Wavelet Analysis of Protein Motion

Abstract

As high-throughput molecular dynamics simulations of proteins become more common and the databases housing the results become larger and more prevalent, more sophisticated methods to quickly and accurately mine large numbers of trajectories for relevant information will have to be developed. One such method, which is only recently gaining popularity in molecular biology, is the continuous wavelet transform, which is especially well-suited for time course data such as molecular dynamics simulations. We describe techniques for the calculation and analysis of wavelet transforms of molecular dynamics trajectories in detail and present examples of how these techniques can be useful in data mining. We demonstrate that wavelets are sensitive to structural rearrangements in proteins and that they can be used to quickly detect physically relevant events. Finally, as an example of the use of this approach, we show how wavelet data mining has led to a novel hypothesis related to the mechanism of the protein γδ resolvase.

1. Introduction

Molecular dynamics (MD) has become a common method for studying the motion of proteins over time, and it is the only available technique for examining continuous fine granularity motion at atomic resolution. By numerically integrating Newton’s equations of motion, one can produce a series of snapshots of a protein’s trajectory through time. These snapshots, when saved at sufficiently high resolution, serve as stop-motion photography and provide a great deal of information about how proteins behave.

In recent years, the decreasing cost of computation has caused MD to grow in popularity. Longer and finer-resolution simulations of larger systems and of a greater number of systems have become common. Our Dynameomics project,^1;2 containing >11,000 simulations, is one such example in which the number of systems has pushed the process of analysis to the edge of intractability. Other groups, by innovating efficient hardware for MD, have pushed their data to a similar position by running simulations with timescales on the order of milliseconds.^3;4 Still others have simulated enormous systems, such as membrane proteins.^5;6 Each of these projects has a similar problem when it comes to data analysis: the analysis itself requires the greatest human cost, due partly to the fact that analysis techniques have historically been more interested in explaining a short simulation than in locating events in a long simulation.

In this paper, we focus on the the analysis of MD simulations using wavelet-based techniques. It is worth noting, however, that any molecular system that evolves over time can be analysed with these same wavelet techniques. Nrownian dynamics simulations and elastic networks are two examples of systems whose data have a similar structure to MD systems and which could benefit from wavelet analysis as well. To demonstrate the effectiveness of wavelets on molecular systems, we examine the simulations in the Dynameomics database.

The Dynameomics project^1;2 is a large-scale MD effort to simulate a representative from every protein fold family.⁷ The Dynameomics database^8;9 currently contains over 2200 proteins, including 807 fold family representatives and several extra members of more populated fold families. Each protein has been simulated for at least one 51 ns at a temperature of 298 K, at least twice at 498 K for 51 ns, and at least three times at 498 K for 2 ns. This makes a total of ~11,000 simulations. These simulated target proteins are selected from our updated consensus domain dictionary¹⁰ based on procedures developed by Day et al.¹¹ These targets constitute a data set that spans a considerable portion of the protein universe, representing more than 80% of all known protein domains. The majority of the remaining 20% of the domains are not in fact autonomous self-contained folds. In fact, the selected targets represent 97% of the known autonomous protein domains (the remaining 3% are membrane proteins or contain complicated co-factors). Consequently, the simulation portion of the Dynameomics project is complete; thus we now turn to mining and using this database.

Because of the incredible amount of information stored in the Dynameomics database, which contains 10⁴ times as many structures as the Protein Data Bank (PDB),¹² analysis is often challenging. Although a vast array of analysis techniques exist for the examination of individual trajectories, these techniques are designed to shed light on the cause and effect of events specific to one protein. Determining the often subtle similarities and differences between hundreds of simulations has never before been possible, and new analysis techniques that focus on hypothesis generation rather than mere description are necessary.

Wriggers et al. have previously examined the topic of event detection in an MD trajectory by analyzing broken and gained contacts throughout a simulation.¹³ Although this method is a powerful tool for the analysis of large, long, or numerous trajectories, it is limited to detecting events that are associated with large changes in contacts. Although many significant events involve both significant motion and significant changes in contacts, some feature a greater change in the former than the latter or vice versa. Our method, which we describe here, aims to build on these event detection abilities by examining the motions of proteins using continuous wavelets by and highlighting events based purely on the significance of these motions.

Wavelet analysis is a signal processing technique that has been around since the early 1900s,¹⁴. Biological uses of wavelets have frequently focused on high-level probles such as voice recognition¹⁵ or brain imaging¹⁶, but wavelets have recently begun to gain popularity in molecular biology (reviewed by Liò¹⁷). Many applications of wavelets to protein science have focused on analysis of sequence or of individual 3D structures.^18;19;20;21 More recently, the discrete wavelet transform (DWT) has been applied to protein trajectories in various forms as well, for example to reaction coordinates of folding²² or to contacts,²³ where it has proven to be a valuable noise reduction method. The continuous wavelet transform (CWT) has been specifically suggested as powerful tools in MD,²⁴ but, to our knowledge, they have never been applied to the time dimension of MD, nor have wavelets been applied to atomic coordinates themselves. Like the Fourier transform, wavelets give information about the frequency domain of a signal, but, unlike the Fourier transform, which gives only average information about each frequency, wavelets give instantaneous information about how a particular frequency is localized in time. Consequently, one can obtain considerable information about the modes of a particular signal without losing information about when these modes occur or how variable they are (Fig. 1).

Fig. 1.

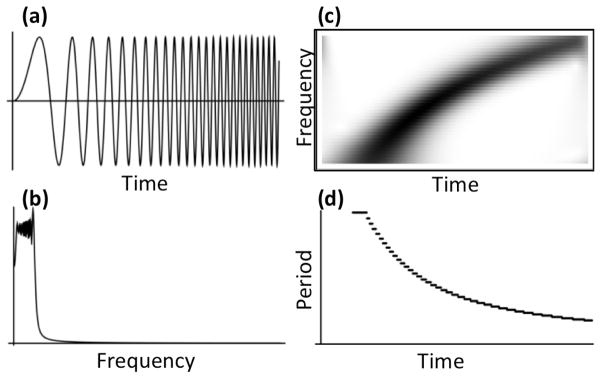
Comparison of Fourier transform and the continuous wavelet transform. (a) A signal whose frequency increases over time. (b) The absolute value of the Fourier transform of the signal in a. (c) The continuous wavelet transform of the signal in a. Notably, the wavelet transform shows clearly that the signal is increasing in frequency over time while the Fourier transform shows only that low frequencies are dominant. (d) Plot of the significant period over time of the signal in (a), calculated by taking the most significant wavelet wavelength from (c) at each time with a minimum significance of 0.2.

The CWT is a wavelet technique, distinct from the more common DWT, that offers high resolution information about a signal at any scale. For our purposes, a signal is the trajectory of an atom over time. The CWT is defined by Equation 1.1, where s is the unitless scale of the wavelet, t is time, q(τ) is the signal over time, ψ(t) is the wavelet function or wavelet, τ is the variable of integration, and * denotes the complex conjugate. Conceptually, this is equivalent to sliding a given wavelet function along the signal and calculating the match of the signal to the wavelet at each time. The wavelet is scaled (or horizontally stretched) by some amount determined by the scale s in order to examine various wavelengths in the signal. In order for wavelets to produce finite values localized in time, they are required to be localized in time and frequency space, meaning they and their Fourier transforms must approach zero as time or frequency approaches negative or positive infinity. We additionally require that they have unit power ( ${\int }_{-\infty }^{\infty }{\mid \mathrm{\Psi }(\omega )\mid }^{2}d\omega =1$ where Ψ(ω) is the Fourier transform of ψ(t)) in order to make them comparable across scales. Wavelets are also required to have a mean of zero. Examples of wavelet functions are shown in Figure 2.

Fig. 2.

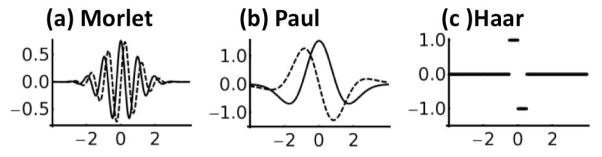
Plots of the three wavelets used in this study, as described in Table 1, each plotted from −4 to 4 with scale s = 1. Solid lines represent the real parts while dashed lines represent the imaginary parts. (a) The Morlet wavelet. (b) The Paul wavelet. (c) The Haar wavelet.

For a discrete signal q of length n, the wavelet coefficients W^(ψ,s) for a scale s and a wavelet function ψ are calculated using Equation 1.2, a discrete version of Equation 1.1. The resulting coefficients can then be examined in terms of time and scale (or wavelength) as shown in Figure 1c. The coefficients can be calculated very efficiently using the discreet Fourier transform and convolution theorem.²⁵ Using this technique, the runtime of our method is O(n log n) where n is the length of the signal. Further details including complete Mathematica codes for calculating wavelets are included in the supplemental materials.

$${\mathbf{W}}^{(\psi ,s)}(t)=\frac{1}{\sqrt{s}}\int q(\tau ){\psi }^{\ast }\left(\frac{\tau -t}{s}\right)d\tau ,$$ (1.1)

$${\mathbf{W}}^{(\psi ,s)}(t)=\frac{1}{\sqrt{s}}\sum _{\tau =0}^{n-1}{q}_k{\psi }^{\ast }\left(\frac{t-\tau }{s}\right).$$ (1.2)

Wavelet coordinates, like Fourier coordinates, can be expressed in terms of period or frequency. Low frequencies (few events per unit of time) are equivalent to long periods (events spread over a long time). Because our atoms do not have constant velocities and because we are interested primarily in the duration of events, we do not consider wavelength here. The scale of a wavelet is related to its period in that if a wavelet has a period of p, then the same wavelet, when scaled by s, will have a period of sp. Equivalently, if a wavelet has frequency ω = 1/p, the wavelet will have frequency s/ω when stretched by s. Because many wavelets have periods close to 1, the scale is often approximately equal to the period of the wavelet.

Because each wavelet function has a unique shape, the scale of a wavelet does not always correspond perfectly to the wavelength at which it best matches the signal. For example, the Paul wavelet (Fig. 2b), when scaled by s, matches a sine or cosine wave with a wavelength of approximately 1.389s. The Morlet wavelet (Fig. 2a), on the other hand, would match a wavelength of 1.01s. These parameters can be calculated using the method outlined by Meyers et al.²⁶ Parameters as well as equations for each of the wavelets used in this paper are given in Table 1.

Table 1.

Formulas and wavelengths for wavelets used in the paper.

Wavelet	Formula	Period of W(ψ,s) (ps)
Morlet (ω = 2π)	ψ(t) = π−1/4e−t22e2πit	1.01s
Paul (order = 4)	$\psi (t)=8\sqrt{\frac{2}{35\pi }}{(1-it)}^{-5}$	1.389s
Haar	$\psi (t)=\{\begin{array}{cc}1& \hfill -1/2\le t<0,\\ -1& \hfill 0\le t<1/2,\\ 0& \hfill \text{otherwise}.\end{array}$	0.87s

Once wavelet coefficients have been calculated, one may determine which scales and times are significant and which are not. To demonstrate how this can be done, suppose that we believe our signal follows white noise, meaning that at every frequency, the signal (an atom’s motion) will tend to have the same amplitude. We would thus expect that at any given time t the square of the absolute value of the wavelet coefficient for a period p would be approximated by the variance of the original signal; note that the absolute value is used because the wavelet coefficient may be a complex number. Generally speaking, we can expect that a wavelet coefficient will be normally distributed around the expected value, thus the square of its absolute value, assuming the coefficients are complex numbers, will be distributed by ${\chi }_2^2{\sigma }^2/2$. By extension, if we believe that the mean amplitude of our signal is distributed by the function ν(p) and that the wavelet coefficients will be normally distributed around their mean amplitudes, then we expect the square of the absolute values of our wavelet coefficients to be distributed by ${\chi }_2^2{\sigma }^2\nu (p)/2$. Using this distribution, we can choose any significance level and examine only those regions of time whose power is in the upper portion of the expected distribution, just like in a standard t-test. For a more complete theoretical description of the continuous wavelet transform, please refer to Daubechies.²⁷ A practical guide to wavelets is discussed by Torrence and Compo.²⁸ Implementation details, including an exact algorithm, are given in the supplemental materials.

The CWT, unlike the discrete wavelet transform, is not a data reduction method; in fact, the CWT produces considerably more data than the original signal (each scale produces as much data as the simple x, y, z coordinates of an atom over time). By using significance testing, however, one can manage these data by storing only those points at which significant wavelet matches occur along with their significance levels. The vast majority of data produced by the CWT carries no more information than the fact that, at a particular time and scale, there is no motion of statistical interest. By storing only the scales and times of significant motion, an entire trajectory of wavelet coordinates can be compressed into a few kilobytes without loss of useful information, allowing the CWT to be used as a data reduction and summary technique.

Here we begin by showing what wavelet analysis provides for a simple 3-helix bundle fold (the engrailed homeodomain, EnHD; PDB: 1enh). We then demonstrate the utility of wavelet analysis by focusing on two proteins: endoglucanase A (CelA; PDB: 1cem) and profilin (ProF; PDB: 1ypr). We compare these wavelet spectra to other analysis methods as well as to the trajectories themselves. With these two proteins, we show that wavelet analysis can be used to discover important events in a simulation including rearrangements and changes in secondary structure. We then show the power of wavelet signatures as a high-throughput metric for identifying subtle features and interactions that are not always obvious using traditional techniques by analyzing the 298 K simulations of all 807 of the targets in our Dynameomics database and examining the most statistically significant result. This result, the identification of a loop in the protein γδ resolvate that oscillates between subtly different conformations, explains how the protein achieves the flexibility required to bind DNA.

2. Methods

2.1. Molecular Dynamics Simulations

Simulations were performed with explicit water using our in-house developed simulation package in lucem molecular mechanics^29;30 and our previously described protein and water force fields.^31;32 Simulation details can be found elsewhere.¹ Here we are focusing on the 298 K trajectories. For each simulation, atomic coordinates from all but the first 1 ns of our trajectories were analyzed from our in-house developed database.⁹ For each ps of the simulation, the protein structure was aligned to the initial structure using a rigid least squares fitting of Cα atoms with the structure’s center of mass held at the origin.³³ The total time of each simulation was at least 51 ns; though only 31 ns were complete at the time this project was started. Haar, Morlet, and Paul wavelet analyses were performed on each Cα atom’s trajectory over time; these wavelet data were then loaded into Mathematica³⁴ for further analysis. At least 31 ns of all 807 ‘simulatable’ (self-contained) folds in our new 2011 consensus domain dictionary,¹⁰ which is an updated version of our 2003 domain dictionary,⁷ were analyzed (~17 μs total).

2.2. Wavelet Analysis

We chose to use the continuous wavelet transform because of its ability to retain very finely detailed information at a wide range of wavelengths. Scales were chosen to fit Equation 2.1,

$$s_k=250\text{ps}·2^{k/10},k=0,1,\dots 60,$$ (2.1)

giving a range of 60 scales from 250 ps to 16 ns. Scales determine how much each wavelet function is stretched or compressed prior to calculation of the wavelet coordinates, thus are roughly equivalent to frequency. Because a wavelet function scaled by a factor s may not match motions occurring in exactly a period s, scales were adjusted for each wavelet function according to the period factor in Table 1 so that, for each wavelet function, the resulting wavelet coordinates describe the motions with periods s_k from Equation 2.1. In other words, each wavelet function examines differently shaped motions (Fig. 2), but each function examines the motions occurring on timeframes (periods) occurring from 250 ps to 16 ns as described in Equation 2.1. The granularity for our simulations is 1 ps, so this range of scales captures both the fast (250 ps) and the slower (10–20 ns) motions that occur in our simulations. Additionally, the large number of wavelet scales gives a very fine resolution.

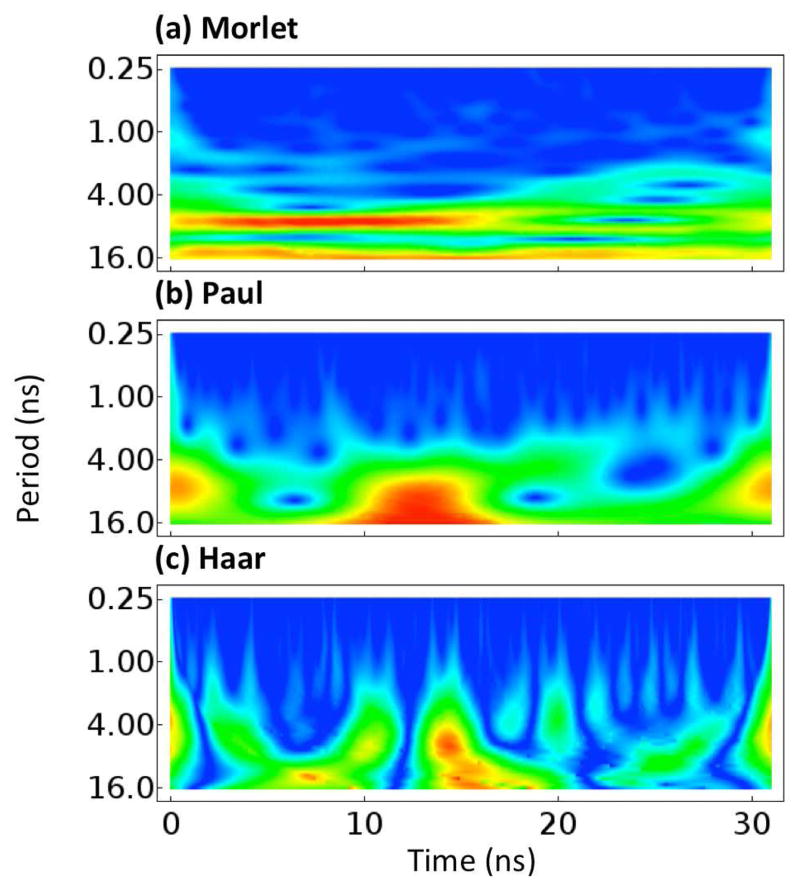
Three wavelet functions were chosen in order to capture the variety of motion that can occur in a simulation. The Morlet wavelet³⁵ consists of a plane wave tempered by a Gaussian. The Morlet has both a real and imaginary component, such that it can capture both the amplitude of the motion and the phase. It best matches motions that are sinusoidal in nature. The Haar wavelet¹⁴ is a very simple wavelet that is zero everywhere except for immediately before and after 0 where it is 1 and −1, respectively. The Haar wavelet best matches sudden changes in a signal and square waves. The Paul wavelet³⁶ is essentially a complex version of the famous Mexican hat wavelet, which is based on the derivative of the Gaussian function. It is similar to the Morlet wavelet but decays more quickly, giving it better resolution in time and lower resolution in frequency. Notably, the imaginary portion of the Paul wavelet can match sigmoidal signals quite well. All wavelets were initially scaled so as to have a single period of approximately 21 ns. Plots of the three wavelets are shown in Figure 2. Example wavelet spectra for the Cα atom of Arg29 of EnHD are show in Figure 3. These spectra demonstrate that the Morlet, Paul, and Haar wavelets have different sensitivities in time and frequency while still highlighting the same events.

Fig. 3.

Plots of the wavelet analyses of the Cα atom of R29 of the engrailed homeodomain (EnHd, PDB: 1enh). The absolute value of each wavelet coordinate is shown with low values illustrated in blue. No scale is given because wavelet values are in arbitrary units. (a) The Morlet wavelet. (b) The Paul wavelet. (c) The Haar wavelet. The scales of each are not identical as they are not directly comparable.

In order to determine which pieces of a wavelet spectrum are of interest, we used the basic significance testing method discussed above and outlined by Torrence and Compo.²⁸ Because the square of the absolute value of a wavelet coordinate is distributed by ${\chi }_2^2{\mu }_p{\sigma }^2/2$, where the variance of the signal is σ² and the mean expected Fourier power (squared amplitude) of a particular period p is μ_p, we only need to know the mean Fourier power of a particular period to determine statistical significance of the oscillations occurring at any given time for that wavelength. We calculated the Fourier spectrum, f_p, for each of our wavelengths over every atom’s trajectory, q, according to Equation 2.2 and found that the mean Fourier power, |f_p|², was approximately described by the equation μ_p = p^1.43/155 + 20, where p is the period measured in picoseconds. Equation 2.2 is similar to the calculation of a single Fourier coefficient but at an arbitrary wavelength. The calculation is made over as much of the signal as possible, but trims from the front when necessary to prevent incomplete sinusoidal waves from biasing the magnitude of the calculation.

$$f_p=\frac{1}{n}\sum _{k=N-n}^{N-1}exp\left(\frac{-2\pi ik}{pn}\right)q_k;n=p\lfloor N/p\rfloor .$$ (2.2)

For each wavelet spectrum, we extracted regions whose values were statistically in the upper 20% of the expected power distribution as strong oscillations of a particular wavelength. For each scale, s, regions within s/2 ps of the beginning or end of the trajectory were ignored in order to avoid the edge effects inherent with a finite signal. Additionally, the first nanosecond was ignored to allow for equilibration. For each picosecond, the wavelength at which a given Cα atom was oscillating according to this analysis was recorded. Whenever multiple frequencies occurred at the same time, the one with the stronger oscillation (greater statistical significance) was used. These data thus formed a “wavelet map” of the wavelengths that were most prevalent at every picosecond for each Cα atom in a given protein.

In order to demonstrate the utility of these wavelet maps, we examined their general properties for all 807 proteins. We hypothesized that an atom experiencing no significant wavelet oscillations over a time regime would be characterized by very little motion or by rapid vibrations, likely due to heat. Similarly, we hypothesized that those residues with low frequency wavelets would be characterized by structural rearrangements and large motions during the time of those wavelets. To test this, we randomly chose 100 residues and time regions from our 807 proteins requiring only that the wavelets for the residue be of a uniform frequency over that time. Time regions were allowed to be low frequency/long period (p > 1 ns), high frequency/short period (p < 1 ns), or no frequency (no significant wavelets) for the entire region in question. These residues were then scored as either arbitrary vibrations or large movements/rearrangements with the actual values of the wavelets during each time region concealed. The results were then tallied and compared. To demonstrate our specific findings, we present wavelets for the two proteins ProF and CelA. Finally, to show how wavelets can be used to mine simulations, we compared the low frequency distributions of all Cα atoms and examined the simulations of those with the greatest statistical significance at low frequencies. The trajectory of one such pair of atoms, G101 and M103 of γδ resolvase, revealed a novel mechanism in which helix αE changes conformation during DNA binding.

3. Results and Discussion

Universally, the Morlet and Paul wavelets were a better fit for MD trajectories than the Haar wavelet. At a given period, the Paul wavelet tended to give the best resolution in time; at a given time, the Morlet wavelet tended to give the best resolution in frequency. The Haar tended to lag behind both. This comparison is demonstrated in Figure 3 for the simple 3-helix bundle fold of EnHD. There were no residues in all of our simulations that could be statistically differentiated from white noise more than 20% of the time using the Haar wavelet; thus, we do not consider it further (note that nothing in Fig. 3c is statistically distinct from white noise).

In the 807-protein data set, high frequency oscillations (p < 1 ns) were common, occurring 22% of the time, but they were frequently correlated with thermal vibrations. Midrange and low frequencies occurred 30% of the time and were almost always correlated with motions ranging from slight rearrangements to loss or gain of secondary structure to broad shifts in backbone conformation. When scored by hand, regions of time with no significant wavelets correlate with arbitrary vibrations 78% of the time while low frequency wavelets correlate with structural movements and rearrangements 73% of the time. High frequency wavelets correlated with movements and rearrangements 50% of the time and with arbitrary vibrations 50% of the time.

Proteins with very stable trajectories have considerably fewer significant oscillations than those that were unstable. EnHD, for example, exhibits only a small amount of motion, mostly at the N-terminal tail (Fig. S1a). Only 20% of the time is there a significant oscillation with p > 1 ns not occurring in the N-terminal tail (Fig. S1a). Conversely, proteins that undergo considerable rearrangement from their crystal structures have more low frequency oscillations. The DNA-binding domain of ADR6 (1kkx) is a protein with a similar topology to the engrailed homeodomain, but which was deemed unstable in our simulation. It undergoes a large set of helical rearrangements in the beginning of its trajectory after which it moves less but has an exposed hydrophobic core. Low frequency oscillations occur in 35% of this simulation, most of which correlate with the protein’s overall shifts (Fig. S1b).

Given that low frequency wavelets correlated strongly with overall rearrangements in a protein simulation, we searched all 807 simulations for wavelet coordinates that whose period was at least 1 ns and whose significance was in the top 5% of the expected power distribution. Two proteins stood out as having highly significant motions during their trajectories: endoglucanase A (CelA) and profilin (ProF). We examine these proteins in more detail here.

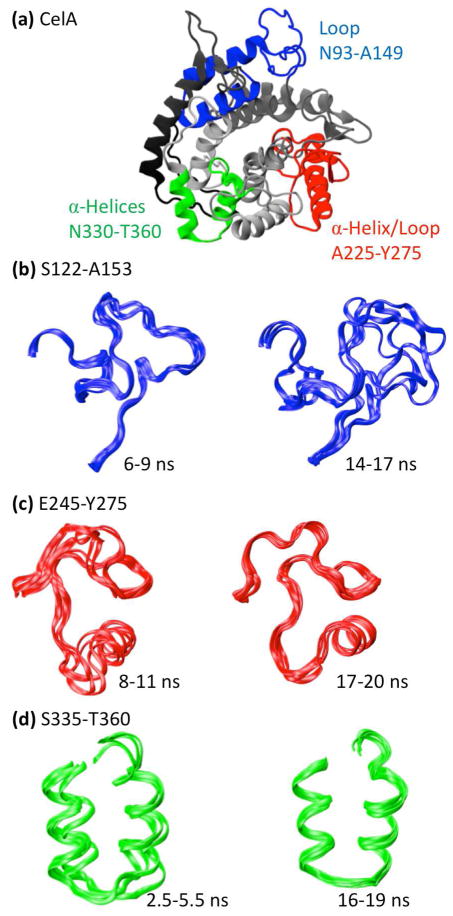
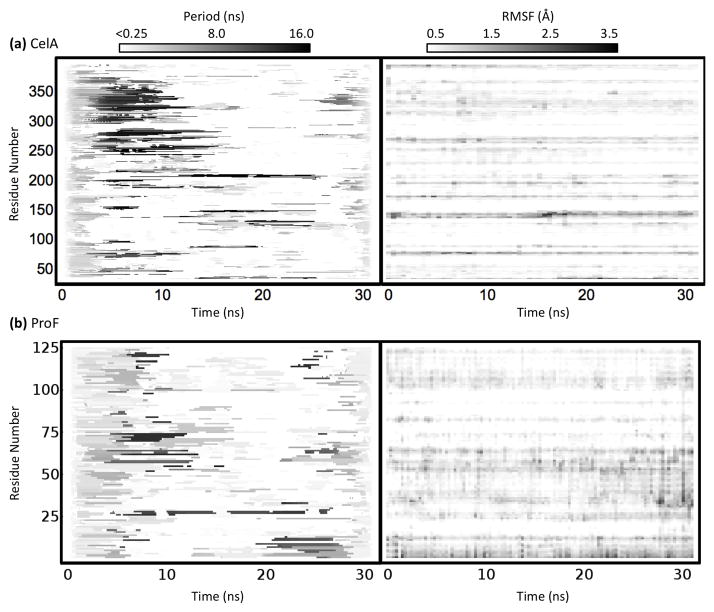
The catalytic core of CelA is an all-helical protein in the α/α toroids family (Fig. 4a). The simulation of CelA contains moderate rearrangement of several mobile loops early on and several subtle changes that occur throughout the simulation. The Paul wavelet map and the root mean square fluctuation (RMSF) plot for CelA are shown in Figure 5a. RMSF is a commonly used metric for the amount of fluctuation occurring in a residue over time relative to its average position. Three main regions are of interest in this wavelet map, the first of which is an empty region around 5–10 ns near residue 125 followed by the long periods around 14 ns. During this time, the loop, shown in blue in Figure 4a, moves over 7 Å from a docked to a completely solvent-exposed configuration. The corresponding structures for these regions are shown in Figure 4b. Another interesting region is the long period block near residue 250 throughout the middle of the simulation. During this time a pair of small β-strands are lost (~10 ns) and the helix shown in red in Figure 4a (α7) moves close to the nearby loop (Fig. 4c). The structures for this region are compared with the region absent of long periods at the end of the simulation in Figure 4c. Finally, Figure 4d shows the subtle helical shift that occurs near residue 350 early in the simulation that result in a change in the orientation and packing of two small helices. None of these fluctuations is visible on the RMSF spectrum due to their subtle nature and their relatively small movements. RMSF and other traditional analyses often fail to detect small movements, even when they are significant, due to their focus on the amount of change rather than the quality of change. Wavelet analysis finds these motions despite their subtlety because they are ordered rearrangements whose magnitude is significant relative to the timescale at which they occur.

Fig. 4.

(a) Protein structures and notable structural features of the protein Endoglucanase A (1cem; CelA) taken at 10 ns in its simulation. (b) Region S122-A153 of CelA colored red, green, blue, magenta in temporal order. (c) Region E245-Y275. (d) Region S335-T360. In each instance, the time period whose wavelet coordinates were significant in the low frequency range are mobile while the time period whose wavelet coordinates were not significant in the low frequency range is stationary.

Fig. 5.

Wavelet maps and RMSF plots of (a) Endoglucanase A (CelA; PDB: 1cem) and (b) profilin (ProF; PDB: 1ypr). The wavelet maps show the most statistically significant frequency of each Cα atom occurring at each time. Notably, RMSF maps and wavelet maps are not correlated in time.

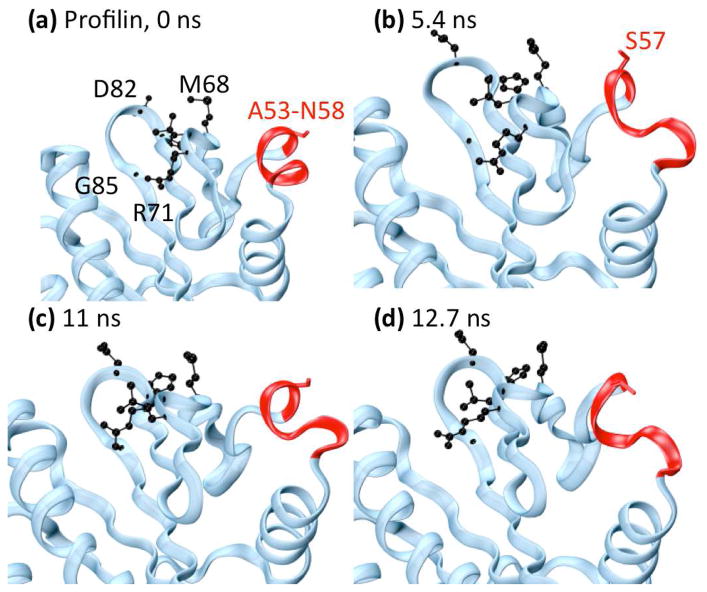
The protein profilin is a member of the profilin-like family that binds actin and regulates the growth of actin filaments. The simulation of ProF, in contrast to CelA, undergoes a few fast rearrangements in the first few ns of the simulation after which little significant motion is observed. The simulation is very stable with even the most flexible residue having a mean RMSF of only ~ 0.76 Å. When examining the Morlet oscillation map of ProF (Fig. 5b), one is immediately drawn to the long period block throughout the middle of the simulation between residues 55 and 75. This midrange oscillation occurs for a long period of time and includes the highly significant motions located by wavelet analysis, which are focused around a band of residues from A53-N58 (Fig. 6a). These residues are in a helix near the binding interface with actin, and S57 participates directly in actin binding. Above this band (further along the sequence) are several other bands of low frequency motion containing 6 other actin-binding residues (M68, L70, R71, H81, D82, and G85). In the crystal structure, S57 points outward into solvent and away from the other binding residues, but during the time frame highlighted by the long period wavelets from ~ 4.5 ns until ~ 14 ns, the helix containing S57 unravels from the C-terminal end, keeping the loop containing S57 and N58 in tact and pushing them toward the other active site residues slightly (Fig. 6).

Fig. 6.

Changes in profilin (ProF) binding residue S57. Helix α3, containing S57, is shown in red. Side-chains of actin binding residues highlighted by wavelet analysis are shown in black, and the side-chain of S57 is shown in red. (a) Minimized crystal structure. (b) 5.4 ns, (c) 11 ns, and (d) 12.7 ns. During this time period, helix α3 twists significantly and unravels from the N-terminal end, changing the orientation of S57 to the binding site.

Figure 5 shows the RMSF for CelA (a) and ProF (b) over time. For these proteins, their RMSF profiles are essentially uncorrelated with their wavelet maps. Notably, there is a slight increase in the RMSF of the region S122-A153 for CelA during the longer periods near 15 ns. However, regions E245-Y275 and S335-T360 show virtually no distinctive patterns in the RMSF spectra. Similarly, the regions around S57 and N58 of ProF show little correlation with the wavelets and, in fact, do not tend to change much over time. Thus, wavelet analysis was able to effectively screen for and detect interesting motion within two unrelated proteins where conventional analysis failed.

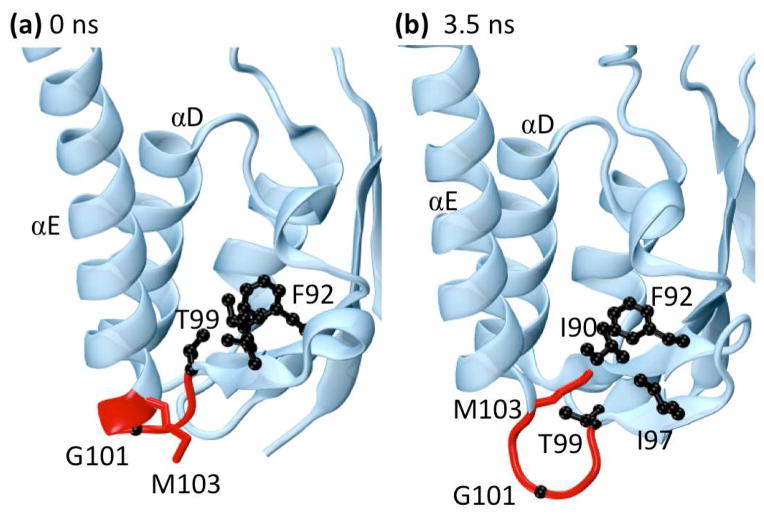
Searching a database of multiple simulations of 807 proteins and > 17 μs of simulation time for interesting or important events is a daunting task. In order to expedite this process, we hypothesized that individual residues dominated by low frequency movements were most likely to be involved in significant conformational events. Accordingly, we examined the trajectories of Cα atoms in our simulations that had the highest portion of significant low frequency (> 1 ns) motion according to the Paul and Morlet wavelets. Two such atoms, both in the upper 5% of the distribution, belong to G101 and M103 of γδ resolvase (1gdt). γδ resolvase is a 183-residue protein belonging to the resolvase and DNA invertase family that forms a homodimer in solution.³⁷ It is known that G101 is a critically flexible residue situated between β-strand 5 and α-helix E (Fig. 7a) that allows αE to pivot away from αD during DNA binding,³⁸ but how this event occurs is unclear.

Fig. 7.

The protein γδ resolvase (PDB: 1gdt). The side-chains of residues forming a hydrophobic pocket (I90, F92, I97, T99, and M103) are shown in black while the backbones of residues 99–103 are shown in red. (a) Residues near loop 5E in the minimized crystal structure. (b) Residues near loop 5E at 3.5 ns. Near 3.5 ns the end of helix αE and part of loop 5E unwind to form an Ω-loop. This motion flips the side-chain of residue M103 into the hydrophobic pocket shown in black while pushing residue G101 into solvent, stabilizing the alternate conformation. Both M103 and G101 are known to be important for the binding and flexibility of αE and were identified as highly significant during this time range by wavelet analysis.

In our simulation of the monomer of γδ resolvase, we observed a slight unraveling of helix αE and β-strand 5 around 3.5 ns as well as periodically throughout the simulation (Fig. 7b). These movements were the cause of the low frequency motion highlighted by wavelet analysis. Closer examination revealed that this separation is accompanied by the formation of an Ω-loop between β5 and αE with G101 at its tip. This loop is stabilized by the movement of the side-chain of M103 from a solvent-accessible state into a hydrophobic pocket consisting of I90, F92, and I97 where it displaces the Cγ of T99 (Fig. 7c and 7d). During this motion, T99 rotates out of the pocket, maintaining its hydrogen bond with the amide of I90 and allowing it to easily rotate back into the pocket when M103 leaves. The result of this event is a slight turning of αE and a loosening of loop 5E, making further rearrangement of αE, such as that required for strand exchange, possible. Interestingly, methionine can be reversibly oxidized, increasing its polarity and hydrophilicity, a process proposed to be involved in protein regulation.^39;40 Theoretically, an oxidized M103 or a mutation such as M103D could stabilize the solvent-accessible state (αE closed) while a reduced M103 or a mutation such as M103L could stabilize the Ω-loop (αE open). Thus, an automated screen for Cα atoms in the upper 5% of the distribution with respect to low frequency motion led to the discovery of interesting cyclic conformational behavior that may be linked to function.

The wavelet analyses explored here are a very effective method of examining both very large and very subtle types of motions occurring in a protein over time. We have demonstrated that wavelets are capable of picking out multiple types of distinct movements that occur within a protein that may not be easy to find via visual inspection of the trajectory or by using traditional analysis methods (for example, CelA, ProF). Additionally, wavelets are capable of pinpointing when a change is occurring in time, allowing them to be used as a high-throughput screening technique for simulations (as with γδ resolvase).

It is not surprising that the Haar wavelet fit our data poorly. The Haar is, by nature, designed for square waves and discrete jumps, neither of which we observe in our simulations. The Paul wavelet, which approximates the Haar wavelet in a smooth form, was much more useful for our purposes. Both the Paul and the Morlet wavelet provided good results, though the Paul is theoretically better suited for analysis across time due to its high temporal resolution.

Although it is initially surprising that wavelets would be able to detect non-oscillatory movements, such as a helical rearrangement, it should be noted that an atom following a sigmoid trajectory can easily match the imaginary part of an appropriately scaled Paul wavelet (Fig. 2b). Thus, the Paul wavelet should not be thought of purely as an indicator of oscillation, but rather as an indicator of non-random motions. The fact that wavelet significance testing is not dependent on the amplitude of the oscillation additionally confers an advantage, in that large motions do not necessarily drown out smaller motions as is often the case in analyses such as RMSF. For example, a large hinge motion between two regions of a protein would not prevent a smaller change in secondary structure within one region from being detected.

Wavelets show clear sensitivity and specificity to all ranges of structural rearrangement in a simulation, including many that are not visible using traditional analyses such as RMSF. This is potentially of great use for studying the effects of mutation, pH, and/or temperature on a structure, as these changes can be difficult to detect. The motions highlighted from CelA (Fig. 4) demonstrate the range of wavelet sensitivity, as these motions include a large loop rearrangement (Fig. 4b), a small change in contacts and secondary structure position (Fig. 4c), and a subtle change in the arrangement of two helices (Fig. 4d).

Wavelets also show promise for detecting biochemically relevant motions that can be otherwise very subtle and difficult to find. Notably, the Cα RMSFs for the oscillating region in ProF are relatively low and show no particular distinction over the time range during which the helical unwindings were occurring (Fig. 6b). In fact, compared with the wavelet maps, the RMSF profile shows very little differentiation over time.

Notably, the Paul and Morlet wavelets excel at detecting different kinds of events. While the Paul wavelet showed excellent sensitivity to changes and rearrangements in protein structure, the Morlet showed sensitivity to periodic oscillations. This sensitivity suggests that the Morlet wavelet may be useful in detecting interactions and communication in long simulations while the Paul wavelet may additionally be useful in examining changes in simulations and simulations in which rearrangements are expected to occur, such as in high-temperature unfolding simulations.

Perhaps most critically, all of these advantages of wavelets can be used in a high-throughput fashion to screen and isolate events in large simulations or sets of simulations, as illustrated with γδ resolvase. Finding an event of interest by hand in even 0.1 μs of simulation data of a single protein is a daunting task and would be virtually impossible for our now complete database containing ~11,000 simulations of all protein folds. As high-throughput computation becomes more common, methods for mining the resulting data, such as wavelets, will also become more important.

4. Conclusions

Wavelet analysis is a powerful tool that can be used to quickly and automatically isolate distinct motions of interest in a protein simulation. Due to their ability to locate subtle changes without being overwhelmed by larger more obvious motions, wavelets represent an ideal method for screening simulations to quickly pinpoint changes or structural rearrangements and for comparing differences in simulations, due to mutation, pH, or temperature changes, for example. Additionally, wavelets can be used to scan large databases of simulations for biochemically relevant events, such as the motion of a catalytic site or of functionally relevant loops.