The Distribution of Pairwise Genetic Distances: A Tool for Investigating Disease Transmission

Abstract

Whole-genome sequencing of pathogens has recently been used to investigate disease outbreaks and is likely to play a growing role in real-time epidemiological studies. Methods to analyze high-resolution genomic data in this context are still lacking, and inferring transmission dynamics from such data typically requires many assumptions. While recent studies have proposed methods to infer who infected whom based on genetic distance between isolates from different individuals, the link between epidemiological relationship and genetic distance is still not well understood. In this study, we investigated the distribution of pairwise genetic distances between samples taken from infected hosts during an outbreak. We proposed an analytically tractable approximation to this distribution, which provides a framework to evaluate the likelihood of particular transmission routes. Our method accounts for the transmission of a genetically diverse inoculum, a possibility overlooked in most analyses. We demonstrated that our approximation can provide a robust estimation of the posterior probability of transmission routes in an outbreak and may be used to rule out transmission events at a particular probability threshold. We applied our method to data collected during an outbreak of methicillin-resistant Staphylococcus aureus, ruling out several potential transmission links. Our study sheds light on the accumulation of mutations in a pathogen during an epidemic and provides tools to investigate transmission dynamics, avoiding the intensive computation necessary in many existing methods.

PATHOGEN genomic data are rapidly becoming abundant, and there is a demand for statistical methods to extract meaningful conclusions from the wealth of information these data provide. One of the most basic and frequently used—yet imperfectly understood—comparative tools is the genetic distance between two samples [commonly defined as the number of single-nucleotide polymorphisms (SNPs) between the isolates]. In the context of epidemiological investigations, genetic distance can be used as a discriminatory value to determine whether infected individuals belong to the same outbreak or cluster or to rule out potential transmission events.

Genetic distance is central to the inference of transmission routes—intuitively, the greater the similarity is between samples taken from two different hosts, the more likely they are to have been involved in a transmission event. While in some cases it may suffice to identify the carrier of the genetically closest pathogen isolate as the source of infection (Jombart et al. 2011), this approach lacks any measure of uncertainty and may result in a high false positive rate; it has been demonstrated that estimation of a transmission network using genetic distance data alone is associated with much uncertainty, making the estimation of individual transmission routes impossible (Worby et al. 2014). However, with a probabilistic interpretation of genetic distances, given the relationship between the hosts of pathogen samples, one can quantify the uncertainty surrounding each potential transmission source and establish general trends of transmission in the epidemic. Furthermore, probabilistically weighted transmission routes may also lead to improved estimates of heterogeneous transmission rates from different subpopulations.

Many studies to date have developed methods to infer routes of transmission based on genomic and epidemiological data (Cottam et al. 2008; Jombart et al. 2011; Morelli et al. 2012; Ypma et al. 2012, 2013; Didelot et al. 2014; Jombart et al. 2014). Each method utilizes a likelihood component that describes the probability that a set of mutations occurs between two pathogen samples from different hosts, given their epidemiological relationship. These are often based on strong assumptions (e.g., transmission bottleneck size of 1 or mutation occurring only at the time of transmission), and many are highly computationally intensive.

The distribution of pairwise genetic distances between samples taken from epidemiologically linked carriers depends on numerous factors, such as the mutation rate, the within-host pathogen population dynamics, and the transmission bottleneck size. It is of interest to understand how each of these factors affects observed genetic distance.

In this study, we aimed to investigate the distribution of pairwise genetic distances to better understand how diversity accumulates during a disease outbreak. In particular, we developed an approximation to this distribution and investigated its use as a tool to assess the likelihood of transmission routes. We used simulated data and real outbreak data, collected during a hospital outbreak of methicillin-resistant Staphylococcus aureus (MRSA), to demonstrate the ability of our method to rule out several patient-to-patient transmission routes.

Methods

The distribution of genetic distance between two samples taken during an outbreak

Consider a disease outbreak, consisting of n cases, where case 1 is the origin, and cases $2,\dots ,n$ each have a source of infection from within the population. Let $t_j^{\text{I}}$ be the infection time of case j, and $t_1^{\text{I}}=0.$ Each case is observed, and we initially assume that one pathogen specimen is taken for sequencing at time $t_j^{\text{s}}$ with genotype $g_j.$ Table 1 describes notations used in this article.

Table 1. Notation used in this article.

Notation	Definition
$i\to j$	Transmission route from person i to person j
$t_j^{\text{I}}$	Time of infection of person j
$t_j^{\text{s}}$	Time of genome sampling from person j
$s_{ij}$	Vector of transmission ancestry common to persons i and j
$d(i,j)$	Time of lineage divergence
μ	Mutation rate per genome per generation
$\psi (a,b)$	Genetic distance (no. SNPs) between genomes a and b
$m(a,b)$	Coalescence time of isolates a and b
$m_t$	Time between coalescence and observation time t
$N(t)$	Effective pathogen population size at time t
$N_{\text{B}}$	Effective transmission bottleneck size

We consider the unobserved transmission network, which consists of infection routes and times. Let $c_j$ be the vector of transmission ancestry for person j, such that the first element is the transmission source of j, and each successive element is the source of the preceding element. Since the network is fully connected, the final element of this vector for any given host will be the outbreak origin, and the vector will have length equal to the number of hosts in the transmission chain from the origin to j. Let $s_{ij}=c_i\cap c_j$ be the vector of ancestry common to both i and j, such that the first element $s_{ij}^{(1)}$ is the most recent common transmission source of both i and j, and the last element is 1.

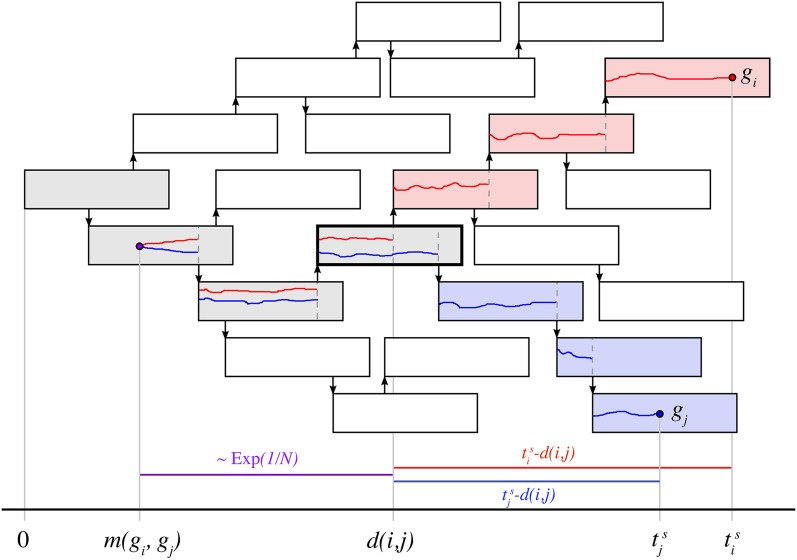
Now consider the genealogy of the sampled isolates. This tree is not necessarily identical to, but must be consistent with, the transmission tree (Ypma et al. 2013). The time of coalescence for samples $g_i$ and $g_j,$ denoted $m(g_i,g_j),$ must occur prior to the divergence of the transmission tree branches to which persons i and j belong and will belong within one of the hosts in $s_{ij}.$ The ancestries of the samples coexist in the same host or chain of hosts for a period of time, before one lineage is transmitted to another person and exists independently of the other. Let $d(i,j)$ be the time of lineage divergence, the time at which the lineages cease to exist within the same host (see Figure 1).

Figure 1.

Two isolates sampled from infected cases during an outbreak. Each infected case is depicted by a rectangle, corresponding to its infectious period. Arrows denote transmission events. Samples $g_i$ (red circle) and $g_j$ (blue circle) are taken from persons i and j, respectively. The colored lines indicate the ancestry of each isolate back to its most recent common ancestor at time $m(g_i,g_j).$ Hosts shaded in gray denote the shared ancestry $s_{ij},$ while blue and red denote the lineages of the genotypes $g_i$ and $g_j,$ respectively. The colored bars at the bottom of the diagram show the distinct time periods in which mutations may occur—between divergence and observation (blue and red) and from divergence to coalescence (purple), which is exponentially distributed, assuming a constant population N.

Let $\psi (g_i,g_j)$ denote the genetic distance between samples $g_i$ and $g_j,$ measured by the number of SNPs. The mutations could have arisen in two distinct periods—first, during the time between observations $t_i^{\text{S}},$ $t_j^{\text{S}}$ and lineage divergence $d(i,j),$ and second, during the (earlier) time between lineage divergence and coalescence $m(g_i,g_j).$ The number of SNPs $\psi (g_i,g_j)$ is then equal to the sum of two random variables, $\psi (g_i,g_j)=X+Y,$ where X represents mutations occurring between lineage divergence and observation, and Y represents mutations occurring prior to lineage divergence. For the former, we can assume that the number of SNPs arising from the time of lineage divergence $d(i,j)$ until observation follows a Poisson distribution with mean $\mu (t_i^{\text{s}}+t_j^{\text{s}}-2d(i,j)).$ For the latter, with a known time of coalescence, $m(g_i,g_j),$ the number of SNPs accumulating between coalescence and divergence is again a Poisson-distributed random variable,

$$Y|m(g_i,g_j)\sim \text{Pois}(2\mu (d(i,j)-m(g_i,g_j))).$$ (1)

However, the time of coalescence for two samples is generally unknown, although it must lie in the interval $0\le m(g_i,g_j)<d(i,j).$ If the size of the transmitted inoculum is equal to one, then $t_{s_{ij}^{(1)}}^{\text{I}}\le m(g_i,g_j)<d(i,j);$ in the scenario depicted in Figure 1, coalescence would have to occur within the host (rectangle) highlighted in a thick black line.

Most epidemic models describe nonlinear dynamics, and estimating the rate of coalescence between two pathogen samples during an outbreak is highly dependent on the demographic model used (Koelle and Rasmussen 2012; Volz 2012). However, in this study, interest lies in the individual-level rather than the population-wide dynamics. Under an assumed or hypothesized set of transmission routes, the time of lineage divergence $d(i,j)$ is known, and the rate of lineage coalescence can be derived from the specification of a model of within-host population dynamics and transmission.

Assuming a constant population size of N, the time to coalescence for two randomly sampled lineages at time t, $m_t,$ is exponentially distributed with rate $1/N.$ Under this assumption, it can be shown that the number of SNPs separating two randomly sampled lineages at time t follows a $\text{Geom}\left(\left(1/N\right)/\left(1/N+2\mu \right)\right)$ distribution, equivalent to $\text{Geom}\left(1/\left(1+\theta \right)\right),$ where $\theta =2N\mu$ (Watterson 1975).

As such, by assuming a constant mutation rate and effective population size prior to lineage divergence, we have

$$X\sim \text{Pois}(\mu (t_i^{\text{s}}+t_j^{\text{s}}-2d(i,j))),$$ (2)

and

$$Y\sim \text{Geom}\left(\frac{1}{1+2N\mu }\right).$$ (3)

However, as the lineage is transmitted from one host to another, the population experiences repeated bottlenecks, violating the assumption of constant population size. We hence considered an approximation to the true population dynamics, using a discrete-time population model. The effective population size remains constant at size N, except during transmission, at which time it spends one generation in a bottleneck of size $N_{\text{B}},$ before recovering to its previous level. The expected time to coalescence under such a model is

$$E(m_t)={\displaystyle \sum }_{k=0}^{t}k{\left(1-\frac{1}{N}\right)}^{k-\phi (k)-1}{\left(1-\frac{1}{N_{\text{B}}}\right)}^{\phi (k)}\left(\frac{1}{N\left(k\right)}\right),$$ (4)

where $\phi (k)$ is the number of bottlenecks a lineage must pass through between times 0 and k, and $N(k)$ is the effective population size at time k and is equal to either N or $N_{\text{B}}.$ We note that $N(k)$ represents the short-term effective population size that takes into account nonrandom sampling during the bottleneck and stochastic variation, while $N_{\text{e}}^{\ast }=1/E[m_{d(i,j)}]$ is the long-term effective population size that also considers the changes in short-term effective population sizes over time. We can then either assume that the time of coalescence is fixed at $\overline{m(g_i,g_j)}=d(i,j)-E(m_{d(i,j)})$ and that

$$\begin{array}{c}\psi (g_i,g_j)\sim \text{Pois}(\mu (t_i^{\text{s}}+t_j^{\text{s}}-2\overline{m(g_i,g_j)}))\\ =\text{Pois}(\mu (t_i^{\text{s}}+t_j^{\text{s}}-2(d(i,j)-E(m_{d(i,j)})))\end{array}$$ (5)

[the sum of random variables (1) and (2)] or that the effective population size $N_{\text{e}}^{\ast }$ prior to divergence is fixed at $1/E[m_{d(i,j)}]$ and that

$$\psi (g_i,g_j)\sim \text{Geom}\left(\frac{1}{1+2E[m_{d(i,j)}]\mu }\right)+\text{Pois}(\mu (t_i^{\text{s}}+t_j^{\text{s}}-2d(i,j)))$$ (6)

[the sum of random variables (2) and (3)], which we refer to as the geometric-Poisson approximation. Finally, we can derive the posterior probability of any transmission route ($i\to j$), given the genetic distance between sampled isolates $g_i$ and $g_j$ and associated parameters $\omega =\{\mu ,E[m_{d(i,j)}]\}$,

$$\begin{array}{l}\pi (i\to j|\psi (g_i,g_j),\omega )=\frac{\pi (\psi (g_i,g_j)|i\to j,\omega )\pi (i\to j|\omega )}{\pi (\psi (g_i,g_j)|\omega )}\\ =\frac{\pi (\psi (g_i,g_j)|i\to j,\omega )}{{\sum }_{k\in S(j)}\pi (\psi (g_k,g_j)|k\to j,\omega )},\end{array}$$ (7)

assuming equal prior probabilities of potential transmission routes, where $S(j)$ is the set of all potential infection sources for individual j.

Simulation studies

We generated the empirical distribution of genetic distances by simulating within-host dynamics on top of a transmission process. We compared the resulting empirical distributions with the geometric-Poisson approximation given in Equation 6, as well as the Poisson approximation in Equation 5. The index case of the disease outbreak is infected with a clonal population of bacteria, and this is allowed to grow under a discrete-time neutral evolutionary process. At each generation, $x\sim \text{Binom}(N(t),N(t)/2N)$ cells die, and the remaining $N(t)-x$ cells are replicated, where $N(t)$ denotes the census population size at time t. We impose the restriction $x<N(t)$ to prevent the population from going extinct. Each replicated cell has a probability μ of being a mutation. All mutations are assumed to be neutral, and back mutations are allowed. A transmission event involves a bottleneck: $N_{\text{B}}$ cells are randomly sampled from the host and passed to the susceptible individual. In reality, this inoculum is unlikely to be a truly random sample from the pathogen population, since a host is not a well-mixed vessel. However, $N_{\text{B}}$ can be thought of as an effective bottleneck size.

Initially, we considered the simple example of a transmission chain, in which each infected individual infects exactly one new person. Transmission events occur at equidistant intervals, and the time from infection to sampling is constant. For each scenario under given parameters, we repeated the transmission chain 100 times and considered the average distribution of pairwise distance across these simulations.

We also simulated more general susceptible–infectious–removed (SIR) outbreaks in an initially susceptible population, using the R package “seedy” version 0.1 (Worby 2014). Genotypes were sampled randomly from the host at regular intervals, and person-to-person mixing in the population was assumed to be homogeneous. Outbreaks were simulated with $R_0=2.$ We investigated the effect of varying the bottleneck size $N_{\text{B}},$ the equilibrium effective population size $N_{\text{eq}},$ and the mutation rate μ.

Data

We applied our approximations to a data set collected during an outbreak of MRSA. Colonization of MRSA strain type ST2371 was detected in a total of 15 newborn infants during an outbreak in a special care baby unit (SCBU) in Cambridge, United Kingdom. A single genome sampled from each of these individuals was sequenced, along with 20 isolates collected from a healthcare worker (HCW), who was found to be MRSA positive several weeks after the 15 cases were observed. The genetic similarity of the pathogen samples indicated potential transmission, (i) from patient to patient, via a transiently colonized HCW (transferring the bacteria from one patient to another, with carriage cleared upon hand washing); (ii) between persistently colonized HCW and patient; or (iii) from external sources. This study was described by Harris et al. (2013), and sequence data are available at the European Nucleotide Archive (www.ebi.ac.uk/ena).

Results

Within-host diversity

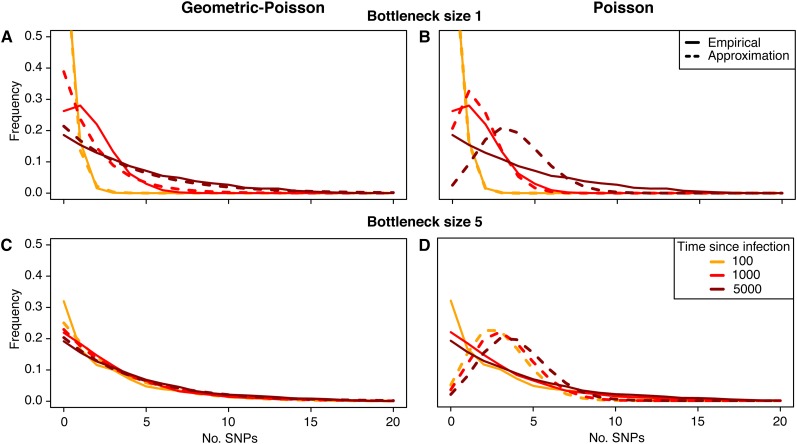
We first considered the distribution of pairwise genetic distances between isolates sampled from a single host. The distance between two isolates sampled at the same time point will be geometrically distributed according to the geometric-Poisson approximation (6), since the Poisson component is equal to zero. However, assuming infection with a single genotype, the empirical distribution generated from simulations can vary from this approximation (Figure 2A). This is a consequence of assuming a constant coalescent rate—under this simplification, it is assumed that the time to coalescence is exponentially distributed, while in reality, coalescence is much more likely to occur in the very early stages of infection, while the total within-host pathogen population is still expanding. With less uncertainty surrounding the coalescent time, pairwise genetic distance is approximately Poisson distributed, as in Equation 5. As the time since infection increases, the probability that coalescence occurred in the initial growth phase decreases, and the constant coalescent rate assumption of the geometric-Poisson approximation becomes more realistic.

Figure 2.

The empirical (solid lines) and estimated (dashed lines) distribution of genetic distances for sampling within host at specified times after infection. Both the geometric-Poisson approximation (A and C) and the simpler Poisson approximation (B and D) are shown. The infected host was infected by an inoculum of size 1 (A and B) and size 5 (C and D). The inoculum was a random sample from a bacterial population having evolved over a period of 5000 generations from an initial clonal population. Mutation rate is 0.002, and effective population size is 2000.

For individuals infected with an inoculum containing multiple genotypes, the coalescence time of sampled lineages may occur within a previous host. As such, the initial diversity within a newly infected host is higher, and equilibrium levels of diversity are approached sooner than for a clonally infected host. This leads to better agreement between the empirical and geometric-Poisson distributions (Figure 2C).

The expected and empirical mean diversities are consistently similar, even when the empirical and expected distributions differ (Figure 3). However, for observations made soon after the time of infection, the approximate distribution may overestimate the frequency of genetically identical isolates. In situations where the timing of coalescence is more certain, for example, shortly after a bottleneck of size 1 (a “strict” bottleneck), a pure Poisson approximation (Equation 5) may be more appropriate (Figure 2B). We used Akaike’s information criterion (AIC) to determine the better approximation at various time points after a strict bottleneck, finding the cutoff for the Poisson approximation to increase with population size $N_{\text{eq}}$ (Supporting Information, Table S1).

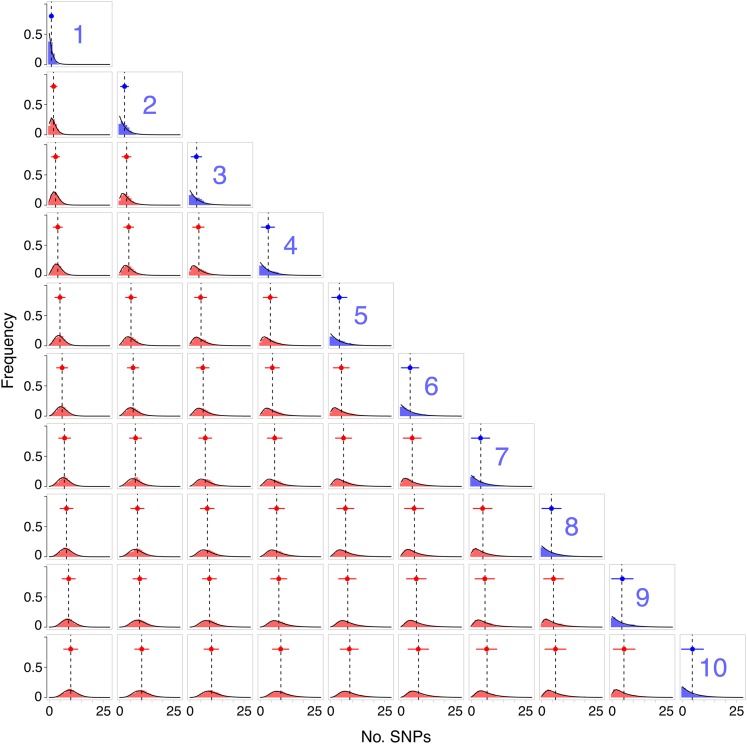
Figure 3.

Genetic distance between each pair of cases in a transmission chain. The $(i,j)$th plot represents the empirical distribution of the genetic distance between samples taken from individuals i and j (red bars). The diagonal represents the within-host diversity for each of the 10 cases in the transmission chain (blue bars). Overlaid on each plot is the expected distribution (black line), based the geometric-Poisson approximation. The expected mean is marked with a dashed line, while the empirical mean and standard error bar are marked in red (blue for within host). The within-host equilibrium pathogen population was 10,000, with a bottleneck size of 5.

Pairwise diversity along transmission chains

We next looked at the distribution of genetic distances arising from each pair of individuals in the transmission chain, simulated as described in Methods. Under most scenarios, the geometric-Poisson approximation correctly described the increasing mean and variance of the distribution as samples were taken farther down the transmission chain (Figure 3), with little apparent bias to the empirical mean (Figure S1). As the chain length increases, the genetic distributions reach an equilibrium, as the expected diversity of each transmission inoculum becomes constant.

Notably, there is considerable overlap between SNP distributions, meaning that the likelihood of observing a genetic distance between samples from two individuals will be similar for a range of transmission network configurations. This has ramifications for identifying the source of infection, since the posterior probability of any particular transmission route will typically be low, and much uncertainty will be associated with the estimated network.

Identifying direct transmission

The geometric-Poisson distribution can be used to calculate the probability that an observed genetic distance arose from a direct transmission event. In the case where the transmission bottleneck is equal to one, the distribution of distances arising from samples taken from a transmission pair does not depend on the previous structure of the transmission network, so a probability for direct transmission can be derived independently of the outbreak structure.

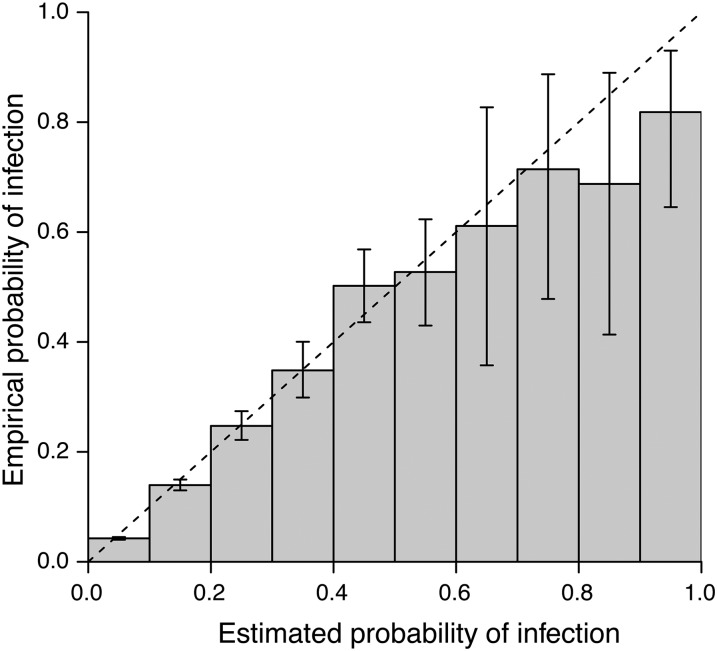
We simulated SIR outbreaks and calculated the posterior probability of transmission for every pair of individuals given observed genetic distances, as derived in Equation 7. We found that the posterior probability of transmission routes corresponded well with the empirical probability calculated under repeated simulation (Figure 4). In File S1 and Figure S2, we describe a simulated disease outbreak and demonstrate the identification of potential transmission routes using the maximum likelihood, as well as the ability to rule out transmission routes at the 5% level.

Figure 4.

The empirical probability that a proposed transmission route is correct for a range of posterior probabilities calculated under the geometric-Poisson assumption. A total of 100 outbreaks were simulated and the posterior probability of direct transmission was calculated for every pair of infected individuals. Counts were collated into 10% probability bins and for each bin, the proportion of true transmission routes was calculated. Error bars depict the 95% exact binomial confidence interval.

To test the approximation as a tool for investigating transmission networks, we repeatedly simulated SIR outbreaks and assessed the likelihood of direct transmission between each pair of individuals, using a single sampled genotype from each host. Identification of the source of infection via maximum likelihood was consistently more successful than selection of the host with the genetically closest genotype. Furthermore, source identification was more successful for higher mutation rates. A heuristic approach, in which the infection route was selected if a potential source was both the maximum-likelihood estimate and the genetically closest host, was successful around one-third of the time (Table 2).

Table 2. Performance of geometric-Poisson distribution.

Performance measure	Mutation rate ($\times {10}^{-4}$)
	1	3	5
Proportion of true infection sources identified by maximum likelihood	0.27	0.32	0.33
Proportion of true infection sources identified by closest genotypea	0.19	0.27	0.29
Proportion of potential links ruled out at 5% level	0.10	0.21	0.24
Proportion of true infection sources ruled out at 5% level	0.04	0.07	0.07
Proportion of cases identified as source by both maximum likelihood and genetic similarity found to be correct	0.27	0.33	0.35

SIR outbreaks with 30 initial susceptibles were simulated and a single genome sample was generated for each infective. Simulations with a final size <20 were discarded. For each infective, the maximum-likelihood source was calculated, and the genetically closest hosts were selected. All previously infected individuals were considered potential sources, regardless of removal times. Simulations for each scenario were repeated 100 times. Baseline parameters were infection rate 0.002, removal rate 0.001, and effective population size 5000.

^aIf the true source and other hosts are genetically equidistant, the true host is assumed to be identified with probability 1/(no. equidistant closest hosts).

With a bottleneck size >1, the time of coalescence of the two sampled lineages may occur in previous hosts, and the expected time of coalescence depends on timing of bottlenecks in the bacterial population. Past population dynamics, and therefore previous transmission history, would be required to assess individual transmission links. To avoid conditioning on the remainder of the tree structure, we calculated the likelihood under the assumption that previous bottlenecks occurred at intervals equal to the expected serial interval. While we found that higher posterior probabilities were often underestimated using this approach (Figure S3), maximum-likelihood identification still consistently outperformed selection of the genetically closest host (Table S2).

We additionally compared our approach to the software “outbreaker” (Jombart et al. 2014) and “seqTrack” (Jombart et al. 2011) and found that it could identify more transmission routes correctly in many scenarios. However, differences in modeling assumptions mean the methods are not directly comparable. More details can be found in File S1 and Table S3.

Investigating transmission routes during a hospital MRSA outbreak

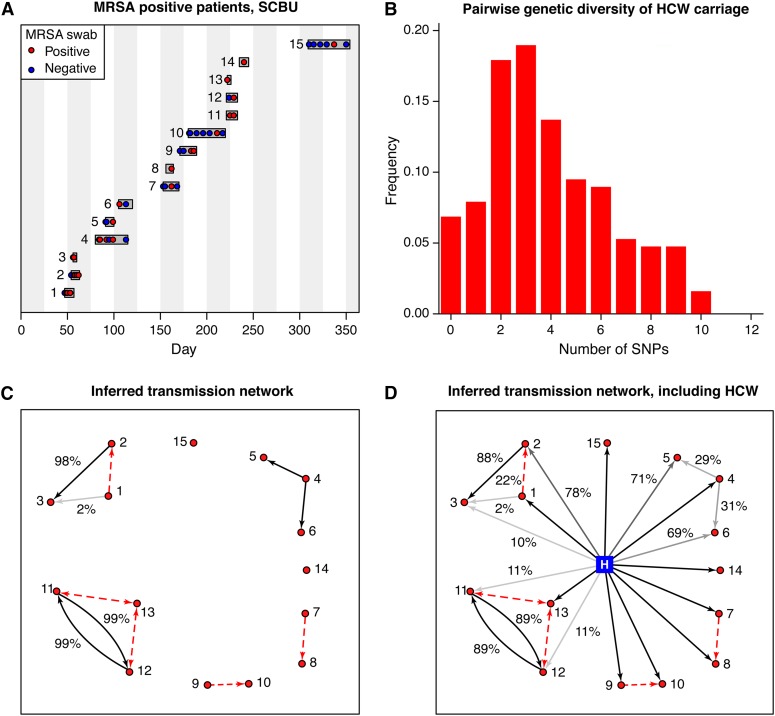
We used the MRSA data set described in Methods to investigate transmission routes in a real outbreak. We compared observed genetic distances to the geometric-Poisson approximation, to determine likely transmission routes. MRSA-positive patient episodes and swab times are shown in Figure 5A.

Figure 5.

Data and transmission route inference for the MRSA outbreak in the SCBU. (A) Patient episodes are shown as horizontal bars, with colored circles representing positive and negative swab results. (B) The observed pairwise genetic distances between the 20 sequenced isolates collected from the HCW. (C) Inferred transmission routes are shown, excluding the possibility of HCW–patient transmission. Red dashed lines indicate routes excluded at the 5% level. All temporally consistent transmission routes are shown. Posterior probability is 100% unless stated. (D) Inferred transmission routes, including the HCW as a potential source. The HCW is marked as a blue square.

We initially investigated potential patient-to-patient transmission, ignoring the possibility that the HCW may have infected patients. We assumed a bacterial generation time of 30 min (Chang-Li et al. 1988; Dengremont and Membré 1995; Ender et al. 2004) and used the mutation rate of one SNP per 15 weeks (equivalent to 0.0002 per genome per generation) quoted in the study by Harris et al. (2013). We assumed a strict bottleneck. We found that, since the time from infection to sampling was typically short, the within-host effective population size made little difference to the approximated distributions. Five temporally consistent transmission routes could be ruled out at the 5% level, leaving five plausible transmission events (Figure 5C). Two of these form a cycle (between 11 and 12)—only one of these events could have occurred, but each route is equally plausible. The lack of any other observed and temporally consistent infection source within the ward suggests transmission from an external source or environmental contamination—however, since the infants in this study were nonambulatory, this possibility was considered less likely.

We next supposed that the HCW could have been the source of infection for any of the patients in the SCBU. The observed mean pairwise distance between the samples collected from the HCW was 3.89 SNPs (Figure 5B), suggestive of a lengthy carriage time or a nonstrict bottleneck size. The time of HCW infection was estimated to be 23 days before the first patient case (Harris et al. 2013). We set the observed genetic distance from patient to HCW as the nearest integer to the mean of the genetic distances to each of the HCW’s 20 samples. We found that all patients could plausibly have been infected by the HCW; however, in three cases this was not the most likely source of infection (Figure 5D). Assuming that infection must have a source from within the SCBU (including the HCW), we found that in addition to the six individuals with no other temporally consistent source, three patients had a posterior probability of >99% of acquiring infection from the HCW, while two others had a >50% probability. We additionally repeated the analysis, using each of the HCW’s isolates individually (Figure S4). Furthermore, we ran the analysis using the Poisson approximation, finding little difference in transmission route probabilities (Figure S5).

We finally investigated the possibility that the HCW was infected by one of the patients on the ward. Assuming that the HCW was infected 2 days after the infection time of the potential source, we could rule out five patients as a source of infection for the HCW at the 5% level. If the HCW was infected by any one of the patients, the observed diversity within the HCW is greater than would be expected to accumulate in the period from infection to observation. At least 16% of the observed HCW within-host pairwise distances would be rejected at the 5% level under any patient–HCW transmission scenario (Table S4).

We found that, while most of our analyses were fairly robust to the specification of the effective population size, there was sensitivity to the choice of mutation rate and the time of HCW infection. We investigate these sensitivities in detail in File S1 and Table S5.

The methods we have described and implemented are for pairwise distances and, as such, cannot account for dependencies between several isolates. This is necessary when considering the transmission network as a whole, rather than just a set of pairwise connections. In addition, it is necessary to consider the conditional distribution of genetic distance to account for multiple samples per host. The degree of dependence varies considerably depending on the transmission bottleneck size (Figure S6, Figure S7). In File S1, we describe the conditional distribution for genetic distances.

Discussion

In this study, we have explored the distribution of the genetic distances arising from samples taken from infected hosts during an outbreak and investigated the impact of factors such as mutation rate, transmission dynamics, and within-host pathogen population dynamics on the expected value of such distances. Under most circumstances, a geometric-Poisson approximation is sufficient to describe genetic distances between samples taken during an outbreak. This allows the distribution to be approximated without knowing the coalescence time of two lineages. With known parameters of pathogen population dynamics, the likelihood of genetic distances arising between a host and various potential transmission sources may be compared, and certain links may be excluded. The transmission bottleneck size can have a large impact on the genetic distance distribution, and our methods can account for this.

The ability to assign a genetic distance threshold to rule out transmission events in a nonarbitrary fashion can be important in establishing distinct subgroups of the transmission tree, as well as identifying pathogen importation from outside of the studied population. This is of much importance when estimating transmission rates within a community, as incorrectly identified importations can introduce bias. Previous studies have used an arbitrary cutoff to determine potential transmission (e.g., Jombart et al. 2014; Long et al. 2014).

We found that the geometric-Poisson approximation deviated from the empirical distribution to the greatest extent when sampling occurred shortly after infection with a clonal inoculum. While the expected genetic distance exhibited no apparent bias, and this deviation was minor for bottleneck sizes >1, it should be noted that this scenario may potentially be important in outbreaks of highly symptomatic pathogens, as samples are more likely to be taken in the earlier stages of infection, compared to asymptomatic, chronic infections. If a strict bottleneck is considered likely shortly before sampling, using the Poisson distribution (Equation 5) with fixed coalescent time is recommended.

Identification of transmission sources using this method is most successful with a high mutation rate. While higher mutation rates (and longer intervals between infection and onward transmission) can lead to more distinct distributions, potentially allowing one to rule out certain relationships, such as direct transmission, it is clear that even under extreme scenarios, uncertainty remains. We found that the success rate of identifying the source of infection was up to 33% better than selection of the genetically closest host, but still too low to identify transmission routes with confidence. We demonstrated that our approach could identify transmission routes more successfully than existing software packages, provided key values, such as mutation rate and infection times, are known. It has been shown previously that identification of transmission routes during an outbreak based on genomic data is likely to be challenging due to high levels of uncertainty (Worby et al. 2014), a finding also reflected in recent investigations (Didelot et al. 2014). The methods provided in this article are likely to be most valuable in the identification of a group of potential sources with a high likelihood, as well as the elimination of potential sources at a given probability level (discriminating, for example, between imported cases and within-population transmission events). Additional data sources, such as spatial location, contact patterns, and infectious periods, will increase the precision of estimates of infection paths (Ypma et al. 2012, 2013; Jombart et al. 2014).

We demonstrated the application of our methods to a data set collected during an MRSA hospital outbreak. We could rule out 5 of the 11 temporally consistent patient-to-patient transmission routes at the 5% level and found evidence supporting the important role played by the colonized HCW in the outbreak. However, our analysis was limited by a number of important parameter values that are uncertain or unknown. This work highlights the importance of deriving estimates for the transmission bottleneck size and gaining an improved understanding of within-host pathogen population dynamics. With less parameter uncertainty, it would be possible to draw more robust conclusions. Our analysis considered only sequence data, but other data sources could contribute valuable information to infection routes. For instance, we assume an uninformative prior distribution for infection sources, but contact patterns could potentially be factored into this, if such information were available.

While using our approximation to the genetic distance distribution can be useful to assess pairwise individuals for evidence of direct transmission, reconstruction of the full transmission network requires us to consider the conditional distribution of genetic distances and a framework to sample over the entire structure. Accounting for dependencies between genetic distances would require inference of the set of coalescent times. This approach has been described in a recent study (Ypma et al. 2013), which used sequence data directly, rather than genetic distance data. It may be possible to implement the distribution approximation described here, accounting for dependencies by conditioning on shared tree branches.

The transmission bottleneck size is important in the analysis of transmission dynamics, using genomic data. Most studies to date assume a strict bottleneck for convenience, as under this condition, the expected distance between two samples does not depend on pathogen population dynamics prior to the divergence of the lineages to different hosts. Previous studies have suggested a diverse transmission inoculum for influenza (Hughes et al. 2012; Murcia et al. 2012), while it is thought that the bottleneck size for bacterial transmission could vary dramatically (Balloux 2010). Conducting inference under the incorrect bottleneck size can generate misleading results. Our methods illustrate the degree to which the bottleneck size can affect the expected genetic distance between individuals and may potentially be used to assess whether a strict bottleneck is a realistic assumption.

There are several assumptions made in this work. First, we have assumed neutral evolution, such that no fitter mutant can arise and dominate the pathogen population. This may be a reasonable assumption in the short term, such as during individual carriage and in small outbreaks, but would have to be taken into account when considering epidemics over a long period of time. However, transmission route inference is most applicable to localized outbreaks within a community or a hospital, and the emergence of fitter variants may be of lesser importance. We have also assumed that the within-host pathogen population remains at equilibrium level and that this is identical for all infected individuals, while in reality this may be unrealistic, especially during antimicrobial use. Within-host pathogen dynamics are still poorly understood, and the effective size may fluctuate and vary considerably between hosts. We have primarily considered long-term bacterial infections, with a relatively stable within-host population, but alternative models could also be considered, provided the expected time of coalescence can be estimated at any given time. With appropriate sampling, methods exist to estimate the within-host effective population size, as well as the mutation rate (e.g., Wang 2001; Minin et al. 2008). With known transmission routes, our approximation can also be used to estimate parameters of interest; however, these estimates are associated with some uncertainty (see File S1, Figure S8 and Figure S9). We assumed that the source of infection must come from the pool of observed infectives at the time of infection and furthermore that the time of infection is known. In some cases, particularly for outbreaks in large, well-mixing communities, it is unlikely that all infected cases will be identified and sampled. Nonetheless, evidence for an external source of infection can be seen when all potential observed sources are ruled out (for instance, cases 2 and 8 in the MRSA outbreak when not considering the HCW). In many cases, transmission times are unknown, although for many infections this can be estimated from the time of symptom onset or at least narrowed down by swabs for pathogen presence. Although one can test the hypothesis that an individual was infected at a certain time, this is a source of uncertainty, particularly for scenarios with a lengthy, asymptomatic infection period and/or a low pathogen mutation rate.

Genetic distances are an important and frequently used feature of genome sequence data, and our work contributes to a better understanding of how such distances arise during an outbreak. While sequence data provide a wealth of information regarding evolutionary history and relatedness of genotypes, the phylogeny derived from such data by itself may not be informative of transmission dynamics, and methods to combine this structure with the transmission tree are complex and computationally intensive (Ypma et al. 2013). Genetic distances offer a simple summary statistic of complex multidimensional data and may be more appropriate in comparative analyses of genomic samples. Genetic distances can crudely be used to determine direct transmission, via selection of the genetically closest host, but our simulations demonstrate that this approach may frequently be misleading. The geometric-Poisson approximation offers a less arbitrary method of quickly assessing the likelihood of direct transmission without requiring computationally intensive Monte Carlo sampling strategies. It may additionally provide an important component in the development of a full transmission network reconstruction methodology based on genetic distance data.