Hybrid Incompatibility Despite Pleiotropic Constraint in a Sequence-Based Bioenergetic Model of Transcription Factor Binding

Abstract

Hybrid incompatibility can result from gene misregulation produced by divergence in trans-acting regulatory factors and their cis-regulatory targets. However, change in trans-acting factors may be constrained by pleiotropy, which would in turn limit the evolution of incompatibility. We employed a mechanistically explicit bioenergetic model of gene expression wherein parameter combinations (number of transcription factor molecules, energetic properties of binding to the regulatory site, and genomic background size) determine the shape of the genotype–phenotype (G-P) map, and interacting allelic variants of mutable cis and trans sites determine the phenotype along that map. Misregulation occurs when the phenotype differs from its optimal value. We simulated a pleiotropic regulatory pathway involving a positively selected and a conserved trait regulated by a shared transcription factor (TF), with two populations evolving in parallel. Pleiotropic constraints shifted evolution in the positively selected trait to its cis-regulatory locus. We nevertheless found that the TF genotypes often evolved, accompanied by compensatory evolution in the conserved trait, and both traits contributed to hybrid misregulation. Compensatory evolution resulted in “developmental system drift,” whereby the regulatory basis of the conserved phenotype changed although the phenotype itself did not. Pleiotropic constraints became stronger and in some cases prohibitive when the bioenergetic properties of the molecular interaction produced a G-P map that was too steep. Likewise, compensatory evolution slowed and hybrid misregulation was not evident when the G-P map was too shallow. A broad pleiotropic “sweet spot” nevertheless existed where evolutionary constraints were moderate to weak, permitting substantial hybrid misregulation in both traits. None of these pleiotropic constraints manifested when the TF contained nonrecombining domains independently regulating the respective traits.

ADAPTIVE changes in phenotype often occur through changes in gene regulation (Wray 2007; Carroll 2008). Regulatory networks map an organism’s genotype to its phenotype through developmental and physiological processes (Wilkins 2002). Such networks consist of interacting loci that can respond to selection by changing the expression levels of individual genes in space and time. In addition to gene interaction (epistasis) (Phillips 2008), gene networks are also characterized by pleiotropy, where single genetic loci have manifold effects (Gibson 1996; Paaby and Rockman 2013).

Gene interactions are pervasive in the evolution of hybrid incompatibility, an important form of reproductive isolation between species (Coyne and Orr 2004). The leading model for the evolution of hybrid incompatibility, the Bateson–Dobzhansky–Muller (BDM) model, requires interactions between at least two genetic loci (Bateson 1909; Dobzhansky 1937; Muller 1942). Interpopulation divergence in regulatory interactions may be expected to result in hybrid incompatibility due to misregulation of the traits they control (Johnson and Porter 2000, 2001; Landry et al. 2007; Ortíz-Barrientos et al. 2007; Maheshwari and Barbash 2011, 2012). Theoretical studies (Johnson and Porter 2000, 2007; Palmer and Feldman 2009) of the molecular basis of evolving regulatory interactions demonstrate that misregulation in hybrids readily arises as a byproduct of adaptation. Tulchinsky et al. (2014) show that the degree of this hybrid incompatibility is determined in large part by the bioenergetic [thermodynamic plus kinetic (Morowitz 1978)] details of the molecular interactions between coevolving transcription factors and the sites to which they bind.

BDM incompatibilities between species often express themselves in traits other than those involved in adaptation to divergent environments, although the traits may share a genetic basis (Schluter 2009). Pleiotropy and genetic linkage have been proposed as possible mechanisms by which selection on one trait may result in hybrid dysfunction in a different trait (Rundle and Nosil 2005; Johnson and Porter 2007; Via 2009). At the same time, opposing selective forces on coregulated traits should impose constraints on the evolution of loci with pleiotropic effects (Stern 2000; Wray 2007). For that reason, several authors have hypothesized that most adaptive changes in gene expression are due to changes in trait-specific cis-regulatory regions rather than in trans-acting transcription factors (TFs) that bind pleiotropically to multiple sites (e.g., Stern 2000; Prud’homme et al. 2007). Expression changes constrained to a trait’s cis-regulatory region would not produce hybrid misregulation, which requires coevolved changes in interacting loci. Nonetheless, cis-by-trans incompatibility between TFs and their binding sites is commonly observed in hybrids (Wittkopp et al. 2004; Landry et al. 2005). The purpose of this study is to explore this apparent contradiction from the perspective of the molecular basis of pleiotropic regulatory interactions, to determine the bioenergetic properties of these interactions that permit BDM incompatibilities to evolve despite evolutionary constraint.

How might cis-by-trans divergence occur if adaptation in trans is constrained by pleiotropy? One possibility is that regulatory incompatibility in hybrids results from changes in the expression level of TFs rather than their coding sequence (Wittkopp et al. 2004). The modular structure of cis-regulatory regions may permit changes in expression to be confined to specific tissues or conditions and therefore affect fewer regulatory targets than would a change in DNA-binding specificity (Stern 2000; Prud’homme et al. 2006). Another possibility is that the sequence of a TF is often less constrained by pleiotropy than its number of downstream targets would suggest (Wagner and Lynch 2008; Baker et al. 2011). Transcription factors are typically modular in structure, consisting of multiple DNA-binding and cofactor-binding domains (Hsia and McGinnis 2003). As with cis-regulatory regions, this modularity may allow tissue-specific or condition-specific evolutionary responses that affect only a subset of the TF’s potential targets (Hsia and McGinnis 2003; Wagner and Lynch 2008). This inherent limit to the extent of pleiotropy is complemented by the possibility that pleiotropic changes occur but their deleterious effects are later compensated (Haag 2007; Kuo et al. 2010; Pavlicev and Wagner 2012). Compensation can contribute to hybrid incompatibility if different combinations of deleterious and compensatory changes occur in diverging populations (Landry et al. 2005). In this study, we examine the conditions under which compensatory evolution between a TF and its binding site may facilitate cis-by-trans regulatory incompatibility despite pleiotropic constraint.

Model

We model, in diploids, a three-locus, two-interaction regulatory network in which a pleiotropic TF regulates the expression of two downstream loci, one under directional selection and the other under stabilizing selection. Our previous results, for a two-locus interaction that regulates expression of a single trait, show that hybrid incompatibilities rapidly evolve as a byproduct of adaptation when that trait is under positive selection (Johnson and Porter 2000; Tulchinsky et al. 2014). Under stabilizing selection, we found that more gradual and parameter-limited evolution of incompatibilities could occur due to compensatory evolution following genetic drift (Tulchinsky et al. 2014). We expect the addition of a regulatory target under positive selection to accelerate evolutionary change in the TF compared to the case of a single conserved trait. Likewise, the addition of a trait under stabilizing selection should constrain TF change compared to the case of a single positively selected trait. If adaptive change occurs at the pleiotropic TF locus, it will select for compensation at the conserved regulatory target (Johnson and Porter 2007), resulting in hybrid misregulation at both interactions in the three-locus network.

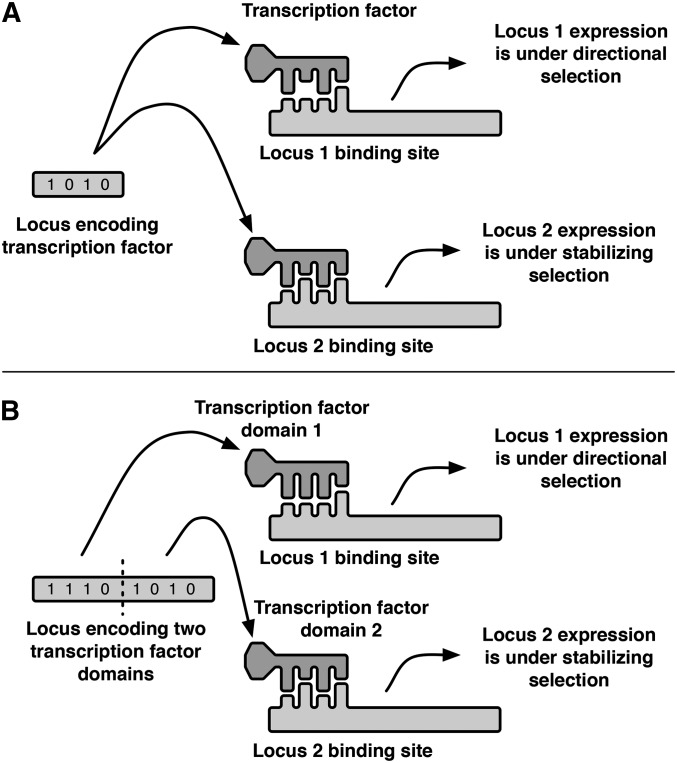
To quantify the extent of pleiotropic constraint, we compare two different TF architectures. In the first, the TF consists of a single DNA-binding domain that binds to the cis-regulatory regions of two downstream loci associated with separate traits as illustrated in Figure 1A. In the second, the TF contains two nonrecombining DNA-binding domains, each of which binds to the regulatory region of one of the downstream loci (Figure 1B). In the terminology of Paaby and Rockman (2013), these correspond to multifunctional TF types showing “developmental pleiotropy” and “molecular gene pleiotropy,” respectively. As shorthand, we refer to these as the “pleiotropic” and “two-domain” models. Our shorthand follows a distinction made by evolutionary geneticists when offering alternative explanations, pleiotropy vs. linkage disequilibrium, for correlations between evolving traits (e.g., Hartl and Clark 2007). We characterize the one-domain TF as being mechanistically pleiotropic, while the two-domain TF serves as a control for the potential effects of maximal linkage disequilibrium between otherwise mechanistically independent regulatory sites.

Figure 1.

Three-locus regulatory network in which a pleiotropic transcription factor (TF) regulates the expression of two downstream loci. Locus 1 is under directional selection while locus 2 is under stabilizing selection. At each locus, expression depends on the fit between the transcription factor and a binding site in the cis-regulatory region. The binding preference of the transcription factor and the nucleotide sequence of the cis-regulatory site are represented as binary strings, whose total number of matching positions determines the binding strength. For illustrative purposes, only 4 bits of the binding interaction are shown. An adaptive change in the expression of locus 1 may be accomplished either by a mutation in its cis-binding site or in the transcription factor. Changes in the transcription factor select for compensatory mutations in the cis-binding site of locus 2. Thus, if selection on locus 1 results in interpopulation divergence in the transcription factor, hybrid misregulation of both loci will occur as each binding interaction evolves a unique fit to produce the favored expression level in parent populations. (A) “Pleiotropic model” where a single domain of the TF regulates both downstream loci. (B) “Two-domain model” where two nonrecombining domains of the TF independently regulate the downstream loci.

We obtain a simple quantitative model of compensatory evolution by applying a bioenergetic, information-based model of transcriptional regulation (Von Hippel and Berg 1986; Gerland et al. 2002; Mustonen et al. 2008; Tulchinsky et al. 2014). We give an overview here and refer the reader to Tulchinsky et al. (2014) for details. The principle is that the phenotype is determined by the level of gene expression and that gene expression is determined by fractional occupancy—the probability that a TF is associated with its cis-regulatory site at any given moment. Fractional occupancy depends on the number of TF molecules and the energetics of their binding to the cis-regulatory region, which depends in turn on the number of matching positions between the TF’s recognition motif and the sequence of the binding site.

The transcription factor’s binding motif(s) and the cis binding-site sequences of the two downstream loci are mutable alleles, each represented by a string of bits. In a motif of length n, the number of mismatched bits m determines the energy of binding between the TF and the binding site, which determines the fractional occupancy θ. Each matching bit increases the fractional occupancy, which is maximal when m = 0. In diploids, fractional occupancy is specific to the allelic combination at the TF and the cis-regulatory site, with TF alleles competing for binding at each allelic copy of that cis-regulatory locus. The fractional occupancy for each allelic combination is

$${\theta }^{\prime }=\frac{N_{\text{TF}}}{N_{\text{TF}}+\alpha e^{-m\Delta G_1-E_{\text{diff}}}},$$ (1)

where N_TF is the number of molecules of the allele-specific TF in the cell, ΔG₁ is the contribution of a single matched bit to the free energy of formation between that TF and the cis-regulatory site allele, $\alpha =1+N_{\text{TF}}{e}^{m_{\text{c}}\Delta G_1+E_{\text{diff}}}$ accounts for the reduction in fractional occupancy of a TF variant from competition with the other variant, and m_c is the number of mismatches in the competing TF allele. E_diff is a heuristic parameter that measures the free energy of TF binding to the nonspecific intracellular background relative to that of a perfectly matched TF–cis site pair, such that E_diff < 0 when fractional occupancy on the genomic background is higher than to the cis-regulatory site. This assumes that N_TF and E_diff are equal between TF alleles.

Expression proceeds when the TF is bound to the cis-regulatory region, so the final level of expression is proportional to the fractional occupancy (Gertz et al. 2009). We treat the phenotype, P, as proportional to the level of expression. We calculate the diploid phenotype as the sum of expression from each of the four allele-specific θ′ values, scaled following Tulchinsky et al. (2014) so that the maximum phenotype P_max = 1.0 for a double homozygote with no mismatches (m = 0).

Fitness is a function of an organism’s deviation from the optimal phenotypic value at each trait. The total organismal fitness is the product of the marginal fitnesses at each trait and these marginal fitnesses are

$$W=\exp \left[\frac{-{\left(P-P_{\text{opt}}\right)}^2}{2{\sigma }_{\text{s}}^2}\right],$$ (2)

where P_opt is the trait’s environmentally determined, optimal phenotypic value and ${\sigma }_{\text{s}}^2$ is the variance of fitness around that optimum (a measure of the degree to which a suboptimal phenotype is tolerated by selection).

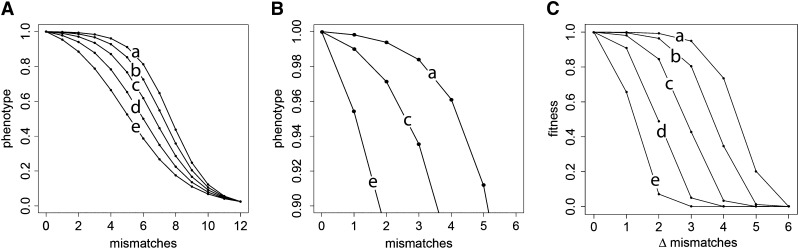
We previously found that hybrid incompatibility occurred more readily in a two-locus, single-trait model under bioenergetic parameters that yield either a shallower fitness landscape around a conserved trait or a steeper fitness landscape around a directionally selected trait (Tulchinsky et al. 2014). Here we examine the effect of the genotype-to-phenotype and phenotype-to-fitness functions on pleiotropically coregulated traits. In our model, the general forms of the genotype–phenotype (G-P) map and fitness landscape are sigmoid, with their explicit shapes determined by the values of N_TF, ΔG₁, and E_diff (and for the fitness landscape, P_opt and ${\sigma }_{\text{s}}^2$ as well). Figure 2 shows this effect as well as the combinations of parameter values we used in this study. Heuristically, it is useful to characterize these shapes qualitatively rather than as vectors of explicit values. To do this, we use the term “slope” as the difference in phenotype between 0 and 1 mismatches; it follows that shape “a” in Figure 2A has the shallowest slope and “e” the steepest. This characterization extends isomorphically to the fitness landscape as well, where slope is also influenced by the value of ${\sigma }_{\text{s}}^2.$

Figure 2.

G-P map shapes determined by bioenergetic parameter combinations, from figure 2 in Tulchinsky et al. (2014), used to assess the effects of bioenergetic parameters on pleiotropic constraint. (A) G-P maps a–e, shown with a motif length of n = 12 bits. (B) G-P maps a, c, and e over the phenotypic range of 0.9–1.0, emphasizing the difference in slopes. Conditions: we held N_TF constant at 100 and varied E_diff in steps of 1.0, covarying ΔG₁ with it to enforce a constant phenotype of P ≈ 0 when none of the n bits matched. (C) Fitness landscapes corresponding to the G-P maps of A, at P_opt = 1 and ${\sigma }_{\text{s}}^2=2.5\times {10}^{-3}$. The conditions are (a) E_diff = 2, ΔG₁ = −0.858; (b) E_diff = 1, ΔG₁ = −0.774; (c) E_diff = 0, ΔG₁ = −0.692; (d) E_diff = −1, ΔG₁ = −0.610; and (e) E_diff = −2, ΔG₁ = −0.530.

Simulations

We conducted individual-based simulations to examine the effects of bioenergetic parameter combinations and fitness landscape on the evolution of net F₂ hybrid misregulation. (We assess the effects of evolutionary rate and mutation effect size in Supporting Information, File S1.) A pair of independent populations was subjected in parallel to trait-specific directional and stabilizing selection. The two loci downstream from the trans-acting TF locus correspond to separate, cis-regulated traits (Figure 1). One of these traits was held under stabilizing selection at a phenotypic value of P_opt = 1.0, such that zero mismatched bits was optimal in its binding interaction. The other trait was placed under directional selection such that the optimal number of mismatches changed from m = n to m = 0 over the course of the simulation. This was accomplished by setting the initial trait optimum to a value near P_opt = 0, corresponding to the phenotypic value produced by the maximum number of mismatches. The initial genotype of all individuals was set such that each trait started at its optimum. Evolutionary change in the directionally selected trait was achieved by adjusting P_opt by a constant amount ΔP_opt each generation to arrive at a final optimum of P_opt = 1.0.

Each generation consisted of viability selection followed by random mating. Population size was kept constant each generation, with no overlap of generations. Thus, populations could experience bottlenecks between viability selection and mating, but returned to carrying capacity each generation. In the fitness function, we set ${\sigma }_{\text{s}}^2$ to 2.5 × 10⁻³ at each trait; the effects of variation in this parameter are presented in File S1. In keeping with our two-locus model (Tulchinsky et al. 2014), mutations occurred in the offspring at a baseline rate of 8.333 × 10⁻⁵ per bit, equivalent to 0.001 per locus with an n = 12 bit motif length. Each mutation changed one bit of information. We varied the mutation rate experimentally as described below.

We studied the effects on F₂ hybrid misregulation of the G-P map and marginal fitness landscapes by varying the E_diff and ΔG₁ parameters, using the range of values in Tulchinsky et al. (2014). As binding to the genetic background increases with decreasing values of E_diff, TF availability at the target binding sites declines rapidly following an exponential function. We adjusted ΔG₁ along with E_diff to keep a constant phenotype of P ≈ 0 (P = 0 is an asymptote and we used P = 0.0245) when all bits were mismatched; parameter values are in the Figure 2 legend. Following Tulchinsky et al. (2014), we used alleles of length n = 12 bits and an evolutionary rate of ΔP_opt = 1/40,000 generations. We held constant the upstream expression level of the TF-determining locus at N_TF = 100. This does not limit the generality of our results, because it is a property of Equation 1 that the effects on fractional occupancy of varying N_TF and E_diff are isomorphic, such that the effect of changing E_diff on a linear scale can be duplicated by changing N_TF on an exponential scale.

If pleiotropy constrains the substitution rate at the TF locus because of its negative side effects on the conserved trait, then mutation rate should influence the extent of that constraint. Low overall availability of mutations should cause more TF mutants to be tolerated despite their side effects. To investigate the extent to which each of the three mutable loci contributes to pleiotropic constraint, we ran simulations in which we varied the overall mutation rate, as well as mutation rates at each locus in the network, between 1/8 and 8 times the baseline rate above. For these, we used G-P map “d” of Figure 2, and the evolutionary rate was set to ΔP_opt = 1/4000 generations.

Net misregulation of each trait in the hybrid phenotype was assessed at the end of the final generation. Tulchinsky et al. (2014) showed that F₁ misregulation is typically less than or equal to F₂ misregulation, depending on the bioenergetic parameter combinations that determine allelic dominance in gene expression, so we report only F₂ misregulation here. The parental populations were cross-mated randomly to create 50 F₁ hybrids, which were then randomly mated with each other to create 50 F₂ hybrids without prior viability selection on the F₁’s. We measured the mean deviation of F₂ hybrids from the optimal phenotype at each trait. This total F₂ hybrid misregulation includes a fraction representing genetic load in the parental populations. We therefore calculated the net F₂ hybrid misregulation by subtracting the mean deviation of the parents at each trait from the total F₂ deviation. This represents the portion of F₂ misregulation that resulted solely from Bateson–Dobzhansky–Muller incompatibilities between populations. While net misregulation in the hybrid phenotype is our primary parameter of interest in assessing BDM incompatibilities, we also report the marginal fitnesses of each trait, assuming the fitness model of Equation 2. These results are based on 200 replicates. Simulations were written in C in the Xcode environment and run in Mac OS X, and graphics were produced using the statistical package R.

Results

Sensitivity of pleiotropic misregulation to bioenergetics of TF binding

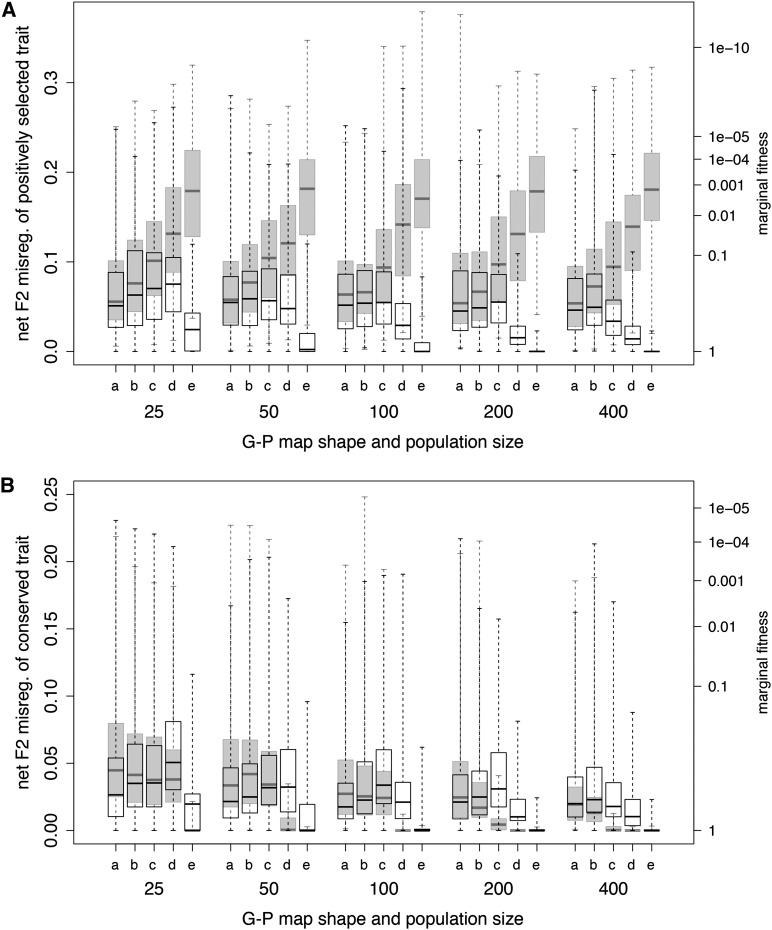
When we varied the bioenergetic parameter values that determine the G-P map and fitness landscape shapes of Figure 2, net F₂ hybrid misregulation occurred at both the directionally selected and conserved traits, but the patterns were different (Figure 3). Misregulation in the two-domain model’s directionally selected trait (Figure 3A, shaded bars) climbed steeply as the G-P map shapes of Figure 2 proceeded from a to e and was not affected by population size. The simple two-locus model of Tulchinsky et al. (2014) (their figure 3) showed the same pattern, indicating that having a second TF domain under stabilizing selection does not constrain evolution at the first domain. In contrast, in the pleiotropic model, net F₂ misregulation of the directionally selected trait (Figure 3A, open bars) climbed gradually, starting at shape a, and then declined rapidly by shape e. The trajectory depended on population size, peaking earlier as population size increased. Misregulation in the directionally selected trait (Figure 3A) was higher than in the conserved trait (Figure 3B) in both the pleiotropic (open bars) and two-domain (shaded bars) models.

Figure 3.

Median net F₂ hybrid misregulation as a function of bioenergetic parameters for the pleiotropic (open boxes) and two-domain (shaded boxes) models, at population sizes 25–400. Bioenergetic parameter combinations determine G-P map and fitness landscape shapes following Figure 2, with shape “a” having the shallowest and “e” having the steepest slope. (A) Misregulation of the directionally selected trait. (B) Misregulation of the conserved trait. Note the different scales. Box plots show median, quartiles, and full ranges. Simulation conditions: directional selection was applied over 40,000 generations, using a 12-bit motif.

For the conserved trait (Figure 3B), the pleiotropy model (open bars) showed the same pattern of misregulation seen in the directionally selected trait. Misregulation in the two-domain model (shaded bars) followed almost the same pattern as that in the two-locus model under stabilizing selection (Tulchinsky et al. 2014, their figure 3), where misregulation was associated with compensatory evolution. Here, compensatory evolution in the second domain of the two-domain TF was largely unaffected by the selection response at the first domain. Thus, the two-domain model behaved as if it were a pair of independently regulated two-locus traits.

The dynamics underlying these patterns in the pleiotropic model are influenced by the slopes of the G-P map and fitness landscape. To illustrate these influences, we can follow the substitution dynamics in the parental populations by referring to Figure 2B, looking first at G-P map e. As P_opt for the directionally selected trait approaches ∼0.95, restoring the mean marginal fitness of that trait to W_dir = ∼1 can be accomplished by fixing a mutant having one mismatch. But, because the slope of the G-P map is steep, any mutation at the TF site will simultaneously drop the marginal fitness of the conserved trait to W_cons = 0.66 (Figure 2C). This is a strong evolutionary constraint on the TF locus. Selection thus favors mutants in the cis-regulatory site of the directionally selected trait, which have no such pleiotropic fitness cost.

In the G-P map c of Figure 2B, with a moderate slope, fixation of a new mutant of the directionally selected trait is favored with a lesser change in P_opt, to ∼0.99. Although a cis-site mutant for this trait yields the highest mean fitness, a substitution at the TF does not diminish the marginal fitness of the conserved trait very much, to W_cons = 0.98. Compensation is ultimately more likely because it need not occur as quickly, and over the course of the simulation, more compensation can take place. More F₂ hybrid misregulation therefore accumulates at the conserved locus, and the pleiotropic constraint is relaxed under the bioenergetic parameter combinations that yield this map.

In contrast, in G-P map a of Figure 2B, the slope is very shallow and the upward trend in phenotypic misregulation reverses. The phenotypes of either trait are little affected until several mismatches become fixed, so selection for compensation at the conserved trait becomes strong only when the number of mismatches remains high (on the order of m > 3 on this map, beyond which W_cons < 0.74). With little to compensate for, less compensation evolves. Moreover, by the end of the simulation, even though parental populations had diverged, hybrids with several mismatches still showed similar phenotypes to those of parents, with little evidence of phenotypic misregulation. As population size increases, selection becomes more efficient, causing pleiotropic constraint to become more evident at shallower slopes.

Net F₂ misregulation in the pleiotropic model was consistently lower in the conserved trait (Figure 3 and Figure S1). This traces to the dynamics of compensatory substitution in the cis site of the conserved trait in the later stages of the simulation. Misregulation of the conserved trait remains relatively lower until compensation is complete, whereupon it reaches that of the directionally selected trait; this holds for both total and net misregulation. Incomplete compensation is more common when the G-P map is shallow because the fitness advantage of the last compensatory mutant is low (for map a of Figure 2, the advantage is only ΔW = 0.005), and complete remediation may not be reached until a great many generations after the bout of directional selection ends.

Sensitivity to mutation rate

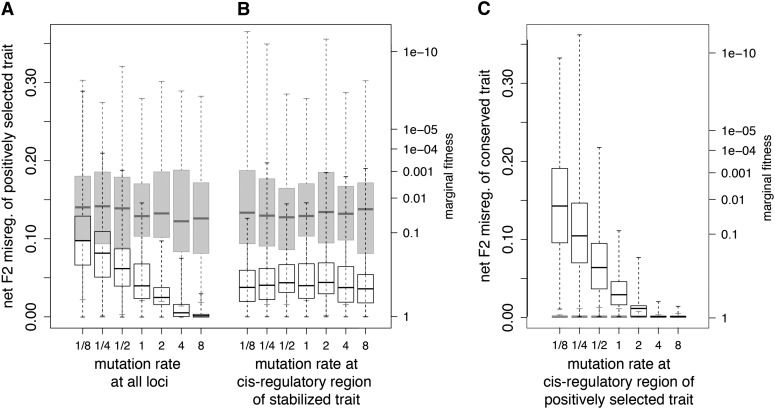
Decreasing the overall mutation rate increased net F₂ hybrid misregulation of the positively selected trait in the pleiotropic model, but not in the two-domain model (Figure 4A). In the former, where the TF is mechanistically pleiotropic, a dearth of new mutations increases the net fitness advantage of any new TF mutant that does arise, provided its favorability at the positively selected trait overcomes its disadvantage at the conserved trait. This promotes the evolution of misregulation. However, as the overall mutation rate increases, enough new mutants arise at the cis locus of the directionally selected trait and more of the adaptive change can occur there. This limits the evolution of misregulation, which requires changes at both the TF and the cis locus.

Figure 4.

Median net F₂ hybrid misregulation under varying mutation rates occurring at cis-regulatory sites of separate traits in the pleiotropic (open boxes) and two-domain (shaded boxes) models. Mutation rates are expressed as multiples (0.125–8) of the baseline mutation rate of 8.333 × 10⁻⁵/bit. (A) Median net F₂ misregulation of the positively selected trait as a function of varying the overall mutation rate. Misregulation was constrained to lower levels in the pleiotropic model relative to the two-domain model and the extent of constraint increased with mutation rate. (B) As in A, but instead varying the mutation rate only at the cis-regulatory locus of the conserved trait. Misregulation was again constrained in the pleiotropic model relative to the two-locus model, but was not sensitive to mutation rate. (C) Misregulation of the conserved trait as a function of the mutation rate at the cis-regulatory locus of the positively selected trait. In the pleiotropy model, misregulation was high at low mutation rates, dropping to zero as mutation rate increases, but no misregulation occurred in the two-domain model. Box plots show median, quartiles, and full ranges. Simulation conditions: directional selection was applied over the course of 4000 generations; population size = 400.

To examine the importance of compensation in the evolution of hybrid incompatibility, we varied the mutation rate at the cis-regulatory locus of the conserved trait while holding it constant at the other two loci and measured the effect on misregulation at the positively selected trait. Pleiotropy constrained misregulation relative to the two-domain model, but neither model was sensitive to mutation rate at this locus (Figure 4B).

Decreasing the mutation rate at the cis-regulatory locus of the positively selected trait alone increased net F₂ hybrid incompatibility at the conserved trait (Figure 4C). A lower availability of mutations at this locus increased divergence at the TF locus by increasing the net fitness advantage of TF mutants, increasing hybrid misregulation. No misregulation of the conserved trait was found in the two-domain model under these conditions.

Discussion

The pleiotropic sweet spot for hybrid incompatibility

Hybrid incompatibility is predicted to arise from the disruption of regulatory genetic networks that have diverged since the hybridized populations shared a common ancestor (Johnson and Porter 2000). These disruptions are the basis of Bateson–Dobzhansky–Muller interactions responsible for hybrid dysfunction. At the same time, pleiotropy is a ubiquitous characteristic of these networks, and pleiotropic regulatory loci typically affect a diversity of traits, most of which are likely to be evolutionarily conserved. We might therefore predict strong evolutionary constraints against divergence at pleiotropic points in the network (Stern 2000; Wray 2007), and indeed, most regulatory divergence between Drosophila species occurs at cis-acting sites (Wittkopp et al. 2008). These predictions are at odds because transcription factors are fundamental to gene regulation and at the same time, typically pleiotropic. We tested these conflicting predictions in this study, using a bioenergetic model of gene regulation. We found that pleiotropy did indeed constrain the evolution of hybrid incompatibility to varying extents and precluded it altogether under some conditions. However, net misregulation of the F₂ hybrid phenotype was reasonably strong under a variety of intermediate bioenergetic parameter values, corresponding to a broad sweet spot of parameter combinations permitting the evolution of Bateson–Dobzhansky–Muller incompatibility.

Adaptation can occur at a pleiotropic locus when the selective advantage due to one trait is greater than the disadvantage due to pleiotropy with others (Otto 2004). This was the case in our pleiotropic model because the bioenergetic properties of molecular interactions yield sigmoid G-P maps (Figure 2), creating a nearly neutral region in the fitness landscape around the conserved trait. Parameters that steepen the fitness landscape decrease the advantage of a pleiotropic mutation relative to a cis-regulatory mutation and impose evolutionary constraint on the pleiotropic locus. These include any factors that reduce the availability of TF molecules in the region of the binding sites, particularly larger genome size, which increases E_diff, the extent that the genetic background attracts TFs away from the binding site, as well as factors that reduce N_TF, particularly the upstream regulators of TF production. The fitness landscape is also steeper if the cis–trans interaction is sensitive to mismatches (high ΔG₁) or if the environment is less tolerant to phenotypic variation (${\sigma }_{\text{s}}^2$ in the fitness function). Increased constraint on the pleiotropic TF restricted adaptive change in the directionally selected trait to its cis-regulatory locus and precluded compensatory evolution in the loci underlying the conserved trait. This constrained the evolution of F₂ hybrid incompatibility because both cis and trans sites must coevolve to produce it.

For a different reason, we also see reduced hybrid misregulation under bioenergetic parameter values that cause the G-P map and fitness landscape to become increasingly plateaued (e.g., shape a in Figure 2). Phenotypes near the upper end of such maps are insensitive to mutation, such that several mismatches are required to substantially change them. F₂ hybrids show relatively little misregulation or incompatibility, not because pleiotropy constrains divergence in the TF but simply because insensitivity of the phenotype to underlying divergence masks it. This is the case under parameter combinations where TFs are superabundant (high N_TF and low E_diff) or binding is robust to mutation (low ΔG₁, in negative magnitude), so that fractional occupancy remains high even with imperfect matching.

These parameter combinations bound a broad sweet spot where hybrid misregulation is most likely to evolve despite pleiotropy. These involve G-P maps and fitness landscapes with moderate slopes (Figure 3), produced likely (but not necessarily) by a balance of moderate background binding and moderate to high TF availability, weaker selection on conserved sites (Figure S2, B and D), smaller population sizes (Figure 3 and Figure S1), and to a lesser extent longer areas of direct interaction between TFs and their binding sites (here represented by bit length; File S1). Although it is ultimately a problem to be resolved empirically, we speculate that many pleiotropic regulatory interactions will fall within these confines.

When separate but nonrecombining domains of the TF locus regulated separate traits, incompatibility always evolved in the directionally selected trait but only at small population sizes in the conserved trait. These results do not differ from those of the simple two-locus model of Tulchinsky et al. (2014). Thus, multifunctional molecules exhibiting Paaby and Rockman’s (2013) molecular gene pleiotropy do not place significant pleiotropic evolutionary constraints on hybrid misregulation or incompatibility. More generally, Via (2009) showed that linkage within or between genes may transfer the effects of selection to a nearby hybrid incompatibility locus through genetic hitchhiking, which at the genomic level can contribute to reproductive isolation between species. However, within the relative confines of our three-locus model, this effect was minimal compared to the direct effect of functional pleiotropy at the level of individual mutations.

To what extent do additional loci under pleiotropic control increase the constraint on the evolution of hybrid incompatibility? Our experiments varying the strength of selection on the conserved trait (File S1) can provide a limited insight into the effects of adding more conserved traits. For example, following from Equation 2, doubling the baseline ${\sigma }_{\text{s}}^2$ of a single conserved trait is equivalent to adding a second trait with the same ${\sigma }_{\text{s}}^2.$ This is only an upper-bound approximation, as it does not consider the potential repercussions of compensation at multiple loci. If more than two loci require compensation, it may take fewer mutations to purge a pleiotropic TF mutation and replace it with one at the cis site of the directionally selected trait. Whether this is the case depends on the number of loci and on the availability of potentially compensatory mutations per pleiotropic mutation. That availability was equal to one in our model, but may be higher in reality (Levin et al. 2000). Regardless, Wittkopp et al. (2008) show that TF changes are often accompanied by numerous cis-regulatory changes across the sites they regulate, indicating that increasing the number of loci under pleiotropic control does not seem to prohibit TF divergence altogether.

Availability of mutations

The results of our fitness landscape experiments suggest that the constraint on substitutions at the pleiotropic TF locus is a consequence of the availability of relatively advantageous nonpleiotropic mutations and not because a pleiotropic mutation reduces fitness. Therefore, we investigated the consequences of mutational availability by manipulating the mutation rates of individual loci in the network. We found that hybrid misregulation was greatly increased if insufficient nonpleiotropic mutations were available to respond to selection (Figure 4C). Under those conditions, adaptation still occurred readily at the pleiotropic locus and was accompanied by compensatory evolution, resulting in hybrid misregulation in the conserved trait. This result demonstrates that the trans-regulatory TF locus is not constrained by the selective effect of pleiotropy directly.

Increasing the compensatory mutation rate may be expected to reduce pleiotropic constraint by allowing pleiotropic mutations to be compensated more quickly. We found this to be true to some extent; however, our results suggest that it is primarily the fixation probability of a pleiotropic mutation that drives the rate of compensatory evolution, rather than vice versa. Stronger selection on the conserved trait causes the population to tolerate less standing variation at the pleiotropic locus. This decreases the potential for compensatory evolution to occur, resulting in less hybrid misregulation (Figure S2, B and D). Increasing the compensatory mutation rate was not able to fully alleviate this effect (Figure 4B and Figure S3B), suggesting that the primary determinant of pleiotropic constraint is net fitness cost and that the availability of compensation is secondary, at least in the range of parameter values we tested. Furthermore, decreasing the availability of nonpleiotropic adaptive mutations (Figure 4C and Figure S3C) had a greater effect than increasing the availability of compensatory mutations (Figure 4B and Figure S3B). This also suggests that pleiotropic divergence is mainly constrained by the initial probability of a pleiotropic mutation reaching high frequency, rather than by the wait for compensation.

Compensation and developmental system drift

The phenomenon called “developmental system drift” (DSD) exists when the underlying genetic basis for the regulation of a phenotype differs between taxa even though the phenotype has remained (largely) unchanged since they shared a common ancestor (True and Haag 2001; Weirauch and Hughes 2010). Empirical cases of this phenomenon are found in diverse taxa (True and Haag 2001; Zinzen et al. 2009; Pavlicev and Wagner 2012), and DSD can be replicated in simulations (Haag 2007; Johnson and Porter 2007; Pavlicev and Wagner 2012; this study). Our results show that the evolution of DSD can occur under neutral drift, but is greatly facilitated by selection on a pleiotropic locus. This finding supports the “selection, pleiotropy, and compensation model” (Pavlicev and Wagner 2012) in which compensation for the pleiotropic side effects of adaptation drives DSD in the loci underlying conserved traits. Although we find that compensatory evolution may be constrained by the bioenergetics of the interacting loci, our results support the general conclusion of Johnson and Porter (2007) that directional selection on pleiotropic loci accelerates DSD.

An important lesson from the discovery of DSD is that it can obscure sources of selection and lessen the utility of candidate-gene approaches (True and Haag 2001). However, when the goal is to discover sources of hybrid incompatibility, DSD becomes a valuable tool. Because DSD and hybrid incompatibility go hand in hand, traits that exhibit DSD between related species are high-priority candidates for sources of hybrid incompatibility. Traits coregulated by upstream TFs are candidates as well and may help to identify the original source of adaptive evolution that drove regulatory divergence. If that divergence was recent enough that compensatory evolution has not caught up, misregulation in those traits may even be higher (Figure 3 and Figure S1).