Physiologically Based Pharmacokinetic Modeling and Simulation in Pediatric Drug Development

Abstract

Increased regulatory demands for pediatric drug development research have fostered interest in the use of modeling and simulation among industry and academia. Physiologically based pharmacokinetic (PBPK) modeling offers a unique modality to incorporate multiple levels of information to estimate age-specific pharmacokinetics. This tutorial will serve to provide the reader with a basic understanding of the procedural steps to developing a pediatric PBPK model and facilitate a discussion of the advantages and limitations of this modeling technique.

In 2012, the US Food and Drug Administration's (FDA) Advisory Committee for Pharmaceutical Science and Clinical Pharmacology unanimously voted to support the motion that modeling and simulation be considered for all pediatric drug development programs (14 March 2012, Gaylord National Resort & Convention Center, National Harbor, MD). During the same meeting, the committee also assessed whether the routine use of physiologically based pharmacokinetic (PBPK) modeling, when possible, be incorporated into the pediatric drug development process. Although the committee expressed concerns regarding limitations and knowledge gaps surrounding pediatric PBPK modeling (i.e., ontogeny of transporters), the motion passed with a slim majority by members who felt PBPK models offered an enhanced ability for predicting and understanding of age-related changes in pharmacokinetics (PK) among children.

Utilization of PBPK modeling among the pharmaceutical industry, as denoted by the annual publication rate, has increased steadily over the past two decades.¹ Within the drug development process, PBPK modeling has been incorporated in a variety of applications. In preclinical stages, models serve to assess the viability of candidate compounds, combining data derived in vitro with in vivo preclinical species (i.e., rat) data to provide estimates of human PK.² During clinical drug development stages, PBPK modeling can permit for efficient trial design, providing suitable starting doses and selection of optimal sampling times.³ In addition, models may be used to extend existing knowledge derived from preliminary clinical investigations into unstudied subpopulations and clinical scenarios. For example, several recent investigational new drug and new drug applications submitted to the US FDA have applied PBPK modeling techniques to estimate the impact of hepatic disease, pharmacogenomics, and drug–drug interactions on drug disposition.⁴

Based on successes of estimating PK within adult populations⁵ and the inherent ability of models to facilitate extrapolation toward different life stages, development of pediatric PBPK models appear to be a natural progression. In recent years, several publications from various research groups have demonstrated the capacity of PBPK models to deliver rational estimates of age-specific PK changes along the developmental age range.^{6,7,8,9,10,11} Additionally, use of pediatric PBPK models is increasing in frequency among sponsors, as demonstrated by the proportion of investigational new drug and new drug applications containing pediatric PBPK modeling techniques received by the US FDA between 2008 and 2013 (ref. 12). Of the 84 applications which incorporated PBPK modeling into their submissions, 21% were utilized to investigate PK among children.

In order to increase efficiencies surrounding the pediatric drug development process, the US FDA introduced the pediatric decision tree, which delineates required clinical investigations in pediatric populations in order to comply with current legislation. The framework provides a venue by which adult efficacy data can be extrapolated to pediatrics, subsequently reducing the number of children required to participate in clinical trials. In recognition that children may display developmentally unique differences in absorption, distribution, metabolism, and excretion (ADME) and resultantly exhibit variable patterns of drug sensitivity when compared to adults, the decision tree does not permit for extrapolation of PK and safety data between adults and children. As a result, clinical assessments of pediatric PK and safety are required. Considering the integral role of PK in drug efficacy, use of pediatric PBPK models can serve to integrate multiple levels of information (i.e., in vitro, preclinical, clinical, etc.) to elucidate PK changes among children and function as a complement to pediatric clinical investigations. Estimates of age-specific PK can be utilized to support dose selection and assess for the potential for concentration-related toxicities within pediatrics. This tutorial will serve to provide the reader with a basic understanding of the procedural steps to developing a pediatric PBPK model and facilitate a discussion of the advantages and limitations of this modeling technique.

Traditional Pediatric Dosing Methods

Traditional methods for estimating pediatric dosages include dosing algorithms such as Clark's rule (i.e., based on body weight (BW)), Young's rule (i.e., based on age), body surface area-based dosing (i.e., same mg/m²), and allometry (i.e., based on BW). These algorithms attempt to convert adult doses to those of children for the purposes of achieving similar exposure as a standard dose in adults. Algorithms aim to account for the effect of growth on dose but do not address the impact early childhood maturation. As a result, Clark's and Young's rules are bounded for use between 2–12 and 1–12 years of age, respectively. Allometry, the most widely evaluated and accepted dosing algorithm (Eq. 1),

uses dose as absolute (e.g., in milligrams) and the child to adult BW (in kilograms) ratio raised to a power of 3/4. Dose may be replaced with clearance (CL) in Eq. 1. The history and use of the ¾ power function has been discussed at length elsewhere.^13,14 In a study assessing CL prediction in children over the age of 6 years using allometry, 100 and 80% of all predictions were within twofold and 30% of observed CLs as taken from FDA databases.¹⁵ Considering that allometry well accounts for size, this result is unsurprising. For younger children, allometry still accounts for size; however, maturation remains unaccounted. As a result, allometry overpredicts CL below an age where the mechanisms of CL become immature.¹⁶ If, however, the purpose of the modeling exercise is to predict PK in children whose metabolic or excretory capacities are fully mature, use of allometric equations, as depicted by Eq. 1, can be utilized to provide age-specific estimates of dose and CL.

Integration of allometry with a maturation modifier on CL can be used to circumvent tendencies of conventional allometric equations (i.e., Eq. 1) to overpredict CL in younger children. Using this approach, a typical CL (CL_adult) for an adult weighing 70 kg is modified for size using allometry along with a maturation function (MF; between 0 and 1) to account for immaturity of CL processes and an organ function (OF; can be greater or less than 1) to account for disease modifications on CL.¹⁷

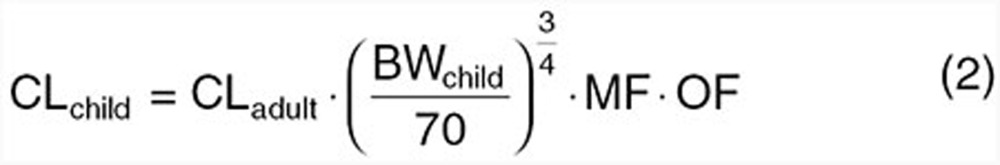To use Eq. 2, however, the MF and OF must be known or rationally predicted.

While the above scaling procedures have utility under predefined boundaries, PBPK models inherently account for both growth and maturation in a mechanistic manner and thus allow for rational extrapolation across the age continuum.

PBPK Model Description

This section will provide a brief description of whole-body PBPK modeling. For a more in-depth description of essential structural elements and theoretical concepts of PBPK modeling, the reader is directed to a previously published tutorial.²

Whole-body PBPK models strive to provide a comprehensive depiction of compound PK throughout the entire body. A general schematic depiction of the structure of such models has been illustrated in a previous tutorial.² Unlike compartmental PK models, where compartments represent the sum of kinetically similar tissues, whole-body PBPK models segregate compartments based on anatomical considerations. Models incorporate multiple compartments each representing a defined organ/tissue space. Drug movement is facilitated by assigning flow rates to each compartment reminiscent of a circulatory system. Flow is unidirectional, permitting movement of drug from the arterial pool, through the tissues, and into the venous pool. Typically, systems operate in a closed loop, permitting venous blood to be recycled back into the arterial pool via the lung. Within the model, CL (elimination or excretion) can be ascribed to any relevant tissue compartment. Commonly, the body's two main eliminatory organs, the liver and the kidneys, play predominant roles in modulating drug CL. To computationally account for CL as well as the rate of drug exchange between the blood and tissue compartments, models utilize a series of differential equations. Simulations should preserve mass balance at any given time point to ensure appropriate mathematical implementation of the model.

Distribution into tissue compartments may be defined as either perfusion-limited or permeability-limited. For smaller lipophilic compounds, distribution into compartments is typically a function of the rate of blood flow to the tissue (i.e., perfusion-limited). For larger hydrophilic molecules, distribution across tissue membranes may be restricted. In these cases, the rate of tissue diffusion can be surmised using permeability-limited kinetics.²

PBPK models provide an integrative platform for incorporating several levels of information: physicochemical, in vitro, preclinical, and clinical. These data may be used to parameterize the model and ultimately generate predictions of compound-specific PK. Parameters within the model can be defined as either system or drug specific. System-specific parameters pertain to the anatomy and physiology of the organism and include organ volume, composition, and blood flow; enzyme/transporter localization and abundance; and plasma protein concentrations. Drug-specific parameters pertain to drug physicochemical properties (i.e., lipophilicity, molecular weight, pKa, solubility, etc.) and their influence on biological binding affinity (i.e., plasma proteins, enzymes, transporters) and membrane permeability. Based on the interrelationship between system- and drug-specific parameters, tissue-to-plasma partition coefficients (K_p) and quantitative measures of specific CL pathways (i.e., intrinsic CL (CL_int)) may be derived. Owing to its physiologically based structure and parameterization, PBPK models permit for extrapolation of PK estimates between developmentally unique age groups as well as different species. As models are mechanistic, extrapolations can be conducted by modifying system-specific parameters toward the organism or age group of interest while maintaining an understanding that drug-specific parameters remain constant. Unlike empiric compartmental models, where compartments typically do not maintain a physiologic basis, PBPK models, if appropriately parameterized, can be used to derive rational predictions outside the range of data used in model development. The ability of PBPK models to extrapolate knowledge between systems is highly advantageous within the field of pediatric drug development where PK data from adults may be leveraged to provide estimates of PK alterations in children.

Pediatric PBPK Model Development Workflow

Pediatric model development begins with an examination of the relevant information available for model building and evaluation. This is greatly dependent on the timing of the pediatric clinical trial and any clinical investigation history.¹⁸ Three scenarios exist: 1, drug approved for use in adults; 2, drug candidate in phase I or phase II of clinical development; and 3, drug candidate for pediatric use only. In all scenarios, there is data available from the preclinical realm. With regard to the clinical investigation history, the most data-rich environment is the first scenario where the drug is approved for use in adults. In this case, PK information in adults is available and may be accompanied by PK data in children if investigated in an off-label manner. In the second scenario, the drug candidate has entered the clinical phase in adults, and there is limited PK data available from healthy individuals and/or an adult patient population. In the third scenario, the first clinical investigation of the drug candidate is the pediatric patient population. There is a decrease in the available information for model building and evaluation from scenarios 1 through 3.

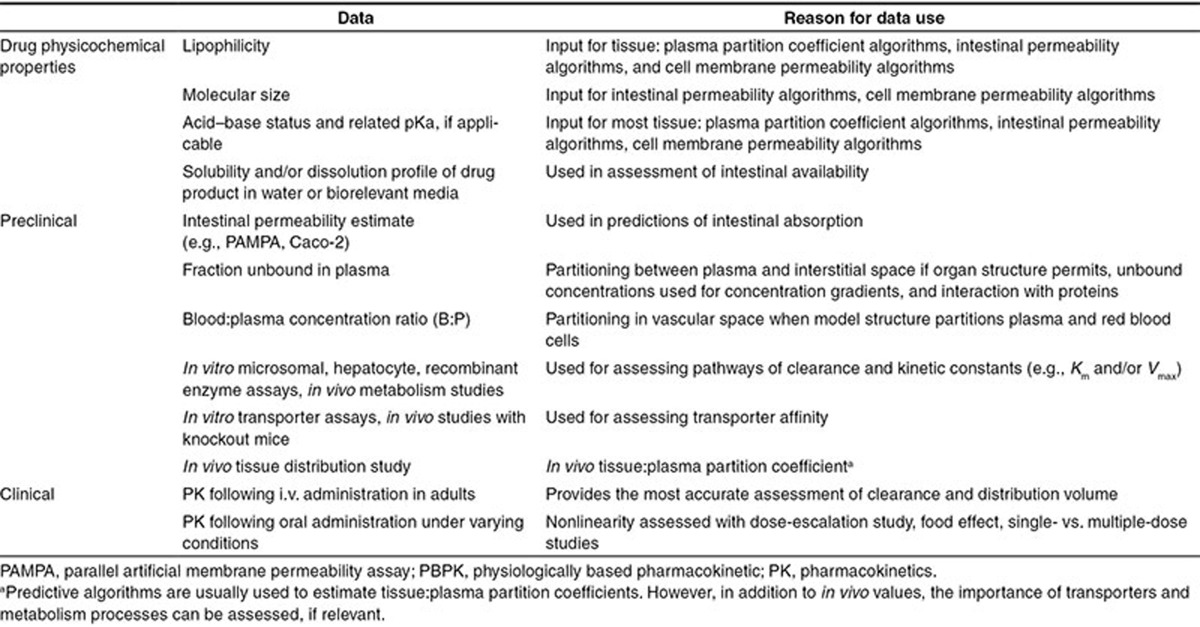
Table 1 provides a list of drug-specific data that can be used for development of the adult PBPK model in scenarios 1 and 2. The required data for PBPK model development depends on the model structure and the level of confidence that is required in the outputs of the model. Naïve predictions of drug PK in children based on drug physicochemistry and preclinical information alone (i.e., scenario 3) will yield outcomes that have a lower confidence than if model development incorporates adult clinical data.

Table 1. Typical drug-specific data needs for pediatric PBPK model development of a drug candidate in the adult clinical phase.

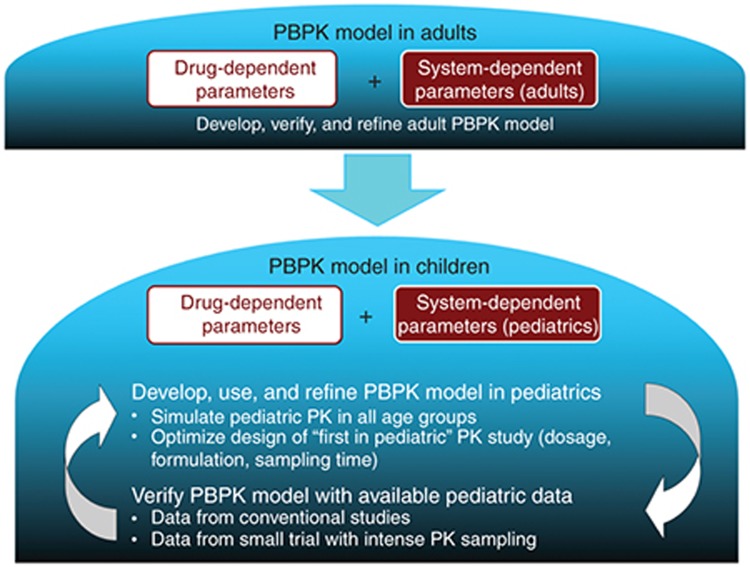
This leads to the importance of a rigorous workflow in the development of pediatric PBPK models. All published workflows^6,19 have a similar structure such that an adult model is first developed using system- and drug-specific inputs along with an iterative process of evaluation and refinement with observed adult PK data (Figure 1). Following finalization of the adult model under the relevant conditions (e.g., i.v. or oral administration), system-specific inputs are modified to children, while drug-specific inputs remain unaltered. In the absence of any pediatric PK data, models function exclusively in simulation mode, providing users with prospective estimates of age-specific PK. To maximize the probability of appropriately depicting PK among children, system-specific parameters should be defined based on the best available biological information within the literature. Since simulations require all parameters to be explicitly defined a priori, parameter selection necessitates appropriate justification. In the presence of some pediatric PK data (e.g., data in older children or sparse samples in the relevant age group from off-label use), simulation results can be evaluated against observed data. Since models are physiologically based, system-specific variables within children associated with high degrees of uncertainty may be modified, within biological plausibility, to establish appropriate fits with observed data. Using this approach, comparisons between observed data and simulated outputs can provide a platform for clarifying anatomical/physiological variables within age-specific cohorts that have not been extensively defined. The described methodology exemplifies an alternative use of PBPK models to function as a learning tool with regard to system-specific parameters.

Figure 1.

Pediatric PBPK model development workflow.¹⁹ PBPK, physiologically based pharmacokinetic.

Within the workflow, the importance of appropriate adult model development cannot be understated. Poor predictive capacity of the adult PBPK model will ensure the same in the pediatric PBPK model. This has been demonstrated using lorazepam where overprediction of the first 20 min following i.v. administration in the adult model translated to the same overprediction in the pediatric model.⁶ The importance of this mismatch is dependent on the question being addressed and may or may not be a consideration; however, low confidence in the adult model leads to low confidence in any pediatric PBPK model developed from it.

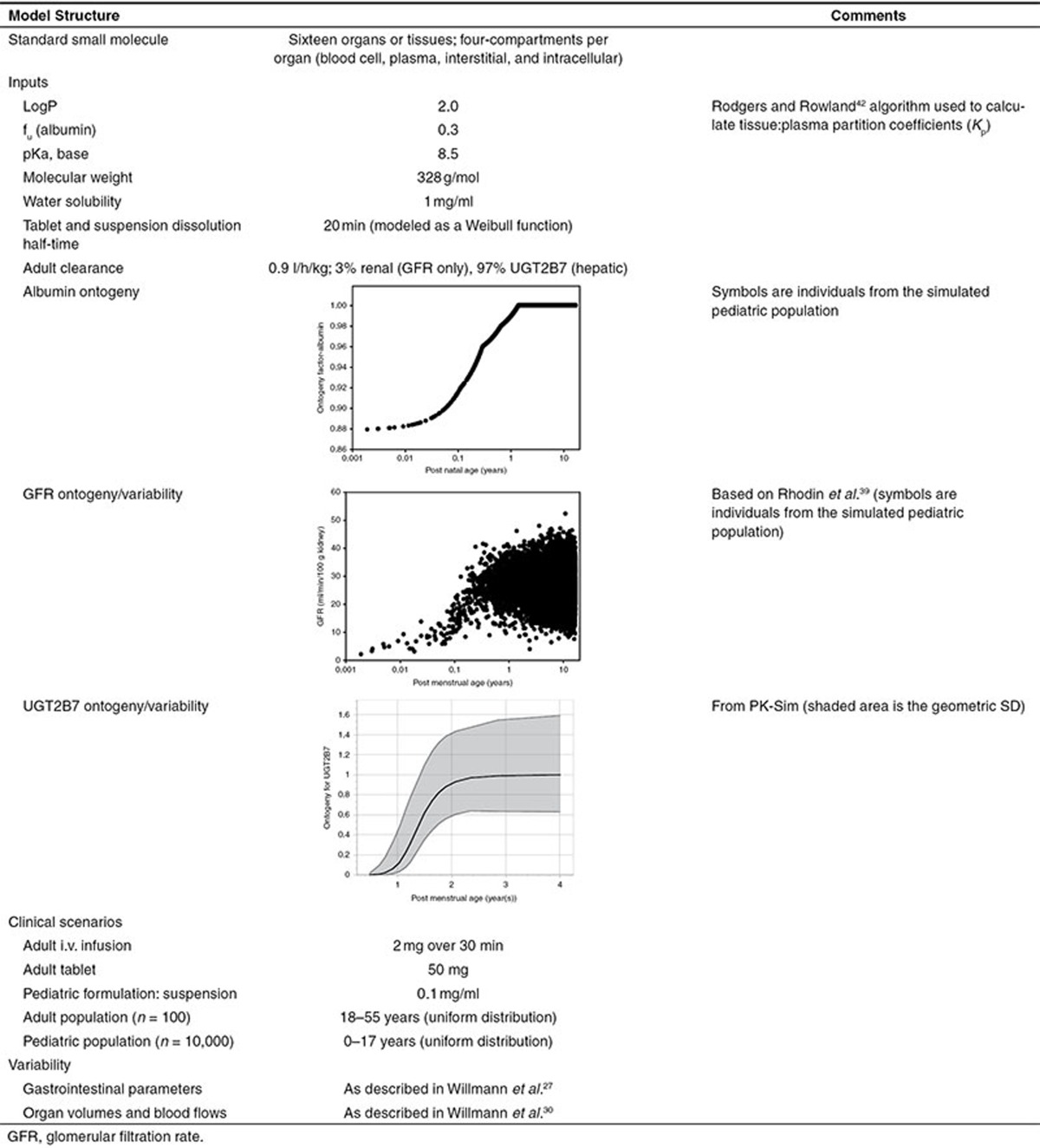
The workflow will be illustrated in the following sections with the use of an example. Despite recent interest in the utilization of PBPK models toward pharmaceutical biologics, the majority of literature regarding this modeling technique pertains to small molecules. Models for biologic compounds require additional physiologic information regarding tissue-specific lymph flows and receptor-mediated disposition. Unfortunately, such parameters lack appropriate characterization within the literature, even among adult subjects.²⁰ Consequently, development of pediatric PBPK models for biologic compounds is an area which requires ongoing investigation. The example presented within this tutorial will highlight key aspects for the development of pediatric PBPK models for small molecules. All models and simulations were completed in PK-Sim (ver 5.2; Bayer Technology Services, Leverkusen, Germany). A hypothetical small molecule will be used, and relevant information for model building is presented in Table 2. The question being addressed is: What is the pediatric equivalent dose (the dose that provides the same exposure as a standard adult dose in an adult) for a group of children aged 0–17 years?

Table 2. Inputs and clinical scenarios for the tutorial example.

Development of Adult i.v. Model

In order to establish a quantitative understanding of the in vivo processes of distribution and CL within adults, PK data depicting i.v. drug administration is typically required. By circumventing the complexities surrounding the oral absorption process, data derived from these investigations permit for clean assessments of CL and the rate and extent of distribution. Correspondingly, the development and assessment of i.v. disposition models provide a suitable basis to ensure simulations appropriately describe the processes of distribution, metabolism, and excretion within adults prior to predicting the contribution of such processes in pediatrics.

In its simplest form, the adult i.v. PBPK model may be parameterized using exclusively perfusion-limited kinetics. Based on this approximation, organs are defined as well-stirred compartments and require, at minimum, volume, blood flow, blood:plasma concentration ratio (B:P), and tissue-specific K_p values for parameterization.² Organ volume and perfusion rates are system-specific parameters pertaining to adult humans, whereas B:P and K_p values are contingent on the relationship between system- and drug-specific parameters and may be determined experimentally (i.e., in vivo) or computationally using in vitro data. Compared to experimental determination of K_p values, the use of in silico–based algorithms such as tissue composition–based models (e.g., Rodgers and Rowland²¹) or correlation models (e.g., Yun and Edginton²²) have decreased the time and cost associated in the development of whole-body PBPK models. Common input parameters incorporated into these algorithms include aspects of drug physicochemistry such as lipophilicity and pKa. In addition, tissue composition–based models require information pertaining to plasma protein binding (i.e., f_u) and organ-specific composition in terms of proportional content of lipids, protein, and tissue water.²³ It is the common practice of the authors to use the best predicting tissue composition–based model,²³ Rodgers and Rowland,²¹ as the default for new molecules. In order to define CL mechanistically, mass balance studies quantifying the fraction of drug excreted renally unchanged (fe), metabolized (fm), excreted via the biliary system (fb), and/or removed by other less-common pathways of CL are required.

Within the model, organ-specific CLs may be described using either first-order intrinsic CLs (CL_int) or, if nonlinearities are present, using V_max and K_m values to denote capacity-limited kinetics (i.e., Michaelis–Menten). CL_int, defined as the tissue-specific drug removal capacity (per gram of tissue) in absence of binding and flow limitations, can be approximated using a constant value (i.e., CL_int ≈ V_max/K_m) at concentrations well below the saturation capacity. Estimation of hepatic CL_int within the adult model can be conducted using two techniques. In vitro to in vivo correlations provides estimates of CL_int based on in vitro assays using human liver microsomes, human hepatocytes, or recombinantly expressed enzymes.²⁴ Estimates of in vivo CL_int using recombinantly expressed enzyme systems can be tabulated based on the following equation²⁴:

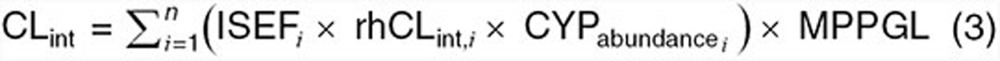where, ISEF_i is the intersystem extrapolation factor, rhCL_int,i is the isozyme-specific CL_int determined within recombinant-based systems, CYP_abundence is the isozyme abundance, and MPPGL is the milligrams of microsomal protein per gram of liver. Using the above equation, in vitro determinations of isozyme-specific CL_int can be combined with system-specific information pertaining to CYP-specific abundance and MPPGL to provide estimates of hepatic CL_int in adults. An alternate approach for estimating hepatic CL_int, which can also be applied to any eliminatory tissue, utilizes the mechanistic framework of PBPK models along with PK data from mass balance studies. Using this approach, tissue-specific CL_int values are initially parameterized within the adult PBPK model using a default value. Simulations are subsequently conducted and outputs in terms of CL devoted to specific pathways (i.e., CL_renal, CL_hepatic) are compared to data from in vivo mass balance investigations. Based on the discrepancy between simulated results and in vivo values, tissue-specific CL_int values within the model are modified until simulated outputs reflect observed PK data. One area of contention with regard to this approach is its lack of specificity for quantifying CL_int for tissues which exhibit high drug-specific extraction ratios. CL values for tissues with highly efficient drug removal capacities approximate a maximum value, the tissue perfusion rate. Consequently, use of the latter approach would not provide definitive estimates for such tissues, since CL_int values ranging from a predefined lower limit to infinity would simulate CLs that approximate tissue blood flow.

Parameterization of CL_int for tissues employing nonenzymatic processes utilize in vivo PK data, as previously described. For renal excretion, drug elimination may transpire as a result to three competing processes: glomerular filtration, tubular reabsorption (TR), and tubular secretion (TS). As an approximation, drugs exhibiting renal CLs less than (or equal to) the product of glomerular filtration rate (GFR) and fraction unbound in adults (i.e., CL_R ≤ GFR_(adult) × f_u(adult)) are denoted to be excreted through the combined effects of glomerular filtration and TR. In contrast, when CL_R > GFR_(adult) × f_u(adult), drug elimination is a composite of both glomerular filtration and TS. For drugs excreted via glomerular filtration and TR, quantitation of intrinsic CL due to glomerular filtration (CL_int,GF) and fractional tubular reabsorption (f_TR) is required. CL_int,GF can be estimated as GFR_adult/Kidney Mass_adult where GFR_adult represents the GFR denoted in vivo (i.e., 120 ml/min). Estimation of f_TR is conducted by comparing model-based simulations to observed data from mass balance studies. Simulations are parameterized using a default value for f_TR along with other adjunctive tissue-specific CL_int values, including the aforementioned CL_int,GF. Model outputs are then compared to in vivo PK data sets, and f_TR is modified until simulated results align with observed renal excretion values (i.e., f_e). For drugs excreted via a combination of glomerular filtration and TS, estimation of both CL_int,GF and CL_int,TS is required. CL_int,GF can be estimated as depicted above. Estimation of Cl_int,TS also follows a simulation-based methodology as described previously. In such cases, simulations are initially parameterized using a default value for CL_int,TS along with other tissue-specific CL_int values including CL_int,GF. Unless in vivo information capable of quantifying the contribution of TR is available (i.e., mass balance studies conducted in conjunction with TS inhibition), f_TR is assigned a value of 0, indicating that drug does not undergo TR. Simulations are utilized to refine CL_int,TS estimates until model outputs reflect observed renal excretion values (i.e., f_e). Although different modalities for CL determination have been described, regardless of what method is applied, simulated results should approximate the contribution of each CL pathway noted within in vivo mass balance studies.

To provide initial estimates of i.v. drug disposition, a naïve adult PBPK model is constructed based on the above-mentioned parameters including drug-specific inputs, quantitative measures of CL, and fraction protein binding (f_u) (Table 2). Preliminary comparisons between observed data sets, depicting mean concentration–time estimates from several subjects, and PBPK simulations can be approximated by parameterizing the model toward the demographics of the average subject within the specific in vivo study. Using this approach, models are additionally parameterized using logistic parameters such as dose, duration of infusion, and length of sampling interval from the in vivo investigation.

Evaluation of model performance is discussed in a forthcoming section but can, in part, be ascertained by superimposing mean observed data onto the simulation results (i.e., plasma- or tissue-specific concentration time data). To ensure that the model encapsulates intricacies depicted in vivo, assessment of the simulations' ability to replicate the general trends within the observed concentration–time curves (i.e., bumps, valleys, peaks, etc.) is conducted. At this point, visual predictive inspections of curve shape provide the most important determinant of the model's capacity to describe the rate and extent of distribution in vivo.

Model Evaluation

Evaluation of the predictive performance of PBPK modeling techniques is an area that lacks consistency within the literature. Most assessments of PBPK model-predictive performance primarily focus on the discrepancy between model-derived outputs and independent observed PK data sets.^5,9,11 For estimating PK measures such as AUC, C_max, t_max, and k_e, a variety of metrics including absolute average fold error (AAFE), root mean squared error (RMSE), mean ratio_(obs/pred), and proportion of estimates falling within a specified fold-error (i.e. 2-fold, 3-fold etc.), have been utilized.^5,9,11 Metrics used to assess the predictive performance of model estimated concentration-time values also vary considerably and include the use of qualitative visual predictive checks (VPC)¹¹ and quantitative discrepancy indexes such as mean relative deviation²⁵ and median absolute percentage error.⁹ Though frequently utilized to assess the validity of model structure and parameterization, comparisons between model predictions and external PK data sets should represent only one facet of PBPK model evaluation. A more holistic approach for model evaluation has been proposed.²⁶ The method establishes a level of confidence in PBPK models directed toward their end use (i.e., fit for purpose) and assesses three fundamental aspects: biological basis, reliability in terms of uncertainty/sensitivity analyses, and comparison of simulations with observed data.

Evaluation of the biological basis of the model assesses fidelity of model structure and parameters. In order to establish confidence in model outputs, PBPK model structure and parameterization should demonstrate biologically plausibility. For example, in whole-body PBPK models, organ perfusion rates should sum to a biologically rational estimate of cardiac output within the organism. Evaluations of model reliability are based on appropriate uncertainty and sensitivity analyses. Uncertainty analyses focus on the spread or distribution of simulated outputs due to the ambiguity surrounding input parameters and model structure. For sensitivity analyses, the emphasis is shifted toward quantitatively describing the influence of model parameters on simulated outputs. Uncertainty analysis can be conducted in an iterative manner by incorporating the potential range of ambiguous parameter values into simulations. The level of uncertainty is then determined based on the ratio of the 95th percentile to the median value for the selected dose metric (i.e., AUC, C_max, etc). Quantitative measures of sensitivity can be attained by varying individual model parameters by 1% and evaluating the impact on simulated outputs.²⁷ Based on the relationship between uncertainty and sensitivity, inferences regarding model reliability can be attained. For example, models possessing parameters with high uncertainty and high sensitivity can be defined as having low reliability. In contrast, models possessing parameters with either low uncertainty or low sensitivity are considered to have a high reliability. The final aspect of evaluating model-predictive performance is the comparison of model simulations with observed data. As described previously, a variety of approaches have been utilized for this purpose including visual predictive checks and quantitative discrepancy indexes. Although qualitative in nature, visual predictive checks can be utilized to instill confidence in the model by ensuring that simulations replicate the general trends (i.e., peaks, bumps, and valleys) present within the data. In addition, inspection of diagnostic plots of residuals can be useful for detection of systematic model errors. Summative discrepancy indexes provide quantitative measures of the average difference between simulated and observed data and can provide a basis for parameter optimization or selection of one model over another. The ability of models to reproduce independent observed data sets, not used in the model-building process, is typically considered the standard comparative measure of model fit, though consideration of in vivo variability associated with observed data is also imperative. Due to intra- and interindividual variation along with small sample sizes, data derived experimentally tends to encompass innate variability. In acknowledgment of this, a common practice is to empirically denote models exhibiting mean estimates falling within twofold error from observed PK data as acceptable.²⁶ An alternative approach which utilizes the mechanistic nature of PBPK models is the incorporation of population-based simulations (Pop-PBPK).^10,24,27 Pop-PBPK simulations provide a rational framework to account for biological variables known to impart PK variation among a population. As such, simulations permit for a priori estimates of the magnitude of in vivo PK variability to be generated. Assessments of model performance using Pop-PBPK techniques may be achieved by examining the proportion of observed data falling within a 90% prediction interval of simulated results.¹⁰

Benchmark values addressing questions such as “What fold error between observed and model-predicted values is appropriate?” or “What proportion of observed data should fall within a specified interval using Pop-PBPK models?” have not yet been defined within the context of pediatrics. One approach is to transpose the frequently utilized twofold error metric from adults into pediatric-based simulations.²⁸ Since this approach is empiric in nature, its use within vulnerable populations such as pediatrics should be contemplated on a case-specific basis and should include consideration the model's end use and the pharmacologic moiety. For example, models designed to inform optimal first dosages within pediatrics or models devoted to compounds known to exhibit narrow therapeutic indexes in adults may require more restrictive benchmark values compared to the empirically based approach.

Workflow for Model Refinement

Model refinement is necessary when simulated profiles fail to follow observed profile trends. All inputs are available for refinement; however, only those with high uncertainty should be modified and then, only within a reasonable range of biological plausibility.

Reasons for a lack of fit with regard to profile shape include, but are not limited to:

1. Undefined or poorly defined transporter activity

2. Tissue: plasma partition coefficients ill defined due to uncertainty in algorithm inputs (e.g., lipophilicity, f_u) or algorithms not applicable to drug–organ interaction (e.g., specific unaccounted binding within an organ as algorithms assume reversible binding)

3. Presence of enterohepatic recirculation that was not incorporated

4. CL modeled as first-order process(es) but enzyme saturation affects profile shape

5. Structural deficiencies such as compartments modeled as well stirred where organ uptake is actually permeability rate limited. Other structural deficiencies include the assumption of well-stirred organs for highly bound compounds where plasma and interstitial space must be separately defined within the model.

Prior knowledge is used to inform the choice of inputs that are available for refinement. An investigators brochure, published literature, and/or grey literature may be used for this selection. A hypothesis testing process ensues which can yield valuable information about the importance of structural (e.g., separation of organ compartments) components and/or can be used to determine the value of uncertain inputs if outcomes are sensitive (e.g., gastric emptying time in a fed state). Some common refinements include lipophilicity (i.e., for K_p and/or permeability refinement), addition of permeability surface area products for defining organs as permeability rate limited, and the addition of transporter activity. Regardless of the refinement made, biological plausibility should be maintained, justification should be provided, and assumptions should be stated. Model refinement may be completed throughout the adult PBPK model development process, and the final adult PBPK structure and drug-specific inputs are held constant in pediatric PBPK model creation.

Development of Adult i.v. Population Model

In addition to providing mean estimates of drug disposition, PBPK modeling techniques can be extended to provide estimates of PK variability within a population. Characterization of the breadth of interindividual PK variability along with relevant covariates within the population is essential to multiple disciplines including clinicians, drug developers, and regulatory organizations. Depending on the magnitude of PK variations induced by the presence of particular covariates, altered dosages or drug avoidance may be suggested.²⁹ Population-based assessments provide a platform for identifying influential covariates and may be conducted in either a top-down or bottom-up approach.

Top-down approaches, such as population PK (Pop-PK) models, are data driven requiring PK data from large groups of diverse subjects. In contrast, bottom-up approaches such as Pop-PBPK models permit for a priori identification of potential covariates in the absence of in vivo data. Such models leverage existing knowledge pertaining to the relationship between patient-specific physiology and anatomy with drug ADME, thereby allowing for estimation of intersubject variability.²⁴ To facilitate this assessment, Pop-PBPK models incorporate virtual populations into their framework. Virtual populations attempt to encompass the biological diversity present among in vivo subjects.^30,31 For example, the algorithm proposed by Willmann et al.³⁰ incorporates demographic databases, such as the National Health and Nutrition Examination Survey III study, to create virtual subjects based on predefined parameters such as race, age, and gender. Virtual subjects are developed based on correlations between the aforementioned parameters and demographic data such as height and weight.

To facilitate PK assessments using whole-body PBPK models, virtual subjects require implicit descriptions of physiology and anatomy (i.e., system-specific parameters) including organ weights, relative blood flows, and in the case of absorption models, gastrointestinal transit rates. Algorithms used in virtual population creation introduce stochastic variation into the parameter selection process, providing a basis of interindividual variability among the population. As a result, each virtual subject is defined by a complete set of unique system-specific parameters. Stochastic variation may be introduced to several parameters including, but not limited to, organ volumes and blood flows, plasma protein concentrations, glomerular filtration, and enzyme/transporter concentrations. Stochastic parameter selection is typically facilitated by a Monte Carlo process incorporating known distributions (i.e., uniform, log-normal, and normal) of variability surrounding each parameter. Generated subjects can be further restricted by specifying anthropometric (i.e. weight, height, and BMI) ranges of interest, permitting for assessment of PK variability within specific subgroups.³⁰ This information can serve to identify potentially vulnerable segments of the population or those who may exhibit poor responsiveness.

In the context of facilitating prospective development of pediatric PBPK models, creation and assessment of adult population i.v. models allow investigators to establish confidence based on an understanding of PK variability in adults. Unlike the mean adult i.v. model, where assessments focus on comparisons to averaged PK data sets, assessments of Pop-PBPK models require PK data that reflect the extent of in vivo variability (i.e., individual data or mean ± SD). Models are developed using logistic parameters (i.e., dose, infusion rate, etc.) from observed i.v. studies. Drug-specific parameters from the finalized mean adult i.v. model are maintained. Virtual populations based on the demographics (i.e., race, age, and gender) of subjects examined within in vivo investigations describe system-specific parameters. Model evaluation is conducted using a similar approach as discussed previously but with an increased emphasis on variability. Based on simulations from the virtual population, a 90% prediction interval can be constructed. Favorable assessments are based on 90% of data points from individual subjects being within the 90% prediction interval. It is the authors' standard practice to accept 80–90% since residual variability is not implicitly input into the model. Depending on PK data available for model evaluation, alternative assessments of model performance may be applied. For example, assessment of the extent to which observed data expressed as mean ± SD corresponds with simulated results. If simulations fail to appropriately reflect observed data, model refinement may be considered. In the context of Pop-PBPK models, refinement focuses on distribution type and variance of parameters. Model refinement with regard to i.v. Pop-PBPK models offer an opportunity to examine the effects of CL and distribution variability in the absence of absorption, a notoriously variable process. An additional point for consideration is the use of individual simulations based on an average subject to refine central estimates of model parameters. Once population influences are incorporated, it is not unusual to see mean curves deviate from the finalized i.v. simulation pertaining to the average subject as log-normally distributed inputs within the population tend to pull means either way.

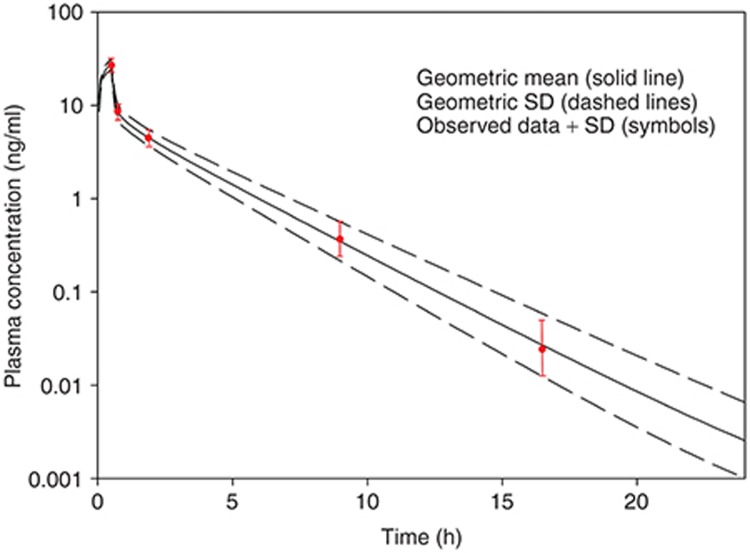
Figure 2 presents the geometric mean plasma concentration vs. time profile along with the SD of a simulation of 100 virtual adults administered 2 mg of a hypothetical drug over a 30-min i.v. infusion. “Observed data” has been overlaid onto the simulated data. The mean and SD are acceptably simulated by the model which allows for continuation to the oral model.

Figure 2.

Simulated (lines) and observed (symbols) plasma concentrations of a hypothetical drug administered as a 30-min i.v. infusion of 2 mg to an adult population.

Development of the Oral Adult PBPK Model

Integration of mechanistic oral absorption models into the aforementioned modeling framework has increased the applicability of PBPK simulations toward a wider variety of pharmaceutical formulations. Simulation of oral absorption requires a quantitative understanding of not only the processes governing absorption but also the processes of distribution, metabolism, and excretion. Based on the previously developed i.v. disposition model, the latter three processes were addressed, subsequently providing a suitable venue to assess the process of absorption in isolation. In this regard, PBPK simulations of adult oral absorption can be conducted by maintaining previously established drug- and systemic-specific parameters from the finalized i.v. model.

To facilitate a priori predictions of oral absorption, most commercially available modeling platforms (i.e., Gastroplus, PK-Sim, and SimCyp) utilize a multicompartmental approach, as originally described by Yu et al.³² These models depict the gastrointestinal lumen as a series of compartments, each representing a defined physiologic segment and include the stomach, duodenum, jejunum, ileum, cecum, and colon. Drug movement between compartments is facilitated via linear transfer kinetics. Compartmental pH values, fluid volumes, transit rates, and surface areas are ascribed based on regional specific (i.e., jejunum vs. ileum) anatomic/physiologic values. Within each compartment, drug may persist in several forms including unreleased, undissolved, dissolved, degraded, metabolized, and absorbed.³³ With the inclusion of empiric as well as mechanistic dissolution functions, models are able to simulate a variety of drug release profiles. Unless contrary evidence suggests otherwise, absorption of dissolved drug is typically assumed to transpire via passive absorption.² Estimates of effective intestinal permeability can be attained using a variety of approaches including in vivo–based perfusion systems (i.e., Loc-I-Gut), in vitro–based assays (i.e., PAMPA, Caco-2), or in silico algorithms which provide estimates based on compound physicochemistry.³⁴ Models can also include phenomena such as luminal degradation by including compartment-specific degradation rate constants.³³ Lastly, with the addition of enterocytic compartments adjacent to the aforementioned luminal compartments, models can incorporate processes such as gut metabolism and active transport (influx/efflux) provided data regarding regional distribution of intestinal enzymes and transporters are available.

Simulation of oral drug disposition for an average study subject may be generated by integrating a mechanistic oral absorption model into the PBPK modeling framework. Parameters obtained from the finalized i.v. disposition model should be maintained within the simulation, while parameters pertaining the oral absorption model should be modified to reflect the gastrointestinal anatomy/physiology of an average adult subject. Oral simulation results (i.e., plasma concentration–time profiles) can then be compared to in vivo data sets depicting mean absorption profiles using the previously suggested evaluation criteria. Due to the inherent biological complexity of the oral absorption process, mismatches between model-predicted and observed data may occur for several reasons. These deviations can be attributed, but not limited to, inadequate parameterization of active transport, gut wall metabolism, luminal degradation, and gastrointestinal transit; complexation of drug with nutrient components such as calcium and iron; inaccurate predictions of solubility and intestinal permeability; and mismatches between in vitro and in vivo disintegration/dissolution rates. In order to address the discrepancy between model-generated estimates and observed data, parameters pertaining to the oral absorption model may be modified based on compelling evidence. Using this approach, observed data is utilized to optimize the model provided a rational basis for parameter refinement can be justified and parameters are maintained within the realm of biological plausibility. Following model refinement, if required, the finalized adult oral absorption model is attained.

In order to provide an assessment of intersubject PK variability associated with oral drug delivery, Pop-PBPK oral simulations can be conducted. In addition to the previously discussed variability incorporated within the whole-body PBPK model, these simulations impart additional variation around oral absorption parameters. These parameters include luminal pH; gastrointestinal transit (i.e., small intestinal transit time, gastric emptying time); intestinal radius, length, and effective surface area; and expression levels of intestinal enzymes and transporters. Evaluation of the Pop-PBPK oral absorption model may be conducted using a similar approach as described in previous sections. Simulations which accurately depict observed data under a variety of dosing scenarios including different dietary states (fed, fasted), formulations, and doses (nonlinearities) increase confidence in the model structure and parameterization.

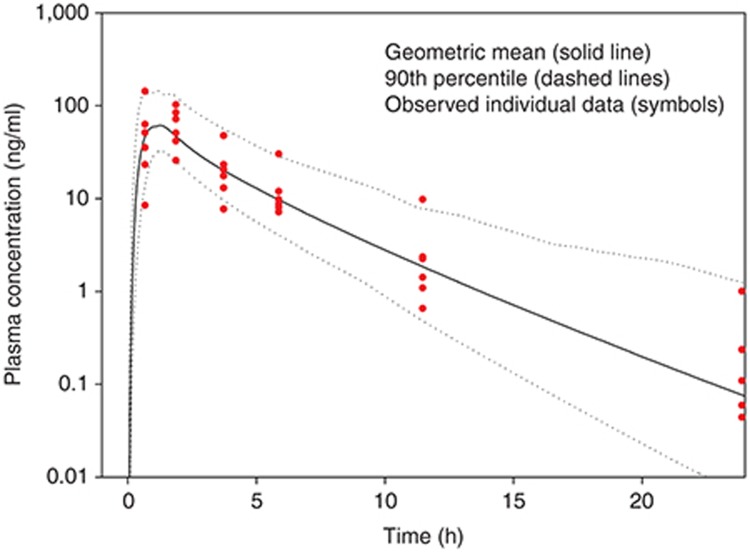
Figure 3 presents the geometric mean and 90th percentile of plasma concentrations following administration of a 50 mg tablet in the same virtual individuals as were used in the i.v. simulations. Eighty-six percent of the individual plasma concentrations are within the simulated 90th percentile and curve shape was well described. As a result, this constituted the final adult PBPK model and was deemed sufficient for the purposes of scaling to pediatrics.

Figure 3.

Simulated (lines) and observed (symbols) plasma concentrations of a hypothetical drug administered orally as a 50 mg tablet to an adult population. Eighty-six percent of all individual (n = 6) observed data points are within the simulated 90th percentile.

Development of Pediatric PBPK Models

As depicted within the presented workflow, formation of pediatric PBPK models follows adult model development and evaluation. This retrograde approach ensures investigators establish a firm understanding of ADME in adults, a relatively homogenous cohort, before extrapolating findings toward developmentally diverse pediatric age groups. In cases where the developed PBPK model does not display appropriate agreement with adult PK data, subsequent development of pediatric models is cautioned as misconceptions depicted within the adult model are likely to be mirrored in pediatrics. By ensuring adult models adequately reflect observed PK data, the workflow provides an appropriate framework by which preexisting PK data from adults can be leveraged for the purposes of pediatric model development.

Development of pediatric PBPK models following appropriate adult model characterization entails several assumptions which should be stated. First, pathways of CL between adults and children are similar. For example, if drug metabolism is modulated exclusively by CYP3A4 and CYP2D6 in adults, both isozymes will be exclusively responsible for drug metabolism in children. Second, PBPK model structure is similar to adults. Preterm neonates displaying significant arterial shunting due to the presence of a patent ductus arteriosus may preclude this assumption. Third, ontogeny factors are based on healthy subjects and do not incorporate any disease-specific changes. Disease modifiers can be included if known. Finally, unless knowledge indicating that variability is a function of age, variability in terms of anatomy, physiology, and biochemistry are considered to be similar between adults and children.

To facilitate predictions of pediatric drug disposition, the workflow exploits the mechanistic nature of PBPK models to establish a rational basis for scaling developed adult simulations toward children. Scaled pediatric models are developed based on an understanding that drug-specific parameters remain constant, whereas system-specific parameters, defining age-dependent anatomy, physiology, and biochemistry, change. Pediatric anatomic values (i.e., organ weights) are derived from databases published by organizations such as the International Committee on Radiological Protection.³⁵ Physiological values such as organ blood flows are typically ascribed assuming a similar proportion of cardiac output as denoted in adults though parameterization could also be informed using in vivo pediatric data.^7,25 Tissue composition (i.e., % interstitial, % intracellular, and % vascular) is commonly considered similar between adults and children for most organs with the exception of adipose and muscle tissue, where neonates and infants are denoted to have higher proportions of interstitial space.^7,25 Tissue composition–based algorithms can account for altered tissue compositions and are typically utilized to estimate pediatric-specific K_p values. In order to effectively parameterize the oral absorption model, information characterizing age-dependent changes in gastrointestinal anatomy and physiology including pH, luminal fluid composition, intestinal fluid volume, gut surface area and length, transit times, and enzyme/transporter localization and abundance is required. Unfortunately, many of these parameters have yet to be fully elucidated within pediatrics. Where information gaps lie, assumptions regarding the oral absorption process within children are required. Assumptions characterizing similarities between pediatric and adult oral absorption parameters may be utilized, where appropriate, but should be explicitly stated within the model description. Estimates of the proportion of drug-plasma protein binding in children can be derived from adult values based on knowledge of age-specific changes in plasma protein concentrations. Plasma proteins responsible for the majority of drug binding in humans, albumin and α-1-acid glycoprotein, are present in lower concentrations at birth relative to adult values. Quantitative equations characterizing age-dependent concentrations of binding protein have been reported by McNamara and Alcorn³⁶ and can be incorporated to compute fraction unbound within the pediatric PBPK model. Information regarding transporter-mediated drug disposition in terms of tissue-specific transporter abundance and ontogeny of specific transporter systems is currently limited. Correspondingly, scaling of adult models utilizing transporter-mediated processes toward pediatrics should be conducted using up-to-date literature resources with assumptions being implicitly stated. Provided sufficient information is available, relative transporter activity expressed in the form of CL_int may be scaled from adults toward pediatrics using age-dependent protein concentration or activity levels.

CL is chiefly responsible for modulating in vivo drug exposure (i.e., AUC) and, as such, requires careful consideration in terms of scaling toward children. For parameterization of pediatric PBPK models, a variety of CL scaling methods have been purported. Allometry has been widely utilized for this purpose but, as previously discussed, fails to account for maturational processes. As such, use of allometry should be restricted for scaling toward pediatric age groups where the eliminatory processes responsible for drug removal have reached full maturation.¹⁵ Within the pediatric PBPK model development process, allometric principles are innately incorporated since PBPK models define organ size/volume using age-dependent relationships. Assuming adult CL_int values, defined as the tissue-specific drug removal capacity (per gram of tissue) in absence of binding and flow limitations, remain constant within children is conceptually similar to allometric CL scaling, as presented in Eq. 1. As such, this approach assumes alterations in CL between adults and children are solely attributed to differences in organ size (i.e., growth).

Physiology-based CL scaling techniques account for differences between adults and children in terms of biochemistry, anatomy, and physiology. As a result, these approaches account for both changes in growth and maturation of CL mechanisms and may be utilized to estimate CL in neonates and infants, where eliminatory pathways are typically immature. Compared to allometry, physiology-based CL scaling is computationally complex, requiring predefined knowledge of the contribution of each specific CL pathway in adults as well as quantitative information regarding the pathway ontogeny. For compounds where hepatic metabolism plays a significant role, pediatric CL_int (per gram of tissue) can be estimated from adult values using the following equation³⁷:

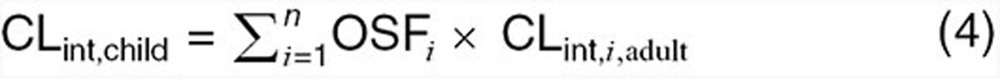where OSF_I is the isozyme-specific ontogeny scaling factor and CL_int,i,adult is the isoenzyme-specific intrinsic CL (per gram of tissue) as denoted in adults. OSF(s) quantitatively describe age-dependent maturational changes, relative to adult values, in enzyme expression or activity per unit of hepatic tissue. Scaling factors are a function of both age and the specific enzyme system responsible for metabolism.^37,38 As denoted in the previous equation, incorporation of maturational functions such as OSF(s) inherently require quantitative CL information regarding the contribution of each specific isozyme in adults. Such data, as derived from in vivo mass balance studies or in vitro metabolic assays, provides a rational basis for proportioning hepatic CL_int into isozyme-specific CL_int values. This process is essential for scaling of adult hepatic CL_int toward children as isozyme ontogeny typically differ from one another with regard to time to reach adult functional levels.

For compounds where renal processes (i.e., glomerular filtration or secretion) play a significant role in total elimination, maturation of renal function must be considered in order to adequately estimate CL in children. When the combined effects of glomerular filtration and TR represent the principle mechanisms of renal elimination in adults (i.e., CL_R ≤ GFR_(adult) × f_u(adult)), pediatric CL_int due to glomerular filtration (i.e., CL_{int,GF(child)}) can be estimated based on developmental changes in GFR as depicted below³⁸:

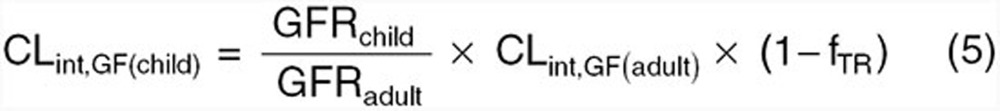where GFR_child and GFR_adult are age-specific GFRs in the children and adults, respectively, CL_{int,GF(adult)} is the intrinsic CL attributable to glomerular filtration in adults, and f_TR is the fractional tubular reabsorption. Quantitative equations describing age-dependent alterations in GFR have been previously published ^39,40 and can incorporated into the above equation. Rhodin et al.³⁹ is the most comprehensive and is suggested by the authors. Since information pertaining to the ontogeny of tubular reabsorption has not been explicitly explored, f_TR values, as determined in adults, are assumed to remain similar in children. If tubular secretion contributes to renal elimination within adults (i.e., CL_R > GFR_(adult) × f_u(adult)), estimation of pediatric renal CL will require scaling of both glomerular filtration and tubular secretion. Scaling of CL_int attributable to tubular secretion toward pediatrics can be conducted using the following equation³⁸:

where TS_child and TS_adult are age-specific tubular secretions rates in the children and adults, respectively, and Cl_{int,TS(adult)} is the intrinsic CL attributable to tubular secretion in adults. Age-dependent estimates of functional tubular secretion (i.e., TS_child and TS_adult) using, for example, the equations published by Hayton⁴⁰ can be incorporated within the above equation to derive pediatric-specific CL_int,TS values. If, however, quantitative information denoting the CL_int (or V_max and K_m) and ontogeny of the specific transporter systems responsible for TS are available, age-dependent effects of transporter-mediated drug disposition can be determined using the equations previously described for scaling of hepatic processes.

By considering the aforementioned ontological changes to anatomy, physiology, and biochemistry, pediatric PBPK models capable of assessing the impact of growth and maturation on drug PK can be developed. For compounds where systemic exposure serves as a surrogate marker of drug effect, assessment of PK alterations within the plasma may suffice. However, for compounds whose effects are mediated via tissue-specific exposure or complex drug–receptor interactions, pharmacodynamic (PD) models can be integrated within whole-body PBPK simulations. Use of integrated PBPK-PD models provides investigators with a system to explore the impact of maturational changes in both PK and PD on the efficacy of drug treatment. For the purpose of this tutorial, it is assumed both adults and children exhibit a similar exposure–response relationship. As such, estimates of plasma exposure (i.e., AUC) were deemed as appropriate measures of drug efficacy for all age groups.

Using a similar procedure as described for adults, virtual populations of various pediatric age ranges can be created to provide assessments of age-specific drug disposition (i.e., Pop-PBPK). Additionally, simulations can be utilized to explore age dependencies of key PK indices such as C_max, T_max, or AUC. If PK data depicting drug administration to children exists, evaluation of model performance may be conducted as described in previous sections pertaining to adult models. Since the pediatric age range encompasses several developmentally distinct age groups (i.e., neonate, infant, toddler, preschool child, school-aged child, and adolescent), evaluation of model performance is typically segmented accordingly. If simulations do not display appropriate agreement with observed PK data, model refinement using a similar modality as described for adult models may be considered. In addition, advanced techniques such as Markov chain Monte Carlo simulations can be employed to refine input parameter distributions using experimental data from pediatric subjects.⁴¹ Due to the prominence of functional immaturities concerning several eliminatory pathways, members of the youngest cohorts (i.e., neonates and infants) commonly display unique age-specific alterations in drug PK when compared to older children. As such, models which establish appropriate fits within older children do not necessarily provide insight into said model's ability to facilitate depictions of PK in progressively younger age groups.

Presentation of Results

The choice of how to present the simulation data is greatly dependent on the question being addressed. Leong et al.¹⁹ presents the application of pediatric PBPK models that were submitted to FDA between 2008 and 2011. Dose predictions, clinical trial design optimization, facilitation of covariate analysis (e.g., What patient-specific data should be collected during the clinical investigation?), and quantification of enzyme ontogeny for a benchmark drug are examples of pediatric PBPK model applications.¹⁹ As a consequence of these diverse applications, the presentation of results is greatly varied, and only a handful will be presented here.

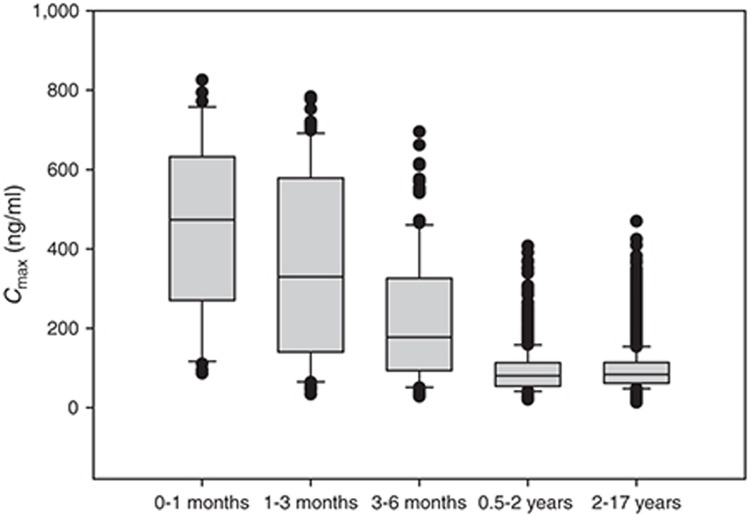
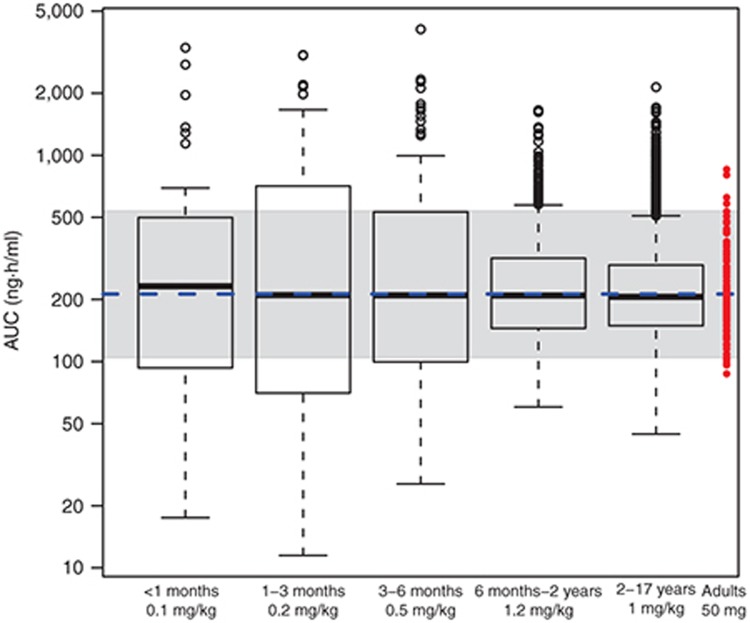
Figure 4 displays box plots of age vs. C_max as derived from 10,000 virtual children administered a 1 mg/kg dose of a hypothetical drug formulated as a pediatric suspension (0.1 mg/ml; Table 2). Other informative plots include body weight vs. exposure as a continuous function (Figure 5) or box plots for assessing dosing cohorts (e.g., by BMI, weight, age, sex, genotype, or any combination of these; Figure 6). The R-code and example data sets used for building Figure 6 can be found in the Supplementary Material.

Figure 4.

A box whisker plot of the maximum concentration (C_max) vs. age class for a hypothetical drug administered orally as a 1 mg/kg dose formulated as a suspension (0.1 mg/ml) to a pediatric population (n = 10,000; ages 0–17 years). The boundaries of the box indicate the 25th and 75th percentile with the line representing the median. Error bars indicate the 90th and 10th percentiles, and the symbols indicate outliers.

Figure 5.

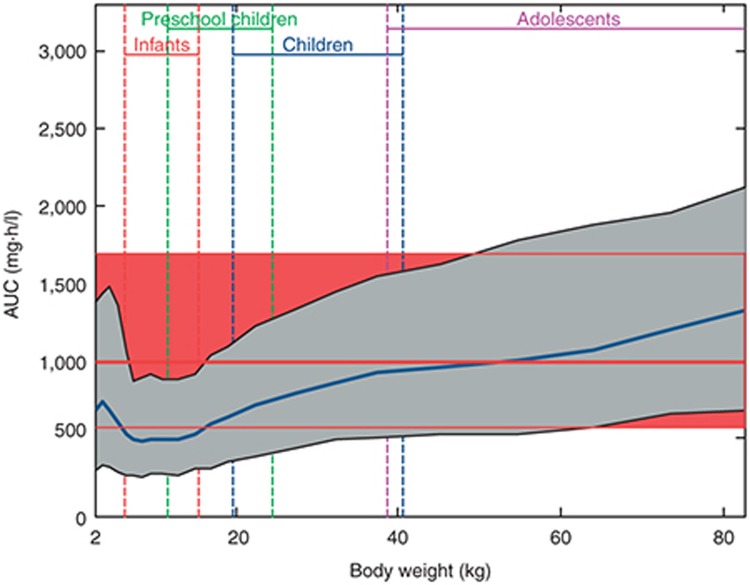
Simulation of area under the plasma concentration–time curve (AUC) vs. body weight for rivaroxaban administered at 0.143 mg/kg body weight and formulated as an oral suspension as compared with the adult reference population. Simulated data of the pediatric population are represented as a geometric mean (blue line) and 90% prediction interval (gray shaded area). Simulated data of the adult reference population are represented as a geometric mean (thick red line) and 90% confidence interval (red shaded area in the background of the graph). Expected weight ranges for infants, preschool children, children, and adolescents are indicated. Taken from Willmann et al.¹⁰

Figure 6.

A box whisker plot of AUC_inf (y-axis) values as a function of age class for a given dose (in mg/kg) of hypothetical drug administered orally as a suspension to a pediatric population (n = 10,000; ages 0–17 years) that would reach equivalent AUC_inf as a 50 mg tablet in adults. The box is the interquartile range (IQR) representing the 25th to 75th percentile. The whiskers represent the last point within 1.5 times the IQR of the 25th and 75th percentile. Circles represent all points above or below the whiskers. The blue dotted line is the geometric mean AUC_inf, and the shaded area is the 90th percentile of adult values. Red dots are the adult individuals.

The aim of the stratification process is again dependent on the question being addressed and is limited to those patient-specific inputs that were included in the pediatric PBPK model. Covariates should be chosen based on their clinical applicability and ease of clinical assessment. A common model application is to derive starting doses for a first-in-pediatric trial with doses aimed at achieving the same exposure as a standard adult dose in an adult. In this case, the dose determination may be dependent on body weight or age with an aim to bin these to achieve a median AUC similar to that in adults with a variability to match (Figure 6). Variability will drive the number of cohorts in the final dosing table. For example, in Figure 6, the variability in the first three age cohorts is greater than that in adults which is a result of the smaller sample size in these age groups and the high rate of change in the ontogeny of processes responsible for ADME. These issues could be addressed through incorporating more virtual children in these age groups and/or having higher resolution in the age bins. Simulations for outcomes should be discussed with the responsible clinicians as they will have restraints not necessarily shared by the modeler. Usually, the end game in dose determination is to derive pediatric equivalent doses. This assumes that the exposure–response relationship is similar to that in adults. In the event that the exposure–response relationship changes as a function of age or disease and this is known a priori, pediatric doses can be determined through Pop-PBPK/PD modeling. In the event that this is not known, the model may help in planning an adaptive trial where children are followed and the exposure response evaluation is completed with the potential for subsequent dose modification.

Presentation of results may also include the testing of assumptions. When significant assumptions have been made—for example, the ontogeny of a transporter is unknown and its activity is assumed to be independent of age—a sensitivity analysis should be included to demonstrate the importance of said assumption. This can be achieved by rerunning the pediatric model for the young age cohorts assuming no transporter activity and assessing the difference in predicted outcomes. By testing at the limits, it is possible to address the consequences of the assumption being incorrect.

Summary

In summary, PBPK models can serve to integrate multiple levels of information (i.e., in vitro, preclinical, clinical, etc.) to elucidate PK changes among children. This tutorial aimed to provide the reader with a basic understanding of the workflow for developing a pediatric PBPK model and to provide examples of PBPK model outputs that may be used to guide pediatric clinical investigations.

Conflict of interest

The authors declared no conflict of interest.