Robustness of Equations that Define Molecular Subtypes of Glioblastoma Tumors Based on Five Transcripts Measured by RT-PCR

Abstract

Glioblastoma (Gb) is one of the most deadly tumors. Its molecular subtypes are yet to be fully characterized while the attendant efforts for personalized medicine need to be intensified in relation to glioblastoma diagnosis, treatment, and prognosis. Several molecular signatures based on gene expression microarrays were reported, but the use of microarrays for routine clinical practice is challenged by attendant economic costs. Several authors have proposed discriminant equations based on RT-PCR. Still, the discriminant threshold is often incompletely described, which makes proper validation difficult.

In a previous work, we have reported two Gb subtypes based on the expression levels of four genes: CHI3L1, LDHA, LGALS1, and IGFBP3. One Gb subtype presented with low expression of the four genes mentioned, and of MGMT in a large portion of the patients (with anticipated high methylation of its promoter), and mutated IDH1. Here, we evaluate the robustness of the equations fitted with these genes using RT-PCR values in a set of 64 cases and importantly, define an unequivocal discriminant threshold with a view to prognostic implications. We developed two approaches to generate the discriminant equations: 1) using the expression level of the four genes mentioned above, and 2) using those genes displaying the highest correlation with survival among the aforementioned four ones, plus MGMT, as an attempt to further reduce the number of genes. The ease of equations' applicability, reduction in cost for raw data, and robustness in terms of resampling-based classification accuracy warrant further evaluation of these equations to discern Gb tumor biopsy heterogeneity at molecular level, diagnose potential malignancy, and prognosis of individual patients with glioblastomas.

Introduction

Glioblastoma is one of the most deadly tumors. Yet its molecular subtypes in relation to its diagnosis, treatment, and prognosis deserve further characterization (Grant et al., 2014; Park et al., 2013; Shao et al., 2013; Tabouret et al., 2014). In this vein, the use of gene-expression microarrays has allowed the characterization of certain types of glioma and glioblastoma (Castells et al., 2012; Colman et al., 2010; de Tayrac et al., 2011; Freije et al., 2004; Gravendeel et al., 2009).

Glioblastoma is clinically classified as primary or secondary subtypes depending on whether it was diagnosed as a de novo tumor or it derived from gliomas of lower grade, respectively (Louis et al., 2007). Secondary Gb is characterized by a high percentage of cases harboring a G to A transition in the central base of the codon 132 of the IDH1 gene (Yan et al., 2009). Although several works have proposed methods to stratify Gb cases based on gene-expression profiling (Colman et al., 2010; Lee et al., 2008; Li et al., 2009; Nigro et al., 2005; Verhaak et al., 2010), there is no consensus so far on potential molecular subtypes, neither on the optimal approach to perform such stratification.

Identification of such groups by automated and fully objective methods is a crucial step due to the data complexity. Several studies have shown the possibility of robustly classifying brain tumors based on omics data (Castells et al., 2010; 2012; Gravendeel et al., 2009). However, the use of high throughput data for diagnostics purposes is not always optimal due to its high cost (despite ongoing trends for reductions in the cost of molecular analyses) particularly in resource-limited regions or the developing world. Hence, the development of supervised statistical methods based on a cost-effective technology such as RT-PCR is an alternative worth consideration for its implementation in clinical routine, so that Gb cases with better prognosis or more likely to respond to therapy can be detected.

We have previously reported a linear discriminant (LDA) equation fitted with the expression values from only four transcripts (CHI3L1, LDHA, LGALS1, and IGFBP3), which was able to distinguish two survival groups in Gb (Castells et al., 2012). These four genes, selected from the publication of Colman and collaborators (2010), showed the highest robustness to detect Gb groups in two independent datasets when compared to genes proposed in another publication (Lee, 2008) and to the most variable genes across the cases in our local dataset (Castells et al., 2012). To our knowledge, this and two other reports (de Tayrac et al., 2011; Kawaguchi et al., 2013) contain the only published equations to distinguish molecular subtypes of glioma based on the expression profile obtained from microarray experiments. The aim of the present study was to evaluate the potential use of RT-PCR data to develop an LDA equation using a similar approach to previous studies (Arimappagan et al., 2013; Colman et al., 2010).

We characterized the Gb groups in terms of the mutational status of the codon 132 of IDH1, so that they could be linked to primary or secondary Gb. We also evaluated the mutational status of codon 172 of IDH2 in an attempt to identify rare mutations also leading to secondary Gb (Yan et al., 2009). Another feature we studied was the average survival time of each group and the expression level of the MGMT gene, as an indirect measurement of its promoter's methylation status. That is, MGMT is a gene involved in the repair of DNA damage by alkylating agents, such as the temozolomide, the standard chemotherapeutic compound used for Gb treatment. The hypermethylation of such promoter produces a decrease in the expression of that gene, and the temozolomide is more effective in those tumors (Hegi et al., 2005). Thus, the patients harboring methylation of MGMT promoter, or low expression of this gene, are more likely to respond to the therapy.

We aimed to describe the classification method developed accurately, so that other people can easily test our molecular-based Gb stratification on their own patients in actual clinical practice or in available retrospective sample cohorts. We followed two approaches: 1) assessment of the reproducibility of the LDA equation using RT-PCR expression values of the four previously reported genes, and 2) fitting an LDA equation with those genes (the four initial ones plus MGMT) most correlated with survival, as a way to select the minimum number of genes required to classify Gb in different molecular types. In both approaches, we normalized the data using two different methods: 1) standardization per gene, and 2) quantiles normalization followed by standardization per gene.

Methods

Sample collection

The 64 Gb biopsies were obtained as described in our previous work (Castells et al., 2012). Among the 47 biopsies used for the report by Castells et al., (2012), there was enough material left for additional analysis in 42 samples. The additional 22 biopsies used in the present work were collected in the Hospital Universitari de Bellvitge (L'Hospitalet de Llobregat). The 271 Gb from The Cancer Genome Atlas (TCGA) were selected based on availability of both gene-expression microarray and survival data (CGARN 2013). The full study protocol was approved by the local Ethics Committees and informed consent was obtained from all patients.

RNA isolation and RT-PCR experiments

RNA was isolated and quantified as described in our previous work (Castells et al., 2012). One microgram RNA was used as input for the reverse transcription using the iScript cDNA synthesis kit (Bio-Rad, Hercules, CA). A 1/20 dilution of the reverse transcription product was used for the RT-PCR reaction and performed using the IQ SYBR Green Supermix kit (Bio-Rad) following the manufacturer instructions. A 25 μL reaction was undertaken in 96 well-plates using the CFX96 Touch™ Real-Time PCR Detection System (Bio-Rad). The MGMT primers described in (Tanaka et al., 2008) were used in this study. The primers for the genes described in our previous work (Castells et al., 2012) were: CHI3L1: Fw-CTGTGGGGATAGTGAGGCAT and Rv-TAGGATGTTTGGCTCCTTGG, LDHA: Fw-CACAGCTATATCCTGATGCTGG and Rv-GACTAGGCATGTTCAGTGAAGGAG, LGALS1: Fw-CTAAGAGCTTCGTGCTGAACCTG and Rv-ATGCACACCTCTGCAACACTTC, IGFBP3: Fw-AGGGCACTCTGGGAACCTAT and Rv-CTCTCTGTCCCTCCTACCCC. The raw data from the RT-PCR experiments can be found in Supplementary Table S1 (supplementary material is available online at www.liebertpub.com/omi).

Sanger sequencing

Twenty nanograms of cDNA were used as input to amplify regions containing the target fragment of codon 132 of IDH1 and codon 172 of IDH2. Amplification products were purified using ExoSAP-IT (Affymetrix) and sequenced using nested primers. One microgram of the purified product was used for the sequencing reaction using BigDye® Terminator v3.1 Cycle Sequencing Kit (Life Technologies). The amplification and sequencing primers for IDH1 were the same than the ones reported by Gravendeel et al., (2009), while specific primers were designed for IDH2. The amplification was performed using the pair CACCCCTGATGAGGCCCG/TTTGGGGTGAAGACCATT and the reverse primer was replaced for sequencing (GCCCGTGTGGAAGAGTTCAA).

Data normalization

Two strategies were followed to normalize both the local and the TCGA dataset: 1) In the local dataset, the Ct mean and standard deviation of each gene from the training set were computed. The corresponding Ct mean was subtracted from all Ct values of the given gene and divided by the standard deviation (i.e., Ct_{gene1-sample1} - Ct_gene1/sd_gene1). For TCGA data, all cases were used to compute the mean and standard deviation. 2) Prior to the standardization, quantiles normalization was undertaken using the normalize.quantiles function available in the preprocessCore R package (Bolstad et al., 2003).

Linear discriminant analysis assumes the hypotheses of normal distribution and independence of variables. To that end, the normalized data were evaluated using the hist function from the graphics R package, the qqplot and cor from the stats R package (all with default settings).

Evaluation of the prediction accuracy

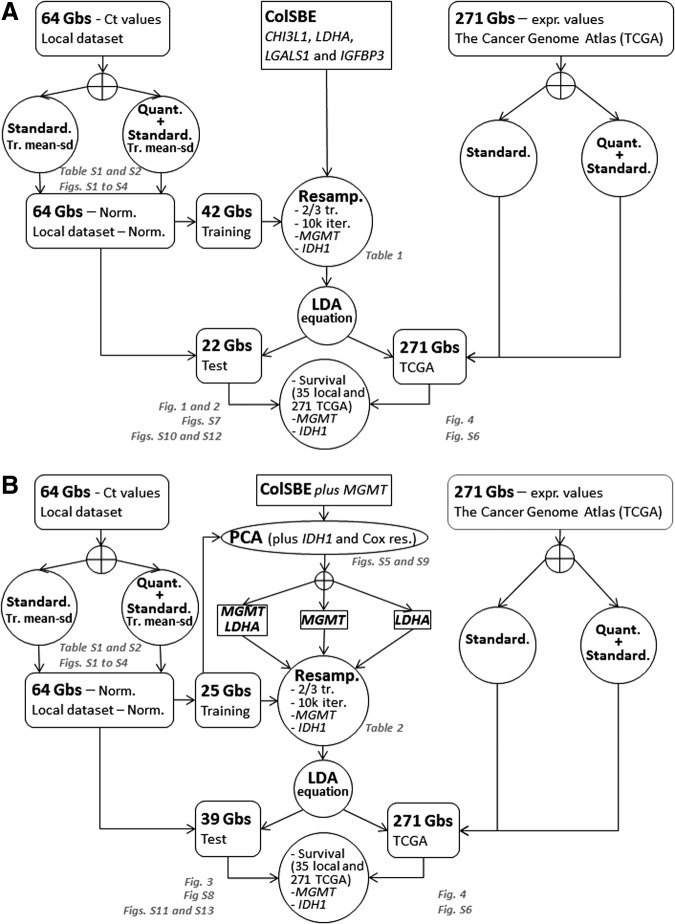
We followed two approaches to fit an equation based on LDA (Fig. 1 and figures cited therein): Approach 1 (Fig. 1A) assessment of the reproducibility of our LDA equation using RT-PCR expression values of the four previously reported genes (CHI3L1, LDHA, LGALS1, and IGFBP3) and Approach 2 (Fig. 1B) fitting an LDA equation with genes most correlated with survival among the four genes in approach 1, plus MGMT. The 64 Gb were divided into training and test sets depending on the approach used. In Approach 1, the 42 cases for which microarray data were available constituted the training set and the remaining 22 ones were used as test set. For Approach 2, those 25 cases with survival information available among the 42 training cases in Approach 1 were used as training set. To assess the differences in survival, those 25 cases plus the 10 cases with survival available in the test set from Approach 1 were used. In contrast, all data available (n=64) were employed to evaluate the differences in terms of MGMT expression level and IDH1 mutational status.

FIG. 1.

Diagram of computations performed. This figure summarizes the computations performed using as input the four genes from ColSBE (CHI3L1, LDHA, LGALS1, and IGFBP3) (top panel A) and the two genes selected from the PCA approach (MGMT and LDHA) (bottom panel B). Sets of genes are represented by a squared-box, datasets by a rounded-edges box, and computations described inside empty circles. The crossed empty circles indicate that only one of the following items are performed at the same time. The gray-colored text provides the figures and/or files containing the output information. “Standard” is an abbreviation for standardization, “Tr. mean-sd” stands for mean and standard deviation from the training set, “Quant” means quantiles normalization, “Norm” denotes normalization, “Cox res” corresponds to Cox residuals and “expr values” means expression values.

The prediction accuracy for each approach was evaluated by fitting an LDA equation by randomly selecting two-thirds of cases (28 out of 42 in Approach 1) and 17 out of 25 in Approach 2 and classifying one-third of cases, which had been left out as a test. This procedure was repeated 10,000 times and at each iteration, the composition of groups in terms of MGMT expression, IDH1 mutational status, and survival time was assessed. In both cases, the discriminant threshold was set to zero.

The accuracy and the specificity were computed as the percentage of cases correctly classified with respect to the “gold-standard” reference in the entire set or separately per group, respectively. Accuracy is defined as [true positive+true negative]/[total positive+total negative], while specificity is defined as [true negative]/[false positive+true negative]. Additionally, sensitivity is defined as [true positive]/[true positive+false negative]. Provided that only two groups are considered, as in this work, the specificity calculated for one group is the sensitivity of the other one and vice versa. We considered as “gold-standard” reference the classification defined in our previous work (Castells et al., 2012) for Approach 1. In contrast, that reference in Approach 2 was the group class defined by the principal component analysis (PCA) performed using as input the expression of the five transcripts measured by RT-PCR (Fig. 1). That is, two groups in the training set (n=25) were determined by selecting those genes most associated with IDH1 status and survival. Such association was computed by including the mutational status of IDH1 and the residuals of a Cox's residual from a null model as supplemental variables in the PCA (Fig. 1), which is an approach similar to the one performed in a precedent work (Freije et al., 2004). The Cox's residuals can be understood as a measure of “excess of death” (Therneau et al., 1990) and the higher their values, the higher the probability of death.

A final LDA equation was fitted using the entire training set in each respective approach and the resulting equation was used to classify all cases (n=64). As the “gold-standard” classification from test samples was unknown, the prediction accuracy was only evaluated by MGMT expression, IDH1 mutational status, and survival time per group.

Statistical tests and software

The survival analysis and the assessment of differences between tumor groups in terms of IDH1 status and MGMT expression or mutation were performed with the freely-available R software (R Core Team 2014) by using the same functions and packages as the ones described in Castells et al. (2012). The PCA analysis was performed using the FactoMineR package (http://factominer.free.fr).

Results

Evaluation of normal distribution and independence of variables (genes)

The hypotheses of normal distribution and independence assumed by the linear discriminant model were assessed prior to developing the equations. The standardization of Ct values produced a low correlation between pairs of genes, while the distribution appears to be normal in most cases, but biased for genes LGALS1 and MGMT (Supplementary Table S1 and Figures S1 and S2). In contrast, a normal distribution was observed for all genes when quantiles normalization was applied before standardization (Supplementary Table S2 and Figures S3 and S4). However, in this case the correlation increased between pairs of genes and was high between LDHA and LGALS1. As no method fully accomplished the assumptions of the LDA model, the analysis was performed using the data normalized through both approaches. A scheme of the computations performed is shown in Figure 1.

Robustness of Gb classifier based on real-time PCR data from previously selected four-gene set (CHI3L1, LDHA, LGALS1, and IGFBP3)

We fitted an LDA equation using the standardized Ct values from two-thirds of cases (28 out of 42) from the training set. The derived LDA equation was used to classify the remaining third of cases (n=14). This procedure was repeated 10,000 times, so that a precise estimation of classification error was obtained (Table 1).

Table 1.

Summary of Resampling Results in Training Dataset for ColSBE Using RT-PCR Values

	Ct standardized
Estimate	Training	Test	All
Sensitivity	89.0	80.3	86.0
Specificity	83.8	80.7	84.1
Accuracy	85.8	80.7	84.1
% IDH1 mut GLE	13.3	7.7	10.6
% IDH1 mut GHE	0	0	0
Fold-change GHE/GLE MGMT	2.1	2.3	2.0
% GLE <mean MGMT	59.6	65.1	62.2
% GHE <mean MGMT	33.3	39.0	35.5

	Ct quantiles normalized+standardized
Estimate	Training	Test	All
Sensitivity	97.0	86.4	93.3
Specificity	83.7	81.6	83.0
Accuracy	88.9	83.6	87.2
% IDH1 mut GLE	12.	7.4	10.0
% IDH1 mut GHE	0.0	0.0	0.0
Fold-change GHE/GLE MGMT	1.8	1.8	1.6
% GLE <mean MGMT	58.5	63.9	61.1
% GHE <mean MGMT	33.4	38.3	35.2

This table depicts the average classification and molecular features across iterations based on the stratification resulting from LDA equations fitted with the RT-PCR values from the ColSBE. On the top panel, Ct values were transformed to a zero centred distribution by subtracting the Ct value of a sample from the mean of all samples for a given gene and divided by the standard deviation (i.e., for a gene 1 and a sample 1 the computation would be [Mean Ct gene1 – Ct gene1-sample1]/standard deviation Ct gene1). On the bottom panel, Ct values were first normalized by the quantiles method and the same standardization than the one described above was undertaken. The 42 cases composing the training set were subjected to an iterative process that was repeated 10,000 times. Such set of samples was split in a further training (2/3 of cases) and test (1/3 of cases) set at each iteration. The training set was used to develop the LDA equation and the obtained discriminant coefficients were multiplied by expression values from the test set, which resulted into a single discriminant score per sample. Those cases displaying a negative score were classified as GLE, while as GHE those ones showing a positive one. The sensitivity, specificity, and accuracy (see Methods) were computed taking as a “gold standard” reference the classification obtained by the ColSBE from gene expression microarrays. Also, the percentage of cases harboring the IDH1 mutation per group is described (% IDH1 mut GLE or GHE), the MGMT fold-change GHE/GLE and the percentage of cases per group having a MGMT expression value below the average of all cases (% GLE or GHE <mean MGMT).

The performance of the classification was very high and none of the iterations classified IDH1 mutated cases into the GHE, as expected from Castells et al. (2012). Also, the fold-change GHE/GLE for the MGMT gene was on average higher than two, and the GHE presented a higher percentage of cases above the MGMT average expression, as previously described (Castells et al., 2012). Subsequent to the iterative process, an LDA equation was fitted using all training samples (ColSBE-RT, Eq. 1):

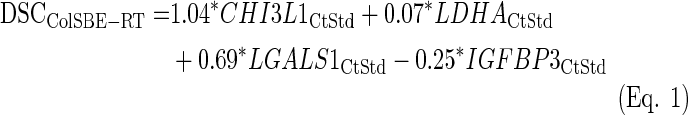The subindex “CtStd” indicates that the Ct value used for a given gene was standardized by using the mean and standard deviation (Mean (StDv)) from the training set and changing the sign of the resulting value to set low Cts as high expression (see discriminant scores in Supplementary Table S1):

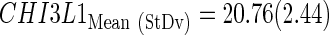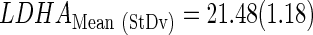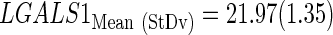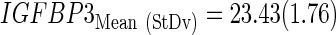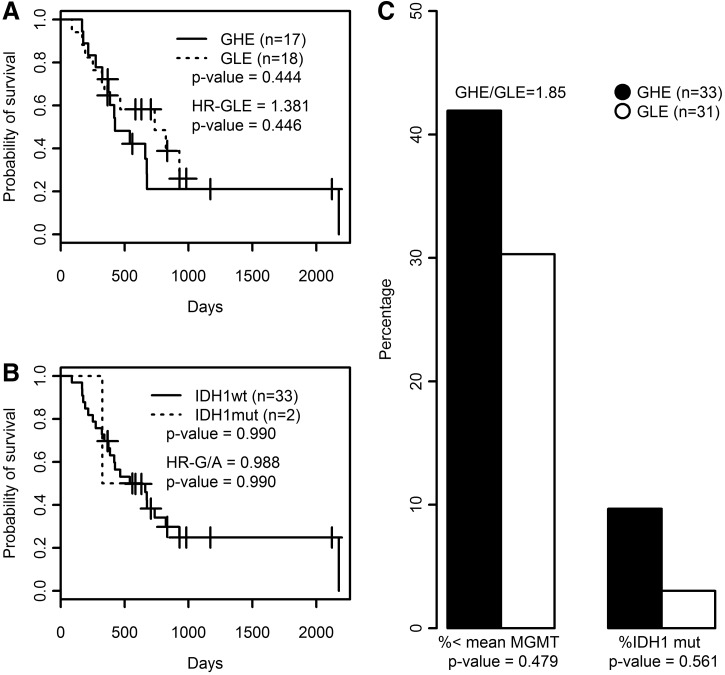
All cases were classified as GLE or GHE by setting to zero the cut-off threshold for the discriminant coefficients (DSC) obtained from applying Equation 1. As shown in Figure 2A, survival differences between GLE and GHE were not significant, but those patients with the highest survival were classified as GLE. Three out of the four IDH1 mutated cases were classified as GLE, and the ratio GHE/GLE for the expression level of MGMT was almost two (GHE/GLE=1.85), although the percentage of cases above the average Ct was higher in GLE than in GHE (Fig. 2C). No case was found mutated in codon 172 of the IDH2 gene. The use of the original classification of training cases from microarrays data did not change the results as depicted in Supplementary Figure S7.

FIG. 2.

Survival and molecular features of ColSBE. (A) Survival curves based on ColSBE as classified by the LDA equation using standardized Ct values for those cases with survival data available. (B) Survival curves for patients harboring or not the mutation in IDH1. In each plot, the amount of cases per group is shown as well as its associated p value, which indicates the probability that curves are equal, the death hazard ratio (HR) computed from the Cox's proportional hazard model is depicted, as well as the p value providing the probability that the HR is different than zero. (C) The histograms summarize the molecular features based on MGMT expression and IDH1 mutational status (codon 132). The left-side bars describe the percentage of cases within each ColSBE group below the MGMT average expression, while the right-side bars provide the percentage of cases showing IDH1 mutation in each ColSBE group. The GHE/GLE indicates the fold-change between groups for the MGMT expression levels. The p value denotes the probability that proportions are equal.

The same procedure was repeated for the data normalized by quantiles prior to the standardization. As Table 1 shows, the percentage of accuracy substantially improved compared to the previous approach. Also, a similar percentage of cases harboring the IDH1 mutation in GLE was found, while the fold-change based on the MGMT expression slightly decreased. As above, an LDA equation was fitted using all training samples (ColSBE-RT, Eq. 2):

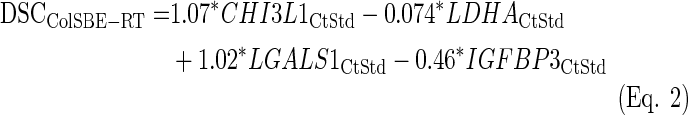Equivalently to the procedure described above, the subindex “CtStd” indicates that the Ct value used for a given gene was standardized after quantiles normalization by using the mean and standard deviation (Mean(StDv)) from the training set and changing the sign of the resulting value to set low Cts as high expression (see discriminant scores in Supplementary Table S3). As quantiles normalization makes the distribution equal for all variables, the mean and standard deviation were identical per gene (mean=23.04 and sd=1.73).

All cases were classified as GLE or GHE by setting to zero the cut-off threshold for the discriminant coefficients (DSC) obtained from applying Equation 1. The differences between groups in terms of survival, IDH1 and MGMT composition were equivalent to the result obtained by data only standardized, regardless that the cases from the training set were labeled by Equation 2 (Supplementary Fig. S10) or the classification provided by microarray data were used instead (Supplementary Fig. S12).

Robustness of Gb classifier based on most correlated genes with survival

The PCA analysis resulted in the selection of genes MGMT and LDHA as input to generate three discriminant equations.(Eq. 3–5) (see Supplementary Figures S5 and S9 for the data). The accuracy of classifying the samples into good or poor prognosis groups (abbreviated as GPG and PPG, respectively) was evaluated through a resampling approach in the training cases from the previous approach with available survival data (n=25). This procedure showed that the LDA function based on the expression level of LDHA-MGMT or MGMT alone provided the best classification results (Table 2).

Table 2.

Summary of Resampling Results in Training Dataset Using PCA Classification

	Ct standardized
	MGMT-LDHA			MGMT			LDHA
Estimate	Training	Test	All	Training	Test	All	Training	Test	All
Sensitivity	99.9	91.4	97.5	85.8	85.5	85.7	42.8	42.9	42.9
Specificity	87.3	86.0	86.9	77.7	78.0	77.8	44.4	44.5	44.4
Accuracy	91.0	87.4	89.8	80.1	79.9	80.0	44.0	44.1	44.0
% IDH1 mut GPG	28.6	13.9	21.8	33.2	9.9	20.0	66.6	5.1	15.4
% IDH1 mut PPG	0.0	0.02	0.006	0.0	0.0	0.0	0.0	0.0	0.0
Fold-change PPG/GPG MGMT	11.0	6.2	7.8	19.3	7.2	10.6	23.3	0.6	1.6
% GPG<mean MGMT	85.7	78.9	82.5	100	100	100	100	53.8	61.5
% PPG<mean MGMT	22.1	20.6	21.6	7.2	5.8	6.7	0.0	46.1	25.0

	Ct quantiles normalized+standardized
	MGMT-LDHA			MGMT			LDHA
Estimate	Training	Test	All	Training	Test	All	Training	Test	All
Sensitivity	100.0	99.9	99.9	100.0	100.0	100.0	39.7	40.4	40.0
Specificity	85.2	81.1	83.8	80.0	80.1	80.0	50.0	50.1	50.0
Accuracy	88.0	85.3	87.0	83.7	84.5	84.0	48.1	48.0	48.0
% IDH1 mut GPG	40.0	15.2	24.4	40.1	13.3	22.2	90.0	5.5	16.7
% IDH1 mut PPG	0.0	0.01	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Fold-change PPG/GPG MGMT	16.4	7.8	9.6	18.8	9.4	11.2	24.5	0.6	1.7
% GPG<mean MGMT	100.0	85.0	90.2	100.0	100.0	100.0	90.0	56.2	66.7
% PPG<mean MGMT	21.8	21.3	21.6	12.5	12.6	12.5	0.0	47.6	23.1

This table depicts the average classification and molecular features across 10,000 iterations. Only those samples having survival data were considered (n=25). Two thirds of cases were used as training set (n=16), and the remaining ones were used as a test set (n=9). The information in this table is equivalent to that provided in Table 1, but in this case the LDA equations were fitted only using the standardized RT-PCR expression values from MGMT and LDHA genes. On the top panel, values were only standardized, while on the bottom one, the Ct values were first normalized by the quantiles method and the same standardization as the one described above was undertaken afterwards.

Then, a final LDA equation based on the 25 Gbs was computed and used to classify the remaining cases with survival available (n=10) and nonavailable (n=29) data. The mean and standard deviation of Ct values from the training set (n=25) were used to standardize the rest of samples:

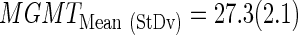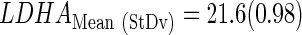LDA equations were fitted with the standardized values from the training set (n=25). The discriminant scores were computed for each sample (both training and test sets, n=64) and equation (see discriminant scores in Supplementary Table S3):

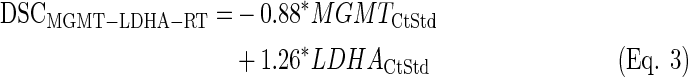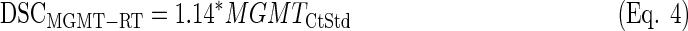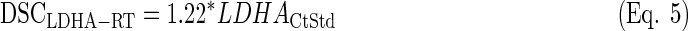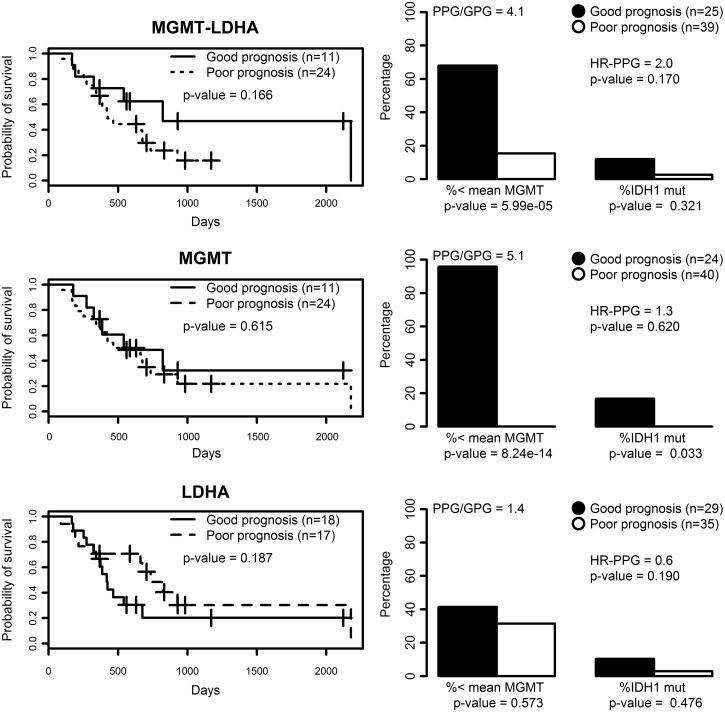
Once again, the LDA function based on MGMT-LDHA (Eq. 3) produced the best overall results, since the difference in survival was the highest among the three equations, the expression of MGMT was very high in PPG, and three out of four IDH1-mutated cases were classified as GPG (see Fig. 3). Actually, Equation 4 provided the best result in terms of MGMT expression and IDH1 mutational status, but the average survival was very similar between GPG and PPG. Equation 5 showed a similar survival difference to the one from Equation 3, but the life expectancy of each group was opposite to that expected. Moreover, the expression of MGMT was approximately identical between groups.

FIG. 3.

Survival and molecular features of LDA functions. Left plots are survival curves based on LDA functions (Equations 2, 3, and 4) fitted with either MGMT-LDHA, MGMT, or LDHA expression values. All samples having survival data available were used (n=35). The p value indicates the probability that curves are equal. Plots on the right depict the percentage of cases showing an MGMT expression below the average of all cases (n=64) and the percentage of cases showing IDH1 mutation in each group (GPG and PPG). The p value denotes the probability that proportions are equal.

The analysis was then repeated using the data standardized per gene after quantiles normalization (see Supplementary Fig. S9). Again, the genes most correlated with survival were MGMT and LDHA. Similar to the data only normalized, equations fitted with LDHA-MGMT and only MGMT displayed the highest classification accuracy through the resampling procedure, as well as the remaining features (see Table 2). Moreover, the values obtained using this approach across the three variables analyzed (survival, MGMT and IDH1) were higher than the ones obtained by only standardizing the data.

The final LDA equation based on the 25 Gbs was computed and used to classify the remaining cases with survival data available (n=10) and nonavailable (n=29). The mean and standard deviation of Ct values from the training set (n=25) were used to standardize the rest of samples, which are the same values than described in previous section (mean=23.04 and sd=1.73).

LDA equations were fitted with the standardized values from the training set (n=25). The discriminant scores were computed for each sample (both training and test sets, n=64) and equation (see discriminant scores in Supplementary Table S3):

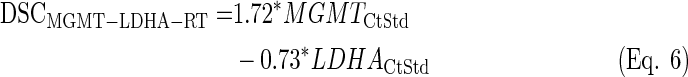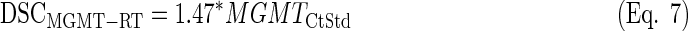By doing so, the survival differences between groups were reduced compared to the only standardized data, but such difference increased between GPG and PPG for the MGMT and IDH1 analysis (see Supplementary Figures S11 and S13).

External validation of equations using TCGA data

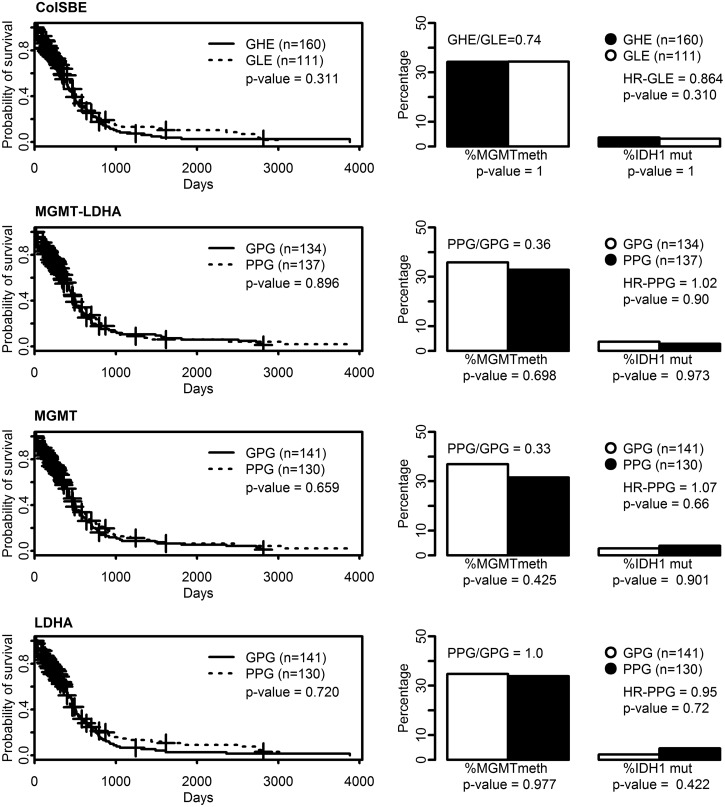
We used data from those 271 cases with gene expression microarray and survival data available in The Cancer Atlas Repository (TCGA) as an approach to validate the equations developed using RT-PCR data, similarly to Arimappamagan and collaborators (2013). We directly fitted Equations 1 and 3–6 with the standardized values from microarray data in TCGA and set the DSC threshold to zero. Our strategy differed from the one performed by Arimappamagan and collaborators in the sense that we kept fixed the DSC threshold, while they modified it for each dataset tested. Equation 3 produced the best result in terms of survival, although it did not achieve significance (see Supplementary Figure S6). An overall non-correlation with the expected features was observed for the remaining equations. IDH1-mutated cases showed a significant higher survival and MGMT expression than wild-type ones, but the HR associated was not significant. Accordingly, IDH1 mutational status should be combined with other information to improve the classification of Gb in terms of survival.

The same analysis was repeated for Equations 2 and 6–8, but TCGA data were first normalized by quantiles and then standardized. As we show in Figure 4, the composition of groups, either GLE/GHE or GPG/PPG, in terms of MGMT and IDH1, showed no differences across the different equations. However, GLE showed a lower probability of death (HR=0.86) than GHE, although the difference was not statistically significant. Such a result was not observed for any of the other equations or for the only standardized data, which rather provided a higher hazard ratio for the GLE (Supplementary Figure S6).

FIG. 4.

Survival and molecular features of LDA functions and IDH1 mutational status based on 271 TCGA cases and data standardized after quantiles normalization. Left plots are survival curves based on classification provided by the IDH1 status and by the LDA functions fitted with ColSBE, MGMT-LDHA, MGMT or LDHA expression values (Equations 2 and 6–8). The discriminant scores for classification were computed by multiplying standardized values from TCGA data by the discriminant coefficients obtained from our training RT-PCR data (n=35, Equations 1–4). The cut-off to classify in one of two groups was set to zero. The p value indicates the probability that curves are equal. Plots on the right depict the percentage of cases showing an MGMT expression below the average of all cases and the percentage of cases showing IDH1 mutation in each group. The p value denotes the probability that proportions are equal.

Discussion

Availability of a classification threshold remains a key point for the clinical application of a diagnostic signature on single patients. Such value must be independent of the group of samples to be tested. In this work we propose a set of equations with a clearly defined discriminant threshold.

Our approach was strict in terms of avoiding overestimated results as much as possible. All cases in Figures 2, 3, and 4 were classified based on the equations proposed, rather than using the classification defined by microarray data in Equation 1 or the classification derived from Supplementary Figures S1 and S9. Actually, the use of the “gold-standard” classification for the training set resulted in a similar result of survival outcome in Equation 1 (see Supplementary Figure S7), but a fair improvement for Equations 3–5 (see Supplementary Figure S8). The use of quantiles normalization prior to normalization gave rise to a similar result than the one obtained with only normalized data when applied to local data (Supplementary Figures S7 and S8 and S10–S13).

However, the validation of equations using TCGA data resulted in the detection of GLE displaying a lower death hazard ratio than GHE by using the data standardized after quantiles normalization, although such difference was not significant (see Fig. 4). Even if the MGMT methylation and the percentage of IDH1-mutated cases were almost equal between these two groups, this result provides evidence of the ColSBE's ability to detect Gb cases of better prognosis. The fact that we have been using microarray data to validate the results obtained from RT-PCR experiments may be hampering the identification of the expected features for each group (GLE: higher survival time, higher % of MGMT methylation and higher % of IDH1 mutated cases than GHE). Therefore, a dataset of equivalent size to the TCGA one analyzed herein should be screened by RT-PCR for a proper validation of our results. Actually, an RT-PCR-based dataset would also be more convenient to assess whether a smaller number than four genes can discriminate Gb groups with better prognosis (increased survival and high % of IDH1 mutated cases) and response to therapy (high methylation level of MGMT).

Although Arimappamagan and collaborators (2013) succeeded in distinguishing two groups of Gb displaying a differential survival time based on a 14 gene-signature, they modified the threshold for classification and set the mid-value of all discriminant scores, called weighted prognostic gene score (WG), as the threshold to classify the TCGA data. To our understanding, an overestimated result can be obtained by following that approach. Colman and collaborators (2010) developed a metagene score based on 9 transcripts measured by RT-PCR and validated their classification threshold on a large test dataset, but the threshold derived by applying recursive partitioning analysis (RPA) was not explicitly described in their work. This makes the direct validation of their equation by other people not possible and forces that RPA is applied on the data to be tested.

On the other hand, we attempted to improve the classification threshold by applying RPA in our local and TCGA datasets, but no improvement was observed in terms of survival difference between GHE and GLE groups (data not shown). In this sense, we also performed a linear regression between the Ct and the microarray values available in the training set (n=42) to mimic the analysis that would have been done in a quantitative RT-PCR setting. However, the result obtained was almost identical to what is described herein (data not shown), which seems to discard the potential benefit of using quantitative RT-PCR to improve the results of our study.

Conclusions

The detailed description of the set of equations provided in this work warrant consideration for further development for applications in clinical or histopathology laboratories and/or research groups to assess the molecular characterization of Gb biopsies. Nevertheless, there are some issues that require further evaluation for a widespread use of our equations, such as the unverified reproducibility of Ct values using other RT-PCR reagents and machines. Still, from the two normalization strategies used, the most convenient one seems to be the quantiles normalization prior to standardization as the LDA assumptions are better fulfilled.

The ease of equations applicability, reduced cost for producing the raw data and robustness in terms of resampling-based classification accuracy still make the reported equations a reliable tool to evaluate tumor biopsy heterogeneity at the molecular level and to identify the potential malignancy and prognosis of individual Gb samples.

Abbreviations Used

CHI3L1

Chitinase 3-like 1

ColSBE-RT

Colman's signature-based equation (described in Castells et al., 2012) based in real-time PCR values

Gb

Glioblastoma

GPG

Good prognosis groups

GHE

Group of high expression

GLE

Group of low expression

IDH1 and IDH2

Isocitrate dehydrogenase 1 and 2

IGFBP3

Insulin-like growth factor binding protein

LDA

Linear discriminant analysis

LDHA

Lactate dehydrogenase isoform A

LGALS1

Lectin, galactoside-binding, soluble

MGMT

O⁶-Methylguanine-DNA methyltransferase

PCA

Principal component analysis

PPG

Poor prognosis groups

RPA

Recursive partitioning analysis

RT-PCR

real-time PCR

Acknowledgments

This work was funded by the EU-funded grant eTUMOUR (FP6-2002-LIFESCIHEALTH 503094) and the Spanish grant MARESCAN (SAF2011-23870). Centro de Investigación Biomédica en Red-Bioingeniería, Biomateriales y Nanomedicina [CIBER-BBN (http://www.ciber-bbn.es/en)], is an initiative of the Instituto de Salud Carlos III (Spain) Co-funded by EU FEDER funds.

We thank Victor Mocioiu for critically revising the manuscript and helping with language corrections.

Author Disclosure Statement

The authors declare that there are no conflicting financial interests.