T cell receptor-ligand interactions: A conformational preequilibrium or an induced fit

Abstract

Kinetic parameters of T cell receptor (TCR) interactions with its ligand have been proposed to control T cell activation. Analysis of kinetic data obtained has so far produced conflicting insights; here, we offer a consideration of this problem. As a model system, association and dissociation of a soluble TCR (sT1) and its specific ligand, an azidobenzoic acid derivative of the peptide SYIPSAEK-(ABA)I (residues 252-260 from Plasmodium berghei circumsporozoite protein), bound to class I MHC H-2K^d-encoded molecule (MHCp) were studied by surface plasmon resonance. The association time courses exhibited biphasic patterns. The fast and dominant phase was assigned to ligand association with the major fraction of TCR molecules, whereas the slow component was attributed to the presence of traces of TCR dimers. The association rate constant derived for the fast phase, assuming a reversible, single-step reaction mechanism, was relatively slow and markedly temperature-dependent, decreasing from 7.0 × 10³ at 25°C to 1.8 × 10² M^-1·s^-1 at 4°C. Hence, it is suggested that these observed slow rate constants are the result of unresolved elementary steps of the process. Indeed, our analysis of the kinetic data shows that the time courses of TCR-MHCp interaction fit well to two different, yet closely related mechanisms, where an induced fit or a preequilibrium of two unbound TCR conformers are operational. These mechanisms may provide a rationale for the reported conformational flexibility of the TCR and its unusual ligand recognition properties, which combine high specificity with considerable crossreactivity.

Resolution of the interaction mechanism between the T cell receptor (TCR) and its ligands, complexes of peptides with the molecules encoded by class I or II MHCs (MHCp), is still a central problem in immunology (1-5). Several models have been suggested to rationalize the apparent contradiction between the observed relatively high specificity and usual modest affinities of TCR-MHCp interactions (6-8). Significant progress has been achieved during the last decade in resolving three-dimensional structures of TCR-MHCp complexes (9-13). These studies revealed that marked structural changes are observed, primarily in the TCR, upon binding the ligands. Moreover, large amounts of data have been accumulated from both time course and affinity measurements of TCR-MHCp interactions (1, 2). These data were essentially all obtained by using the surface plasmon resonance (SPR) method (14). Equilibrium and kinetic studies using this method established the 0.1- to 100-μM affinity range for the interactions of the different TCR-MHCp couples examined. These low affinities were interpreted to be a result of relatively slow association (10³ to 10⁵ M^-1·s^-1) and fast complex dissociation (0.1 to 100 s^-1) rate constants. Practically all values of the association rate constants were calculated by assuming the operation of a reversible, single-step reaction mechanism. However, in view of the ample crystallographic evidence for conformational changes taking place in the TCR upon interaction with its ligands, a more complex mechanism for TCR-MHCp interaction must be considered.

Here, we present results of time course measurements of the TCR-MHCp interactions by SPR and their detailed, in-depth analysis. This analysis revealed that the apparent rate of the association process is significantly affected by the dissociation process. Therefore, the universally used reversible, single-step process model is not a unique solution, and mechanisms involving additional steps, e.g., induced-fit or a preequilibrium of two free TCR conformers, fit the kinetic data equally well. Furthermore, these mechanisms provide agreement with the well documented structural transitions accompanying TCR-ligand interactions (9).

Materials and Methods

The recombinant water-soluble single-chain TCR, sT1, was prepared and was purified on H57-Sepharose as described (15). Synthesis and purification of the peptide SYIPSAEK(ABA)I derivative, [PbCS(ABA), residues 252-260 from Plasmodium berghei circumsporozoite protein], was described elsewhere (16). H-2K^d-PbCS(ABA) complexes with the heavy chain biotinylated at its C terminus were prepared and purified as described (15). All protein samples were centrifuged at 20,000 × g for 30 min before the SPR measurements, which were performed by using a BIAcore 2000 (BIAcore AB, St Albans, U.K.) in standard BIAcore buffer [10 mM Hepes (pH 7.4)/150 mM NaCl/0.005% (vol/vol) surfactant P20] at 25°C and 4°C. C-terminal biotinylated heavy-chain H-2K^d-PbCS(ABA) complexes and a control protein (biotinylated goat anti-mouse IgG, Molecular Probes) were bound to streptavidin coated sensor chip (Sensor chip SA, BIAcore) at surface densities of 0.45-0.65 ng/mm^-2 [450-650 response units (RU)]. Special attention detailed below was paid to performing all of the kinetic measurements under experimental conditions that are not affected by mass transfer or analyte rebinding. Pilot experiments were carried out at 25°C at three immobilization levels of H-2K^d-PbCS(ABA) (250, 450, and 900 RU) and two flow rates of TCR (10 and 20 μl/min). We found that at 25°C the reaction time courses normalized on the same binding amplitude were the same in the limit of experimental accuracy for 150 and 450 RU immobilization levels when the analyte was injected at 20 μl/min. To obtain maximal accuracy, all of the kinetic experiments were carried out at the highest available immobilization level (450 RU) at 25°C and 20 μl/min analyte flow rate. Because the binding was considerably slower at 4°C, a slightly higher immobilization level (650 RU) was used. All experiments were performed at least in duplicates at all tested concentrations. Fitting of the data were carried out by the use of a nonlinear least-squares optimization program GLSA (Alango Ltd., Haifa, Israel).

Results and Discussion

SPR was used to measure the time courses of interactions between the recombinant, water-soluble TCR sT1 and the immobilized H-2K^d-PbCS(ABA). We first formally analyzed separately the apparent association and dissociation phases so as to obtain a satisfactory fit to the following model:

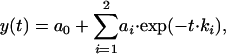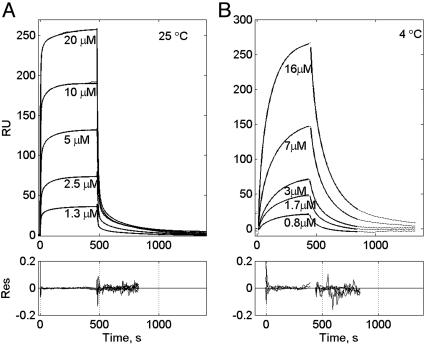
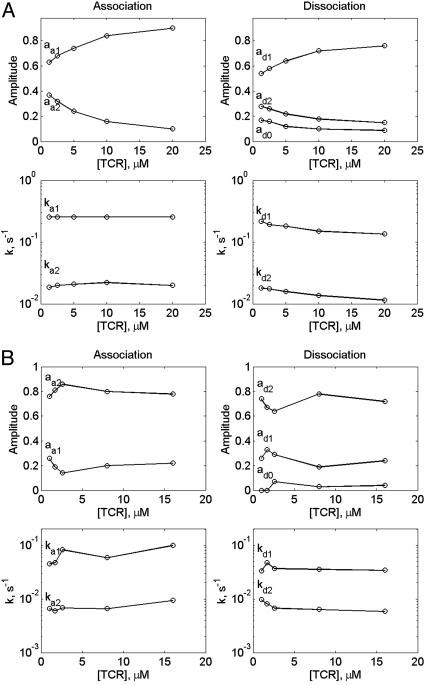
where a_i and k_i are amplitudes and corresponding rate constants (Fig. 1). The resultant fitting parameters are listed in Tables 1 and 2 and are plotted in Fig. 2. These results show that k_a1, the apparent rate constant of the association process, is essentially TCR concentration-independent and close in its value to the dissociation rate k_d1. The observed normalized amplitudes provided by the preexponential coefficients, a₁ increased and a₂ decreased upon increasing TCR concentration at 25°C.

Fig. 1.

Observed association and dissociation time courses of sT1 TCR and the H-2K^d-PbCS(ABA) complex monitored by SPR. A biotin-labeled H-2K^d-PbCS(ABA) was bound to a streptavidin coated sensor chip at surface density 0.45 at 25°C or 0.65 ng/mm^-2 at 4°C. sT1 TCR solutions, at the concentrations indicated, were injected at a flow rate of 20 μl/min, and the time courses were recorded at 25°C (A Upper) and 4°C (B Upper). The association and dissociation time courses were separately fitted to a two-exponential model

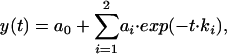and the evaluated parameters are listed in Tables 1 and 2 are plotted in Fig. 2. The corresponding residuals are plotted in Lower.

Table 1.

Parameters derived by fitting of the observed association and dissociation time courses of the sT1 TCR-H-2K^d-pPbS^AB interaction at 25°C shown in Fig. 1A to a two-exponential model

[sT1], μM	20		10		5		2.5		1.3
Phase	Association	Dissociation	Association	Dissociation	Association	Dissociation	Association	Dissociation	Association	Dissociation
a0	1	0.09	1	0.10	1	0.12	1	0.16	1	0.17
a1	−0.90	0.76	−0.84	0.72	−0.74	0.64	−0.68	0.58	−0.63	0.54
k1, 10−1·s−1	2.6	1.4	2.6	1.5	2.6		2.6	1.9	2.6	2.2
a2	−0.10	0.15	−0.16	0.18	−0.26	0.24	−0.32	0.26	−0.37	0.28
k2, 10−2·s−1	2.0	1.1	2.2	1.4	2.1	1.6	2.0	1.8	1.9	1.8

The total amplitudes of each time course (a₀ + a₁ + a₂) were normalized to 1.

Table 2.

Parameters derived by fitting of the observed association and dissociation time courses of the sT1 TCR-H-2K^d-pPbS^AB interaction at 25°C shown in Fig. 1B to a two-exponential model

[sT1], μM	16		8		2.6		1.7		1
Phase	Association	Dissociation	Association	Dissociation	Association	Dissociation	Association	Dissociation	Association	Dissociation
a0	1	0.04	1	0.03	1	0.07	1	0	1	0
a1	−0.22	0.24	−0.2	0.19	−0.14	0.29	−0.19	0.33	−0.26	0.26
k1, s−1	1.0·10−1	3.5·10−2	5.9·10−2	3.6·10−2	8.3·10−2	3.7·10−2	4.8·10−2	5.5·10−2	4.6·10−2	7.1·10−2
a2	−0.78	0.72	−0.80	0.78	−0.86	0.64	−0.81	0.67	−0.76	0.74
k2, s−1	9.4·10−3	5.9·10−3	6.6·10−3	6.4·10−3	6.8·10−3	5.9·10−3	6.0·10−3	7.3·10−3	6.6·10−3	1.0·10−2

The total amplitudes of each time course (a₀ + a₁ + a₂) were normalized to 1.

Fig. 2.

Amplitudes of the H-2Kd-PbCS(ABA)-TCR interaction time courses (Upper) and their rate constants (Lower) as derived from the fitting to the two-exponential model (Left, association; Right, dissociation) monitored at 25°C (A) and 4°C (B).

Significantly, similar biphasic binding and dissociation patterns of several MHCp-TCR have been reported earlier (17-19).Some authors interpreted this observation as a reflection of structural adjustment or conformational changes taking place in one or both reactants (17). Others, to exclude the possibility that the biphasic reaction pattern is due to mass transfer or to inhomogeneous ligand immobilization, carried out their SPR experiments at a relatively low ligand immobilization level (711 RU), fast flow rate (20 μl/min), and immobilized the ligand by means of a biotin group introduced into the MHC molecule (18). Even more strict precautions were taken by Ding et al. (19), who carried out their experiments at 100 μl/min flow rate and at an ≈3-fold lower ligand immobilization level. Nevertheless, the binding and dissociation time courses were still found to be biphasic. Thus, we conclude that neither inhomogeneous ligand immobilization nor mass transfer are responsible for the observed biphasic reaction pattern. In view of the generality of this observation, we have carried out a rigorous analysis of our data and examined the possible causes for the observed complex kinetic patterns.

We first tried to exclude the possibility that the above observed reaction patterns are due to mass transfer (20). To this end, we have carried out the kinetic experiments at several immobilization levels and at different flow rates and found that the normalized time courses were almost identical at 150 and 450 RU. In addition, we used the “two-compartments” mass transfer model (21, 22) and simulated the reaction time curves at 500 RU immobilization level and the k_a = 5 × 10⁴ M^-1·s^-1. We found that under these conditions the model does not predict any significant mass transfer distortion of the kinetic data. Other possible causes considered were analyte heterogeneity and a possible additional reaction step or both. Analysis of the present data by these models is described in Supporting Materials and Methods, which is published on the PNAS web site. This analysis showed that the additional minor phase observed in the binding pattern might be due to the presence of traces of a higher-affinity fraction in the TCR. This higher-affinity component could be due to traces of TCR dimers, produced by the specific mAb used for the TCR immunoisolation and causes the observed reaction pattern in both our study and probably other reported cases (17-19). Thus, in the following, we concentrate on the results obtained for the major reaction component. This reaction phase is attributed to the interaction between the TCR and the MHCp. The association rate constants (k₁) derived from its analysis according to the reversible, single-step mechanism

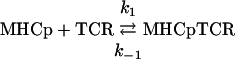1

are as follows: 7.0 × 10³ and 1.8 × 10² M^-1·s^-1 at 25°C and 4°C, respectively (see Table 4, which is published as supporting information on the PNAS web site) i.e., a 39-fold decline over this temperature range. This result, together with their remarkably slow values, which are at least two orders of magnitude slower than those expected for diffusion controlled processes (23), clearly suggest that the association process involves crossing of a relatively high activation barrier. Moreover, a survey of essentially all published studies of TCR-MHCp reaction kinetics shows that very similar values have been reported for the association rate constants (1, 2).

An important additional feature of this TCR-MHCp reaction phase is that the observed association step, being rather slow, is markedly affected by the relatively fast dissociation process. Assuming the operation of a reversible, single-step reaction mechanism, one can see that k₁·[TCR] < k_-1 (Table 4 and Supporting Materials and Methods). This reaction results in a slight concentration dependence of the apparent association rate constant k_ap = k₁·[TCR] + k_-1. Therefore, employing this model for the data analysis does not yield a unique solution. To rationalize the current data and the relatively large body of published kinetic and structural results, we examined whether the MHCp-TCR interactions could be described by either of the following two related mechanisms. One mechanism describes an induced-fit transformation from an intermediate (int) to a stable (st) state:

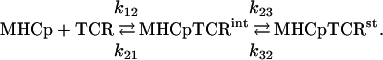2

The other mechanism assumes the existence of two conformers of the TCR's free binding site:

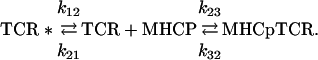3

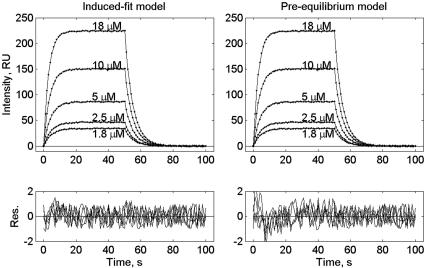
The good agreement between these two models and the observed data is illustrated by fitting a set of simulated time courses. The simulated data were produced by addition of 1 RU amplitude of uniform noise to the major component (k₁ = 7.0·10³ M^-1·s^-1 and k_-1 = 0.20 s^-1) resolved by the two-species model (Supporting Materials and Methods, Eqs. 7-11, Table 4). Both of these models predict biphasic kinetic patterns, however, at certain combinations of the rate constants, they can also resemble the reversible, single-step process occurring within the time scale of the data. Thus, the induced-fit model (Fig. 3 Left) provides a perfect global fit to the simulated time courses. These simulations show that for the induced-fit model operation the reaction starts with the formation of an intermediate complex (TCR-MHCp)^int at a rate close to a diffusion-controlled process. This initial complex is stabilized in the following step of the reaction, which determines the overall association rate. Because this step involves a ligand-induced conformational transition in the TCR, its rate may also be a function of the ligand's structure, including that of the bound peptide. This step can rationalize the remarkable T cell specificity, which allows resolution between two MHC complexes with peptides differing by only one amino acid residue (24, 25).

Fig. 3.

Global fitting of simulated by the bimolecular model time courses by the induced fit and preequilibrium of two conformers models. The simulated time courses were produced by adding 1 RU amplitude of uniform noise to the major component resolved by the two-species model (k₁ = 7.0·10³ M^-1·s^-1and k_-1 = 0.20 s^-1). The simulated time curves (dotted lines) were globally fitted with following parameters of the induced-fit model (Eq. 1) k₁₂ = 1 × 10⁶M^-1·s^-1, k₂₁ = 3 × 10³ s^-1, k₂₃ = 20.7 s^-1, k₃₂ = 0.2 s^-1,(Left, smooth lines) or the model assuming the existence of two conformers of the binding site in the unbound TCR (Eq. 2) k₁₂ = 7.4 × 10² M^-1·s^-1, k₂₁ = 1.2 × 10⁵ s^-1, k₂₃ = 1 × 10⁶M^-1·s^-1, k₃₂ = 0.2 s^-1 (Right, smooth lines).

The alternative model involving the existence of two free-site conformers (Eq. 3) accounts for the flexibility of the TCR-binding site. The model assumes that one of these conformers binds the specific MHCp ligand. By switching between different conformations, the binding site can screen structures of potential ligands. This model also allows a good fit to the experimental data (Fig. 3 Right). We found that this model fits the simulated data when k₁₂ << k₂₁, and therefore the free TCR exists mostly in the binding inactive conformation. This binding conformer readily associates with the ligand at close to the diffusion-limited rate k₂₃. Hence, a conformational transition within the TCR-binding site controls the overall association time course and its rate would then be independent of the ligand structure. Clearly, the existence of several conformers may explain the reported remarkable crossreactivity of TCR (11, 26, 27). Operation of the above two mechanisms has been established for antigen-antibody interactions (28-30). Published results (30) have unambiguously demonstrated that the induced fit step significantly increases the complex affinity, whereas the presence of multiple conformations may endow some antibodies with multispecificity or crossreactivity (30).

In conclusion, the experimentally observed slow MHCp-TCR association rates may be due to the fact that the reaction's elementary steps are not resolved by the used experimental methods. At this stage, we cannot distinguish between the above mechanisms, and it is also possible that both are operating. The problem with resolving between these mechanisms arises on one hand from the design of SPR experiments where the ligand immobilized on the chip can accumulate significant amounts of a high-affinity reagent, present in the analyte at a trace concentration, due to its continuous supply from the analyte flow. On the other hand, the temporal resolution limit of the SPR method provided by commercially available equipment has been reached in this study. Therefore, application of kinetic methods with higher temporal resolution may provide further and clearer understanding of this important process.