Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Jan 8;5:7669. doi: 10.1038/srep07669

Control of microtubule trajectory within an electric field by altering surface charge density

Naoto Isozaki 1,*, Suguru Ando 1,*, Tasuku Nakahara 1, Hirofumi Shintaku 1, Hidetoshi Kotera 1, Edgar Meyhöfer 2, Ryuji Yokokawa 1,3,a
PMCID: PMC4286733  PMID: 25567007

Abstract

One of challenges for using microtubules (MTs) driven by kinesin motors in microfluidic environments is to control their direction of movement. Although applying physical biases to rectify MTs is prevalent, it has not been established as a design methodology in conjunction with microfluidic devices. In the future, the methodology is expected to achieve functional motor-driven nanosystems. Here, we propose a method to guide kinesin-propelled MTs in multiple directions under an electric field by designing a charged surface of MT minus ends labeled with dsDNA via a streptavidin-biotin interaction. MTs labeled with 20-bp or 50-bp dsDNA molecules showed significantly different trajectories according to the DNA length, which were in good agreement with values predicted from electrophoretic mobilities measured for their minus ends. Since the effective charge of labeled DNA molecules was equal to that of freely dispersed DNA molecules in a buffer solution, MT trajectory could be estimated by selecting labeling molecules with known charges. Moreover, the estimated trajectory enables to define geometrical sizes of a microfluidic device. This rational molecular design and prediction methodology allows MTs to be guided in multiple directions, demonstrating the feasibility of using molecular sorters driven by motor proteins.

Intracellular transport has been extensively studied for potential applications as in vitro nanoactuators. Kinesins comprise a class of biomolecular motors that function in intracellular transport by hydrolyzing adenosine triphosphate (ATP) to generate a mechanical motion along MT filaments1. This process has been recapitulated in vitro by inverting the molecular configuration to allow MTs to glide on a kinesin-coated surface2; in this case, MTs act as molecular shuttles that are loaded with cargo through avidin-biotin3 and antigen-antibody4 binding and DNA hybridization5. Autonomous cargo loading and unloading have also been reported6,7.

Molecular systems comprising a sorter8 and a concentrator9 have been demonstrated in microfabricated structures and although they have used molecular shuttles, certain limitations must be overcome before they replace current biochemical methods. One is to confer MTs with the ability to define their gliding directions according to the cargo, producing an autonomous shuttle that transports specific molecules to a predefined destination. For example, in a molecular separator, molecules will be automatically divided once they are loaded onto an appropriate MT. However, MTs behave in a similar manner whether they are subjected to external fields8,10,11,12,13, photoresist tracks9,14,15, or fluid shear force16,17. Cargo destinations can be multiple only when the field is actively controlled8. This limitation of active control necessitates designing MTs that can autonomously assume precise gliding directions under given conditions. The other issue is to establish from an engineering perspective design rules for fabricating a microfluidic device by predicting MT trajectories. Traditionally, adjusting the size of such a device to the MT trajectory18 or else optimizing external fields to control MT gliding within the device11 have been employed; however, a design rule for molecular systems could circumvent the labor-intensive optimization and engineering obstacles caused by the instability of molecular motors.

To address these issues, MTs were designed with different electrophoretic mobilities that allowed them to glide in different directions depending on their surface charge densities in a given electric field. Short, biotinylated seed MTs (B-seeds) were labeled with negatively charged 20- or 50-bp DNA via streptavidin (SA)-biotin interaction, given that the electrophoretic force acting on the free leading tips (minus ends) of MTs clamped at the frontmost kinesin rectifies their gliding directions on a kinesin-coated surface. The measured electrophoretic mobilities enabled the prediction of significantly different curvatures among seed MTs with a cantilever model8,11. B-seeds were polymerized into longer MTs with biotinylated short minus ends and non-labeled plus ends, because the MT gliding directions were defined by the surface charge densities and lengths of the leading tip, but not by those of longer non-labeled tail segment bound to kinesin; this design prevented the steric hindrance that would obstruct MT gliding if the entire MT surface were to be covered with labeled molecules19,20, and left a non-labeled tail free to be used as a cargo carrier in future applications. A quantitative evaluation of the trajectories of three MTs with 20- or 50-bp DNA tips or a biotinylated tip (control) in an electric field revealed their biased gliding directions, which were in accordance with calculated trajectories. Moreover, the fact that the effective charge of the MT-loaded DNA—which was calculated from the electrophoretic mobility—was similar to that of freely dispersed DNA molecules in a buffer solution indicated that the surface charge of MTs could be adjusted by varying DNA length. This study demonstrated the broad applicability of this molecular design and prediction methodology for a nanosystem based on molecular shuttles.

Results

Electrophoretic mobilities of short seed MTs

According to the cantilever model, the freely suspended tip of a MT is deflected by the externally applied force, because the other portion of the MT is anchored to a glass surface by kinesin molecules without compliance11. The tip experiences both electro-osmotic flow (EOF) and electrophoretic force under an electric field, however, the former acts evenly to any MT tips in a given microfluidic environment. Therefore, our strategy in this report is to alter the electrophoretic force by designing surface charge density of MT tips, which is achieved by labeling DNA molecules to tips. Here, we prepared seven seed MTs (Fig. 1) and measured their electrophoretic mobilities (Fig. 2a): TAMRA (red)-tagged seed MT (R-seed), AlexaFluor 488 (green)-tagged seed MT (G-seed), biotinylated R-seed (B-R-seed), AlexaFluor 488-tagged SA (FSA)-labeled R-seed (FSA-R-seed), 20-bp DNA (AlexaFluor 488)-labeled R-seed (20-bp DNA(G)-R-seed), 50-bp DNA (AlexaFluor 488)-labeled R-seed (50-bp DNA(G)-R-seed), and 50-bp DNA (TAMRA)-labeled G-seed (50-bp DNA(R)-G-seed).

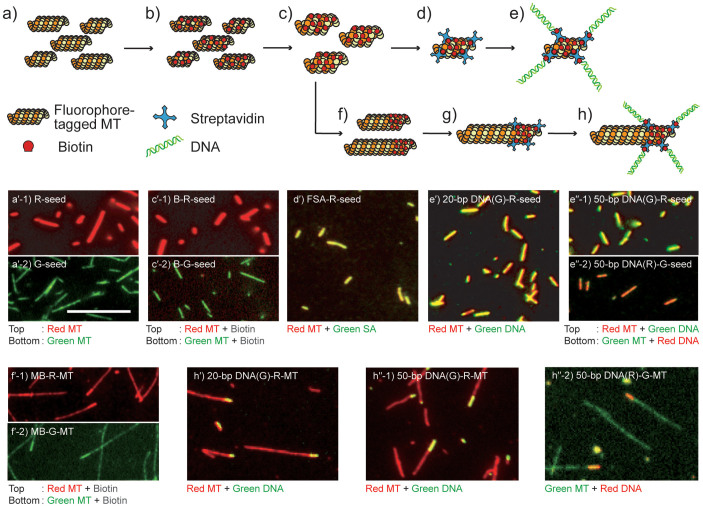
Figure 1. Schematic views and fluorescence images of designed seed MTs and minus-end labeled MTs.

Figure 1

Open in a new tab

(a) Schematic for fluorophore-tagged seeds polymerized with GMPCPP, and corresponding (a′-1) TAMRA-tagged seeds (R-seeds) and (a′-2) AlexaFluor 488-tagged seeds (G-seeds); (b) Biotinylated seeds (B-seeds) before syringe shearing; (c) B-seeds after shearing to reduce the length distribution; (c′-1) Biotinylated R-seeds (B-R-seeds) after shearing; (c′-2) Biotinylated G-seeds (B-G-seeds) after shearing; (d) Schematic for SA-labeled seeds; (d′) AlexaFluor 488-tagged SA (FSA)-labeled R-seeds (FSA-R-seeds); (e) DNA-labeled seeds; (e′) 20-bp DNA(G)-R-seeds; (e″-1) 50-bp DNA(G)-R-seeds; (e″-2) 50-bp DNA(R)-G-seeds; (f) Minus-end biotinylated MTs (MB-MTs); (f′-1) MB-R-MTs; (f′-2) MB-G-MTs; (g) SA-labeled MB-MTs; (h) DNA-labeled MB-MTs; (h′) 20-bp DNA(G)-R-MTs; (h″-1) 50-bp DNA(G)-R-MTs; (h″-2) 50-bp DNA(R)-G-MTs. Fluorescence images show that the biotinylated parts of B-seeds and MB-MTs were uniformly labeled with SA and dsDNA. Scale bar = 10 μm.

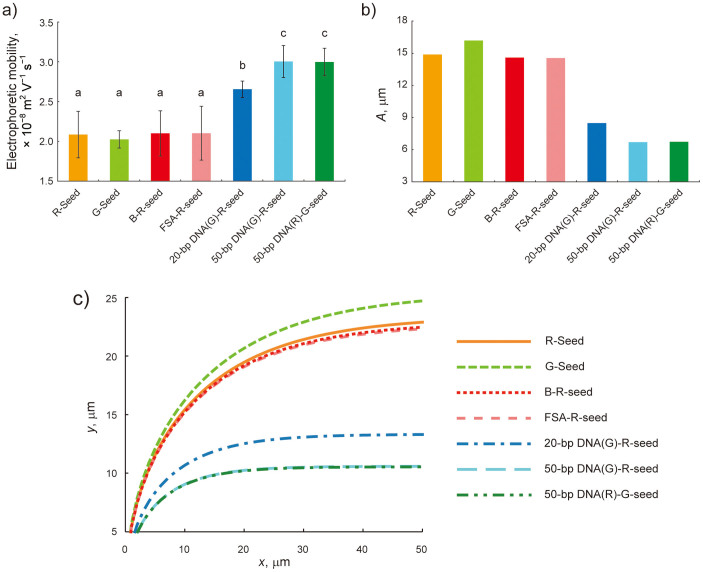
Figure 2. Measured electrophoretic mobilities and predicted trajectories of seven seed MTs.

Figure 2

Open in a new tab

(a) Electrophoretic mobilities of each seed MT measured with the laser Doppler method. Bars represent mean ± SD (n = 34 measurements for R-seed, n = 36 for G-seed and 50-bp DNA(R)-G-seed, n = 32 for B-R-seed, n = 33 for FSA-R-seed and 20-bp DNA(G)-R-seed, and n = 40 for 50-bp DNA(G)-R-seed). There were no significant differences between identical lowercase letters by the Tukey-Kramer test at a critical value of p < 0.01. (b) A values calculated from measured MT electrophoretic mobilities. (c) MT trajectories in an electric field predicted by the cantilever model.

To prepare seed MTs labeled with DNA molecules, guanylyl-(α,β)-methylene-diphosphonate (GMPCPP), a slowly hydrolyzable guanosine 5′-triphosphate (GTP) analog, was used to polymerize two fluorophore-tagged seeds (F-seeds) as illustrated in Fig. 1a. Their fluorescence images are shown in Fig. 1a′-1 for R-seeds and Fig. 1a′-2 for G-seeds (hereafter, F-seeds indicate both R-seeds and G-seeds). These were biotinylated by adding amine-reactive biotin to tubulin dimers at a molar ratio of 20:1 (Fig. 1b), which resulted in 3.2 biotin molecules with respect to the tubulin dimer. Based on the assumption that MTs were uniformly biotinylated, the total charge provided by labeled DNA molecules was proportional to the length of B-seeds (hereafter, B-seeds indicate both B-R-seeds and B-G-seeds). However, GMPCPP-polymerized B-seeds varied widely in length, which was 3.09 ± 1.81 μm (mean ± SD). The lengths of B-seeds were standardized by actuating a syringe 30 times to apply shear force, which resulted in short B-seeds with a more homogeneous length distribution of 2.28 ± 0.99 μm. The polydispersity index, which is a measure of the molecular distribution in a given sample, was reduced from 1.34 to 1.1921, indicating that the distribution of B-seed length was reduced by the shearing (Fig. 1c, c′-1, c′-2, and Supplementary Fig. S1 online).

B-seeds were further labeled with SA for DNA labeling. Although non-fluorophore-tagged SA was used for producing DNA-labeled seeds (Fig. 1d), the binding of SA to B-seeds was confirmed by FSA binding to R-seeds. B-seeds were incubated with SA at a molar ratio of 1:3 and uniform labeling was confirmed by those fluorescence images (Fig. 1d, d′). In our molecular design, double-stranded (ds)DNAs were prepared before conjugating to SA-labeled seeds. The 20- and 50-bp dsDNAs were hybridized from two complementary single-stranded (ss)DNAs, one of which was tagged with AlexaFluor 488 or TAMRA and the other with biotin at the 5′ end. Given that a dsDNA molecule has a bare charge of 2 e− per bp, the total bare charges of 20- and 50-bp dsDNA were expected to be 40 e− and 100 e−, respectively22. SA-labeled seeds were conjugated with a dsDNA at 37°C for 20 min (Fig. 1e), resulting in uniform labeling of dsDNA on B-seeds as observed in Fig. 1e′ for 20-bp DNA(G)-R-seeds, Fig. 1e″-1 for 50-bp DNA(G)-R-seeds, and Fig. 1e″-2 for 50-bp DNA(R)-G-seeds.

Electrophoretic mobility measurements were made for R-seed and G-seed (Fig. 1a), B-R-seed (Fig. 1c), FSA-R-seed (Fig. 1d), and 20-bp DNA(G)-R-seed, 50-bp DNA(G)-R-seed, and 50-bp DNA(R)-G-seed (Fig. 1e). Seed MTs were diluted with BRB80 buffer solution (80 mM PIPES, 1 mM MgCl2, and 1 mM EGTA, pH 6.8 with KOH) containing 20 μM taxol and flushed into a fused silica channel by pressure-driven flow. The length, height, and width of the channel were 26.0, 1.4, and 5.0 mm, respectively. Seed MT velocities were measured by the laser Doppler method, and electrophoretic mobilities (μe,⊥) without the effects of EOF—which were eliminated with the Mori-Okamoto equation—were calculated as: (2.09 ± 0.29) × 10−8 m2 V−1 s−1 for R-seed, (2.03 ± 0.11) × 10−8 m2 V−1 s−1 for G-seed, (2.11 ± 0.29) × 10−8 m2 V−1 s−1 for B-R-seed, (2.11 ± 0.34) × 10−8 m2 V−1 s−1 for FSA-R-seed, (2.66 ± 0.10) × 10−8 m2 V−1 s−1 for 20-bp DNA(G)-R-seed, (3.02 ± 0.20) × 10−8 m2 V−1 s−1 for 50-bp DNA(G)-R-seed, and (3.01 ± 0.17) × 10−8 m2 V−1 s−1 for 50-bp DNA(R)-G-seed (Fig. 2a). There were no significant differences among R-seed, G-seed, B-R-seed and FSA-R-seed by the Tukey-Kramer test (p > 0.01); these were therefore considered as the control groups for DNA-labeled seeds. Significant differences were found between 20- or 50-bp DNA-labeled seeds and each of the control seed MTs, as well as between 20- and both 50-bp DNA-labeled seeds (p < 0.01). Also, there was no significant difference between R-seed and G-seed or 50-bp DNA(G)-R-seed and 50-bp DNA(R)-G-seed. It supports that the difference of electrophoretic mobilities is attributed to the DNA charges, but not to the fluorophore charges.

Effective charges of the tubulin dimer and DNA molecules

To determine whether differences in μe,⊥ among labeled seed MTs originated from DNA charges (which are reported as 0.06–0.9 e− per bp in a buffer solution)23,24,25,26,27, the surface charge density σ of seed MTs was derived from μe,⊥ via two equations: the perpendicular electrophoretic mobility of an MT28

graphic file with name srep07669-m1.jpg

and the linear Grahame equation29

graphic file with name srep07669-m2.jpg

where η = 8.90 × 10−4 kg m−1 s−1 and ε = 6.93 × 10−10 C V−1 m−1 are the viscosity and dielectric constant of the buffer, respectively; g⊥ = 1.18 is the Henry function8; and λD = 0.74 nm is Debye length (see Supplementary equation (S1) online). Taken together with measured μe,⊥, the zeta potential ζ was derived from equation (1), yielding the average surface charge density σ of an MT from equation (2). The values of μe,⊥, ζ, and σ are summarized for seven seed MTs in Table 1. To obtain the effective DNA charge, the surface areas of tubulin dimers and 20- and 50-bp DNA were assumed as 508, 47, and 117 nm2 30, respectively. In addition, a tubulin dimer was estimated to be conjugated to 5.1 DNA molecules via SA-biotin binding, because SA binds to 80% of the biotin on MTs31 and 200% of SA binds to biotinylated DNA32. Consequently, the effective charges of the TAMRA- and AlexaFluor 488-tagged tubulin dimer and 20- and 50-bp DNA were calculated as 10 e−, 9.7 e− per dimer and 0.62 e− and 0.69 e− per bp, respectively (see Supporting Information online for details). These values were in good agreement with previous studies that have measured the effective charges of tubulin8 and freely dispersed DNA molecules23,24,25,26,27. The correlation confirmed that this method allows the total amount of charge (surface charge density) of seed MTs (μe,⊥) to be altered according to the effective charge of cargo molecules.

Table 1. Calculated ζ and σ values from measured μe,⊥ for seed MTs.

  R-seed G-seed B-R-seed FSA-R-seed 20-bp DNA(G)-R-seed 50-bp DNA(G)-R-seed 50-bp DNA(R)-G-seed
μe,⊥ (× 10−8 m2 V−1 s−1) 2.09 2.03 2.11 2.11 2.66 3.02 3.01
ζ (mV) 34.1 33.1 34.4 34.4 43.5 49.2 49.1
σ (e− nm−2) 0.20 0.19 0.20 0.20 0.25 0.29 0.29
Open in a new tab

Prediction of MT trajectories in an electric field

Since we have determined electrophoretic mobilities for multiple seed MTs, which are long enough to predict the deflection of the tip, MT trajectories can be calculated according to the cantilever model. When an electric field was applied in the negative x direction of the xy-plane and MTs entered the field at the origin in the positive y direction, the MT trajectory was defined as follows:

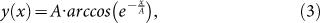graphic file with name srep07669-m3.jpg
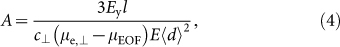graphic file with name srep07669-m4.jpg

where EyI is the flexural rigidity of an MT, c⊥ is the perpendicular Stokes drag coefficient per unit length of an MT tethered to the surface via kinesin, E is the field intensity, μEOF is the electro-osmotic mobility, and 〈d〉 is the distance between active kinesins8,11. MT gliding direction is represented by A, which defines the curvature of the trajectory in a given electric field. Based on equations (3) and (4), trajectories of seven seed MTs were predicted using directly measured μe,⊥ and other values for a given experimental condition. EyI has been measured by thermal fluctuation33,34,35,36,37,38, hydrodynamic flow35, atomic force microscopy39,40, MT trajectory11, and electric field41, and values have varied between 0.34 × 10−24 and 26 × 10−24 N m2, and were strongly dependent on buffer conditions in the MT polymerization process as well as MT-stabilizing reagents34. Therefore, EyI = (8 ± 3) × 10−24 N m2—which was reported for MTs polymerized in the presence of GMPCPP and stabilized with taxol in PIPES-based buffer34—was used. The equation

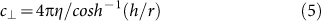graphic file with name srep07669-m5.jpg

was derived for an MT gliding at height h above the kinesin-coated surface42,43. From equation (5), c⊥ = 1.39 × 10−2 kg m−1 s−1 for an MT with radius r = 1.25 × 10−8 m and h = 1.68 × 10−8 m8,44. A value for μEOF was calculated during the electrophoretic mobility measurement of each seed MT by measuring the EOF velocity distribution in the z-direction in a flow cell (FC), which yielded μEOF = (1.33 ± 0.40) × 10−8 m2 V−1 s−1 from the Mori-Okamoto equation45. To compare estimated trajectories with those obtained in the MT gliding experiment described below, an average electric field of E = 7 kV m−1 was used for both the calculation and the experiment. Measured values of μe,⊥, μEOF, c⊥, and 〈d〉 = 1.66 μm36 yielded calculated A values of 14.9 μm for R-seed, 16.2 µm for G-seed, 14.6 μm for B-R-seed, 14.5 μm for FSA-R-seed, 8.48 μm for 20-bp DNA(G)-R-seed, 6.71 μm for 50-bp DNA(G)-R-seed, and 6.74 µm for 50-bp DNA(R)-G-seed (Fig. 2b) with associated predicted trajectories (Fig. 2c).

Trajectories of minus end-labeled MTs in an electric field

Since a free tip segment of a seed MT, of which length was much larger than 〈d〉, was regarded as a beam in the cantilever model, it was expected that MTs polymerized from the seed MTs would show the same trajectories as those of seed MTs. In other words, trajectories can be defined by the μe,⊥ measurement for seed MTs. To test this hypothesis, the plus ends of B-seeds were elongated by incubation with a mixture of non-fluorophore-tagged, N-ethylmaleimide (NEM)-treated, and fluorophore-tagged tubulins in the presence of dithiothreitol (DTT) and GMPCPP46. The mixture ratio of fluorophore-tagged to non-fluorophore-tagged tubulins for plus ends was set lower than that for B-seeds (1:7.5 vs. 1:2). This produced minus end-biotinylated TAMRA-tagged MTs (MB-R-MTs, Fig. 1f, f′-1) and AlexaFluor 488-tagged MTs (MB-G-MTs, Fig. 1f, f′-2), which had a short biotinylated segment at the minus end corresponding to B-seeds and an additional polymerized longer segment at the plus end (Fig. 1f), since NEM inhibited polymerization at the minus ends of B-seeds (hereafter, minus-end biotinylated MTs (MB-MTs) indicate both MB-R-MTs and MB-G-MTs). Although the same fluorophore-tagged tubulins were used for B-seeds and the longer plus end, the brighter parts corresponding to B-seeds were distinguished from dimmer plus end in the fluorescence images (Fig. 1f′-1, f′-2). The same SA (Fig. 1g) and biotinylated dsDNA (Fig. 1h) labeling protocol that was used for B-seed labeling was applied to MB-MTs to create MTs partially labeled with DNA at their minus end. Thus, resulting MTs polymerized were 20-bp DNA (AlexaFluor 488)-labeled MB-R-MTs (20-bp DNA(G)-R-MTs, Fig. 1h′), 50-bp DNA (AlexaFluor 488)-labeled MB-R-MTs (50-bp DNA(G)-R-MTs, Fig. 1h″-1), and 50-bp DNA (TAMRA)-labeled MB-G-MTs (50-bp DNA(R)-G-MTs, Fig. 1h″-2). Trajectories of three types of MTs—MB-R-MTs and 20- and 50-bp DNA-labeled MB-MTs—were evaluated in an electric field. MB-G-MTs, FSA-labeled MB-R-MTs, and non-labeled MTs were omitted from this experiment, because they were not expected to have trajectories that differed significantly from those of MB-R-MTs based on their μe,⊥ values (Fig. 2a).

FCs were constructed with spacers consisting of two 50-µm pieces of double-sided tape attached to a glass coverslip cleaned in 10 N KOH solution41, with another coverslip placed on top to form a channel. Two pipet tips were fastened with epoxy glue to the end of the channel as reservoirs (see Supplementary Fig. S2 online). The FC was filled with BRB80 buffer solution with 0.50–1.0 mg ml−1 casein and 0.08–0.10 mg ml−1 kinesin for nonspecific adsorption of kinesin to the glass surface. A mixture of 20-bp DNA(G)-R-MT and MB-R-MT (FC-20), 50-bp DNA(G)-R-MT and MB-R-MT (FC-50), or 20-bp DNA(G)-R-MT, 50-bp DNA(R)-G-MT, and MB-R-MT (FC-mix) was introduced into the FCs and incubated to immobilize MTs on the kinesin-coated surface. MT gliding was stimulated by injecting a 0.5 mM ATP solution with an O2-scavenging system into the reservoirs, into which platinum electrodes were immersed. When an electric field of 7 kV m−1 was applied, MTs changed their trajectories toward the anode owing to their negatively charged minus ends (see Supplementary Movies S1–S3 online for FC-20, -50, and -mix, respectively). Sequential fluorescence images for a 20-bp DNA(G)-R-MT with 50-s intervals and a 50-bp DNA(R)-G-MT with 20-s intervals under an electric field of 7 kV m−1 in FC-mix are shown in Fig. 3a and b, respectively.

Figure 3. DNA-labeled MB-MTs gliding under an electric field (E = 7 kV m−1).

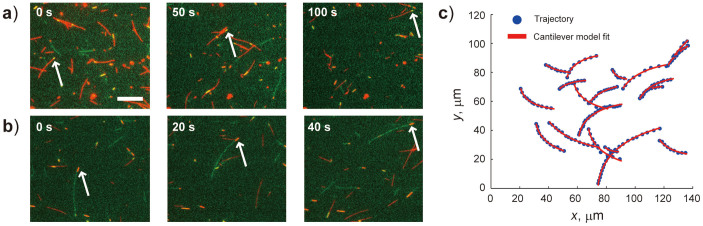
Figure 3

Open in a new tab

Sequential images obtained for an A value measurement of a gliding (a) 20-bp DNA(G)-R-MT and (b) 50-bp DNA(R)-G-MT. The anode and cathode is located at the right- and left-hand side of images, respectively. White arrows indicate the leading tips of the MTs. Similar images for MB-R-MTs were also obtained for their A value measurements. Scale bar = 10 μm. (c) Trajectories and fitted results for 20-bp DNA(G)-R-MTs in FC-20. Blue dots and red solid lines indicate leading tip trajectories of 20-bp DNA(G)-R-MTs (0.17 frame/s) and curves fitted with the cantilever model, respectively. Trajectories of MB-R-MTs, 50-bp DNA(G)-R-MTs, and 50-bp DNA(R)-G-MTs were also analyzed in the same manner.

The trajectories of MT leading tips were obtained using Mark2 image analysis software. Although MTs were designed to have DNA-labeled minus end using NEM-treated tubulins, we found some MTs labeled at their plus end or at the middle (see Supplementary Movies S1–S3 online). In the analysis, MTs labeled at their leading tips (minus end) were considered as DNA-labeled MB-MTs and other MTs as MB-R-MTs. The equation,

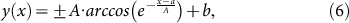graphic file with name srep07669-m6.jpg

modified from equation (3) expressed the trajectory of an MT that is initially located at an arbitrary coordinate (x, y) = (a, b) and is gradually re-oriented parallel to the external electric field. By fitting equation (6) to the trajectories with the least squares method, values for A and R2 were calculated with a custom-written MATLAB algorithm. Figure 3c shows trajectories and fitted curves for 20-bp DNA(G)-R-MTs under an electric field of 7 kV m−1 in FC-20. A mean R2 > 0.98 for MB-R-MTs and DNA-labeled MB-MTs showed that the model fit not only conventional TAMRA-tagged MTs but also our DNA-labeled MB-MTs.

A values were 24.6 ± 10.8 µm for MB-R-MT and 16.4 ± 6.7 µm for 20-bp DNA(G)-R-MT in FC-20, and 21.0 ± 7.5 µm for MB-R-MT and 10.3 ± 4.1 µm for 50-bp DNA(G)-R-MT in FC-50 (see Supplementary Fig. S3 online). In each FC, significant differences were found between MB-R-MT and DNA-labeled MB-MT (p < 0.01). Although ATP and Mg2+ concentrations and the surrounding temperature were kept constant throughout the experiments, different batches of protein and glass coverslip can cause variation in kinesin activity, i.e., in the distance 〈d〉 between active kinesins47. Thus, mean A values for DNA-labeled MB-MT were normalized to those of corresponding MB-R-MT in each FC. The resulting ratios for 20-bp DNA(G)-R-MT and 50-bp DNA(G)-R-MT were 0.66 and 0.49, respectively (see Supplementary Fig. S3 online), demonstrating that a larger negative charge on labeled molecules results in a smaller A value.

To demonstrate that MT trajectories depend on the length of labeled-DNA molecules, 20-bp DNA(G)-R-MT, 50-bp DNA(R)-G-MT, and MB-R-MT were assayed in the FC-mix (see Supplementary Movie S3 online). A values for all MTs were normalized to the mean A value for MB-R-MT in each FC, resulting in 1.0 ± 0.43 for MB-R-MT (n = 96), 0.73 ± 0.29 for 20-bp DNA(G)-R-MT (n = 43), and 0.44 ± 0.16 for 50-bp DNA(R)-G-MT (n = 46) as shown in Fig. 4a. There were significant differences among the three MTs by the Tukey-Kramer test (p < 0.01). Interestingly, normalized A values for 20-bp DNA(G)-R-MT and 50-bp DNA(R)-G-MT were in good agreement with those obtained for 20-bp DNA(G)-R-MT in FC-20 and 50-bp DNA(G)-R-MT in FC-50, which shows the consistency of relative A values in a given FC condition. To compare trajectories obtained from three measurements, A values for 20-bp DNA(G)-R-seed and 50-bp DNA(R)-G-seed calculated from μe,⊥ were normalized to that for B-R-seed, A values in FC-20 and -50 were normalized to that for MB-R-MT in each FC, and then their trajectories were plotted with those measured in FC-mix (Fig. 4b). Trajectories were categorized into three colored groups; differences in A values and trajectories emerged from this normalization process, supporting the association of A values to MT groups labeled with 20- or 50-bp DNA molecules. Therefore, even without conducting a MT gliding assay in an electric field, one can predict MT trajectories from cargo molecules with known charges and/or electrophoretic mobilities of cargo-labeled seed MTs that are simply measured using a bulk MT solution.

Figure 4. Evaluation of A values measured in FC-mix.

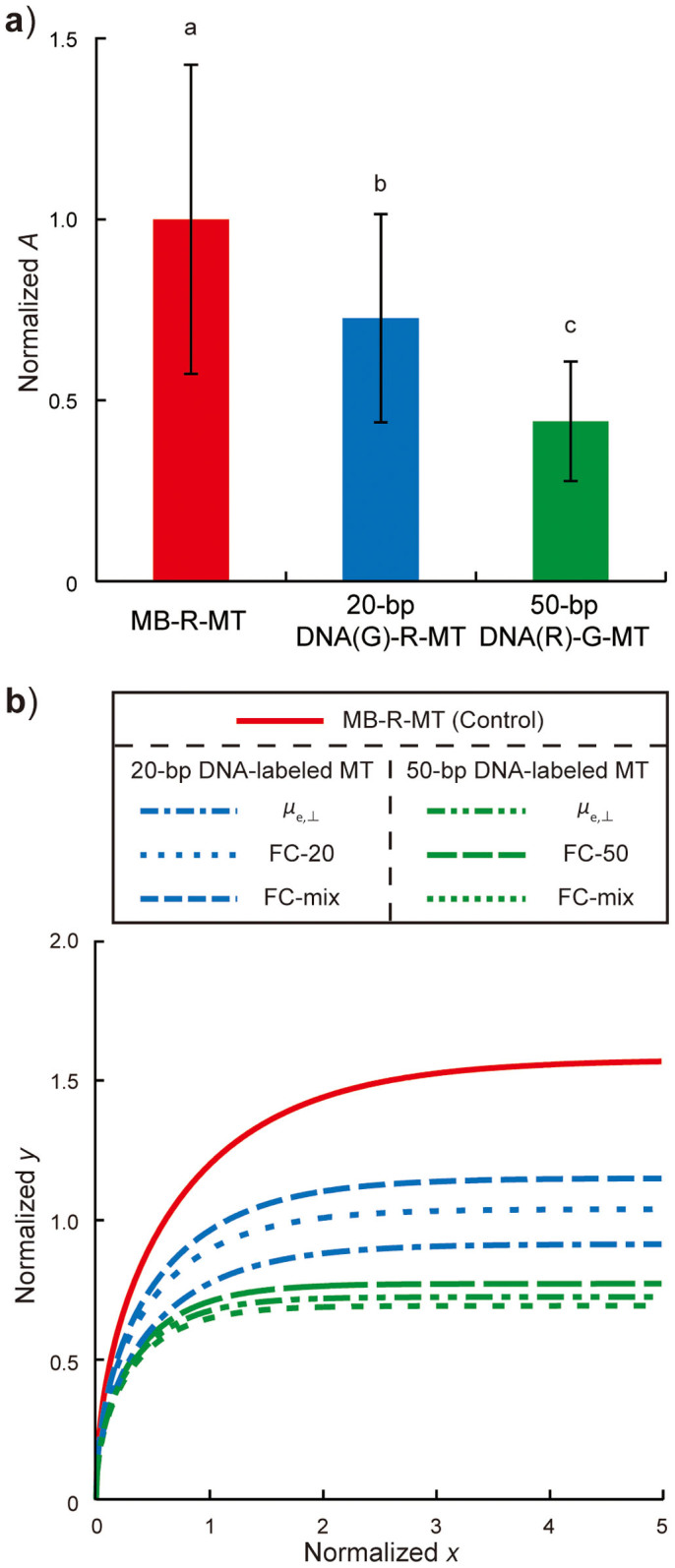
Figure 4

Open in a new tab

(a) Ratios of A values normalized to mean A value for MB-R-MT. Bars represent mean ± SD. There were significant differences between different lowercase letters by the Tukey-Kramer test at a critical value of p < 0.01. (b) MT trajectories predicted by A values obtained from electrophoretic mobility measurements and A values in FC-20, -50, and -mix. Trajectories were categorized into three groups colored in red, blue, and green, corresponding to MB-R-MTs and 20- and 50-bp DNA-labeled MB-MTs, respectively.

Discussion

A method was established for predicting A values based on the cantilever model11, and it was demonstrated that these values could be decreased by labeling DNA molecules. The optimization of the A value is critical for a molecular system such as a sorter that separates target molecules carried by MTs8,9,48. When designing MTs for a molecular sorter, the ratio of A values between cargo-carrying MTs and the absolute A value to achieve the designated curvature is critical. The former reflects the relative distance between trajectories of two MT groups labeled with different molecules; obtaining an optimum ratio requires adjusting μe,⊥ and EyI values in equation (4), because μEOF, E, and 〈d〉 are considered constants in a FC. In this experiment, μe,⊥ values were varied; EyI can be also altered by changing MT-polymerizing conditions34,36 or MT-associated proteins39,49. GMPCPP-polymerized MTs have a higher EyI than GTP-polymerized MTs (~8 × 10−24 N m2 vs. ~2.5 × 10−24 N m2)34. A large difference in A values allows the separation of MT groups according to effective charge with high precision. Thus, MTs can be designed with a wide range of ratios of A values by adopting large μe,⊥ and small EyI for one group of MTs with small A, and small μe,⊥ and large EyI for another group with large A.

Once ratios of A values have been defined for two MT groups, absolute A values can be optimized by adjusting E and 〈d〉 to obtain appropriate curvature in the molecular sorter, with the objective of guiding two labeled MT groups toward two areas spaced apart denoted by the y coordinates y(∞) = Aπ/2, that MTs ultimately reach in an electric field. Optimizing parameters EyI, μe,⊥, E, and 〈d〉 for two labeled MT groups according to the proposed steps determines MT trajectories, and provides a design strategy for further developments in the construction of a molecular sorter. For example, when E is altered to 4 kV m−1 and EyI for 50-bp DNA(R)-G-MT to 2.5 × 10−24 N m2 by polymerization in the presence of GTP34, the difference in values of y(∞) between 20-bp DNA(G)-R-MT and 50-bp DNA(R)-G-MT in FC-mix will increase from 16.6 µm to 59.4 µm. Here, we calculated these values using the A value for MB-R-MT in FC-mix (36.4 ± 16.4 µm, n = 96). This difference is large enough to sort two DNA-labeled MB-MT groups in a typical microfluidic device with channel width of several micrometers to several hundred micrometers.

In summary, a methodology was presented for designing MTs whose trajectories can be predicted, and whose gliding directions on a kinesin-coated surface when loaded with cargo can be controlled under an electric field. DNA labeling that locally increased surface charge density or electrophoretic mobility at MT tips decreased the A value, which was consistent with that estimated by the cantilever model. More importantly, even after conjugation, the tubulin dimer and DNA molecules retained their effective charges, which reflected their electrophoretic mobilities; thus, MT trajectories can be specified by selecting a cargo molecule with known charge. Further optimization of parameters other than electrophoretic mobility—i.e. bending stiffness, field intensity, and kinesin density—were also discussed with respect to a molecular sorter. The strategy described herein can serve as a guideline for any molecular shuttle-based nanosystem.

Methods

Protein and DNA preparation

Phosphocellulose (PC) tubulin was purified from porcine brains after two cycles of assembly-disassembly and PC chromatography50 and stored in liquid nitrogen. Fluorophore-tagged tubulin was prepared by adding a 10-fold molar excess of TAMRA (C-1171; Invitrogen, Carlsbad, CA, USA) or AlexaFluor 488 (A-20000; Invitrogen) to tubulin for a labeling stoichiometry of 0.45–0.70 or 0.27–0.30, respectively51. Recycled tubulin was purified from PC tubulin after an assembly-disassembly cycle that eliminated non-polymerizable tubulins. Human kinesin (amino acid residues 1–573) with an N-terminal histidine tag was purified as previously described52, and dsDNAs were hybridized by incubating 5′-biotinylated ssDNA and the complementary 5′-AlexaFluor 488- or TAMRA-tagged ssDNA at 37°C for 20 min. The sequences were 5′-TGT TGT CGA AAA TGT CAA CG-3′ for 20-bp DNA and 5′-GAG GTC TTA ACG GTG GAG GAT GGG GGT TAG TCC GGG GCG CAG ATT CGA AT-3′ for 50-bp DNA.

Seed MT preparation and electrophoretic mobility measurement

Recycled tubulin and fluorophore-tagged tubulin were mixed at 2:1 in the presence of 1 mM DTT and 1 mM GMPCPP and polymerized into F-seeds at 37°C for 30 min. The polymerized F-seeds were biotinylated by incubating with biotin-XX succinimidyl ester (B1606; Invitrogen) at 37°C for 30 min. Unreacted biotin was quenched by adding a 10-fold molar excess of K-glutamate at room temperature (RT) for 10 min, followed by centrifugation at 163,000 × g and 27°C for 15 min. Precipitated B-seeds were resuspended in BRB80 buffer solution containing 20 µM taxol, and biotinylation ratio was measured by a biotin quantitation assay kit (F30751; Invitrogen)9. The lengths of F- and B-seeds were shortened by syringe actuation using a 30-G syringe with a needle diameter of 0.16 mm (90030; Osaka Chemical Co. Ltd., Osaka, Japan). SA- and FSA-labeled seeds were prepared by incubating B-seeds with SA (192-11644; Wako Pure Chemical Industries, Ltd., Osaka, Japan) and FSA (S-11223; Invitrogen), respectively, at RT for 15 min. For 20- or 50-bp DNA-labeled seeds, SA-labeled seeds were incubated with a 20-fold excess of dsDNA molecules at 37°C for 20 min. The electrophoretic mobilities of F-, B-R-, FSA-R-, and 20- and 50-bp DNA-labeled seed were measured by the laser Doppler method (ELSZ-2; Otsuka Electronics Co. Ltd., Osaka, Japan).

Preparation of minus end-labeled MTs

To obtain minus end-labeled MTs, shortened B-seeds were elongated before SA or DNA labeling. The tubulin mixture for elongation was prepared by mixing non-fluorophore-tagged, NEM-treated, and fluorophore-tagged tubulin at a molar ratio of 6.6:0.9:1 in the presence of 1 mM DTT and 1 mM GMPCPP. NEM-treated tubulin consisted of recycled tubulin in 1 mM GMPCPP, 1 mM NEM, and 3% 2-mercaptoethanol (β-ME). The tubulin mixture for elongation was incubated with B-seed solution at a molar ratio of 9:1 at 37°C for 60 min, which yielded MB-MTs; these were incubated with a two-fold excess of SA, and SA-labeled MB-MTs were incubated with a 20-fold excess of dsDNA to obtain 20- and 50-bp DNA-labeled MB-MTs.

MT gliding assay

Fused silica glass coverslips (20 × 30 × 0.17 mm3 and 10 × 15 × 0.17 mm3, Senyo-Kogaku, Inc., Osaka, Japan) were cleaned in 10 N KOH solution at RT for 24 h and rinsed twice by ultrasonication in deionized water (DIW) at RT for 20 min. Coverslips were immersed in 20% ethanol solution at RT for 10 min, rinsed in DIW, and dried with nitrogen gas. FCs were constructed by securing two cleaned coverslips with double-sided tape (400P50; Kyodo Giken Chemical Co., Ltd., Saitama, Japan) and attaching 200-μl pipet tips as reservoirs41. The width and length of each channel were 3.5 mm and 15 mm, respectively, and the FC volume was ~2.6 µl.

Casein, kinesin and MT solutions were sequentially introduced into the FC and incubated for 5–10 min at RT. MTs started gliding after injection of an ATP solution consisting of 0.5 mM ATP in BRB80 with 0.30 mg ml−1 casein and an O2-scavenging system composed of 8.0 µg ml−1 catalase, 25 mM d-glucose, 20 µg ml−1 glucose oxidase, 1% β-ME, 20 mM DTT, 3.0 mM 1,1′-ferrocenedimethanol (322-49071; Wako Pure Chemical Industries, Ltd.), 10% glycerol, and 20 µM taxol, followed by application of an electric field with an average intensity of 7 kV m−1 (E3612A; Agilent Technologies, Tokyo, Japan).

Optical imaging and analysis

MTs and labeled molecules were observed under an IX71 or IX73 inverted epifluorescence microscope (Olympus, Tokyo, Japan) with an excitation filter (GFP/DsRed-A-OMF; Opto-Line International, Inc., Wilmington, MA, USA), absorbance filter (A11400-04; Hamamatsu Photonics, Hamamatsu, Japan), charge-coupled device camera (ORCA-D2; Hamamatsu Photonics), and 60× (NA 1.35) and 100× (NA 1.4) oil-immersion objectives. Exposure time was 500 ms (1 frame/s) using a ND6 filter with a shutter (VMM-D3; Uniblitz, Rochester, NY, USA). Optical images were stored as sequential image files in TIFF format using HCImage software (Hamamatsu Photonics). B-seed lengths > 0.5 µm were measured using ImageJ software (National Institutes of Health, Bethesda, MD, USA) with the Lines8 plug-in. Trajectories were defined by tracking MT leading tips with the Mark2 image analysis software (provided by Dr. Kenya Furuta, National Institute of Information and Communications Technology, Kobe, Japan) at the sampling rate of 0.5 frame/s. Coordinate data were exported to MATLAB software (MathWorks, Natick, MA, USA); each trajectory was fitted with equation (6) by a least squares method, and A and R2 values were exported through a custom-written MATLAB algorithm.

Author Contributions

N.I., E.M. and R.Y. designed the experiments. N.I. and S.A. performed the experiments and analyzed data. N.I., S.A., T.N., H.S., H.K., E.M. and R.Y. discussed and interpreted the results. N.I., S.A. and R.Y. wrote the paper. All authors have approved the final version of the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep07669-s1.pdf (478.5KB, pdf)
Supplementary Information

Movie S1

Download video file (3.6MB, avi)
Supplementary Information

Movie S2

Download video file (2.8MB, avi)
Supplementary Information

Movie S3

Download video file (9.8MB, avi)

Acknowledgments

This research was partially supported by Precursory Research for Embryonic Science and Technology (PRESTO) from the Japan Science and Technology Agency (JST); Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number 25709018; Kyoto University Supporting Program for Interaction-Based Initiative Team Studies (SPIRITS) as part of the Program for Promoting the Enhancement of Research Universities, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. N.I. is supported by Grant-in-Aid for JSPS Fellows (26·2439).

References

  1. Schnitzer M. J. & Block S. M. Kinesin hydrolyses one ATP per 8-nm step. Nature 388, 386–390 (1997). [DOI] [PubMed] [Google Scholar]
  2. Rahim M. K. A., Fukaminato T., Kamei T. & Tamaoki N. Dynamic photocontrol of the gliding motility of a microtubule driven by kinesin on a photoisomerizable monolayer surface. Langmuir 27, 10347–10350 (2011). [DOI] [PubMed] [Google Scholar]
  3. Bachand G. D. et al. Assembly and transport of nanocrystal CdSe quantum dot nanocomposites using microtubules and kinesin motor proteins. Nano Lett. 4, 817–821 (2004). [Google Scholar]
  4. Ramachandran S., Ernst K. H., Bachand G. D., Vogel V. & Hess H. Selective loading of kinesin-powered molecular shuttles with protein cargo and its application to biosensing. Small 2, 330–334 (2006). [DOI] [PubMed] [Google Scholar]
  5. Taira S. et al. Selective detection and transport of fully matched DNA by DNA-loaded microtubule and kinesin motor protein. Biotechnol. Bioeng. 95, 533–538 (2006). [DOI] [PubMed] [Google Scholar]
  6. Fischer T., Agarwal A. & Hess H. A smart dust biosensor powered by kinesin motors. Nat. Nanotechnol. 4, 162–166 (2009). [DOI] [PubMed] [Google Scholar]
  7. Hiyama S., Moritani Y., Gojo R., Takeuchi S. & Sutoh K. Biomolecular-motor-based autonomous delivery of lipid vesicles as nano- or microscale reactors on a chip. Lab Chip 10, 2741–2748 (2010). [DOI] [PubMed] [Google Scholar]
  8. van den Heuvel M. G., de Graaff M. P. & Dekker C. Molecular sorting by electrical steering of microtubules in kinesin-coated channels. Science 312, 910–914 (2006). [DOI] [PubMed] [Google Scholar]
  9. Lin C. T., Kao M. T., Kurabayashi K. & Meyhofer E. Self-contained, biomolecular motor-driven protein sorting and concentrating in an ultrasensitive microfluidic chip. Nano Lett. 8, 1041–1046 (2008). [DOI] [PubMed] [Google Scholar]
  10. Hutchins B. M., Platt M., Hancock W. O. & Williams M. E. Directing transport of CoFe2O4-functionalized microtubules with magnetic fields. Small 3, 126–131 (2007). [DOI] [PubMed] [Google Scholar]
  11. van den Heuvel M. G., de Graaff M. P. & Dekker C. Microtubule curvatures under perpendicular electric forces reveal a low persistence length. Proc. Natl. Acad. Sci. U.S.A. 105, 7941–7946 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dujovne I., van den Heuvel M., Shen Y., de Graaff M. & Dekker C. Velocity modulation of microtubules in electric fields. Nano Lett. 8, 4217–4220 (2008). [DOI] [PubMed] [Google Scholar]
  13. Kim T., Kao M. T., Hasselbrink E. F. & Meyhofer E. Active alignment of microtubules with electric fields. Nano Lett. 7, 211–217 (2007). [DOI] [PubMed] [Google Scholar]
  14. Hiratsuka Y., Tada T., Oiwa K., Kanayama T. & Uyeda T. Q. Controlling the direction of kinesin-driven microtubule movements along microlithographic tracks. Biophys. J. 81, 1555–1561 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Clemmens J., Hess H., Howard J. & Vogel V. Analysis of microtubule guidance in open microfabricated channels coated with the motor protein kinesin. Langmuir 19, 1738–1744 (2003). [Google Scholar]
  16. Agayan R. R. et al. Optimization of isopolar microtubule arrays. Langmuir 29, 2265–2272 (2013). [DOI] [PubMed] [Google Scholar]
  17. Kim T., Meyhofer E. & Hasselbrink E. F. Biomolecular motor-driven microtubule translocation in the presence of shear flow: modeling microtubule deflection due to shear. Biomed. Microdevices 9, 501–511 (2007). [DOI] [PubMed] [Google Scholar]
  18. Nitta T., Tanahashi A. & Hirano M. In silico design and testing of guiding tracks for molecular shuttles powered by kinesin motors. Lab Chip 10, 1447–1453 (2010). [DOI] [PubMed] [Google Scholar]
  19. Korten T. & Diez S. Setting up roadblocks for kinesin-1: mechanism for the selective speed control of cargo carrying microtubules. Lab Chip 8, 1441–1447 (2008). [DOI] [PubMed] [Google Scholar]
  20. He S., Lam A. T., Jeune-Smith Y. & Hess H. Modeling negative cooperativity in streptavidin adsorption onto biotinylated microtubules. Langmuir 28, 10635–10639 (2012). [DOI] [PubMed] [Google Scholar]
  21. Jeune-Smith Y. & Hess H. Engineering the length distribution of microtubules polymerized in vitro. Soft Matter 6, 1778–1784 (2010). [Google Scholar]
  22. Pitard B. et al. Virus-sized self-assembling lamellar complexes between plasmid DNA and cationic micelles promote gene transfer. Proc. Natl. Acad. Sci. U.S.A. 94, 14412–14417 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Smith S. B. & Bendich A. J. Electrophoretic charge density and persistence length of DNA as measured by fluorescence microscopy. Biopolymers 29, 1167–1173 (1990). [DOI] [PubMed] [Google Scholar]
  24. Gurrieri S., Smith S. B. & Bustamante C. Trapping of megabase-sized DNA molecules during agarose gel electrophoresis. Proc. Natl. Acad. Sci. U.S.A. 96, 453–458 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Laue T. M. et al. Insights from a new analytical electrophoresis apparatus. J. Pharm. Sci. 85, 1331–1335 (1996). [DOI] [PubMed] [Google Scholar]
  26. Keyser U. F. et al. Direct force measurements on DNA in a solid-state nanopore. Nat. Phys. 2, 473–477 (2006). [Google Scholar]
  27. Mazur S., Chen C. Y. & Allison S. A. Modeling the electrophoresis of short duplex DNA: Counterions K+ and Tris+. J. Phys. Chem. B. 105, 1100–1108 (2001). [Google Scholar]
  28. Stigter D. Shielding effects of small ions in gel electrophoresis of DNA. Biopolymers 31, 169–176 (1991). [DOI] [PubMed] [Google Scholar]
  29. Butt H.-J., Graf K. & Kappl M. Physics and chemistry of interfaces. 1st edn, 49 (Wiley-VCH, Weinheim, 2003). [Google Scholar]
  30. van Dorp S., Keyser U. F., Dekker N. H., Dekker C. & Lemay S. G. Origin of the electrophoretic force on DNA in solid-state nanopores. Nat. Phys. 5, 347–351 (2009). [Google Scholar]
  31. Dinu C. Z. et al. Parallel manipulation of bifunctional DNA molecules on structured surfaces using kinesin-driven microtubules. Small 2, 1090–1098 (2006). [DOI] [PubMed] [Google Scholar]
  32. Caruso F., Rodda E., Furlong D. N., Niikura K. & Okahata Y. Quartz crystal microbalance study of DNA immobilization and hybridization for nucleic Acid sensor development. Anal. Chem. 69, 2043–2049 (1997). [DOI] [PubMed] [Google Scholar]
  33. Gittes F., Mickey B., Nettleton J. & Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 120, 923–934 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hawkins T. L., Sept D., Mogessie B., Straube A. & Ross J. L. Mechanical properties of doubly stabilized microtubule filaments. Biophys. J. 104, 1517–1528 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Venier P., Maggs A. C., Carlier M. F. & Pantaloni D. Analysis of Microtubule Rigidity Using Hydrodynamic Flow and Thermal Fluctuations. J. Biol. Chem. 269, 13353–13360 (1994). [PubMed] [Google Scholar]
  36. Mickey B. & Howard J. Rigidity of microtubules is increased by stabilizing agents. J. Cell Biol. 130, 909–917 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Pampaloni F. et al. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. U.S.A. 103, 10248–10253 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Janson M. E. & Dogterom M. A bending mode analysis for growing microtubules: evidence for a velocity-dependent rigidity. Biophys. J. 87, 2723–2736 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Felgner H., Frank R. & Schliwa M. Flexural rigidity of microtubules measured with the use of optical tweezers. J. Cell Sci. 109, 509–516 (1996). [DOI] [PubMed] [Google Scholar]
  40. Kikumoto M., Kurachi M., Tosa V. & Tashiro H. Flexural rigidity of individual microtubules measured by a buckling force with optical traps. Biophys. J. 90, 1687–1696 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Kim T., Kao M. T., Hasselbrink E. F. & Meyhofer E. Nanomechanical model of microtubule translocation in the presence of electric fields. Biophys. J. 94, 3880–3892 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Hunt A. J., Gittes F. & Howard J. The force exerted by a single kinesin molecule against a viscous load. Biophys. J. 67, 766–781 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Jeffrey D. J. & Onishi Y. The slow motion of a cylinder next to a plane wall. Q. J. Mech. Appl. Math. 34, 129–137 (1981). [Google Scholar]
  44. Kerssemakers J., Howard J., Hess H. & Diez S. The distance that kinesin-1 holds its cargo from the microtubule surface measured by fluorescence interference contrast microscopy. Proc. Natl. Acad. Sci. U.S.A. 103, 15812–15817 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Mori S. & Okamoto H. An improved method of determining the zeta-potential of mineral particles by micro-electrophoresis. Fusen 27, 117–126 (1980). [Google Scholar]
  46. Howard J. & Hyman A. A. Preparation of marked microtubules for the assay of the polarity of microtubule-based motors by fluorescence microscopy. Methods Cell. Biol. 39, 105–113 (1993). [DOI] [PubMed] [Google Scholar]
  47. Schmidt C. et al. Tuning the "roadblock" effect in kinesin-based transport. Nano Lett. 12, 3466–3471 (2012). [DOI] [PubMed] [Google Scholar]
  48. Schroeder V., Korten T., Linke H., Diez S. & Maximov I. Dynamic guiding of motor-driven microtubules on electrically heated, smart polymer tracks. Nano Lett. 13, 3434–3438 (2013). [DOI] [PubMed] [Google Scholar]
  49. Felgner H. et al. Domains of neuronal microtubule-associated proteins and flexural rigidity of microtubules. J. Cell Biol. 138, 1067–1075 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Williams R. C. Jr & Lee J. C. Preparation of tubulin from brain. Methods Enzymol. 85 Pt B 376–385 (1982). [DOI] [PubMed] [Google Scholar]
  51. Hyman A. et al. Preparation of modified tubulins. Methods Enzymol. 196, 478–485 (1991). [DOI] [PubMed] [Google Scholar]
  52. Yokokawa R., Tarhan M. C., Kon T. & Fujita H. Simultaneous and bidirectional transport of kinesin-coated microspheres and dynein-coated microspheres on polarity-oriented microtubules. Biotechnol. Bioeng. 101, 1–8 (2008). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep07669-s1.pdf (478.5KB, pdf)
Supplementary Information

Movie S1

Download video file (3.6MB, avi)
Supplementary Information

Movie S2

Download video file (2.8MB, avi)
Supplementary Information

Movie S3

Download video file (9.8MB, avi)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES