Free-energy landscape of ion-channel voltage-sensor–domain activation

Significance

Voltage-gated cation channels (VGCCs) shape cellular excitability. Their working cycle involves the complex conformational change of modular protein units called voltage sensor domains (VSDs). For over 40 y, these rearrangements have been recorded as “gating” currents, the intensities and kinetics of which are unique signatures of VGCC function. We show that the atomistic description of VSD activation obtained by molecular dynamics simulations and free-energy calculations is consistent with the phenomenological models adopted to account for the macroscopic observables measured by electrophysiology. Our findings pave the way for in silico studies of the VGCC electrophysiological response and hold promise to uncover the molecular underpinnings of inherited channelopathies and modulation of VGCCs by drugs and toxins.

Abstract

Voltage sensor domains (VSDs) are membrane-bound protein modules that confer voltage sensitivity to membrane proteins. VSDs sense changes in the transmembrane voltage and convert the electrical signal into a conformational change called activation. Activation involves a reorganization of the membrane protein charges that is detected experimentally as transient currents. These so-called gating currents have been investigated extensively within the theoretical framework of so-called discrete-state Markov models (DMMs), whereby activation is conceptualized as a series of transitions across a discrete set of states. Historically, the interpretation of DMM transition rates in terms of transition state theory has been instrumental in shaping our view of the activation process, whose free-energy profile is currently envisioned as composed of a few local minima separated by steep barriers. Here we use atomistic level modeling and well-tempered metadynamics to calculate the configurational free energy along a single transition from first principles. We show that this transition is intrinsically multidimensional and described by a rough free-energy landscape. Remarkably, a coarse-grained description of the system, based on the use of the gating charge as reaction coordinate, reveals a smooth profile with a single barrier, consistent with phenomenological models. Our results bridge the gap between microscopic and macroscopic descriptions of activation dynamics and show that choosing the gating charge as reaction coordinate masks the topological complexity of the network of microstates participating in the transition. Importantly, full characterization of the latter is a prerequisite to rationalize modulation of this process by lipids, toxins, drugs, and genetic mutations.

Voltage sensor domains (VSDs) are key players of diverse physiological processes involving changes in transmembrane (TM) potential: electrical impulse propagation, cellular contraction, and activation of metabolic pathways are only few possible examples (1). As such, they are the target of toxins produced by many venomous animals (2) and are becoming a popular target for drug development (3). Most of what we know about VSDs comes from the study of voltage-gated cation channels, mainly potassium and sodium selective ones, each containing four distinct VSDs. VSDs are formed by a bundle of four TM helices (S1–S4) (4–7). The S4 segment contains a series of positively charged residues, called gating charges, arranged along its inward-facing side. This segment confers to VSDs their sensitivity to external voltages, by translating vertically in response to voltage changes (Fig. 1A), and determines their voltage dependency, which is tuned by the number of S4 charges and their specific interactions with their environment (8, 9).

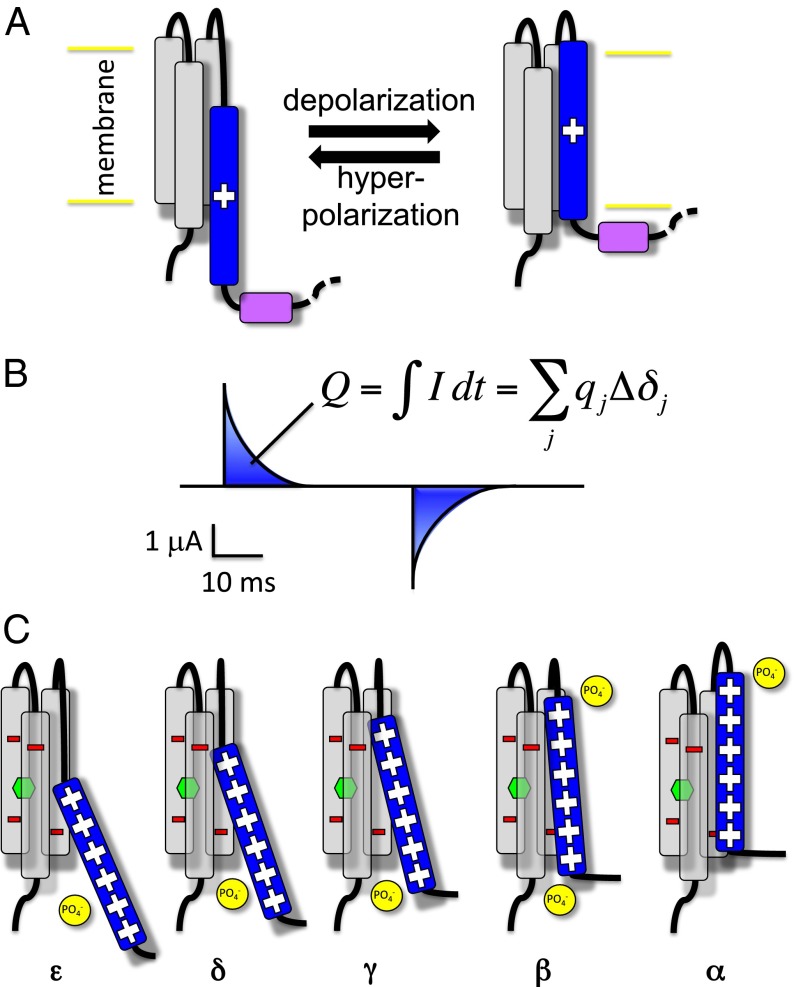
Fig. 1.

Activation of voltage sensor domains (A) VSDs are formed by four transmembrane helices. Upon changes in the membrane potential, the positively charged S4 (blue) moves across the membrane relative to a static S1–S3 bundle (gray), transmitting the electrical signal to a linker peptide (purple). (B) This movement is reported by the measurement of transient currents called gating currents. The time integral of these, the gating charge $Q$, can be expressed as the sum of the contributions of the charges of the system. (C) Cartoon depiction of the stepwise activation of the Kv1.2 VSD. From the most resting (ε) to the most activated conformation (α), S4 proceeds in a ratchet-like upward motion in which its positively charged residues jump from a negative binding site to the next. The negative charges of S1–S3 are depicted in red and the ones of the lipid headgroups in yellow. The hydrophobic gasket at the center of the VSD is represented by a green hexagon.

For several decades, the molecular details of the VSD activation mechanism have been investigated extensively using diverse experimental techniques such as single-channel and macroscopic current measurements, mutagenesis (cysteine accessibility experiments and disulfide or cadmium bridging experiments), chimeragenesis, fluorescence or luminescence resonance energy transfer experiments, investigations of toxin binding to VSDs, electron paramagnetic resonance measurements of spin label mobility, and alteration of the lipid matrix embedding the channel (see ref. 10 for an extensive review). A large part of this work has focused on a remarkable property of VGCC function: during the onset of depolarization and upon repolarization of the membrane, structural rearrangements of VSDs generate positive and negative transient gating currents, respectively (11–13). The time integral of these on- and off-gating currents reflects the gating charge ($Q$) moved by the voltage sensors in response to changes in the TM potential (Fig. 1B). Analyses of gating currents have provided estimates of the number of elementary charges involved in the gating of a single channel (14), in agreement with mutagenesis studies (15, 16). Interestingly, fluctuation analyses revealed that gating currents result from a series of discrete transitions (17, 18). Accordingly, discrete-state Markov models (DMMs) gained popularity to describe gating kinetics (19). In this framework, rate constants are treated as free adjustable parameters, and are interpreted in light of Eyring’s transition state theory (20). The ability of DMMs to faithfully reproduce electrophysiology recordings has determined their tremendous success and made them standard tools to analyze activation kinetics on physiologically relevant timescales (21).

The quest to link the putative kinetic states of these phenomenological models to conformational states of the VSD started with simplified models constrained by early mutagenesis experiments (22–24) and culminated in recent years with high-resolution molecular models resulting from ingenious experiments such as double mutant experiments (25), charge reversal mutagenesis (26), disulfide locking (27, 28), cadmium binding (29), and X-ray crystallography (6). Additionally, independent long timescale molecular dynamics (MD) simulations suggested the existence of metastable intermediate states compatible with this large body of experimental data (30–32). According to the emerging consensus, each VSD conformational state (resting, intermediates, and activated) is stabilized by a different network of salt bridges involving on one hand the gating charges and, on the other, negatively charged residues from S1–S3 along with the head groups of neighboring lipid molecules. During activation, each gating charge jumps from a negatively charged binding site to the next in an upward ratchet-like motion, displacing S4 across the membrane toward the extracellular medium (Fig. 1C) (26, 31–38). It is noteworthy, however, that the only conformational state of the VSD solved experimentally is the activated state (an exception is constituted by Ci-VSP, a voltage sensor with a possibly different activation mechanism). The structures of other states, including the ones studied in the present work, are theoretical models that still lack full experimental validation. Despite the fact that the different techniques mentioned above are able to probe the VSD's conformation at atomic resolution, they are not, in general, suitable to quantitatively assess the stability of the conformational states. Indeed, all of the aforementioned experimental techniques involve mutations of selected residues that alter the intrinsic equilibrium between states; typical MD simulations, on the other hand, suffer from severe limitations in statistical sampling and thus are not able to distinguish between slowly diffusive regions of configurational space and local free-energy minima. Thus, the precise conformational ensemble corresponding to each distinct kinetic state remains to be characterized.

The equilibrium between conformational states of a VSD is determined by their free-energy difference, i.e., by the reversible work performed when going from one state to another. The reversible work can be expressed as a sum involving the intrinsic Gibbs free energy (i.e., the conformational free energy) and contributions arising from generalized thermodynamic forces such as voltage and chemical potential as: $\delta W=\delta G+V\delta Q+Q\delta V+\mu \delta n+\cdots$ In a voltage-clamped setup such as the one used in electrophysiology experiments, i.e., in the presence of a constant voltage V, this expression simplifies to $\delta W=\delta G+V\delta Q$ (39, 40). The second term of this equation, the electrostatic contribution to the reversible work, is experimentally characterized by measuring the instantaneous response of the membrane-embedded channel to the applied V, i.e., by the recording of gating currents and their time integral, $Q$ (11). Using the available atomistic models of voltage-gated ion channels, it is rather straightforward to calculate the electrostatic contribution to the reversible work along the activation pathway (32, 41–43). In contrast, calculating the Gibbs free energy, which results from the intrinsic conformational equilibrium of the system, is a challenging task. MD simulations enable, in principle, sampling of the equilibrium probability distribution provided that the obstacle of short timescales can be overcome. Crucial steps in this direction have been taken by adopting two alternative strategies: Kim and Warshel used coarse graining in an implicit membrane and solvent and approximated the conformational free energy to solely the hydrophobic contribution (44); Schwaiger et al., on the other hand, used an atomistic description of the system together with umbrella sampling along one of the degrees of freedom associated with activation, namely the vertical displacement of S4 (45). Here, we compute the energetics of the activation landscape of the Kv1.2 VSD using atomistic MD simulations and an enhanced sampling approach, namely well-tempered metadynamics. To do so, we initially enhance the sampling along abstract, custom-designed collective variables, in a manner such that we make minimal assumptions about the activation mechanism. We then project the free energy obtained along $Q$, the gating charge degree of freedom, which is the experimental reaction coordinate (RC). Specifically, we investigate the first transition of the activation mechanism of the K⁺ selective channel Kv1.2, described in ref. 31, which involves the transition from the putative resting state ε to the putative first intermediate state δ.

Modeling Strategy

Among possible schemes for computing the free energy, we have chosen well-tempered metadynamics, a method that enhances sampling by adding a repulsive history-dependent potential along a set of a few RCs (46). This potential discourages the system from assuming repeatedly the same value of the RC, thus effectively increasing the scope of exploration of the configuration space. A proper choice of the history-dependent potential provides an increased sampling rate of rare events and an estimate of the free-energy profile along the chosen RCs. The success of this method relies crucially on the choice of the RCs or collective variable(s) (CVs) along which the repulsive bias is applied. Because the electrostatic potential is the driving force for the conformational change, an intuitive choice for the RC is its conjugate thermodynamic variable, the gating charge $Q$. This particular choice ensures that the free-energy difference between the two terminal states corresponds to the reversible electrical work performed on/by the system. However, because $Q$ depends on the position of all the charged particles of the system (SI Materials and Methods), applying a biasing potential on this CV results in external forces acting uniformly on all particles with the same charge. Hence this biasing potential barely increases the sampling rate of the activation transition, because the latter relies on specific displacements of few selected particles.

To circumvent this problem, we have adopted a two-stage strategy whereby a free-energy surface is first obtained by biasing a set of abstract CVs and is then recomputed as a function of $Q$, thanks to a mathematically rigorous reweighting procedure. This approach allows us to achieve optimal sampling of the conformational space and, at the same time, to characterize the Gibbs free energy of experimentally relevant thermodynamic states. To design a set of CVs enabling an enhanced sampling of the activation pathway, we considered the two major molecular determinants of VSD activation, as determined in ref. 28: (i) the unbinding (binding) of the gating charge (R_i) from (to) the initial (final) binding site and (ii) the spatial translation of the gating charges along the vector between two binding sites (Fig. 2). Hence, progression along the activation pathway is mathematically described by expressions of the form

$$C{V}_{R_i}=(B_{fin}-B_{init})+\kappa \hspace{0.17em}x,$$ [1]

where B_init and B_fin are variables reporting the unbinding (B = 0) or binding (B = 1) of charge R_i to the initial and final binding sites, respectively; x is the spatial translation of the charge along the vector joining the two binding sites. κ makes Eq. 1 dimensionally homogeneous and can be used to fine-tune the relative weight of the two components (SI Materials and Methods).

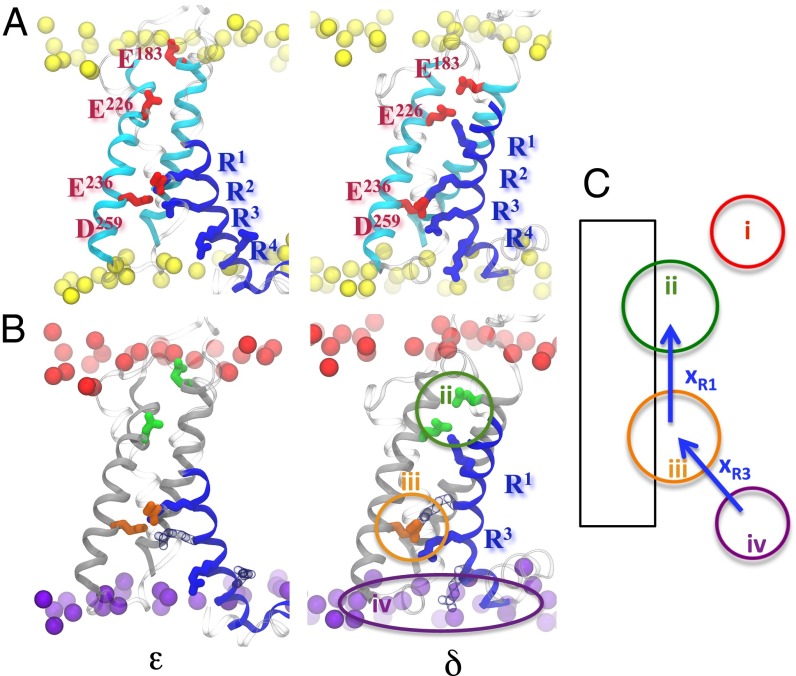
Fig. 2.

ε/δ-transition in the 2D CV space. (A) The activation step involves a concerted rearrangement of salt bridges between the positive charges of S4, R1–R6 (blue) and the negative charges of S1–S3 (red) and of the lipid headgroups (yellow). (B) Due to the spatial clustering of negative charges, four binding sites can be identified: (i) top phosphate groups (red); (ii) top protein binding site (green); (iii) bottom protein binding site (orange); and (iv) bottom phosphate groups (purple). (C) In this space, during the ε/δ-transition, R1 transfers from site iii to ii and R3 from sites iv to iii.

Taking advantage of the spatial proximity of several negatively charged groups of the VSD, the number of binding sites can be reduced to four: (i) phosphate groups of the top lipid layer; (ii) top protein binding site comprising E183 and E226; (iii) bottom protein binding site comprising E236 and D259; and (iv) phosphate groups of the bottom lipid bilayer (Fig. 2B). The binding collective variables B_init and B_fin depends on the coordination number S between the gating charges and the negative binding sites via a sigmoid function (hence the quasi-binary, on/off behavior): $B\left(S\right)=1/1+a{e}^{-b\left(S-c\right)}$, with $S\left(r_{ij}\right)={\displaystyle {\sum }_i{\displaystyle {\sum }_j\exp \left[-{\left(r_{ij}-d_0\right)}^2/2r_0^2\right]}}$, where i and j are the indices of the atoms belonging to the positively and negatively charged groups, respectively and r_ij is the distance between them. The parameters d₀, r₀, a, b, and c were chosen to fit the equilibrium distributions of bound pairs and are listed in Table S1. In this framework, each gating charge transfer can be treated separately. The transition between the models describing the putative resting state ε and first intermediate δ is thus investigated using two CVs: CV_R1 describes the transfer of R1 (R294) from binding sites iii to ii and CV_R3 the one of R3 (R300) from binding sites iv to iii (Fig. 2C).

Free-Energy Surface in the Extended Collective Variable Space

Multiple walkers well-tempered metadynamics reveals that this choice of CVs enables efficient sampling of the configurational space, allowing the system to explore conformations outside the initial stable configuration basins (Fig. 3A). Indeed, whereas all trajectories started from configurations within the ε and δ basins (21 walkers each), the other regions of the 2D space are sampled over the course of 4 μs. Interestingly, out of the 42 walkers, 10 of them fully cross the barrier separating the two basins (5 in the δ => ε direction and 5 in the ε => δ direction). The resulting free-energy surface reveals that the most favorable activation pathways involves either the sequential transition of R1 and R3 or the concerted transfer of both charges simultaneously, the transfer of R3 before R1 being forbidden.

Fig. 3.

Free-energy landscape of the ε/δ-transition. (A) Free-energy map in 2D CV_R1/CV_R3 space. Regions of low free energy are depicted in cold colors (green to blue) and regions of high free energy in hot colors (orange to red). (B) Mapping of the average value of the gating charge $Q$ as a function of CV_R1 and CV_R3. (C) Reweighted free-energy profile along $Q$. The free-energy profiles at −100 mV and +100 mV were obtained by adding a linear component to the profile obtained under 0 mV using $\mathrm{\Delta }\text{G}\left(Q,V\right)=\mathrm{\Delta }\text{G}\left(Q,V=0\right)-\text{QV}$. Starting with the geometrical definition of the two putative activation intermediates ε and δ, we have obtained two larger ensembles of structures corresponding to stable thermodynamic states of the experimental (voltage-clamped) ensemble E and Δ. All free energies are reported in kcal/mol.

Importantly, the landscape is rough: numerous local minima are apparent throughout the surface, several of which feature comparable free energies. Of note is the set of metastable configurations in the region surrounding the ε and δ states: the ensemble corresponding to the thermodynamic ground state (regions colored in green in Fig. 3A) encompasses several distinct configurations of R1 and R3. The presence of nearly degenerate states can be attributed, at least in part, to the different possible binding geometries involving the guanidinium and carboxylate groups, i.e., stacked, single, or bidentate H bond, with or without participation of one or more water molecules. Therefore, the bumpiness of the landscape ultimately reflects the combinatorial diversity resulting from the presence of multiple gating charges and multiple binding modes. As a consequence, several possible pathways of comparable free energy can potentially link any two points on the surface. This suggests that a coarser description of the thermodynamic states may be appropriate and raises the possibility that a projection of the configurational space onto a different manifold can potentially give rise to a smoother free-energy landscape.

Projection of the Free-Energy Surface onto the Gating Charge $\mathit{Q}$ Reaction Coordinate

To characterize the reversible work needed to perform the transition, we calculated the free energy as a function of the gating charge by calculating the value of $Q$ for each configuration visited during the simulation. $Q$ can be expressed as a sum of contributions from each individual charge i as $Q={\displaystyle {\sum }_i{q}_i\mathrm{\cdot }\left[\mathrm{\delta }\left({\mathit{r}}_i^{{\lambda }_2}\right)-\delta \left({\mathit{r}}_i^{{\lambda }_1}\right)\right]}$. The function $\delta \left({\mathit{r}}_i^{\lambda }\right)$, the so-called electrical distance, is evaluated at the position r_i of charge q_i in conformation λ and is defined as the linear variation of the electrostatic potential ϕ with the applied potential V: $\delta \left(\mathit{r}\right)=\left(\partial /\partial V\right)\varphi \left(\mathit{r}\right)$ (Fig. S1).

The average value of $Q$ for each point in the 2D CV space is shown in Fig. 3B. To calculate the free-energy profile along this new CV, we used all of the configurations visited during the biased metadynamics trajectories after assigning an appropriate weight to each of them, as described in Bonomi et al. (47). Strikingly, the free energy as a function of $Q$ is extremely smooth (Fig. 3C). The profile shows two major stable states, separated by a gating charge of ∼0.7 e. Thus, by starting from a purely geometrical definition of the two putative activation intermediates, we have obtained two larger ensembles of structures both encompassing the starting configurations, and corresponding to stable thermodynamic states of the experimental (voltage-clamped) ensemble. Hereafter, we will call these states E and Δ. E and Δ have defined values of the gating charge but feature heterogeneous patterns of salt bridges. Indeed, it is apparent from Fig. 3B that the value of $Q$ largely depends on a combination of the position of R1 and R3.

The E and the Δ state are of similar stability. The barrier separating the two states is ∼5 kcal/mol. These free-energy differences are consistent with a situation in which equilibrium properties and kinetics of activation are modulated by an external potential of the order of tens of mV. Fig. 3C shows the reshaping of the profile by an applied potential of ±100 mV when the contribution of the external field to the electrostatic energy is added using the relationship $\mathrm{\Delta }\text{G}\left(Q,V\right)=\mathrm{\Delta }\text{G}\left(Q,V=0\right)-\text{QV}$ (39). It is apparent that potentials of these magnitudes alter the equilibrium free-energy values and the height of the barrier between the states by a few kcal/mol. Note that despite the vastness of the configurational space, we obtained a rather converged free-energy profile (Fig. S2): over the course of the last 3 μs, the free-energy difference between the two stable minima showed an oscillatory behavior with fluctuations of the order of ∼0.2 kcal/mol.

Discussion

The task of quantitatively characterizing the conformational free energy associated with the VSD activation is hampered by limitations in both the experimental and computational approaches to the problem. Electrophysiology typically relies on the analysis of macroscopic currents to infer the parameters of a Markov chain encompassing the functional states of the VSD. Whereas this top-down approach is firmly rooted in a quantitative analysis of experimental observables, it hinges on two strong assumptions: (i) separation of timescales: few free-energy barriers are larger than the typical roughness of the landscape and (ii) parsimony: the number of states is the minimum sufficient to fit the electrophysiology data. Computational approaches are, in principle, able to offer a complementary perspective: atomistic MD modeling can be used to obtain the thermodynamic behavior of the system as well as explore the microscopic dynamics. However, being based on the need to thoroughly sample the configuration space, this approach suffers from either the limited timescales accessible to atomistic MD simulations or the additional approximations implied by a coarse-grain description of the system; both these issues cause uncertainties in the free-energy surface.

Here, we bridge the gap between top-down and bottom-up approaches and reconcile the macroscopic and microscopic views of VSD activation dynamics by using two distinct levels of coarse graining. We first use well-tempered metadynamics to bias the exploration of the configurational space along aptly defined CVs describing the activation process; we then use the ensemble of configurations explored in the metadynamics run to calculate the free-energy profile along the experimentally relevant degree of freedom, the gating charge $Q$. The computational complexity of this task requires an extensive use of high-performance computing facilities; in particular, for this specific transition ∼4 μs of MD trajectory were collected. However, thanks to massively parallel simulations (here the free-energy surface was calculated using 42 semiindependent walkers), completion of the calculations can be obtained in few days on large supercomputers.

The design of the first set of CVs was informed by our previous investigations of the activation process with the goal of finding the most parsimonious choice of variables (in terms of dimensionality) able to report all the major molecular events observed in previous MD trajectories of VSD activation, i.e., binding and unbinding and spatial displacement of the gating charges. Thus, at the heart of our modeling strategy is an informed guess about the manifold containing the reactive trajectories. As customary in metadynamics, the validity of this ansatz is verified a posteriori, by checking the convergence of the calculated free-energy surface and, specifically, the absence of hysteresis effects as the simulations progress. Our choice provides a reasonable tradeoff between the volume of configurational space over which statistics is collected (kept low by the small number of collective variables) and assumptions about the molecular degrees of freedom involved in the process. Importantly, despite the abstract nature of the collective variables involved, a clear and transparent physical picture of the process is recovered once the free-energy profile is recomputed as a function of the experimentally probed reaction coordinate, i.e., the gating charge $Q$. Concerning this modeling strategy, nonlinear dimensionality reduction approaches offer a viable alternative to our first supervised coarse-graining and, more in general, a fascinating perspective for studying complex biomolecular systems in an almost-reaction-coordinate-free fashion (48–53). Despite the potential of these approaches, they all rely on a set of empirical parameters that could potentially affect the nature of the nonlinear maps and, thus, the ability of recalculating the free-energy surface as a function of $Q$. Extensive testing will enable us to assess the applicability of these methods to problems as complex as the VSD activation.

This approach has enabled us to sample efficiently the configurational space of the first transition of the activation process of Kv1.2, i.e., the transition from the fully resting state ε to the first activation intermediate δ. Starting from a geometric description of the putative states, the simulations have explored the entire ensemble of microstates (distinct conformational states) contributing to the thermodynamically stable states E and Δ. The resulting free-energy surface is rough and features numerous local minima with several seemingly equiprobable pathways linking any two of them. This roughness is masked by a projection of the free-energy surface along the gating charge reaction coordinate; on this manifold, the first step of the activation process is described by two minima separated by a concave barrier of ∼5 kcal/mol. Because the variation of the total free energy can be written as $\delta W=\delta G+V\delta Q$, knowing $\delta G$ as a function of $Q$ allows us to compute the total free energy (and hence the relative population of the individual states) at any given voltage.

This framework can be naturally extended to the other three transitions of the Kv1.2 VSD activation (δ−γ, γ−β, and β−α). Along the δ–γ transition, R2 (R297) is transferred from binding sites iii to ii and R4 (R303) from binding sites iv to iii. Studying the γ−β and β−α transitions, however, introduces an additional level of complexity because of the transfer of one of the gating charges to the top lipid-binding site (site i). Indeed, during γ−β, R1 moves from binding sites ii to i, R3 moves from binding sites iii to ii, and K5 (K306) moves from binding sites iv to iii. Similarly, along the β−α transition, R2 moves from binding sites ii to i, R4 from binding sites iii to ii, and R6 (R309) from binding sites iv to iii. Thus, these transitions require the calculation of the free energy along one additional degree of freedom, corresponding to an exponential increase of the volume of the configurational space to be explored. Completion of this task will, however, enable us to assess the relative stability of each of the five thermodynamic states at any given voltage. In this respect, an interesting open question concerns the states populated at the physiologically relevant resting potential. In particular, whether or not the E state is populated at physiological conditions has been the object of a debate that has so far reached no consensus (54). Extending our calculations to the entire activation profile will enable us to provide a quantitative answer to this question. Another intriguing property that is potentially made accessible by our calculations is the kinetics of the process. With such a simple free-energy profile, indeed, we can use a derivation of Eyring’s transition state theory to compute the forward and backward kinetic constants associated with the process. This simply amounts to calculating the diffusion coefficient of the reaction coordinate $Q$ in the barrier region. Additional insight could be gathered by solving a generalized Langevin equation in the space spanned by the collective variables CV_R1 and CV_R3 (by computing the position-dependent diffusion coefficient and combining this information with the free energy). This would allow us to assess, at the same time, the equilibrium population of the various microstates at any given voltage and the time-dependent response of the system to external voltage pulses.

An earlier set of experiments that is interesting to compare with our results is the ones measuring the fast component of the gating charge upon pulse application (55). Using Kramers’ large-friction theory to fit the voltage dependence of the rate constants, Sigg et al. were able to infer the free-energy profile governing the behavior of a single gating particle, which is then directly comparable to our free-energy profile along $Q$. Interestingly, both the height of the activation barrier (∼5 kcal/mol) and the magnitude of the gating charge between the two states E and Δ (∼0.7 e) are in excellent agreement. The other features (curvature at the minima and the barrier, for example) will have to be further examined in the context of the entire channel and upon completion of the full free-energy profile of activation.

Our results shed light also on the presence of voltage-independent relaxation processes (56). Using non–voltage-driven probes, such as the change in environment of a fluorophore attached to the extracellular end of S4, Villalba-Galea et al. revealed the presence of voltage-independent conformational changes. The proposed explanation of this relaxation was a change in the secondary structure of S4 (α-helical to 3₁₀ helical). Despite the fact that we cannot confirm or disprove this hypothesis, the roughness of the landscape suggests that voltage-independent relaxations can occur, even without major changes in secondary structure. Specifically, a conformational transition that does not involve a change in the value of the gating charge $Q$ is energetically uncoupled to the external potential and, as such, is voltage-independent; the presence of valleys separated by barriers potentially implies slow diffusion along voltage-uncoupled dimensions (for instance along CV_R3).

The free-energy landscape of VSD activation will be altered by changes in its environment. Indeed, because the VSD is mechanically coupled to the pore, our calculations do not provide an exact description of the VSD activation energetics in the context of the entire channel. However, we note that characterizing the intrinsic conformational equilibrium of VSD activation constitutes an important milestone toward a satisfactory understanding of the energetics of activation of the whole channel. Indeed this piece of information, together with a characterization of the intrinsic free energy of pore gating, will no doubt help to shed light on the energetic coupling between the domains. Moreover, other environmental factors such as the lipid composition of the embedding membrane can possibly affect the free-energy surface. Finally, a comment is in order concerning the potential ability of this approach to uncover the molecular determinants of VSD activation. In addition to providing a theoretical justification to the assumptions underlying the kinetic models of activation used to interpret electrophysiology recordings, our calculations unveil the ensemble of microscopic configurations contributing to each metastable thermodynamic state. This information is of crucial relevance for the study of any state-dependent modulatory agent such as mutations involved in channelopathies, binding of drugs, or toxins. Intriguingly, knowing the ensemble of conformations contributing to each thermodynamic state opens the door to the design of drugs that selectively stabilize a chosen state of the VSD.

Materials and Methods

VSD Models Generation.

To produce models of states of the Kv1.2 VSD other than the ones solved in the crystal structure (57), we used a procedure similar to the one described in Wood et al. (36). Building alignments in which the S4 stretch is shifted by three residues (corresponding to one helical turn) toward the N terminus produced a homology model of a first intermediate state downward of α, which we call β, using the nomenclature proposed in previous work (31). The alignments in which S4 is manually shifted by 6, 9, and 12 residues relative to the original alignment produced states closer to the resting state, called γ, δ, and ε.

System Preparation and MD Simulations.

The δ− and ε-state models of the VSD of Kv1.2 [residues 163 (S1) to 324 (S4–S5 linker)] were inserted in a fully hydrated 110 × 110 Ų 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine. The system was then ionized in 0.15 M NaCl. The systems were equilibrated under normal constant temperature and pressure conditions, i.e., at 298 K and under 1 atm (see SI Materials and Methods for details).

Well-Tempered Metadynamics.

The history-dependent repulsive potential added along the set of collective variables s(x) has the shape of a sum of Gaussians of form $V\left(s,t\right)={\displaystyle {\sum }_{t^{\prime }=t_G,2t_G,3t_G,\dots }^{t<t^{\prime }}W{e}^{-V\left(s\left(x\left(t^{\prime }\right),t^{\prime }\right)\right)/\mathrm{\Delta }T}\text{exp}\left(-{\displaystyle {\sum }_{i=1}^d\frac{{\left(s_i\left(x\right)-s_i\left(x\left(t^{\prime }\right)\right)\right)}^2}{2{\sigma }_i^2}}\right)},$ where W is the initial height of the Gaussian at its center, $\mathrm{\Delta }T$ is the decrease rate of the Gaussian height along CV exploration, and σ is its width at half-maximum height. Here, W is set to 0.1 kJ/mol, $\mathrm{\Delta }T$ to 30 k_BT, and σ to 0.15 for s(x)=CV_R1 and to 0.05 for s(x)=CV_R3. The metadynamics simulations were performed using the PLUMED2.0 (58) plugin patched to gromacs 4.6.5 (59).

Reweighting Procedure.

We used the procedure described in Bonomi et al. to calculate the time-dependent probability distribution of the conformations along the gating charge variable $Q$ and thus estimate the free-energy profile along this CV (47). Briefly, assuming that the system is at instantaneous equilibrium under the internal potential U(r) and the bias potential along a collective variable s(r), V(s(r)), the probability distribution at time t can be written as $P\left(r,t\right)=\frac{e^{-\beta \left\{U\left(r\right)+V\left(s\left(r\right),t\right)\right\}}}{{\displaystyle \int e^{-\beta \left\{U\left(r^{\prime }\right)+V\left(s\left(r^{\prime }\right),t\right)\right\}}d{r}^{\prime }}}$. P(r,t) can be expressed as a function of P₀(r), the Boltzmann distribution using $P\left(r,t\right)=e^{-\beta \left\{V\left(s\left(r\right),t\right)+c\left(t\right)\right\}}\mathrm{\cdot }{P}_0\left(r\right)$ where c(t) is the time-dependent bias offset: $c\left(t\right)=-\frac{1}{\beta }\text{log}\left(\frac{{\displaystyle \int e^{-\beta F\left(s\right)}ds}}{{\displaystyle \int e^{-\beta \left\{F\left(s\right)+V\left(s,t\right)\right\}}ds}}\right)$.

The biased distribution is evolved along time using $P\left(r,t+\mathrm{\Delta }t\right)=e^{-\beta \left\{\dot{V}\left(s\left(r\right),t\right)+\dot{c}\left(t\right)\right\}}\mathrm{\cdot }P\left(r,t\right)$, where the derivative of the time-dependent bias offset can be approximated by $\dot{c}\left(t\right)=-\langle \dot{V}\left(s,t\right)\rangle .$