Abstract
The nature of factors governing the tempo and mode of protein evolution is a fundamental issue in evolutionary biology. Specifically, whether or not interactions between different sites, or epistasis, are important in directing the course of evolution became one of the central questions. Several recent reports have scrutinized patterns of long-term protein evolution claiming them to be compatible only with an epistatic fitness landscape. However, these claims have not yet been substantiated with a formal model of protein evolution. Here, we formulate a simple covarion-like model of protein evolution focusing on the rate at which the fitness impact of amino acids at a site changes with time. We then apply the model to the data on convergent and divergent protein evolution to test whether or not the incorporation of epistatic interactions is necessary to explain the data. We find that convergent evolution cannot be explained without the incorporation of epistasis and the rate at which an amino acid state switches from being acceptable at a site to being deleterious is faster than the rate of amino acid substitution. Specifically, for proteins that have persisted in modern prokaryotic organisms since the last universal common ancestor for one amino acid substitution approximately ten amino acid states switch from being accessible to being deleterious, or vice versa. Thus, molecular evolution can only be perceived in the context of rapid turnover of which amino acids are available for evolution.
Keywords: molecular evolution, fitness landscape, epistasis
Introduction
Whether or not epistasis, a situation when fitness is dependent on the interaction of alleles, plays a major role in molecular evolution is the subject of scrutiny and debate (de Visser et al. 2011; Lehner 2011; Breen et al. 2012; Hansen 2013; McCandlish et al. 2013; de Visser and Krug 2014). Two types of approaches are being used to reveal the type and amount of epistasis in protein evolution: First, studies aiming to reconstruct recent evolutionary trajectories revealing potential epistatic interactions among substitutions that occurred recently (Weinreich et al. 2006; Bridgham et al. 2009; Lozovsky et al. 2009; Romero and Arnold 2009; Lunzer et al. 2010; Khan et al. 2011; Zhang et al. 2012; Covert et al. 2013); second, studies quantifying the degree of epistasis among substitutions that occurred across long evolutionary periods (Miyamoto and Fitch 1995; Huelsenbeck 2002; Kondrashov et al. 2002; Choi et al. 2005; Bazykin et al. 2007; Wang et al. 2007; Rogozin et al. 2008; Rokas and Carroll 2008; Bollback and Huelsenbeck 2009; Povolotskaya and Kondrashov 2010; Gloor et al. 2010; Soylemez and Kondrashov 2012; Naumenko et al. 2012; de Juan et al. 2013; Wellner et al. 2013). Such studies are often statistical in nature and usually cannot identify specific interactions, yet they provide a broader outlook on the nature of the fitness landscape across different areas of the sequence space. Many of these studies claimed that different aspects of molecular evolution are not compatible with evolutionary models devoid of epistatic interactions. However, the dynamics of protein sequence divergence has not been subject to modeling with explicit parameters of epistasis.
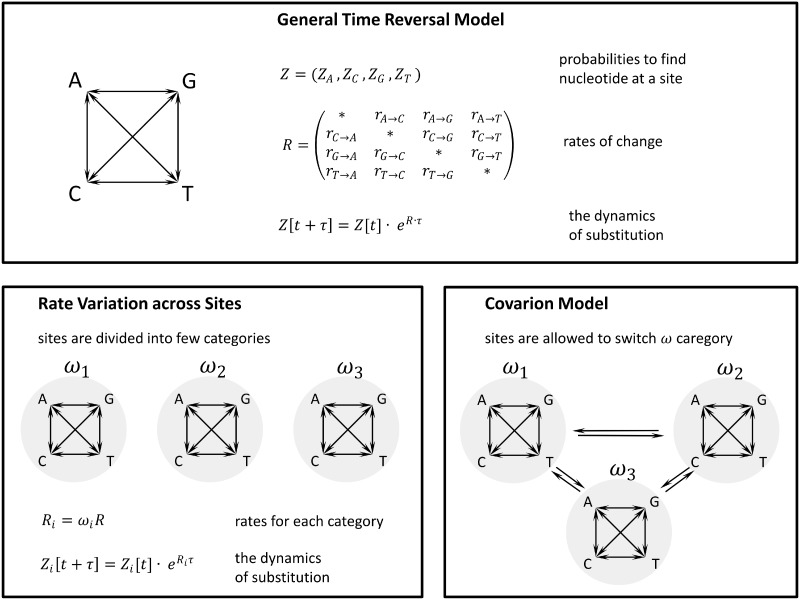
Modeling protein (or DNA) sequence evolution is often concerned with estimating the rate at which two sequences diverge typically describing sequence divergence as a Markov chain process. Initially, such models considered the neutral divergence of DNA sequences. The most general neutral, site-independent, general time-reversible (GTR) model (Tavare 1986), which was created following more restricted models (Jukes and Cantor 1969; Kimura 1980; Felsenstein 1981), allows different substitution rates for each nucleotide pair (see O’Meara 2012 for review). Within the existing Markov chain models, the probabilities of each site being occupied by each of the four nucleotides are estimated across time using a 4 × 4 matrix of nucleotide substitution rates (fig. 1). Amino acid substitution models are analogous in a sense that a 20 × 20 matrix of amino acid substitution rates can be used to estimate the probabilities of a site being occupied by each of the 20 amino acids.
Fig. 1.
Three categories of Markov chain models of protein evolution. The general time reversal models estimate the probability that a site is occupied by a specific nucleotide, Z. The probability of finding specific nucleotides at a site changes with time and the rate of change is described by a 4 × 4 matrix, R, because each of the four nucleotide can change into the other three nucleotides with a certain rate ri→j. The ri→j rates typically reflect the rate of mutation and, therefore, models the neutral rate of change of nucleotides across sites. As selection influences the rate of substitution in sites it is introduced as a parameter ω, with models. In that case ω > 1 reflects the action of positive selection and accelerates the rate of evolution and ω < 1 reflects negative selection slowing down the rate of change of Z. As the action of selection may be different in different sites, some models attempt to capture the resulting rate variation across sites by assigning a different ω to different sites. The covarion models reflect the possibility that the rate of evolution of a site is itself subject to change with time. They introduce extra parameters allowing for sites to switch among the different ω categories.
The first level of complication of these models arises from the impact of selection on sequence divergence. When the matrix of substitution rates reflects only the rate of mutation the Markov chain models reflect neutral sequence divergence. The typical way to introduce selection to these models is to assume a multiplier of the mutation rate, ω, which models selection by slowing down the rate of substitutions at sites under selection (fig. 1). For DNA sequence models the rate of evolution can be estimated separately for synonymous and nonsynonymous sites, with the matrix of nonsynonymous substitution rates multiplied by ω, which is the single parameter determining the strength of selection. Amino acid sequence divergence models often use a precomputed matrix of amino acid substitution rates, such as BLOSUM or PAM (Dayhoff et al. 1978; Henikoff S and Henikoff JG 1992; Whelan and Goldman 2001).
The second level of complication of these models comes from the realization that the strength of selection may be different at different sites. A class of Markov chain models with variable rate of evolution across sites has been created (Nei and Gojobori 1986; Yang 1994) in which ω follows a specific distribution, typically a Gamma distribution. Practically, a discrete Gamma distribution is used and sites are, therefore, classified into a number of categories with a different rate multiplier ωi. Within this approach some sites may be completely invariable, in that case for those sites ωi = 0.
The final level of complication considers the possibility that the strength of selection at a site changes with time. Such covarion models (Fitch and Markowitz 1970) introduce parameters, which describe the rate of change between different substitution rate multipliers. The first such models allowed a site to switch between invariable and variable states (Tuffley and Steel 1998; Huelsenbeck 2002) the second ones to switch between several ωi categories (Galtier 2001). Wang et al. (2007) combined both approaches into a more general covarion model.
The models that incorporate selection do so by varying the rate of evolution across different sites without varying the probability of different substitution across sites. Biologically speaking we know that the fitness impact of a L→C substitution in one site may be radically different from that of the L→C substitution at a different site. However, assuming a different substitution matrix for different sites is impractical as it overparametrizes the model. Therefore, for the time being the assumption that sites differ from each other only in their rate of evolution, which in a covarion model is time-dependent, remains widely accepted. This assumption may not interfere with the models ability to reliably estimate the overall rate of evolution. However, such models may not be appropriate when differences in the rate of the same type of substitutions across different sites contribute substantially to the sequence divergence process.
A widely utilized verbal model of molecular evolution has been formulated by Maynard Smith (1970), which compares protein evolution to a word game, whereby two words (proteins) with meaning (function) are connected by a series of one letter (amino acid) changes (substitutions) such that a continuous pathway between these two words is created. The example used by Maynard Smith is that of the word “WORD” evolving into the word “GENE” through meaningful intermediates comprising a trajectory of substitutions in sequence space: WORD↔WORE↔GORE↔GONE↔GENE. This trajectory reveals an important property of time-dependence, or epistasis, of substitutions in different sites. For example, the substitution of R→N at the third site is meaningful only after D→E and W→G substitutions occurred in the fourth and first sites, respectively. If R→N at the third site was to be the first substitution in WORD, it would lead to the sequence of WOND, which does not have meaning in the English language. The existing Markov chain based models may accurately estimate the rate of evolution of sequences where such time-dependence is common. However, such models cannot be used to study the time-dependence itself. Here, we develop a mathematical model of long-term protein evolution focusing on the evolutionary dynamics of evolving sequences through sequence space in a similar way to that described by Maynard Smith (1970). Instead of focusing on the rate of amino acid substitution as the estimated parameter of the model we focus on the prevalence of epistatic interactions between amino acid states as the parameter of interest. We then attempt to fit our model to several recent observations of long-term evolution. We do not investigate issues related to phylogeny inference.
Results
The Concept of the Model
Verbal Model
We take Maynard Smith’s (1970) analogy as the basis for our model of sequence evolution, which investigates the impact of interactions of sites across the protein sequence. An exhaustive description of all possible interactions is impossible for a sequence even of moderate length (L) as it requires to consider all 20L sequences in sequence space. This vast number can be reduced by focusing on evolutionary trajectories within the sequence space. For the trajectory considered by Maynard Smith (1970) WORD→WORE→GORE→GONE→GENE the entire sequence space, in English, is 264 = 456,976. However, to understand the local restrictions imposed by the interactions of letters in different places across the word it is sufficient to describe the fitness landscape one substitution away from each of the five words in the trajectory (fig. 2). The current sequence as well as the potential fitness impact of all single letter substitutions can be shown in a matrix, which we call the fitness matrix. In the case of a four letter word in English, a cell of the fitness matrix may have three different states, A, B, or C. First, C, or the “current” letter represents the current state of the letter in a specific position. For example, the second letter of WORD is O and, therefore, the (2,O) cell of the matrix has the state C. Second, A stands for a letter that is currently “available” for evolution. In the second letter of the word WORD, the (2,A) cell has the state A because O→A substitution in the second letter creates the word WARD, which has meaning in English. Finally, a substitution may be “blocked” (B), whereby if the substitution were to occur it would not create a meaningful word, but this letter at the same site may be present in another word. All substitutions in WORD in the second site other than O→A are of such type. For example, O→J substitution creates a meaningless WJRD; however, the letter J at the second site can be part of an actual word, AJAR and, therefore, the (2,J) cell is occupied by state B (see table 1 for a list of all abbreviations).
Fig. 2.
The fitness matrices of words encountered in the trajectory of substitutions WORD→GENE described by Maynard Smith (1970). The fitness matrix of a specific sequence reflects both the current (C) sequence, with the state C in the corresponding cell of the matrix, as well as the fitness impact of all possible single letter substitutions. For example, in the first word in the trajectory, “WORD” there are 16 available (A) substitutions, out of 100 total possible ones, that would lead to another word in English (having high fitness). All other 84 states are blocked (B), meaning that if such a substitution were to occur would not lead to a meaningful sequence of letters. A substitution that actually occurred in the trajectory is reflected by a bidirectional C↔A switch in two cells of the matrix. With every substitution the potential impact of other substitution also changes (changes between the current and the previous fitness matrix are shown in orange).
Table 1.
Abbreviations.
| Possible states of cells in the fitness matrix | |
| C | Current |
| An | Available and neighboring |
| Af | Available and far |
| Bn | Blocked and neighboring |
| Bf | Blocked and far |
| F | Forbidden |
| Constants | |
| L | Length of protein sequence |
| m | Number of non-F amino acids per site |
| α | Fraction of A cells among A and B cells |
| γ | Number of switches A↔B occurring with one amino acid substitution |
| δ | Fraction of n cells among n and f cells |
| φ | Number of n↔f switches occurring with one amino acid substitution |
| Rates of switches | |
| Markov process variables | |
| Z = (ZC, ZAn ZAf, ZBn, ZBf) | Vector of probabilities that a cell is in a particular state |
| R | Rate matrix of switches |
| Empirical observations (Povolotskaya and Kondrashov 2010) | |
| D | Protein distance |
| U | Amino acid usage |
| Nt | Number of substitutions toward the reference sequence |
| Na | Number of substitutions away from the reference sequence |
| Kc | Rate of convergent evolution |
| Kd | Rate of divergent evolution |
| K4 | Rate of synonymous evolution in 4-fold sites |
Given a trajectory of substitutions in sequence space, it is possible to track not only the substitutions that have occurred but also the associated changes in the fitness impact of other substitutions. The first substitution in the given trajectory is the D→E substitution in the fourth letter. This is reflected in the A→C switch of the cell (4,E) and the reciprocal C→A switch of the (4,D) cell. Thus, a C↔A switch represents one substitution. Furthermore, each substitution may cause a number of A→B and B→A switches. In this case, the D→E substitution at site 4 causes two B→A switches in cells (2,E) and (2,I). This occurs because these substitutions, O→E and O→I, now lead to meaningful words (WERE and WIRE, respectively), whereas the same substitutions prior to the D→E substitution did not lead to a meaningful combination of letters (WERD and WIRD). If we consider the second substitution in the sequence W→G in the first letter (leading to WORE→GORE), another B→A switch occurs in the cell (2,Y), which leads to the word GYRE, and three A→B switches at the same site in the cells (2,A), (2,E), and (2,I), which lead to the meaningless combinations of GARE, GERE, and GIRE, respectively.
The fitness matrix approach to investigating the trajectory of substitutions in the WORD↔GENE analogy can be further dissected to reveal various parallels with protein evolution. Some letters (sites) tend to have more substitutions available at any given moment (the first letter compared with the second in the example), some substitutions can transition rapidly between allowed and blocked, whereas others switch between these states at a much slower rate, etc. However, investigating many or long trajectories of substitutions using the full fitness matrix may still be troublesome, although this has been done experimentally for a small number of proteins with very short trajectories (McLaughlin et al. 2012; Gong et al. 2013; Roscoe et al. 2013; Thyagarajan and Bloom 2014). Therefore, for ease of mathematical treatment we follow site-independent models and assume that all sites across the sequence have the same properties. Our model aims to study the probability that a cell in the fitness matrix is one of these three states (C, A, or B) and the rate of A↔B switches with every sequence substitution (A↔C switch). The GTR models investigate the rate of nucleotide substitutions on average across the entire sequence without tracking individual sites yet they can reconstruct the expected sequence divergence between the evolving and the ancestral sequence. Similarly, our model investigates the rate of switches between different states of the fitness matrix cells across the entire matrix without tracking individual sites and retains the ability to determine the expected divergences between the evolving and the ancestral sequence.
Fitness Matrix
The protein fitness matrix has L columns and 20 rows, where L is the length of the protein and 20 is the number of all amino acids. In addition to the three aforementioned states A, B, and C we introduce another state F, or a “forbidden” amino acid, which confers low fitness in all possible genetic backgrounds. In the WORD↔GENE analogy, forbidden states do not appear because for each letter of the alphabet at each of the four sites there exists at least one word in English in which that letter is used at the site in question. The fitness matrix as we define it assumes a binary distribution of fitnesses, such that a genotype can have a high, 1, or low, 0, fitness without intermediate values (C and A correspond to high fitness whereas B and F to low fitness).
Because we consider trajectories of amino acid substitutions we must also take into account properties of the genetic table. Some amino acid substitutions may be available from a fitness perspective; however, they cannot occur at the present moment because more than one nucleotide substitution is required on the DNA level. We, therefore, segregate the available (A) and blocked (B) cells into mutationally “neighboring” (n) states, An and Bn, or nonneighboring states labeled with the f subscript (for “far”), Af and Bf. Thus, we define six distinct states: C, An, Af, Bn, Bf, F with An and Af forming set A whereas Bn and Bf forming set B. Conversely, An and Bn form set n, all amino acid states that can be reached by a single substitution and Af and Bf form set f, those amino acid states that cannot. Each cell of the fitness matrix has one of these six states and the model considers the rate of switches among them (fig. 3).
Fig. 3.
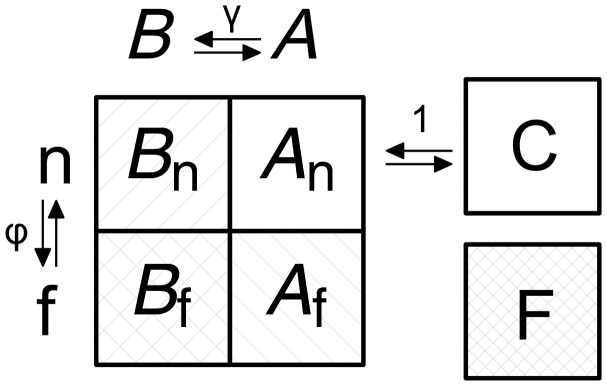
Switches between five states in the fitness matrix. The current amino acid state can switch into an available amino acid that is one nucleotide substitution away (C↔An), which reflects one amino acid substitution. With every C↔An switch γ amino acid states that were previously available to evolution become blocked (An/f→Bn/f) and vice versa, other γ amino acid states that were blocked become available (Bn/f→An/f). Furthermore, with every C↔An switch φ amino acid states that were previously in the mutational neighborhood become unreachable with one nucleotide mutation (An→Af or Bn→Bf switches) and vice versa (Af→An or Bf→Bn) switches. F never changes because it reflects those amino acid states that can never be found in a protein sequence.
Evolution and Switches between States in the Fitness Matrix
Three types of switches of the cell state are possible in the fitness matrix. First, an amino acid substitution causes one cell to switch from state C to state An and another cell to have the opposite switch—from state An to state C. Second, in the same site the sets of n-labeled and f-labeled cells also change, with some amino acids that were previously more than one nucleotide substitution away become neighboring amino acids and vice versa. Third, with every substitution some previously blocked amino acids became available and some available amino acids became blocked. Thus, the dynamics of accumulating substitutions in a sequence can be described with the change of the state of cells of the fitness matrix with a total of ten different switches: C→An, An→ C, An→Af, Af→An, Bn→Bf, Bf→Bn, An→Bn, Bn→An, Af→Bf, and Bf→Af (fig. 3).
Markov Process for States of a Single Cell in the Fitness Matrix
We introduce an approach to analyze the state of a single cell of the fitness matrix. We describe a non-F cell with a vector Z that contains probabilities that the cell is in one of the five possible states, Z = (ZC, ZAn, ZAf, ZBn, ZBf). The probability a state F of a cell is not included because non-F cells never become F and vice versa. Vector Z changes with time because states switch between each other. We measure the rate of the switches as the expected number of switches occurring with every substitution in a site. Therefore, . Moreover, we consider the fitness impact of an amino acid state to be an independent parameter from its mutational neighborhood, that is, whether a site is in state A or B is independent of whether or not it is n or f. Therefore, , , , . The switches form a Markov process with the rate matrix, R:
where diagonal entries are determined by the constraint that rows sum to 0.
The transition probabilities between different states can then be obtained by taking the exponent of the product of the rate matrix and time measured as the number of substitutions per site, or . The distribution of probabilities to obtain a cell of a specific particular state at time t equals:
| (1) |
Figure 4 shows an example of evaluation Z[t] for Z[0] = (1,0,0,0,0) and for switching rates in the same value range as that obtained for real proteins families (see next section).
Fig. 4.
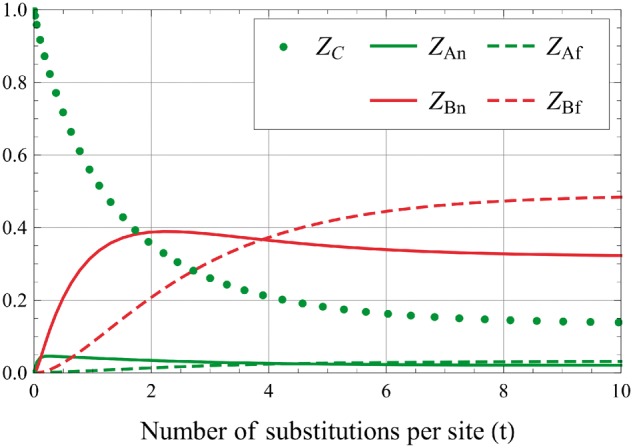
Numerical evaluation of components of Z[t]. The initial condition is Z[0] = (1,0,0,0,0) with constants α = 0.06, γ = 5, m = 7.3.
Constants
To estimate rates in the rate matrix, several constants are necessary. First, we introduce m, the average number of non-F cells per column. Biologically m is the number of amino acids per site that can confer nonzero fitness in at least one genetic background. Second, we introduce α, the fraction of cells with state A among all cells with states A and B. Third, we introduce γ, the number of switches A↔B that happen with one amino acid substitution. The α and γ constants have an affinity in that α describes the relative amount of A and B states and γ describes the rate of change between them. Two more constants are estimated from the genetic code. The fraction of cells with state n among all cells with state n and f, δ = 0.4 calculated considering two amino acids as neighbors if any of their codons are separated by one nucleotide substitution. The number of switches n↔f, φ0 = 3.3, also calculated as an average across all codons for all 20 amino acids. The δ and φ constants are related in that δ stands for the number of neighboring amino acids whereas φ stands for how rapidly this set of neighboring amino acids changes. However, we are interested only in switches between non-F states. Thus, we define the number of possible n↔f switches per site as
| (2) |
The constant −1 appears in the numerator and denominator because at each site one amino acid is C, which is neither n nor f.
Using these constants we calculate the number of cells with different states in one column of the fitness matrix and the stationary probabilities of non-F states to which components of vector Z converge independently of the initial state (table 2). We then derive rates of switches as the number of switches divided by the number of cells from which a switch could have occurred:
Table 2.
Number of Cells with Various States in the Fitness Matrix.
| C | ||||||
|---|---|---|---|---|---|---|
| Nj, number of cells with state j in one column of fitness matrix | 1 | |||||
| , equilibrium frequency of state j for non-F cell | — |
Thus, our model has five constants, with two of them, δ and φ, characterizing the genetic code whereas the other three, m, α and γ, characterize the fitness landscape. To estimate realistic ranges of m, α, and γ, we use empirical data on evolution of protein sequences.
Fitting Observations to Model
Our model is aimed at testing recent statements regarding the epistatic nature of long-term protein evolution. Specifically, the model is used to fit previously obtained data on protein sequence divergence from Povolotskaya and Kondrashov (2010) and Breen et al. (2012). We thus provide a brief description of the previously published data that we investigate here with the present model.
Polarization of amino acid substitutions with one or more outgroup sequences reveals the directionality of evolution. For example, if one sequence has an Alanine (A) and another sequence in the orthologous site contains a Threonine (T) and closely related outgroup sequences also contain a Threonine then an T→A substitution is inferred. Such polarized substitutions can then be related to a fourth, reference, sequence when the reference sequence is an outgroup to all three sequences involved in the polarization. Following our example, if the orthologous site in the reference sequence is occupied by a T then the T→A substitution can be inferred to be a substitution away from the reference sequence. Conversely, if the orthologous site in the reference sequence is occupied by an A then the T→A substitution can be inferred to be a substitution toward the reference sequence. The ratio of the sum of all toward substitutions (Nt) and the sum of all away substitutions (Na), Nt/Na, can then be taken as a measure of the relative rate of divergence of the sister sequences and the reference sequence. The observation that sister and reference sequences that have already diverged considerably continue to do so, that is, Nt/Na < 1 for large values of sequence divergence (protein distance, D), has been claimed to be a consequence of epistatic interactions between sites in the evolving sequences (Povolotskaya and Kondrashov 2010).
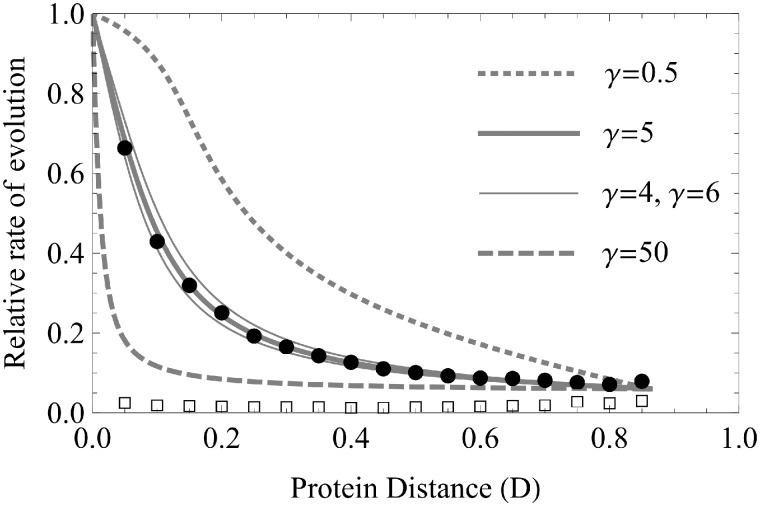
The rate of divergence of sequences from each other can be estimated in an analogous manner to the Nt/Na measure by deconstructing Nt/Na into two independent rates of evolution—the rate of divergent evolution (Kd) and the rate of convergent evolution (Kc). The rate of divergent evolution is estimated as Na divided by the number of sites in which an away substitution could have occurred. The estimate of the number of such divergent sites is equal to the number of sites in which the ancestral state of the two sister sequences matches the reference sequence. Similarly, Kc is Nt divided by the number of convergent sites, in which a toward substitution could have occurred. The number of sites that are occupied by a different amino acid in the ancestor of the sister sequences and the reference sequence and are separated with only a single nucleotide substitution is the target number of convergent sites. Kd was estimated to be substantially slower than the rate of synonymous divergence in 4-fold sites (K4), independently of D (Povolotskaya and Kondrashov 2010). Alternatively, Kc is comparable to K4 when D is near 0 and rapidly declines as D increases reaching a plateau slightly above Kd (fig. 5). The dependence of Kc/K4 but not Kd/K4 on D, and similar observations (Kondrashov et al. 2002; Choi et al. 2005; Rogozin et al. 2008; Rokas and Carroll 2008; Bollback and Huelsenbeck 2009; Gloor et al. 2010; Naumenko et al. 2012; Soylemez and Kondrashov 2012), has been claimed to show support for epistasis in protein evolution but has not been modeled.
Fig. 5.
Relative rate of protein evolution. Kc/K4 is shown by • and Kd/K4 by □ (from Povolotskaya and Kondrashov 2010). We fit the observed Kc/K4 to that calculated by the solution of equation (4) varying γ as a parameter. The optimal fit was found for γ ∼ 5 (thick solid line). Two near fits for γ = 4 and γ = 6 are depicted with thin solid lines. Thick dashed line shows Kc/K4 for γ significantly higher and thick dotted line for significantly lower values of γ.
The final observation that at present requires more formal modeling deals with amino acid usage (U), the number of different amino acids in an orthologous site. In a large multiple sequence alignment, U ∼ 9 (Breen et al. 2012), or approximately half of all possible amino acids. However, the same proteins exhibit a short-term rate of nonsynonymous evolution (Kn) up to an order of magnitude lower than Kn ∼ 0.5 that is expected if an amino acid state has the same effect in all species. The reason why amino acids are accepted in the long-term yet rejected in the short term may be due to epistatic interactions being common (Fitch and Markowitz 1970; Maynard Smith 1970; Povolotskaya and Kondrashov 2010; Breen et al. 2012); however, this parameter has also not been put into a formal context of a macroevolutionary model.
We obtained quadruplet alignments from Povolotskaya and Kondrashov (2010) where each quadruplet alignment consisted of two sister sequences, one outgroup sequence and one reference sequence. Such quadruplet alignments were available for 572 clusters of orthologous groups (COGs), functional gene families that were predicted to have been present in the last universal common ancestor, LUCA (Mirkin et al. 2003). Reference sequence from the alignments corresponds to the sequence at t = 0 in our model.
Distance
As a sequence diverges from the sequence it was at t = 0, we can estimate the protein distance between them as a function of time. The protein distance (D) between two sequences is defined as 1 minus the sequence identity. The sequence identity between the sequence at time t and at t = 0 equals the probability that a cell that was in state C at t = 0 is at state C at time t, that is, ZC[t] when Z[0] = (1,0,0,0,0). This gives:
| (3) |
We then consider the value of D at equilibrium, at t = ∞ as . In Povolotskaya and Kondrashov (2010), the distance limit has been estimated as the time when Nt/Na = 1. In principle, we can use D∞ to estimate one of the constants, the number of non-F amino acids m, as
| (4) |
From Povolotskaya and Kondrashov (2010) the divergence equilibrium (Nt/Na = 1) was estimated as . However, from equation (4) it is clear that when D∞ is large a difference of just 5% leads to a large scatter of m with m = 10 − 20. Thus, although it appears that m is likely to be high, consistent with a large U observed by Breen et al. (2012), this approach is not suitable for an accurate estimation of m.
Sequence Divergence and Convergence
The ratio Kd/K4 relates the rate of divergence of nonsynonymous substitutions to the rate of 4-fold synonymous evolution. In terms of our model, a nucleotide substitution leading to amino acid with state A fixes with the same probability as a synonymous substitution. Thus, Kd/K4 equals to the proportion of substitutions that lead to an amino acid with state A, in other words it is the ratio of the number of cells with state A and the number of cells with all non-C states. Therefore,
| (5) |
The ratio Kc/K4 relates the rate of convergent amino acid substitutions to the 4-fold synonymous rate of evolution. Kc measures the rate of substitution toward the reference sequence, or toward cells in the fitness matrix which were C at t = 0. Amino acids with state A fix with the same probability as synonymous substitutions. But when calculating Kc only amino acids in the mutational neighborhood are taken into account. Thus, Kc/K4 equals the probability that a cell that was in state C at time t = 0 is in state An at time t divided by the probability that a cell is in state n:
| (6) |
We then explore equation (6) as t→0. At t = 0 ZAn = 0 and ZBn = 0 whereas Kc/K4 is not defined, because there are no convergent sites. Applying L’Hôpital’s rule, we find . That is in a good agreement with Kc/K4 from Povolotskaya and Kondrashov (2010). Second, we explore Kc/K4 [t] when t→∞. From table 2:
| (7) |
From data we estimate Kc/K4→0.06, which implies α = 0.06. Kd/K4 is approximately constant and equals 0.02, substituting it and α into equation (5) we get m = 7.3. From equation (2), we calculate φ = 1.1.
Estimating the Degree of Epistasis in Protein Evolution
In the previous sections, we estimated values for all constants used in the model except for γ, which reflects the amount of epistasis in evolution. To obtain it, we fit the empirically obtained Kc/K4 from Povolotskaya and Kondrashov (2010) to the estimated Kc/K4[D] that we obtain from our model. We evaluate equation (1) numerically varying γ as a parameter. For a given γ, we use the functions ZC(t), ZAn(t), ZAf(t), ZBn(t), and ZBf(t) obtained from equation (1) to calculate Kc/K4[t] in equation (7) and D[t] in equation (3). We repeat this process varying the γ parameter until we obtain a good fit between the observed and predicted Kc/K4 across D (fig. 5). Mathematically speaking we minimize relative errors of fit:
| (8) |
where ND is the number of data points for Kc/K4[D]. provides the best fit (fig. 5).
Evolution Relative to a Reference Sequence, Nt/Na
As we have estimated all parameters of the model, we can now estimate Nt/Na:
| (9) |
where is amount of convergent (divergent) sites in protein, and defines how many substitutions from one convergent (divergent) site toward (away) the reference are possible. Convergent sites are those from which a single nucleotide substitution can lead to reference amino acids that is currently available. Thus, . For every convergent site, only one substitution can lead toward the reference amino acid: . Sites with the amino acid which matches reference are divergent, so . equals the average number of available and neighboring amino acids per column in the fitness matrix: . Therefore, we get:
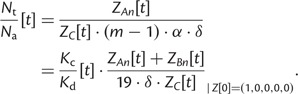 |
(10) |
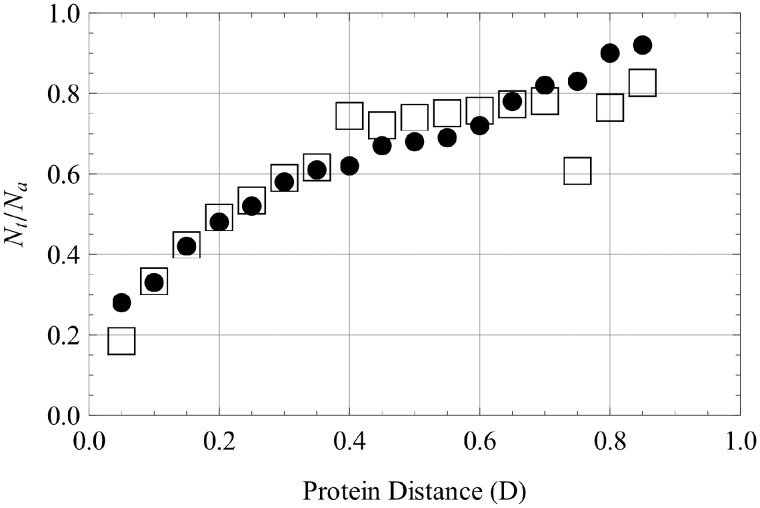
Equation (10) allows us to convert into and vice versa. We calculate using rates of divergent and convergent evolution from Povolotskaya and Kondrashov (2010) and estimate Z from equation (1) when Z[0] = (1,0,0,0,0) and with the five estimated constants. Figure 6 shows the comparison of data (fig. 3 from Povolotskaya and Kondrashov 2010) and the estimate obtained with our model.
Fig. 6.
Observed and predicted relative rates of sequence divergence. The observed values of Nt/Na shown by • and the predicted fit with our model using optimal parameters shown with □.
Usage
NA = α(m
− 1) = 0.06·(7.3 − 1) = 0.38 indicates how many amino acid substitutions are available at a given moment. Thus, on average less than 1 amino acid substitution per site is acceptable at a time. However, when longer time periods are taken into account, up to eight different amino acids may be found at the same site across different species (Breen et al. 2013). These two observations can be reconciled if γ, the number of A↔B switches associated with one C↔An switch, is relatively high. For the data from Povolotskaya and Kondrashov (2010), our model predicts 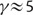 . Such a high γ implies that per site there are five times more switches between the available and blocked states of amino acids than there are actual amino acid substitutions at the same site. It follows that the distribution of available amino acids changes substantially even for a very small number of substitutions in that site. Therefore, we can model all non-F amino acids (m) as having an equal probability to occur at a site after a substitution and the usage expected to be observed after a certain amount of sequence divergence is a simple combinatorial problem.
. Such a high γ implies that per site there are five times more switches between the available and blocked states of amino acids than there are actual amino acid substitutions at the same site. It follows that the distribution of available amino acids changes substantially even for a very small number of substitutions in that site. Therefore, we can model all non-F amino acids (m) as having an equal probability to occur at a site after a substitution and the usage expected to be observed after a certain amount of sequence divergence is a simple combinatorial problem.
Let N be the number of substitutions observed per site with every substitution being a random choice from m. Reformulating the problem, we have a pool of objects of m different colors, we then take N random objects from the pool and calculate n, the number of different colors out of N objects taken from the pool. The value of n varies across trials but we consider amino acid usage to be equal expectation of n distribution. The probability to get n different colors in set of N objects is given by the number of possible sets with n different colors divided by the total number of possible sets, which is mN. The number of ways to partition N objects into n nonempty subsets equals the Stirling number of the second kind, S(N,n). There are m!/(m − n)! ways to associate these subsets with n different colors:
| (11) |
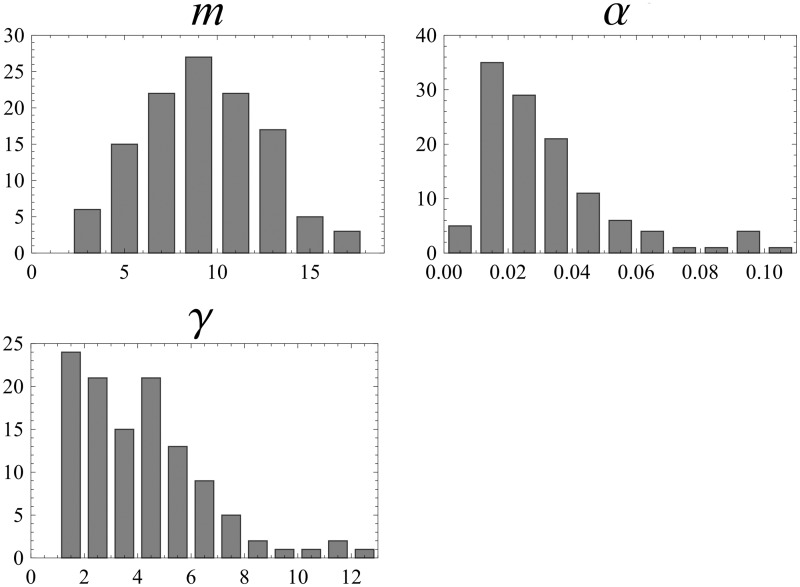
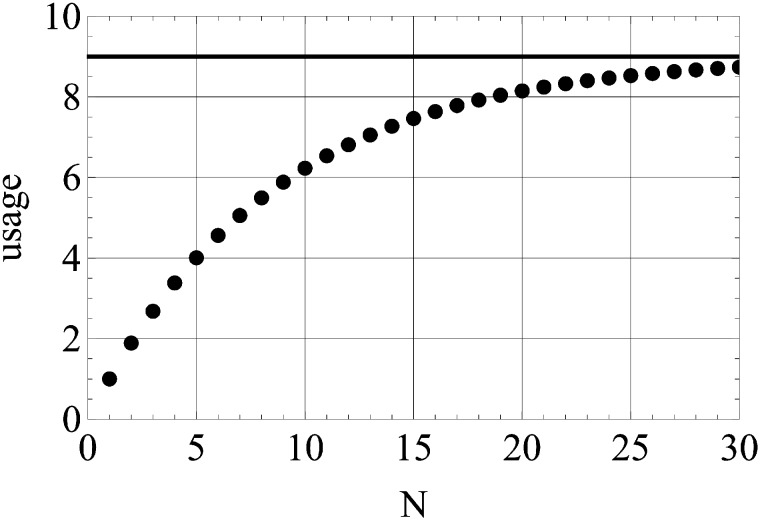
We estimate m = 9 (see next section) as the mean value of m distribution among different COGs (fig. 7) and using equation (11) calculate the dependence of usage on N (fig. 8). Due to the high γ value, the amino acid usage is considerable even for N ∼ 10, number of substitutions per site, with usage almost approaching its maximal value with 30 substitutions per site.
Fig. 7.
Distribution of estimated parameters for 119 COGs. The distribution of the number of nonforbidden amino acids per site (m), proportion of available amino acids over all available and blocked states (α), and the rate of A↔B switches (γ) are shown.
Fig. 8.
Estimating amino acid usage. Usage calculated as the most probable number of amino acids to be observed at a site as a function of the number of accumulated substitutions per site. The solid line represents the number of nonforbidden amino acids at a site (m).
Considering the Distribution of Parameters across Gene Families
In the previous sections, we used data which were obtained by taking average values across all 572 COGs (Povolotskaya and Kondrashov 2010). Here, we use data on the same variables that were obtained for each COG separately. For some protein families, there are not enough data to calculate Kc/K4 and Kd/K4 with an acceptable degree of precision. Therefore, we selected 119 COGs for which Kd/K4 and Kc/K4 were defined across distances 0.1–0.8 without strong outliers. For each COG, we obtained Kd/K4 as an average Kd/K4 across different D between the trios and the reference sequence in bins of 0.1 of D. We presume that α is a limit of Kc/K4 when D→1. Then, we calculate m using equation (5) and φ using equation (2). Finally, we fit Kc/K4 with numerical evaluation of equation (1) and find γ. Distributions of these parameters for the 119 COGs are shown on figure 7.
Discussion
The model presented here makes three assumptions. The first assumption is that fitness is either 0 or 1. Binary fitness landscapes, while unrealistic in certain situations, are nevertheless useful when recapitulating the multidimensionality of the sequence space (Gavrilets 1997; Gavrilets and Gravner 1997; van Nimwegen et al. 1999; Aita et al. 2003; Gravner et al. 2007). When fitness values are either 1 or 0 mutations are either neutral or lethal and all permitted substitutions have an equal probability of occurrence. Thus, the impact of slightly deleterious and beneficial substitutions on molecular evolution cannot be taken into account, even though their contribution may be considerable (Ohta 1998; Andolfatto 2005; Popadin et al. 2007; McCandlish et al. 2013). The reason for excluding the effects of such substitutions is 2-fold. First, the practical considerations of modeling a complex and multidimensional fitness landscape in which substitutions are not equal in effect. The nonepistatic impact of slightly deleterious and beneficial substitutions on evolution in the absence of epistasis is well characterized (Crow and Kimura 1970), whereas the effects of epistasis on long-term molecular evolution have not been subject to the same level of scrutiny. Our work develops a null model that may be expanded to incorporate these effects. Second, it appears certain that neither the fixation of slightly deleterious or beneficial alleles can serve as the basis for explaining the measurements considered here, at least without the impact of epistasis. The fixation of slightly deleterious alleles is compatible with a large U under some circumstances (McCandlish et al. 2013). However, slightly deleterious alleles alone cannot lead to large sequence divergence in fast-evolving proteins and are incompatible with reaching maximum sequence divergence distances substantially slower than the rate of divergence of neutral sequences (Kondrashov et al. 2010). There is a tradeoff between the contribution of slightly deleterious alleles toward amino acid usage and sequence divergence; it is not possible to have a high U and a high D at the same time solely due to the contribution of fixation of deleterious alleles (Breen et al. 2013). Furthermore, periodic fixation of nonepistatic slightly deleterious alleles cannot lead to a decline in the rate of convergent evolution, in contrast to the observed Kc/K4 relationship (Povolotskaya and Kondrashov 2010). Therefore, slightly deleterious alleles may contribute to molecular evolution but a model based on the accumulation of slightly deleterious alleles alone cannot explain all of the available data (also see Kondrashov et al. 2010). A similar argument is applicable to the impact of beneficial alleles on observations of molecular evolution considered here. Large sequence divergence observed between sequences is compatible with most differences between sequences having been fixed by positive selection. However, the high values of Kc/K4, especially for small D, are incompatible with sequence divergence being largely driven by the accumulation of beneficial alleles.
The second assumption is that all sites in the protein are expected to have the same properties (described by α, γ, φ, m, and δ). This includes genetic properties, such as the number of mutational neighbors at each site, or the properties of the protein, such as the number of available, blocked, and forbidden amino acids at a site. Indeed, it may be possible to alleviate this assumption by introducing a variation of our model in a manner similar to that has been done for models of the rate of protein evolution (Nei and Gojobori 1986; Yang 1994). We hope that the present work will be a stepping stone in this direction. The third assumption is that all of these five parameters are independent of each other. This may not be entirely the case, for example amino acids in the mutational neighborhood of each other are more likely to be available (Freeland et al. 2000).
Our model is not unique in modeling interactions between different alleles to describe the fitness landscape. However, the model presented here differs substantially from models developed previously. Previous efforts were principally concerned with the issue of the shape of the fitness landscape (Kauffman and Levin 1987; Macken and Perelson 1989; Gavrilets 1997; Gavrilets and Gravner 1997; Ohta 1998; Kondrashov FA and Kondrashov AS 2001; Gravner et al. 2007; Ferrada and Wagner 2010; Crona et al. 2013; Lobkovsky et al. 2013). Our model, on the other hand, considers patterns of long-term divergent and convergent molecular evolution as a factor of the epistatic interactions arising on a multidimensional fitness landscape. Our model shares the same conceptual basis as covarion models (Fitch and Markowitz 1970; Tuffley and Steel 1998; Galtier 2001; Huelsenbeck 2002), which allow the rate of evolution at a site to change over time. Our model approaches the same issue but from a perspective that, in our opinion, more accurately reflects the biological basis for interaction between sites.
Our analysis has revealed several important aspects of protein evolution. The crucial aspect of our model is that we can find a limited parameter space that is consistent with all of the available observations of protein evolution. The three estimated parameters that reveal the nature of the fitness landscape are the number of amino acids that in principle can confer nonzero fitness (m), the fraction of them which allowed for substitution in one moment (α), and the number of switches between amino acids in available and blocked states per a single amino acid substitution (γ).
We estimate an m between 5 and 15 for most protein families (fig. 7), which indicates that few states are forbidden, that is, correspond to low fitness regardless of the amino acid composition of other sites. Here, a modest number of universally forbidden amino acids implies that most amino acid sites can accept most of the possible amino acids given the right combination of states at other sites (Fitch and Markowitz 1970; Maynard Smith 1970; Povolotskaya and Kondrashov 2010). Conversely, this implies that a single amino acid site can accept many different amino acids, consistent with the previous observations of a high amino acid usage (Breen et al. 2012).
We estimate α = 0.06, the fraction of available amino acids at a given time as just a small fraction of all amino acid states. Therefore, at any given time many sites cannot accept any substitutions. This estimate is consistent with the observation of slow rate of sequence divergence of sequences in our data set, with Kd/K4 ∼ 0.02 and with mutational studies (Guo et al. 2004). Evidently, for faster evolving protein families α is likely to be higher, however, as we considered old gene families, which tend to be conservative, our estimate is unlikely to be representative of the entire diversity of protein rates of evolution found across all taxa.
Within the confines of our model, it is not possible to maintain γ = 0 while maintaining a fit to all of the observed parameters of protein evolution. Specifically, γ appears to be the key parameter that allows the model to fit the observation of the decline in the rate of convergent evolution, Kc/K4 (fig. 5). Because the model is scaled to the number of amino acid substitutions that occur in a protein the γ = 5 estimate cannot be taken as a direct indication that epistatic interactions are intragenic. Individual proteins do not evolve in isolation and cases of intergenic epistatic interaction have been documented (Lehner 2011). Indeed, our model does not imply a causative interaction between amino acid substitutions and switches between available and blocked states of amino acids in the fitness matrix. Indeed, a general interpretation of γ = 5 is that on average five switches between available and blocked states occur on the same timeframe as a single amino acid substitution. These switches may either be a consequence of changes in the same protein or in the rest of the genome. If most interactions are intragenic then the best fit of γ = 5 implies that the fitness matrix of a protein is changing faster than its sequence implying that the inherently epistatic nature of the fitness landscape is an inseparable and defining factor of molecular evolution.
Our model can be used to analyze the patterns of molecular evolution of specific gene families, as was done here (fig. 7). We observed that all parameters, including γ, vary substantially across different gene families, implying that the nature of the fitness landscape is a feature that may differ across protein families. The application of this model to a broader set of proteins than considered here can lead the way toward a more general characterization of fitness landscapes and evolutionary trajectories in nature.
Acknowledgments
The work was supported by grants from Agence Nationale de la Recherche (ANR-12-JSV7-0007), HHMI International Early Career Scientist Program (55007424), the EMBO Young Investigator Programme, MINECO (BFU2012-31329 and Sev-2012-0208), and an ERC Starting Grant (335980_EinME). All authors participated in the design of the model. D.R.U. and L.F. performed the mathematical analysis. D.R.U and I.S.P. obtained and analyzed data on protein evolution. D.R.U. and F.A.K. wrote the draft.
References
- Aita T, Ota M, Husimi Y. An in silico exploration of the neutral network in protein sequence space. J Theor Biol. 2003;221:599–613. doi: 10.1006/jtbi.2003.3209. [DOI] [PubMed] [Google Scholar]
- Andolfatto P. Adaptive evolution of non-coding DNA in Drosophila. Nature. 2005;437:1149–1152. doi: 10.1038/nature04107. [DOI] [PubMed] [Google Scholar]
- Bazykin GA, Kondrashov FA, Brudno M, Poliakov A, Dubchak I, Kondrashov AS. Extensive parallelism in protein evolution. Biol Direct. 2007;2:20. doi: 10.1186/1745-6150-2-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollback JP, Huelsenbeck JP. Parallel genetic evolution within and between bacteriophage species of varying degrees of divergence. Genetics. 2009;181:225–234. doi: 10.1534/genetics.107.085225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breen MS, Kemena C, Vlasov PK, Notredame C, Kondrashov FA. Epistasis as the primary factor in molecular evolution. Nature. 2012;490:535–538. doi: 10.1038/nature11510. [DOI] [PubMed] [Google Scholar]
- Breen MS, Kemena C, Vlasov PK, Notredame C, Kondrashov FA. Reply to: The role of epistasis in protein evolution. Nature. 2013;497:E2–E3. [Google Scholar]
- Bridgham JT, Ortlund EA, Thornton JW. An epistatic ratchet constrains the direction of glucocorticoid receptor evolution. Nature. 2009;461:515–519. doi: 10.1038/nature08249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi SS, Li W, Lahn BT. Robust signals of coevolution of interacting residues in mammalian proteomes identified by phylogeny-aided structural analysis. Nat Genet. 2005;37:1367–1371. doi: 10.1038/ng1685. [DOI] [PubMed] [Google Scholar]
- Covert AW, 3rd, Lenski RE, Wilke KO, Ofria C. Experiments on the role of deleterious mutations as stepping stones in adaptive evolution. Proc Natl Acad Sci U S A. 2013;110:E3171–E3178. doi: 10.1073/pnas.1313424110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crona K, Greene D, Barlow M. The peaks and geometry of fitness landscapes. J Theor Biol. 2013;317:1–10. doi: 10.1016/j.jtbi.2012.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow JF, Kimura M. An introduction to population genetics theory. New York: Harper and Row; 1970. [Google Scholar]
- Dayhoff MO, Schwartz RM, Orcutt BC. Atlas of protein sequence and structure. Vol. 5. Washington (DC): National Biomedical Research Foundation; 1978. A model of evolutionary change in proteins; pp. 345–352. [Google Scholar]
- de Juan D, Pazos F, Valencia A. Emerging methods in protein co-evolution. Nat Rev Genet. 2013;14:249–261. doi: 10.1038/nrg3414. [DOI] [PubMed] [Google Scholar]
- de Visser JA, Cooper TF, Elena SF. The causes of epistasis. Proc Biol Sci. 2011;278:3617–3624. doi: 10.1098/rspb.2011.1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Visser JA, Krug J. Empirical fitness landscapes and the predictability of evolution. Nat Rev Genet. 2014;15:480–490. doi: 10.1038/nrg3744. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Evolutionary trees from DNA sequences: a maximum likelihood approach. J Mol Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
- Ferrada E, Wagner A. Evolutionary innovations and the organization of protein functions in genotype space. PLoS One. 2010;5:e14172. doi: 10.1371/journal.pone.0014172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitch WM, Markowitz E. An improved method for determining codon variability in a gene and its application to the rate of fixation of mutations in evolution. Biochem Genet. 1970;4:579–593. doi: 10.1007/BF00486096. [DOI] [PubMed] [Google Scholar]
- Freeland SJ, Knight RD, Landweber LF, Hurst LD. Early fixation of an optimal genetic code. Mol Biol Evol. 2000;17:511–518. doi: 10.1093/oxfordjournals.molbev.a026331. [DOI] [PubMed] [Google Scholar]
- Galtier N. Maximum-likelihood phylogenetic analysis under a covarion-like model. Mol Biol Evol. 2001;18:866–873. doi: 10.1093/oxfordjournals.molbev.a003868. [DOI] [PubMed] [Google Scholar]
- Gavrilets S. Evolution and speciation on holey adaptive landscapes. Trends Ecol Evol. 1997;12:307–312. doi: 10.1016/S0169-5347(97)01098-7. [DOI] [PubMed] [Google Scholar]
- Gavrilets S, Gravner J. Percolation on the fitness hypercube and the evolution of reproductive isolation. J Theor Biol. 1997;184:51–64. doi: 10.1006/jtbi.1996.0242. [DOI] [PubMed] [Google Scholar]
- Gloor GB, Tyagi G, Abrassart DM, Kingston AJ, Fernandes AD, Dunn SD, Brandl CJ. Functionally compensating coevolving positions are neither homoplasic nor conserved in clades. Mol Biol Evol. 2010;27:1181–1191. doi: 10.1093/molbev/msq004. [DOI] [PubMed] [Google Scholar]
- Gong LI, Suchard MA, Bloom JD. Stability-mediated epistasis constrains the evolution of an influenza protein. Elife. 2013;2:e00631. doi: 10.7554/eLife.00631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravner J, Pitman D, Gavrilets S. Percolation on fitness landscapes: effects of correlation, phenotype, and incompatibilities. J Theor Biol. 2007;248:627–645. doi: 10.1016/j.jtbi.2007.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo HH, Choe J, Loeb LA. Protein tolerance to random amino acid change. Proc Natl Acad Sci U S A. 2004;101:9205–9210. doi: 10.1073/pnas.0403255101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen TF. Why epistasis is important for selection and adaptation. Evolution. 2013;67:3501–3511. doi: 10.1111/evo.12214. [DOI] [PubMed] [Google Scholar]
- Henikoff S, Henikoff JG. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci U S A. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsenbeck JP. Testing a covariotide model of DNA substitution. Mol Biol Evol. 2002;19:698–707. doi: 10.1093/oxfordjournals.molbev.a004128. [DOI] [PubMed] [Google Scholar]
- Jukes T, Cantor C. Evolution of protein molecules. In: Munro H, editor. Pages in mammalian protein metabolism. New York: Academic Press; 1969. pp. 21–132. [Google Scholar]
- Kauffman S, Levin S. Towards a general theory of adaptive walks on rugged landscapes. J Theor Biol. 1987;128:11–45. doi: 10.1016/s0022-5193(87)80029-2. [DOI] [PubMed] [Google Scholar]
- Khan AI, Dinh DM, Schneider D, Lenski RE, Cooper TF. Negative epistasis between beneficial mutations in an evolving bacterial population. Science. 2011;332:1193–1196. doi: 10.1126/science.1203801. [DOI] [PubMed] [Google Scholar]
- Kimura M. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. J Mol Evol. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- Kondrashov FA, Kondrashov AS. Multidimensional epistasis and the disadvantage of sex. Proc Natl Acad Sci U S A. 2001;98:12089–12092. doi: 10.1073/pnas.211214298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov AS, Povolotskaya IS, Ivankov DN, Kondrashov FA. Rate of sequence divergence under constant selection. Biol Direct. 2010;5:5. doi: 10.1186/1745-6150-5-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov AS, Sunyaev S, Kondrashov FA. Dobzhansky-Muller incompatibilities in protein evolution. Proc Natl Acad Sci U S A. 2002;99:14878–14883. doi: 10.1073/pnas.232565499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehner B. Molecular mechanisms of epistasis within and between genes. Trends Genet. 2011;27:323–331. doi: 10.1016/j.tig.2011.05.007. [DOI] [PubMed] [Google Scholar]
- Lobkovsky AE, Wolf YI, Koonin EV. Quantifying the similarity of monotonic trajectories in rough and smooth fitness landscapes. Mol Biosyst. 2013;9:1627–1631. doi: 10.1039/c3mb25553k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lozovsky ER, Chookajorn T, Brown KM, Imwong M, Shaw PJ, Kamchonwongpaisan S, Neafsey DE, Weinreich DM, Hartl DL. Stepwise acquisition of pyrimethamine resistance in the malaria parasite. Proc Natl Acad Sci U S A. 2009;106:12025–12030. doi: 10.1073/pnas.0905922106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunzer M, Golding GM, Dean AM. Pervasive cryptic epistasis in molecular evolution. PLoS Genet. 2010;6:e1001162. doi: 10.1371/journal.pgen.1001162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macken CA, Perelson AS. Protein evolution on rugged landscapes. Proc Natl Acad Sci U S A. 1989;86:6191–6195. doi: 10.1073/pnas.86.16.6191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith J. Natural selection and the concept of a protein space. Nature. 1970;225:563–564. doi: 10.1038/225563a0. [DOI] [PubMed] [Google Scholar]
- McCandlish DM, Rajon E, Shah P, Ding Y, Plotkin JB. The role of epistasis in protein evolution. Nature. 2013;497:E1–E2. doi: 10.1038/nature12219. [DOI] [PubMed] [Google Scholar]
- McLaughlin RN, Jr, Poelwijk FJ, Raman A, Gosal WS, Ranganathan R. The spatial architecture of protein function and adaptation. Nature. 2012;491:138–142. doi: 10.1038/nature11500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirkin BG, Fenner TI, Galperin MY, Koonin EV. Algorithms for computing parsimonious evolutionary scenarios for genome evolution, the last universal common ancestor and dominance of horizontal gene transfer in the evolution of prokaryotes. BMC Evol Biol. 2003;3:2. doi: 10.1186/1471-2148-3-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyamoto MM, Fitch WM. Testing the covarion hypothesis of molecular evolution. Mol Biol Evol. 1995;12:503–513. doi: 10.1093/oxfordjournals.molbev.a040224. [DOI] [PubMed] [Google Scholar]
- Naumenko SA, Kondrashov AS, Bazykin GA. Fitness conferred by replaced amino acids declines with time. Biol Lett. 2012;8:825–828. doi: 10.1098/rsbl.2012.0356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M, Gojobori T. Simple methods for estimating the numbers of synonymous and nonsynonymous nucleotide substitutions. Mol Biol Evol. 1986;3(5):418–426. doi: 10.1093/oxfordjournals.molbev.a040410. [DOI] [PubMed] [Google Scholar]
- Ohta T. Evolution by nearly-neutral mutations. Genetica. 1998;102–103(1–6):83–90. [PubMed] [Google Scholar]
- O’Meara BC. Evolutionary inferences from phylogenies: a review of methods. Annu Rev Ecol Evol Syst. 2012;43(1):267–285. [Google Scholar]
- Popadin K, Polishchuk LV, Mamirova L, Knorre D, Gunbin K. Accumulation of slightly deleterious mutations in mitochondrial protein-coding genes of large versus small mammals. Proc Natl Acad Sci U S A. 2007;104:13390–13395. doi: 10.1073/pnas.0701256104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Povolotskaya IS, Kondrashov FA. Sequence space and the ongoing expansion of the protein universe. Nature. 2010;465:922–926. doi: 10.1038/nature09105. [DOI] [PubMed] [Google Scholar]
- Rogozin IB, Thomson K, Csürös M, Carmel L, Koonin EV. Homoplasy in genome-wide analysis of rare amino acid replacements: the molecular-evolutionary basis for Vavilov’s law of homologous series. Biol Direct. 2008;3:7. doi: 10.1186/1745-6150-3-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rokas A, Carroll SB. Frequent and widespread parallel evolution of protein sequences. Mol Biol Evol. 2008;25:1943–1953. doi: 10.1093/molbev/msn143. [DOI] [PubMed] [Google Scholar]
- Romero PA, Arnold FH. Exploring protein fitness landscapes by directed evolution. Nat Rev Mol Cell Biol. 2009;10:866–876. doi: 10.1038/nrm2805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roscoe BP, Thayer KM, Zeldovich KB, Fushman D, Bolon DN. Analyses of the effects of all ubiquitin point mutants on yeast growth rate. J Mol Biol. 2013;425:1363–1377. doi: 10.1016/j.jmb.2013.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soylemez O, Kondrashov FA. Estimating the rate of irreversibility in protein evolution. Genome Biol Evol. 2012;4:1213–1222. doi: 10.1093/gbe/evs096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavare S. Some probabilistic and statistical problems on the analysis of DNA sequences. Lect Math Life Sci. 1986;17:57–86. [Google Scholar]
- Thyagarajan B, Bloom JD. The inherent mutational tolerance and antigenic evolvability of influenza hemagglutinin. Elife. 2014:e03300. doi: 10.7554/eLife.03300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuffley C, Steel M. Modeling the covarion hypothesis of nucleotide substitution. Math Biosci. 1998;147:63–91. doi: 10.1016/s0025-5564(97)00081-3. [DOI] [PubMed] [Google Scholar]
- van Nimwegen E, Crutchfield JP, Huynen M. Neutral evolution of mutational robustness. Proc Natl Acad Sci U S A. 1999;96:9716–9720. doi: 10.1073/pnas.96.17.9716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang HC, Spencer M, Susko E, Roger AJ. Testing for covarion-like evolution in protein sequences. Mol Biol Evol. 2007;24:294–305. doi: 10.1093/molbev/msl155. [DOI] [PubMed] [Google Scholar]
- Weinreich DM, Delaney NF, Depristo MA, Hartl DL. Darwinian evolution can follow only very few mutational paths to fitter proteins. Science. 2006;312:111–114. doi: 10.1126/science.1123539. [DOI] [PubMed] [Google Scholar]
- Wellner A, Raitses Gurevich M, Tawfik DS. Mechanisms of protein sequence divergence and incompatibility. PLoS Genet. 2013;9:e1003665. doi: 10.1371/journal.pgen.1003665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whelan S, Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol Biol Evol. 2001;18:691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
- Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J Mol Evol. 1994;39(3):306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
- Zhang W, Dourado DF, Fernandes PA, Ramos MJ, Mannervik B. Multidimensional epistasis and fitness landscapes in enzyme evolution. Biochem J. 2012;445:39–46. doi: 10.1042/BJ20120136. [DOI] [PubMed] [Google Scholar]