Bacterial growth laws reflect the evolutionary importance of energy efficiency

Significance

Bacterial cells are remarkable machines. When food is present, bacteria shift gears into a fast-growth mode, whereby they duplicate all their proteins quickly. Cells do this by producing proportionately more ribosomes relative to other proteins. Ribosomes are the 55-protein complexes that a cell makes to synthesize all the cells proteins. Here, we develop a mathematical model of the mechanism of the cell’s gear-shifting and energy utilization under different growth conditions. A major conclusion from this modeling is that we can understand an evolutionary choice made by bacteria. We find that fast growing cells operate close to their optimal energy efficiency, which is a balance between the rates of translation and turnover of proteins and ribosomal assembly.

Abstract

We are interested in the balance of energy and protein synthesis in bacterial growth. How has evolution optimized this balance? We describe an analytical model that leverages extensive literature data on growth laws to infer the underlying fitness landscape and to draw inferences about what evolution has optimized in Escherichia coli. Is E. coli optimized for growth speed, energy efficiency, or some other property? Experimental data show that at its replication speed limit, E. coli produces about four mass equivalents of nonribosomal proteins for every mass equivalent of ribosomes. This ratio can be explained if the cell’s fitness function is the the energy efficiency of cells under fast growth conditions, indicating a tradeoff between the high energy costs of ribosomes under fast growth and the high energy costs of turning over nonribosomal proteins under slow growth. This model gives insight into some of the complex nonlinear relationships between energy utilization and ribosomal and nonribosomal production as a function of cell growth conditions.

Since the work of Monod in the 1940s, there has been interest in understanding the principles of bacterial growth laws (1–12). Monod observed that increasing glucose increases Escherichia coli’s growth rate, up to a maximum rate beyond which the cells cannot replicate any faster (1). On the one hand, such growth laws are experimentally observable. On the other hand, growth laws, per se, do not give insight into the evolutionary driving forces that lead to them.

Evolutionary principles are expressed by fitness landscapes (13), which are mathematical surfaces that represent how the organism’s fitness depends on some cellular property that can be altered by evolution over time. Peaks on fitness landscapes represent states of maximal fitness. To understand why a cell has a particular growth law, we need a mathematical model that relates its growth law (how the growth rate of the cellular population depends on food concentration) to its underlying fitness landscape (how the cell’s growth parameters can be altered through evolution). Thus far, this is relatively uncharted territory for cellular modeling. Here, we develop a model to explore how bacteria balance their fluxes of energy and ribosomal (RPs) and nonribosomal proteins (NRPs). By comparing the model with data, we can explore possible fitness objectives for bacterial replication. Are bacteria evolutionarily optimized to maximize their duplication speed? Or, are bacteria evolutionarily optimized to maximize the energy efficiency of their duplication processes? Or, something else? By “evolutionarily optimized,” we mean the tradeoffs that a cell must make. By evaluating extensive growth data on E. coli through the lens of the present model, which relates growth observables to fitness landscapes, we conclude that a principal evolutionary driving force for bacteria is the energy efficiency of the fastest-growing cells.

Modeling E. coli’s Balance of Energy Flux and Protein Synthesis

Fig. 1 shows our kinetic model of bacteria growing in the exponential phase. This model defines relationships among four dynamical quantities: the rate of synthesis of ribosomal proteins, the synthesis and degradation rates of NRPs, the production and utilization rates of energy (ATP), and the steady-state specific growth rate of the cell. After Scott et al., Klumpp et al., and others (10, 14, 15), we develop a coarse-grained model based on the following observations: (i) half of the biomolecular mass in a cell are proteins (16); (ii) under fast growth, ∼86% of the total RNA investment of a cell is in ribosomes (6); (iii) under fast-growth conditions, more than 80% of the cell’s ATP requirements for biomass is spent on protein and rRNA synthesis (17, 18); and (iv) bacterial fitness costs, defined as relative loss of fitness, increase with excess production of protein (19, 20). Hence our coarse-grained modeling here focuses on just three internal cell components: ATP (our surrogate quantity that represents internal energy supplies, taken broadly), ribosomes (R), and nonribosomal protein (P).*

Fig. 1.

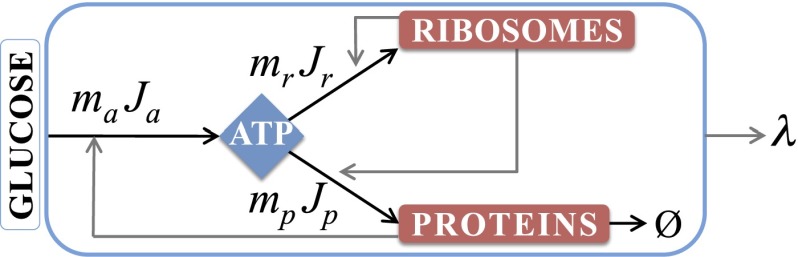
Minimal model of E. coli. Extracellular sugar is converted to ATP, which powers a two-compartment proteome: RPs and NRPs. In turn, the proteome catalyzes the energy-conversion process and growth of the cell. The black arrows show the ATP fluxes: $m_a{J}_a$ is the influx of sugar conversion to ATP, $m_r{J}_r$ is the flow of ATP to produce ribosomes, $m_p{J}_p$ is the flow of ATP to produce NRPs, $\to \varnothing$ indicates the degradation of NRPs, and λ is the specific growth rate of E. coli.

We model the concentration dynamics as follows:

$$\frac{dR}{dt}=J_r-\lambda R,$$ [1]

$$\frac{dP}{dt}=J_p-\left(\lambda +\gamma \right)P,$$ [2]

$$\frac{dA}{dt}=m_a{J}_a-m_r{J}_r-m_p{J}_p-\lambda A,$$ [3]

$$\rho =M_{r}R+M_{p}P.$$ [4]

Here, R, P, and A are the concentrations of ribosomes, NRPs, and ATP, respectively, and λ is the specific growth rate of cells. $m_a$ is the stoichiometric number of ATP molecules derived by the cell per glucose molecule, and $m_r$ and $m_p$ are the stoichiometric numbers of ATP molecules required to synthesize a ribosome (i.e., ribosomal proteins plus ribosomal RNAs) and an NRP, respectively. $M_r$ is the sum of molecular weights of all of the RPs in a ribosome, and $M_p$ is the average molecular weight of an NRP. γ denotes degradation rate of the NRPs (22–24),^† whereas ribosomes are assumed to be stable (25). The total protein density of a cell is denoted by ρ, and it is conserved over a range of growth rates as observed in experiments. For specific values, see Table 1. The rate equations (Eqs. 1–3) contain dilution terms $\left(\lambda R\right)$, $\left(\lambda P\right)$, and $\left(\lambda A\right)$, respectively. As the cell grows, its volume increases, so even if the numbers of cellular protein molecules were fixed, their concentrations would diminish as the cell grows. We set $\lambda A=0$, because this term is negligible compared with the other fluxes in Eq. 3.^‡

Table 1.

Structural, rate, and bioenergetic constants

Constants	Symbol	Value	Reference
Physical constants
Protein density	ρ	0.25 g⋅cm−3	(46)
Molecular weight of RPs per ribosome	$M_r$	7,336 aa × 110 g/mol/aa = 806,960 g⋅mol−1	(6)
Molecular weight of an NRP	$M_p$	325 aa × 110 g/mol/aa = 35,750 g⋅mol−1	(47)
Molecules of ATP produced per glucose molecule	$m_a$	30	(32)
Molecules ATP consumed to create one ribosome	$m_r$	(7,336 aa × 6) + (4,566 nu × 10) ∼ 89,700	†
Molecules of ATP consumed to create one NRP	$m_p$	325 aa × 6 = 1,950
Rate of NRP elongation per ribosome, 20 aa/s	${k\prime }_p$	20 × 3,600 (aa/h)/7,336 aa ∼ 10 aa/h/(RP aa)	(6)
Nonribosomal protein degradation rate	γ	0.1 NRP per total NRP per hour	(22)
Derived constants
Maximum number of protein molecules translated  per hour per ribosome (capacity)	$k_p$	$M_r{k\prime }_p/M_p$ = 215 h−1
NRP translation rate per ribosome scaled by pathway efficiencies	${\lambda }_p$	$\left({\epsilon }_r/{\epsilon }_p\right){k\prime }_p\sim 5$ h−1
Maximum number of ribosomes synthesized per hour per ribosome $\left(={\lambda }_p\right)$	$k_r$	5 h−1
Ribosomal pathway efficiency, grams of RPs synthesized per mole ATP	${\epsilon }_r$	$M_r/m_r\sim 9$ g⋅mol−1
Protein pathway efficiency, grams of NRPs per mole ATP	${\epsilon }_p$	$M_p/m_p\sim 18$ g⋅mol−1
Relative pathway efficiency between P and R pathways	${\epsilon }_{rp}$	$\left({\epsilon }_p-{\epsilon }_r\right)/{\epsilon }_r\sim 1$

^†Average cost of making 1 aa is ∼2 ATP; average cost of making a peptide bond is ∼4 ATP and adding these together gives ∼6 ATP. The average cost of making an average RNA nucleotide and joining a pair of nucelotides is ∼10 ATP (ref. 16, table 1, chapter 4).

Now, we express the production–rate fluxes $J_r$ of ribosomal proteins, $J_p$ of NRPs, and the consumption–rate flux of glucose, $J_a$, for ATP generation in Eqs. 1–3 in terms of concentrations, R, P, A, and extracellular glucose, G

$$J_r=k_r{f}_r\left[A\left(G\right)\right]\cdot R,$$ [5]

$$J_p=k_p{f}_p\left[A\left(G\right)\right]\cdot R,$$ [6]

$$J_a=k_a\left(G\right)\cdot P,$$ [7]

where $k_a$, $k_p$, and $k_r$ are rate coefficients. These functions are given explicitly in Eqs. S1–S5 and Fig. S1A. We note here for example that $f_r\left(A\right)$ is a step-like activation function that saturates with ATP concentration (which, in turn, depends on glucose) to $f_r^{\infty }$, whereas $f_p\left(A\right)=f_p^{\infty }$ is nearly independent with cell’s energy status (26). We express these functional dependences explicitly above to indicate that even though this coarse-grained model is simple in having few equations, it retains considerable complexity of the nonlinearities and feedback that are essential for treating cells beyond common linear approximations.

Our interest here is in the cell growth dynamics over a timescale of hours, so we now focus on steady-state conditions. We obtain the three steady-state relationships from this model by setting the time derivatives in Eqs. 1–3 to zero, giving

$$\frac{R}{P}=\left(\lambda +\gamma \right)/k_p{f}_p,$$ [8]

$$\lambda =k_r{f}_r,$$ [9]

$$m_a{J}_a=m_r{J}_r+m_p{J}_p.$$ [10]

Eq. 9 shows that the maximum growth rate of the cell, the “speed limit,” is the product (also see ref. 10)

$${\lambda }^{\infty }=k_r{f}_r^{\infty },$$ [11]

of model quantities that depend on how fast ribosomes are made.

Deriving Monod’s Growth Law from the Underlying Fitness Landscape

Using this simple coarse-grained model, we develop the central result of this work, namely a mathematical relationship between a growth law (how the growth rate of an average cell depends on food concentration, on timescales shorter than its lifetime) and its fitness landscape (the fitness costs to a cell lineage from altering its machine properties and growth parameters through evolutionary changes on long timescales). We seek an expression for the cell’s growth rate $\lambda \equiv \lambda \left(G,{\mathbf{c}}_{\mathbf{m}}\right)$, as a function of G, the extracellular sugar concentration, and ${\mathbf{c}}_{\mathbf{m}}$, the vector of biophysical machine-property set points, such as the degradation and elongation rates of NRPs and maximum rate of ribosomal synthesis. If we had a mathematical function $\lambda \equiv \lambda \left(G,{\mathbf{c}}_{\mathbf{m}}\right)$, then varying G at fixed ${\mathbf{c}}_{\mathbf{m}}$ would express the growth law: how the concentrations and fluxes of A, R, and P depend on sugar as a cell grows. Alternatively, the dependence of λ on ${\mathbf{c}}_{\mathbf{m}}$ expresses the fitness landscape, namely how the cellular growth rate depends on the cell’s intrinsic biochemical and biophysical properties, which have been established through evolution.

To find this function, we solve the set of equations above in the steady-state limit. That leads us to an expression for the growth rate as a cubic polynomial (SI Text)

$$a_3{\lambda }^3+a_2{\lambda }^2+a_1\lambda +a_0=0.$$ [12]

where the coefficients $a_0$, $a_1$, $a_2$, and $a_3$ depend on the glucose concentration, biophysical constants (Table 1), and metabolic parameters (Table 2). Its solution gives $\lambda =\lambda \left(G,{\mathbf{c}}_{\mathbf{m}}\right)$, providing both the Monod’s growth law and the evolutionary fitness landscape of the model.

Table 2.

Parameters of E. coli ODE numerical model obtained from fit of the model to data

ODE model parameters	Symbol	Value
Affinity constant between NRPs and glucose for glucose transport	$D_g$	0.07 mM
Number of glucose molecules metabolized to ATP per hour per protein molecule	$k_a^{\infty }$	120 h−1
Affinity constant between proteins and ATP for ATP generation	$D_a$	4.0 mM
ATP concentration threshold for ribosome synthesis	$D_r$	0.18 mM
Maximum fraction of ribosomes translating RPs	$f_r^{\infty }$	0.2
Maximum fraction of ribosomes translating NRPs	$f_p^{\infty }$	0.7

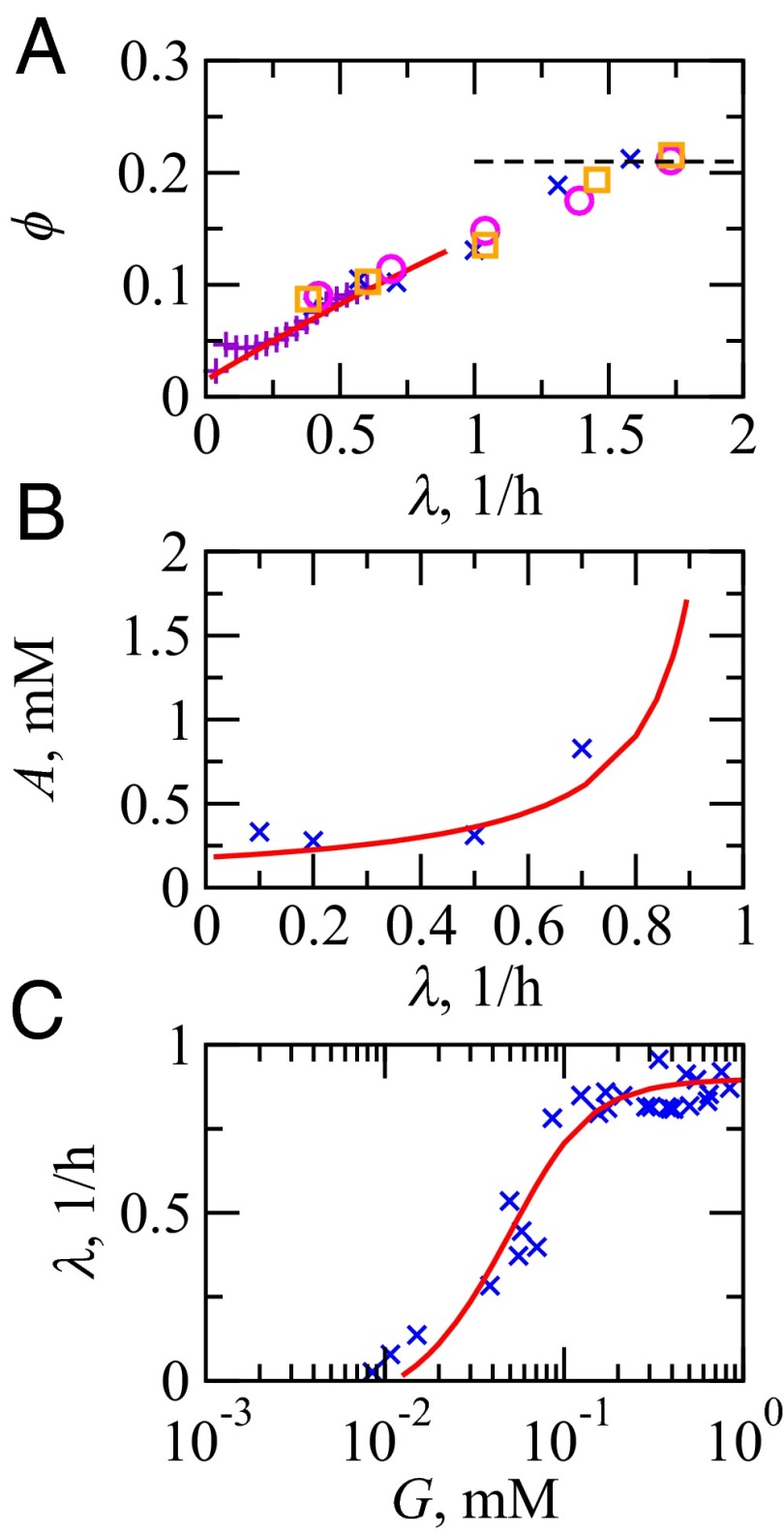
Here is how we use this model. First, we use experimental data to determine the parameters of the model (Fig. 2). In particular, we require three types of experimental data: (i) the growth rate vs. sugar, $\lambda =\lambda \left(G\right)$, such as in Monod’s growth law; (ii) the ribosomal fraction vs. growth rate, $\varphi =\varphi \left(\lambda \right)$; and (iii) the ATP concentration as a function of growth rate, $A=A\left(\lambda \right)$. These three types of experiments fully specify the model (SI Text). We are especially interested in the energy-mass balance topology and the principles and limits arising out of it over evolutionary timescales. Then, given the fully specified model, we can explore the fitness landscape. In particular, we ask what E. coli is optimized to do, in the context of how its energy is trafficked between RPs and NRPs.

Fig. 2.

Comparison of model results (—) vs. experiments (symbols) at 37 °C. (A) The RP as a fraction of total protein weight in E. coli: °, Bremer and Dennis (6); ×, Scott et al. (10); and □ Forchhammer et al. (44). To get ϕ, the (rRNA/protein) ratio from ref. 10 is scaled by a factor of 0.46 (6). +, fraction of ribosomal promoter activities of Zaslaver et al. (33) uniformly scaled to align with (°, ×, □). At fast growth, ϕ reaches a limit of 0.21 (- - -). (B) ATP concentration, A, in E. coli K-12 strain vs. specific growth rates of cells: ×, Ishii et al. (45). (C) E. coli specific growth rate vs. extracellular glucose concentration: ×, Monod (1).

Cells Are Optimized for Energy Efficiency of the Fast-Growing Cells and Not Just Growth Rate or Efficiency Alone

We are interested in the cell’s energy efficiency. We define the energy efficiency as the growth rate λ divided by the rate, $J_a$, of conversion of sugar to ATP, specifically

$$\epsilon \left(\lambda ,f_p^{\infty }\right)=\left(\frac{\rho }{m_a}\right)\left(\frac{\lambda }{J_a}\right),$$ [13]

(27). ε is a measure of how effectively the organism converts its input energy into its duplication speed. The energy efficiency ε is a function of the values of the machine constants that have resulted from evolutionary optimization (18, 28, 29).

The present model can be used to explore what values of the biophysical constants are optimal. We can compute its point of maximum fitness to address how E. coli chooses one of its important operating parameters. Here, we focus on one particular biophysical constant. We suppose some properties are largely fixed by chemical and physical limits, including the rate constants of protein synthesis $\left({k\prime }_p\right)$, degradation (γ), and ribosomal assembly $\left(k_r\right)$, and the relative costs of P vs. R $\left({\epsilon }_p/{\epsilon }_r\right)$.^§ We suppose that evolution can optimize a cell’s ribosome utilization by altering the value of $f_p^{\infty }$, the fraction of ribosomes that are producing NRPs under fast-replication conditions $\left(\lambda \to {\lambda }^{\infty }\right)$. We ask what value, $f_p^{\infty }=f_p^{\mathrm{\infty },\mathrm{\ast }}$, maximizes the cell’s energy efficiency ε? In SI Text, we show that the value of $f_p^{\mathrm{\infty },\mathrm{\ast }}$ that maximizes the energy efficiency of the cell under the fast-growth condition is

$$f_p^{\mathrm{\infty },\mathrm{\ast }}\approx 1-\frac{1}{k_r}\frac{\gamma }{{\epsilon }_{rp}}\left(1-\frac{{k\prime }_p}{k_r}\right)-\frac{1}{k_r}\sqrt{\frac{\gamma }{{\epsilon }_{rp}}{k\prime }_p}.$$ [14]

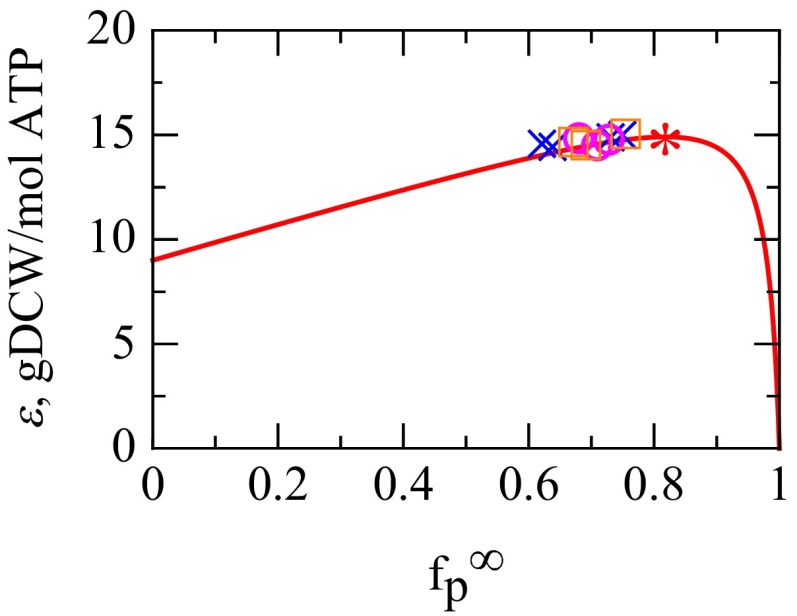
Substituting the known machine constants from Table 1 into Eq. 14 gives the value $f_p^{\mathrm{\infty },\mathrm{\ast }}\sim 0.8$ and therefore $f_r^{\mathrm{\infty },\mathrm{\ast }}=1-f_p^{\mathrm{\infty },\mathrm{\ast }}\sim 0.2$. This result is quite robust, independent of the substrates for growth and the mode of energy metabolism, e.g., fermentation vs. oxidative phosphorylation. A key uncertainty is in ${\mathit{ϵ}}_r$. If we increase ${\mathit{ϵ}}_r$ by 50%, then the model predicts the peak at $f_p^{\mathrm{\infty },\mathrm{\ast }}=0.69$, which is within the error of the experimental data. This result predicts that, at its maximum speed, each ribosome produces about four mass units of NRP for every mass unit of ribosome it produces. Remarkably, these predicted values are very close to the observed values of $f_p$ for fast-growing aerobic E. coli under different conditions (Fig. 3 and Fig. S2A).

Fig. 3.

The fitness landscape of energy efficiency ε vs. $f_p^{\infty }$—the fractional amount of ribosomes translating NRPs at fast growth. The solid line is Eq. S18, grams of cell dry weight (gDCW) per mole of ATP, with machine constants ${k\prime }_p$ , $k_r$, and $\left(\gamma /{\epsilon }_{rp}\right)$ from Table 1. * Predicted maximum. The symbols ○, ×, and □ show values of $f_p$ (same as Fig. S2A) from experiments across all nutrients and growth rates $\lambda \hspace{0.17em}\mathrm{\gtrsim }\hspace{0.17em}0.7$ 1/h obtained from Eq. 16 with γ = 0.1 h⁻¹ and ${k\prime }_p$ = 9.7 h⁻¹, whereas the symbol heights are model-efficiency transformed from $\varphi \left(\lambda \right)$ data via Eq. S17. ○, Bremer and Dennis (6); ×, Scott et al. (10); □, Forchhammer et al. (43). The $f_p$ values are consistent with the predicted fitness peak, if the evolutionary target is to maximize the energy efficiency of the fastest-growing cells.

Here is our interpretation. Consider two idealized limiting cases: (i) if a bacterial cell had only one ribosome $\left(f_p^{\mathrm{\infty },\mathrm{\ast }}\to 1\right)$, the cell would require years to duplicate; or (ii) if a bacterial cell was a “bag of ribosomes” $\left(f_p^{\mathrm{\infty },\mathrm{\ast }}\to 0\right)$, the cell could duplicate in about 6 min. In reality, the observed speed limit for duplicating E. coli is about 20–30 min. Therefore, to first approximation, E. coli has evolved to nearly reach the bag of ribosomes limit under fast-growth conditions. However, to second approximation, this is not exactly true. Why is E. coli not able to squeeze out the remaining factor of 3–4 in speed? Why must each ribosome duplicate about four times its own weight in NRPs at the cell’s speed limit? On the one hand, there could be biological reasons why there is a minimal essential set of NRPs that must be duplicated. On the other hand, we simply note that it is remarkable that the observed mass ratio of four can be derived from a simple principled general energy-balance argument.

Put metaphorically, this evolutionarily optimized energy balance in E. coli is akin to optimizing a race car. A race car has a front end (fuel system) and back end (engine). The best race car is one in which the fuel system is matched to the engine, neither too big for the engine nor too small for it. For E. coli, the front end entails conversion of glucose to ATP and the back end entails the expenditure of ATP. In short, if the cell invests too heavily in ribosomes, it will not have enough NRPs to catalyze the biochemical conversion of glucose to ATP. The optimization of energy efficiency for fast-replicating cells occurs within the maximal growth rate, which corresponds to a matching of the catabolic and anabolic fluxes

$${\lambda }^{\infty }=k_r{f}_r^{\infty }={\lambda }_a{f}_p^{\infty },$$ [15]

where ${\lambda }_a$ is related to the NRP’s rate constant for energy generation (SI Text).^¶

This argument can also be framed in terms of energy costs. Making ribosomes is more expensive than making NRPs per unit weight. The evolutionary tradeoff is between the intrinsic cost of energy-expensive ribosomes needed for fast growth, on the one hand, and the unavoidable cost of NRP turnover at slow growth. As a caveat, to be clear, we note that our efficiency quantity describes the conversion of ATP, not glucose, to proteins and ribosomes. Therefore, our arguments about optimizing energy efficiency do not address the relative importance of fermentation to respiration. Also, the energy optimization described here pertains to evolutionary timescales, over which cells can alter their machine constants. Stressing cells can certainly lead to nonoptimality under daily growth conditions, in ways that could only be improved by evolutionary changes.

The Cell Shifts Its Energy Flows Under Different Growth Conditions

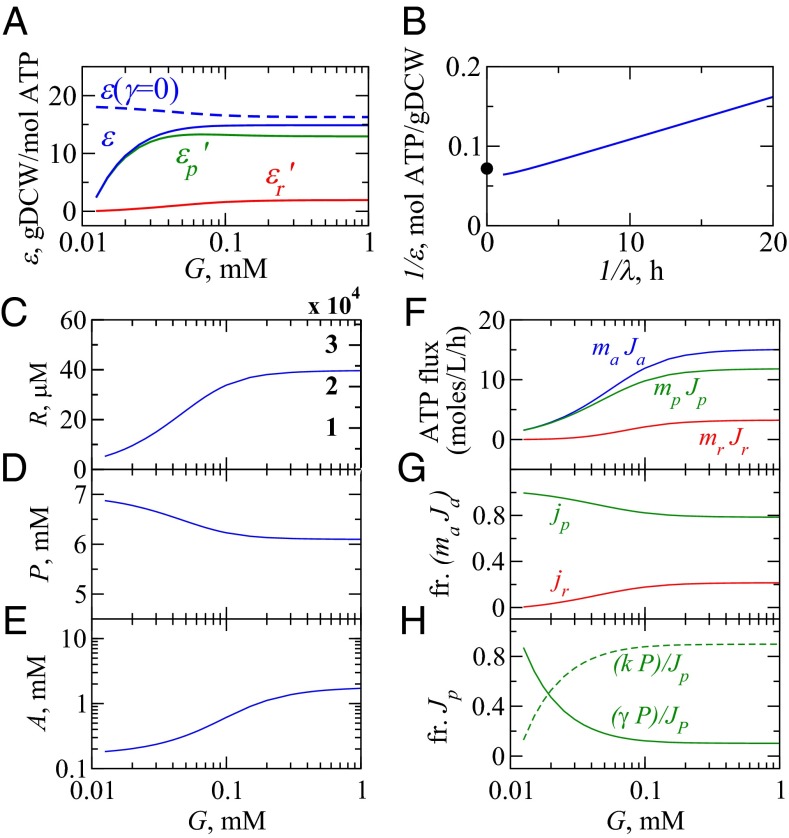
What are the cellular activities under different growth conditions? Fig. 4 gives a summary of the model results. First, under slow-growth conditions, the cell is not efficient at converting energy to proteins or ribosomes (Fig. 4A). Under slow growth, the cell invests its energy in maintenance, replenishing proteins that are degrading.^‖ The blue dashed curve shows that the efficiency would be much higher if there were no protein degradation (i.e., $\gamma =0$). Fig. 4 F and G shows that the cell is producing mostly NRPs, and Fig. 4H shows that most of energy in NRPs is going into protein degradation and not dilution under slow-growth conditions.

Fig. 4.

Behaviors of the model cell. (A) Growth efficiency ε (30, 31) (solid blue) and its components ${\epsilon }_p\prime$ (solid green) and ${\epsilon }_r\prime$ (solid red) (Eq. S20); efficiency in the absence of protein turnover $\epsilon \left(\gamma =0\right)$ (dashed blue). (B) A Lineweaver–Burk plot linearizes the reciprocals of yield $\left(1/\epsilon \right)$ and growth rate $\left(1/\lambda \right)$ from the model. •, experimental maximum biomass yield per unit ATP, ${\epsilon }_{max}=13.9$ gDCW/mol ATP (30). (C–E) How the concentrations of ribosomes (R), NRPs (P), and ATP (A) depend on glucose concentration G. Ribosomal density in units of ${10}^4$ ribosomes/fL is displayed in red and compares well against ref. 46. (F) The flux of ATP into R and P for different growth conditions, G, total ATP generation flux $m_a{J}_a$ (blue), and ATP consumption fluxes for biosynthesis of ribosomes $m_r{J}_r$ (red) and NRPs $m_p{J}_p$ (green) in units of moles per liter per hour (Eq. 10). (G) Predictions of fractional ATP flux toward synthesis of ribosomes $j_r=\left(m_r{J}_r\right)/\left(m_a{J}_a\right)$ (red) and NRPs $j_p=\left(m_p{J}_p\right)/\left(m_a{J}_a\right)$ (green). (H) Fraction of ATP flux used for NRP synthesis split between dilution $\left(\lambda \cdot P\right)/J_p$ (dashed green) and degradation $\left(\lambda \cdot \gamma \right)/J_p$ (solid green).

Second, at higher glucose levels, growth efficiency increases. Under fast-growth conditions, protein degradation happens at a negligible rate, so less of the cell’s energy is devoted to repairing degrading proteins. Now, the cell converts more sugar directly to cell growth. Maximal values of yield of biomass from ATP have been widely estimated before in aerobic E. coli grown in glucose and other carbon sources (30, 31); our model is consistent with that data. Third, increasing sugar leads to upshifting the production of ribosomes relative to NRPs (6, 10, 32, 33). Experiments are often used to determine ϕ, the mass fraction of all of the cellular proteins that are ribosomal. Previous work has shown that $\varphi \left(\lambda \right)\propto \lambda$, i.e., ϕ increases linearly with the growth rate of the cell (10). Here, we show how $\varphi \left(\lambda \right)$ is related to machine constants of the cell. Using Eq. 8, we find that ϕ is given by

$$\varphi \left(\lambda ;f_p\right)=\frac{M_{r}R}{M_{r}R+M_{p}P}=\frac{\lambda +\gamma }{\lambda +\gamma +{k\prime }_p{f}_p},$$ [16]

where ${k\prime }_p=\left(M_p{k}_p/M_r\right)$ is the speed of protein translation. In E. coli, ${k\prime }_p$ is a constant of 20 amino acids per second per ribosome at 37 °C (6). We find that**

$$\varphi \left(\lambda \right)={\varphi }_0+\frac{\lambda }{{k\prime }_p{f}_p^{\infty }},$$ [17]

where ${\varphi }_0=\left(\gamma /{k\prime }_p{f}_p^{\infty }\right)$. Eq. 17 predicts the observed linear relationship (6, 10) in terms of the physical variables in our model: γ, the protein degradation rate, and $f_p^{\infty }$, the fraction of ribosomes that are translating NRPs at the speed limit for growth. Also, we noted above that, under the fast-growth limits, ribosomes produce about four mass equivalents of NRPs for every mass equivalent of RPs. This comes from using $\varphi \hspace{0.17em}\mathrm{\lesssim }\hspace{0.17em}{f}_r^{\infty }=f_r^{\mathrm{\infty },\mathrm{\ast }}\sim 0.2$, which gives $\left(RP/NRP\right)=\varphi /\left(1-\varphi \right)\sim 1/4$ (Fig. 2A).

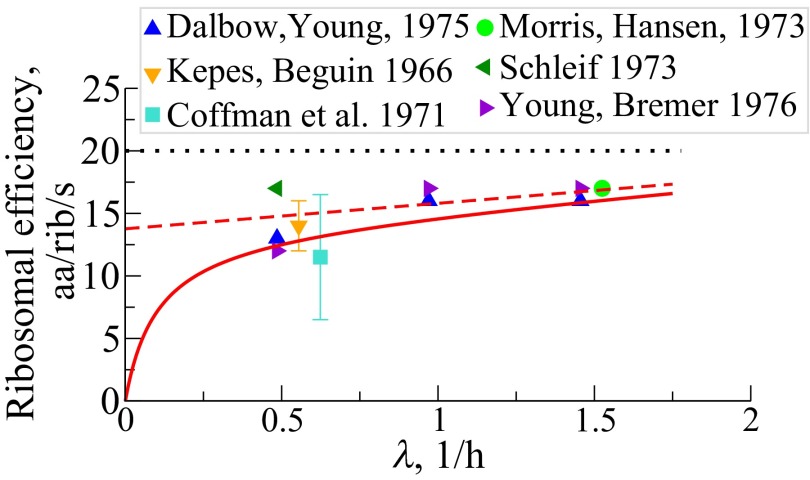
Fourth, the model predicts that the net protein elongation rate per ribosome, $k_{per}$, should increase with the cell’s growth rate, consistent with direct measurements of single peptide chain extension rates (34–39) (Fig. 5). The error in prediction is within 20% arising from discounting inactive ribosomal fraction (39). Sometimes called ribosomal efficiency, here its growth rate dependency (14, 40, 41) stems mainly from the synthesis of nonribosomal proteins against their tendency to turnover, especially at small growth, and also on the demand to make more energy-sensitive ribosomes at increased growth rates. Fig. S2B shows the average time, the inverse of the rate, for extending the NRP chain by one amino acid per ribosomal catalyst. This time varies from 0.65 s under slow growth to 0.15 s at fast growth.

Fig. 5.

Net peptide elongation rate, per ribosome, $k_{per}$, in units of amino acids per second per ribosome vs. cell growth rates, taken over both RPs and NRPs. The solid symbols are direct observations of peptide chain elongation (34–39). The red solid and the dashed lines are predictions with NRP turnover rate $\gamma =0.1$ h⁻¹ and $\gamma =0$, respectively [Eq. S14a; $f_p=f_p^{\infty }$. (…) indicates maximal translation rate].

Limitations of the Model

To focus on the essentials, our modeling has neglected certain factors of lesser importance for our purposes. First, the model only treats implicitly, and not explicitly, certain processes such as glucose transport across membrane, transcription of RNA, and translation of ribosomal proteins. These are implicit in quantities ${\lambda }_a$ and $k_r$. The slowest rate coefficient (under fast growth) is ${\lambda }_a$, which characterizes metabolism and not the production of protein. With these simplifications, there are energy sources and sinks in the cell that we have not modeled here. Second, we have only considered respiration. It is well known that aerobic E. coli uses fermentative metabolism at fast growth rates. In quantitative terms, fermentation contributes increasing energy at faster growth rates. However, the amounts are small. We estimate this contribution to be ∼10% at $\lambda =0.6$ h⁻¹.^†† Interestingly, the cell’s optimal energy efficiency state (Eq. 14) is given by properties unrelated to the mode of energy generation. Third, we considered the efficiency of energy to biomass, a property that is difficult to measure. More experiments for accurate estimates are required. However, based on indirect measurements, it has been suggested that maximal energy efficiency seems to lie close to maximal growth rates (18). Fourth, our model is relevant in the growth speed regime $0.1\hspace{0.17em}\mathrm{\lesssim }\hspace{0.17em}\lambda \hspace{0.17em}\mathrm{\lesssim }\hspace{0.17em}1$ h⁻¹ as observed in glucose-limited cultures. At slower growth rates, stress machineries and chaperones are activated, whereas at very fast growth, additional nutrient supplements are required, which we do not consider.

Discussion

We developed a coarse-grained model of the concentrations and fluxes of the basic energy and biomass flows in a typical bacterial cell such as E. coli. With three dynamical equations and one constraint relationship, taken in the steady-state limit, this is about the simplest model of the energy–biomass balance of a simple cell, which is a complex and nonlinear system. It predicts the fluxes and concentrations of ATP and RPs and NRPs as a function of glucose concentration. The model also gives an expression for the linear law of ribosomal increase with growth rate and how it depends on the cell’s machine constants, and it expresses the basic behavior that cells invest energy in repairing proteins when sugar is low vs. duplicating when sugar is high. The model gives a relationship between the cell’s growth law and its fitness landscape. It explains why each ribosome in E. coli duplicating at full speed produces about four mass equivalents of NRP for every unit mass of RP. The present model shows that the observation can be explained if the evolutionary fitness function for E. coli is the energy efficiency of the fast-growing cells instead of the maximum speed itself or some other property. This appears as a result of evolution in which a cell achieves a balance between the cost of energy-expensive ribosomes required for fast replication, on the one hand, and the unavoidable costs of maintaining proteins against instability, denaturation, and turnover, on the other hand, which are important under slow-growth conditions.