The Adaptive Biasing Force Method: Everything You Always Wanted To Know but Were Afraid To Ask

Abstract

In the host of numerical schemes devised to calculate free energy differences by way of geometric transformations, the adaptive biasing force algorithm has emerged as a promising route to map complex free-energy landscapes. It relies upon the simple concept that as a simulation progresses, a continuously updated biasing force is added to the equations of motion, such that in the long-time limit it yields a Hamiltonian devoid of an average force acting along the transition coordinate of interest. This means that sampling proceeds uniformly on a flat free-energy surface, thus providing reliable free-energy estimates. Much of the appeal of the algorithm to the practitioner is in its physically intuitive underlying ideas and the absence of any requirements for prior knowledge about free-energy landscapes. Since its inception in 2001, the adaptive biasing force scheme has been the subject of considerable attention, from in-depth mathematical analysis of convergence properties to novel developments and extensions. The method has also been successfully applied to many challenging problems in chemistry and biology. In this contribution, the method is presented in a comprehensive, self-contained fashion, discussing with a critical eye its properties, applicability, and inherent limitations, as well as introducing novel extensions. Through free-energy calculations of prototypical molecular systems, many methodological aspects are examined, from stratification strategies to overcoming the so-called hidden barriers in orthogonal space, relevant not only to the adaptive biasing force algorithm but also to other importance-sampling schemes. On the basis of the discussions in this paper, a number of good practices for improving the efficiency and reliability of the computed free-energy differences are proposed.

Introduction

Although the statistical-mechanical foundations of free-energy calculations were laid a long time ago,¹⁻³ their practical applications became possible only with the advent of modern computers. From the inception of computer-based free-energy calculations^4,5 it has been clear to theorists that direct Boltzmann sampling of rugged energy landscapes is inefficient. The subsequent development of the field is a history of efforts to remedy this problem.

In free-energy calculations, the quantity of interest is almost always the free-energy difference between physical states of the system rather than the absolute free energy of a given state. From this standpoint, calculations can be categorized on the basis of variables used to transform the system between states of interest. Then, two main classes can be distinguished, namely alchemical and geometrical transformations.⁶ They rely, respectively, on changes of a parameter in the Hamiltonian or a function of atomic coordinates. The first class encompasses structural modifications of chemical species that rest upon the remarkable malleability of the potential energy function in molecular-mechanics-based simulations,^7,8 reminiscent of the fabled ability of alchemists to transmute base metals into noble ones. Alchemical transformations are often associated with the free-energy perturbation method^2,3 on account of the progressive and perturbative nature of the change incurred by the system of interest, although, strictly speaking, alchemical free-energy calculations can be carried out by way of alternate approaches, such as thermodynamic integration.¹ The very first application of alchemical transformations to a nontrivial chemical problem was published nearly 30 years ago by William Jorgensen, to whom the present contribution is dedicated.⁹ In noteworthy agreement with experiment, this pioneering simulation reproduced the relative hydration free energy of methanol with respect to ethane.

The second class of transformations embraces virtually any geometric modification in a molecule or a collection of molecules by means of selected collective variables tailored to address the problem at hand, which could vary from changes in the internal degrees of freedom in a molecule to intricate recognition and association phenomena.⁷ Such collective variables form the transition coordinate, a low-dimensional representation of a multidimensional mathematical object.

The distinction between the two types of transformations is theoretically important. For geometric transformations, the transition coordinate is, in effect, a generalized coordinate, the evolution of which is usually described by Hamilton’s equations of motion. In contrast, for a parameter in the Hamiltonian, no equations of motion naturally exist, although it is possible to extend the formalism of dynamics to include such a parameter.¹⁰ As a consequence, a number of methods for calculating free energy by way of geometric transformations cannot be applied to alchemical transformations without such extension. The adaptive biasing force method can serve as an example.⁷

A considerable number of ingenious techniques have been developed to improve the efficiency of mapping free-energy landscapes associated with geometrical transformations along a transition coordinate.¹¹⁻²⁵ A common feature of these methods is their reliance on importance-sampling techniques. The central idea of these techniques is to depart from sampling from the Boltzmann distribution defined by the original Hamiltonian and, instead, sample from another distribution that favors regions of phase space that would be visited only infrequently but are important to achieving reliable free-energy estimates. Because this procedure is clearly biased, it is essential to know how to correct, or unbias, it to recover the true underlying distribution. Importance sampling is commonly used not only in statistical mechanics of condensed phases but also in other fields of science, usually as a variance reduction technique most frequently combined with the Monte Carlo method.

Probably the most popular, and also the oldest importance-sampling technique used in free-energy calculations is umbrella sampling.¹¹ It relies on introducing a bias in simulations that favors states corresponding to large values of the free energy along the transition coordinate. Local elevation,¹⁵ conformational flooding,¹⁶ metadynamics,^20,24 and the Wang–Landau algorithm^26,27 are examples of more recent importance-sampling algorithms, united by the common denominator that a memory-dependent potential disfavors regions of conformational space that have already been frequently visited.

In a sense, the adaptive biasing force method¹⁹ rewove the fabric of free-energy calculations of geometrical transformations, as it is characterized by both conceptual and practical simplicity and requires, at least in principle, little intervention from the end user. In spite of apparent similarities with the local-elevation and conformational-flooding strategies in its aim to sample efficiently all values of the transition coordinate, its theoretical underpinnings are quite different, as we will argue further in this paper. Furthermore, in contrast with seemingly similar strategies, the adaptive biasing force algorithm requires no prior knowledge of the free-energy landscape at hand.

At its core, the adaptive biasing force method is an adaptive importance-sampling strategy in which the quantity being adjusted is the average force acting along the transition coordinate. It helps the system under study escape from kinetic traps in which it would otherwise have remained for a very long time. The method constitutes a highly efficient route to estimating free energies, which, since its inception, has been used to tackle a number of challenging problems of chemical and biological interest, such as mechanical proteins,²⁸ transport phenomena,²⁹⁻³¹ or protein–ligand and protein–protein recognition and association.³² More generally, it is a versatile, adaptive, importance-sampling strategy that can be utilized in many fields, whenever sampling of a probability measure is thwarted by metastability of the sampling dynamics.

In this self-contained contribution, the multiple facets of the adaptive biasing force algorithm are discussed in an exhaustive manner, tackling a number of issues that have not been addressed so far, or only rarely so. In the following section, we present the theoretical foundations of the method, discussed in the context of other free-energy approaches. Next, we briefly address a number of practical issues related to a proper choice of the transition coordinate. Then, an analysis of the convergence properties of the method and approaches to calculating and controlling statistical errors associated with the calculated free-energy values are presented. The discussion of convergence and errors continues with the focus on nonergodicity scenarios, and ways to identify and circumvent them. Subsequently, we examine for the first time how the adaptive biasing force algorithm is used in conjunction with geometrical restraints, which have to be enforced in many problems of interest. Finally, we discuss some new strategies for combining thermodynamics and kinetics in importance-sampling simulations, before closing with recommendations for ”good practices” in applying the adaptive biasing force method and an outlook toward further promising statistical mechanical and algorithmic developments.

The adaptive biasing force algorithm

In this section, the essential idea behind the adaptive biasing force algorithm is first explained in terms appealing to physical intuition, followed by the theoretical underpinnings of the method presented in a more formal language. Then, the reader is guided through the common expressions for the mean force, and the adaptive algorithm, both of which are at the core of the method. Finally, the method is compared with related importance-sampling schemes.

The Adaptive Biasing Force in Plain Language

The adaptive biasing force method is aimed at improving the efficiency of molecular dynamics simulations in which the potential energy surface is sampled ineffectively due to free-energy barriers. In practice, these barriers appear as bottlenecks in the dynamics of certain privileged coordinates that describe the transitions between physically important states (transition coordinates). They also cause the system to become trapped in some states for durations exceeding the time scale of the simulation, resulting in incomplete sampling.

The free energy along a transition coordinate can be seen as a potential resulting from the average force acting along the coordinate (i.e., the negative of the gradient of this potential), hence the name potential of mean force. In the formalism of thermodynamic integration, on which the adaptive biasing force is based, the average force is the quantity that is calculated directly. Subsequently, this force is integrated to yield the potential. The instantaneous force acting along the coordinate may be decomposed into the sum of the average force (which depends only on the value of the transition coordinate) and a random force with zero average, reflecting fluctuations of all other degrees of freedom. Hence, in a low-dimensional view of the process, the transition coordinate evolves dynamically in its time-independent potential of mean force, and this evolution is driven by the random force. In many instances, the random force can be satisfactorily approximated as diffusive, leading to a simple physical picture in which the system diffuses along the transition coordinate in the potential of mean force.

The idea behind the adaptive biasing force algorithm is to preserve most characteristics of this dynamics, including the random fluctuating force, while flattening the potential of mean force to remove free-energy barriers, and thus accelerate transitions between states. This is done adaptively, without any prior information about the potential of mean force. To accomplish this, the instantaneous force acting along the coordinate is calculated, and its running time average is recorded, thus providing an on-the-fly estimate of the derivative of the free energy at each point along the pathway. At the same time, an external biasing force is applied, exactly canceling the current estimate of the average force. Over time, as the estimate converges to the average force at equilibrium, the total, biased average force stabilizes at values very close to zero. Then, the system experiences a nearly flat potential of mean force and displays accelerated dynamics along the transition coordinate. The fact that the biasing force is exactly equal to the mean force is actually not crucial. What is important is that the biasing force yields sufficiently uniform sampling of the transition coordinate that the remaining barriers can be easily traversed in response to thermal fluctuations.

Theoretical Backdrop

Let us now define the adaptive biasing force algorithm in a formal way. The adaptive biasing force algorithm is not inherently tied to any specific type of dynamics but does rely on sampling of the canonical ensemble. In explicit-solvent simulations, Langevin dynamics with sufficiently soft damping and small stochastic forces becomes a mere perturbation of Hamiltonian dynamics and may be used as one simple way to achieve canonical sampling. For convenience, but without loss of generality, we will base our description below on Langevin dynamics. Langevin dynamics can be written as

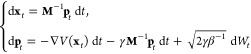1

where (x_t, p_t) denotes the positions and momenta of the particles at time t, M is the mass tensor, V : 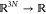is the potential energy function, γ is the friction coefficient, W_t is the Wiener process that underlies the random force (white noise), and β^–1 = k_BT, where k_B is the Boltzmann constant and T is temperature. The dynamics of eq 1 is ergodic (under mild conditions on V) with respect to the canonical measure Z_p^–1 exp[−βp^TM^–1p/2] dp μ(dx), where μ(dx) = Z_x^–1 exp[−βV(x)] dx. Ergodicity means that long-time averages converge to canonical averages:

2

and that the law at time t of the stochastic process converges to the canonical measure in the long-time limit:

3

where 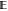is the expected value. The first limit in eq 2 is of particular interest for practical applications because it allows for computing canonical averages from trajectory averages.

For a typical potential V, the associated Boltzmann measure μ is multimodal: high-probability regions are separated by low-probability regions. The former correspond, for instance, to the most likely conformations of a biological object, which are typically separated by transition regions of very low probability. For these reasons, estimating averages with respect to the probability measure μ is, in general, a difficult task. In particular, the ergodic properties of the dynamics of eq 1 are not sufficient to devise reliable numerical methods, because under these premises, the stochastic process remains trapped in large-probability regions, and, as a consequence, the long-time asymptotic regime t → ∞ is very difficult to reach in the ergodic limits in eqs 2 and 3. The fact that the system remains for a very long time in some region of phase space before hopping to another region is called metastability, and the corresponding states of the system are called metastable. The inability to reach the ergodic limit is often called quasi nonergodicity; the system appears nonergodic on the time scales of the simulations. A typical example of a metastable state is a local free-energy minimum in the conformational space of a protein.

The adaptive biasing force method relies on modifying the potential V in such a way that the energy landscape is flattened along a given transition coordinate ξ: 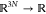. Here, we restrict ourselves to a one-dimensional transition coordinate, leaving generalization to high-dimensional transition coordinates for the section Expressions for the Mean Force. More precisely, the potential V is changed to x → V(x) – A_t[ξ(x)] and A_t is updated in such a way that it converges to the free energy A, defined (up to an additive constant) by

4

where the measure δ_ξ(x)–z (dx) is supported by the subset {x, ξ(x) = z} and is such that δ_ξ(x)–z (dx) dz = dx.

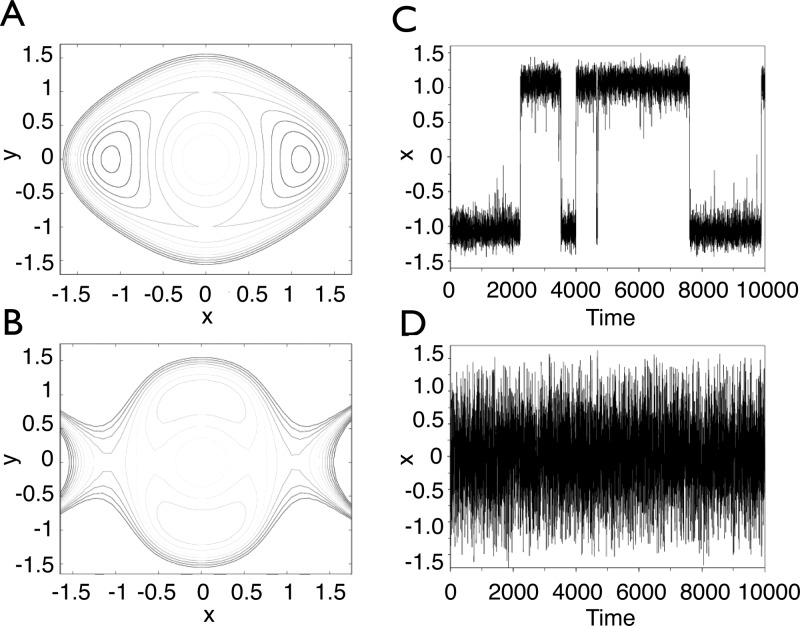
In practice, the bias is only applied in a window [z_min, z_max] as explained in the section Justification of a Stratification Strategy. Notice that, by the definition of A, the canonical measure associated with the biased potential V(x) – A[ξ(x)] is such that ∫exp(−β{V(x) – A[ξ(x)]})δ_ξ(x)–z (dx) = C, where C is a constant independent of z. Therefore, if the biased potential V(x) – A[ξ(x)]1_{ξ(x)∈[zmin,zmax]} is used, the marginal along ξ is a uniform law over [z_min, z_max]. Here, 1_{ξ(x)∈[zmin,zmax]} is an indicator function, which is one when ξ(x) ∈ [z_min, z_max] and zero otherwise. Let us recall that the marginal law is defined as follows: if x is distributed according to a probability distribution μ, then the law of ξ(x) is called the marginal of μ along ξ. If we knew the free energy A, it would be a good idea to use −A◦ξ as a biasing potential, because sampling along ξ would be easier. This is illustrated in simple two-dimensional examples in Figures 1 and 2. Notice in particular that the free energy seems to be a good biasing function for efficient sampling of both energetic barriers (Figure 1) and entropic barriers (Figure 2).

Figure 1.

Upper row: (A) original two-dimensional, double-well potential displayed as level sets; (C) time trajectory of the first coordinate x in the stochastic process, showing oscillations between the two metastable wells. Lower row: (B) level sets of the same potential biased by the free energy associated with the transition coordinate ξ(x,y) = x; (D) time trajectory of the transition coordinate x in the adaptively biased dynamics, showing no metastability.

Figure 2.

Upper row: (A) the original two-dimensional potential is zero inside the hourglass shape, and +∞ outside; (C) time trajectory of the first coordinate x in the stochastic process, showing oscillations between the two metastable wells. Lower row: (B) free energy along the transition coordinate ξ(x,y) = x, featuring a purely entropic barrier; (D) time trajectory of the transition coordinate x in the free-energy-biased dynamics, showing no metastability.

The main ingredient that we now need is an update rule for A_t such that lim_t→∞A_t = A. This is based on the following formula,³³⁻³⁵ which defines the mean force, namely, the negative of the derivative of the free energy. More general formulas can be derived, which give rise to many variants of the adaptive biasing force method (see section Expressions for the Mean Force),

5

where the instantaneous force is defined by

6

Equation 5 is a consequence of the definition of the free energy in eq 4 and of the co-area formula (which is a generalization of the Fubini theorem); see for instance ref (8). From eq 5 it follows that A′ is the conditional average of the instantaneous force, F_ξ, with respect to the canonical measure conditioned to a fixed value of the transition coordinate: A′(z) = 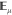[F_ξ(x)ξ(x) = z]. An important observation is that eq 5 remains true if the potential V is changed to V – A_t◦ξ: for any function A_t

7

In other words, a biasing potential A_t depending solely on ξ leaves averages conditioned by ξ unchanged. This is the intuition behind the adaptive biasing force dynamics, which can be written as

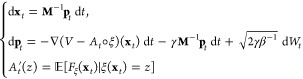8

Indeed, if (x_t, p_t) were at equilibrium with respect to the biased canonical measure Z_p^–1 exp(−βp^TM^–1p/2) dpZ_t^–1 exp[−β(V – A_t◦ξ)(x)] dx, then A_t^′ would be equal to A′. In practice, of course, the sampling is not sufficiently fast for the process to be instantaneously at equilibrium with respect to the time-varying biased potential V – A_t◦ξ, and this is why this heuristic is not sufficient to fully understand the convergence of the adaptive biasing force dynamics (see the section Convergence and Error Analysis). However, this simple reasoning is sufficient to check that if A_t converges to some limit A_∞, then necessarily, A_∞ = A′.

From a practical viewpoint, the conditional expectation in eq 8 can be computed using two procedures: either time averages over a single long trajectory or averages over many replicas run in parallel. These procedures will be discussed in ample detail in the section Multiple-Walker Strategies below.

Intuitively, the adaptive biasing force dynamics thus consists of adding a force A_t^′[ξ(x)]∇ξ(x) that exactly compensates the average of the original force, −∇V(x), along a given transition coordinate. If ξ is well-chosen, the hope is to observe a fast convergence (at least compared to the original dynamics embodied in eq 1 at equilibrium) of A_t to the mean force A′.

Expressions for the Mean Force

Given a transition coordinate ξ(x), the mean force is a well-defined quantity, yet its expression as an ensemble average of an instantaneous force F_ξ is not unique, as we will see below. In adaptive biasing force simulations, the choice of a convenient expression for F_ξ is driven by practical considerations, notably ease of implementation and numerical behavior, such as variance.

The classic expression for the instantaneous force involves an explicit coordinate transformation Ξ from Cartesian to generalized coordinates, which include the transition coordinate ξ. That is, Ξ : 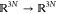, with Ξ₁ = ξ and components Ξ_i for i > 1 are generalized coordinates of no particular physical significance, but necessary to the mathematical framework. A valid expression for the instantaneous force is then¹²

9

which in the physics literature is more commonly written as

10

where |J| is the determinant of the Jacobian matrix (∂_iΞ_j^–1)_(i,j). From the arbitrary choice of Ξ_i,i>1 is derived a (somewhat arbitrary) function F_ξ, whose ξ-restricted ensemble average nevertheless yields the uniquely defined mean force (eq 5). Equation 10 provides an intuitive view that different choices of Ξ and F_ξ correspond to different ways of projecting the Cartesian forces, −∇V, onto the transition coordinate. The direction along which the forces are projected in this expression is the vector ∂₁Ξ^–1, which we call “inverse gradient”.³⁶ As the gradient of ξ can be seen as the changes in ξ corresponding to infinitesimal changes in x, the inverse gradient is the vector along which a change in ξ is propagated in Cartesian coordinates, other generalized coordinates (Ξ_i,i>1) being constant, hence the dependence of the inverse gradient on the explicit coordinate transformation. The alternate notation for the inverse gradient, ∂x/∂ξ, has the drawback of hiding this dependence on the choice of Ξ.

Numerically, eq 10 is impractical for two reasons. One is that defining Ξ_i,i>1 explicitly can be exceedingly difficult, especially if ξ is a collective coordinate (e.g., the radius of gyration of a set of particles). Supposing that this step is done, the second difficulty comes with the numerical computation of the Jacobian derivative, as it involves second derivatives of Ξ^–1 whose analytical derivation and numerical implementation may be cumbersome, again, depending on the nature of the transition coordinate.

To circumvent this issue, the original adaptive biasing force method was introduced with an instantaneous force estimator based on a constraint force that is calculated iteratively, but never applied.¹⁹ In the initial implementation of the adaptive biasing force algorithm³⁷ in the popular molecular dynamics program NAMD,³⁸ eq 10 was used because the small set of implemented coordinates made it practical. As this set was greatly extended in the framework of the collective variables module,³⁹ more versatile expressions of the instantaneous force were required.³⁶

Den Otter put forward the idea that the inverse gradient can be replaced with an arbitrary vector field (satisfying certain requirements).⁴⁰ In other words, changes in ξ may be propagated along an arbitrary direction in Cartesian coordinates, without explicitly defining a complete set of generalized coordinates. That idea was extended to a multidimensional case by Ciccotti et al.⁴¹ Consider a vector transition coordinate (ξ_i), in the presence of a set of constraints of the form σ_k(x) = 0. For each coordinate ξ_i, let v_i be a vector field 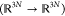satisfying, for all j and k:

11

12

The ith partial derivative of the free energy can then be calculated as the conditional average of the following instantaneous force:

13

of which eq 6 is a special case, limited to a single coordinate and choosing v = ∇ξ/|∇ξ|², which satisfies the condition (eq 11) above. Note that this estimator still requires the calculation of second derivatives, in the form of the divergence of the vector field v, although the relative freedom in choosing v can be taken advantage of to make the divergence calculation practical. The choice v = ∇ξ/|∇ξ|² is always valid, and as such, convenient for theoretical purposes, but certainly not always optimal when implementing specific generalized coordinates. Expressions that were chosen in practice for those coordinates implemented in the collective variables module are listed in ref (39).

Darve et al. described an estimator that does not require second derivatives, but rather first derivatives with respect to time and space, and is valid for multidimensional adaptive biasing force calculations.⁴² This estimator resembles a statistical form of Newton’s equation of motion: instead of relating acceleration to the potential energy gradient, it relates the mean acceleration to the gradient of the free energy. In a considerable simplification, only the first derivative of the force with respect to ξ needs to be derived. The time derivative is calculated numerically in the same fashion and at the same level of accuracy as time derivatives of other quantities in molecular dynamics. Other ways of simplifying calculations of instantaneous forces will be discussed in the context of extended adaptive biasing force simulations, or eABF, in the section The Extended Adaptive Biasing Force Method.

Adaptive Algorithm

The final, essential ingredient of the theory underlying the adaptive force method is an algorithm for deriving the current estimate of the average force as simulations progress. In its generic, one-dimensional implementation, the transition coordinate, ξ, connecting two end points, is divided into M equally sized bins of width δξ in which forces are accrued in the course of the simulation. In a naïve approach, the approximation to the average force, F̅_ξ(N_step, k) in bin k after N_step molecular dynamics steps is just the simple, unweighted average of all force samples in this bin

14

provided that the bin has already been visited at least once. N_step^k is the number of samples accrued in bin k after N_step steps and F_μ abbreviates the μth force sample in this bin. This approach would work well for large N_step^k. However, when only a few samples are available in a given bin k, the running average might be a poor estimate of the actual average force in this bin. Moreover, adding additional samples might markedly change F̅_ξ(N_step,k). Large fluctuations in the running estimate of the average force are undesirable, as they may drive the system away from equilibrium, thus slowing the convergence of the algorithm and reducing the efficiency of the method. To control these effects, a procedure is needed to reduce variations in early estimates of F̅_ξ(N_step,k). A number of schemes can be applied for this purpose. In current implementations, the biasing force in bin k at time t is applied in full only if the number of samples N_t is above a threshold, N_full. It is ramped up smoothly as N_t^k varies from 0 to N_full. In one implementation,⁴² the ramp is linear and the force is proportional to N_t/N_full; in another,^36,37 the biasing force is zero for N_t^k < N_full/2 and is ramped linearly above that value, proportionally to 2N_t/N_full – 1. Both implementations have proven to be efficient in a number of applications, but other, more advanced schemes are possible. So far, there have been no systematic studies on the efficiency of different adaptive algorithms, but it is anticipated that it may be strongly system-dependent.

For a sufficiently large N_step, F̅_ξ(N_step,k) approaches the correct average force in each bin. Then, the free-energy difference, ΔA_ξ, between the end point states can be estimated simply by way of summing the force estimates in individual bins.

15

If the average force is a rapidly changing function of ξ, a more sophisticated integration algorithm may be required. It might be also possible to develop binless integration algorithms, similar to those proposed for some other free-energy calculation methods.^43,44

A common trait of importance-sampling algorithms is the discretization of the transition coordinate, ξ, in bins of width δξ in which statistical information is accrued in the course of the simulation.⁷ In the umbrella-sampling scheme,¹¹ for instance, a histogram is constructed, corresponding to the biased probability of occurrence of the molecular assembly of interest at the different values of the transition coordinate. In the adaptive biasing force algorithm,¹⁹ bins are utilized to store instantaneous values of the thermodynamic force that acts along the transition coordinate. As has been observed in practice previously for diffusive dynamics, the instantaneous force in any given bin obeys a normal distribution.³⁷ At thermodynamic equilibrium, by definition, its average is exactly equal to −A′(z), that is, the gradient of the free energy along the transition coordinate. Insisting upon being at thermodynamic equilibrium is pivotal here, as application of a poorly estimated time-dependent bias, i.e., from a distribution out of equilibrium, will not yield a Hamiltonian bereft of a mean force acting along the transition coordinate.

The adaptive algorithms described above contain two adjustable parameters: bin width, δξ, and the number of samples, N_init, below which R(N_step^k) is not equal to 1 or, equivalently, averaging does not follow eq 14. The choice of these parameters should be done with some care.

At constant δξ, large values of N_init yield better estimates of the average force once the number of samples collected in a given bin reaches this threshold value and conventional averaging begins, at the price of delayed application of the full averaging and slow, initial progress along the transition coordinate. Small values of N_init, in turn, tend to drive the system out of equilibrium. Typically, setting N_init in the range between 200 and 500 appears to be a good compromise that allows for avoiding both types of problems.

At constant N_init, large values of δξ prevent capturing variations of the average force on short length scales. This may have adverse effects on the accuracy of integration in eq 15. On the other hand, small values of δξ require longer simulation times to collect sufficient force statistics in every bin. If the transition coordinate is a distance in an atomistic system, the choice of δξ as 0.1 or 0.2 Å usually represents a satisfactory trade-off.

Differences with Other Importance-Sampling Algorithms

In the last four decades a number of strategies have been developed for computing free-energy changes as a function of geometrical transformations, each endowed with advantages, as well as limitations.^11−25,45 To a large extent, umbrella sampling, whether in its original formulation or variants thereof,^11,18,46 remains one of the most widely utilized routes to address rare events in molecular simulations. In its original form, umbrella sampling referred to incorporating an external biasing potential in the simulation, i.e., an umbrella,¹¹ ideally the negative of the free energy, which would yield a broad, if not uniform exploration of the transition coordinate. In other words, in ideal circumstances, the system would evolve in the collective-variable space on a flat free-energy hyperplane, as is also the case for the adaptive biasing force method. Under most circumstances, however, the form of the optimal umbrella is unknown. Thus, for any qualitatively new problem, the end-user must resort to an educated guess regarding the shape of the biasing umbrella potential, usually on the basis of prior knowledge of this and related problems. This may constitute a daunting task.⁴⁷ Poorly predicted biasing potentials yield nonuniform probability distributions across the transition coordinate. This decreases the efficiency of umbrella sampling, which, in extreme cases, may reduce rather than improve the efficiency compared to results with unbiased calculations. This common shortcoming led to the development of an adaptive variant of the umbrella-sampling algorithm,¹⁸ wherein the initial guess of the biasing potential is progressively refined in light of a series of short simulations.

Adaptive umbrella sampling is one member of a broader family of techniques called adaptive biasing potential methods.⁴⁸ Local elevation,¹⁵ conformational flooding,¹⁶ or its more recent avatar, metadynamics,^20,49 adaptive biasing molecular dynamics,²³ and the Wang–Landau algorithm^26,27 belong to the same family. In the former methods, the idea is to penalize the already visited states by changing the potential V to V – A_t◦ξ, A_t(z) being related to the occupation time of the value z of the transition coordinate up to time t. The longer the time spent in a bin {x, ξ(x) ∈ [z₀, z₁]}, the larger the biasing potential A_t(z), z ∈ [z₀, z₁]. The local elevation technique and metadynamics are based on a similar idea. The biasing potential A_t is built as a sum of Gaussian kernels that are periodically added to the Hamiltonian along the ξ variable. This pushes the system away from states that have already been visited and, by doing so, improves sampling. It ought to be noted that the potential A_t, rather than its derivative, is computed in these two cases, hence, the name adaptive biasing potential methods. One important downside of the adaptive biasing force algorithm, compared to the class of adaptive biasing potential methods, lies in its inability to handle discrete transition coordinates, for instance, coordination numbers. This drawback can be understood by considering that the free energy is now a map from integers to reals, and, thus, has no derivative and, hence, no mean force.

From a mathematical viewpoint, the adaptive biasing force method, just like adaptive biasing potential methods, is an adaptive importance-sampling procedure. There is, however, a salient difference between these two techniques. In the latter, the potential of mean force or, equivalently, the corresponding probability distribution along the transition coordinate is being adapted. In contrast, the former relies on biasing the force, i.e., the gradient of the potential. This difference is more important than it might appear at first sight, as potentials and probability distributions are global properties whereas gradients are defined locally. In terms of probability distributions, it means that the count of samples in the neighborhood of a given value of the transition coordinate is insufficient to estimate probability. Knowledge of the underlying probability distribution over a much broader range of ξ is required. This may considerably impede efficient adaptation. In contrast, all that is needed to estimate the gradient is the knowledge of local behavior of the potential of mean force. Other regions along the transition coordinate do not have to be visited. Thus, in many instances, adaptation proceeds markedly faster. Using a common metaphor, the difference between the adaptive biasing potential and adaptive biasing force methods can be compared to inundating the valleys of the free-energy landscape as opposed to plowing over its barriers to yield an approximately flat terrain, conducive to unhampered diffusion.

There are also a number of important technical differences between these two methods. For example, in metadynamics and its ancestors, the widths and weights of Gaussian functions and the frequency with which the biasing potential is updated have to be carefully chosen, which often requires considerable experience. In the adaptive biasing force method, estimating the biasing gradient happens automatically by way of a simple algorithm, described in the previous subsection. Another technical concern about adaptive methods is to ensure that adaptation vanishes once A_t approaches the converged free energy.⁵⁰ There are a number of ways to fulfill this condition more-or-less automatically,^51,52 but adaptive biasing force and adaptive biasing potential techniques remain intrinsically different from this point of view. In the adaptive biasing force algorithm, if the correct free energy is given as an initial guess (namely if V is replaced by V – A◦ξ in eq 8), then the biasing force will not be updated (A_t^′ in eq 8 will be constant over time). This is not the case for an adaptive biasing potential strategy. Moreover, if the derivative of the biasing potential is needed (for example to bias the Langevin dynamics as in eq 8), the advantage of the adaptive biasing force algorithm is that A_t is directly computed, whereas in adaptive biasing potential algorithms, one needs to differentiate the evaluated biasing potential A_t, which may lead to very noisy results because A_t is estimated along a stochastic trajectory.

Because the basic quantity calculated, and subsequently integrated, in the adaptive biasing force method is the force, this approach belongs to the thermodynamic integration class of methods. However, in contrast to conventional implementations of thermodynamic integration and its generalizations, such as the blue-moon ensemble approach,¹² the adaptive biasing force algorithm does not rely on constrained molecular dynamics, but instead is based on unconstrained simulations; i.e., the free-energy difference is not determined at discrete values of the transition coordinate through solving constrained equations of motion. Sampling of the transition pathway proceeds in a continuous, unhampered fashion, guided by the diffusion properties of the system of interest, obviating the need for re-equilibration at fixed, predefined values of the transition coordinate, even in stratified simulations. As will be discussed further in this paper, this may improve ergodic behavior of the system.

It is also of interest to compare the adaptive biasing force method with reconstructions of free-energy landscapes from nonequilibrium trajectories that represent repeated pulling experiments.⁵³⁻⁵⁵ The latter are based on the groundbreaking Jarzynski identity,⁵⁶ or its extension to bidirectional transformations,⁵⁷ combined with steered molecular dynamics. Even though both approaches involve molecular dynamics trajectories that are initially away from equilibrium, there is a fundamental distinction between them. In the adaptive force method, only the average, or systematic force is removed to erase the ruggedness of the free-energy landscape, preserving the random force responsible for diffusion. Once a good estimate of the average force becomes available, the equilibrium behavior of the system is restored. In pulling experiments, the transformation always proceeds away from equilibrium at constant velocity and, therefore, the instantaneous force acting along the transition coordinate is nil. The random force actually appears in the formalism after averaging over the ensemble of pulling experiments. Moreover, achieving convergence in calculations based on Jarzynski’s identity usually requires large numbers of independent realizations,²¹ which comes at a significant computational cost. Taken together, when a geometrical transformation can be undertaken at equilibrium, it is not clear whether there is any practical advantage of handling the problem at hand by means of nonequilibrium work experiments rather than the adaptive biasing force method.

An important advantage of gradient-based methods^7,8 is the possibility of formally decomposing the free-energy change into physically meaningful contributions,^58,59 thereby helping to dissect qualitatively the nature of the intermolecular interactions at play. It is worth noting that different energy terms contribute to the mean force both explicitly through force terms and implicitly through the Boltzmann weights in the canonical average; contributions can only be separated numerically at the former level, not at the latter. Decomposition of the free energy is generally handled a posteriori through computing the thermodynamic force between, for instance, groups of atoms of interest. This force is then projected onto the transition coordinate determined for each stored configuration, prior to the construction of a histogram from which the average force is inferred. Integration of the latter yields the desired contribution to the total free-energy change across the entire transition pathway.

Among many options for reconstructing free-energy landscapes along a transition coordinate, which one is the best? Considering that the efficiency of different methods strongly depends on their implementation in software packages and, very likely, on a system of interest, attempts to answer this question appear somewhat misguided and unproductive. That said, one aspect of the adaptive biasing force algorithm pleading in its favor is its simplicity.^36,37 How the algorithm operates is physically intuitive,^7,42 requiring, in principle, very little prior knowledge of the free-energy landscape, or input from the end-user, even for qualitatively new problems.

TRANSITION COORDINATE

Central to geometric transformations is the concept of a transition coordinate. In this section, this concept is illuminated in the context of free-energy calculations aimed at tackling rare events. Specifically, we will discuss how the transition coordinate is explored with the adaptive biasing force algorithm and delve into the practical aspects of defining this coordinate. Stratification,⁶⁰ a common technique for improving the efficiency of free-energy calculations by partitioning the reaction pathway into ranges of the transition coordinate, will be discussed with the focus on the justification for and limitations of this strategy.

Transition Coordinates and Rare Events

For any transition from a macrostate, A, to another macrostate, B, of the same system there exists an exact one-dimensional transition coordinate: the committor probability.⁶¹⁻⁶⁴ In most cases, this coordinate is difficult to calculate and usually offers very limited insight into the nature of the process of interest. For these reasons, it is often more useful to employ a transition coordinate that is only an approximation to the committor probability but is physically more meaningful and easier to handle. Sometimes it might be helpful to extend the reduced representation of the transition to a transition coordinate that extends beyond one dimension. Not only physical significance but also efficiency of sampling, given a transition coordinate, is of concern. These two factors are often closely related.

As in any enhanced sampling method based on a reduced representation, adaptive biasing force sampling relies on stochastic exploration along the transition coordinate, ξ, enhanced by the adaptive bias, combined with equilibration of other, orthogonal degrees of freedom. Equilibration in the orthogonal space is critical in two respects: It affects the mobility along ξ (see Figure 1B for a diffusive example), and it determines the rate of convergence of A′(z) = ⟨−F_ξ(x)⟩_ξ, which is an average over the orthogonal degrees of freedom. In the ideal situation of time scale separation, all slow degrees of freedom are captured by the transition coordinates, and relaxation in the orthogonal space is comparatively fast. In other words, the adaptive biasing force algorithm removes metastability along the transition coordinates, provided that other degrees of freedom are not metastable. Complex systems such as biological macromolecules, however, possess many slow, coupled degrees of freedom, making time scale separation difficult or impossible to achieve.

Fortunately, empirical results suggest that time scale separation is not an absolute requirement of adaptive biasing force sampling. One reason behind it might be that enhanced diffusion in the transition coordinate space reduces metastability in the orthogonal space, by letting the dynamics sidestep orthogonal barriers rather than cross them, making some “multichannel” cases (see the section Hidden Barriers and Other Challenges to Obtaining Accurate Results) tractable with standard adaptive biasing force simulations. More encouraging still, convergence in such multichannel cases can be markedly accelerated by multiple-walker formulations of the adaptive biasing force algorithm (see the section Multiple-Walker Strategies).

Yet, not all intuitive choices of the transition are appropriate. As will be extensively discussed further in this paper, the end-to-end distance of the α-helical deca-alanine peptide provides a good example of an inadequate transition coordinate. Depending on the range of values, the coordinate exhibits completely different behavior. For values corresponding to the stable α-helix (14 Å) and larger, separation of time scales is obeyed and the adaptive biasing force converges well.³⁷ In contrast, smaller values of the end-to-end distance correspond to a rich set of metastable, compact states that are not resolved by the transition coordinate.³⁶ As a result, adaptive biasing force dynamics becomes trapped in these states, and the free-energy estimator does not converge in accessible simulation times.⁶⁵ Attempts to resolve these metastable states by two- and three-dimensional coordinates give improved results, allowing the exploration of all metastable basins, yet those basins are not all resolved even in three dimensions. Furthermore, the adaptive biasing force dynamics retains some metastability.³⁶ These difficulties are not due to specific deficiencies of the adaptive biasing force method, but rather, to shortcomings of the reduced representation, which would constitute an obstacle to any sampling method.

Practical Design of a Transition Coordinate

In practice, finding an effective reduced representation is still a process largely guided by physical intuition about the process of interest, as well as trial-and-error. More systematic and robust approaches for this dimension reduction step are an area of active research.⁶⁶ A limiting factor is often the availability of usable numerical implementations of the generalized coordinates of choice. The collective variables module³⁹ is an attempt to overcome this limitation, by providing a rich and flexible toolbox to define many types of coordinates, in particular those useful for the description of biological macromolecules. In this module, the adaptive biasing force is implemented, among other algorithms.

Once an intuitive understanding of the relevant generalized coordinate has been obtained, some technical choices remain to be made to express this coordinate as a function ξ of atomic Cartesian coordinates. Though these decisions may seem ancillary, they have a strong influence on the accuracy, convergence, and computational performance of the adaptive biasing force algorithm.

When objects of interest are composed of many atoms, there are often several nearly equivalent ways to define the transition coordinate. In sufficiently long simulations, different definitions produce nearly identical potentials of mean force, but the efficiency might vary considerably. For example, the distance between two proteins could be defined by selecting one central atom in each protein, or by selecting the centers of mass of large groups of atoms. The largest contribution to the instantaneous force on each atom in a molecule is due to rapidly oscillating bonded interactions; more generally, in all applications, forces on the particles will contain some background noise. If many atoms contribute to the projected force (e.g., the first right-hand-side term in eq 13), contributions from those noisy terms average out, which lowers the variance of the instantaneous force estimator.

In the initial stage of an adaptive biasing force simulation, nonequilibrium effects occur if the biasing force applied to some degrees of freedom varies faster than coupled degrees of freedom can relax. This can be mitigated by defining “smooth” collective variables that involve many Cartesian coordinates with smoothly varying contributions to the gradient (hence, to the biasing force vector). At equilibrium, a smooth motion may be described by a nonsmooth variable and this may make the convergence of the adaptive bias more difficult. In the deca-alanine stretching toy example, the geometric process of interest involves all atoms in the peptide, yet our classic approach uses the end-to-end distance as a biasing coordinate, with the implicit assumption that biasing forces exerted on the terminal atoms propagate, and that the entire peptide relaxes rapidly, so that the biased trajectory remains close to equilibrium. A more robust approach is to replace that coordinate with the radius of gyration of the peptide. The gradient of the radius of gyration has components on each atom proportional to its distance from the center of the group, so that atoms close to the center also experience moderate biasing forces and do not lag behind the terminal atoms when the biasing force varies rapidly over time. A more elaborate discussion of this problem can be found in ref (42).

In some cases, however, coordinates involving large collection of atoms will have less resolution than more local ones. A biophysical example is permeation through an interface, such as a lipid bilayer. The common choice of transition coordinate is the distance of the permeant molecule to the center of the bilayer center, projected onto the bilayer normal. In such a case, the physically relevant phenomenon is interaction of the permeant with the membrane surface, on a local scale. If the bilayer patch is large enough, it will experience fluctuations away from planarity, thus the local position of the interface will fluctuate with respect to the bilayer center. In turn, this will cause spurious fluctuations in the transition coordinate. A comparable situation arose in a study of glycerol permeation through the water channel protein GlpF.³⁰ Interaction of the permeant with the protein depended on distances to neighboring pore-lining residues, which fluctuated with respect to the bulk of the protein. Therefore, the global coordinate measured between the protein and glycerol molecule had insufficient resolution on a local scale, and a more local coordinate had to be defined to resolve the structure of the free-energy profile in the constricted region of the selectivity filter.

Performance

Depending on system size and implementation details, choices of coordinates may impact performance noticeably. A common application case is a biomolecular simulation performed with the NAMD package,³⁸ with the adaptive biasing force algorithm implemented³⁶ in the collective variables module.³⁹ NAMD is highly parallelized and can simulate large systems on supercomputers with nearly linear scaling. The current implementation of the adaptive biasing force algorithm is not parallelized and runs on one node, leading to two potential bottlenecks: (1) Poor serial performance on the master node: for the most expensive variables (e.g., those involving sums on atom pairs), the bias calculation on the master node might take longer than the force calculation on other nodes. (2) Scaling may suffer even for computationally simple coordinates, if too many atom coordinates and forces have to be communicated across nodes, increasing latency. This second case may affect any highly parallel application with coordinates defined on many atoms. In practice, one often has to find an acceptable trade-off between variance and performance by selecting a reasonable number of Cartesian coordinates that are most representative of the quantity of interest. To describe conformational fluctuations of a protein, for example, the root-mean-square deviation of α carbon coordinates is often a good compromise.

Justification of a Stratification Strategy

To increase the efficiency of exploring the transition coordinate in adaptive biasing force¹⁹ or umbrella sampling,¹¹ it is common to break down the transition path into a series of sequential strata or windows. This idea⁶⁰ arises from the intuition that the time to convergence grows as the square of the range of the transition coordinate. Simple considerations provide the rationale for this strategy.

Consider a transition path of length 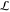. Convergence of the free energy over the entire range 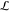is achieved after t₀. Let us now divide the transition path into N nonoverlapping windows of lengths 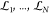, for which convergence is attained after t₁^′, ..., t_N. As shown in the Supporting Information, t₀ > Σ_it_i^′.

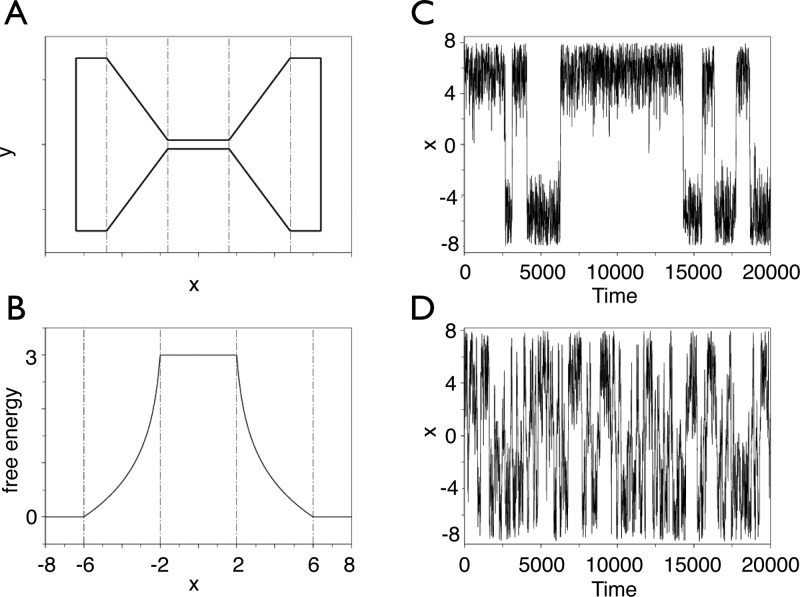
We illustrate this result in a simple example of a tagged water molecule diffusing in a bulk environment over a stretch of 20 Å. The transition coordinate is the projection of the distance separating the centers of mass of the tagged water molecule and the simulation cell along a given direction of Cartesian space. Translational invariance due to the isotropic nature of the liquid imposes the condition that the free-energy change along the transition coordinate be zero. For this system, the potential of mean force was determined in a single, 20 Å long stratum, two 10 Å strata, four 5 Å strata, and eight 2.5 Å strata. The simulations continued until the root-mean-square deviation between the computed potential of mean force and the reference zero free-energy profile was less than 0.1 kcal/mol.

As can be observed in Figure 3, t₀, the time necessary to attain convergence within this preset tolerance without stratification is on the order of 100 ns. When the transition coordinate is divided into two strata, convergence in each 10 Å stratum is reached in approximately 40 ns, i.e., in 80 ns over the full 20 Å range. The effect of stratification increases further, as the reaction coordinate is decomposed into four and eight windows. In these cases, convergence is achieved in approximately 6 and 2 ns per window, respectively, which corresponds to 24 and 16 ns for the complete 20 Å range.

Figure 3.

Stratification strategies for the translationally invariant toy model of a tagged water molecule diffusing in a bulk aqueous medium. The transition path spans 20 Å and is handled in a single window (A), in two 10 Å windows (B), in four 5 Å windows (C), and in eight 2.5 Å windows (D). For each stratification strategy, a potential of mean force calculation is carried out until the root-mean-square deviation with respect to the accurate zero free-energy profile is less than 0.1 kcal/mol.

Both theoretical considerations and a simple example given above appear to suggest that extensive stratification should be always preferred. This, however, does not have to be the case. First, simulations in each window require initial equilibration, which may erase benefits gained from stratification into many windows. Perhaps more importantly, extensive stratification may impede ergodic sampling of the phase space. This behavior, shared with the standard thermodynamic integration, will be discussed in section Addressing Nonergodicity Scenarios.

In contrast to umbrella sampling and its adaptive variants, the adaptive biasing force algorithm does not require that consecutive windows of a dissected transition coordinate overlap. Provided that convergence has been achieved in each window, the gradient, ∇A(ξ), can be reconstructed merely by joining the gradients from individual windows at the boundaries. This improves efficiency, as the requirement for overlap between windows may frequently add as much as 50% to the total simulation time. If the gradient between consecutive windows is not continuous to within statistical error, this is usually a sign of difficulties with ergodic sampling. Again, this problem will be considered in section Addressing Nonergodicity Scenarios.

Convergence and Error Analysis

In this section, we examine the convergence properties of the adaptive biasing force algorithm and the reliability of the computed free-energy estimates. First, the reader is invited to follow a demonstration that the numerical scheme formally converges. Then, we discuss how statistical errors associated with the reconstructed free-energy landscapes can be measured and managed.

Formal Convergence of the Adaptive Biasing Force Algorithm

The aim of this section is to explain convergence properties of the adaptive biasing force algorithm. For more details, the reader is referred to the Supporting Information.

We restrict ourselves to the following simple setting. We consider the overdamped Langevin dynamics,

16

where x_t is defined in the N-dimensional torus 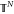(namely, in [0, 1]^N with periodic boundary conditions) and ξ(x₁,...,x_N) = x₁. We direct the reader to refs (67) and (68) for extensions to more general situations of the results presented below.

Starting from eq 16 and using the above choice of the transition coordinate ξ, the adaptive biasing force dynamics can be represented as

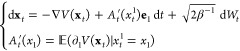17

where x_t¹ denotes the first coordinate of the vector x_t, e₁ is the vector with coordinates (1, 0, ..., 0), and ∂₁V denotes the partial derivative of V(x₁,...,x_N) with respect to x₁.

As explained in the section Theoretical Backdrop, it is clear at least formally that the only possible stationary state for A_t is the free energy (up to an additive constant). Indeed, if A_t converges to some stationary state A_∞, then the law of x_t converges to Z_∞^–1 exp(−β{V(x) – A_∞[ξ(x)]}) dx, which implies that 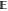(∂₁V(x_t)x_t¹=x₁) is A′(x₁). Yet, this does not provide a proof of the convergence of A_t to A′, and it does not explain why the adaptive biasing force dynamics of eq 17 indeed converges faster to equilibrium than the original, unbiased dynamics of eq 16.

One way to understand this convergence is to look at the way the law of x_t evolves. Let us denote ψ(t,x) the density of x_t. For the original dynamics of eq 16, the density ψ satisfies the Fokker–Planck equation:

18

For the adaptive biasing force dynamics, the density ψ satisfies

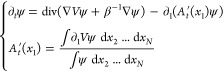19

It ought to be noted that eq 19 is a nonlinear partial differential equation (PDE), which makes the study of its long-time behavior much more complicated than for the linear Fokker–Planck PDE (18).

Using appropriate mathematical tools (namely, entropy techniques, see the Supporting Information), one can show that if the transition coordinate is well chosen, the convergence to equilibrium for the adaptive biasing force dynamics of eq 19 is much faster than for the original unbiased dynamics of eq 18. Roughly speaking, the assumption on the transition coordinate is that the canonical measure Z^–1 exp[−βV(x)] dx is “more multimodal” than the conditional measures at a fixed value x₁ of the transition coordinate

This is typically the case for the simple illustrative two-dimensional potentials in Figures 1 and 2 if ξ(x₁,x₂) = x₁. This can be fully quantified, and it actually gives a way to measure the quality of the transition coordinate.

In the analysis outlined above, it is assumed that the conditional expectation appearing in the adaptive biasing force dynamics is computed exactly. This analysis is therefore well adapted to discretizations that involve many replicas in parallel, which indeed converge to the adaptive biasing force dynamics with the exact conditional expectation; see ref (69). Analysis of the adaptive algorithms (adaptive biasing force or adaptive biasing potential) with estimates of the conditional expectations based on trajectory averages along a single path are much more complicated. See refs (70) and (71) for preliminary results for the Wang–Landau algorithm.

Distinguishing Sources of Error

Just like any experimental measurement, free-energy calculations, of either alchemical or geometrical nature, ought to be reported with the associated error bars. In the absence of an error estimate, a free-energy difference is generally of limited utility, making direct comparison with experiment difficult and speculative. Although much effort has been devoted in recent years to the characterization of errors that are associated with free-energy calculations,^7,8,72−81 estimating the reliability of such calculations remains an intricate task. This explains why it is not unusual that calculated free energies are still being published without error estimates.

Ideally, any free-energy difference should be determined from a series of N independent simulations. If this were, indeed, the case, the best possible estimate of the target free-energy difference would be the expected value over the N simulations, i.e., 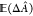, where ΔÂ denotes the estimate of the exact quantity, ΔA, inferred from one individual free-energy calculation. Then, the associated mean-square error can be written as

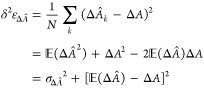20

The first term of eq 20, σ_Δ² = 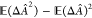, is the variance, or the precision⁸² of the free-energy calculation. In other words, it is a measure of its statistical error. The second term, 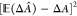, is the square of the bias of the free-energy estimator, i.e., the square of the difference between the expected value of the estimator and the actual free-energy change, ΔA. The bias, also referred to as the accuracy⁸² of the free-energy calculation, is a measure of systematic error of the latter.

How to estimate statistical error for the adaptive force method will be discussed in the next section. Unfortunately, a similar, formal treatment does not exist for systematic error. One important source of bias arises from incomplete sampling in finite-length simulations due to quasi nonergodic behavior of the system. Although this behavior cannot be quantified, in many instances it can be detected. Then, a number of remedial tools are at our disposal. How to recognize and remedy problems with quasi nonergodicity will be discussed in section Addressing Nonergodicity Scenarios. Other common sources of bias are inaccurate treatment of intermolecular interactions and algorithmic artifacts arising primarily from imprecise numerical integration of the equations of motion. These contributions to bias, which are common to all simulation methods, will not be discussed here.

Measure of the Statistical Error

The adaptive biasing force method is typically applied to nanoscale molecular processes under physiological conditions, a realm dominated by thermal noise. Thus, estimating free-energy differences using adaptive biasing force requires careful consideration of statistical error.⁸³ Within the adaptive biasing force framework, free-energy differences are determined by integrating the estimated mean force of the system exerted along the transition coordinate. Namely, a free-energy difference on the interval z_a ≤ ξ ≤ z_b can be expressed as⁸³

21

where ⟨F_ξ⟩_z is the average of the instantaneous force on the transition coordinate ξ at the position ξ(x) = z.

Thus, to determine the statistical error of the free-energy differences, we must delve into the statistics of the mean system force. We assume that the transition coordinate, ξ, is discretized and instantaneous forces calculated during the course of the simulation are collected in appropriate bins along ξ. As derived in the Supporting Information, one way to estimate the error of the mean force in bin i is given by

22

where ΔF_ξ(x_t) = F_ξ(x_t) – ⟨F_ξ⟩_i is the random component of the instantaneous force, n_i is the number of samples accrued in bin i, Δt is the time step of the simulation, and τ_i and ⟨ΔF_ξ²⟩_i are the autocorrelation time and variance of ΔF_ξ(x_t) in bin i.

Given a reliable estimate of the error of the mean force in each bin, we are prepared to analyze how these estimates are propagated to yield free-energy differences. On a discrete grid along the transition coordinate, the integral in eq 21 becomes

23

where i_a and i_b are bin indices delimiting the ξ-interval [z_a, z_b]. Assuming independent behavior in each bin, the error of a sum of mean forces is approximated from from the Bienaymé formula as equal to the square root of the sum of squares of the errors of these mean forces,⁸⁴

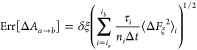24

A notable property of this formula is that the error increases with the size of the interval over which the free-energy difference is calculated.⁸³

Application to the Toy-Model Deca-alanine

For concreteness, we now consider the error in free-energy differences for the reversible folding of deca-alanine in vacuum. We define the transition coordinate of interest ξ as the end-to-end distance of the peptide, specifically the distance between the carbonyl carbon atoms of the first and the tenth residue. Below we discuss the behavior of the three quantities that enter eq 22, namely. The number of samples in each bin n_i, the standard deviation of the random force (⟨F_ξ²⟩_i)^1/2, and the autocorrelation time of this force τ_i. See the Supporting Information for further comments on calculating these quantities.

The black curve in Figure 4A is the number of samples in each bin of width δξ = 0.1 Å for the adaptive biasing force calculated in the range from 12 to 32 Å (the red curve will be discussed later in the paper). The number of samples, n_i, in this range varies from 17 000 to 36 000. Thus, as expected from the adaptive biasing force algorithm, the number of samples in each bin approaches uniformity. In this case, nonuniformity of sampling exceeds only slightly a factor of 2, which corresponds to the variations of the biased free energy not exceeding 0.5 kcal/mol. For comparison, the unbiased free energy changes in the same range by approximately 30 kcal/mol.

Figure 4.

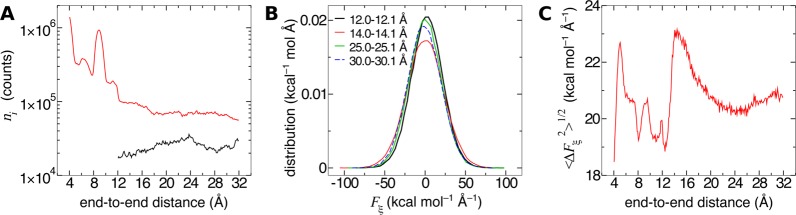
Coordinate dependence of sampling and the system force distribution in reversible folding of deca-alanine. (A) Samples in each bin for a 10 ns adaptive biasing force calculation on the domain ξ ∈ [4, 32] Å (black curve) and a 100 ns calculation on the domain ξ ∈ [4, 32] Å (red curve). Note the logarithmic scale on the vertical axis. (B) Distribution of the ξ-component of the instantaneous system force for different ranges of ξ. (C) Standard deviation of the ξ-component of the instantaneous system force as a function of ξ.

In Figure 4B, we show the distribution of instantaneous forces in four different bins. The forces in each bin are approximately normally distributed, with similar standard deviations of about 20 kcal mol^–1 Å^–1. This point is underscored in Figure 4C, which illustrates that, for deca-alanine in vacuum with Langevin dynamics emulating buffeting of the molecule by solvent, the standard deviation of the force acting along the transition coordinate changes very modestly, even though the peptide explores structures that are as disparate as can be imagined. The peptide courses through different compact forms for ξ < 10 Å, remains mostly α-helical for 10 < ξ < 16 Å, and forms extended structures with diminishing helical fractions as ξ increases beyond 16 Å.⁸⁵ The approximate uniformity of ⟨F_ξ²⟩_i^1/2 seen here is also characteristic of many other systems. For example, it has been previously found⁸⁶ that the standard deviation of the instantaneous force on the center of mass of a water molecule is about 2 kcal mol^–1 Å^–1, irrespective of whether the molecule lies in the bulk aqueous phase or in the hydrophobic core of a lipid bilayer. On the other hand, the transfer of a solute across a liquid–vapor interface is an example of a transition for which ⟨F_ξ²⟩_i^1/2 is expected to vary considerably with ξ.

Note that ⟨F_ξ²⟩_i^1/2 is considerable. Because this term enters prominently the expression for statistical error in eq 22, there are significant merits in reducing the dispersion of instantaneous forces. We have already pointed out two potential paths toward this goal. First, because the expression for the ensemble average of instantaneous force is not unique we can, in principle, choose one that reduces ⟨F_ξ²⟩_i^1/2. Second, variation of forces can be also reduced by a thoughtful choice of the transition coordinate.

The third variable in eq 22, the correlation time of the instantaneous system force τ_i, is also the most difficult to calculate. The sampling in a single bin is rarely sufficient to obtain a converged autocorrelation function of the system force; thus, in Figure 5A we plot the autocorrelation function averaged over 40 bins along different regions of ξ. The correlation time for each region, τ, is determined by fitting an unscaled exponential function e^–t/τ to the positive values of the autocorrelation function. Figure 5B reveals only modest variations in correlation time for different regions.

Figure 5.

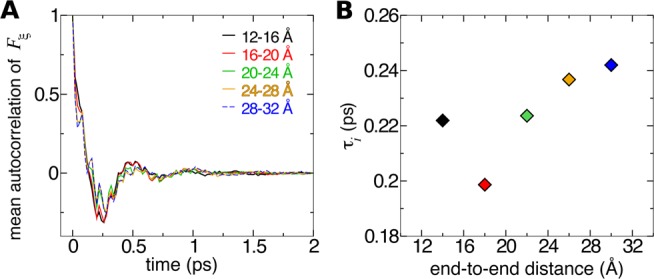
Coordinate dependence of correlations in the system force in reversible folding of deca-alanine. (A) Autocorrelation functions of the random component of the instantaneous system force for different ranges of ξ. The functions are normalized by the variance ⟨ΔF_ξ²⟩_i so that correlation at t = 0 is unity. (B) Correlation time for ξ-ranges in panel A.

Using the calculated values of n_i, ⟨F_ξ²⟩_i and τ_i, we now estimate the uncertainties of free-energy differences between deca-alanine structures with different end-to-end distances. The mean system force, with uncertainties calculated by eq 22, is shown in Figure 6A. Because only free-energy differences between two points along ξ, rather than free energies at single points, have a clear physical meaning, we focus on errors associated with these differences. To compute the error in the free-energy difference at points z_a and z_b, we must accumulate the uncertainties of the force between these two points, in accord with eq 24. If stratification is used and points z_a and z_b are in different windows, then the Bienaymé formula needs to be used across all windows separating these points.

Figure 6.

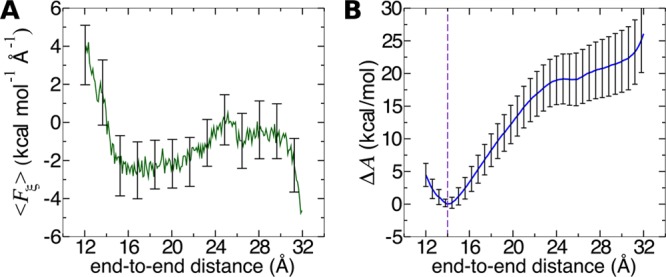
Propagation of error in the mean force to the error of free-energy differences. (A) Mean system force on ξ for a 10 ns adaptive biasing force calculation, with error bars determined according to eq 22. (B) Error of free-energy differences A(ξ) – A(z_a) with the reference position z_a = 14 Å. This position is denoted by a violet dashed line.

In Figure 6B we show the estimated error of ΔA between the α-helical minimum free-energy state (z_a = 14) and other states within the interval z_b ∈ [12, 32] Å. If we want to calculate, for instance, the difference in free-energy between the minimum and ξ = 16 Å, we obtain 3.6 ± 1.8 kcal/mol. Larger distances in ξ yield larger error: the free-energy difference between the minimum and the plateau at 25.5 Å is 19 ± 4 kcal/mol.

It is expected that, for sufficiently long total simulation time, t, statistical errors of both the average forces and free-energy differences will decay proportionally as t^1/2.⁴² The same dependence on t should apply to deviations from nonuniform sampling. If force statistics is collected in M bins, then the root-mean-square deviation from the uniform distribution can be defined as the square root of the variance, Var(t),

25

where N_step^k and N_step are the number of samples in bin k and the total number of samples at time t, respectively. For large t, the variance is expected to be proportional to 1/t or, equivalently to 1/N_step. In other words, N_step × Var(t) should be constant. An example of how Var(t) behaves in a typical simulation is shown in Figure 7. This is the expected behavior for diffusive motion. Errors that clearly deviate from such behavior are a sign of insufficient sampling. If the problem persists with increasing t, and especially if errors exhibit large fluctuations, then most likely problems with quasi nonergodic behavior have been encountered.

Figure 7.

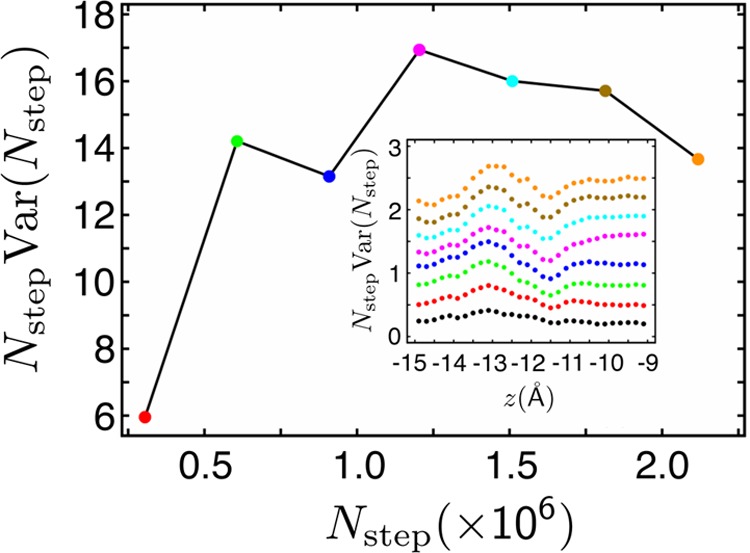
N_step × Var(t) as a function of the number of molecular dynamics steps, N_step. This quantity was calculated for the permeation of K⁺ through a transmembrane hexametric channel of a peptaibol, trichotoxin in a window along the normal to the membrane spanning the range between z equal to −15 and −9 Å. z = 0 is located in the middle of the membrane.⁸⁷ Note that for N_step between 0.6 × 10⁶ and 2.3 × 10⁶, N_step × Var(t) differs from its average value in this range by no more than 10%. The inset: the number of force samples along z in the window as a function of N_step.

ADDRESSING NONERGODICITY SCENARIOS

A common manifestation of pathological free-energy calculations, in particular those of geometrical nature, is quasi nonergodicity, wherein sampling along the selected transition coordinate appears to be hampered. Here, we inspect closely the effects that impede accurate results to be obtained from free-energy methods, including the adaptive biasing force scheme (notably hidden barriers in the slow manifolds), and discuss how to identify these effects and outline possible remedies, by increasing the dimensionality of the transition coordinate, improved stratification, or sampling aided by multiple-replica strategies.

Hidden Barriers and Other Challenges to Obtaining Accurate Results

The primary objective of importance-sampling schemes is to facilitate exploration of the transition pathway with a uniform probability.^7,8 Among these schemes, as has been previously emphasized, the adaptive biasing force algorithm uses a local estimate of the gradient, A′, acting along the transition coordinate, to erase progressively the original ruggedness of the free-energy landscape. As has already been discussed in section Formal Convergence of the Adaptive Biasing Force Algorithm, this feature is valid from a theoretical standpoint. How true is this in practice? In most instances, satisfactorily uniform sampling is achieved quite efficiently. Occasionally, however, the adaptive biasing force algorithm does not perform as expected. The reminder of this section is devoted to explaining and identifying these special, yet important cases.

Potential difficulties in applying the adaptive biasing force algorithm are intimately related to the choice of transition coordinate. A basic, yet seldom verified assumption that underlies this choice is the separation between time scales of motions along the transition coordinate and orthogonal degrees of freedom (see section Transition Coordinates and Rare Events). For complex, rugged free-energy landscapes, notably those formed by parallel valleys separated by considerable barriers in the direction orthogonal to the transition coordinate (Figure 8),⁸⁸ assuming time scale separation may turn out to be unwarranted. Because the adaptive biasing force algorithm exerts no direct action in the orthogonal space, it will not improve sampling at constant ξ. Returning to the foundational expression for the adaptive biasing force method, eq 8, which relates the gradient of the free energy to an ensemble average at constant value of the transition coordinate, the inability to cross hidden barriers in the orthogonal space is tantamount to incomplete ensemble averages and, hence, poor estimates of free-energy changes.

Figure 8.

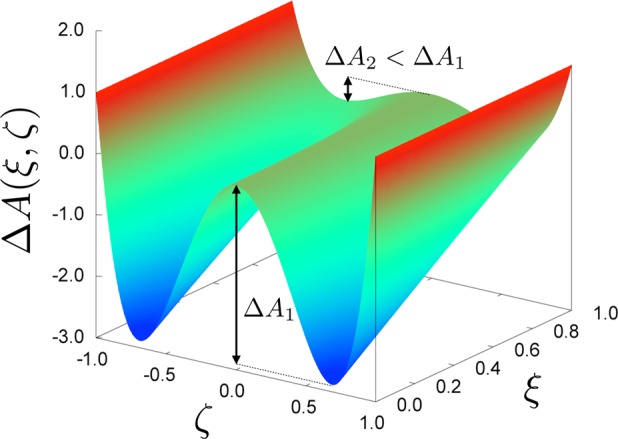
Common free-energy landscape featuring parallel valleys, collinear to the transition coordinate, ξ. These valleys are separated by substantial free-energy barriers in the direction ζ, orthogonal to ξ. ζ can be interpreted as a slow degree of freedom coupled to ξ and hampering progression along the latter direction. Excessively stratified reaction pathways preclude spontaneous crossing of high barriers, typically ΔA₁. Wider windows should allow diffusion toward values of ξ, where the barrier separating valleys in the direction ζ is smaller, typically ΔA₂.

What are common symptoms of quasi nonergodic behavior? Several of them can be readily identified. Their presence is a guaranteed sign of flawed free-energy calculations, but their absence is not a sufficient condition to ensure that such calculations converged to the correct value. As has been discussed previously, sampling along the transition coordinate in well-behaved simulations should approach uniformity with time, and the statistical error associated with the biasing force or, equivalently, the free-energy differences should decrease in a predictable fashion. If this is not the case, difficulties in equilibrating the system along orthogonal degrees of freedom are, most likely, at play. To illustrate this point, we return to the toy model of deca-alanine reversibly folding in vacuum and to Figure 4A. In the range of ξ between 12 and 32 Å, sampling is fairly uniform even in 10-ns simulations. In contrast, in the [0, 12] Å range, sampling remains quite nonuniform, even after 100 ns (red curve). As has already been pointed out in the section Transition Coordinates and Rare Events, there are a number of metastable states in this region, all corresponding to similar values of ξ. Difficulties in properly averaging over these states markedly impedes equilibration along ξ. In the context of stratified simulations, the presence of hidden barriers along degrees of freedom orthogonal to ξ often leads to discontinuous biasing forces between adjacent windows.

Another strategy for exposing apparent nonergodic behavior is to carry out bidirectional calculations, i.e., initiate the adaptive biasing force simulation from both end points along the transition coordinate. Just as in free-energy perturbation calculations,⁸¹ the resulting hysteresis is a good indicator (although not necessarily a measure) of error. If the hysteresis markedly exceeds statistical error, the calculated free-energy values are, most likely, poorly converged. In such a case, simply combining data from both directions is not likely to improve accuracy significantly, as their proper weighting remains unknown.

When quasi nonergodicity scenarios are encountered, additional simulation strategies, such as multiple walkers or multidimensional transition coordinates, should be brought to bear. Also, the chosen stratification scheme might require reevaluation. These issues are discussed in more detail below.

Balancing Ergodic Sampling and Efficiency in Window Sizes

Formally, the adaptive biasing force algorithm does not prescribe a particular window size nor does it require that consecutive windows along a stratified transition coordinate overlap. Provided that convergence has been achieved in each window, the gradient, ∇A(ξ), can be reconstructed merely by joining the gradients from individual windows at the boundaries. As we have already argued, from the efficiency point of view it might appear that using small windows is always beneficial. This is, however, not necessarily true. One concern about extensive stratification is that efficient sampling of rugged landscape along orthogonal degrees of freedom may require temporary excursions beyond the window’s boundaries, where the barrier separating adjacent valleys is smaller. This is illustrated in Figure 8. The barrier between the minima along the orthogonal degree of freedom, ζ, may be difficult to cross at ξ in the range of [0, 0.2], but not in the [0.8, 1] range. In this case, stratification will create kinetic traps, most likely reducing rather than improving efficiency.

A similar problem was observed in simulations aimed at determining the potential of mean force for a small, proline-rich peptide, p41, bound to the SH3 domain of Abl kinase using the root-mean-square deviation (RMSD) with respect to the native conformation as the transition coordinate. There, a second minimum was only discovered through creation of a window that did not encompass the native state (see Figure 2A in ref (89)). This second minimum represents a shift in register of the peptide in its binding site, and although it would occur spontaneously given sufficiently long time, its probability can be enhanced by first driving the peptide to higher values of RMSD, which disrupts some of the bonds characteristic of the native state, and then letting it come back.

Because it is often not possible to predict orthogonal barriers a priori, determining an appropriate windowing scheme typically requires an adaptive procedure. The basic criterion here is the continuity of the biasing force across consecutive windows. If one is concerned about quasi nonergodicity, a good strategy is to start with large windows. If the continuity of forces appears to be satisfactory, one might attempt to improve efficiency through further stratification. The advantage of this strategy is that the approximation to the biasing force acquired from the large-window simulation can be used in smaller windows. If no windowing scheme yields continuous forces, then other strategies, described in the next section, should be employed.

Multiple-Walker Strategies

Simulations involving multiple replicas are perhaps the most powerful strategies to accelerate ergodic sampling along degrees of freedom orthogonal to the transition coordinate. Beyond the “embarrassingly parallel” strategy of running independent simulations to obtain more sampling than is possible with a single simulation in the same real time, a number of schemes have been devised that significantly enhance sampling, at the cost of transferring information between replicas. In a prototype example of multiple-replica algorithms, originating with Monte Carlo simulations,⁹⁰⁻⁹² replicas are run at different temperatures and exchanges of system configurations are attempted periodically between replicas, so as to maintain a canonical ensemble at each temperature.⁹³ The advantage of this method is that replicas at higher temperatures cross energetic barriers more quickly and can pass the resulting configurations to replicas at lower temperatures, preventing the latter from remaining in metastable states. Exchange of replicas with different umbrella-sampling potentials, known as Hamiltonian exchange, has also been widely successful.⁹⁴⁻⁹⁶

With the adaptive biasing force method, each replica can be thought of as a “walker” exploring the transition coordinate space. Multiple-walker strategies range from simply running similar independent adaptive biasing force calculations in parallel, to more complex ones, involving communication between replicas.^85,97 Here we consider two communication strategies that can be used in concert. In the first strategy, which we refer to as shared adaptive biasing force, the instantaneous forces sampled from each walker are collected in a single shared buffer as the simulations progress simultaneously. In the current implementation, the shared buffer is merely conceptual: each walker retains its own buffer, which is synchronized with all the others at fixed intervals. Regardless, shared adaptive biasing force can result in significantly faster exploration of the transition coordinate and improved convergence of the free energy, as compared to the case for independent walkers.^85,97 A second strategy, complementary to the first, is the application of so-called walker selection rules. These selection rules eliminate replicas with values of the transition coordinate that are already well sampled, while duplicating replicas in relatively unexplored regions, enforcing more uniform sampling.

Selection rules may be implemented using a so-called resampling procedure and weights that are associated with each replica.⁸ There are many ways to choose the weights and to implement this idea in practice. The basic requirement is that the selection mechanism automatically vanishes at equilibrium, namely when the biasing force is the mean force. Here, we calculate the weight of each walker in a somewhat simpler way than in previous studies,^48,97 while obtaining similar results. The weight assigned to each walker is the inverse of the number of samples accrued in a neighborhood of bins near the walker. Specifically,

26

where j is the bin occupied by walker i at the time of application of the selection rules, n_j(t) – n_j(t_last) is the number of samples that have been accrued in bin j since the last selection and resampling step, and h defines the number of bins surrounding j that are included in the sum. The walkers are resampled on the basis of these weights, and the selection mechanism is switched off when the smallest and largest n_i(t) differ by less than 20%, i.e., when [max(1/w_tⁱ) – min(1/w_t)/min(1/w_tⁱ) < 0.2].

Application to the Toy-Model Deca-alanine

We consider reversible unfolding of deca-alanine as a model system for testing different multiple-walker strategies. In Figure 9A we compare the results of adaptive biasing force calculations of 8 ns total simulated time to a converged free-energy profile. A single, 8-ns long simulation gave the poorest results, whereas 16 short, independent calculations perform somewhat better, even though the region 31.4–32 Å has not been sampled at all. In contrast, shared adaptive biasing force yields complete and more uniform sampling, and a smoother, more reliable free-energy profile. The best free-energy profile, almost indistinguishable from the converged one, was obtained from shared adaptive biasing force combined with walker selection. Note that, as expected, the free energies converge to the same values for sufficiently long simulations, irrespective of the multiple-walker strategy, as demonstrated in Figure 9B. An implementation of the shared adaptive biasing force algorithm with the selection rules used here is expected to be available in future releases of the molecular dynamics program NAMD.

Figure 9.

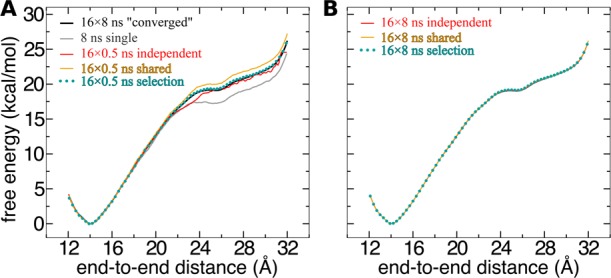
Improving the rate of convergence with multiple-walker strategies. (A) Potentials of mean force obtained for different multiple-walker strategies and total simulation times of 8 ns. For reference, the black curve shows the result for a total simulation time of 128 ns. “Single” refers to a single long 8 ns simulation, and “independent” denotes the result of combining force samples for 16 walkers after they ran independently for 0.5 ns. For the curves marked “shared” and “selection”, force samples were synchronized among walkers every 20 ps. “Selection” also included the application of walker selection, as described in the text, on the same interval. (B) Potentials of mean force obtained for different multiple-walker strategies and total simulation times of 128 ns.

Multidimensional Adaptive Biasing Force Simulations

Algorithmic Backdrop

There are several reasons to perform adaptive biasing force calculations with a transition coordinate of dimension greater than one. First, we may be simply interested in how the free energy varies as a function of more than one coordinate. For example, to study the interaction between two molecules, it may be of interest to obtain the free energy as a function of both their distance and relative orientation. A second reason to use multiple dimensions is practical. As described in section Hidden Barriers and Other Challenges to Obtaining Accurate Results, sampling along a single collective variable may be hampered by barriers in orthogonal dimensions. If one can identify these orthogonal dimensions, the application of adaptive biasing force along them will remove the barriers and improve sampling.

By itself, obtaining a multidimensional free-energy landscape requires more sampling than is needed to calculate a one-dimensional profile. For example, if one uses N bins along collective variable ξ and M bins along collective variable χ, each component of the gradient over both collective variables, ∇A(ξ, χ), requires MN bins. With one sample obtained per time step, the time required to generate a statistically significant number of samples in all bins will increase approximately proportionally. Despite the additional, substantial computational effort, adding a second or third dimension may improve efficiency, as it accelerates convergence and increases uniformity in sampling by allowing the system to more rapidly cross between multiple parallel valleys.⁹⁸ Subsequently, one can recover the potential of mean force along a single dimension through integrating out the additional dimensions.⁹⁹ However, when one wishes to include a large number of dimensions, the generalized adaptive biasing force algorithm (see section The Generalized Adaptive Biasing Force Algorithm) may be more appropriate.

If the transition coordinate involves angular degrees of freedom that span their full range (e.g., [0, 2π]), an additional complication develops. The exact forces and free energies are periodic in these variables, but this is not necessarily true for these quantities burdened with statistical errors. One way to restore the required periodicity is to approximate the free energy as a function of angular variables with spline functions, coefficients of which are computed to distribute errors smoothly across the whole hyperspace spanned by these variables. How to do this has been described by Darve et al.⁴²

Application to the Toy-Model Deca-alanine

As an example application of multidimensional adaptive biasing force, we consider the free-energy landscape of deca-alanine as a function of the root-mean-square displacement (RMSD) from three reference structures. Figure 10A shows these reference structures: an α-helix, a 3₁₀-helix, and a particular compact conformation that we refer to as the ω conformation due to its visual similarity to this Greek letter. In agreement with the one-dimensional calculations, extensively discussed above, the free-energy minimum occurs when the structure is close to the α-helix, i.e., when RMSD_α = 0.3 Å. In Figure 10B the three-dimensional potential of mean force is represented by three isosurfaces. Two low-energy regions can be seen in this figure. The violet region on the left corresponds to the α-helix, whereas the region on the right is closer to the ω conformation than to the other two structures. The minimum in the latter region is only 1.2 kcal/mol higher than the minimum for α-helix and lies at (RMSD_α RMSD₃₁₀ RMSD_ω) = (4.3 5.0 2.7) Å. In Figure 10C, examples of representative structures in these two low-energy regions are shown. The multidimensional free-energy landscape thus yields more insight into the correspondence between the free energy and molecular conformations, revealing, in particular, a minimum for a compact structure that was not identified when the one-dimensional transition coordinate was used.

Figure 10.

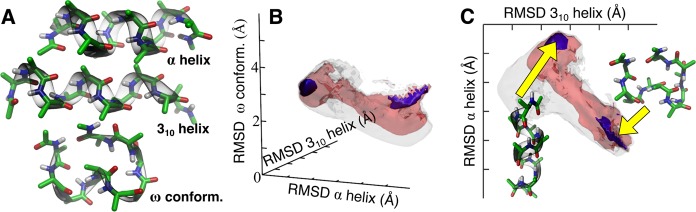
Three-dimensional adaptive biasing force calculation. (A) Three reference structures of deca-alanine. The root-mean-square deviation of selected atoms from their positions in each of the three reference structures defines each of the three transition coordinates. (B) Free-energy isosurfaces as a function of the three transition coordinates. The violet, pink, and gray surfaces contain all points for which the free energy is less than 5, 10, and 20 kcal/mol, respectively. In all cases the tick marks represent a root-mean-square deviation of 1 Å. The minimum value of the free energy, which occurs at (RMSD_α RMSD₃₁₀ RMSD_ω) = (0.3 2.6 2.7) Å, is defined to be zero. (C) Another view of the surface shown in panel B, with representative structures shown for the two energetically favorable regions.

The Generalized Adaptive Biasing Force Algorithm

Previously, we considered one particular approach to multidimensional adaptive biasing force. Here we discuss two further possibilities. First, it is easy to check that if the dimension of the transition coordinate is larger than one, the biasing force cannot be in general derived from a gradient (it is not conservative).⁴² On the other hand, this is of course true of the expected long-time limit. A natural idea is, therefore, to project, using, for example, the classical Helmholtz–Hodge projection: Change the biasing force F_t to ∇φ_t where φ_t = arg min_φ ∥F_t – ∇φ∥_L². Because this is consistent with the expected stationary state, this should not alter the convergence properties. Moreover, the interest of this projection is that the variance of the force is reduced, because the nonconservative part is set to zero. This aspect is analyzed in ref (100).

Second, it would be interesting to develop efficient adaptive biasing force techniques for higher dimensional transition coordinates. The standard implementation of the adaptive biasing force algorithm is currently limited to a dimension up to 3, because it relies on a Cartesian grid of the transition coordinate values, whose complexity is exponential with respect to the dimension of the transition coordinate. It would not be very useful, however, to develop a technique that yields a flat energy landscape along the transition coordinate if the dimension is high, as mapping a high-dimensional cube would be quite time-consuming. One alternative idea, explored in ref (101), is to use a bias of the form ∑_i=1^mA_t◦ξ_i, where (ξ₁, ..., ξ_m) denotes an m-dimensional transition coordinate. Under appropriate assumptions, one can show the convergence of the method, and preliminary numerical results are encouraging; see ref (101). Another route would be to consider a bias of the form ∏_i=1^mA_t◦ξ_i, or even following greedy algorithms and tensor product approaches used in nonlinear approximation theory (see, for instance, ref (102)), ∑_k≥1∏_i=1^mA_t◦ξ_i, where the functions (A^1,k, ..., A^m,k)_k≥1 would be iteratively computed. This method is currently under study.

Combining the adaptive biasing force algorithm with geometrical restraints

The objective of this section is to assess the influence of geometrical restraints on the free-energy landscape and how such restraints ought to be treated in the context of adaptive biasing force simulations. Toward this end, the nature of the forces at play, either thermodynamic forces or forces arising from external harmonic potentials, will be clarified, and the current strategy for handling the latter, using an extended-Lagrangian formalism, will be outlined.

Distinguishing the Thermodynamic Force from the Restraint Force

One subtlety of the adaptive biasing force algorithm that is often overlooked is its dependence on the measure of the thermodynamic force, which is not necessarily synonymous with the total force acting on the transition coordinate. For most biomolecular simulations, this is due to the imposition of various constraint and/or restraint forces. For example, hydrogen-bond lengths are often constrained in a simulation via the RATTLE algorithm.¹⁰³ If only the heavy atom of the bonded pair is involved in the transition coordinate, then the adaptive biasing force algorithm will include the constraint force emanating from the hydrogen in addition to the thermodynamic force, thus contaminating its estimate. A straightforward solution is to include both the hydrogen and its parent atom in the collective variable(s) defining the transition coordinate, causing the constraint forces to cancel each other. In other words, if the constraint/restraint force is zero in the collective variable’s center of mass, it will not contribute to the measured potential of mean force. Alternatively, if restraints nonuniformly affect atoms in the collective variable(s) but are not accounted for in the thermodynamic force used by the adaptive biasing force algorithm, then convergence is impossible; the adaptive biasing force scheme cannot remove forces that it does not measure.

Though it may seem apparent that one will always want to calculate what the potential of mean force would be in the absence of artificial restraints, there are cases in which externally imposed restraints are meant to be included. A key example is in calculating protein–ligand binding free energies, which utilizes a staged procedure involving a series of geometrical restraints.^32,89 By design of the procedure, these restraints must involve the same atoms also being biased at each stage and their contributions are individually determined and tabulated at the end. In this case, to ensure that all necessary forces are included, a procedure such as extended adaptive biasing force is required.

The Extended Adaptive Biasing Force Method

As mentioned above, it may be cumbersome to write an analytical expression for the instantaneous force in dimensions larger than one or for complicated transition coordinates. One possible way around this issue is to extend configurational space with a fictitious degree of freedom λ and define an extended potential,

27

where k > 0 is a (large) force constant that couples λ to the transition coordinate, and proceed utilizing the extended transition coordinate, ξ^ext(x,λ) = λ, instead of ξ. It can be checked that the free energy associated with this extended system is the convolution of the original free energy with a Gaussian kernel, A^ext(λ) = ∫dz χ_k(λ–z) A(z), where χ_k(z) = Z^–1 exp[(−β/2k)|z|²] is the Gaussian kernel with variance kβ^–1. The constant k should thus be chosen sufficiently large to ensure that A^ext is a good approximation of A. This enables quick convergence to equilibrium.

The adaptive biasing force algorithm can be applied to the extended system,⁸ the potential energy being V^ext and the transition coordinate being ξ^ext. Notice that the instantaneous force on the extended degree of freedom, corresponding to free energy A^ext, is trivial to compute, because it is equal to the harmonic spring force. The original free energy A can then be recovered by using either deconvolution procedures¹⁰⁴ or simple unbiasing techniques based on formulas such as eq 34.

Provided that a good estimate of the biased marginal of the transition coordinate, ρ̃(z), has been collected, the following unbiased estimator of the free-energy derivative can be used,

28

where ⟨λ⟩_z is the conditional average value of λ for ξ(x) = z. Here, the biased marginal of ξ is used as a correction to the inaccurate biasing force. It should be noted that this is valid in a more general context, including the absence of biases (removing the second term of the right-hand side), in which case one recovers the trivial histogram-based estimator of the potential of mean force.

Combining thermodynamics and kinetics

Although the adaptive biasing force algorithm is often considered merely a free-energy calculation technique, it is, at its core, an importance-sampling scheme that can have applications beyond obtaining free energies. One such application is to calculate kinetic parameters, such as the diffusivity along a transition coordinate, where an importance-sampling scheme is often essential to obtain reliable estimates in all regions of the coordinate, particularly near all-important free-energy barriers. Together, the diffusivity and free energy as functions of the transition coordinate can be used to construct a kinetic model of a process of interest, which yields insight beyond the static picture of molecular phenomena given by free-energy calculations. In this section, we describe a recently developed scheme leveraging adaptive biasing force to compute simultaneously the free energy and diffusivity along a transition coordinate. This scheme is just an example, as a number of other approaches in which the adaptive biasing force is used to improve kinetic descriptions of different systems are being investigated. Also note that, although this scheme was designed with the adaptive biasing force method in mind, it can be straightforwardly applied to other importance-sampling techniques.

Determining kinetic parameters can be more subtle than mapping the free-energy landscape, because kinetic descriptions are usually approximations and cannot be exactly derived from statistical mechanics.¹⁰⁵ A commonly invoked diffusive model is overdamped Langevin dynamics, in which the following equation of motion^106,107 is assumed for a set of M collective variables z = (z¹, z², ..., z^M),

29

where ż_tⁱ is the time derivative of the ith collective variable at time t, D_ij(z_t) is the (i, j) component of the diffusivity tensor for the configuration of the collective variables at time t, f_j(z_t,t) is the total force on collective variable j for the configuration at time t, ∇_j = ∂/∂z^j, and ζ_i(t) is a stochastic variable with ⟨ζ_i(t) ζ_j(t′)⟩ = 2D_ij(z_t) δ(t′–t). The total force on variable j, f_j(z_t,t), is the sum of the biasing force, f_j(t), and the system force, which can be expressed as the negative of the gradient of the potential of mean force F_j(z) = −∇_jA(z).

Here, we will focus on diffusive models along a single collective variable, but note that multidimensional transitions have been analyzed by similar approaches.^86,108,109 In one dimension, the overdamped Langevin model has two free parameters, the free-energy profile A(z) and the position-dependent diffusivity D(z). The adaptive biasing force method, as well as other techniques, provides a route to A(z), whereas a number of methods have been applied to determining position-dependent diffusivity.^{105,108−117} However, some of the most basic methods are not compatible with nonuniform free-energy landscapes,¹¹² and others are based on the assumption that the free energy can be approximated as a harmonic well.^105,110,112 In methods specifically designed for compatibility with the adaptive biasing force method, it is assumed that the dependence of diffusivity on position is weak.⁸⁷ To parametrize a diffusive model, A(z) and D(z) should be determined consistently, because, for example, coarsening A(z) results in a reduction of the associated D(z).¹¹⁸ Furthermore, to save computational resources, it would be desirable to obtain both the free energy and the diffusivity in the same calculation. However, in many methods cited above, equilibrium or steady-state statistics is assumed, which is likely to yield erroneous results with time-dependent biasing forces. Solutions to the problem of calculating diffusivity in simulations with time-dependent biases take advantage of statistical tools such as maximum likelihood¹¹⁴ or Bayesian inference.¹¹⁷ Conceptually, these methods rely on optimizing the parameters of the diffusive model such that the observed trajectory has the greatest likelihood of occurring.

Optimizing the Diffusive Model

The Bayesian inference scheme described below^86,99,117 begins with assuming a particular dynamical model for the collective variable (or collective variables) of interest. In practice, we represent the functions D_ij(z) and F_i(z) by piecewise cubic interpolation¹¹⁷ from a discrete grid in M-dimensional z-space. We seek the optimal parameters comprising the values of the functions D_ij(z) and F_i(z) at each grid node that best correspond to the simulated trajectory, denoted by T. For simplicity, we represent these optimal parameters as H*. We consider the trajectory as a set of discrete hops of duration Δt. Given trial parameters H, as well as the biasing forces f^bias(t_α), we compute for each hop p ({z_α+1, t_α+1}{z_α, t_α}, f^bias(t_α), H₀), the conditional probability of arriving at transition-coordinate configuration z_α+1 at time t_α+1, given that the system occupied the configuration z_α at time t_α. The probability of the complete trajectory given the parameters is the product of the probabilities at each step^105,114,117

30

This equation yields the probability of the trajectory given an assumed set of parameters. Using Bayes’ theorem,^119,120 we can infer the probability of the parameters given the trajectory:

31

An advantage of the Bayesian approach is that it permits inclusion of any prior knowledge about the form of the parameters in a consistent way by defining the prior probability p_prior(H) of the parameters.^119,120 For example, one can assume scale invariance of the function values¹²¹ or smoothness of the functions.^86,105,117 Finding the optimal parameters then becomes a problem of finding the set of parameters H* that maximizes posterior probability P(H*|T), which can be carried out by generating a Markov chain of states H_k using the Metropolis–Hastings algorithm.¹²²

Trajectory Likelihood in One Dimension

In the one-dimensional case (or for independent motions along multiple dimensions), we can simplify and discretize eq 29 to yield

32

where g_t is a random variable with a standard normal distribution. From the properties of g_t, it is evident that eq 30 becomes

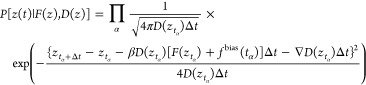33

Below, using this formula and eq 31, we are able to reconstruct D(z) and F(z) for deca-alanine, yielding a complete diffusive model.

One might note that we have assumed nothing about f^bias(t). Indeed, we may even set f^bias = 0 and construct the diffusive model from an equilibrium simulation. However, the accuracy of the results of a Bayesian scheme are wholly dependent on the quality of sampling near each point along z, necessitating importance sampling for rugged free-energy landscapes. In the Supporting Information, we discuss assessment of the precision and reliability of the results of the Bayesian scheme, which includes estimating the statistical error, as well as checking the consistency of the diffusive model with itself and the output of adaptive biasing force.

Application to the Toy-Model Deca-alanine

The z-dependent diffusivity for reversible unfolding of deca-alanine is shown in Figure 11B. The variation with z could not have been inferred in any simple way from knowledge of the system force or free-energy profiles. Diffusion along z, which can be thought of as the rate at which the end-to-end distance randomly changes, is highest near z = 16 Å, corrsponding to slightly unfolded α-helical structures. The ensemble of diverse compact structures in the range z ∈ [5, 10] Å seems to be associated with the lowest diffusivity values, whereas a secondary minimum appears near z = 22 Å. Given these data, one might hypothesize that the diffusivity is inversely related to the conformational degeneracy at z. Note that Figure 11B shows considerable dependence of the calculated diffusivity on Δt, the time over which the trajectory is discretized in eq 33, which implies that the motion on the observed times is not well modeled by overdamped Langevin dynamics, and that a more sophisticated model of motion along z may be needed.

Figure 11.

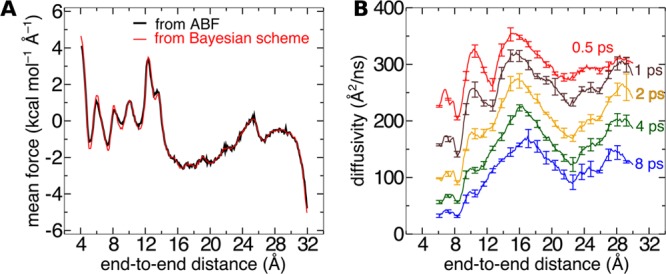
Combining thermodynamics and kinetics for reversible unfolding of deca-alanine. (A) Comparison of the system force as determined by adaptive biasing force and that calculated from the Bayesian scheme on the same trajectory. (B) Diffusivity as a function of the end-to-end distance of deca-alanine for different observation time intervals Δt.

Summary and outlook

Free-energy calculations have become standard tools of statistical mechanics applied to a wide variety of problems in chemistry and biology. This has been possible due to significant theoretical advances in this area, their highly efficient implementations in software packages developed for modern, parallel computers, and remarkable improvements in computational power available for free-energy calculations. Yet, these calculations are still not sufficiently mature to be carried out without careful supervision of the end user. This may be fortunate, as there is no substitute for physical insight of the researcher. This also implies that a number of good practices should be followed in free-energy calculations in general, and in applying the adaptive biasing force in particular. These good practices are usually quite simple and involve careful design of simulations, monitoring their progress and postprocessing analysis. In favorable circumstances, they will simply increase confidence that the calculated free energies are reliable. In less favorable cases, they are even more important, as they allow for identifying and correcting shortcomings of the calculations that might adversely affect the results and their interpretation. Below, we recapitulate these good practices, which have been already discussed in a considerable detail in the preceding sections.

• (1)Careful choice of the transition coordinate is a key step toward successful free-energy calculations. In making this choice, it is desirable not only to capture the physical nature of a problem of interest but also to ensure small variance and smoothness of the biasing force.⁴² Ignoring the latter issues may adversely affect efficiency and even correctness of the calculation. Reducing the variance should be balanced with the cost of calculating the instantaneous value of the transition coordinate, as usually the former will decrease and the latter will increase with the number of atoms involved. This balance will depend on implementation details and, therefore, some familiarity with the underlying code might be required.
• (2)A suitable stratification strategy should be planned in advance. If there are concerns about possible quasi nonergodic behavior of the system, and in particular the existence of parallel channels between the end point states, it is recommended to use large windows. If these concerns prove to be unjustified, it is always possible to switch to smaller windows without losing information about the biasing force that has already been accrued. In other instances it is usually more efficient to stratify the transition coordinate into smaller windows throughout a simulation.
• (3)Free-energy calculations should always be accompanied by estimates of statistical errors. For the adaptive biasing force algorithm, a formula to do so exists and should be applied whenever possible. Without error estimates the reliability of the calculated free-energy values is questionable and the ability to compare them with experimental measurements is seriously hampered.
• (4)In stratified simulations, lack of continuity in the biasing force across consecutive windows that clearly exceeds statistical errors is a sure sign of problematic free-energy calculations. This issue should not be ignored, and any attempt to circumvent it by way of some sort of averaging is unlikely to succeed. Instead, remedial steps aimed at improving ergodic behavior of the system, such as applying the multiple-walker strategy, should be taken.
• (5)It is usually very useful to monitor the behavior of the total, biased force, as it should converge to zero in long simulations. Moreover, the rate of convergence at sufficiently long times t should become proportional to 1/√t. If the biased force along the transition coordinate or within a window exhibits large deviations from nonuniformity, which clearly does not decrease with time, or the convergence rate is erratic, we have, again, a likely indication of quasi nonergodicity in orthogonal degrees of freedom. Then, there is no basis for assuming that a reliable free-energy dependence on the transition coordinate can be extracted from the calculated forces. Instead, in such circumstances, techniques for removing quasi nonergodicities along orthogonal degrees of freedom should be brought to bear.

Following these simple good practices guarantees the improved quality of free-energy calculations carried out by way of the adaptive biasing force method but does not ensure that all problems encountered in such calculations, especially those related to quasi nonergodicity, have been identified. To this end, the toughest challenges to practitioners of the adaptive biasing force algorithm and related methods are linked to multiple slow degrees of freedom leading to orthogonal barriers. One way to address these problems is through a multiple-walker strategy, which has proven effective in a test system that exhibits metastability in the orthogonal space, a significant challenge to the classic adaptive force method.⁹⁷ Along the same lines, the basic method can be integrated with other enhanced sampling techniques that involve multiple-copy schemes, such as parallel tempering and Hamiltonian exchange.⁸⁵ Another promising research direction is to increase the dimensionality of the bias, as is done in an implicit way in the generalized adaptive biasing force scheme.¹⁰¹ “Real-life” applications would, however, require an accessible and well-documented implementation, now available as part of the independent collective variables module.³⁹

Although better sampling of orthogonal degrees of freedom is the most promising direction for increasing the efficiency of the adapting biasing force method, there is also room for improvement in achieving convergence along the transition coordinate. For example, it would be of interest to develop adaptive algorithms for the early stages of simulations that would converge faster than the currently used step or ramp functions. One possibility along these lines is to employ a kernel function along ξ. In other words, adaptation in a given bin would depend not only on samples accrued in this bin but also on samples in neighboring bins. Developing binless algorithms is also of interest. Another avenue to improve convergence along the transition coordinate, which has not been explored so far, is to exploit the freedom in defining the ensemble average of instantaneous force and identify choices that reduce the variance.

Several steps can be taken to obtain better estimates of free energies. For example, the error in integrating force to calculate free energy that is due to binning of force values could be reduced by using improved, smooth interpolation schemes. Further, we observe that the best accuracy is obtained not when the free energy is flat but rather when the statistical error of the average force is the same everywhere along the transition coordinate. To achieve this, the number of samples, N_k, in bin k should be such that σ_k/(N_k)^1/2 rather than N_k is constant for all bins, where σ_k is the standard deviation of estimated average force in bin k. This is realized if the biasing potential due to the average force used in the standard adaptive biasing force method is supplemented by the term 2k_BT ln(σ_k/σ₀), where σ₀ is the standard deviation at a reference point. In practice, σ_k and σ₀ are estimated from their running values or their approximations during the course of a simulation. The additional term becomes important whenever the friction coefficient changes markedly with ξ or parts of the system undergo large fluctuation, for example because they are near phase transition.

A number of extensions to the adaptive biasing force method have not been explored yet. For example, the method could be straightforwardly extended to transformations along a parameter of the Hamiltonian if an equation of motion was associated with this parameter, as is done in metadynamics. It would be of interest to check whether such application of the adaptive biasing force method were more efficient and reliable than other, related methods currently used for this purpose, such as conventional thermodynamic integration, metadynamics, or the Wang–Landau algorithm. Another extension of the method that was outlined in one of the original studies on the adaptive biasing force¹²³ but has not been pursued so far, is to add to the biasing force another contribution that would depend only on ξ and would favor certain states of particular interest to the user or drive the dynamics in a specified direction. The latter would make the adaptive biasing force method a more efficient and better controlled alternative to steered dynamics.

Finally, we emphasize that the adaptive biasing force is not just a free-energy calculation technique but can also be seen as a general adaptive biasing scheme (see, for instance, ref (124) for applications in Bayesian statistics). Indeed, once a correct sampling of the biased measure Z_p^–1 exp(−βp^TM^–1p/2) dp Z_t0^–1 exp{−β[V – A_t0◦ξ](x)} dx has been obtained (t₀ being a fixed time, and the bias being fixed from time t₀: ∀t ≥ t₀, A_t = A_t0, it is easy to recover canonical averages using standard unbiasing procedures:

34

Although the adaptive biasing force dynamics has been applied so far almost exclusively to chemical and biological systems, it could also be very useful for sampling a multimodal measure (namely, a probability measure for which high-probability regions, called “modes” in this context, are separated by low-probability regions) in other fields, e.g., among others, free-energy computations in material sciences¹²⁵ or Markov chain Monte Carlo techniques for Bayesian inference.¹²⁴ In summary, the combination of simplicity, versatility, and strong mathematical underpinnings makes the adaptive biasing force method an attractive target for a wide variety of extensions in statistical mechanics and beyond.

Supporting Information Available

Further derivation for the justification of stratification, the convergence of the adaptive biasing force algorithm, statistical error measurement and a discussion on assessing the accuracy of kinetic modeling. This material is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States