Exact Stochastic Simulation of a Calcium Microdomain Reveals the Impact of Ca²⁺ Fluctuations on IP₃R Gating

Abstract

In this study, we numerically analyzed the nonlinear Ca²⁺-dependent gating dynamics of a single, nonconducting inositol 1,4,5-trisphosphate receptor (IP₃R) channel, using an exact and fully stochastic simulation algorithm that includes channel gating, Ca²⁺ buffering, and Ca²⁺ diffusion. The IP₃R is a ubiquitous intracellular Ca²⁺ release channel that plays an important role in the formation of complex spatiotemporal Ca²⁺ signals such as waves and oscillations. Dynamic subfemtoliter Ca²⁺ microdomains reveal low copy numbers of Ca²⁺ ions, buffer molecules, and IP₃Rs, and stochastic fluctuations arising from molecular interactions and diffusion do not average out. In contrast to models treating calcium dynamics deterministically, the stochastic approach accounts for this molecular noise. We varied Ca²⁺ diffusion coefficients and buffer reaction rates to tune the autocorrelation properties of Ca²⁺ noise and found a distinct relation between the autocorrelation time τ_ac, the mean channel open and close times, and the resulting IP₃R open probability P_O. We observed an increased P_O for shorter noise autocorrelation times, caused by increasing channel open times and decreasing close times. In a pure diffusion model the effects become apparent at elevated calcium concentrations, e.g., at [Ca²⁺] = 25 μM, τ_ac = 0.082 ms, the IP₃R open probability increased by ≈20% and mean open times increased by ≈4 ms, compared to a zero noise model. We identified the inactivating Ca²⁺ binding site of IP₃R subunits as the primarily noise-susceptible element of the De Young and Keizer model. Short Ca²⁺ noise autocorrelation times decrease the probability of Ca²⁺ association and consequently increase IP₃R activity. These results suggest a functional role of local calcium noise properties on calcium-regulated target molecules such as the ubiquitous IP₃R. This finding may stimulate novel experimental approaches analyzing the role of calcium noise properties on microdomain behavior.

Introduction

Ca²⁺ is a versatile second messenger, orchestrating a great variety of vital cellular functions such as cell motility (1), regulation of gene transcription (2), neurotransmitter release (3), and cytoskeleton dynamics (4). Its low intracellular resting concentration is maintained and tightly regulated by ion channels, ion pumps, and Ca²⁺ buffers (5). A central element of this regulation apparatus is the inositol 1,4,5-trisphosphate receptor (IP₃R), a large homotetrameric Ca²⁺ release channel protein accounting for Ca²⁺ flux from intracellular stores (endo-/sarcoplasmic reticulum) into the cytosol. It is regulated by IP₃, a second messenger produced by the membrane protein Phospholipase C, to transduce extracellular stimuli into intracellular Ca²⁺ signals. In addition to an IP₃ binding site, each of the four channel subunits has two Ca²⁺ binding sites that are responsible for the characteristic bell-shaped calcium response curve of IP₃R (6). While for low Ca²⁺ concentrations ([Ca²⁺]) the high-affinity activating Ca²⁺ binding site accounts for the positive feedback mechanism known as calcium-induced calcium release, the low-affinity inactivating Ca²⁺ binding site induces a negative feedback mechanism, inactivating the IP₃ receptor at elevated [Ca²⁺] (7). IP₃Rs are not uniformly distributed. They are organized in channel clusters, each including a few tens of IP₃Rs and spaced 1–7 μm apart (8).

The synchronized openings of such clusters, carried by calcium-induced calcium release, are the foundation of experimentally observed elementary calcium release events called “calcium puffs” (9). Diffusion, the presence of Ca²⁺ pumps (e.g., SERCA), and Ca²⁺ buffers limit the spatiotemporal extent of these ECRE and control the coupling strength of adjacent IP₃R clusters. This quantization of Ca²⁺ signals in dynamic microdomains is the basis of more complex spatiotemporal signaling patterns such as calcium oscillations and calcium waves (10). It also introduces stochasticity into the process of signal generation. Microdomains only contain a small copy number of Ca²⁺ ions and IP₃Rs and therefore do not behave deterministically, which is reflected on a macroscopic level by spontaneous occurrences of Ca²⁺ puffs. It is now believed that global cellular Ca²⁺ signals are based on the stochastic occurrence of elementary calcium release events that, in turn, are carried by single channel noise (8,11–13).

These perceptions motivated the use of mathematical descriptions of Ca²⁺ signaling, which take into account the discrete and stochastic nature of molecular interactions (14,15). Consequently, a large number of simulation strategies for IP₃R-containing calcium microdomains have been proposed over the last decade (16,17). The fully stochastic description of complex reaction-diffusion systems (RDS) is computationally demanding, and therefore most existing approaches implement hybrid algorithms. Hybrid algorithms are able to cover the hierarchical structure of calcium signals, spanning several orders of magnitude in space and time by treating functionally important nonlinear components such as the IP₃R stochastically, whereas passive bulk reactions and diffusion are treated deterministically (11,18–20). Because noise-induced effects on nonlinear systems have received special attention over the last few years (21–26), we chose a fully stochastic framework to investigate the effects of Ca²⁺ noise, arising from buffer association/dissociation reactions and diffusion, on the nonlinear behavior of IP₃Rs. Our model represents a Ca²⁺ microdomain with a single nonconducting IP₃R, integrating channel gating and Ca²⁺ dynamics in a common stochastic simulation framework based on Gillespie’s algorithm. We started investigating the influence of pure diffusive Ca²⁺ noise on the nonlinear gating dynamics of the IP₃R, and then extended the model by introducing artificial Ca²⁺ buffers. In summary, we found that IP₃R gating is susceptible to Ca²⁺ noise in general, and to the Ca²⁺ noise autocorrelation time in particular.

Materials and Methods

Stochastic description of chemical reaction diffusion systems

An exact stochastic description of chemical systems is provided by the chemical master equation (CME) (27). The CME describes the evolution of a chemical reaction system, comprised of a set of N molecular species S = {S₁,…,S_N}, inside a system with volume Ω. The system state at time t is represented by the system state vector x(t) = (x₁(t),…,x_N(t)), where x_k(t) denotes the molecular count of species S_k at time t. The system state is advanced by a set of M reaction events R = {R₁,…,R_M} that are defined as state change vectors v_j = (d_j1,…,d_jN), j = 1,…,M. Here d_ji represents the change in the molecular count of species S_i due to R_j. The CME reads as

$${\partial }_{t}P\left(\mathit{x},t\right)=\sum _{j=1}^M\left[a_j\left(\mathit{x}-{\mathit{v}}_j,t\right)P\left(\mathit{x}-{\mathit{v}}_j,t\right)-a_j\left(\mathit{x},t\right)P\left(\mathit{x},t\right)\right]$$

and states that the probability P(x,t) of the system being at state x at time t is calculated from the net probability flow from state x − v_j to x, and vice versa. The propensity function a_j(x,t) denotes the transition probability of R_j, given a system state x at time t. All these considerations are based on the basic assumption of a well-stirred chemical system, where nonreactive molecular collisions are far more likely than reactive events and exact positions, and velocities of single molecules are ignored (28).

It is possible to extend the CME to reaction diffusion systems by subdividing Ω into u smaller subvolumes (voxels) Ω_k, k = 1,…,u. Subsequently, an additional spatial dimension is introduced into the CME, which leads to the reaction diffusion master equation (RDME) (29). This approach uses the classic CME in each voxel separately and connects the voxels by adding diffusion events to the set of state transitions R.

Gillespie’s algorithm

For complex chemical reaction diffusion systems, the RDME quickly becomes analytically intractable. Gillespie’s algorithm is a Monte Carlo procedure that simulates the time evolution of a system as a discrete multivariate Markov process (30). It is based on the joint probability density function

$$P\left(j,\tau |\mathit{x},t\right)=a_j\left(\mathit{x},t\right)\times \text{exp}\left(-\sum _{j=1}^M{a}_j\left(\mathit{x},t\right)\tau \right),$$ (1)

which determines the probability of state transition R_j to occur in the infinitesimal time interval [t + τ, t + τ + dτ), given system state x at time t. The propensity functions a_j(x,t) can be obtained from the deterministic reaction rate constants. In this study, we use the following.

• 1.First-order reactions. These are independent of the system volume Ω. Their propensity functions are directly proportional to the respective reaction rate constants a_j(x,t) = k_j × x_j(t).
• 2.Second-order reactions. They require molecular collisions of two educts, and therefore depend on Ω. We have a_j(x,t) = k_j/Ω × h_j(x,t), where h_j(x,t) denotes the number of unique reactant combinations at time t for R_j.
• 3.Diffusion events. These are characterized by a diffusion coefficient D and depend on the spatial extent of the considered system. Assuming a cubic simulation voxel with volume Ω = l³ and diffusion area A = 6 × l², the propensity function reads a_j(x,t) = D_j/l² × x_j(t).

A rigorous derivation of these propensity functions has been presented by several authors before (31–33). One way of performing state transitions is the generation of exponentially distributed random waiting times τ_j for each R_j and executing the state transition with the minimum waiting time (first reaction method) (31). This requires the generation of M uniformly distributed random variables r₁,…,r_M and the computation of

$$\begin{array}{c}{\tau }_j=\frac{-\text{log}{r}_j}{a_j\left(\mathit{x},t\right)},\\ j=1,\dots ,M.\end{array}$$ (2)

Let R_k be the state transition with the smallest associated τ_k. The system time t is then advanced to t → t + τ_k and the system state is updated as x(t) → x(t) + v_k. The resulting simulation trajectories are exact solutions of the underlying RDME.

Many improvements to the classic version of Gillespie’s algorithm have been proposed in the past (33). In this study, we use Gibson and Bruck’s next reaction method (34). Its main advantages are the reuse of random numbers and the introduction of an optimized data structure.

Calcium buffer reactions

Ca²⁺ ions interact with a great variety of cytosolic buffer proteins (35):

$${\text{Ca}}^{2+}+\text{B}\underset{k^{-}}{\overset{k^{+}}{\rightleftharpoons }}\text{CaB}.$$ (3)

Buffer molecules are characterized by their rate constants for association (k⁺) and dissociation (k⁻) reactions. The implementation of Ca²⁺ buffers to Gillespie’s algorithm requires the definition of a second-order reaction for buffer association and a first-order reaction for the dissociation reaction. A summary of numerical values is given in Table 1.

Table 1.

Model data

Reactant	K+ (μM−1 ms−1)	k− (ms−1)	Kd (μM)	D (μm2/s)	c (μM)
Ca2+	—	—	—	50–500	0.1–500
IP3	—	—	—	0	10
B1	0.01	0.1	10	0	300
B2	0.05	0.5	10	0	300
B3	0.1	1	10	0	300

Channel kinetics	Association (μM−1 ms−1)	Dissociation (ms−1)
IP3 binding site	a1,a3 = 0.08	b1 = 6.4 × 10−4
		b3 = 0.04
Active Ca2+ binding site	a5 = 0.015	b5 = 0.012
	a2 = 4 × 10−5	b2 = 4.8 × 10−4
Inactive Ca2+ binding site	a4 = 4 × 10−4	b4 = 7.68 × 10−5
Subunit activation	a0 = 0.55 ms−1	b0 = 0.08

Overview of system parameters used. We use IP₃R subunit transition rates as suggested by Rüdiger et al. (19) that were obtained from fitting experimental data from Mak et al. (7). The value k⁺ is the buffer association reaction rate constant, k⁻ is the buffer dissociation reaction rate constant, and K_d is the respective buffer dissociation constant. D is the diffusion coefficient, and c is the concentration of the respective substance. Subunit state transition rates a_i,b_j refer to the De Young-Keizer model detailed in Fig. 1.

Model geometry and diffusion

In this study, we consider a model consisting of a single simulation voxel surrounded by equilibrated boundary voxels, to account for diffusive transfer across the surface area as illustrated in Fig. 1 A. Inside the boundary voxels, we set all concentrations to their constant equilibrium concentrations and thus obtain a constant influx rate of diffusing molecular species (36). Introducing diffusion events considerably increases computation times. In this study, we only consider stationary Ca²⁺ buffers, limiting diffusion processes to Ca²⁺ ions. In all simulations, a cubic voxel geometry with box length l = 0.5 μm and thus Ω = 0.125 fL is used.

Figure 1.

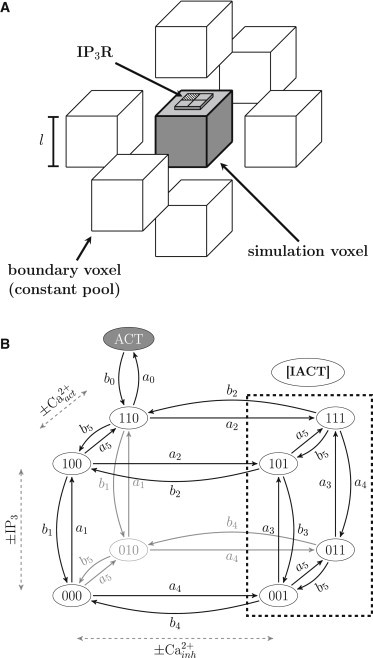
(A) Schematic illustration of the model geometry (shaded box in the center). Main simulation voxel, including a single IP₃R on top. Surrounding blank boxes represent the constant pool boundary voxel used in spatially resolved models. (B) De Young and Keizer state transition model of an IP₃R subunit (37) with an additional, ligand-independent [ACT] state (38). Four homotetrameric subunits form the channel protein that is in an open state whenever ≥3 subunits are active. A subunit exhibits three binding sites, represented by the numeration of the states. First digit, activating IP₃R binding site; second digit, activating Ca²⁺ binding site; third digit, inactivating Ca²⁺ binding site. Subunit states with an occupied inactivating Ca²⁺ binding site are summarized as inactive states ([IACT]) (dashed box). State transition rates are shown in Table 1 (19).

Implementation of the IP₃R

A widely used gating scheme for the IP₃Rs is given by the eight-state subunit transition model proposed by De Young and Keizer in 1992 (37). It has been further refined by Shuai et al. (38), who introduced an additional active state that locks the subunits and prevents the dissociation of its ligands, reproducing experimentally observed ligand-independent channel flickering (39). Fig. 1 B illustrates the model with rate constants as proposed by Rüdiger et al. (19), shown in Table 1. Subunit state transition rates used in their study were obtained by fitting data from single channel recordings from Mak et al. (7) and are thus a solid foundation for the here presented simulations of an IP₃R. The three binding sites exposed by each subunit are represented by the numeration of the states where the first digit represents the IP₃ binding site, the second digit the activating Ca²⁺, and the third digit the inactivating binding site. A value of 0 indicates a free binding site, whereas 1 represents an occupied binding site. The channel is considered to be in an open state whenever at least three subunits are in the active state [ACT]. If more than one IP₃R subunit has an occupied inactivating binding site ([IACT]), the channel is unable to open and thus considered to be completely inactivated.

In our implementation of Gillespie’s algorithm, we consider each subunit state as a distinct molecular species. State transitions are implemented as second-order ligand binding reactions and first-order ligand dissociation reactions. The open channel is included as a further molecular species whereby its count is increased by 1 whenever at least three out of four subunits are active. Within this framework, the implementation of clusters of IP₃R channels as well as Ca²⁺-conducting channels is straightforward. In this study, we only consider a single, nonconducting IP₃R, in analogy to experimental results from lipid bilayer studies (7).

As discussed earlier, simulation trajectories resulting from the here-used algorithm are exact. They are unevenly spaced time series of the system state, whereat each data point represents the system state after a single system state transition. It is therefore possible to track the exact points in time when the IP₃R opens or closes and the determination of channel open/close times is straightforward. Because no event is missed, the resulting statistical analysis of channel open/close times does not require correction.

Characteristics of Ca²⁺ noise

All systems considered here obey combinatorial kinetics and, in the absence of channel flux, a constant detailed balanced equilibrium condition. The resulting Ca²⁺ noise distributions at equilibrium are therefore Poissonian (40) and for sufficiently large [Ca²⁺], they are well approximated by a normally distributed random variable $\mathcal{N}$(μ,σ²) with μ = σ². In these cases, noise intensities at equilibrium depend solely on the mean [Ca²⁺], and are independent from kinetic system properties. The resulting Ca²⁺ signal is stationary and ergodic (41). In this study, we focus on the temporal characteristics of Ca²⁺ noise, in particular on the two-time autocorrelation function, which reveals information about properties of the underlying microscopic processes (42,43). By varying buffer reaction rates and diffusion coefficients, it is possible to tune the Ca²⁺ noise autocorrelation time (41). The autocorrelation function is well approximated by an exponentially decaying function (29,43,44) characterized by its decay rate τ_ac, which we will refer to as the “autocorrelation time” (Fig. 2). For a detailed theoretical analysis of the origins of Ca²⁺ fluctuations, the reader is referred to this recent publication (41).

Figure 2.

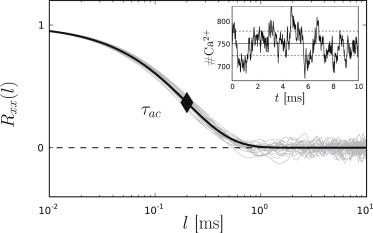
Estimated autocorrelation time of a plain diffusion system with D_Ca = 200 μm² s⁻¹ and [Ca²⁺] = 10 μM. Semilogarithmic representation of 20 exemplary autocorrelation functions R_xx(l) (shaded curves) with exponential fit (solid curve) and a resulting autocorrelation time of τ_ac = 0.207 ms (solid diamond). On the right, a representative simulation trajectory of purely diffusive Ca²⁺ noise with mean (solid line) and standard deviation (dashed lines) is shown (T = 10 ms).

Computation times

Simulations presented in this study were carried out on an Intel Core 2 Quad CPU Q9550 @ 2.83 GHz (Santa Clara, CA) and a cache size of 6144 Kb. Fig. 3 is based on data from simulation runs of at least 1.5 × 10³ s for [Ca²⁺] = 0.1–50 μM and at least 5 × 10² s for [Ca²⁺] = 100–500 μM. Simulation times ranged from ∼72 s to 6.5 × 10⁵ s. RDS data presented in Figs. 4 and 5 result from simulation runs of at least 1 × 10³ s. Here, simulation times ranged from ∼${10}^3\text{s}$ to 4.5 × 10⁴ s.

Figure 3.

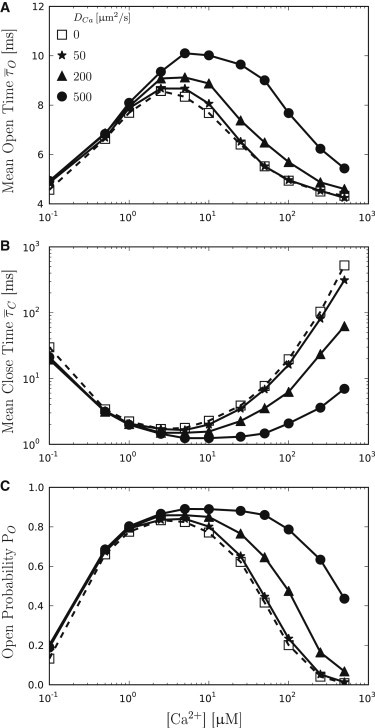
Summary of gating properties of the IP₃R for varying diffusion coefficients D_Ca. Open squares (dashed curve) are the result of zero noise models and represent the results expected from algorithms that treat Ca²⁺ dynamics deterministically. (Solid curves) Results for three different diffusion coefficients D_Ca = 50 μm² s⁻¹ (stars), 200 μm² s⁻¹ (triangles) and 500 μm² s⁻¹ (circles). For low [Ca²⁺], Ca²⁺ noise has no obvious influence on the IP₃R. Starting at [Ca²⁺] = 1 μM, (A) mean open times ${\overline{\tau }}_O$ increase with increasing D_Ca, whereas (B) mean close times ${\overline{\tau }}_C$ decrease. (C) Consequently, the channel open probability P_O increases with increasing D_Ca.

Figure 4.

Summary of the relationship between IP₃R gating and τ_ac of Ca²⁺ noise at [Ca²⁺] = 10 μM. In addition to purely diffusive models (circles), results from a RDS with D_Ca = 200 μm² s⁻¹, including a single buffer with K_d = 10 μM and varying association reaction rates k⁺ (see Table 1), are shown (stars). The zero noise model is included at an arbitrary x-intercept and represents a model with infinite τ_ac (open square). Mean open times ${\overline{\tau }}_O$ (A), mean close times ${\overline{\tau }}_C$ (B), and open probabilities P_O (C) are shown as a function of τ_ac.

Figure 5.

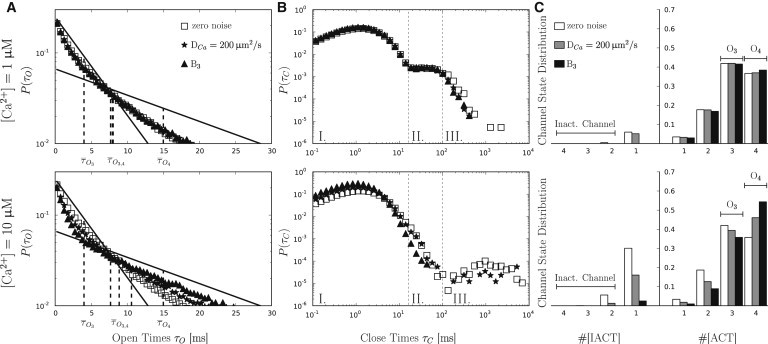
Open time distributions (left column), close time distributions (middle column) and subunit distributions (right column) at [Ca²⁺] = 1 μM (upper row) and at [Ca²⁺] = 10 μM (lower row). Results are shown for a zero noise model (open squares, open bar), pure diffusive noise with D_Ca = 200 μm² s⁻¹ (stars, shaded bar) and noise arising from a RDS including B₃ (k⁺ = 0.1 μM⁻¹ ms⁻¹, k⁺ = 1 ms⁻¹) and diffusion with D_Ca = 200 μm² s⁻¹ (triangles, solid bar). (A) Expected open time distributions for O₃ and O₄ openings (solid lines) and the resulting biexponential open time distribution. (Dashed lines) Mean open times. (B) Within the close time distributions, we identify three distribution regions: Region I, channel closings resulting from channel flickering; Region II, channel closings resulting from a superposition of close states where the channel is not inactivated; and Region III, long close intervals resulting from channel inactivation. (C) Channel state distributions in terms of activated ([ACT]) and inactivated ([IACT]) subunits.

Results

To study the noise susceptibility of a single, nonconducting IP₃R, we chose a saturating IP₃ concentration ([IP₃]_sat = 10 μM). In a first step, we used purely diffusive Ca²⁺ noise with varying diffusion coefficients to examine its influence on IP₃R gating dynamics over a range of [Ca²⁺] = 0.1–500 μM. Consequently, we extended the system by introducing Ca²⁺ buffers and examined their additional influence on the IP₃R. In contrast to pure diffusion models that reveal constant Ca²⁺ noise τ_ac for different [Ca²⁺], the influence of a Ca²⁺ buffer on Ca²⁺ noise depends on its saturation level. With increasing buffer saturation, its influence decreases and noise characteristics are dominated by the remaining dynamic processes such as diffusion. Due to computational feasibility, the total buffer concentration [B]_tot is limited in our models. To avoid buffer saturation phenomena, we therefore focused on a fixed [Ca²⁺] = 10 μM and a Ca²⁺ buffer with dissociation constant K_d = 10 μM and constant [B]_tot = 300 μM. The choice of these model parameters reflects a compromise between a realistic Ca²⁺ buffer dissociation constant and an acceptable level of buffer saturation (50%). To vary temporal characteristics of Ca²⁺ noise, different on/off reaction rates have been used (see Table 1). All RDS models of the second part use a Ca²⁺ diffusion coefficient of D_Ca = 200 μm² s⁻¹.

The case of multibuffer systems can be effectively reduced to a single buffer system with a compound τ_ac (45). Temporal Ca²⁺ noise characteristics are dominated by the fastest present dynamic process involving Ca²⁺. This means that a multibuffer system induces Ca²⁺ noise τ_ac comparable to a single buffer system, which only contains the fastest buffer (as long as the buffer is far from saturated).

IP₃R gating dynamics in a pure diffusion model

To investigate the noise susceptibility of the IP₃R, we used three different Ca²⁺ diffusion coefficients (D_Ca = 50 μm² s⁻¹, 200 μm² s⁻¹, and 500 μm² s⁻¹) to introduce Ca²⁺ noise to the system. Channel dynamics are evaluated in terms of the mean open times ${\overline{\tau }}_O$, mean close times ${\overline{\tau }}_C$, and open probabilities P_O, for varying [Ca²⁺] = 0.1–500 μM. We included results from a zero noise model in order to compare with earlier results from hybrid models. The mean open/close times and open probabilities of the zero noise model are in good accordance with results from hybrid algorithms used by Shuai et al. (38) and Rüdiger et al. (19).

Fig. 3 summarizes the results and clearly shows that IP₃R gating dynamics are affected by Ca²⁺ noise. Ca²⁺ diffusion is modeled as a random walk between adjacent voxels (32) with a rate constant derived from the voxel geometry and the diffusion coefficient D_Ca. The corresponding τ_ac is equal to the inverse of the diffusion rate; therefore, increasing D_Ca leads to decreasing τ_ac (41). We found the estimated τ_ac from our simulations to be in good accordance with the expected values, as given in parentheses: For D_Ca = 50 μm² s⁻¹, we found an autocorrelation time of ${\tau }_{ac}^{50}$ = 0.820 ± 0.084 ms (0.833 ms); for D_Ca = 200 μm² s⁻¹, we found ${\tau }_{ac}^{200}$ = 0.204 ± 0.021 ms (0.208 ms); and for D_Ca = 500 μm² s⁻¹, we found ${\tau }_{ac}^{500}$ = 0.082 ± 0.0085 ms (0.083 ms).

Because the noise variance is constant for fixed [Ca²⁺], noise-induced effects can be attributed to as the autocorrelation time of Ca²⁺ noise. Fig. 3 A shows that ${\overline{\tau }}_O$ increases for decreasing τ_ac. Ca²⁺ diffusion with D_Ca = 500 μm² s⁻¹ shows a maximum of ${\overline{\tau }}_O$ = 10.07 ms ([Ca²⁺] = 5 μM) compared to the zero noise model with a maximum of ${\overline{\tau }}_O$ = 8.56 ms ([Ca²⁺] = 2.5 μM). Furthermore, short τ_ac values are associated with a delay of the negative Ca²⁺ feedback, and ${\overline{\tau }}_O$ remains on a high level, even for large [Ca²⁺]. This effect is also shown in Fig. 3 B, where long ${\overline{\tau }}_C$ intervals, resulting from Ca²⁺-dependent subunit inactivation, only appear at much larger [Ca²⁺] values as expected from the zero noise model. Fig. 3 C shows how the open probability P_O increases accordingly. While the zero noise model reveals a maximum P_O = 84% ([Ca²⁺] = 2.5 μM), the fast diffusion model shows a maximum of P_O = 89% ([Ca$2^{+}$] = 10 μM). Open probabilities remained high even for large [Ca²⁺] when diffusive noise is considered.

IP₃R gating dynamics in the vicinity of Ca²⁺ buffer

Introduction of Ca²⁺ buffer

To investigate the additional impact of Ca²⁺ buffers on Ca²⁺ noise and IP₃R gating, we simulated a RDS with a standard value of D_Ca = 200 μm² s⁻¹ (46) and an immobile Ca²⁺ buffer with K_d = 10 μM. From Fig. 3, the clearest effects of Ca²⁺ noise on the IP₃R are expected for high [Ca²⁺]. However, to avoid buffer saturation phenomena, we kept the [Ca²⁺] equilibrium concentration at [Ca²⁺]_eq = K_d = 10 μM. We obtained different τ_ac values by varying the buffer association rate k⁺, keeping K_d constant. We used three different Ca²⁺ buffers B₁–B₃ (see Table 1 for numerical values) and found the corresponding Ca²⁺ noise τ_ac to be as follows: ${\tau }_{ac}^{\left(1\right)}$ = 0.153 ± 0.035 ms, ${\tau }_{ac}^2$ = 0.087 ± 0.027 ms, and ${\tau }_{ac}^{\left(3\right)}$ = 0.058 ± 0.012 ms.

In Fig. 4, mean channel open times ${\overline{\tau }}_O$, mean channel close times ${\overline{\tau }}_C$, and channel open probability P_O are shown as a function of Ca²⁺ noise τ_ac. In addition to the RDS models, we included the results from Fig. 3 to show that the impact on IP₃R gating is independent of the underlying noise generating mechanism. The zero noise model is included at an arbitrary x-intercept to represent a model with infinite τ_ac.

We found a dependency of ${\overline{\tau }}_O$, ${\overline{\tau }}_C$, and P_O on Ca²⁺ noise τ_ac. The decreasing τ_ac induced by Ca²⁺ buffers and diffusion leads to an increase in ${\overline{\tau }}_O$ and P_O, and to a decreasing ${\overline{\tau }}_C$. It is also observed that slow Ca²⁺ diffusion (D_Ca = 50 μm² s⁻¹) inducing relatively long Ca²⁺ noise τ_ac values has only very small effect on the IP₃R (see also Fig. 3).

Detailed channel gating analysis

Because the IP₃R opens whenever at least three out of four subunits are in the [ACT] state (see Fig. 1), it has two distinct open states. They can be distinguished by the maximum number of active subunits during an open interval, and are termed O₃ and O₄ (38). Data from patch-clamp experiments (47) and deterministic analysis of the IP₃R model (38) both reveal independent, exponential open time distributions for each open state. Our simulations reveal the same behavior, and we found dwell times for the O₃ and O₄ states that are in good accordance with previously published data (38), ${\overline{\tau }}_{O_3}$ ≈ 4 ms and ${\overline{\tau }}_{O_4}$ ≈ 15 ms. In contrast to only two open states, many more distinct close states exist (9⁴–2). Mean close time distributions therefore show a more complex, multiexponential behavior. Nevertheless, it is possible to distinguish two major types of channel closings: 1) short close intervals, resulting from the ligand-independent inactivation of a single active subunit that underlies the typical channel flickering and 2) long close intervals that occur whenever Ca²⁺ binds to an inactivating binding site, accounting for the strong negative feedback at high [Ca²⁺].

While short closings only last for a few milliseconds, long close intervals can last up to seconds, and account for the burstlike opening pattern of IP₃Rs.

Fig. 5 shows a detailed channel gating analysis of three different models: a zero noise model, a purely diffusive noise model (D_Ca = 200 μm² s⁻¹), and an RDS model including the buffer B₃ (k⁺ = 0.1 μM⁻¹ ms⁻¹, k⁻ = 1 ms⁻¹), as well as Ca²⁺ diffusion (D_Ca = 200 μm² s⁻¹). The upper row shows results from models with [Ca²⁺] = 1 μM; the lower row shows results from models with [Ca²⁺] = 10 μM.

Open/close time distributions

Open time distributions are shown in the left column of Fig. 5. The biexponential decay results from the superposition of the open time distributions of O₃ and O₄ states (solid lines). Vertical dashed lines indicate the ${\overline{\tau }}_O$ value of the respective distribution. While the open time distribution for [Ca²⁺] = 1 μM is unaffected by noise, we find a clear effect for [Ca²⁺] = 10 μM. A decreasing Ca²⁺ noise τ_ac induces a shift of the open time distributions toward the expected distribution for isolated O₄ openings. Mean open times ${\overline{\tau }}_O$ increase accordingly from 7.68 to 10.59 ms.

The middle column depicts the corresponding close time distributions. Based on theoretical mean waiting times ${\overline{\tau }}_w$ resulting from subunit transition rates, we subdivided the distributions roughly into three regions.

Region I. This distribution shows short channel closings, resulting from subunit transitions from [110] → [ACT] (channel flickering). This ligand-independent transition reveals a theoretical mean waiting time of ${\overline{\tau }}_w$ = 0.090 ms.

Region II. This distribution is a superposition of close channel states with less than two inactivated subunits.

Region III. This distribution shows channel close states resulting from complete channel inactivation with more than one inactivated subunit. Assuming the IP₃R to be saturated with IP₃, the dissociation of Ca²⁺ from an inactivating Ca²⁺ binding site ([1x1] → [1x0]) reveals a theoretical mean waiting time ${\overline{\tau }}_w$ = 2083.3 ms. The shape of the distribution changes from [Ca²⁺] = 1 μM to [Ca²⁺] = 10 μM, where especially the fraction of prolonged close times increase for higher [Ca²⁺]. This is mainly caused by increasing subunit inactivation, i.e., negative Ca²⁺ feedback. Again, noise only influences the close time distribution at [Ca²⁺] = 10 μM. The zero noise model shows a well-defined second peak in Region III, which slowly vanishes for decreasing τ_ac. Remarkably, the IP₃R does not completely inactivate at small τ_ac (triangles) values, explaining the large mean channel open times ${\overline{\tau }}_O$ in Fig. 3. Consequently, mean channel close times ${\overline{\tau }}_C$ decrease with decreasing τ_ac from 2.28 to 1.14 ms (Fig. 4 B).

Channel state distribution

The right column of Fig. 5 shows the channel state distribution as histograms. Because the IP₃R consists of four subunits with nine different subunit states each, the resulting total number of possible channel states is 9⁴ = 6561. Here, we simplify the situation by defining a state solely by its number of active ([ACT]) or inactive ([IACT]) subunits (see Fig. 1). The right side of Fig. 5 C shows the channel state distribution in terms of the number of [ACT] subunits, the left side in terms of the number of [IACT] subunits. For [Ca²⁺] = 1 μM, the average number of [ACT] states are insusceptible to noise and average numbers of [IACT] differ only slightly. Invariant open time distributions go along with a nearly constant ratio of O₃/O₄ openings (≈1.14).

It is also observed that complete channel inactivation ([IACT] > 1) occurs very rarely, leading to invariant close time distributions. In contrast, the histogram for Ca²⁺ = 10 μM shows a strong, τ_ac-dependent deviation from this pattern. The O₃/O₄ ratio varies considerably ranging from 0.67 in RDS models to 1.17 in zero noise models, explaining the skewed open time distributions. With increasing [Ca²⁺], subunit inactivation becomes more likely and we find an increased fraction of inactivated channel states ([IACT] > 1). However, noise also influences channel inactivation. While the zero noise model reveals a fraction of 5% inactivated channels, this value decreases to 1.5% for the purely diffusive noise model, and vanishes for the RDS model. The channel state distribution explains the vanishing peak in Region III of the close time distribution for decreasing Ca²⁺ noise τ_ac.

In summary, we can explain the initially observed, noise-induced alteration of mean channel open times ${\overline{\tau }}_O$, mean channel close times ${\overline{\tau }}_C$, and open probabilities P_O with a shift in the channel state distribution away from inactivated states and toward the O₄ open states.

Discussion

Our motivation to study the influence of Ca²⁺ noise on the IP₃R arose from the contemporary interest in the stochastic nature of complex Ca²⁺ signals (11,20,26,41). Just recently, Thurley et al. (13) showed that stimulus intensities of input signals are reliably encoded in stochastic sequences of random spikes, and the body of literature, emphasizing the functional relevance of noise in biological systems, is constantly growing (24,48–52).

The exact stochastic description of chemical RDS is universal and therefore, models of arbitrary complexity can be implemented in a consistent framework. However, running the model can be computationally demanding and in practice, the spatio-temporal dimensions of realistic models are limited. An alternative modeling strategy is represented by hybrid algorithms that treat nonlinear system components stochastically and bulk reactions deterministically (11,19,38,53–55). In terms of Ca²⁺ signaling, hybrid approaches explicitly ignore Ca²⁺ noise.

As noise-induced effects on nonlinear systems have received much interest over the past years (21,56), we designed a reduced, computationally feasible, fully stochastic model of a Ca²⁺ microdomain, to investigate the influence of Ca²⁺ noise on IP₃R gating dynamics.

We observed that the Ca²⁺ noise autocorrelation time τ_ac has a significant effect on mean open times, mean close times, and the open probability of the IP₃R (see Fig. 4). As shown in Fig. 3, the effect becomes apparent for [Ca²⁺] > 1 μM and mainly affects channel inactivation. This is confirmed in Fig. 5, where open and close time distributions are noise-invariant for [Ca²⁺] = 1 μM, whereas the distributions are clearly skewed for [Ca²⁺] = 10 μM. The corresponding channel state histograms emphasize that decreasing τ_ac induces a shift in the channel state distribution from [IACT] toward [ACT], decreasing channel inactivation and stabilizing channel open states. Our data shows that Ca²⁺ noise reduces the probability for subunit inactivation, which in turn increases the number of [ACT] subunit states and consequently the number of O₄ openings. At [Ca²⁺] = 10 μM, for example, the proportion of inactivating subunit state transitions was ≈0.35% for the zero noise model, ≈0.18% for the pure diffusive model, and ≈0.07% for the RDS model. Subunit inactivations are rare events compared to channel openings, but with a strong impact on the IP₃R channel state distribution. A single inactivated subunit prevents O₄ openings for a duration up to seconds, and two inactive subunits prevent the IP₃R completely from opening. Therefore, minimal changes in the channel inactivation probability lead to significant changes of mean channel open/close times and open probabilities.

Both the functionally important association of Ca²⁺ to the activating binding site and the inactivating binding site are second-order reactions. The influence of fluctuations in the educt species of simple second-order reactions has been studied analytically by Morita (57) and Katsumoto and Morita (58) in closed systems. They showed in their work that fluctuations not only alter equilibrium concentrations but also influence the dynamics of the reaction. The here used gating scheme of IP₃R subunits consists of eight interconnected, Ca²⁺-dependent second-order reactions and exponentially correlated Ca²⁺ noise (compared to uncorrelated noise in Morita and Katsumo’s work). The situation here is therefore much more complex, and a rigorous physical explanation for the observed effects would require an analytically solution of the proposed model. But an analytical solution is, to the best of our knowledge, not available at the moment. We can therefore only hypothesize about the origin of the noise-induced delay of subunit inactivation. Fig. 6 shows the distributions of the most frequent subunit states ([ACT], [IACT], [110]) as a function of [Ca²⁺], whereby the shaded curve represents the zero noise model and the solid curve a purely diffusive model (D_Ca = 200 μm² s⁻¹).

Figure 6.

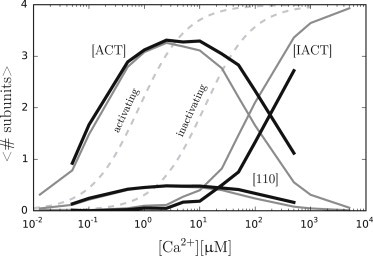
Subunit distribution of the three most frequent subunit states [ACT], [IACT], and [110] are shown as a function of [Ca²⁺]. The distributions of the zero noise model (shaded curve) and a pure diffusion model with D_Ca = 200 μm² s⁻¹ (solid curve) are shown. As a reference, isolated binding curves of the activating and inactivating binding site are shown (light-shaded dashed curves). Note that due to crucially shorter computation times, data of the zero noise model is available for a greater range of [Ca²⁺] than for the diffusive model.

It becomes clear that subunit activation and inactivation does not follow the binding curves expected from the rate constants of the respective binding sites. This shift can be attributed to the ligand-independent subunit activation transition that locks [110] subunits with a high rate. The binding curve of the activating binding site is therefore shifted to lower [Ca²⁺], while the binding curve for the inactivating binding site is shifted to higher [Ca²⁺]. This effect explains the late inactivation of channel subunits, even for the zero noise model. Ca²⁺ noise, here introduced by diffusion, clearly shifts the binding curve of the inactivating site further to higher [Ca²⁺], while leaving the binding curve of the activating binding site mainly unaffected. There are three main differences between the two Ca²⁺ binding sites that could serve as an explanation for this behavior: 1) the activating binding site has a much higher association rate than the inactivating binding site; 2) the dissociation constants of the two binding sites differ by a factor of 10; and 3) the lockable subunit [110] is a product of subunit activation, while it is an educt for subunit inactivation.

The consequent examination of the influence of these differences on the noise susceptibility of IP₃Rs would go beyond the scope of this study. However, future investigations should be directed toward this problem to gain a deeper understanding of the effect of Ca²⁺ noise on the nonlinear dynamics of the De Young and Keizer subunit transition model for IP₃Rs.

The biphasic Ca²⁺ feedback of the IP₃R is the functional basis of Ca²⁺ waves and oscillations (59). Noise-induced delay of negative Ca²⁺ feedback therefore affects the fundamental mechanism of spatiotemporal Ca²⁺ signal formation. We showed that not only diffusion, but also the presence of Ca²⁺ buffers shape the temporal properties of Ca²⁺ fluctuations and consequently IP₃R gating. The influence of Ca²⁺ buffers on Ca²⁺ signaling has previously been studied, both theoretically (54,60–62) and experimentally (63–66). These studies mainly focused on the influence of mobile and immobile buffers on global Ca²⁺ signals, whereas only a very few studies are concerned with the functional role of buffer-dependent Ca²⁺ fluctuations (26). The expression profiles for Ca²⁺ buffers with widely differing kinetic properties are highly variable among different cell types (35,46).

There is a large number of naturally occurring Ca²⁺ buffers and their dissociation constants range from only a few nM (e.g., α-Parvalbumin, K_d = 4–9 nM (35)) to up to tens of μM (e.g., α-Secretagogin, K_d = 25 μM (67)). Furthermore, there are slow (e.g., α-Parvalbumin, k⁺ = 1 × 10⁻³ μM⁻¹ ms⁻¹) and fast Ca²⁺ buffers (e.g., Calbindin-D9k, k⁺ = 1 μM⁻¹ ms⁻¹), as characterized by their Ca²⁺ association rates k⁺. Specific buffer expression profiles may therefore constitute a powerful tool that allows the cell to influence Ca²⁺ signaling on different levels, ranging from the modulation of stochastic Ca²⁺ fluctuations up to the spatiotemporal modulation of ECRE, waves, and oscillations. Another thought should be dedicated to the fact that most experimental settings include artificial Ca²⁺ buffers, either to control [Ca²⁺] or in the form of fluorescent Ca²⁺ dyes. The range of physico-chemical properties of artificial Ca²⁺ buffers adds to the complexity of the problem (68). As we have shown in this study, artificial Ca²⁺ buffers may significantly alter the properties of calcium noise and possibly, the behavior of the observed calcium microdomain.

So far, we have only investigated the noise susceptibility of the IP₃R in silico. We used the nine-state De Young-Keizer subunit state transition model as proposed by Shuai et al. (38) with parameters from Rüdiger et al. (19). In accordance with structural and mutational studies (69), the model assumes that the IP₃R consists of four identical subunits with an IP₃-binding site, an activating Ca²⁺ binding site and an inactivating Ca²⁺ binding site (70). The originally proposed eight-state De Young-Keizer model (37) was extended by a ligand-independent [ACT] state in order to account for experimental observations including channel flickering (39) and calcium-independence of the activated open state (38,71). Following other studies showing the functional relevance of noise experimentally (20,72–74), our findings await experimental verification.

For instance, an IP₃R channel incorporated into a lipid bilayer could be exposed to a defined calcium microenvironment. This setting should allow for the observation of IP₃R gating in a controlled Ca²⁺-buffer system. Statistical properties of Ca²⁺ noise and the corresponding two-time correlation function in particular could be measured with fluorescence correlation spectroscopy (75). This approach would allow to investigate experimentally the influence of both natural Ca²⁺ buffers and widely used fluorescence dyes on Ca²⁺ fluctuations and IP₃R gating. A further interesting focus for future investigations is the noise susceptibility of the ryanodine receptor, structurally closely related to the IP₃R and representing the main Ca²⁺ release channel in cardiac and striated muscle cells (76). Due to a similar biphasic Ca²⁺ dependency, a similar influence of stochastic Ca²⁺ fluctuations on the gating behavior of the ryanodine receptor is expected (77).

To understand our findings in the global context of Ca²⁺ signaling, it is necessary to extend our models to clusters of IP₃R channels, and beyond. Furthermore, it is necessary to consider Ca²⁺ flux through the channel pore, because it has been shown that the magnitude of Ca²⁺ fluctuations reveals a dependency on total buffer concentration and buffer kinetics in systems with constant Ca²⁺ influx (41). Because our model and software framework are capable of simulating both channel clusters and Ca²⁺ flux, the investigation of more complex models will be the subject of future investigations (14,15,17,36).

The spatial extent of our models is so far also limited by computational feasibility. A more efficient strategy would be the approximation of the CME by a Fokker-Planck equation or a chemical Langevin equation (78) but there are limitations to find a satisfactory approximation, namely the existence of a macroscopically infinitesimal time domain (79). An adequate approximation requires the existence of a time interval during which changes in the propensity functions are negligibly small, whereas each state transition is expected to occur sufficiently frequently (n ≫ 1). Given the model parameters used in this study, this condition is not met, mainly due to the large timescale of IP₃R subunit state transitions and the low copy number of both Ca²⁺ ions and IP₃Rs. The rarely occurring and functionally essential Ca²⁺-dependent channel inactivation constitutes the limiting factor.

Ca²⁺ microdomains are a fundamental entity of Ca²⁺-mediated cell functions (80). Morphologically predetermined structures, such as neuronal dendritic spines or the dyadic cleft of cardiac myocytes, are prominent examples for their vital roles in learning, memory (81), and heart-beat generation (82). Even though some recent work about stochastic fluctuations in the dyadic cleft exists (26), the question how such fluctuations influence the Ca²⁺ signaling apparatus as a whole, remains unanswered.

Beyond the scope of Ca²⁺ signaling, our work illustrates the important role of mesoscopic chemical noise for intracellular signaling networks. Nonlinearities such as allosteric regulation, positive and negative feedback mechanisms, and covalent modifications are ubiquitous and low-copy numbers of key molecules appear frequently. In these situations it is necessary to recognize noise as an active element within biological signaling networks.