A Kernel Machine Method for Detecting Effects of Interaction Between Multidimensional Variable Sets: An Imaging Genetics Application

Abstract

Measurements derived from neuroimaging data can serve as markers of disease and/or healthy development, are largely heritable, and have been increasingly utilized as (intermediate) phenotypes in genetic association studies. To date, imaging genetic studies have mostly focused on discovering isolated genetic effects, typically ignoring potential interactions with non-genetic variables such as disease risk factors, environmental exposures, and epigenetic markers. However, identifying significant interaction effects is critical for revealing the true relationship between genetic and phenotypic variables, and shedding light on disease mechanisms. In this paper, we present a general kernel machine based method for detecting effects of interaction between multidimensional variable sets. This method can model the joint and epistatic effect of a collection of single nucleotide polymorphisms (SNPs), accommodate multiple factors that potentially moderate genetic influences, and test for nonlinear interactions between sets of variables in a flexible framework. As a demonstration of application, we applied the method to data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) to detect the effects of the interactions between candidate Alzheimer's disease (AD) risk genes and a collection of cardiovascular disease (CVD) risk factors, on hippocampal volume measurements derived from structural brain magnetic resonance imaging (MRI) scans. Our method identified that two genes, CR1 and EPHA1, demonstrate significant interactions with CVD risk factors on hippocampal volume, suggesting that CR1 and EPHA1 may play a role in influencing AD-related neurodegeneration in the presence of CVD risks.

1 Introduction

Genetic components play a significant role in most brain-related illnesses. The discovery of genetic effects can elucidate the biological pathways and processes underlying neurological disorders, and ultimately yield prevention and treatment strategies. In the field of imaging genetics, this goal is approached by using quantitative brain image derived measurements as intermediate or endophenotypes [Biffi et al., 2010; Ge et al., 2014; Gottesman and Shields, 1972; Gottesman and Gould, 2003; Meyer-Lindenberg and Weinberger, 2006; Sabuncu et al., 2012], which are biomarkers of disease, and are believed to be closer to the disease process and have a simpler genetic architecture than clinical diagnoses.

However, heritability analyses and genome-wide association studies (GWAS) [Visscher et al., 2012] of complex genetic phenotypes ranging from human height [Yang et al., 2010], body mass index, von Willebrand factor [Yang et al., 2011], schizophrenia [Lee et al., 2012b], to various volume-, surface- or connection-based brain measurements computed from structural, functional or diffusion images [Thompson et al., 2013], indicate that phenotypic variation cannot be solely explained by genetics. The interactions between genetic and non-genetic variables such as disease risk factors, environmental exposures and epigenetic markers may play an important role in the variation of complex phenotypes [Sullivan et al., 2012], and the influence of genetic variants on the likelihood, development, and progression of a brain illness may be indirect and interactive. The presence of interactions implies that genetics can modulate the effects of various risk factors on the disease, producing variations across subjects even exposed to the same environment. Alternatively, the effect of the genotype on outcomes can depend on one or more risk factors or environmental exposures. For example, Caspi et al. [2002] reported that the effect of maltreatment of children from birth to adulthood on the development of antisocial behavior is moderated by a functional polymorphism in the MAOA gene. The genotype of a locus known as 5-HTTLPR located in the promoter region of the serotonin transporter gene was found to moderate the influence of stressful life events on depression [Caspi et al., 2003]. Therefore, identifying potential genetic interactions with non-genetic variables can be critical in understanding the true relationship between genotype and phenotype.

Thanks to recent advances in genotyping technology, it is now possible to investigate genetic interaction effects involving specific genetic risk factors, candidate genes, or even the entire genome, in unrelated individuals. Current statistical methods to test for interactions largely utilize multiple linear regression models with quantitative phenotypes, or logistic regression models with binary outcomes, in both the genetics community [Aschard et al., 2011; Kraft et al., 2007; Paré et al., 2010], and the imaging community (e.g., psychophysiological interactions analysis [Friston et al., 1997]). In these analyses, both main effects are typically univariate variables, and the interaction is modeled by their product. Although a number of recent papers have tried to improve the power of the classical univariate interaction test [Hsu et al., 2012; Mukherjee and Chatterjee, 2008; Murcray et al., 2011], they suffer from two main drawbacks when detecting interactions between genetic variants and non-genetic variables. First, converging evidence has shown that many complex brain disorders are polygenic and influenced by up to thousands of genetic variants with small effects [Purcell et al., 2009; Sullivan et al., 2012]. Analyzing each individual locus may not identify any reliable results with a small to moderate sample size, which is typical in imaging genetic studies. And second, it is now not uncommon to collect a large number of disease risk factors, environmental variables, or epigenetic markers in a single study. The product of all possible pairs of genetic variants and non-genetic variables may be dauntingly large, which dramatically increases the burden of computation and multiple testing correction. More critically, Lin et al. [2013] showed that if the main effects of a set of genetic variants are associated with the phenotype, testing each single genetic variant for interactions can be biased.

In this paper, inspired by Li and Cui [2012], we present a semiparametric kernel machine based method to detect interactions between multidimensional variable sets. Kernel machine based methods have been previously used in association studies between single nucleotide polymorphism (SNP) sets and complex diseases or imaging phenotypes [Kwee et al., 2008; Liu et al., 2007; Wu et al., 2010, 2011], and have been applied to voxel-wise genome-wide association studies to obtain boosted statistical power [Ge et al., 2012; Stein et al., 2010]. Here, to jointly model the genetic and non-genetic variables, and their interactions, we extend the original kernel machine based method, and include three appropriately selected kernels in the model; one for genetic variants, one for non-genetic variables, and a third one, which is the Hadamard product of the genetic and non-genetic kernel, for the interaction effect. The genetic kernel provides a biologically-informed way to capture epistasis in a set of SNPs and model their joint effect on the phenotype. SNP sets can be formed by SNPs located in or near a gene, within a gene pathway or a haplotype structure; risk SNPs identified by previous studies or other a priori biological information [Wu et al., 2010]. Examining the collective contribution of SNPs further opens possibilities to investigate cumulative effects of rare variants [Wu et al., 2011], and often provides improved reproducibility, biologically informed insights, and increased power relative to univariate methods. The non-genetic kernel allows for modeling the joint effect of multiple variables. By using a connection to linear mixed effects models, the interaction effect can be tested by a variance component score test [Lin, 1997; Liu et al., 2007]. The proposed method thus offers a flexible framework to account for epistatic effects, multiple non-genetic factors, and test for the overall interaction effect between sets of multidimensional variables.

As a demonstration of application, we applied the proposed method to detect the interaction effects between candidate late-onset Alzheimer's disease (AD) risk genes and cardiovascular disease (CVD) risk factors including age, gender, body mass index (BMI), hypertension, current smoking status and diabetes, on hippocampal volume derived from structural brain magnetic resonance imaging (MRI) scans, which is associated with AD risk and future AD progression [Sperling et al., 2011].

AD, the most common form of dementia, is characterized by memory loss, cognitive decline, and other symptoms. The cause and progression of AD are not well understood. As a disease that often co-occurs with AD in the elderly population, vascular pathology is among the potential factors to increase the risk of AD. In particular, increasing evidence shows that many CVD risk factors including hypertension, smoking and diabetes are associated with cognitive decline and neurodegeneration, and may increase the risk and accelerate the progression of AD [Helzner et al., 2009; Kivipelto et al., 2001; Lo et al., 2012; Luchsinger et al., 2005; Purnell et al., 2009]. For example, the neurovascular hypothesis of AD suggests that neurovascular dysfunction reduces the clearance of amyloid beta (Aβ) peptide across the blood-brain barrier, which could initiate a series of pathological processes and ultimately lead to neuronal injury and loss [Zlokovic, 2005]. Moreover, recent studies have identified that the interaction within multiple CVD risk factors, and the interaction between CVD risk factors and the apolipoprotein E (APOE) polymorphism, the largest genetic determinant of late-onset AD susceptibility, may significantly influence the risk and progression of AD [Borenstein et al., 2005; Irie et al., 2008; Purnell et al., 2009; Qiu et al., 2003]. We therefore hypothesized that genetic components play a role in the development and progression of AD in the presence of CVD risk factors and events. Testing for the interactions between AD risk genes and CVD risk factors on hippocampal volume may shed light on the underlying mechanisms of AD-related neurodegeneration, and suggest potential therapeutic treatment as many CVD risk factors are largely modifiable.

The remainder of the paper is organized as follows. In the Materials and Methods section, we present the kernel machine based method and the statistical test for interaction detection between multidimensional variable sets. Simulation studies are then introduced to evaluate the proposed method. In the Results section, simulation results, as well as our findings on the real data are shown, and compared to alternative interaction detection methods. The advantages and weaknesses of the method, and the implication of the findings, are summarized in the Discussion section. Some theoretical aspects of the kernel method and supplementary analyses are provided in Appendix.

2 Materials and Methods

2.1 Kernel methods for interaction detection

2.1.1 The model

We assume that there are N unrelated subjects under investigation. y_i, i = 1, ···, N, is a quantitative phenotype for the i-th subject, such as an image derived disease marker. We are interested in detecting the interaction between a collection of genetic variants and a set of non-genetic variables such as disease risk factors, environmental exposures, or epigenetic markers. In particular, let ${\mathit{G}}_i={[G_{i,1},\cdots ,G_{i,L}]}^{\mathsf{T}}$ denote the L SNP markers, where G_i,s, s = 1, ···, L, is the genotype coded to be the number of copies of the minor allele that the i-th subject possesses for the s-th SNP, and takes the values of 0 (homozygotic major alleles), 1 (heterozygote), and 2 (homozygotic minor alleles). Let ${\mathit{W}}_i={[W_{i,1},\cdots ,W_{i,R}]}^{\mathsf{T}}$ denote the R non-genetic variables for the i-th subject. We associate the phenotype with the genetic and non-genetic variables via the following semiparametric model:

$$y_i={\mathit{x}}_i^{\mathsf{T}}\beta +f({\mathit{G}}_i,{\mathit{W}}_i)+{∊}_i,i=1,\cdots ,N,$$ (1)

where x_i is a p × 1 vector of covariates (e.g., age, sex) for the i-th subject, β is a p × 1 vector of fixed effects, ε_i is random residual with zero-mean and homogeneous variance σ², f is an unknown function on the product domain $\mathcal{X}={\mathcal{X}}_G\otimes {\mathcal{X}}_W$, with ${\mathit{G}}_i\in {\mathcal{X}}_G$ and ${\mathit{W}}_i\in {\mathcal{X}}_W$. According to the ANOVA decomposition of functions [Gu, 2002], f can be expanded as

$$f({\mathit{G}}_i,{\mathit{W}}_i)=h_G\left({\mathit{G}}_i\right)+h_W\left({\mathit{W}}_i\right)+h_{G\times W}({\mathit{G}}_i,{\mathit{W}}_i),$$ (2)

where h_G(G_i) and h_W(W_i) are the main effects of genetics and non-genetic factors, respectively, and h_G×W (G_i, W_i) captures interactions. The overall mean of f can be absorbed into the intercept contained in x_i, and is therefore omitted here. A reproducing kernel Hilbert space (RKHS) $\mathcal{H}$ of smooth real-valued functions on $\mathcal{X}$ can be constructed [Gu and Wahba, 1993; Wahba et al., 1995]. In particular, the functional space $\mathcal{H}$ has an orthogonal decomposition:

$$\mathcal{H}={\mathcal{H}}_G\oplus {\mathcal{H}}_W\oplus {\mathcal{H}}_{G\times W},$$ (3)

where ${\mathcal{H}}_G$ and ${\mathcal{H}}_W$ are RKHSs of functions on ${\mathcal{X}}_G$ and ${\mathcal{X}}_W$, respectively, ${\mathcal{H}}_{G\times W}$ is a RKHS of functions on $\mathcal{X},\oplus$, denotes direct sum. Each component in Eq. (2) lies in the corresponding subspace in Eq. (3). Therefore, $\mathcal{H}$ is a RKHS with the associated reproducing kernel as the sum of the reproducing kernels of the three component subspaces. We assume that $\mathcal{H}$ is equipped with an inner product < ·, · > and a norm ${\Vert \cdot \Vert }_{\mathcal{H}}$.

2.1.2 Model estimation

The function $f\in \mathcal{H}$ can be estimated by minimizing the penalized squared-error loss function of model (1):

$$\mathcal{L}(\mathit{y},\beta ,f)=\frac{1}{2}\sum _{i=1}^N{[y_i-{\mathit{x}}_i^{\mathsf{T}}\beta -f({\mathit{G}}_i,{\mathit{W}}_i)]}^2+\frac{\lambda }{2}\mathcal{J}\left(f\right),$$ (4)

where $\mathcal{J}(\cdot )={\Vert \cdot \Vert }_{\mathcal{H}}^2$ is a roughness penalty, and λ is a tuning parameter. Since the entire functional space $\mathcal{H}$ has the orthogonal decomposition (3), the penalty function $\mathcal{J}(\cdot )$ can be decomposed accordingly, and Eq. (4) can be more explicitly written as

$$\mathcal{L}(\mathit{y},\beta ,f)=\frac{1}{2}\sum _{i=1}^N{[y_i-{\mathit{x}}_i^{\mathsf{T}}\beta -h_G\left({\mathit{G}}_i\right)-h_W\left({\mathit{W}}_i\right)-h_{G\times W}({\mathit{G}}_i,{\mathit{W}}_i)]}^2+\frac{{\lambda }_G}{2}{\Vert h_G\Vert }_{{\mathcal{H}}_G}^2+\frac{{\lambda }_W}{2}{\Vert h_W\Vert }_{{\mathcal{H}}_W}^2+\frac{{\lambda }_{G\times W}}{2}{\Vert h_{G\times W}\Vert }_{{\mathcal{H}}_{G\times W}}^2=\frac{1}{2}{(\mathit{y}-\mathit{X}\beta -{\mathit{h}}_G-{\mathit{h}}_W-{\mathit{h}}_{G\times W})}^{\mathsf{T}}(\mathit{y}-\mathit{X}\beta -{\mathit{h}}_G-{\mathit{h}}_W-{\mathit{h}}_{G\times W})+\frac{{\lambda }_G}{2}{\Vert h_G\Vert }_{{\mathcal{H}}_G}^2+\frac{{\lambda }_W}{2}{\Vert h_W\Vert }_{{\mathcal{H}}_W}^2+\frac{\lambda {\zeta }_{G\times W}}{2}{\Vert h_{G\times W}\Vert }_{{\mathcal{H}}_{G\times W}}^2,$$ (5)

where $\mathit{y}={[y_1,\cdots ,y_N]}^{\mathsf{T}}$, $\mathit{X}={[{\mathit{x}}_1,\cdots ,{\mathit{x}}_N]}^{\mathsf{T}}$, ${\mathit{h}}_G={[h_G\left({\mathit{G}}_1\right),\cdots ,h_G\left({\mathit{G}}_N\right)]}^{\mathsf{T}}$, ${\mathit{h}}_W={[h_W\left({\mathit{W}}_1\right),\cdots ,h_W\left({\mathit{W}}_N\right)]}^{\mathsf{T}}$, ${\mathit{h}}_{G\times W}={[h_{G\times W}({\mathit{G}}_1,{\mathit{W}}_1),\cdots ,h_{G\times W}({\mathit{G}}_N,{\mathit{W}}_N)]}^{\mathsf{T}}$, λ_G, λ_W, and λ_G×W are positive smoothing parameters that balance the goodness of fit and complexity of the model.

By the representer theorem [Kimeldorf and Wahba, 1971; Wahba, 1990], the functions h_G, h_W and h_G×W that minimize the functional (5) take the forms

$$\begin{array}{cc}\hfill h_G\left({\mathit{G}}^{\ast }\right)=& \sum _{j=1}^N{\alpha }_{G,j}{k}_G({\mathit{G}}^{\ast },{\mathit{G}}_j),\hfill \\ \hfill h_W\left({\mathit{W}}^{\ast }\right)=& \sum _{j=1}^N{\alpha }_{W,j}{k}_W({\mathit{W}}^{\ast },{\mathit{W}}_j),\hfill \\ \hfill h_{G\times W}({\mathit{G}}^{\ast },{\mathit{W}}^{\ast })=& \sum _{j=1}^N{\alpha }_{G\times W.j}{k}_{G\times W}(({\mathit{G}}^{\ast },{\mathit{W}}^{\ast }),({\mathit{G}}_j,{\mathit{W}}_j)),\hfill \end{array}$$ (6)

for arbitrary G* and W*, where α_G,j, α_W,j and α_G×W,j, j = 1, 2, ···, N, are unknown coefficients, k_G, k_W and k_G×W are reproducing kernel functions of the Hilbert spaces ${\mathcal{H}}_G$, ${\mathcal{H}}_W$ and ${\mathcal{H}}_{G\times W}$, respectively. Since the reproducing kernel of a tensor product of two RKHSs is the product of the two reproducing kernels [Aronszajn, 1950], the kernel function k_G×W is connected to the kernel functions k_G and k_W by

$$k_{G\times W}(({\mathit{G}}^{\ast },\mathit{W}),({\mathit{G}}_j,{\mathit{W}}_j))=k_G({\mathit{G}}^{\ast },{\mathit{G}}_j)\cdot k_W({\mathit{W}}^{\ast },{\mathit{W}}_j).$$ (7)

Define the N×N symmetric kernel matrices K_G = {k_G(G_i, G_j)}, K_W = {k_W (W_i, W_j)} and ${\mathit{K}}_{G\times W}=\left\{k_{G\times W}(({\mathit{G}}_i,{\mathit{W}}_i),({\mathit{G}}_j,{\mathit{W}}_j))\right\}={\mathit{K}}_G\odot {\mathit{K}}_W$, where $\odot$ is the Hadamard product (element-wise product) of two matrices. Then

$${\mathit{h}}_G={\mathit{K}}_G{\alpha }_G,{\mathit{h}}_W={\mathit{K}}_W{\alpha }_W,{\mathit{h}}_{G\times W}={\mathit{K}}_{G\times W}{\alpha }_{G\times W},$$ (8)

where ${\alpha }_G={[{\alpha }_{G,1},\cdots ,{\alpha }_{G,N}]}^{\mathsf{T}}$, ${\alpha }_W={[{\alpha }_{W,1},\cdots ,{\alpha }_{W,N}]}^{\mathsf{T}}$ and ${\alpha }_{G\times W}={[{\alpha }_{G\times W,1},\cdots ,{\alpha }_{G\times W,N}]}^{\mathsf{T}}$. Substituting h_G, h_W and h_G×W into Eq. (5), and making use of the reproducing kernel property, we obtain

$$\mathcal{L}(\mathit{y},\beta ,{\alpha }_G,{\alpha }_W,{\alpha }_{G\times W})=\frac{1}{2}{∊}^{\mathsf{T}}∊+\frac{{\lambda }_G}{2}{\alpha }_G^{\mathsf{T}}{\mathit{K}}_G{\alpha }_G+\frac{{\lambda }_W}{2}{\alpha }_W^{\mathsf{T}}{\mathit{K}}_W\times {\alpha }_W+\frac{{\lambda }_{G\times W}}{2}{\alpha }_{G\times W}^{\mathsf{T}}{\mathit{K}}_{G\times W}{\alpha }_{G\times W},$$ (9)

where ε = y – Xβ – K_Gα_G – K_Wα_W – K_G×Wα_G×W.

The gradients of $\mathcal{L}$ with respect to the parametric coefficients β and nonparametric coefficients α_G, α_W and α_G×W are

$$\begin{array}{cc}\hfill \frac{\partial \mathcal{L}}{\partial \beta }=-{\mathit{X}}^{\mathsf{T}}∊,& \frac{\partial \mathcal{L}}{\partial {\alpha }_G}=-{\mathit{K}}_G^{\mathsf{T}}∊+{\lambda }_G{\mathit{K}}_G{\alpha }_G,\hfill \\ \hfill \frac{\partial \mathcal{L}}{\partial {\alpha }_W}=-{\mathit{K}}_W^{\mathsf{T}}∊+{\lambda }_W{\mathit{K}}_W{\alpha }_W,& \frac{\partial \mathcal{L}}{\partial {\alpha }_{G\times W}}=-{\mathit{K}}_{G\times W}^{\mathsf{T}}∊+{\lambda }_{G\times W}{\mathit{K}}_{G\times W}{\alpha }_{G\times W}.\hfill \end{array}$$ (10)

Therefore, setting the gradients to zero, this first-order condition is given by the linear system:

$$\left[\begin{array}{cccc}\hfill {\mathit{X}}^{\mathsf{T}}\mathit{X}\hfill & \hfill {\mathit{X}}^{\mathsf{T}}{\mathit{K}}_G\hfill & \hfill {\mathit{X}}^{\mathsf{T}}{\mathit{K}}_W\hfill & \hfill {\mathit{X}}^{\mathsf{T}}{\mathit{K}}_{G\times W}\hfill \\ \hfill {\mathit{K}}_G^{\mathsf{T}}\mathit{X}\hfill & \hfill {\mathit{K}}_G^{\mathsf{T}}{\mathit{K}}_G+{\lambda }_G{\mathit{K}}_G\hfill & \hfill {\mathit{K}}_G^{\mathsf{T}}{\mathit{K}}_W\hfill & \hfill {\mathit{K}}_G^{\mathsf{T}}{\mathit{K}}_{G\times W}\hfill \\ \hfill {\mathit{K}}_W^{\mathsf{T}}\mathit{X}\hfill & \hfill {\mathit{K}}_W^{\mathsf{T}}{\mathit{K}}_G\hfill & \hfill {\mathit{K}}_W^{\mathsf{T}}{\mathit{K}}_W+{\lambda }_W{\mathit{K}}_W\hfill & \hfill {\mathit{K}}_W^{\mathsf{T}}{\mathit{K}}_{G\times W}\hfill \\ \hfill {\mathit{K}}_{G\times W}^{\mathsf{T}}\mathit{X}\hfill & \hfill {{\mathit{K}}_{G\times W}^{\mathsf{T}}}_G\hfill & \hfill {\mathit{K}}_{G\times W}^{\mathsf{T}}{\mathit{K}}_W\hfill & \hfill {\mathit{K}}_{G\times W}^{\mathsf{T}}{\mathit{K}}_{G\times W}+{\lambda }_{G\times W}{\mathit{K}}_{G\times W}\hfill \end{array}\right]\zeta \left[\zeta \begin{array}{c}\hfill \beta \hfill \\ \hfill {\alpha }_G\hfill \\ \hfill {\alpha }_W\hfill \\ \hfill {\alpha }_{G\times W}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathit{X}}^{\mathsf{T}}\mathit{y}\hfill \\ \hfill {\mathit{K}}_G^{\mathsf{T}}\mathit{y}\hfill \\ \hfill {\mathit{K}}_W^{\mathsf{T}}\mathit{y}\hfill \\ \hfill {\mathit{K}}_{G\times W}^{\mathsf{T}}\mathit{y}\hfill \end{array}\right].$$ (11)

Liu et al. [2007] showed that this first-order linear system is equivalent to the normal equation of the linear mixed effects model

$$\mathit{y}=\mathit{X}\beta +{\mathit{h}}_G+{\mathit{h}}_W+{\mathit{h}}_{G\times W}+∊,$$ (12)

where β is a coefficient vector of fixed effects, h_G, h_W and h_G×W are independent random effects, and distributed as ${\mathit{h}}_G\sim \mathrm{N}(0,{\tau }_G^2{\mathit{K}}_G)$, ${\tau }_G^2={\lambda }_G^{-1}{\sigma }^2$, ${\mathit{h}}_W\sim \mathrm{N}(0,{\tau }_W^2{\mathit{K}}_W)$, ${\mathit{h}}_W\sim \mathrm{N}(0,{\tau }_W^2{\mathit{K}}_W)$, ${\tau }_W^2={\lambda }_W^{-1}{\sigma }^2$, ${\mathit{h}}_{G\times W}\sim \mathrm{N}(0,{\tau }_{G\times W}^2{\mathit{K}}_{G\times W})$, ${\tau }_{G\times W}^2={\lambda }_{G\times W}^{-1}{\sigma }^2$, ε is independent of random effects and follows ε ~ N(0, σ²I), and I is an identity matrix. This connection indicates that the fixed effects β, and the random effects h_G, h_W and h_G×W, obtained by minimizing the loss function in Eq. (4), are equivalent to the best linear unbiased predictors (BLUPs) of the linear mixed effects model (12). The variance components ${\tau }_G^2$, ${\tau }_W^2$, ${\tau }_{G\times W}^2$ and σ² can be estimated via the restricted maximum likelihood (ReML) approach [Harville, 1977; Lindstrom and Bates, 1988] (see Appendix A for details), and the estimates of random effects ĥ_G, ĥ_W, ĥ_G×W can be obtained by solving the linear system (11) and inserting the $\widehat{\alpha }$ estimates into Eq. (8).

2.1.3 Selection of kernels

There are a variety of choices for the kernel functions to characterize the similarity between subjects with respect to the genetic variants and non-genetic factors, as long as they are nonnegative definite [Schaid, 2010a,b]. Possible candidates are the linear kernel, the polynomial kernel, the Euclidean distance (ED) kernel, the Gaussian kernel, and the identity-by-state (IBS) kernel [Kwee et al., 2008].

Here we use the IBS kernel for the genetic effect. The IBS kernel measures the similarity of the genotypes between the i-th and j-th subject by

$$k_G({\mathit{G}}_i,{\mathit{G}}_j)=\frac{1}{2L}\sum _{s=1}^L(2-\mid G_{i,s}-G_{j,s}\mid ),$$ (13)

where L is the number of SNP markers to be combined. The IBS kernel is a nonparametric function of the genotypes, as it does not depend on the selection of basis or any assumption on the types of genetic interaction. Therefore, in principle, it can capture any epistatic effect between genetic variants and their nonlinear influences on the phenotypes.

We propose the linear kernel to combine multiple non-genetic factors. The linear kernel can be represented as

$$k_W({\mathit{W}}_i,{\mathit{W}}_j)=\frac{1}{R}\langle {\mathit{W}}_i,{\mathit{W}}_j\rangle =\frac{1}{R}\sum _{s=1}^R{W}_{i,s}{W}_{j,s},$$ (14)

where R is the number of non-genetic factors under investigation. We evaluate the performance of the two kernels by simulation studies.

2.1.4 Score test

We note, from the linear mixed effects model representation (12), that testing an overall genetic and non-genetic effect ${\mathcal{H}}_0:h_G(\cdot )=h_W(\cdot )=h_{G\times W}(\cdot )=0$ is equivalent to testing the variance components: ${\mathcal{H}}_0:{\tau }_G^2={\tau }_W^2={\tau }_{G\times W}^2=0$. To address the issue that, under the null hypothesis, the parameters ${\tau }_G^2$, ${\tau }_W^2$, and ${\tau }_{G\times W}^2$ are on the boundary of the parameter space, Liu et al. [2007] proposed a score test based on the ReML. In particular, let K = K_G + K_W + K_G×W, and the score test statistic is defined as:

$$\mathcal{S}\left({\sigma }_0^2\right)=\frac{1}{2{\sigma }_0^2}{\left(\mathit{y}-\mathit{X}{\widehat{\beta }}_0\right)}^{\mathsf{T}}\mathit{K}\left(\mathit{y}-\mathit{X}{\widehat{\beta }}_0\right)=\frac{1}{2{\sigma }_0^2}{\mathit{y}}^{\mathsf{T}}{\mathit{P}}_0\mathit{K}{\mathit{P}}_0\mathit{y},$$ (15)

where ${\widehat{\beta }}_0$ is the maximum likelihood estimate (MLE) of the regression coefficients under the null model y = Xβ₀ + ε₀, ${\sigma }_0^2$ is the variance of ε₀, ${\mathit{P}}_0=\mathit{I}-\mathit{X}{\left({\mathit{X}}^{\mathsf{T}}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{T}}$ is the projection matrix under the null. $\mathcal{S}\left({\sigma }_0^2\right)$ is a quadratic function of y and follows a mixture of chi-squares under the null. We use the Satterthwaite method to approximate the distribution of $\mathcal{S}\left({\sigma }_0^2\right)$ by a scaled chi-square distribution $\kappa {\chi }_{\nu }^2$. In practice, the unknown value of the model parameter ${\sigma }_0^2$ in $\mathcal{S}$ is replaced by its ReML estimate ${\widehat{\sigma }}_0^2$ under the null model. To account for this substitution, the fitted scale parameter κ and the degrees of freedom ν are adjusted, giving $\widehat{\kappa }$ and $\widehat{\nu }$ (see Appendix B for details). The p-value of an observed score statistic $\mathcal{S}\left({\widehat{\sigma }}_0^2\right)$ is then computed using the scaled chi-square distribution $\widehat{\kappa }{\chi }_{\widehat{\nu }}^2$.

To test the interaction effect, we notice that testing the null hypothesis ${\mathcal{H}}_0^I:h_{G\times W}(\cdot )=0$ is equivalent to testing the variance component: ${\mathcal{H}}_0^I:{\tau }_{G\times W}^2=0$. Let $\Sigma ={\tau }_G^2{\mathit{K}}_G+{\tau }_W^2{\mathit{K}}_W+{\sigma }^2\mathit{I}$, where ${\tau }_G^2$, ${\tau }_W^2$, and σ² are model parameters under the null model y = Xβ + h_G + h_W + ε. We follow Li and Cui [2012] and design a score test statistic

$${\mathcal{S}}_I({\tau }_G^2,{\tau }_W^2,{\sigma }^2)=\frac{1}{2}{\mathit{y}}^{\mathsf{T}}{\mathit{P}}_I{\mathit{K}}_{G\times W}{\mathit{P}}_I\mathit{y},$$ (16)

where ${\mathit{P}}_I={\Sigma }^{-1}-{\Sigma }^{-1}\mathit{X}{\left({\mathit{X}}^{\mathsf{T}}{\Sigma }^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{T}}{\Sigma }^{-1}$ is the projection matrix under the null hypothesis ${\mathcal{H}}_0^I$. Analogously, the Satterthwaite method is used to approximate the distribution of ${\mathcal{S}}_I$ by a scaled chi-square distribution ${\kappa }_I{\chi }_{{\nu }_I}^2$. In practice, the unknown model parameters ${\tau }_G^2$, ${\tau }_W^2$ and σ² in ${\mathcal{S}}_I$ are replaced by their ReML estimates ${\widehat{\tau }}_G^2$, ${\widehat{\tau }}_W^2$ and ${\widehat{\sigma }}^2$ under the null model. The fitted scale parameter κ_I and the degrees of freedom ν_I are adjusted to account for this substitution, giving ${\widehat{\kappa }}_I$ and ${\widehat{\nu }}_I$ (see Appendix B for details). The p-value of an observed score statistic ${\mathcal{S}}_I({\widehat{\tau }}_G^2,{\widehat{\tau }}_W^2,{\widehat{\sigma }}^2)$ is then computed using the scaled chi-square distribution ${\widehat{\kappa }}_I{\chi }_{{\widehat{\nu }}_I}^2$.

2.2 The ADNI data

Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California – San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older subjects, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

2.2.1 Data preprocessing and SNP grouping

All ADNI-1 1.5T structural brain MRI scans were processed using FreeSurfer (freesurfer.nmr.mgh.harvard.edu) [Dale et al., 1999; Fischl, 2012; Fischl et al., 1999], version 4.3. Subject specific intra-cranial volume (ICV) and bilateral hippocampal volumes were automatically computed by FreeSurfer, after skull stripping, B1 bias field correction, segmentation and labeling [Fischl et al., 2002, 2004], and passed rigorous visual quality control checks. For more details regarding the imaging processing and quality control, we refer the reader to the official website of ADNI (http://adni.loni.usc.edu).

CVD risk factors considered in the present study included age, gender, body mass index (BMI), systolic blood pressure, current smoking status and diabetes. A CVD risk score summarizing these six risk factors can be calculated using the non-laboratory, office-based cardiovascular risk profile prediction function from the Framingham Heart Study (FHS) [D'Agostino et al., 2008]. The score can be treated as a continuous variable, and higher values indicate higher risks of developing individual CVD events. We use the FHS risk score as a benchmark variable to compare the results obtained with the proposed multivariate method.

We followed the ENIGMA2 1KGP cookbook (v3) (The Enhancing Neuroimaging Genetics through Meta-Analysis (ENIGMA) consortium, http://enigma.loni.ucla.edu/wp-content/uploads/2012/07/ENIGMA2_1KGP_cookbook_v3.doc, version July 27, 2012), developed by the ENIGMA2 Genetics support team, to preprocess and impute the ADNI genome-wide SNP data. In brief, we used PLINK [Purcell et al., 2007] for preprocessing and quality control, which included sex discrepancy check, removing subjects with low genotype call rate (< 95%), and filtering individual markers that contained an ambiguous strand assignment and that did not satisfy the following quality control criteria: genotype call rate ≥ 95%, minor allele frequency (MAF) ≥ 1%, and Hardy-Weinberg equilibrium p ≥ 1 × 10^–6. We then used the MaCH software [Li et al., 2010] to impute ungenotyped SNPs based on the 1,000 genomes reference [1000 Genomes Project Consortium, 2012]. 697 subjects (cognitive normal controls N = 203, subjects with mild cognitive impairment N = 334, and AD patients N = 160) that have complete imaging and genetic data, and CVD risk factors, were included in the following analyses. Among the 334 subjects with mild cognitive impairment (MCI), 183 subjects were stable and did not convert to AD throughout the follow-up, and 151 subjects progressed to AD in at least one of the follow-up visits.

In addition to APOE, the major genetic risk factor for late-onset AD, a recent two-stage meta-analysis of GWAS with 74,046 individuals identified 20 susceptibility loci for late-onset AD [Lambert et al., 2013]. A very recent article suggested that the REST gene may play a critical role in normal aging in human cortical and hippocampal neurons, and may distinguish neuroprotection from neurodegeneration [Lu et al., 2014]. We therefore used these 21 genes as our candidate gene set and extracted all the SNPs on the coding regions as well as 20kb up/downstream of each of these genes in the ADNI data set. Some of these genes, e.g., BIN1, CR1 and PICALM, have been associated with quantitative imaging phenotypes, such as hippocampal volume, amygdala volume and entorhinal cortical thickness, in ADNI [Biffi et al., 2010; Bralten et al., 2011; Furney et al., 2010; Weiner et al., 2013]. Table 1 lists the 21 genes and the final number of SNPs located on them after preprocessing and quality control.

Table 1.

A list of 21 candidate risk genes for late-onset Alzheimer's disease and the final number of SNPs located on and near them.

Chr	Gene	SNP num	Chr	Gene	SNP num
19	ABCA7	240	6	HLA-DRB5	62
2	BIN1	301	2	INPP5D	495
20	CASS4	165	5	MEF2C	272
6	CD2AP	421	11	MS4A6A	63
19	CD33	85	11	PICALM	360
11	CELF1	97	8	PTK2B	419
8	CLU	116	4	REST	146
1	CR1	264	14	SLC24A4	716
18	DSG2	219	11	SORL1	233
7	EPHA1	115	7	ZCWPW1	74
14	FERMT2	242

2.3 Alternative methods

No standard method exists in the literature that can detect interactions between a collection of SNPs and a set of non-genetic variables such as CVD risk factors. Below in both simulation studies and real data analysis, we consider alternative methods based on burden tests and principal component analysis (PCA) that can summarize multiple variables into a single regressor and convert the problem into standard multiple regression analyses.

Burden tests collapse a set of variants in a genetic region into a single burden variable. They can be powerful when most variants in a region are causal and the effects are in the same direction, but suffer from dramatic power loss when these assumptions are violated [Lee et al., 2012a]. Different variants of burden tests have been proposed and are mainly aimed at rare variant association tests. Here we adapt two methods to our context: (1) the rare variant test (RVT), proposed by Morris and Zeggini [2010], which calculates the proportion of minor alleles in the set of genetic variants for each subject as the burden regressor, and (2) the weighted sum test (WST) [Madsen and Browning, 2009], which calculates a genetic score as the burden variable. The genetic score is a weighted average of the count of minor alleles for each subject. Specifically, if G_i,s ∈ {0, 1, 2} is the count of minor alleles in genetic variant s for the i-th subject, then the genetic score is ${\gamma }_i={\sum }_{s=1}^L{G}_{i,s}∕w_s$, where L is the number of SNP markers, $w_s=\sqrt{N_s{q}_s(1-q_s)}$ is the weight, in which q_s = (m_s + 1)/(2N_s + 2), N_s is the total number of subjects genotyped for variant s, and m_s is the number of minor alleles observed for variant s. Many other burden tests are similar to these two methods. We note that the underlying assumptions of these collapsing methods are that the interactions have similar effect sizes and the same direction for all the genetic variants being collapsed. The tests can be biased or have inflated type I error if these assumptions are violated.

For the second alternative method, we perform PCA on the set of SNP regressors or CVD risk factors to extract the first principal component that explains the largest possible variance of the original regressors.

After reducing the dimension of the SNP set and the CVD risk factors, we can carry out a standard multiple regression analysis, in which the interaction effect between the derived univariate SNP regressor and the CVD risk factor is modeled by their product.

2.4 Simulation studies

We conducted simulation studies to evaluate the performance of the ReML algorithm and the accuracy of the score tests. The simulation was based on real ADNI demographic information, genetic data and CVD risk factors with N = 697 subjects, in order to best mimic the situation of our real data application. To synthesize quantitative phenotypes, we employed the following model:

$$y_i={\mathit{x}}_i^{\mathsf{T}}\beta +{\alpha }_M[h_G\left({\mathit{G}}_i\right)+h_W\left({\mathit{W}}_i\right)]+{\alpha }_I{h}_{G\times W}({\mathit{G}}_i,{\mathit{W}}_i)+\sigma {∊}_i,$$ (17)

where x_i is a vector comprising an intercept, the ICV, and the education (in years) of the i-th subject, β is a vector of all ones, ε_i is a Gaussian distributed random error with zero mean and unit variance, σ is the standard deviation of the error and was set to 5 in our simulation studies. α_M and α_I are two free parameters. We followed Liu et al. [2007] and designed the function h_G to have the following complex form:

$$h_G\left({\mathit{G}}_i\right)=2\cos \left(G_{i,1}\right)-3G_{i,2}^2+2{\mathrm{e}}^{G_{i,3}}{G}_{i,4}-1.6\sin \left(G_{i,5}\right)\cos \left(G_{i,3}\right)+4G_{i,1}{G}_{i,5}.$$ (18)

The main non-genetic effect was designed as h_W(W_i) = W_i,1 + W_i,2. Finally, we introduced a linear interaction effect between the genetic variants and CVD risk factors: h_G×W(G_i, W_i) = 3h_G(G_i)h_W(W_i).

Since previous work has performed extensive simulations to characterize the overall score test for the semiparametric model [Hua and Ghosh, 2014; Liu et al., 2007], we focused our simulations on testing for the interaction effect. Our major concern is to assess whether the main effects “bleed” into the interaction, yielding false positives, or “cloud” the interaction, reducing sensitivity.

In the first simulation study, we generated data under different values of α_M and α_I to evaluate the performance of the score tests. Specifically, when α_M = α_I = 0, both main and interaction effects vanish, and we studied the false positive rate of the score test for overall effect. When α_M > 0 and α_I = 0, there are main effects but no interaction, and we therefore assessed the power of the overall score test, and the false positive control of the score test for interaction effect. We also set α_M and α_I at a number of different values to test the power of both score tests in different situations. 1,000 simulations were performed for each setting. For each run, we randomly picked a gene from Table 1 and randomly selected five adjacent SNPs on the gene, reflecting the linkage disequilibrium (LD) between genetic markers, and randomly selected two variables from the six CVD risk factors (age, gender, BMI, systolic blood pressure, smoking and diabetes). The phenotypic data were then generated using the five SNPs and two CVD risk variables following Eq. (17). We note that for all the genes the signal only comes from a very small proportion of the SNPs. Likewise, only part of the CVD risk factors were used in producing the phenotypic data.

We then evaluated the performance of the kernel method. As a comparison, we summarized genetic variants and CVD risk factors into a single regressor respectively using different collapsing methods (for genetic data: PCA, RVT and WST; for CVD risk factors: PCA and the FHS risk score¹), and conducted standard univariate interaction tests between all possible combinations of these univariate genetic and CVD risk variables, which amounted to six multiple regression analyses.

In the second simulation study, we fixed α_M = 1, and for each run α_I was assigned a random number uniformly distributed on [0, 1] with a probability of 0.5, and was fixed at 0 otherwise. We then generated data following the same approach described above, and compared the Receiver Operating Characteristic (ROC) curves of the kernel method and alternative methods for interaction detection.

2.5 Real data application

As a sanity check, we started with some standard regression analyses of real data from ADNI. Specifically, we tested the association between hippocampal volume (averaged between two hemispheres) and APOE-ε4 status (carriers vs. non-carriers), after controlling for ICV, age, gender and education. We conducted multiple regression analyses to assess the main effects of the FHS CVD risk score and each CVD risk factor, and their interaction effects with APOE-ε4 status on hippocampal volume, after properly controlling for covariates. Using logistic regression, we also analyzed the association between diagnosis (AD patients vs. cognitive normal controls) and the FHS CVD risk score and each CVD risk factor.

We then applied the kernel method to detect interaction effects between each of the 21 candidate AD risk genes listed in Table 1, and the collection of six CVD risk factors, on hippocampal volume. ICV and education were included in the model as covariates. The IBS kernel was used to combine SNPs located on and near each gene, and a linear kernel was used for the CVD risk factors. All CVD risk factors were standardized (subtracting the mean and devided by the standard deviation) to transform variables measured with different units onto the same scale. Bonferroni correction was used to control the family-wise error (FWE) rate, and a gene was identified to have a significant interaction with the CVD risk factors if the p-value was smaller than 0.05/21 ≈ 2.38 × 10^–3. Analogous to the simulation studies, we compared the proposed kernel machine based method to six univariate interaction tests based on different dimension reduction methods.

In order to reveal the direction of a significant interaction effect, we collapsed genetic variables and CVD risk factors into scalar variables; the RVT burden variable and the FHS risk score, respectively, and defined four regimes, low genetic risk and low CVD risk, high genetic risk and low CVD risk, low genetic risk and high CVD risk, high genetic risk and high CVD risk, by splitting the data with respect to the medians of the RVT burden variable and the FHS risk score. We then averaged the estimated interaction effect ĥ_G×W within each of the four regimes. A smaller average indicates a higher risk of the interaction effect (smaller hippocampal volume). Jackknife resampling was used to get accurate standard error estimates of these average statistics. We also compared ĥ_G×W between the 183 stable MCI subjects (who remained MCI throughout the follow-up) and the 151 MCI subjects that progressed to AD to investigate the predictive power of the interaction effect on disease progression.

3 Results

3.1 Simulation results

Table 2 shows the simulation results for the overall and interaction score tests. Here we used a nominal p-value threshold of 0.05. In more than 99% of the situations, the ReML algorithm converged within 50 iterations (convergence was declared when the difference between successive log ReML likelihoods was smaller than 10^–4), the maximum number of iterations we set in this simulation study, and in most cases it converged very quickly within 10 iterations and a few seconds with a MATLAB implementation on a MacBook Pro with 8GB of memory and a 2.4 GHz Intel Core i7 processor.

Table 2.

Simulation results of the overall and interaction score tests, and the alternative methods for interaction detection based on dimension reduction and multiple regression. Nominal p-value threshold was set to 0.05. The first row corresponds to simulating the null hypothesis for both the overall and interaction effects. The second and third rows correspond to the null hypothesis of the interaction effect only. Thus, corresponding detection rates in the first three rows are desired to be below the p-value threshold of 0.05. PCg: first principal component of the genetic data; PCw: first principal component of the cardiovascular disease risk factors; RVT: rare variant test burden variable; WST: weighted sum test burden variable; FHS: the Framingham Heart Study vascular disease risk score.

	Kernel method		Alternative methods
(αM, αI)	Overall	Interaction	PCg × FHS	PCg × PCw	RVT × FHS	RVT × PCw	WST × FHS	WST × PCw
(0, 0)	0.048	—	0.051	0.043	0.051	0.040	0.049	0.038
(0.5, 0)	0.908	0.046	0.061	0.046	0.063	0.043	0.062	0.054
(1, 0)	1.000	0.051	0.052	0.052	0.068	0.049	0.061	0.052
(0, 0.5)	0.961	0.918	0.622	0.499	0.578	0.444	0.572	0.455
(0,1)	0.983	0.950	0.681	0.546	0.620	0.508	0.631	0.505
(1, 0.1)	0.999	0.585	0.292	0.242	0.229	0.204	0.226	0.216
(1, 0.25)	0.995	0.865	0.506	0.405	0.432	0.324	0.433	0.325
(1, 0.5)	0.997	0.926	0.591	0.481	0.542	0.413	0.536	0.425
(0.1, 1)	0.984	0.951	0.681	0.529	0.622	0.478	0.610	0.476
(0. 25, 1)	0.986	0.944	0.665	0.521	0.600	0.459	0.601	0.469
(0.5, 1)	0.983	0.951	0.654	0.517	0.612	0.472	0.587	0.446
(0.5, 0. 5)	0.984	0.918	0.625	0.488	0.587	0.423	0.575	0.431
(1, 1)	0.994	0.958	0.660	0.527	0.629	0.488	0.620	0.489

It can be seen that when α_M = α_I = 0, the size of the overall score test is close to the nominal p-value threshold of 0.05. When α_M > 0 and α_I = 0, the false positive rate of the score test for interaction effect is also well controlled. When α_I > 0, the power of the interaction test quickly exceeds 0.90. In contrast, we observe that dimension reduction methods can have slightly inflated false positive rates and are dramatically under-powered when compared to the kernel machine based method.

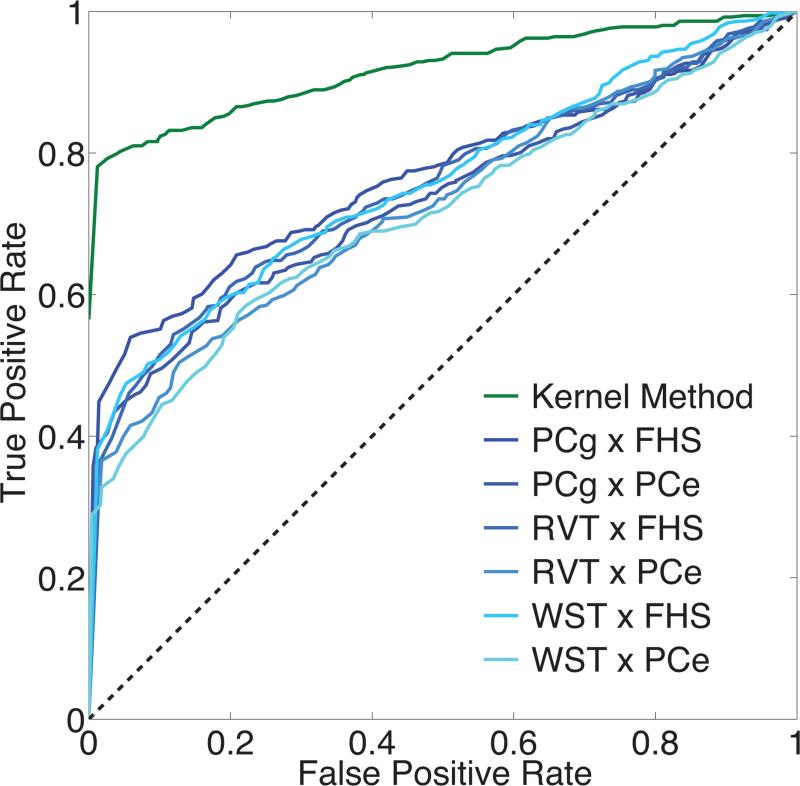
Fig. 1 shows the ROC curves of the kernel method and alternative methods for interaction detection, obtained with the second simulation data. The power gain of the kernel method relative to the alternative methods is evident.

Figure 1.

Receiver operating characteristic (ROC) curves of the kernel method and alternative methods for interaction detection in the simulated data. False positive rates are plotted against true positive rates with the p-value threshold varying between 0 and 1 with a step size of 0.01.

3.2 Application to ADNI data

APOE-ε4 status is significantly associated with hippocampal volume (p = 3.97 × 10^–16), after controlling for ICV, age, gender and education. Table 3 shows the main effects of the CVD risk factors, and their interaction effects with APOE-ε4 status on hippocampal volume obtained by conventional interaction analyses, as well as the association between diagnosis (AD patients vs. cognitive normal controls) and each CVD risk factor obtained by logistic regression analyses. As expected, the association between age and hippocampal volume is highly significant, indicating the reduction in the size of the hippocampus over time. The FHS CVD risk score is also significantly associated with hippocampal volume. Specifically, higher CVD risk scores suggest smaller hippocampal volumes. Age also shows a suggestive significant interaction with APOE-ε4 status but did not survive a Bonferroni correction for the total number of statistical tests performed here.

Table 3.

Results of standard regression analyses with two different outcomes: hippocampal volume and Alzheimer's disease (AD) diagnosis (AD vs. control). The p-values for the main effects of the Framingham Heart Study (FHS) cardiovascular disease (CVD) risk score and each CVD risk factor, and their interaction effects with APOE-ε4 status on hippocampal volume obtained by conventional interaction analyses are presented. The p-values for the association between diagnosis (AD patients vs. cognitive normal controls) and each CVD risk factor obtained by logistic regression analyses are shown. Significant associations, with Bonferroni corrected p-values smaller than 0.05, are highlighted in bold.

Risk factor	Covariates adjusted	Hippocampal volume (linear regression)		AD vs. control (logistic regression)
		Main effect	Interaction with APOE-ε4
FHS risk score	ICV, Edu a	5.12 × 10–4	0.132	0.761
Age	ICV, Edu, Gender	3.99 × 10–18	4.03 × 10–3	0.301
Gender	ICV, Edu, Age	0.103	0.982	0.467
Body mass index (BMI)	ICV, Edu, Age, Gender	2.37 × 10–3	0.227	0.011
Systolic blood pressure	ICV, Edu, Age, Gender	0.832	0.591	0.077
Smoking status	ICV, Edu, Age, Gender	0.062	0.112	0.974
Diabetes	ICV, Edu, Age, Gender	0.609	0.541	0.247

Table 4 lists the ReML estimates of ${\tau }_G^2$, ${\tau }_W^2$, ${\tau }_{G\times W}^2$ and σ², and the p-values for the interaction effects between each of the 21 candidate AD risk genes and the CVD risk factors on hippocampal volume. Two genes, CR1 (p = 4.85×10^–4) and EPHA1 (p = 5.64×10^–4), are identified to have significant interaction with the CVD risk factors.

Table 4.

Results of the multivariate interaction analyses. The restricted maximum likelihood (ReML) estimates of ${\tau }_G^2$, ${\tau }_W^2$, ${\tau }_{G\times W}^2$ and σ², and the p-values for the interaction effects between each of the 21 candidate Alzheimer's disease (AD) risk genes and the cardiovascular disease (CVD) risk factors on hippocampal volume, using the kernel method and the alternative methods based on dimension reduction and multiple regression, are shown. p-values that survive multiple testing corrections are highlighted in bold. PCg: first principal component of the genetic data; PCw: first principal component of the CVD risk factors; RVT: rare variant test burden variable; WST: weighted sum test burden variable; FHS: the Framingham Heart Study vascular disease risk score.

Gene	Kernel method					Alternative methods
	${\tau }_G^2$	${\tau }_W^2$	${\tau }_{G\times W}^2$	σ 2	p-value	PCg × FHS	PCg × PCw	RVT × FHS	RVT × PCw	WST × FHS	WST × PCw
ABCA7	3.44E-7	3.24E-2	9.03E-4	0.286	0.479	0.138	0.253	0.215	0.183	0.291	0.258
BIN1	6.41E-4	1.66E-2	2.03E-2	0.279	0.167	0.861	0.615	0.165	0.296	0.049	0.441
CASS4	2.17E-3	3.31E-2	3.44E-7	0.284	0.492	0.522	0.889	0.971	0.565	0.742	0.838
CD2AP	3.44E-7	4.31E-2	3.44E-7	0.290	0.954	0.150	0.737	0.145	0.618	0.229	0.728
CD33	7.76E-5	4.39E-2	3.44E-7	0.289	0.845	0.196	0.245	0.807	0.543	0.734	0.807
CELF1	3.44E-7	2.74E-2	6.52E-3	0.284	0.284	0.591	0.626	0.102	0.115	0.230	0.216
CLU	1.62E-3	3.60E-2	3.44E-7	0.286	0.602	0.920	0.998	0.140	0.479	0.154	0.563
CR1	3.44E-7	7.21E-3	4.68E-2	0.273	4.85E-4	0.559	4.08E-4	0.268	0.023	0.354	0.109
DSG2	3.44E-7	3.51E-2	3.44E-7	0.286	0.566	0.232	0.135	0.823	0.367	0.617	0.202
EPHA1	3.44E-7	3.44E-7	5.12E-2	0.273	5.64E-4	0.323	0.133	0.182	0.270	0.939	0.979
FERMT2	2.05E-2	3.17E-2	5.93E-3	0.278	0.342	0.556	0.817	0.767	0.794	0.852	0.876
HLA-DRB5	3.44E-7	3.80E-2	3.44E-7	0.286	0.759	0.764	0.388	0.763	0.388	0.763	0.388
INPP5D	6.18E-4	3.44E-2	3.44E-7	0.285	0.527	0.910	0.395	0.267	0.022	0.375	0.156
MEF2C	1.74E-3	2.08E-2	1.77E-2	0.279	0.058	0.125	0.408	0.085	0.436	0.067	0.418
MS4A6A	9.32E-4	3.77E-2	3.44E-7	0.287	0.902	0.769	0.969	0.779	0.945	0.781	0.926
PICALM	1.89E-2	3.91E-2	3.44E-7	0.281	0.679	0.473	0.295	0.580	0.390	0.922	0.294
PTK2B	1.68E-3	3.25E-2	9.00E-4	0.284	0.460	0.779	0.615	0.630	0.406	0.043	0.048
REST	3.66E-2	2.11E-2	1.95E-2	0.273	0.189	0.732	0.497	0.800	0.578	0.694	0.671
SLC24A4	8.22E-3	1.64E-2	2.35E-2	0.277	0.211	0.345	0.029	0.634	0.222	0.942	0.268
SORL1	2.30E-3	4.77E-2	3.44E-7	0.290	0.919	0.663	0.521	0.129	0.481	0.126	0.455
ZCWPW1	3.44E-7	2.85E-2	3.80E-3	0.284	0.265	0.634	0.373	0.600	0.422	0.574	0.437

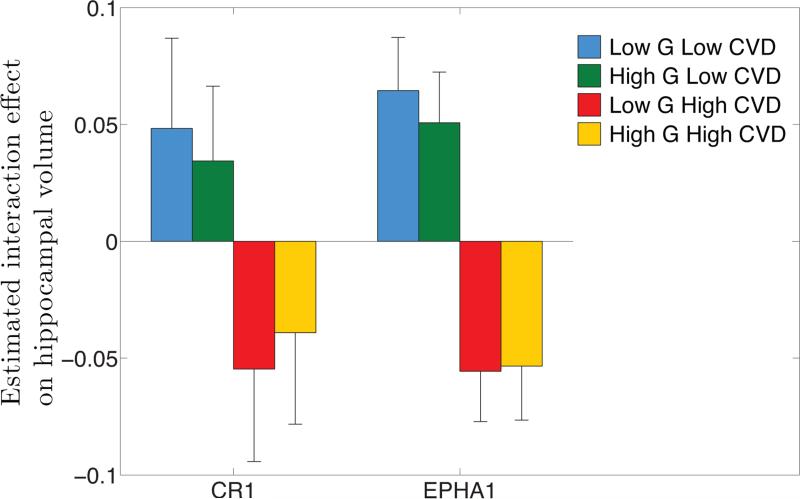
Fig. 2 shows the average of the estimated interaction effect ĥ_G×W within each of the four regimes (low genetic risk and low CVD risk, high genetic risk and low CVD risk, low genetic risk and high CVD risk, high genetic risk and high CVD risk) for the two genes CR1 and EPHA1 that show a significant interaction effect. For both genes, CVD risks largely dominate the interaction effect with higher CVD risk associated with higher risk of interaction and vice versa. The genetic risk appears to have an opposite effect of its marginal effect on interaction under high CVD risk, i.e., high genetic risk reduces the interaction effect in the presence of high CVD risk. One interpretation of this interaction pattern is that under low genetic risk, CVD risk factors have a more detrimental effect.

Figure 2.

Direction of significant interaction effects. For genes CR1 and EPHA1 that show significant interaction effect, genetic variables and cardiovascular disease (CVD) risk factors were collapsed into scalar variables; the RVT burden variable and the FHS risk score, respectively. The average of the estimated interaction effect ĥ_G×W within each of the four regimes (low genetic risk and low CVD risk, high genetic risk and low CVD risk, low genetic risk and high CVD risk, high genetic risk and high CVD risk) is shown with a standard error estimate obtained by Jackknife resampling. A smaller average indicates a higher risk of the interaction effect (smaller hippocampal volume).

Two-sample t-tests showed that subjects with stable MCI have significantly larger ĥ_G×W (lower risk) than subjects that progressed to AD for both genes (CR1, p = 0.049; EPHA1, p = 0.044), suggesting that disease progression is predicted by the interaction effect.

3.3 Comparison to alternative methods

Table 4 also shows the p-values for the alternative methods to test the interaction effect. PCA on both the genetic data and CVD risk factors, followed by multiple linear regression analyses, also identified CR1 with a FWE-corrected significant p-value, but failed to find EPHA1. Other alternative methods did not identify any significant interaction effect.

4 Discussion

In this paper, we have proposed a kernel machine based method to test for interactions between multidimensional variable sets. Compared to traditional collapsing and PCA-based methods, the proposed method provides a more flexible and biological plausible way to model epistasis between genetic variants, accommodates multiple factors that potentially moderate genetic effects, and can test for complex interaction effects between multidimensional variable sets. Although multivariate methods typically produce more powerful and reproducible results, which can also be biologically more insightful, the interpretation of model parameters is often challenging. In this paper, we made some preliminary attempts to reveal the direction of interaction between multidimensional variable sets and investigate the prediction of disease progression by interaction effects. Further improvement of model interpretation would be facilitated by incorporating more biological information when a better understanding of the underlying mechanisms is achieved.

One particular case where model interpretation might be straightforward is when we use a linear kernel, as we did to model non-genetic effects. In our analyses, the non-genetic effect h_W can be represented as a linear combination of the CVD risk factors: h_W = Wβ_W, where $\mathit{W}={[{\mathit{W}}_1,\cdots ,{\mathit{W}}_N]}^{\mathsf{T}}$ are the individual CVD risk factors. The linear coefficients β_W reflect the influence of each variable on the phenotype. The covariance matrix of the coefficient estimates can be computed as

$$\mathbf{cov}({\widehat{\beta }}_W-{\beta }_W)=({\tau }_W^2∕R)\mathit{I}-{({\tau }_W^2∕R)}^2{\mathit{W}}^{\mathsf{T}}\mathit{PW},$$ (19)

where R is the number of non-genetic variables, $\mathit{P}={\mathit{V}}^{-1}-{\mathit{V}}^{-1}\mathit{X}{\left({\mathit{X}}^{\mathsf{T}}{\mathit{V}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{T}}{\mathit{V}}^{-1}$, and $\mathit{V}={\tau }_G^2{\mathit{K}}_G+{\tau }_W^2{\mathit{K}}_W+{\tau }_{G\times W}^2{\mathit{K}}_{G\times W}+{\sigma }^{2}I$. An estimate of this covariance structure can be obtained by inserting the ReML estimates of the variance component parameters ${\tau }_G^2$, ${\tau }_W^2$, ${\tau }_{G\times W}^2$ and σ² into Eq. (19), assuming that the error of the ReML estimation can be ignored. Supplementary Table S1 presents the point estimates and standard errors for each element of β_W, for the ADNI analyses corresponding to each one of the 21 candidate AD risk genes. The above strategy does not apply to nonlinear kernels, but individual subjects can be examined by inspecting the estimated main and interaction effects ĥ_G, ĥ_W, ĥ_G×W, and their variabilities. More specifically, $\mathrm{cov}({\widehat{\mathit{h}}}_{G\times W}-{\mathit{h}}_{G\times W})={\tau }_{G\times W}^2{\mathit{K}}_{G\times W}-\left({\tau }_{G\times W}^2{\mathit{K}}_{G\times W}\right)\mathit{P}\left({\tau }_{G\times W}^2{\mathit{K}}_{G\times W}\right)$, and the variability of ĥ_G and ĥ_W can be quantified analogously. Analyses of individual subjects may provide additional information about the model, but we consider this beyond the scope of the present paper.

Due to the moderate sample size in the present study, we constrained our analysis to a list of candidate late-onset AD risk genes. However, the proposed method can be applied to genome-wide interaction studies. In particular, we note that when testing for the overall genetic and non-genetic effect, the variance component parameters ${\tau }_G^2$, ${\tau }_W^2$, and ${\tau }_{G\times W}^2$ need not be estimated. Therefore, the overall score test offers an efficient and non-iterative approach to screen the whole genome for genetic variants that might show significant contribution to the phenotypic variation. Fitting the full model, estimating the variance components, and testing for interactions can then focus on genetic components with significant overall effect, which will dramatically reduce computational burden. A similar argument applies to voxel-/vertex-wise interaction studies.

We would like to note that most of the CVD risk factors we employed in our ADNI analyses are largely endogenous and thus are, to some extent, under genetic control. Although, this might make the interpretation of the results difficult, this challenge, we believe, exists in many interaction effects probed and detected in the genetics literature. Furthermore, even though the non-genetic variables we used are collectively associated with cardiovascular risk, and thus our interpretation of the detected interaction effects as genetic influences modified by cardiovascular risk is highly likely, alternative explanations that do not involve cardiovascular mechanisms are also possible. Finally, while hippocampal volume is a sensitive biomarker of AD, it is not solely related to this condition. In fact, we conducted additional analyses with entorhinal cortex thickness and volume (also MRI markers of late-onset AD) as alternative outcome variables. These analyses (not included here) did not reveal any statistically significant interaction effect. Although our presented results demonstrated that the detected interaction effects with hippocampal volume predict future MCI-to-AD conversion, one possibility is that these associations might not be specific to AD. Elucidating these issues is beyond the scope of this paper and will require careful follow-up studies that will consider all alternative possibilities.

Another potential concern in the present study is that we took the coding regions and 20kb up/downstream of the 21 candidate genes as units for interaction detection. Although Lambert et al. [2013] examined all SNPs that have strong associations with the top SNPs to confirm the relevance of these genes, we are aware that they are likely not the causative genes. Also, the size of the regulatory region of different genes may vary substantially. Therefore, an alternative strategy is to group SNPs in high LD with the most associated SNP, whether or not they are in or close to the nearest gene.

The choice of kernels may have an impact on the validity and power of the method too. In the present study, we employed an IBS kernel for the genetic data and a linear kernel for the CVD risk factors, as both kernels are parameter free and can in principle capture complex epistatic effects between genetic variants and model the joint effect of multiple non-genetic variables. We found, through simulation studies, that the proposed selection of kernels appears to work well in our setting, both in terms of false positive rate control and statistical power. Using other kernel functions, e.g., the Gaussian kernel for combining non-genetic factors, is certainly possible, but might require preselecting or estimating additional parameters. Our preliminary implementation (results not shown) suggests that incorporating the estimation of the spread parameter in the Gaussian kernel into the ReML algorithm might lead to unstable estimates and failure of convergence. The performance of various kernel functions in different data structures, and the optimal selection of kernels, deserve future investigation.

Although we illustrated the proposed method using a univariate quantitative image derived phenotype, genes as units to group SNPs, and CVD risk factors as non-genetic variables, the modeling framework is general and can be applied to other types of phenotypic and genetic data, and to detecting other types of interactions such as genotype-by-environment interactions. Our method can also be extended to accommodate binary outcomes, and thus has potential wide applications to case-control studies. Recently, a series of papers have been published on the proper modeling of longitudinal and time-to-event data in neuroimaging studies [Bernal-Rusiel et al., 2013a,b; Sabuncu et al., 2014]. Incorporating genetic components and interactions in longitudinal and survival models, and investigating the genetic contributions to the progression of a brain-related illness and the timing of a clinical event of interest, seem promising directions for future research.

Two genes, CR1 and EPHA1, were identified to have significant interaction effects with the CVD risk factors in the present study. The associations between the two genes and AD have been identified and replicated by a number of independent studies [see e.g., Harold et al., 2009; Hollingworth et al., 2011; Lambert et al., 2009; Naj et al., 2011], in addition to Lambert et al. [2013], and their potential contributions to the mechanism of AD have been under active investigation [Biffi et al., 2012; Chibnik et al., 2011; Thambisetty et al., 2013]. Moreover, recent studies show that many of the AD risk genes have potential roles in relationship with CVD risk factors, such as hypertension, hypercholesterolemia, and obesity [Guerreiro et al., 2012; Liu et al., 2014]. In particular, excess adiposity may act as an enhanced substrate for CR1-related inflammatory events [Guerreiro et al., 2012]. Our findings indicate that genetic components may contribute to the etiology of late-onset AD in the presence of CVD risks, and warrant further investigations.

Highlights.

• Novel kernel machine based method for detecting interaction effects

• Method can model epistatic effects

• Method can accommodate multiple environmental variables

• We show novel gene-cardiovascular risk interaction relevant to Alzheimer's

Appendix

A The ReML estimation of the linear mixed effects model

The variance component parameters ${\tau }_G^2$, ${\tau }_W^2$, ${\tau }_{G\times W}^2$ and σ² in the linear mixed effects model (12) can be estimated via the restricted maximum likelihood (ReML) approach [Harville, 1977; Lindstrom and Bates, 1988].

Specifically, let $\theta ={({\tau }_G^2,{\tau }_W^2,{\tau }_{G\times W}^2,{\sigma }^2)}^{\mathsf{T}}$, and $\mathit{V}\left(\theta \right)={\tau }_G^2{\mathit{K}}_G+{\tau }_W^2{\mathit{K}}_W+{\tau }_{G\times W}^2{\mathit{K}}_{G\times W}+{\sigma }^2\mathit{I}$. The log ReML likelihood can be written as

$$\ell ({\tau }_G^2,{\tau }_W^2,{\tau }_{G\times W}^2,{\sigma }^2)=-\frac{1}{2}\log \mid \mathit{V}\left(\theta \right)\mid -\frac{1}{2}\log \mid {\mathit{X}}^{\mathsf{T}}{\mathit{V}}^{-1}\left(\theta \right)\mathit{X}\mid -\frac{1}{2}{(\mathit{y}-\mathit{X}\widehat{\beta })}^{\mathsf{T}}{\mathit{V}}^{-1}\left(\theta \right)(\mathit{y}-\mathit{X}\widehat{\beta }),$$ (20)

where $\widehat{\beta }$ is the BLUP of the regression coefficients β. The score equation of each unknown component of θ is

$$\begin{array}{cc}\hfill \frac{\partial \ell }{\partial {\theta }_i}=& -\frac{1}{2}\mathbf{tr}\left\{\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}\right\}+\frac{1}{2}{(\mathit{y}-\mathit{X}\widehat{\beta })}^{\mathsf{T}}{\mathit{V}}^{-1}\frac{\partial \mathit{V}}{\partial {\theta }_i}{\mathit{V}}^{-1}(\mathit{y}-\mathit{X}\widehat{\theta })\hfill \\ \hfill =& -\frac{1}{2}\mathbf{tr}\left\{\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}\right\}+\frac{1}{2}{\mathit{y}}^{\mathsf{T}}\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}{\mathit{P}}_{\mathit{y}}=0,\hfill \end{array}$$ (21)

where $\mathit{P}={\mathit{V}}^{-1}-{\mathit{V}}^{-1}\mathit{X}{\left({\mathit{X}}^{\mathsf{T}}{\mathit{V}}^{-1}\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathsf{T}}{\mathit{V}}^{-1}$, $\partial \mathit{V}∕\partial {\tau }_G^2={\mathit{K}}_G,\partial \mathit{V}∕\partial {\tau }_W^2={\mathit{K}}_W$, $\partial \mathit{V}∕\partial {\tau }_{G\times W}^2={\mathit{K}}_{G\times W}$, and ∂V/∂σ² = I. The element of the observed information matrix is

$$-\frac{{\partial }^2\ell }{\partial {\theta }_i\partial {\theta }_j}=-\frac{1}{2}\mathbf{tr}\left\{\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_j}\right\}+{\mathit{y}}^{\mathsf{T}}\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_j}\mathit{Py}.$$ (22)

The element of the Fisher information (expected information) matrix is

$$\mathbf{E}\left[-\frac{{\partial }^2\ell }{\partial {\theta }_i\partial {\theta }_j}\right]=\frac{1}{2}\mathbf{tr}\left\{\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_j}\right\}.$$ (23)

Here we employ the Newton-Raphson method, and in particular, the Fisher's scoring algorithm, to solve Eq. (21) [Kenward and Roger, 1997]. Given an estimate of the unknown variance component parameters at the k-th iteration θ^(k), the parameters are updated by

$${\theta }^{(k+1)}={\theta }^{\left(k\right)}+{\phantom{\mid }{\left[{\mathcal{I}}^{\left(k\right)}\right]}^{-1}\frac{\partial \ell }{\partial \theta }\mid }_{{\theta }^{\left(k\right)}},$$ (24)

where $\mathcal{I}$ is the Fisher information matrix. At the beginning of the iteration process, all the variance components are initialized to var[y]/4. We use the following expectation maximization (EM) algorithm [Laird et al., 1987] as an initial step to determine the direction of the updates as EM algorithm is robust to poor starting values:

$$\begin{array}{c}\hfill {\sigma }^2={\mathit{y}}^{\mathsf{T}}\mathit{Py}∕(N-p),\hfill \\ \hfill \theta s_i^{\left(1\right)}=\frac{1}{N}\left[{\left[{\theta }_i^{\left(0\right)}\right]}^2{\mathit{y}}^{\mathsf{T}}\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}\mathit{Py}+\mathbf{tr}\left\{{\theta }_i^{\left(0\right)}\mathit{I}-{\left[{\theta }_i^{\left(0\right)}\right]}^2\mathit{P}\frac{\partial \mathit{V}}{\partial {\theta }_i}\right\}\right],i=1,2,3.\hfill \end{array}$$ (25)

After one EM update, we then switch to the Fisher's scoring algorithm for the remaining iterations until the difference between successive log ReML likelihoods, $\mid {\ell }^{(k+1)}-{\ell }^{\left(k\right)}\mid$, is smaller than 10^–4. In the iteration process, any component that escapes from the parameter space, i.e., negative estimate, is set to 10^–6 × var[y]. The approach to fit the null model, when ${\tau }_{G\times W}^2$ is fixed at zero, is analogous.

B Satterthwaite approximation to the score test

The score test statistic $\mathcal{S}\left({\sigma }_0^2\right)$ defined in Eq. (15) is approximated by a scaled chi-square distribution $\kappa {\chi }_{\nu }^2$. The scale parameter κ and the degrees of freedom ν are calculated by matching the mean and variance of $\mathcal{S}\left({\sigma }_0^2\right)$ with those of $\kappa {\chi }_{\nu }^2$. Specifically,

$$\{\begin{array}{c}\delta =\mathbf{E}\left[\mathcal{S}\left({\sigma }_0^2\right)\right]=\frac{1}{2}\mathbf{tr}\left\{{\mathit{P}}_0\mathit{K}\right\}=\mathbf{E}\left[\kappa {\chi }_{\mu }^2\right]=\kappa \nu ,\hfill \\ \rho =\mathbf{var}\left[\mathcal{S}\left({\sigma }_0^2\right)\right]=\frac{1}{2}\mathbf{tr}\left\{{\mathit{P}}_0\mathit{K}{\mathit{P}}_0\mathit{K}\right\}=\mathbf{var}\left[\kappa {\chi }_{\nu }^2\right]=2{\kappa }^2\nu .\hfill \end{array}\phantom{\}}$$ (26)

Solving the two equations leads to κ = ρ/2δ and ν = 2δ²/ρ. In practice, the unknown model parameter ${\sigma }_0^2$ in $\mathcal{S}$ is replaced by its ReML estimate ${\widehat{\sigma }}_0^2$ under the null model y = Xβ₀ + ε₀. To account for this substitution, we follow Liu et al. [2007] and Li and Cui [2012], and replace ρ by $\widehat{\rho }$ based on the efficient information [Zhang and Lin, 2003]. It can be seen from Eq. (23) that the elements of the Fisher information matrix of θ are

$${\mathcal{I}}_{\tau \tau }=\frac{1}{2}\left[\begin{array}{ccc}\hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_G{\mathit{P}}_0{\mathit{K}}_G\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_G{\mathit{P}}_0{\mathit{K}}_W\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_G{\mathit{P}}_0{\mathit{K}}_{G\times W}\right)\hfill \\ \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_W{\mathit{P}}_0{\mathit{K}}_G\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_W{\mathit{P}}_0{\mathit{K}}_W\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_W{\mathit{P}}_0{\mathit{K}}_{G\times W}\right)\hfill \\ \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_{G\times W}{\mathit{P}}_0{\mathit{K}}_G\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_{G\times W}{\mathit{P}}_0{\mathit{K}}_W\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_{G\times W}{\mathit{P}}_0{\mathit{K}}_{G\times W}\right)\hfill \end{array}\right].$$

$${\mathcal{I}}_{\tau {\sigma }^2}=\frac{1}{2}{[\mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_G\right),\mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_W\right),\mathbf{tr}\left({\mathit{P}}_0{\mathit{K}}_{G\times W}\right)]}^{\mathsf{T}},{\mathcal{I}}_{{\sigma }^2{\sigma }^2}=\frac{1}{2}\mathbf{tr}\left({\mathit{P}}_0{\mathit{P}}_0\right).$$

The efficient information is defined as ${\widehat{\mathcal{I}}}_{\tau \tau }={\mathcal{I}}_{\tau \tau }-{\mathcal{I}}_{\tau {\sigma }^2}{\mathcal{I}}_{{\sigma }^2{\sigma }^2}^{-1}{\mathcal{I}}_{\tau {\sigma }^2}^{\mathsf{T}}$, and $\widehat{\rho }=\mathbf{var}\left[\mathcal{S}\left({\widehat{\sigma }}_0^2\right)\right]$ is estimated by the sum of all the elements in the matrix ${\widehat{\mathcal{I}}}_{\tau \tau }$. With the adjusted parameters $\widehat{\kappa }=\widehat{\rho }∕2\delta$ and $\widehat{\nu }=2{\delta }^2∕\widehat{\rho }$, the p-value of an observed score statistic $\mathcal{S}\left({\widehat{\sigma }}_0^2\right)$ is then computed using the scaled chi-square distribution $\widehat{\kappa }{\chi }_{\widehat{\nu }}^2$.

Analogously, the score test statistic ${\mathcal{S}}_I({\tau }_G^2,{\tau }_W^2,{\sigma }^2)$ defined in Eq. (16) for the interaction effect is approximated by a scaled chi-square distribution ${\kappa }_I{\chi }_{{\nu }_I}^2$. The scale parameter κ_I and the degrees of freedom ν_I are calculated by matching the mean and variance of ${\mathcal{S}}_I$ with those of ${\kappa }_I{\chi }_{{\nu }_I}^2$. Specifically,

$$\{\begin{array}{c}{\delta }_I=\mathbf{E}\left[{\mathcal{S}}_I\right]=\frac{1}{2}\mathbf{tr}\left\{{\mathit{P}}_I{\mathit{K}}_{G\times W}\right\}=\mathbf{E}\left[{\kappa }_I{\chi }_{{\nu }_I}^2\right]={\kappa }_I{\nu }_I\hfill \\ {\rho }_I=\mathbf{var}\left[{\mathcal{S}}_I\right]=\frac{1}{2}\mathbf{tr}\left\{{\mathit{P}}_I{\mathit{K}}_{G\times W}{\mathit{P}}_{G\times W}\right\}=\mathbf{var}\left[{\kappa }_I{\chi }_{{\nu }_I}^2\right]=2{\kappa }_I^2{\nu }_I.\hfill \end{array}\phantom{\}}$$ (27)

Solving the two equations gives κ_I = ρ_I/2δ_I and ${\nu }_I=2{\delta }_I^2∕{\rho }_I$. In practice, the unknown model parameters ${\tau }_G^2$, ${\tau }_W^2$ and σ² in ${\mathcal{S}}_I$ are replaced by their ReML estimates ${\widehat{\tau }}_G^2$, ${\widehat{\tau }}_W^2$ and ${\widehat{\sigma }}^2$ under the null model y = Xβ+h_G+h_W+ε. To account for this substitution, ρ_I is replaced by ${\widehat{\rho }}_I$ based on the efficient information [Zhang and Lin, 2003]. Specifically, ${\widehat{\kappa }}_I={\widehat{\rho }}_I∕2{\delta }_I$ and ${\widehat{\nu }}_I=2{\delta }_I^2∕{\widehat{\rho }}_I$, where ${\widehat{\delta }}_I=\mathbf{tr}\left\{{\mathit{P}}_I{\mathit{K}}_{G\times W}\right\}∕2$, and ${\widehat{\rho }}_I=\mathbf{tr}\left\{{\mathit{P}}_I{\mathit{K}}_{G\times W}{\mathit{P}}_I{\mathit{K}}_{G\times W}\right\}∕2-\Psi {\Lambda }^{-1}{\Psi }^{\mathsf{T}}∕2$, in which

$$\Psi =[\mathbf{tr}\left({\mathit{P}}_I{\mathit{K}}_{G\times W}{\mathit{P}}_I\right),\mathbf{tr}\left({\mathit{P}}_I{\mathit{K}}_{G\times W}{\mathit{P}}_I{\mathit{K}}_G\right),\mathbf{tr}\left({\mathit{P}}_I{\mathit{K}}_{G\times W}{\mathit{P}}_I{\mathit{K}}_W\right)],$$

and

$$\Lambda =\left[\begin{array}{ccc}\hfill \mathbf{tr}\left({\mathit{P}}_I^2\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_I^2{\mathit{K}}_G\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_I^2{\mathit{K}}_W\right)\hfill \\ \hfill \mathbf{tr}\left({\mathit{P}}_I^2{\mathit{K}}_G\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_I{\mathit{K}}_G{\mathit{P}}_I{\mathit{K}}_G\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_I{\mathit{K}}_G{\mathit{P}}_I{\mathit{K}}_W\right)\hfill \\ \hfill \mathbf{tr}\left({\mathit{P}}_I^2{\mathit{K}}_W\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_I{\mathit{K}}_W{\mathit{P}}_I{\mathit{K}}_G\right)\hfill & \hfill \mathbf{tr}\left({\mathit{P}}_I{\mathit{K}}_W{\mathit{P}}_I{\mathit{K}}_W\right)\hfill \end{array}\right].$$

The p-value of an observed score statistic ${\mathcal{S}}_I({\widehat{\tau }}_G^2,{\widehat{\tau }}_W^2,{\widehat{\sigma }}^2)$ is then computed using the scaled chi-square distribution ${\widehat{\kappa }}_I{\chi }_{{\widehat{\nu }}_I}^2$.