Cells as liquid motors: Mechanosensitivity emerges from collective dynamics of actomyosin cortex

Significance

Animals have muscles to act on their environment. The molecules endowing them with this faculty are actin and myosin and are also present in nonmuscle cells. Our modelling breaks down the motor-like properties of the actomyosin network in single nonmuscle cells, which show striking similarity to the properties of muscles. In particular, an internal friction sets the maximum speed of contraction of both cells and muscles when myosins do not have time to detach after pulling, just as rowers lifting their oars too slowly after their stroke. The same modelling explains cell-scale mechanosensing: the combination of myosin-driven contraction and actin polymerization-driven protrusivity regulates cell length in a force-dependent manner, making response to rigidity a property of the very material of the cell cortex.

Abstract

Living cells adapt and respond actively to the mechanical properties of their environment. In addition to biochemical mechanotransduction, evidence exists for a myosin-dependent purely mechanical sensitivity to the stiffness of the surroundings at the scale of the whole cell. Using a minimal model of the dynamics of actomyosin cortex, we show that the interplay of myosin power strokes with the rapidly remodeling actin network results in a regulation of force and cell shape that adapts to the stiffness of the environment. Instantaneous changes of the environment stiffness are found to trigger an intrinsic mechanical response of the actomyosin cortex. Cortical retrograde flow resulting from actin polymerization at the edges is shown to be modulated by the stress resulting from myosin contractility, which in turn, regulates the cell length in a force-dependent manner. The model describes the maximum force that cells can exert and the maximum speed at which they can contract, which are measured experimentally. These limiting cases are found to be associated with energy dissipation phenomena, which are of the same nature as those taking place during the contraction of a whole muscle. This similarity explains the fact that single nonmuscle cell and whole-muscle contraction both follow a Hill-like force–velocity relationship.

When placed in different mechanical environments, living cells assume different shapes (1–5). This behavior is strongly dependent on the contractile activity of the actomyosin network (6–10). One of the cues driving the cell response to its environment is rigidity (11). Cells are able to sense not only the local rigidity of the material with which they are in contact (12) but also, the one associated with distant cell substrate contacts. This ability has been demonstrated by tracking the amount of extra force needed to achieve a given displacement of microplates between which the cell is placed (13, 14) (Fig. 1B), of an atomic force microscope (AFM) cantilever (15, 16) or elastic micropillars (17). This cell-scale rigidity sensing is totally dependent on myosin-II activity (13). A working model of the molecular mechanisms at play in the actomyosin cortex is available (18), where myosin contraction, actin treadmilling, and actin cross-linker turnover are the main ingredients. Phenomenological models (19, 20) of mechanosensing have been proposed but could not bridge the gap between the molecular microstructure and this cell-scale phenomenology. Here, we show that the collective dynamics of actin, actin cross-linkers, and myosin molecular motors are sufficient to explain cell-scale rigidity sensing: depending on the tension that can be borne by the environment, there is a change of the fraction of myosin molecules which perform mechanical work that is effectively transmitted rather than dissipated. The model derivation is analogous to the one of rubber elasticity of transiently cross-linked networks (21), with the addition of active cross-linkers accounting for the myosin. It involves four parameters only: myosin contractile stress, speed of actin treadmilling, elastic modulus, and viscoelastic relaxation time of the cortex, which arises from cross-linker unbinding. We obtain quantitative predictions of the dynamics and statics of cell contraction depending on the external stiffness. The crucial dependence of this behavior on the fact that cross-linkers have a short lifetime is reminiscent of the model of muscle contraction by Huxley (22), in which the force dependence of muscle contraction rate is explained by the fact that, for lower muscle force and higher contraction speed, the number of myosin heads contributing to filament sliding decreases in favor of those resisting it transiently before they unbind. Although it is known that many molecules associated with actomyosin exhibit stress-dependent dynamics (23, 24) and can lead to microscale response to rigidity (25, 26), collective effects govern the linear response of actomyosin and are sufficient to explain the observations in both the model by Huxley (22) and this model: we show that force-dependent binding kinetics tune the system’s efficiency without essential alterations to its behavior, as Huxley (22) noted himself. Despite very dissimilar organization of actomyosin in muscles, where it forms well-ordered sarcomeres, and nonmuscle cell cortex, where no large-scale patterning is observed, we show that similar mechanisms explain their motor properties. The collective dynamics that we describe are consistent with the fact that the actin network behaves as a fluid at long timescales. We show how myosin activity can contract this fluid at a given rate that depends on external forces resisting cell contraction, which arise, for example, from the stiffness of the environment. This contractility combined with actin protrusivity result in both a sustained retrograde flow and a regulation of cell shape. In addition, this regulation explains the elastic-like behavior observed in cell-scale rigidity sensing and justifies ad hoc models based on this observation (19).

Fig. 1.

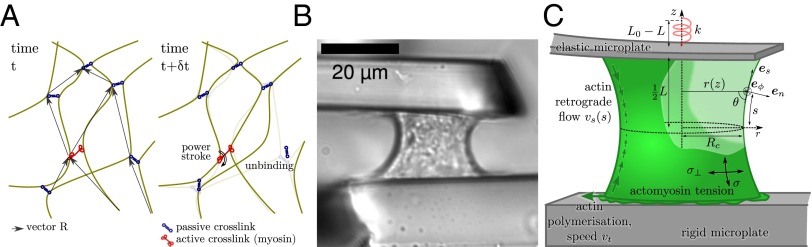
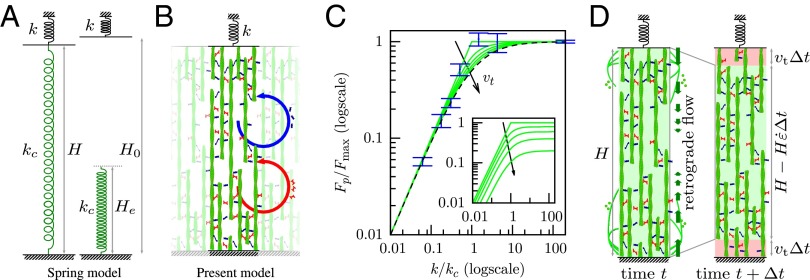
Model of the actomyosin behavior and experimental setup. (A) Sketch of a transiently cross-linked actin network with myosin bipolar filaments. Unbinding of a cross-linker releases elastic tension locally; the cross-linker will rebind to the network, preserving its elastic properties but causing a loss of stored elastic energy. Myosin power strokes have the effect of modifying the equilibrium length of the adjacent strands $\mathit{R}$, leading to an increase of the tension (SI Text, S2). (B) Transmission image of a cell and setup. (C) Model of the mechanical components of the cell and microplate system. Microplates impose that the vertical force equilibrating the cortical tension is linked to the cell length L with $F=k\left(L_0-L\right)$. Tension along the actomyosin cortex (green surface) is anisotropic and has values σ and ${\sigma }_{\perp }$ along directions ${\mathit{e}}_s$ and ${\mathit{e}}_{\varphi }$. Actin treadmilling provides a boundary condition at the cell leading edge, and the actin cortex undergoes a retrograde flow away from the plates.

Results

Intrinsic Sensitivity to Rigidity of Actomyosin.

The actin cortex of nonmuscle cells is a disordered network located at the cell periphery. Actin filaments are cross-linked by proteins, such as α-actinin, which experience a rapid turnover (e.g., on the order of 10 s for α-actinin) (27), and actin itself has a scarcely longer turnover time (28). The actin network is, thus, only transiently cross-linked. Following ref. 21, we describe the behavior of such a network by a rubber-like model. Up to the first order, this model leads to a stress–strain relationship of a Maxwell viscoelastic liquid, in which the relaxation time is a characteristic unbinding time ${\tau }_{\alpha }$ (SI Text, S2),

$${\tau }_{\alpha }\stackrel{\mathrm{▿}}{\mathit{\sigma }}+\mathit{\sigma }-2{\tau }_{\alpha }E\dot{\mathit{\epsilon }}=0,$$ [1]

where $\dot{\mathit{\epsilon }}$ is the rate-of-strain tensor, and $\stackrel{\mathrm{▿}}{\mathit{\sigma }}$ is the objective time derivative of the stress tensor $\mathit{\sigma }$: in the linear setting, $\mathit{\sigma }=2E\left({\beta }^2\langle \mathit{RR}\rangle -\mathit{I}\right)$, where E is the elastic modulus of the cross-linked actin network, $\mathit{R}$ is a basic element of this network (namely the strand vector spanning the distance between any two consecutive actin–actin bonds) (Fig. 1A), and $1/\beta$ is its reference length when submitted to thermal fluctuations only. As long as these two bonds hold (for times much shorter than ${\tau }_{\alpha }$), this basic element behaves elastically, and the stress tensor $\mathit{\sigma }$ grows in proportion with the strain. When a cross-linker unbinds, the filaments can slide relative to one another, and the elastic tension that was maintained by this cross-linker is relaxed: this behavior corresponds to an effective friction and happens at a typical rate of $1/{\tau }_{\alpha }$. In sum, the actin network behaves like an elastic solid of modulus E over a time shorter than ${\tau }_{\alpha }$, because cross-linkers remain in place during such a solicitation, but it has a viscous-like response for longer times with an effective viscosity ${\tau }_{\alpha }E$, because the network yields as cross-linkers unbind.

Such a viscoelastic liquid is unable to resist mechanical stresses (29). However, living cells are able to generate stress themselves (30) thanks to myosin bipolar filaments, which act as actin cross-linkers but are, in addition, able to move along one of the filaments to which they are bound using biochemical energy. Let us call ${\alpha }_{\mathrm{myo}}$ the fraction of cross-linkers that are myosin filaments and effectuate a power stroke of step length $\ell$ at frequency $1/{\tau }_{\mathrm{myo}}$. The power stroke corresponds to a change of the binding location of the myosin head along the actin filament and thus, affects the length of the neighboring strand $\mathit{R}$ (Fig. 1A). Eq. S4 includes the additional term that describes this myosin-driven evolution of the network configuration. When this equation is integrated to give the local macroscopic stress tensor $\mathit{\sigma }$, this term results in a contractile stress ${\mathit{\sigma }}_{\text{a}}=\left({\tau }_{\alpha }/{\tau }_{\mathrm{myo}}\right)E{\alpha }_{\mathrm{myo}}{\left(\ell \beta \right)}^2$ (SI Text, S2):

$${\tau }_{\alpha }\hspace{0.17em}\stackrel{\mathrm{▿}}{\mathit{\sigma }}+\mathit{\sigma }-2{\tau }_{\alpha }E\dot{\mathit{\epsilon }}={\mathit{\sigma }}_{\text{a}}.$$ [2]

The three-parameter model obtained (${\tau }_{\alpha }$, E, and ${\mathit{\sigma }}_{\text{a}}$) is in line with early continuum models (31) and active gel models (32); however, we do not supplement this active stress with an elastic stress unlike in previous models of mechanosensitive active gels (17, 20), where cells are treated as viscoelastic solids (SI Text, S4.2). Consistent with prior computational models (25), this equation shows that the contractile stress ${\mathit{\sigma }}_{\text{a}}$ gives rise to either the buildup of a contractile tension $\mathit{\sigma }$ (if clamped boundary conditions allow no strain) or a contractile strain rate ${\mathit{\sigma }}_{\text{a}}/\left(2{\tau }_{\alpha }E\right)$ proportional to ${\alpha }_{\mathrm{myo}}/{\tau }_{\mathrm{myo}}$ [if free boundary conditions allow strain but not tension buildup (e.g., in the case of superprecipitation in vitro) (33)] or a combination of these.

We then asked whether this simple rheological law for the actomyosin cortex could explain the behavior of cells in our microplate experiments (Fig. 1B). Although the microplate setup is less common than flat substrates (11) or imbedding in a gel (5), it has the advantage of offering direct measurements of force and shape evolutions while preserving the well-studied basal and apical structures with lamellae and lamellipodia (34). To do so, we investigated the equilibrium shape and force of a thin shell of actomyosin surrounding a liquid (the cytosol) in the 3D geometry of the experimental setup in Fig. 1C and SI Text, S5. Surprisingly, the response to rigidity of cells is adequately recovered by this simple model of a contractile viscoelastic shell: although a fixed maximum force is predicted above a certain critical stiffness $k_c={\sigma }_{\text{a}}S/L_0$ of the microplates, the actomyosin-generated force is proportional to k when $k<k_c$ (Fig. 2A). Here, $L_0$ is the initial plate separation, and S is the section area of the actin cortex. Thus, the contractile activity of myosin motors is enough to endow the viscoelastic liquid-like actin cortex with a spring-like response to the rigidity of its environment (13, 35), a property that was introduced phenomenologically in previous models (19). To get a clear understanding of the mechanism through which this is possible, we simplified the geometry to a 1D problem (Fig. 3B) and found that the spring-like behavior of the contractile fluid was retained (Fig. 3C and SI Text, S3). Indeed, for an environment (external spring) of stiffness k much beyond the critical value $k_c$, the contractile fluid is unable to significantly strain the microplates, and equilibrium is reached when it exerts its maximal contractility ${\sigma }_{\text{a}}$. In contrast to computational models (25, 26) discussed in SI Text, S4.1, where such a maximum force arises because myosin molecules reach their specific stall force, the maximal contractility ${\sigma }_{\text{a}}$ emerges from collective dynamics: we assume a fixed rate of power strokes $1/{\tau }_{\mathrm{myo}}$ (SI Text, S3.9 and Fig. S1), and each of them increases the stress in the network of modulus E, but the competing phenomenon of cross-linker detachment at rate $1/{\tau }_{\alpha }$ limits the number of power strokes before the network relaxes. Thus, ${\sigma }_{\text{a}}\propto \left({\tau }_{\alpha }/{\tau }_{\mathrm{myo}}\right)E$ is an emergent stalling stress, and the actomyosin cortex contracts and deflects the microplates until this stalling stress is attained.

Fig. 2.

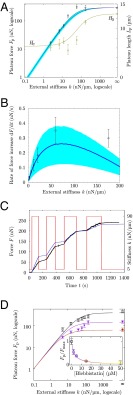
Predictive modeling of the stiffness-dependent cell mechanical response. (A) The force and cell length at equilibrium are adapted to the stiffness of the environment up to a maximum force at high stiffness, and for vanishing stiffness, there is a well-defined equilibrium length $L_e$ [independent of microtubules (Fig. S6)]. Circles show experimental results (13) for force (black) and length (green). The black line shows the force predicted by the 3D model. The green line shows the length predicted by the 3D model. The blue curve and shaded area show the force and confidence interval in the 1D model. Two of four parameters of the model were adjusted in this plot using the force at infinite stiffness and the length at zero stiffness. (B) During the transient part of the experiment, the rate of loading of the cell is adapted to the stiffness of the environment. Boxes show experimental results (13). The blue curve and shaded area show the force and confidence interval in the 1D model. One parameter of the model is fitted in this plot, and the last one is adjusted on Fig. 4A. (C) Instantaneous adaptation to a change of the microplate stiffness k. The red line shows stiffness imposed using a feedback loop. Black dots show the force measured (14). The blue line shows the 1D model prediction of force using the stiffness changes imposed in the experiment (red line) and the four parameters obtained in A and B without any additional adjustment. (D) Blebbistatin treatment modifies the contractility set point but preserves the mechanosensitivity. (Inset) The plateau force recorded experimentally for $k=\infty$ (○) decreases with the dose of blebbistatin. When decreasing the contractility parameter ${\sigma }_{\text{a}}$ of the model by the inhibitory factor of blebbistatin, the model predicts these observations (SI Text, S3.7). Depending on the contractility set point (control, □; model prediction, black line; 5 μM blebbistatin treatment, ▽; corresponding model prediction, purple line; model prediction for 15 μM blebbistatin treatment, red line), the mechanosensitivity is preserved as the force depends on k but with a shift in the saturation force at high stiffness and a different critical stiffness $k_c$ from which force saturates. Color codes blebbistatin concentration in both D and D, Inset.

Fig. 3.

A 1D simplification of the 3D model preserves the essential mechanisms and results. (A) The spring model with spring stiffness $k_c$ and rest length $L_e$ used elsewhere in the literature with which this model is compared (SI Text, S4.2). (B) Sketch of the 1D model. Actin filaments (green) are bound together by myosin (red) and other cross-linkers (blue), forming a structure of elastic modulus E. Cross-linkers and myosin unbind at a fixed frequency, which is at the origin of the viscoelastic behavior (SI Text, S2), and rebind so that their average number per filament unit length remains constant in time. In addition, myosins perform power strokes at a fixed frequency. The resulting rheology is sketched in Fig. S5C. (C) Equilibrium state of models and cells as a function of microplate stiffness k normalized by critical stiffness $k_c$ and maximum force $F_{\max }$ in each case. Blue, experimental results plotted with $k_c={\sigma }_{\text{a}}/\left(L_0+4{\tau }_{\alpha }{v}_{\text{t}}\right)=41$ nN/$\mathrm{\mu }\text{m}$ (no adjustment) (SI Text, S3.6); dashes, tension of the spring model; green, tension calculated in the 1D model for different values of the speed of treadmilling $v_{\text{t}}$. The stiffness dependence of force in experiments is well-matched by both the spring model and the 1D model. (Inset) Tension calculated in the 1D model for different values of the speed of treadmilling $v_{\text{t}}$ and normalized by $F_{\max }$ in the absence of treadmilling $v_{\text{t}}=0$: treadmilling reduces the force transmitted to the microplates. (D) A dynamic equilibrium is attained when the retrograde flow exactly balances the speed of polymerization at the boundaries (here, sketched in the 1D model geometry).

If, however, k is much below $k_c$, deflecting the plates is easier than tensing the actin network. Thus, a maximal strain may be reached before the stalling stress is attained, leading to a plateau stress $\sigma ={\sigma }_p\left(k\right)$ lower than ${\sigma }_{\text{a}}$. The next section discusses how actin polymerization can limit the myosin-powered contraction, thus setting an equilibrium cell length. In any case, this strain has to be less than $100\text{\%}$, leading to ${\sigma }_p\left(k\right)\le k{H}_0$. With a fixed maximal strain, the force finally achieved is proportional to k—just as for a prestretched spring of stiffness $k_c$ (Fig. 3A) or alternatively, just as cells do when exhibiting a mechanosensitive behavior (17, 19) (SI Text, S4.2). This spring-like behavior is supported by our previous report (14) that, when the external spring stiffness is instantaneously changed in experiments, cells adapt their rate of force buildup $dF/dt$ to the new conditions within 0.1 s. This observation was repeated using an AFM-based technique (15). In ref. 16, an overshoot of the rate adaptation, which relaxed to a long-term rate within 10 s, was noted in addition to the initial instantaneous change of slope. Although this instantaneity at the cell scale is not explained by mechanochemical regulation, this behavior is fully accounted for by the mechanical model proposed here (Fig. 2 B and C and SI Text, S3.4). This spring-like behavior is not independent of biochemical regulation of the kinetics of actin and myosin: down-regulation of the myosin contractile activity by blebbistatin results in a reduction of the maximal force that cells can exert (Fig. 2D and SI Text, S3.7), but for a given biochemical set-point, the mechanosensitivity is still present as a function of external stiffness as predicted by the model. Thus, the actomyosin cortex is mechanosensitive by essence: its peculiar active viscoelastic nature, which arises from collective effects, provides a built-in system of adaptation to changes of the mechanical environment.

Force-Dependent Regulation of Cell Length.

In microplate experiments, cells are observed to spread laterally simultaneously as they deflect microplates (Fig. S2). The features of this spreading are similar to those of cells spreading on a single plate both qualitatively and quantitatively (Fig. S3C) (34). Lateral cell spreading and plate deflection both affect the arc distance between the cell adhesions on each plate (Fig. S3 A and B). Cell spreading is known to be mediated by actin treadmilling (36, 37), which controls the extension of the lamellipodium (38). An effect of treadmilling is the net flow of filamentous actin from the lamellipodial region to the proximal part of the actomyosin cytoskeleton between adhesions (37, 39), which persists even if the cell and its adhesions are immobile (18). Thus, the length of the cell is regulated by a combination of the myosin-driven contraction rate $-\dot{\epsilon }$ of the cytoskeleton (the retrograde flow described above) and the speed $v_{\text{t}}$ at which newly polymerized actin is incorporated into the cortex. This feature can be included in the model as a boundary condition, prescribing a difference $v_{\text{t}}$ between the speed of the cell edge and the one of the actin cortex close to the edge (SI Text, S3.2 and S5). We find that this reduces the maximum tension that the actomyosin network can develop; however, the shape of the dependence vs. the external stiffness k is little altered (Fig. 3C). In particular, the force continues to be linearly dependent on k for low stiffnesses, albeit with a reduced slope, in direct consequence of a mechanical regulation of cell length to a target length $L_e$, which maintains the microplate deflection to $L_0-L_e$ when k varies; thus, $F=k\left(L_0-L_e\right)$ varies linearly with k in this range.

Indeed, the equilibrium length of the cell is attained when there is an exact balance between actin polymerization at the cell edge and the retrograde flow that drives it away (Fig. 3D). However, the interpretation here is not that polymerization generates this flow but rather, that it stems from myosin contraction and that the equilibrium length is reached when the force balance between myosin contraction and external forces acting on the cell is such that retrograde flow exactly balances polymerization speed. In the case when they do not compensate, the cell edge will move at a speed that is the difference between the speed of polymerization and the retrograde flow at the edge until equilibrium is reached. For our setup, it is found that cell length is initially decreasing, indicating that retrograde flow is faster than polymerization. Concurrently, because of the resistance of the microplates to cell contraction, the tension σ increases. In turn, this higher tension reduces the retrograde flow until it is exactly equal and opposite to the polymerization speed. Treadmilling and myosin contraction, thus, work against one another, which has been noted for a long time (36) and is specifically described by Rossier et al. (18).

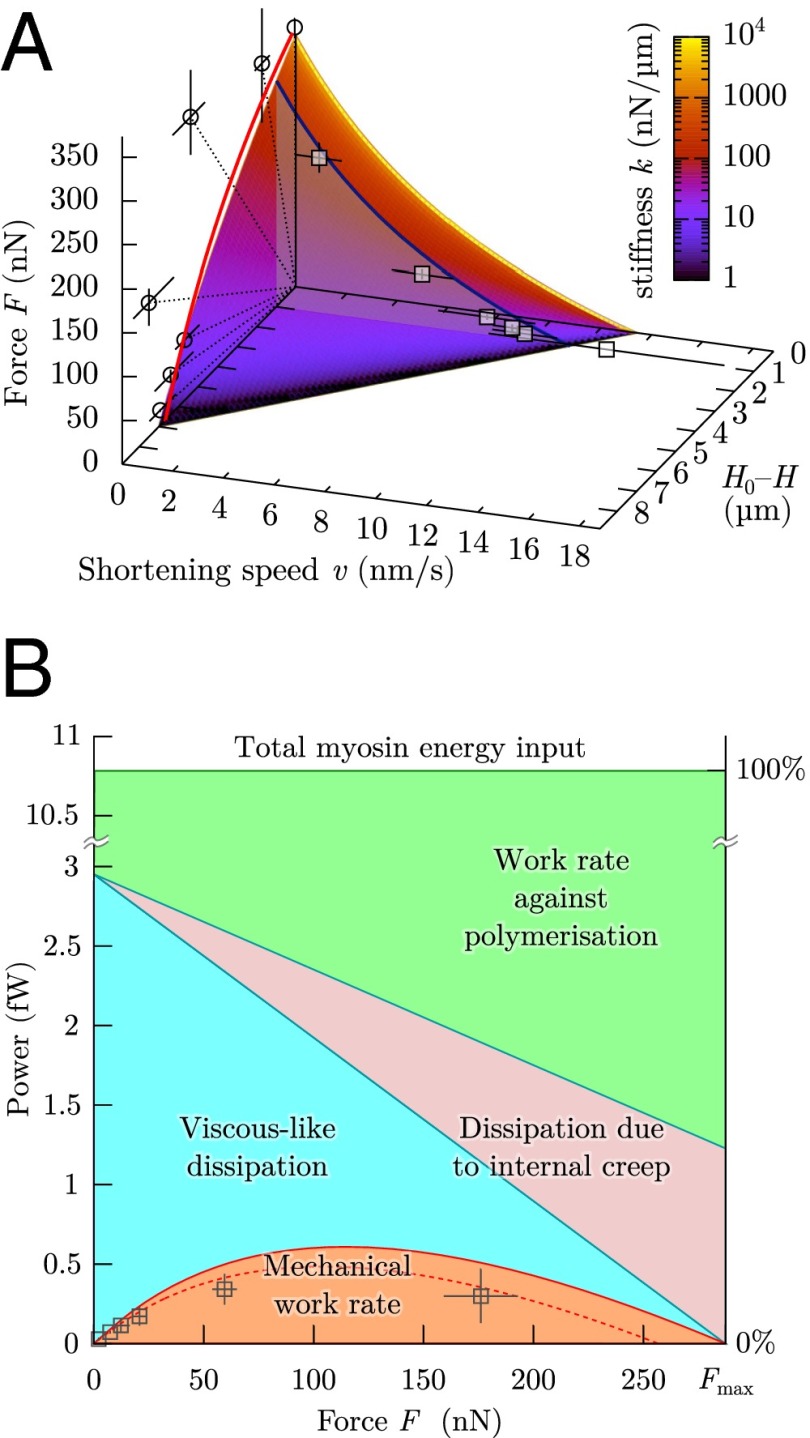
These phenomena regulate cell length. For low external force, myosin-driven retrograde flow is high, because the tension that opposes it is small, and the balance between retrograde flow and polymerization speed is obtained when the cell has significantly reduced its length $L_e$ (Fig. 2A). This length $L_e$ is, thus, a tradeoff between the speed $v_{\text{t}}$ at which actin treadmilling produces new cortex (SI Text, S3) and the rate of myosin-generated contractile strain $1/{\tau }_c={\sigma }_{\text{a}}/\left(2{\tau }_{\alpha }E\right)={\alpha }_{\mathrm{myo}}{\left(\ell \beta \right)}^2/\left(2{\tau }_{\mathrm{myo}}\right)$, which is itself the result of the frictional resistance of cross-linkers to myosin contraction. Indeed, in the 1D toy problem, the equilibrium length of the system is $2{\tau }_c{v}_{\text{t}}$ for $k\ll k_c$, and thus, the force developed by the external spring is $F=k\left(L_0-2{\tau }_c{v}_{\text{t}}\right)$. In the 3D full model of the cell cortex, this equilibrium length is slightly modified as a function of its geometry but still proportional to the product ${\tau }_c{v}_{\text{t}}$ (SI Text, S5.3). This equilibrium length is reached when the treadmilling speed balances exactly the speed at which myosin in the bulk contracts the boundaries of the existing cortex through a retrograde flow that involves the whole of the cortex but is maximum in distal regions (Fig. 3D). This type of competition between the protrusive contribution of actin polymerization and the contractile contribution of myosin is, of course, noted in crawling cells (40); it is also observed in immobile cells, where centripetal movement of actin monomers within filaments is noted, even when adhesive structures are limited to a fixed location on a micropattern (18). Thus, the cell-scale model and experiments allow us to determine the speed of treadmilling, which is a molecular-scale quantity. We find $v_{\text{t}}=6.5\pm 1.5$ nm/s in the 1D model and 4 nm/s for the 3D model, values that are in agreement with the literature value (18) of $4.3\pm 1.2$ nm/s. From the 1D model, we also obtain the relaxation time of the cross-linked actomyosin network, ${\tau }_{\alpha }=\mathrm{1,186}\pm 258$ s, consistent with elastic-like behavior for frequencies higher than ${10}^{-3}$ Hz, the contractile characteristic time ${\tau }_c=521\pm 57$ s, consistent with a 24-min completion of actin superprecipitation (33), and ${\sigma }_{\text{a}}S=\left(2.0\pm 0.9\right)\cdot {10}^3$ nN (SI Text, S3.6). These values fit both the plateau $\left(v=0\right)$ force vs. stiffness experimental results (Fig. 2A) and the dynamics of the experiments (Fig. 2B and Fig. S4). Without additional adjustment, they also lead to predictions of the dynamical adaptation of the loading rate of a cell between microplates of variable stiffness (14) (Fig. 2C) and the force–velocity–length phase portrait of the experiments (Fig. 4A).

Fig. 4.

Liquid-like motor properties of cells. (A) The rheological model leads to a Hill-type Eq. 3, which matches quantitatively the experimental data both during loading (blue curve at $L_0-L=1\mu \text{m}$, force velocity in 1D model; boxes, experiments) and at equilibrium (surface intercept with $v=0$, 1D model; red curve, 3D model; circles, experiments). Dotted lines correspond to the force–distance relationship imposed by a given microplate stiffness k. Same parameters are used as in Fig. 2. (B) Power use in a microplate experiment as a function of the external load F: only a small part of the load-independent myosin power is being transmitted to the cell environment as mechanical power; the rest is dissipated internally or compensates the antagonistic role of polymerization. Boxes are the experimental results to be compared with the dashed line, which is mechanical power at $L_0-L=1\mu \text{m}$. Solid lines correspond to $L=L_0$. Same parameters are used as in Fig. 2.

From an energetic point of view, it may seem very inefficient to use up energy for these two active phenomena that counterbalance one another. However, in a great number of physiological functions, such as cytokinesis and motility, either or both of actin polymerization and myosin contraction are crucial. It is, therefore, highly interesting that, combined together, they provide a spring-like behavior to the cell while preserving its fluid nature, endowing it with the same resilience to sudden mechanical aggression as the passive mechanisms developed by some organisms, such as urinary tract bacteria (41) and insects (42).

Single Cells Have Similar Energetic Expenses to Muscles.

These antagonistic behaviors of polymerization and myosin contractility entail energy losses, which define a range of force and velocity over which the actomyosin cytoskeleton is effective. The study of the energetic efficiency of animal muscle contraction was pioneered by Hill (43) (Fig. S5A), who determined a law relating force F and speed of shortening v: $\left(F+a\right)\left(v+b\right)=c,$ where a, b, and c are numerical values that depend on two values specific of a given muscle, namely a maximum force, a maximum speed, and a universal empirical constant. Hill’s law (43) was then explained using a model based on the muscle molecular structure by Huxley (22). Recently, we have shown that a law of the same form describes the shortening and force generation of cells in this setup (13). In particular, the maximum attainable force and velocity are caused by energy losses. The model can shed light on the molecular origin of these losses and leads to the quantitative force–velocity diagrams in Fig. 4A. Indeed, in terms of F and v, Eq. 2 yields (SI Text, S3.5)

$$\left(\frac{F}{S}+E\right)\left(v+2v_{\text{t}}+v_{\alpha }\right)=\left({\sigma }_{\text{a}}+E\right)v_{\alpha }-\frac{L\dot{F}}{2S}.$$ [3]

Here, $v_{\alpha }=L/\left(2{\tau }_{\alpha }\right)$ can be understood as an internal creep velocity. The right-hand side corresponds to the source of power (minus the internal elastic energy storage term $L\dot{F}/2$), and the left-hand side is the power use (up to a constant $E{v}_{\alpha }$ added to both sides). The formal similarity of this law with Hill’s law for muscles is not a surprise when one compares this model with Huxley’s model of striated muscle contraction. Indeed, the main components in both models are an elastic structure with transient attachments and an ATP-fueled prestretch of the basic elements of the systems, which when released, generates tension, contraction, or a combination of the two. Treadmilling $v_{\text{t}}$ in our model superimposes an effect similar to the ones already present. It is easiest to understand this law in the extreme cases of zero speed or zero load, which correspond to maximum contractile force and maximum contraction speed, respectively (Fig. S5B).

The case of zero load, $F=0$, corresponds to the highest velocity. In the case of muscle contraction, the fastest sliding of actin relative to myosin filaments is limited in Huxley’s model by the rate at which myosin heads detach after their stroke, because myosin heads that remain bound to actin will get entrained and exert an opposing force to the motion. This transient resistance is similar to friction. In our nonmuscle actomyosin model, cross-linkers also need to unbind so that the actomyosin network, which is elastic at short times, fluidizes and flows. The velocity reached is, thus, a decreasing function of the relaxation time ${\tau }_{\alpha }$.

Zero speed, $v=0$, corresponds to microplates of infinite stiffness. If, in addition, protrusion through actin treadmilling is blocked, $v_{\text{t}}=0$, there is no net deformation of the network (or sliding of the filaments in Huxley’s model); however, energy is still being dissipated: indeed, myosin motors will still perform power strokes and generate tension in the network, but nearby cross-linkers and myosins themselves will also detach at the rate $1/{\tau }_{\alpha }$. This detachment will result in the local loss of the elastic energy that had been stored as tension of the network without resulting in a global deformation, corresponding to some internal creep. This time, the maximum force is an increasing function of relaxation time ${\tau }_{\alpha }$. In nonmuscle cells, actin treadmilling is still present when the cell edge is immobile (18) and reduces the maximum force that can be attained, because part of the myosin power will be used to contract this newly formed cortex.

In the intermediate regimes where neither F nor v are zero, the term $Fv$ corresponds to the actual mechanical work performed against the external load (Fig. 4B). This work uses up the part of myosin energy that is not dissipated by internal creep, by effective friction or working against the actin-driven edge protrusion.

Discussion

The model described here is based on a simple description of collective dynamics of actin and myosin that is consistent with observations at the protein scale (18) but does not include molecular sensitivity of the dynamics or actively driven reorganization of the actomyosin cortex (SI Text, S3.9 and Fig. S1). We find that the linear rheological law that arises from this description predicts accurately the rigidity-sensing experiments that we performed over a wide range of external rigidity (Fig. 2A). The dynamics of cell pulling are also recovered (Fig. 2 B and C), and we show that their similarity with the dynamics of muscle contraction (43) are caused by the parallelism that exists between actomyosin dynamics in nonmuscle cells and the dynamics of thin and thick filaments in muscle (22) (Fig. S5). Because the model is based on the collective dynamics of myosin and actin filaments, it yields an understanding of their role in mechanosensitivity: myosin provides a contractile stress ${\sigma }_{\text{a}}$, which will, in turn, generate traction forces at the cell–substrate contact area. In cases where ${\sigma }_{\text{a}}$ is in excess to these traction forces (which resist cell contraction), a retrograde flow is generated, and the cell contracts and deforms its environment. This retrograde flow is limited by the time needed by the actin network to fluidize (viscoelastic relaxation time ${\tau }_{\alpha }$), and force-dependent. Retrograde flow also works against actin protrusion at the cell edge: we hypothesize that this antagonism regulates cell shape and show in the case of our parallel microplates setup that this regulation of cell length determines the mechanosensitive features of cells. Because cells between microplates present similar features as cells spreading on a flat substrate, we suggest that a competition of retrograde flow and protrusion modulated by the stiffness of the environment could be the means by which cell area is regulated (Fig. S3C). The existence of a deformation set-point had already been speculated on micropillar array experiments (35) and used as a hypothesis in modeling work (19); here, we shed light on its relationship with molecular processes and retrograde flow. Because the deformation set-point is obtained as a balance between protrusion and contraction, it is versatile and can be tuned by the many pathways known to affect either of these. Indeed, biochemical regulation tunes the material properties, thus shifting the mechanosensitive response that we predict (Fig. 2D). Undoubtedly, cells lose energy in such an antagonistic mechanism, which we quantify in Fig. 4B. However, the total power of myosin action that we calculate for a single cell is of the order of 10 fW, which is three orders of magnitude less than the total power involved in cell metabolism (SI Text, S3.8). It is, thus, not surprising that this energy expense is not optimized in nonmuscle cells, because the evolutionary pressure on this cost can be deemed very low, whereas the same structure confers to the cell its mechanical versatility and reactivity to abrupt mechanical challenges. Thus, the cell may be likened to a wrestler ready to face a sudden struggle and a commuter ready for a sudden jerk: they will maintain a higher muscle tone than necessary for standing, having their own muscles work against one another. Maintaining this muscular tone is an expense of energy, but the benefit of resisting assaults greatly exceeds this cost.

Materials and Methods

Cell Culture, Fibronectin Coating, and Drugs.

The rat embryonic fibroblast-52 (Ref52) line with YFP-paxillin, provided by Alexander D. Bershadsky (Weizmann Institute, Rehovot, Israel), and the C2-7 myogenic cell line, a subclone of the C2 line derived from the skeletal muscle of adult CH3 mice provided by Denise Paulin and Zhigang Xue (Université Paris-Diderot, Paris), were both cultured and prepared using the procedure described in ref. 13. Glass microplates and in the case of the experiment shown in Fig. S3B, the glass coverslip at the bottom of the chamber were coated with 5 μg/mL as described in ref. 13. In experiments described in SI Text, S1 and Fig. S6, 1 μM Colchicin was used. For blebbistatin treatment discussed in SI Text, S3.7, cells were illuminated through a high-pass colored glass filter (03FCG089; Melles Griot), transmitting only wavelengths higher than 575 nm to avoid phototoxicity and photoinactivation of blebbistatin.

Experimental Procedure.

Ref52 or C2-7 cells were used in microplate experiments as described in ref. 14 with the same equipment and reagents. Cells were then suspended in a temperature-controlled manipulation chamber filled with culture medium, and fibronectin-coated microplates were brought in contact with a single cell as described in ref. 13. After a few seconds, the two microplates were simultaneously and smoothly lifted to 60 $\mathrm{\mu }\text{m}$ from the chamber’s bottom to get the desired configuration of one cell adherent between two parallel plates. One of the plates was rigid, and the other could be used as a nanonewton force sensor (44). By using flexible microplates of different stiffness values, we were able to characterize the effect of rigidity on force generation up to a stiffness of about 200 nN/$\mathrm{\mu }\text{m}$. To measure forces at an even higher stiffness, we used a flexible microplate of stiffness $\simeq 10$ nN/$\mathrm{\mu }\text{m}$ but controlled the plate-to-plate distance using a feedback loop, maintaining it constant regardless of cell force and plate deflection (14, 44). Concurrently, we visualized cell spreading under bright-light illumination at an angle perpendicular to the plane defined by the main axis of the two microplates and analyzed the dynamics. For conditions referred to as low stiffness, such experiments with $n=5$ Ref52 cells and $n=4$ C2-7 cells were analyzed. For conditions referred to as infinite stiffness, again, $n=5$ Ref52 cells and $n=4$ C2-7 cells were analyzed. In both cases, the distribution of values obtained for the different cell types was not significantly different (Fig. S7). Additionally, experimental data in Figs. 2 A and B, 3C, and 4A are replotted from ref. 13.

Additionally, $n=4$ Ref52 cells were used in experiments using another experimental procedure, allowing us to image the adhesion complexes at one of the plates as in ref. 34. Briefly, total internal reflection fluorescence (TIRF) microscopy is performed through the rigid glass plate at the bottom of the chamber. A fibronectin-coated flexible plate is put in contact with the cell after sedimentation, and its deflection is imaged on a photosensitive detector. A feedback procedure is applied as in ref. 13 to mimic an infinite stiffness of the flexible microplate.

Image Analysis and Geometric Reconstruction.

Images were treated with ImageJ software (National Institutes of Health). For side-view experiments, six geometrical points were identified at each time position corresponding to the four contact points of the cell surface with the microplates and the two extremities of the cell equator (i.e., the midpoints where cell surface is perpendicular to microplates). Assuming a symmetry of revolution, these points define uniquely the cell equatorial radius $R_c$, the average radius at the plates $R_p$, the cell length L, and the average curvature of the cell surface κ (average of the inverse of the radii of the circles shown in Fig. S3A). For bottom-view experiments, only the radius $R_p$ at the bottom plate can be acquired dynamically. The initial diameter of cells when still spherical was measured using transmission image microscopy; it was used as the value $L_0$ and found to be consistent with side-view measurements of $L_0$. In the case of infinite stiffness, we assumed that the curvature of fully spread cells viewed from the bottom behaved as the curvature of side-viewed cells: $\kappa L_0=1.80\pm 0.06$ $\left(n=9\right)$. This assumption allowed us to estimate the fully spread radius at the equator, $R_c$, and use $n=13$ experiments for identifying data in the fully spread configuration for infinite stiffness.