The heat released during catalytic turnover enhances the diffusion of an enzyme

Abstract

Recent studies have shown that the diffusivity of enzymes increases in a substrate-dependent manner during catalysis^1,2. Although this observation has been reported and characterized for several different systems^3–10, the precise origin of this phenomenon is unknown. Calorimetric methods are often used to determine enthalpies from enzyme-catalysed reactions and can therefore provide important insight into their reaction mechanisms^11,12. The ensemble averages involved in traditional bulk calorimetry cannot probe the transient effects that the energy exchanged in a reaction may have on the catalyst. Here we obtain single-molecule fluorescence correlation spectroscopy data and analyse them within the framework of a stochastic theory to demonstrate a mechanistic link between the enhanced diffusion of a single enzyme molecule and the heat released in the reaction. We propose that the heat released during catalysis generates an asymmetric pressure wave that results in a differential stress at the protein–solvent interface that transiently displaces the centre-of-mass of the enzyme (chemoacoustic effect). This novel perspective on how enzymes respond to the energy released during catalysis suggests a possible effect of the heat of reaction on the structural integrity and internal degrees of freedom of the enzyme.

Externally induced temperature spikes—through the use of laser pulses, for example—can have dramatic effects on enzyme catalysis and protein conformations¹³. Thus, pyramine and green fluorescent protein have been shown to blink with characteristic frequencies when excited with a laser. Some authors^14,15 have related this blinking to local temperature and pH changes. Yet, no equivalent effect has been attributed to the heat exchanged in an enzyme-catalysed reaction despite the fact that some enzymes, like catalase, release enough heat to unfold a protein¹⁶.

Fluorescence correlation spectroscopy (FCS) results obtained in experiments similar to those presented here^1,2 have demonstrated that the diffusion coefficient (D) of urease increases in the presence of its substrate¹. These authors explored various potential mechanisms that might account for this enhanced diffusion, including global temperature increase of the solution, charged product induced electrophoresis, and pH changes around the enzyme immediately following catalysis. Recently, the same group has shown that the diffusion coefficient of catalase, which mediates the conversion of hydrogen peroxide into water and oxygen, also increases in a substrate-dependent manner², ruling out charge or pH as a general explanation. They have also ruled out global or local temperature changes of the solution to explain the enhanced enzyme diffusion phenomenon¹. More recently, these authors have proposed that the enzyme diffusion coefficient increase arises from chemo-tactic behaviour in which the enzyme preferentially diffuses towards higher substrate gradients, although they provided no mechanism by which this may occur².

Here we performed a series of experiments and carried out a number of crucial controls to show that when enzymes catalyse reactions, the heat released in the process is responsible for accelerating the protein’s centre-of-mass, giving rise to the enhanced diffusion coefficient observed by FCS. We present a stochastic theory that predicts the linear dependence observed between the diffusion coefficient (measured by FCS) and the reaction rate V (measured by bulk enzymatic assays), and demonstrate that the coefficient of proportionality depends linearly on the enthalpy released by a single chemical reaction.

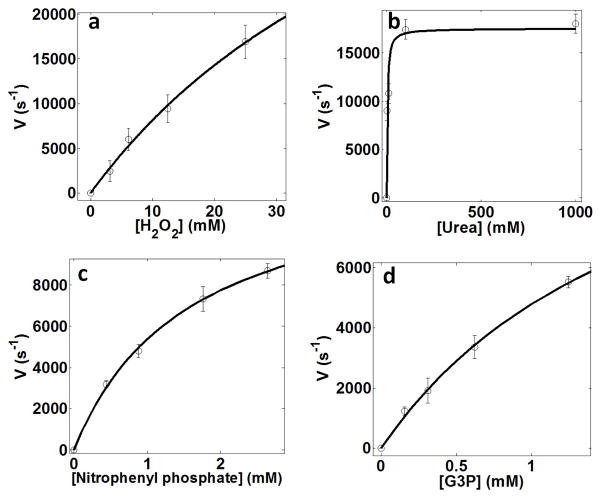
We studied four enzymes: catalase, urease, alkaline phosphatase and triose phosphate isomerase (TIM) (see Supplementary Information for more details on the enzymes). The rates of reaction catalysed by these enzymes and normalized by theenzyme concentration, were determined as a function of the substrate concentrations, V([S]), using bulk enzymatic assays (Extended Data Fig. 1). All enzymes followed Michaelis–Menten kinetics with k_cat and K_M values in agreement with those previously reported in the literature^17–20 (Table 1).

Table 1.

Kinetic, calorimetric parameters of the enzymes and chemical reactions studied

	KM (mM)	kcat (s−1) ×104	ΔH (kJ mol−1)	α(m2) × 10−16
Catalase	62	5.8	−100	10 (9.6–11)
Urease	3	1.7	−59.6	4.5 (3.8–5.3)
Alkaline phosphatase	1.6	1.4	−43.5	16 (14–18)
Triose phosphate isomerase	1.8	1.3	−3.00	−2.5 (−6.1–1.1)

The Michaelis constant K_M and maximum turnover number k_cat are obtained from the fit to a Michaelis–Menten curve for the reaction rate as a function of substrate concentration (Extended Data Fig. 1). Values are in agreement with the ones from the supplier (Sigma) and found in the literature^17–20. ΔH is the enthalpy of the chemical reaction measured in bulk; values are reported in the literature for catalase³⁰, urease¹, triose phosphate isomerase²² and measured by isothermal titration calorimetry for alkaline phosphatase (see Extended Data Fig. 2). α is the coefficient of proportionality between the diffusion coefficient and the reaction rate, in parentheses is the 95% confidence interval.

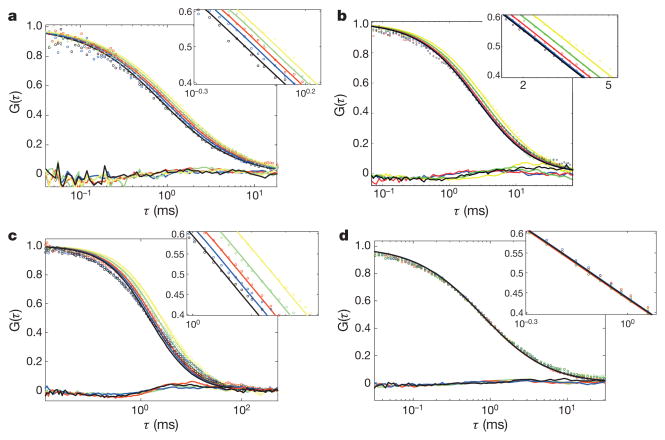
FCS experiments of the fluorescently labelled enzymes were carried out in parallel to bulk assays to generate fluorescence intensity correlation functions, G(τ), as a function of substrate concentrations and initial velocities using previously described protocols for monitoring each enzymatic activity^12,13. These correlation functions were fit by the normal diffusion of a single species in a dilute solution to obtain the diffusion time (τ_D) and molecular occupancy of the labelled molecules within the confocal volume of observation²¹ (see Methods). Measurements were performed at a protein concentration of 1 nM for all enzymes. The FCS curves are shown in Fig. 1. The diffusion coefficient D can be calculated from the diffusion time τ_D using the radius, r, of the illuminated circular area crossed by the molecules according to: D =r²/4τ_D. The radius r was determined to be 500 nm by monitoring the diffusion of a free dye with a known diffusion coefficient through the illuminated area. Using the bulk assays to relate the substrate concentration to the enzyme’s specific activity, we find a linear dependence between the normalized relative increase in diffusion coefficient, (D − D₀)/D₀, and the reaction rate for the enzyme systems (Fig. 2a–d).

Figure 1. FCS data and residuals of the fits.

G(τ) is the normalized correlation function. Insets: zoom around the inflexion point. Lines are fits by a normal diffusion model with a single diffusive species. a, Catalase. Hydrogen peroxide concentration: yellow, 0 mM; green, 3 mM; red, 6 mM; blue, 12 mM; black, 25 mM. b, Urease. Urea concentration: yellow, 0 mM; green, 1 mM; red, 10 mM; blue, 100 mM; black, 1 M. c, Alkaline phosphatase. p-Nitrophenylphosphate concentration: yellow, 0 mM; green, 0.44 mM; red, 0.88 mM; blue, 1.74 mM; black, 2.64 mM. d, TIM. D-Glyceraldehyde 3-phosphate concentration: yellow, 0 mM; green, 0.15 mM; red, 0.31 mM; blue, 0.62 mM; black, 1.3 mM.

Figure 2. Enhanced diffusion as a function of the reaction rate.

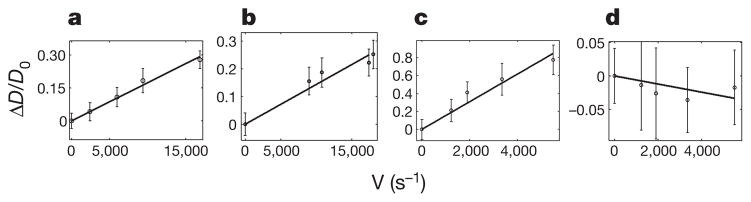
a–d, Dimensionless change in diffusion coefficient (ΔD =(D − D₀)/D₀) as a function of the reaction rate for catalase (a), urease (b), alkaline phosphatase (c) and triose phosphate isomerase (d). Error bars represent the standard deviation of 10 measurements.

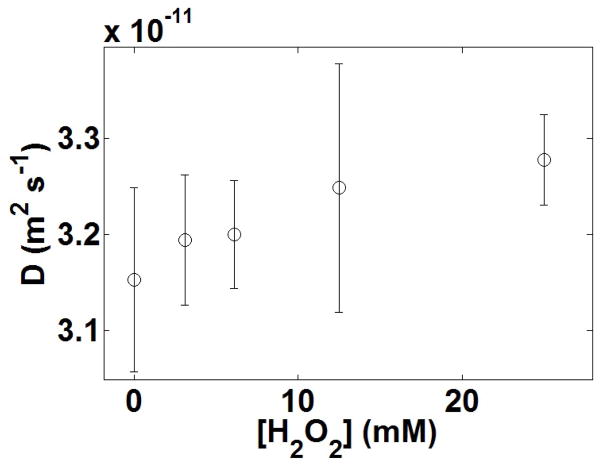
To confirm that the observed increase in diffusion coefficient is a result of the chemical reaction itself and not simply due to the binding or unbinding of the substrate, we performed control experiments with catalase using its non-competitive reversible inhibitor, sodium azide. FCS measurements were repeated for catalase in the presence of 5 mM sodium azide and a high concentration of substrate (25 mM hydrogen peroxide). Under these conditions, the enzyme is known to associate with and dissociate from the substrate without forming any product¹⁷. In the presence of inhibitor, we observe no increase in the diffusion coefficient relative to the measurements performed in the absence of substrate, indicating that the enhanced diffusion of catalase depends on the enzymatic reaction taking place and not just on the association or dissociation of the substrate to the enzyme.

To rule out other potential indirect effects on the apparent diffusion coefficient of the labelled diffusing enzymes (such as convective flows owing to oxygen bubbling, as in the case of catalase), we carried out experiments in which non-labelled, catalytically active catalase, in the presence of its substrate, was mixed with fluorescently labelled urease in the absence of its substrate. Increased diffusion of the labelled urease molecules was observed only under conditions when the concentration of hydrogen peroxide was greater than 100 mM and catalase concentration was above 5 nM. These results show that, below these concentrations, neither oxygen bubbling, nor global heating of the solution owing to the heat released by other molecules in the reaction, are responsible for the enhanced diffusion of enzymes observed in the presence of their substrate. Accordingly, all the results analysed here were obtained below these concentrations to ensure that only first-order, direct effects were being monitored (see Extended Data Fig. 3 for more details). Local heating of the solvent around the enzyme following a turnover event can also be eliminated because assuming the reaction heat is moved into a 1 nm thick spherical shell surrounding catalase, which we assume to be a 4 nm radius spherical molecule, and using water’s heat capacity, the local temperature of this shell would only increase by 0.15 K (see Supplementary Information).

Catalase, urease and alkaline phosphatase, which exhibit enhanced diffusion in the presence of their substrate (Fig. 2a–c), catalyse chemical reactions that are strongly exothermic (above 40 kJ mol⁻¹). Thus, we wondered whether the effect of the heat of the reaction on the enzyme itself could be responsible for the increased in diffusion coefficient observed upon catalysis. To test this idea we performed a negative control with triose phosphate isomerase (TIM). If the heat of the reaction is responsible for the increase in the diffusion coefficient observed, it follows that no such effect should be seen if the reaction is not exothermic or if it is only slightly so. TIM catalyses the reversible interconversion of the triose phosphate isomers dihydroxyacetone phosphate and D-glyceraldehyde 3-phosphate. The enthalpy of this reaction is small (−3 kJ mol⁻¹; ref. 22). Consistent with the hypothesis formulated here, FCS experiments with TIM and diffusion coefficient analysis revealed no enhancement in the diffusion of the enzyme in the presence of its substrate throughout the range of substrate concentrations studied here (0 to 1.2 mM of D-glyceraldehyde 3-phosphate corresponding to reaction rates ranging from 0 to ~6,000 s⁻¹) (Fig. 2d). Table 1 summarizes thermodynamic and kinetic parameters of each enzyme investigated.

On the basis of these observations, we propose that the increase in diffusion coefficient of the enzyme upon catalysis has its origin in an effect similar to that observed in photoacoustic spectroscopy. Here a vibrationally excited protein relaxes by dissipating its energy into the solvent through acoustic waves that are generated from the transient expansion and recompression of the protein immediately following excitation that can be detected by a microphone²³. Likewise, we propose that an enzyme expands, albeit asymmetrically, following the release of the heat of reaction (a process we call ‘chemoacoustic effect’). The asymmetry is due to the location of the catalytic site with respect to the enzyme’s centre-of-mass, as is the case in urease, catalase and alkaline phosphatase. The asymmetric pressure wave—following a catalytic event—should result in differential stress at the protein–solvent interface. The solvent’s response is twofold: it dissipates energy through an acoustic wave and, more importantly, pushes back on the enzyme as dictated by Newton’s third law, transiently displacing its centre-of-mass. In the Supplementary Material we compute an upper bound on the pressure exerted by the expanding protein on the solvent (about 500 pN nm⁻²).

To validate this interpretation, we performed experiments in which we directly excited the catalase haem group using a laser line at 402 nm (the Soret band of catalase is centred at 405 nm (ref. 24) and this transition possesses a fluorescence quantum yield Q <10⁻⁵)²⁵. In these experiments we sought to determine if the heat released upon radiationless de-excitation of the enzyme could also lead to an increased diffusion coefficient of the catalyst. Indeed, an increase of about 50% in the diffusion coefficient of the enzyme in the range of power between 0 and 1 mW was observed in these experiments (Extended Data Fig. 4), indicating that the local heat released by the haem in its transition from the excited to the ground state also generates a centre-of-mass motion of the enzyme (see Supplementary Discussion).

A stochastic model (detailed in the Supplementary Information and Extended Data Figs 6, 7 and 8) describes the enhanced diffusion upon catalysis in terms of the heat released by the chemical reaction. In this model, we assume that enzymes transiently diffuse more quickly—with diffusion coefficient D₁—for some short period of time, δt, following a chemical reaction. Otherwise, the enzyme displays its diffusion coefficient in the absence of substrate, D₀. The net diffusion coefficient in the presence of substrate, D, is therefore the ensemble average over both subpopulations with the probability of observing an enhanced diffusion proportional to V, the reaction rate. We then relate the enhanced diffusion coefficient, D₁, to the amount of heat, Q, evolved by an enzymatic reaction. To do so, we assume that the kinetic energy of the enzyme’s centre-of-mass immediately following a reaction is proportional to some fraction γ of Q. From this simple model, we obtain the following expression

$$D=D_0+\frac{2\gamma Q}{3{\zeta }^2}mV\equiv D_0+\alpha V$$

which shows a diffusion coefficient enhancement linear in V and Q, where m is the mass of the enzyme, δt =m/ζ is the relaxation timescale associated with the enzyme displacement following an enzymatic turnover, and ζ is an effective friction coefficient for the enzyme (see Supplementary Materials).

The parameter α describes the proportionality between the diffusion coefficient and the rate of the reaction. α itself depends on γ, the proportion of catalytic heat contributing to the enhanced translation of the centre-of-mass of the enzyme. As the protein’s structure may dictate the precise mechanism by which enzymes dissipate catalytic heat, there is no simple correlation between the enhanced diffusion quantified by α and the enthalpy of the chemical reaction (see Table 1). For instance, the active sites of urease (two nickel atoms, see Extended Data Fig. 5a) are situated at the protein–solvent interface. By contrast, the haem sites of catalase (Extended Data Fig. 5b) are buried deep inside a highly conserved structure situated more than 20 Å from the nearest molecular surface²⁶. Accordingly, the heat released during catalysis may partition differently between the centre-of-mass and the internal degrees of freedom in these two proteins. In fact, time-resolved crystallography coupled with single-crystal microspectroscopy has been used to measure the correlation of electronic transitions with structural transitions during catalysis in catalase from Proteus mirabilis. This study indicates that the catalytic event is accompanied by small structural changes of the enzyme²⁷. It is possible that for catalase, part of the heat released during the chemical reaction is either absorbed by changes in the enzyme’s conformation and/or dissipated through the protein’s internal degrees of freedom, reducing its effect on the displacement of its centre-of-mass. Future simulations and experiments with different systems may shed light on the structural basis for energy dissipation and the partitioning of the heat of the reaction between the centre-of-mass and the internal degrees of freedom of the enzyme.

Here we considered catalytic reactions by globular proteins with freely diffusing substrates. However, many processive molecular machines (for example DNA polymerases, RNA polymerases, theribosome, and soon) hydrolyse NTPs and generate forces to achieve directed motion along linear templates. It is interesting to speculate that some of these systems may have evolved to absorb or indeed actively ‘channel’ the energy released by enzyme catalysis towards useful purposes (for example, enhanced diffusion, swimming, or even directed motion).

It is traditionally assumed that the heat released by a turnover event does not perturb an enzyme. Yet atomic force microscopy experiments have shown enhanced fluctuations of a cantilever tip placed atop a molecule of egg-white lysozyme in the presence of its substrate²⁸. The results presented here, in turn, indicate that the heat of the reaction can result in a centre-of-mass acceleration of the catalyst, suggesting a critical rethinking of how the reaction may affect the enzyme. For example, it is possible that the structural stability of catalase contributes to its high catalytic efficiency and observed turnover number, and that this parameter in many cases may be determined by the effect of the heat of the reaction on the structural integrity of the enzyme. In fact, studies of adenylate kinase have led to the suggestion of local unfolding of a protein domain near the active site by some unknown causing agent²⁹ during the enzymatic cycle—a phenomenon that has been termed “cracking”. Future fluorescence correlation spectroscopy-fluorescence resonance energy transfer experiments will probe how an enzyme’s internal degrees of freedom and structural integrity are perturbed by the heat of the reaction.

Methods, along with any additional Extended Data display items and Source Data, are available in the online version of the paper; references unique to these sections appear only in the online paper.

METHODS

Labelling and purification

Catalase from bovine (Bos taurus) liver, urease from jack bean (Canavalia ensiformis) and alkaline phosphatase from bovine intestinal mucosa were purchased from Sigma Aldrich. Triose phosphate isomerase from Saccharomyces cerevisiae was expressed from a plasmid provided by P. Harbury. Catalase and urease were purified using a size exclusion column (Superdex 75 HiLoad 16/60 Prep Grade, Amersham Bioscience) and stored in sodium phosphate buffer at 0.1 M and pH 7.

Catalase and urease were labelled with Atto 647–maleimide (excitation/emission wavelengths: 647/665 nm, Molecular Probes). First, the protein was reacted with a tenfold excess of dithiothreitol for two hours at room temperature in order to reduce the cysteines. Dithiothreitol was removed using a desalting column (Micro Biospin 6 chromatography column, Biorad). The reaction with the dyes was then performed for four hours at room temperature and 12 h at 4 °C. Finally, the excess of dye was removed using a biospin column. Comparison of the absorbance at 280 nm and the absorbance at 647 nm indicated a labelling efficiency of one dye per molecule. Following the labelling, glycerol was added to 50% and the enzymes were stored at −20 °C.

TIM and alkaline phosphatase were labelled using Atto 647-NHS (N-hydroxy-succinimide. The proteins were dialysed against phosphate buffered saline (PBS), followed by reaction with dye in PBS +20% DMSO for one hour at room temperature. Excess dye was removed by dialysis, and labelling efficiencies of 1–2 dyes per molecule were achieved. Labelled TIM was stored in MOPS 25 mM pH 6.5, 200 mM NaCl at −80 °C. Labelled alkaline phosphatase was stored in 5 mM Tris pH 7.9, 2.5 mM MgCl₂, 50 μM ZnCl₂ + 50% glycerol at 4 °C.

Bulk enzymatic assays

Bulk enzymatic assays were performed using a Jasco V 650 spectrophotometer at 25 °C.

For catalase, we used a 3-ml cuvette agitated with a magnet stir bar to reduce bubbling. The reaction rate V was calculated from the variation of absorbance (ΔA) of hydrogen peroxide (extinction coefficient ε =43.5 M⁻¹ cm⁻¹ at 240 nm^31,32) and the enzyme concentration.

For urease, the reaction was stopped at different times by transferring 100 μl of the reaction mixture to a 1.5-ml microcentrifuge tube containing 500 μl of a 5% (w/v) phenol-nitroprusside solution. 500 μl of a 2% alkaline hypochlorite solution and 150 μl water were added, the mixture was then shaken, and the colour complex was allowed to develop for a minimum of 10 min at room temperature. Ammonia concentrations generated from the urease reaction, represented by the colour complex, were determined at 625 nm and compared to a standard curve made with NH₄Cl³³. Experiments were performed at a final concentration of enzyme c_e = 10 nM.

Alkaline phosphatase assays were performed in diethanolamine 2 M pH 9.8, 1 mM MgCl₂ and 20 μM ZnCl₂, with 20 pM protein and different concentrations of p-nitrophenylphosphate (Sigma). The absorbance of nitrophenoxide at 405 nm was used to follow the reaction (ε =18,000 M⁻¹ cm⁻¹).

TIM assays were performed in triethanolamine 100 mM pH 7.9, in the presence of 0.125 mM NADH, 4 units per ml of glycerol 3-phosphate dehydrogenase (Sigma), and 40 pM TIM. Different concentrations of DL-glyceraldehyde 3-phosphate (MPbio) were added and the change in absorbance of NADH at 339 nm (ε = 6,220 M⁻¹ cm⁻¹) was measured.

The activity of all labelled enzymes was compared to the non-labelled enzymes to ensure that the labelling did not affect the activity of the enzymes.

Isothermal titration calorimetry

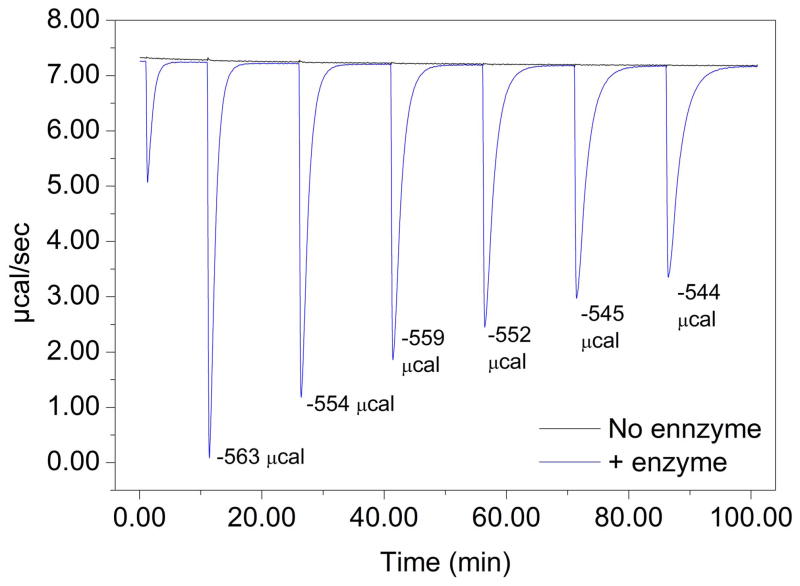
The enthalpies of the reactions catalysed by TIM, catalase and urease in the conditions we used are published elsewhere^1,22,30. We used isothermal titration calorimetry to measure the enthalpy of the hydrolysis of p-nitrophenylphosphate catalysed by alkaline phosphatase in the buffer we used. Reactions were performed at 25 °C in diethanolamine 2 M pH 9.8, 1 mM MgCl₂ and 20 μM ZnCl₂, with 5 nM protein in the cell and 26.5 mM of p-nitrophenyl phosphate in the syringe. Aliquots of 2 μl (0.053 μmol) of substrate were added, and the released heat was measured for 15 min before adding more. The heat of the reaction was calculated by integrating the peaks and dividing by the amount of substrate added. Six additions were performed per experiment, and the experiment was carried out in triplicate. The heat of dilution of substrate alone without enzyme was negligible.

Fluorescence correlation spectroscopy

Fluorescence correlation spectroscopy measurements were performed with a purpose-built confocal microscope. Briefly, a 635 nm line from a high-stability diode LabLaser (Coherent Inc.) was coupled into a single-mode fibre (Thor Labs). The output from this fibre was collimated, reflected off of a polychroic mirror (z488/543/633rpc, Chroma Corp.) and under-filled (β~3) into the back aperture of an infinity-corrected PSF-grade Uplan S apochromat 60×1.2NA water-immersion objective (Olympus America) mounted atop a custom-machined microscope body. Typical incident laser powers were roughly 10–50 μW and were low enough to avoid dye blinking and/or bleaching effects. Emitted fluorescent photons were collected, focused onto a 100-μm pinhole, collimated, split into two emission paths to minimize spurious correlations due to after-pulsing, and finally refocused onto the active areas of two avalanche photodiode (APD) detectors (Perkin Elmer Optoelectronics). The APD outputs were connected to the input channels of an ALV-5000 Multiple Tau Digital correlator. FCS correlation functions were acquired using ALV’s commercial software suite. Experiments were performed at an enzyme concentration of 1 nM. At this nanomolar concentration, subunit dissociation can result in decreased enzyme activity. In order to control protein dissociation and have the same activity in both bulk and FCS experiments, enzymes were kept in ice and measurements were performed simultaneously, in the same substrate solution, at the same temperature (25 °C).

Data analysis

The ALV-5000 Multiple Tau Digital correlator software outputs the data points generating the fluorescence intensity correlation functions, G(τ), presented in Fig. 1 of the main manuscript. These data are fitted (using custom-built Matlab code) by the normal diffusion of a single species in a dilute solution³⁴:

$$G(\tau )=\frac{1}{N}{\left(1+\frac{\tau }{{\tau }_{\mathrm{D}}}\right)}^{-1}{\left(1+\frac{\tau }{{\omega }^2{\tau }_{\mathrm{D}}}\right)}^{-1/2}$$

where N is the average number of molecules in the confocal volume, τ_D is the characteristic diffusion time across the illuminated region and ω is the aspect ratio of the sampling volume (for our custom-built setup: ω =5). Therefore, the only two unknown parameters are N and τ_D. Although the enzyme’s mobility shows small deviation from the free diffusion, as it can be seen in Fig. 1 the determination of τ_D is accurate. We are working at the single molecule level and N is randomly distributed between 1 and 3 for the four enzymes studied. Furthermore, we note that we are working in a regime with no second order effects -meaning that the activity of one enzyme does not affect the diffusion of another enzyme- and that the diffusion coefficient is therefore independent of N. Thus, τ_D is determined by the overall fit, and D =r²/4τ_D where r is size of the beam waist perpendicular to the direction of the propagation of light³⁴.

Extended Data

Extended Data Figure 1. Reaction rate per enzyme molecule as a function of the concentration of substrate.

a, Catalase; b, urease; c, alkaline phosphatase and d, triose phosphate isomerase. Lines are fit to a Michaelis–Menten curve. Error bars represent the standard deviation of 3 measurements.

Extended Data Figure 2. Isothermal titration calorimetry measurement of the heat of hydrolysis of p-nitrophenylphosphate by alkaline phosphatase.

Each peak corresponds to the hydrolysis of 0.053 μmol of substrate. The reaction rate slows as more substrate is added owing to the accumulation of phosphate product inhibiting the enzyme.

Extended Data Figure 3. Diffusion coefficient of non-reactive urease in the presence of active, non-labelled, catalase (1 nM) for different concentrations of hydrogen peroxide.

Even at the highest catalase activity no indirect effects (due to bubbling or global heating of the solution) appreciably increase the diffusion coefficient of freely diffusing urease. Error bars are computed from the standard deviation over 10 measurements.

Extended Data Figure 4. Haem excitation experiment.

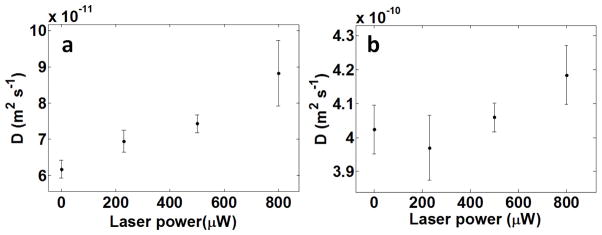
a, Diffusion coefficient of catalase as a function of the laser power at 402 nm. The heat released by the haem enhances the diffusion of the enzyme. b, Diffusion coefficient of free dyes in the presence of non-labelled heat-emitting catalase. Neither the heat generated by the laser power nor the heat released by catalase significantly enhances the diffusion of the dyes. Error bars are computed from the standard deviation over 10 measurements.

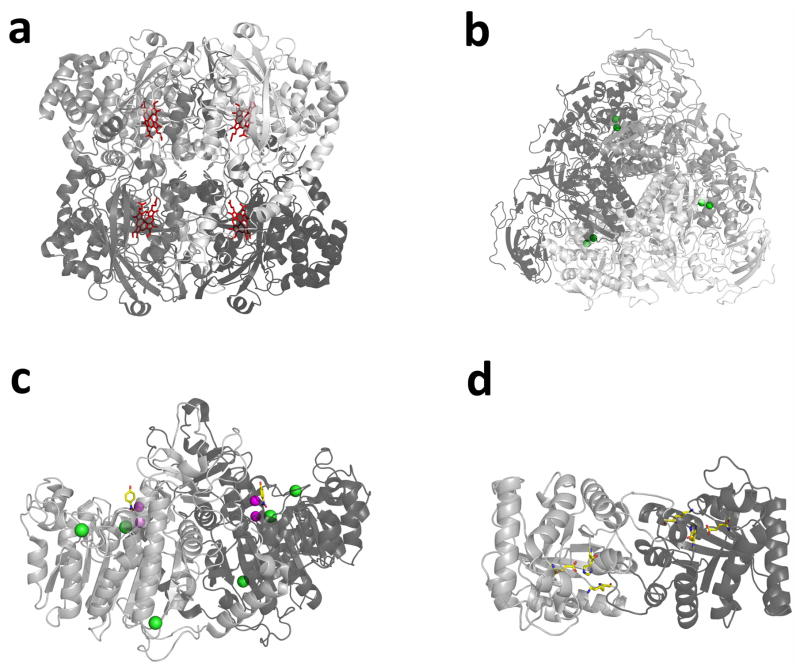
Extended Data Figure 5. Structures of the enzymes studied with active site components highlighted.

Different shades of grey indicate different monomers. a, Catalase (PDB 3NWL). Haem groups are shown as red sticks. b, Urease (PDB 4GY7). Active site nickel ions are shown as green spheres. c, Alkaline phosphatase (PDB 4KJG). Magnesium ions are shown in green; zinc ions are shown in magenta; 4-nitrophenol (hydrolysis product bound at the active site) is shown as yellow sticks. d, Triose phosphate isomerase (8TIM). Active site residues Lys 12, His 95 and Glu 165 are shown as yellow sticks.

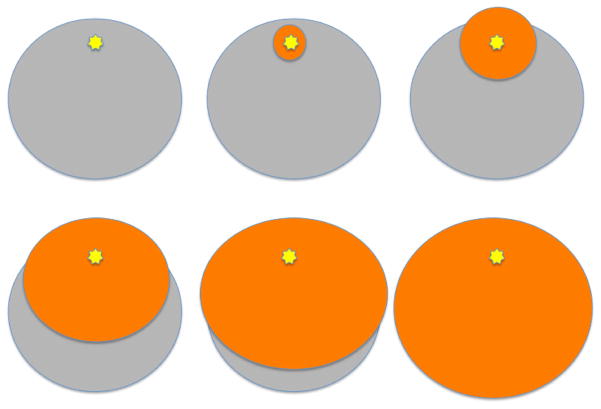
Extended Data Figure 6. Protein deformation progression.

Spread of a radial deformation wave (red) emanating from the catalytic site (yellow star). The protein (grey) has an approximate radius of 4 nm and the deformation wave speed is an estimated 3 nm ps⁻¹.

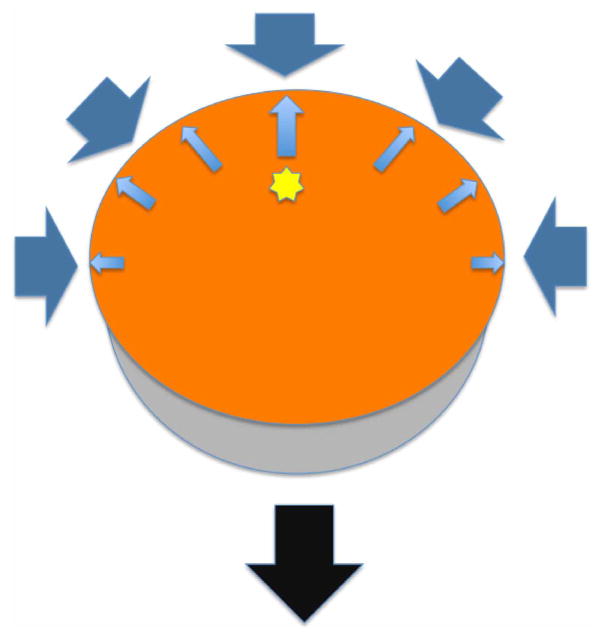
Extended Data Figure 7. Centre of mass translation.

The protein exerts forces on the solvent (small blue arrows). The solvent restoring forces (thick blue arrows) give rise to a protein centre of mass translation (black arrow).

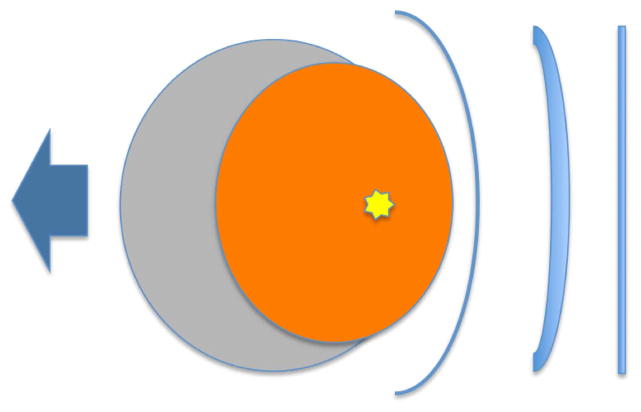
Extended Data Figure 8. Acoustic wave due to deformation.

Here we assume the protein deforms and this generates acoustic waves in the solvent. If these acoustic waves were reflected back on the protein, they would give rise to a centre of mass translation denoted by the blue arrow.