Interbeat Interval Modulation in the Sinoatrial Node as a Result of Membrane Current Stochasticity—A Theoretical and Numerical Study

Abstract

A single isolated sinoatrial pacemaker cell presents intrinsic interbeat interval (IBI) variability that is believed to result from the stochastic characteristics of the opening and closing processes of membrane ion channels. To our knowledge, a novel mathematical framework was developed in this work to address the effect of current fluctuations on the IBIs of sinoatrial pacemaker cells. Using statistical modeling and employing the Fokker-Planck formalism, our mathematical analysis suggests that increased stochastic current fluctuation variance linearly increases the slope of phase-4 depolarization, hence the rate of activations. Single-cell and two-dimensional computerized numerical modeling of the sinoatrial node was conducted to validate the theoretical predictions using established ionic kinetics of the rabbit pacemaker and atrial cells. Our models also provide, to our knowledge, a novel complementary or alternative explanation to recent experimental observations showing a strong reduction in the mean IBI of Cx30 deficient mice in comparison to wild-types, not fully explicable by the effects of intercellular decoupling.

Introduction

The heart rate of a healthy subject shows normal fluctuation behavior called heart rate variability (HRV). HRV sustains complex temporal pattern and not all of its components are well understood. While it is well established that the HRV is modulated by the autonomic nervous system that innervates the sinoatrial node (SAN) via both sympathetic and parasympathetic tracts, a single isolated sinoatrial pacemaker cell also presents intrinsic interbeat interval (IBI) variability (1). Those IBI fluctuations are believed to result from the stochastic characteristics of the opening and closing processes of membrane ion channels, which is at the center of this work.

The ion channels behave stochastically, but because a typical cardiac myocyte contains greater than O(10³) ion channels of each type (2), continuous deterministic equations (e.g., of the Hodgkin-Huxley type) are considered sufficient to describe their kinetics in most models. Recently, however, there is an increasing interest to incorporate ion-channel stochasticity into cardiac electrophysiology models, due to accumulating evidence regarding its importance in both simulation and experimental studies. For example, the stochastic behavior of ion channels in ventricular myocytes of guinea pigs was shown to cause action potential duration (APD) variability even when the heart rate was kept constant (3). Tanskanen et al. (4) have demonstrated in simulations using canine ventricular myocyte kinetics that fluctuations in the L-type Ca²⁺ current during the plateau phase of the AP result in APD variability and in an increased likelihood of early-after-depolarizations. Lemay et al. (5), Pueyo et al. (6), and Heijman et al. (7) showed that stochastic gating of K⁺ and Na⁺ channels in ventricular myocytes affect beat-to-beat variability of repolarization in canine, guinea pig, and human hearts; Lemay et al. (5) showed additionally that ion-channel stochasticity may cause variability in conduction time. These studies clearly point out the relevance of ion-channel stochasticity, at least when considering ventricular myocyte models.

In the SAN pacemaker cells, Wilders and Jongsma (1) were among the first to observe that stochastic channel gating may cause intrinsic stochastic IBI. They showed that a single isolated cell of a rabbit SAN does not beat in a constant rate but actually beats irregularly and that this IBI irregularity could be reconstructed by the SAN kinetic model when adding stochasticity to the ion channels. Consistent findings were later published by Guevara and Lewis (8) using a Monte Carlo model, further supporting the hypothesis that the irregular beating of a single SAN cell is due to the random behavior of the channels. Ponard et al. (9) have extended these studies to pacemaker cell tissues, and evaluated the effect of IBI irregularity in single cells on the rate variability of the global tissue. By modeling three putative origins for IBI, i.e., stochastic gating, stochastic calcium release, and turnover of ion channels, the authors found that the ion channel long-term turnover induces variability pattern that may explain the power-law behavior of HRV.

Although a single pacemaker cell (10) or a ventricular myocyte cell (3) presents IBI and APD variability (respectively), this variability is normally suppressed in the tissue cells congregation due to the gap-junction electrotonic coupling (3,10). The electrotonic coupling is a term referring to the continuous conductive network formed by the expression of conductance channels, or gap-junctions, linking the intracellular space of one myocyte to its neighboring myocytes. Thus, direct spread of current in the myocardium is possible without the generation of new current by APs. The gap-junctions are formed by connexin proteins (Cx), and there are several types of connexins in the mammalian heart. In the mice SAN cells, e.g., gap-junctions are predominantly formed by Cx45, Cx30, and Cx30.2 (11,12). While Cx45, and Cx30.2 are not unique to the SAN, Cx30 is uniquely expressed in the SAN (13).

A previous study has found that when N individual pacemaker cells are coupled with gap-junctions, the IBI variability decreases proportionally to $\sqrt{1/N}$ (10). In other words, the rate variability is impeded by an increased electrical coupling among cells. The electrical coupling among SAN cells was also found experimentally to affect the mean IBI. Gros et al. (13) characterized the role of Cx30 in adult mouse hearts, by comparing several cardiac physiology parameters in control and in Cx30-deficient mice. They found that Cx30-deficient mice exhibited a ∼10% faster heart rate in comparison to control mice. This moderate tachycardia was present even after the injection of atropine and propranolol that inhibits the autonomic nervous system (ANS), suggesting that the rate difference between the two mouse groups was strictly related to the intrinsic electrical properties of the SAN pacemaker cells. The moderating effect of the intercellular electrical coupling via gap-junctions on both IBI variability and mean value is intuitively attributed to the low-pass effect of the electrotonic network established by this coupling. Nevertheless, the exact interrelations among cellular stochasticity, IBI variability, mean IBI, and intercellular coupling are not fully known.

In this work we conduct a theoretical analysis using the Fokker-Planck equation (also known as the Kolmogorov forward equation) and we establish a mathematical relationship between the membrane voltage variance and the mean IBI. Using this novel formulation, we show that with the increasing voltage membrane stochasticity, in addition to the increased beat interval stochasticity, the mean IBI decreases as well. We then demonstrate this principle in numerical simulations of the SAN by employing an updated rabbit SAN model (14). The simulations include single-cell and SAN pacemaker tissue. Our mathematical analysis and numerical simulations show how gap-junction coupling, which reduces the membrane voltage variance, also affects the mean heart rate, in a consistent way with the in vivo experiments of Gros et al. (13) on Cx30-deficient mice.

Materials and Methods

Theoretical modeling

In this section, we develop a mathematical framework that links between stochasticity in the ion-channel gating and the mean IBI in a sinoatrial pacemaker cell. Using the conventional parallel conductor formulation and Kirchhoff’s current law, the cellular membrane voltage, v_m (mV), is described by the following differential equation:

$$\frac{\partial v_m}{\partial t}=-\sum I_{\text{ion}}.$$ (1)

Here, $\sum I_{\text{ion}}$ (pA/pF) represents the summation over all membrane ionic currents (ion channels, pumps, and exchangers). Next, we incorporate an additional stochastic global current I_fluct, which represents the fluctuations of the transmembrane current that are caused due to the stochastic opening and closing of the ion channels (10). I_fluct is defined similarly to the work by Ponard et al. (9) by employing the following Ornstein-Uhlenbeck process:

$$I_{\text{fluct}}\left(t+dt\right)=I_{\text{fluct}}\left(t\right)-\beta I_{\text{fluct}}\left(t\right)\times \Delta t+\xi \times \sqrt{2\times \beta \times \Delta t}\times n\left(t\right),$$ (2)

where n(t) is a normalized zero-mean Gaussian white noise value with a standard deviation of 1 and β = 0.7 ms⁻¹ is a rate constant. This results in I_fluct having a Gaussian distribution with zero mean and a standard deviation of ξ (pA/pF). In this way, the need of explicitly developing and using Markovian models for each channel separately was avoided, dramatically reducing the computational complexity of the simulations. Consequently, a noise term is added to Eq. 1, so that

$$\frac{\partial v_m}{\partial t}=-\sum I_{\text{ion}}+\xi \times n\left(t\right).$$ (3)

Without loss of generality, the first term in the right-hand side of Eq. 3 can be rewritten by separating all elements that are multiplied by v_m or by a nonlinear function of v_m, yielding

$$\frac{\partial v_m}{\partial t}=-g_m\left(v_m,t\right)\left[v_m-\mu \left(v_m,t\right)\right]+\xi \times n\left(t\right),$$ (4)

where g_m(v_m,t) is a general normalized conductivity term (μS/μF) and is a nonpolynomial function of v_m and of time, and μ(v_m,t) is a general voltage term that is also a nonpolynomial function of v_m and of time. For an example of how Eq. 4 is derived for a basic Hodgkin-Huxley model, refer to Section SA in the Supporting Material. Using Eq. 4, we can assume that v_m is normally distributed with a time-varying mean M(t) and a constant variance σ, so that its probability density function, P(v_m,t), is

$$P\left(v_m,t\right)=\frac{1}{\sqrt{2\pi }\sigma }\times \text{exp}\left\{-\frac{{\left(v_m-M\left(t\right)\right)}^2}{2{\sigma }^2}\right\}\triangleq G.$$ (5)

The temporal evolution of P(v_m,t) can be established by solving the following Fokker-Planck equation (15) applied to Eq. 4:

$$\frac{\partial P\left(v_m,t\right)}{\partial t}=\frac{\partial }{\partial v_m}\left\{P\left(v_m,t\right)\times g_m\left(v_m,t\right)\times \left(v_m-\mu \left(v_m,t\right)\right)\right\}+\frac{{\partial }^2}{\partial v_m^2}\left\{P\left(v_m,t\right)\times \xi \right\}.$$ (6)

Using Eq. 5, the left-hand side of Eq. 6 becomes

$$\frac{\partial P\left(v_m,t\right)}{\partial t}=G\times \frac{\left(v_m-M\left(t\right)\right)}{{\sigma }^2}\times \frac{\partial M\left(t\right)}{\partial t},$$ (7)

the first term in the right-hand side of Eq. 6 becomes

$$\frac{\partial }{\partial v_m}\left\{P\left(v_m,t\right)\times g_m\left(v_m,t\right)\times \left(v_m-\mu \left(v_m,t\right)\right)\right\}=G\times g_m\left(v_m,t\right)-G\times g_m\left(v_m,t\right)\times \frac{\partial }{\partial v_m}\mu \left(v_m,t\right)-G\times g_m\left(v_m,t\right)\times \frac{\left(v_m-\mu \left(v_m,t\right)\right)\times \left(v_m-M\left(t\right)\right)}{{\sigma }^2}+G\times \left(v_m-\mu \left(v_m,t\right)\right)\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}=G\times g_m\left(v_m,t\right)-G\times g_m\left(v_m,t\right)\times \frac{\partial }{\partial v_m}\mu \left(v_m,t\right)-G\times g_m\left(v_m,t\right)\times \frac{\left({\left(v_m-M\left(t\right)\right)}^2+M\left(t\right)\left(v_m-M\left(t\right)\right)-\mu \left(v_m,t\right)\left(v_m-M\left(t\right)\right)\right)}{{\sigma }^2}+G\times \left(\left(v_m-M\left(t\right)\right)+\left(M\left(t\right)-\mu \left(v_m,t\right)\right)\right)\frac{\partial g_m\left(v_m,t\right)}{\partial v_m},$$ (8)

and the second term of the right-hand side of Eq. 6 becomes

$$\frac{{\partial }^2}{\partial v_m^2}\left\{P\left(v_m,t\right)\times \xi \right\}=-\xi \times \frac{1}{{\sigma }^2}\times G+\xi \times \frac{1}{{\sigma }^4}\times G\times {\left(v_m-M\left(t\right)\right)}^2.$$ (9)

Inserting Eqs. 7–9 into Eq. 6, and equating the sum of coefficients of v_m – M(t) in both sides of the obtained equation to ensure the solution to any v_m, yield

$$\frac{\partial M\left(t\right)}{\partial t}\times \frac{G}{{\sigma }^2}=-g_m\left(v_m,t\right)\times M\left(t\right)\times \frac{G}{{\sigma }^2}+g_m\left(v_m,t\right)\times \mu \times \frac{G}{{\sigma }^2}+\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}\times G.$$ (10)

By dividing Eq. 10 by G/σ², we finally get

$$\frac{\partial M\left(t\right)}{\partial t}=-g_m\left(v_m,t\right)\times M\left(t\right)+g_m\left(v_m,t\right)\times \mu \left(v_m,t\right)+\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}\times {\sigma }^2.$$ (11)

Note that Eq. 11 is essentially the same as Eq. 4 when ξ = 0 and for v_m = M(t). As we show later in Fig. 6, the IBI is mostly determined by the stochasticity in the phase-4 depolarization of the AP, rather than by the stochasticity in the APD or the minimal v_m value (end-diastolic value, v_min). This can be understood from the much larger impact of the membrane voltage fluctuations on the phase-4 depolarization slope in comparison to the impact on the two other parameters (as will be demonstrated later in Fig. 5). Because we are interested in the relationship between the ion-channel stochastic fluctuations and the sinoatrial cell IBI, we henceforward focus on the depolarization phase, phase 4, of the pacemaker AP. This phase can be typically approximated as linear during the time interval between the minimal v_m value and the threshold value of v_m = −40 mV (Fig. 1 A). Consequently, we can approximate M(t) during this phase by

$$M\left(t\right)\approx M_{min}+\frac{\partial M\left(t\right)}{\partial t}\times t,$$ (12)

and Eq. 11 becomes

$$\frac{\partial M\left(t\right)}{\partial t}=-g_m\left(v_m,t\right)\times \left(M_{min}+\frac{\partial M\left(t\right)}{\partial t}\times t\right)+g_m\left(v_m,t\right)\times \mu \left(v_m,t\right)+\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}\times {\sigma }^2.$$ (13)

To find an approximation for M_min, we return to Eq. 11 and apply it for M(t) = M_min + δ (δ << 1, ≠ 0) because

$$\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}\to -\infty$$

at v_min (see Section SB in the Supporting Material). As in the vicinity of the minimum point ∂M(t)/∂t ≈ 0, we get

$$0\approx -g_m\left(v_{\text{min}},t\right)\times M_{\text{min}}+g_m\left(v_{\text{min}},t\right)\times \mu \left(v_{\text{min}},t\right)+{\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\times {\sigma }^2,$$ (14)

and solving for M_min, we get

$$M_{\text{min}}\approx \mu \left(v_{\text{min}},t\right)+\frac{1}{g_m\left(v_{\text{min}},t\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\times {\sigma }^2.$$ (15)

Because in the deterministic case M_min (σ² = 0) = v_min,det, we can write

$$M_{\text{min}}\approx v_{\text{min,det}}+\frac{1}{g_m\left(v_{\text{min}},t\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\times {\sigma }^2.$$ (16)

Inserting Eq. 16 into Eq. 13, we obtain for phase 4,

$$\frac{\partial M\left(t\right)}{\partial t}\approx -g_m\left(v_m,t\right)\times \left(v_{\text{min,det}}+\frac{1}{g_m\left(v_{\text{min}},t\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\times {\sigma }^2+\frac{\partial M\left(t\right)}{\partial t}\times t\right)+g_m\left(v_m,t\right)\times \mu \left(v_m,t\right)+\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}\times {\sigma }^2,$$ (17)

and thus,

$$\frac{\partial M\left(t\right)}{\partial t}\times \left(1+g_m\left(v_m,t\right)\times t\right)\approx -g_m\left(v_m,t\right)\times \left(v_{\text{min,det}}+\frac{1}{g_m\left(v_{\text{min}},t\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\times {\sigma }^2\right)+g_m\left(v_m,t\right)\times \mu \left(v_m,t\right)+{\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{\text{phase}4}\times {\sigma }^2.$$ (18)

In the deterministic case (σ² = 0, M(t) = v_m(t)), the kinetic model yields a phase-4 slope of ∼112 mV/s and v_min,det = −58 mV. Therefore, by setting σ² = 0 in Eq. 18, we get

$$112\times \left(1+g_m\left(v_m,t\right)\times t\right)\approx g_m\left(v_m,t\right)\times 58+g_m\left(v_m,t\right)\times \mu \left(v_m,t\right),$$ (19)

so when applied back to Eq. 18, we have

$$\frac{\partial M\left(t\right)}{\partial t}\approx 112-\frac{112}{\left(\mu \left(v_m,t\right)+58\right)}\times \left(\frac{1}{g_m\left(v_{\text{min}},t\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\times {\sigma }^2\right)+\frac{112}{g_m\left(v_m,t\right)\times \left(\mu \left(v_m,t\right)+58\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{\text{phase}4}\times {\sigma }^2.$$ (20)

We now apply the mean operator, E{⋅}, on both sides of Eq. 20 to obtain

$$E\left\{\frac{\partial M\left(t\right)}{\partial t}\right\}\approx 112-A\times {\sigma }^2,$$ (21)

where A is defined by

$$A=E\left\{\frac{112}{\left(\mu \left(v_m,t\right)+58\right)}\times \left(\frac{1}{g_m\left(v_{\text{min}},t\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\right)-\frac{112}{g_m\left(v_m,t\right)\times \left(\mu \left(v_m,t\right)+58\right)}\times {\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{\text{phase}4}\right\}.$$ (22)

It is reasonable to assume that the mean values in Eq. 22 equal the deterministic values. As shown in Section SB in the Supporting Material, during the deterministic phase-4,

$$\mu \left(v_m,t\right)\approx -37\text{mV},$$

$$g_m\left(v_m,t\right)\approx 10\mu \text{S}/\mu \text{F},$$

and

$$\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}\approx 0.34{\text{s}}^{-1}/\text{mV},$$

while at v_min + δ,

$$g_m\left(v_{\text{min}}+\delta ,t\right)\approx 6.6\mu \text{S}/\mu \text{F},$$

and

$${\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }\approx -10{\text{s}}^{-1}/\text{mV}.$$

Substituting these values in Eqs. 22 and 21, we eventually obtain

$$E\left\{\frac{\partial M\left(t\right)}{\partial t}\right\}\approx 112+8.3\times {\sigma }^2.$$ (23)

Equation 23 provides a direct relationship between the mean stochastic depolarization slope (∂M(t)/∂t) and the voltage variance σ² (which is a product of the stochastic I_fluct from Eq. 2). The slope directly affects the IBI and hence the activation rate. When the slope increases, the IBI accordingly decreases, and vice versa. Therefore, Eq. 23 suggests that when the membrane voltage variance σ² increases, ∂M(t)/∂t increases in direct proportion, and so the IBI is decreased.

Figure 6.

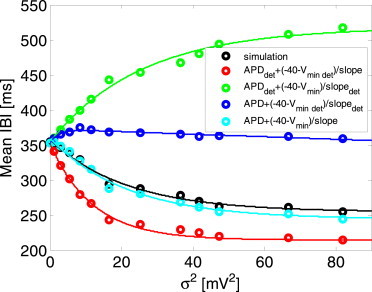
Analysis of the relative contribution of varying APD, v_min, and slope (with respect to their deterministic values) to the mean IBI. (Black) Reference simulation curve. (Cyan graph) Mean IBI was calculated from the three major determinants using Eq. 28. (Red, green, and blue graphs) Only one determinant was free to vary due to stochasticity (slope, v_min, and APD for the red, green, and blue graphs, respectively), while the other two were fixed to their deterministic value. To see this figure in color, go online.

Figure 5.

The effect of membrane voltage variance (σ²) on main determinants of the IBI. (A) Examples for typical APs of deterministic (thin dashed line) and stochastic (thin line) models. (Bold lines) Best-fit phase-4 depolarization linear slopes. (B) APD as a function of σ². (C) End-diastolic voltage, v_min, as a function of σ². (D) Phase-4 depolarization slope as a function of σ².

Figure 1.

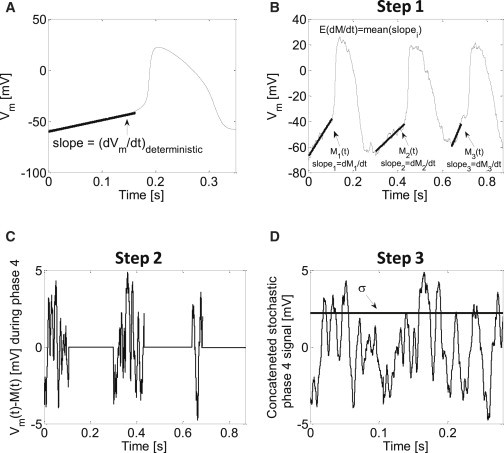
(A) Linear approximation of phase-4 depolarization in a deterministic model of a pacemaker cell. The linear phase can be roughly attributed to the depolarization phase from end-diastolic voltage to v_m = −40 mV. (B–D) Procedure steps for extracting M(t), ∂M(t)/∂t, and σ² from stochastic simulation data. In the first step, M_i(t) during each phase-4 depolarization interval i is approximated by linear curve fitting (B, bold traces). Next, the fitted M_i(t) values are subtracted from the membrane voltage signal v_m(t) during the phase-4 intervals. All other intervals are assigned with an artificial value of 0 (C). Finally, a phase-4 signal is generated by concatenating the subtracted signal segments that temporally correspond to phase-4 depolarization (D).

Biophysical modeling

We employed a recent mathematical model of the ion kinetics of a rabbit pacemaker SAN cell as described by Severi et al. (14). It includes 33 state variables, with (ACh) = 0. Simulations were conducted for either a single SAN cell or a two-dimensional tissue. Single-cell simulations were performed by numerically solving Eq. 1 using Euler temporal integration with a resolution of Δt = 10⁻⁷ s, and setting the membrane capacitance in the kinetic model in Severi et al. (14) to C_m = 3.2 × 10⁻⁵ μF. Two-dimensional simulations were performed by solving the following reaction-diffusion partial differential equation, which is an expansion of Eq. 1 using the cable theory under the mono-domain approximation:

$$\frac{\partial v_m}{\partial t}=-\sum I_{\text{ion}}+\nabla \left(D\nabla v_m\right).$$ (24)

Here D (mm²/s) is the diffusion coefficient. Our two-dimensional models consisted of a SAN region of size 4 × 6 mm (similar to the physiological dimension of the rabbit SAN tissue (16)), surrounded by a rabbit atrial region, giving a total tissue size of 6 × 10 mm (see Fig. 2). For the atrial region in the model geometry, the rabbit atrial myocyte ionic kinetics of Lindblad et al. (17) were adopted with a membrane capacitance of C_m = 5 × 10⁻⁵ μF. The reference diffusion coefficients were set to D = 4.5 and D = 100 mm²/s for the SAN and atrial regions, respectively. This yielded planar physiological conduction velocities of 0.065 and 0.45 m/s in the SAN and the atrial regions, correspondingly (18,19). Equation 24 was discretized and linearized using the finite-difference method and Euler temporal integration with spatial and temporal resolutions of Δx = 0.1 mm and Δt = 10⁻⁷ s, respectively. The 100-s- and 200-s-long electrical activity was simulated for single-cell and two-dimensional simulations, respectively, to ensure reaching steady state.

Figure 2.

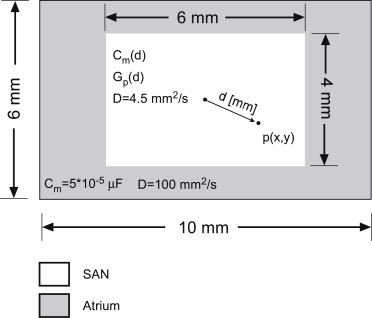
Two-dimensional model geometrical configuration. A 4 × 6 mm SAN region is surrounded by atrial tissue, resulting in a 6 × 10 mm overall tissue size. The capacitance and conductivity within the SAN region were a function of the distance d (mm) between a local point, p(x,y), and the center of the tissue.

The SAN tissue is highly heterogenic; this heterogeneity can be observed when comparing cellular biophysics of cells from the center of the SAN tissue or its periphery, close to the atrial tissue (20). The central SAN cells present lower activation rate; e.g., the IBI ratio between a central and peripheral cell is ∼3:2. A second heterogeneity relates to the AP magnitude, which is higher in peripheral cells than in central cells. These differences in cellular biophysics can be attributed to spatial gradients in membrane capacitance and ion-channel conductance. To account for these spatial heterogeneities inside the SAN, we followed the work of Zhang et al. (18) that originally modeled the capacitance and conductance gradients along a one-dimensional model, and expanded it to two-dimensional SAN tissue. Consequently, the pacemaker membrane capacitance (in μF) was modeled as

$$C_m\left(d\right)=3.2\times {10}^{-5}+\frac{1.07\times \left(d-0.1\right)}{3\times \left[1+0.7745\times e^{-\left(\frac{d-2.05}{0.295}\right)}\right]}\left(6.08\times {10}^{-5}-3.2\times 0^{-5}\right),$$ (25)

where d is the distance in millimeters of the cell from the SAN tissue center (Fig. 2). Using Eq. 25, the minimal C_m is obtained at the center of the SAN tissue (d = 0, C_m = 3.2 × 10⁻⁵ μF, equal to the original model value from Severi et al. (14)), while the maximal C_m is obtained at a peripheral cell (d = 7.2, C_m = 10.5 × 10⁻⁵ μF). The spatial modulation in the maximal conductivity of an ion channel was implemented by setting

$$G_p\left(d\right)=\frac{\left(10.5\times {10}^{-5}-C_m\left(d\right)\right)+5\times \left(C_m\left(d\right)-3.2\times {10}^{-5}\right)}{10.5\times {10}^{-5}-3.2\times {10}^{-5}}\times G_p\left(0\right),$$ (26)

where G_p(0) (μS) is the conductivity of an ion channel of specific type (e.g., p = I_f or p = L – type Ca²⁺) at the SAN center, as defined in the model of Severi et al. (14). From Eq. 26, the peripheral currents can be up to five times stronger than the central currents, in accordance with previous publications (21).

Simulation methods and data analysis

All simulations were performed using C++ code, running on a high-performance computing cluster computer (Altix X86-PTO; Silicon Graphics International, Milpitas, CA) with a master node (eight cores, Xeon 2.5 GHz processor; Intel, Santa Clara, CA) and two computational nodes (48 cores, Xeon 2.8 GHz; Intel). Data analysis and visualization were performed with MATLAB R2014b (The MathWorks, Natick, MA). Typical 1-s-long electrical activity simulation in a two-dimensional model with Δt = 10⁻⁷ s took ∼20 min. Where relevant, results are represented as mean values and standard deviation.

Using the notion of I_fluct defined in Eq. 2, it is understood that in single-cell models I_fluct exhibits the sole contribution to membrane voltage fluctuations (as manifested by σ²). However, in two-dimensional models, both I_fluct as well as the diffusion coefficient, D, determine σ². Therefore, in single-cell simulations we demonstrated the effect of σ² on the mean IBI and in two-dimensional models we showed the effect of ξ², the fluctuation current variance, on the mean IBI during intercellular decoupling. To measure the IBI, activation times were first determined as the times that the membrane voltage crosses the threshold of v_m = −30 mV during depolarization (9). The beat interval between adjacent beats was determined as the time between two successive activations.

In several simulations, we numerically estimated E{∂M(t)/∂t} and σ² from Eq. 23. For that purpose, we first extracted M(t) and its slope ∂M(t)/∂t during phase-4 of the APs by performing linear regression best-fit analyses. The best linear fit was subtracted from the phase-4 voltage data to isolate the stochastic component of the signal (see an example in Fig. 1, B–D). This procedure was repeated for all APs along the 100-s-long simulation. E{∂M(t)/∂t} was calculated as the mean of ∂M(t)/∂t for all beats. The variance for the combined phase-4 segments was defined as σ², and it was updated for each case of stochastic simulation.

Results

Single-cell simulations—stochasticity effect on mean IBI

Ion-channel stochasticity was applied in single-cell simulations by the addition of I_fluct as in Eq. 2 with standard deviation values, ξ, between 0 and 2 (pA/pF), and the resulting AP phase-4 variance, σ², was estimated as detailed in the Materials and Methods. The upper limit for ξ of 2 pA/pF was set following Ponard et al. (9), showing that higher standard deviation values result in unrealistic oscillations. The relationship between σ² and ${\xi }^2$ is shown in Fig. 3, demonstrating a strong linear correlation between the two variances (σ² ≈ 20ξ², R² = 0.98, p-value < 0.05). As σ² is a more direct parameter when examining the effect of stochasticity on the single SAN pacemaker cell AP and IBI than ξ² (see, e.g., Eq. 23), and because σ² and ξ² are linearly correlated (Fig. 3), we will henceforward present and analyze the role of σ² in the single SAN pacemaker cell activity. An example for the effect of stochasticity in membrane voltage on the IBI is given in Fig. 4. The figure presents the IBI signal (thin line) as a function of the beat number for single-cell simulations with two levels of stochasticity: low stochasticity (σ² = 5.5 mV², Fig. 4 A) and high stochasticity (σ² = 11.5 mV², Fig. 4 B). The bold solid line in each panel represents the deterministic intrinsic IBI value (355.0 ms), while the dashed line represents the mean IBI value, E{IBI}.

Figure 3.

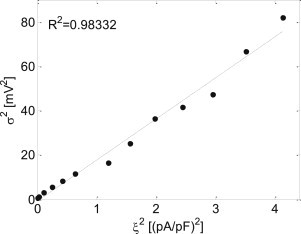
The relationship between the membrane voltage variance, σ², and the stochastic fluctuation current variance, ξ². A linear fit was found (p-value < 0.05).

Figure 4.

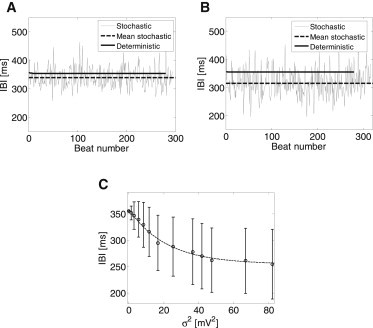
The effect of current (and thus voltage) stochasticity on the IBI. (A and B) IBI as a function of the beat number for deterministic (bold line) and stochastic (thin line) models. (Dashed bold line) Mean stochastic IBI. Two levels of stochasticity are presented: σ² = 5.5 mV² (A) and σ² = 11.5 mV² (B). (C) Mean IBI as a function of σ².

As can be seen from these two examples, increased stochasticity resulted in a reduction of the mean IBI, from a value of 355.0 ms in the deterministic case to 339.0 ms and to 315.5 ms (for σ² = 5.5 mV² and σ² = 11.5 mV², respectively), or alternatively to increased mean activation rate from 2.8 Hz in the deterministic case to 3.0 Hz and to 3.2 Hz. Fig. 4 C summarizes the relationship between the mean IBI and σ². The data are comprised of all the beats during the 100-s-long simulation for each value of σ². The results show a monotonic and significant decrease in the mean IBI as σ² increases, which can be approximated by the following exponential expression (R² = 0.99, Spearman correlation coefficient ρ = −0.61, p-value < 0.05):

$$E\left\{\text{IBI}\right\}=254.439+103.8245\times \text{exp}\left(-0.0462\times {\sigma }^2\right).$$ (27)

To establish the relative importance of the slope of phase-4 depolarization in determining E{IBI}, the following approximation was employed:

$$E\left\{\text{IBI}\right\}\approx E\left\{{\text{APD}}_{0÷3}\right\}+\frac{-40-E\left\{v_{\text{min}}\right\}}{E\left\{\text{slope}\right\}}.$$ (28)

Here E{v_min} (mV) is the mean minimal v_m value (end-diastolic value), E{APD₀₊₃} (ms) denotes the mean duration of the AP excluding the linear segment of phase 4 (i.e., from the point of positive crossing of the threshold of v_m = −40 mV to the next v_min), and

$$E\left\{\text{slope}\right\}=E\left\{\frac{\partial M\left(t\right)}{\partial t}\right\}$$

is the mean linear slope of phase 4. Fig. 5 demonstrates the effect of σ² on E{APD₀₊₃}, E{v_min}, and E{slope}. Panel A shows two examples of the SAN membrane voltage corresponding to deterministic (σ² = 0, in dashed thin line) and stochastic (σ² = 11.5 mV², in solid thin line) simulations. The fitted linear curves during phase-4 depolarization are marked in bold lines. Other than the obvious noisier signal for the stochastic case, stochastic current fluctuations resulted in reduced v_min (−70.8 vs. −58.0 mV, for the stochastic and deterministic cases, respectively) and in increased phase-4 depolarization slope (374.8 vs. 112.3 mV/s, for the stochastic and deterministic cases, respectively). In contrast, APD₀₊₃ did not change significantly (194.0 vs. 192.0 ms, for the stochastic and deterministic cases, respectively).

The results for all beats and for all values of σ² are summarized in Fig. 5, B–D. While no monotonic effect of σ² on E{APD₀₊₃} was found (Fig. 5 B, ρ = −0.08, p-value < 0.05), a monotonic exponential decrease in E{v_min} and a monotonic linear increase in E{slope} were found as σ² increased (Fig. 5, C and D). The exponential relationship between E{v_min} and σ² followed the expression (R² = 0.99, ρ = −0.63, p-value < 0.05)

$$E\left\{v_{\text{min}}\right\}=-76.6+18.57\times \text{exp}\left(-0.04\times {\sigma }^2\right),$$ (29)

while the linear relationship between E{slope} and σ² followed the expression (R² = 0.99, ρ = 0.55, p-value < 0.05)

$$E\left\{\text{slope}\right\}=112.3+9.5\times {\sigma }^2.$$ (30)

These results also demonstrate a much larger relative impact of membrane voltage fluctuations on the phase-4 depolarization slope in comparison to the impact on the two other parameters. The increase of σ² from 0 to 80 mV² resulted in an ∼700% increase in E{slope} from ∼100 to ∼800 mV/s, whereas E{v_min} decreased by a much lower relative value of ∼30% and E{APD₀₊₃} exhibited a maximum increase of ∼15%. Equation 30 provides a numerical validation to the theory leading to Eq. 23, by which a linear relationship between E{slope} and σ² was indeed predicted. Moreover, the numerical slope of this linear correlation obtained from Eq. 30 (9.5 mV⁻¹/s) is relatively close to the predicted value of 8.3 mV⁻¹/s, given by Eq. 23. The ∼13% deviation between the numerical and theoretical slopes may be attributed to inaccuracies due to the assumptions and simplifications taken for the analytical analysis leading to Eq. 23, as well as to numerical estimation errors for either the σ² or phase-4 slope.

Following the dependencies of E{APD₀₊₃}, E{v_min}, and E{slope} on σ², as established in Fig. 5, Eq. 28 was employed to assess which of these three parameters exhibits the largest relative impact on E{IBI}. Fig. 6 shows E{IBI} as a function of σ² in five curves. The black curve is a reference curve in which E{IBI} was directly retrieved from the simulation results (essentially the same curve as Fig. 4 C). For the cyan curve, E{IBI} was calculated using Eq. 28, employing E{APD₀₊₃}, E{v_min}, and E{slope} values for the various σ² from Fig. 5, B–D. The similarity between the reference black curve and the cyan curve suggests the validity of the approximation in Eq. 28. For each one of the last three curves, two of the parameters (E{APD₀₊₃}, E{v_min}, or E{slope}) were fixed to their corresponding deterministic values at σ² = 0, while the third parameter (the free parameter) was varied as a function of σ² in accordance with the ones in Fig. 5, B–D.

The free parameters for the blue, green, and red curves were E{APD₀₊₃}, E{v_min}, and E{slope}, respectively. As shown in Fig. 6, the original trend of reducing E{IBI} with increasing σ² (black and cyan curves) was preserved only in the red curve, in which E{slope} was the free parameters and E{APD₀₊₃} and E{v_min} were fixed to their deterministic values. This curve also presented the closest distance to either the black or the cyan curves. When E{slope} was fixed to its deterministic value, increasing σ² had either a minor effect on E{IBI} (blue curve, for which E{APD₀₊₃} was the free parameter), or even an opposite effect of increasing rather than decreasing E{IBI} (green curve, for which E{v_min} was the free parameter). In conclusion, the analysis in Fig. 6 supports our notion that the modulations in E{slope} due to varying σ² values sustain the major impact on the resulting consequential modulations in E{IBI}. While the variations in E{v_min} due to varying σ² values are substantial, as can be seen from Fig. 5 C, they exhibit only a secondary minor effect on E{IBI}.

Two-dimensional tissue simulations—the gap-junction effect on channel stochasticity

Two-dimensional simulations were performed using the heterogenic SAN model as described in Materials and Methods. Using Eqs. 25 and 26, intrinsic physiological spatial variations in the pacemaker activation rates were obtained when the cells were isolated from the tissue matrix. For example, Fig. 7 A shows the membrane voltage of two isolated, single pacemaker cells: a peripheral cell in red and a central cell in blue. These graphs were obtained without the addition of a fluctuation current, I_fluct, and demonstrate IBI values of 356 and 265 ms for the central and peripheral cells, respectively. This implies a 2:3 ratio between the two cells activation rates, in accordance with published data for rabbit sinoatrial cells (20). Although, in agreement with Fig. 4, the addition of fluctuation current resulted in the overall decreased mean IBIs (and thus in faster activation rates) of –285 and 215 ms for the central and peripheral cells, respectively, the 2:3 ratio between the central and peripheral activation rates was conserved (see, e.g., Fig. 7 B obtained with ξ² = 1.2 (pA/pF)²). Moreover, the voltage oscillations resulting from the added I_fluct were qualitatively consistent with typical experimental signals (see, e.g., Fig. 4B in Bucchi et al. (22)).

Figure 7.

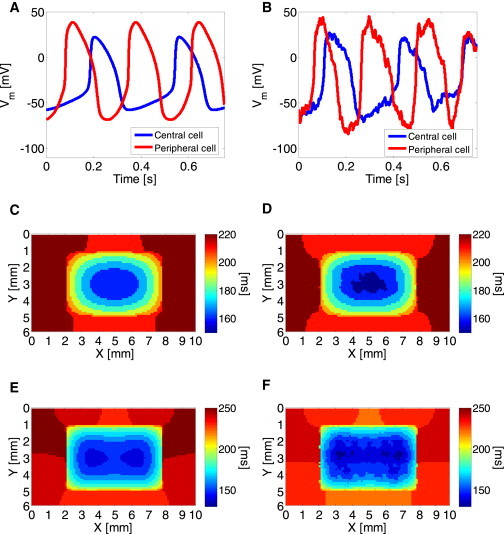
(A and B) Intrinsic physiological spatial variations in the pacemaker activation rates were reproduced in simulated single peripheral (red) and central (blue) cells, demonstrating a 3:2 activation rate between the two cell types in both deterministic (A) and stochastic (B) models. (C and D) Two-dimensional activation maps of one beat for deterministic (C) and stochastic (D) models using normal coupling level (D = 4.5 mm²/s). The maps demonstrate centrally originated activity. (E and F) When cellular decoupling was modeled (D = 1.5 mm²/s), activity was originated at two peripheral foci. To see this figure in color, go online.

As in physiological scenarios, when the cells were embedded in the two-dimensional tissue matrix, the global pacing rhythm was uniform across the tissue and, more importantly, not necessarily determined by the inherently faster peripheral cells. The dominant rate and the origin of conduction were the outcome of two additional factors—the surrounding nonpacemaker atrial cells that obstruct the potential dominance of the peripheral cells, and the degree of electrotonic coupling in the cellular matrix. This phenomenon is demonstrated in Fig. 7, C–F. Using the reference SAN electrotonic coupling with a diffusion coefficient of D = 4.5 mm²/s resulted in pacing conduction originated and dominated by the inherently slower central cells, as can be seen in Fig. 7, C and D, with mean IBI values of 365 and 363 ms for ξ² = 0 and ξ² = 1.2 (pA/pF)², respectively. These panels show typical activation maps for one of the activation waves, from which it is clear that the activation was focal, originated in the central SAN region. In contrast, when coupling was hampered by reducing the diffusion coefficient to D = 1.5 mm²/s, the origin of conduction was shifted to the inherently faster peripheral cells. This is shown in the activation maps in panels E and F, from which it is evident that activity simultaneously originated from two focal sources along the x axis. In this case, the mean IBI values were 345 and 331 ms for ξ² = 0 and ξ² = 1.2 (pA/pF)², respectively.

In the two-dimensional models, the way by which the IBI was affected by ξ² was also determined by the degree of electrotonic coupling. As shown in Fig. 8, A and B, at normal coupling level (D = 4.5 mm²/s), increasing ξ² resulted in a concave downward trend, with decreasing mean IBIs, while at reduced coupling state (D = 1.5 mm²/s), increasing ξ² resulted in a concave upward trend, with decreasing mean IBIs, similar to what was observed in single cells (Fig. 4 C). Moreover, the extent by which ξ² variations affected the mean IBI was thrice higher for D = 1.5 mm²/s than for D = 4.5 mm²/s (−7.6% compared to −2.5% when ξ² was increased from 0 to 3.5, respectively). The effect of the diffusion coefficient values on the IBI is summarized in Fig. 8 C. The deterministic IBI (in gray) and the stochastic mean IBI (for ξ² = 1.2 (pA/pF)², in black) are plotted as a function of D, with D ranging between 1.5 and 4.5 mm²/s. The lower limit of D = 1.5 mm²/s was chosen as it was the minimal value to still allow successful propagation between the SAN and the surrounding atrial tissue regions.

Figure 8.

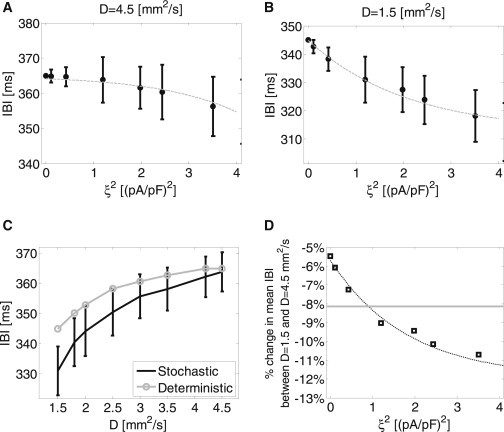
The effect of stochastic current fluctuations and of cellular electrotonic coupling on the IBI. (A) IBI as a function of ξ² in a two-dimensional model using normal intercellular coupling (D = 4.5 mm²/s). (B) IBI as a function of ξ² in a two-dimensional model using low intercellular coupling (D = 1.5 mm²/s), simulating cellular decoupling conditions. (C) IBI as a function of the diffusion coefficient (marking the level of intercellular coupling) for deterministic (shaded) and stochastic (ξ² = 1.2 (pA/pF)², solid) models. (D) The percentage of change in the mean IBI between normal and maximal cellular decoupling condition as a function of ξ². (Horizontal shaded line) Experimental result of −8.13% change measured in wild-types versus Cx30 deficient mice by Gros et al. (13).

The graph shows that a gradual decoupling of the SAN cells as established by decreasing values of D resulted in a monotonous decrease of the IBI. In other words, the more the electrotonic coupling between the cells was hampered, the greater the dominance of the peripheral SAN cells that was achieved, thus the higher the activation rate. This trend was similar for both the deterministic and stochastic models; still, the effect of cell decoupling was significantly stronger for the stochastic model. For example, while the deterministic model yielded a ∼5.5% lower IBI at D = 1.5 mm²/s than at D = 4.5 mm²/s, the stochastic model yielded a ∼9% lower IBI between the same levels of D. Finally, the percentage of change in the mean IBI values between D = 1.5 mm²/s and D = 4.5 mm²/s is plotted as a function of the fluctuation current variance, ξ², in Fig. 8 D. The graph demonstrates an exponential increase in the absolute difference percentage as ξ² increases.

Discussion

In this article we addressed the effect of current fluctuations due to the stochastic nature of ion-channel gating on the interbeat intervals (IBIs) of sinoatrial pacemaker cells. For this purpose, we developed a mathematical framework that relates the variance in the membrane voltage due to current fluctuations to the mean IBI as mediated by the slow phase-4 depolarization. In addition, we conducted computer simulations in single cells and in two-dimensional SAN models for demonstrating the applicability of the developed mathematical theory. Our main findings are as follows.

• 1.As the membrane voltage stochastic variance (σ²) increases, the mean IBI decreases monotonically, hence the activation rhythm increases.
• 2.The major determinant of the mean IBI is the phase-4 depolarization slope, which in turn strongly depends on the minimal transmembrane voltage, v_min.
• 3.The value v_min monotonically decreases with σ², explaining the (indirect) effect of σ² on phase-4 depolarization slope and thus on the mean IBI.
• 4.Intercellular gap-junctional coupling works to extenuate the variance of the intrinsic cellular transmembrane voltage.

This is in addition to the known moderating effect of electrotonic coupling on the spatial variability of intrinsic IBIs. Thus, pathological decoupling acts to further reduce the IBI (therefore to increase activation rhythm) via its effect on the membrane voltage variance of each SAN cell.

Our mathematical analysis leading to the theoretical relationship between membrane voltage fluctuations and the mean phase-4 slope (Eq. 23) required using the Fokker-Planck formalism, also known as the Kolmogorov diffusion equation, which originally describes the time evolution of the probability density function of the velocity of a particle under both drift and random diffusion forces. The approach of using Fokker-Planck formalism on a membrane voltage differential equation was previously proven successful for modeling firing neurons and for modeling neurons with current synapses (23). The application of this formalism for cardiac myocytes (to our knowledge developed here for the first time), although being conceptually similar, required several adaptations to fit to the biophysics of the stochastic current fluctuations of the SAN pacemaker cell. In our case, the particle velocity was replaced by the membrane voltage, v_m, and its probability density function was assumed Gaussian (Eq. 5). Consequently, from the differential equation that established the temporal evolution of v_m (Eq. 4), we could define the drift force as –g_m(v_m,t)[v_m – μ(v_m,t)] and the random diffusion force as the coefficient ξ. These definitions sustained the analogy between the physics underlying the Fokker-Planck equation and the biophysics of the sinoatrial cell membrane.

Gros et al. (13) have conducted in-vivo experiments regarding the modulation of the heart rate by the degree of Cx30 in the mouse sinoatrial node. In the population of ANS-inhibited mice, they found an 8.13% reduction in the mean IBI of Cx30 deficient mice in comparison to the reference mice (111 vs. 121 ms). They speculated that the maximal diastolic potential of the subepicardial nodal cells adjoining the atrial cells are less negative in the Cx30 deficient mice than that of the reference cells, resulting in an increase in heart rate. Our work may suggest two other possible synergic mechanisms for these results:

• 1.Cx30 deficient mice exhibit lower electrotonic connectivity (lower diffusion coefficient), thus leading to intercellular decoupling between peripheral SAN cells and adjacent atrial cells. This increases the source/sink for these peripheral cells, making them dominant in determining the pacing rate due to their intrinsic higher rate of activation (see Fig. 7, C and D, in comparison to Fig. 7, E and F).
• 2.The lower electrotonic connectivity in Cx30 deficient mice also results in a noisier environment, i.e., in increased single-cell membrane voltage fluctuations, due to the lack of the mediating, low-pass filtering effect of diffusion. This in turn also works to increase activation rhythm, as shown in Figs. 4 C and 8 B.

Assuming that, in our modeling, wild-types and Cx30 deficient phenotypes can be represented by diffusion coefficients of D = 4.5 mm²/s and D = 1.5 mm²/s, respectively, the experimental decrease in the IBI can be now compared to the simulation results. It should be noted that because our model does not include any ANS input, and because the ANS input is known to directly affect the heart rate as well as the standard deviation of normal RR intervals, our comparison to work of Gros et al. (13) is only possible for the ANS-inhibited mice population in that work. As shown in Fig. 8 D, our simulations demonstrate that a similar reduction in the IBI under intercellular decoupling conditions could only be achieved using stochastic modeling, with ξ² ≈ 1 (pA/pF)² (as extracted from the intersection between the experimental value, marked by the horizontal shaded line, and the simulation graph). In contrast, the deterministic model exhibited a lower 5.5% reduction in the mean IBI.

An additional experimental support for the stochastic modeling regards the mean IBI value and its standard deviation. Under control coupling level (D = 4.5 mm²/s), our results show a typical mean IBI value of 363 ms with standard deviation value of ∼6 ms for ξ² ≈ 1 (pA/pF)² (Fig. 8 A). This result is consistent with an experimental study by Janousek et al. (24), showing, in isolated rabbit hearts, mean IBI values of 366 ms with standard deviation of 5 ms. Therefore, only by accounting for the stochastic current fluctuations, specifically with ξ² = 1 (pA/pF)², similar experimental and numerical observations could be achieved under both control and intercellular decoupling conditions.

While our work focused on basic modeling and understanding regarding the effects of current/voltage stochastic fluctuations on the mean IBI in the SAN, it may lead to some possible practical applications. One such application may involve using the heart rate signal measurements to monitor the degree of electrotonic coupling in patients suffering from intercellular decoupling, e.g., due to increased SAN fibrosis. Such patients may be treated with drugs that increase gap-junctional coupling, e.g., anti-arrhythmic peptide drugs (25). According to Fig. 8 C, it is expected that an improvement in cellular coupling after therapy will be reflected by a decreasing mean heart rate (increasing mean IBI).

Study limitations

Several limitations of this model should be noted.

• 1.Our kinetic model accounted for a global fluctuation current that integrates the effect of stochastic ion-channel gating. Intracellular stochastic processes were not modeled, e.g., the stochastic gating of ryanodine receptors (9), which are beyond the scope of this article.
• 2.Peripheral currents five-times larger than central currents were modeled for all currents (Eq. 26). While this approximation may seem rough or oversimplified, it is based on previous measurements (21) as well as on our observation that it keeps a 2:3 ratio in the activation rate between central and peripheral cells, as in the SAN model of Severi et al. (14). For our purposes, this approximation is therefore adequate.
• 3.A uniform I_fluct standard deviation ξ (pA/pF) was assumed across the entire SAN tissue, due to a lack of any experimental data showing physiological distributions.
• 4.
  Our mathematical modeling suggests that the main effect of membrane current stochasticity on the phase-4 depolarization slope (and thus on the IBI) is achieved indirectly through its effect on v_min. This can be seen from Eqs. 21 and 22, in which the negative value of

  $${\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }$$

  is significantly larger (absolutely) than

  $${\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{\text{phase}4},$$

  and from Eq. 16 stating that stochastic M_min is linked to σ² via

  $${\frac{\partial g_m\left(v_m,t\right)}{\partial v_m}|}_{v_{\text{min}}+\delta }.$$

  Thus, when σ² increases, v_min decreases, resulting in increased slope. It is plausible that the decrease in v_min due to the increased stochasticity increases the inactivation gate values (i.e., the channels are less inactivated), leading to faster phase-4 depolarization. Nevertheless, future work should investigate the exact ionic mechanism that correlates among current stochasticity, phase-4 slope, and v_min. Such an investigation may also support an intuitive explanation to our findings, potentially via a nonsymmetrical reaction of the membrane voltage to symmetric (or zero-mean) current perturbations during phase-4 depolarization.
• 5.Finally, our theoretical and numerical analysis provide, to our knowledge, a plausible novel explanation regarding one of the mechanisms that may underlie the faster sinus rate that was observed in Cx30 knock-out mice by Gros et al. (13). Nevertheless, other possible mechanisms that cannot be ruled out include, e.g., compensatory ionic remodeling in the Cx30 deficient mice.

Conclusions

Although the relationship between membrane voltage stochasticity that originates from membrane current fluctuations and beat variability has been established in several articles, its relationship to the mean beat rate has not been studied thus far. In this article we have established this relationship using, to our knowledge, novel mathematical and numerical modeling. We conclude that the phase-4 depolarization slope (the major determinant of the IBI) linearly increases with membrane voltage stochastic variance (σ²). This is indirectly related to the effect of σ² on the minimal diastolic voltage, v_min. This work also contributes to better understanding of the impact of cellular coupling (or decoupling) in the intact SAN tissue, via its effect on the level of membrane voltage noise. Finally, this work has the potential of laying the foundations for novel diagnostic methodologies, e.g., for monitoring the level of cellular decoupling in the SAN.

Supporting Citations

Reference (26) appears in the Supporting Material.