Structural Phenotyping of Stem Cell-Derived Cardiomyocytes

Summary

Structural phenotyping based on classical image feature detection has been adopted to elucidate the molecular mechanisms behind genetically or pharmacologically induced changes in cell morphology. Here, we developed a set of 11 metrics to capture the increasing sarcomere organization that occurs intracellularly during striated muscle cell development. To test our metrics, we analyzed the localization of the contractile protein α-actinin in a variety of primary and stem-cell derived cardiomyocytes. Further, we combined these metrics with data mining algorithms to unbiasedly score the phenotypic maturity of human-induced pluripotent stem cell-derived cardiomyocytes.

Highlights

• •Image processing metrics for characterizing the contractile cytoskeleton
• •Unbiased data mining strategies to assess cardiomyocyte maturation
• •Structural phenotyping of stem cell-derived cardiomyocytes

In this article, Parker and colleagues develop metrics to quantitatively characterize myofibrillogenesis and sarcomerogenesis, the processes by which striated muscle cells assemble their contractile cytoskeleton. Further, they coupled these metrics with machine-learning algorithms to unbiasedly score the phenotypic maturity of primary and stem cell-derived cardiomyocytes.

Introduction

Several efforts have been reported in the emerging field of structural phenotyping for the integration of image acquisition, processing, and analysis to assess the response of cells and tissues to various challenges (Eliceiri et al., 2012). All of these methodologies are predicated on the assumption that cell shape is an important indicator of the cell pathophysiological state and rely on (1) image-processing algorithms for the extraction of morphological features and (2) machine-learning strategies to mine the cell morphology data (Crane et al., 2012; Jones et al., 2009; Treiser et al., 2010).

Many intracellular structures, such as the contractile cytoskeleton in striated muscles, are also predictors of cell function (Feinberg et al., 2007). Additionally, while a cell specifies along the myocyte lineage (Mummery et al., 2012; Qian and Srivastava, 2013), it also progresses through myofibrillogenesis as force-generating units, known as sarcomeres, self-assemble along the actin cytoskeleton (Grosberg et al., 2011; Parker et al., 2008). Moreover, the contractile proteins of mature myocytes are continuously turned over and their spatial organization remodeled to adapt to pathophysiological stimuli (McCain et al., 2013; Sun et al., 2012; Wang et al., 2014). Therefore, while the presence of contractile proteins is necessary for myocytes function (Cahan et al. 2014; Mummery et al., 2012), it is not sufficient to define the developmental stage (Sheehy et al., 2014), the health status (Wang et al., 2014), or the functional capabilities of these cells (Feinberg et al., 2012).

Here, we designed a set of 11 metrics (Figure S1; Table 1) that intrinsically score myocyte structural phenotypes by the increasing degree of organization and alignment that sarcomeres acquire during myofibrillogenesis. We utilized these metrics to score the phenotypic maturity of primary and stem cell-derived cardiomyocytes based on the degree of sarcomeric structural organization observed in α-actinin images.

Table 1.

List of Metrics of Sarcomere Organization Developed, Integrated, or Updated for This Study

Metric Number	Metric Name	Metric Description
1	sarcomere length (SL)	The average distance between Z-disks in the entire field of view.
2	total energy	The total amount of spatially varying immunosignal.
3	sarcomeric energy	The amount of immunosignal with a spatial periodicity given by SL.
4	sarcomeric packing density (SPD)	The fraction of immunosignal that localized in a regular lattice at a distance SL.
5	orientational order parameter (OOP)	The degree of alignment of all foreground elements in the field of view.
6	sarcomeric OOP (OOP1)	The degree of alignment of foreground elements that are oriented orthogonally to the actin bundles (Z-disks).
7	nonsarcomeric OOP (OOP2)	The degree of alignment of foreground elements that are oriented parallel to the actin bundles (Z-bodies).
8	Z-disks relative presence (γ)	The fraction of foreground elements that are recognized as Z-bodies.
9	weighted OOP	Calculated by multiplying the sarcomeric OOP (OOP1) and the weight γ. In this sense, it represents both the abundance and relative alignment of the Z-disks in the imag.
10	coverage quality control	Calculated as the percentage of the image pixels that have an intensity value higher than user-specified threshold. It estimates the α-actinin coverage.
11	coherency quality control	Calculated as the percentage of α-actinin-positive pixels that have a value of the coherency higher than a user-selected threshold. It is useful for artifact removal and for image quality control.

See Figure S1 for a schematic representation of the role of each parameter.

Results

Quantitative Analysis of the Contractile Cytoskeleton in Striated Muscle Cells

Sarcomeres are ∼2 μm long ultrastructures delimited by Z-disks that are rich in the contractile protein α-actinin (red in Figure 1A). The localization of this protein can be taken to indicate the maturity of cardiac myocytes (Grosberg et al., 2011): in differentiating cells, α-actinin is diffuse in the cytoplasm (Figure 1Aii); in immature myocytes, it appears as a fibrous structure or as aperiodically spaced puncta known as Z-bodies (Figure 1Aiii); and in mature myocytes, α-actinin localizes into the regular lattice of Z-disks (Figure 1Aiv). Therefore, we focused our analysis (Figure 1B) on identifying how regularly spaced and well-aligned sarcomeric α-actinin-positive structures were in the images. We first associated each sarcomeric α-actinin-positive pixel with the orientation (color coded in Figure 1Ci) of its local neighborhood and then fitted a bimodal distribution to the resulting orientation histogram (red and black curves in Figure 1Cii). This enabled the extraction of several metrics: the global orientational order parameter (Grosberg et al., 2011) (OOP) a value that ranges from 0 to 1 as contractile elements become more aligned and separate OOPs for the two fitted modal distributions, representing Z-disks and Z-bodies, as well as their relative presence. Further, we radially integrated the image power spectrum (Figure 1Ciii), yielding a 1D representation (Figure 1Civ) that highlights the relative importance of each spatial frequency. In particular, the peaks (red curve) represent α-actinin-positive elements arranged at a distance on the order of the sarcomere length (SL) and therefore become more prominent as sarcomerogenesis progresses. Through nonlinear fitting, we separated this component from the aperiodic contribution of Z-bodies and other image artifacts (black curve). Relevant metrics in this case included the area (shaded in red) under the periodic component, the total area under the data curve, and their ratio, a quantity we termed sarcomere packing density (SPD). Taken together, this set of metrics has a direct biophysical interpretation: substantially more mature myofibrillar architectures exhibit a regular lattice of well-oriented Z-disks, resulting in elevated values of SPD and OOP. Additionally, this analysis is robust to common imaging artifacts such as out-of-focus blurriness, salt-and-pepper noise, or poor contrast (Figure S2).

Figure 1.

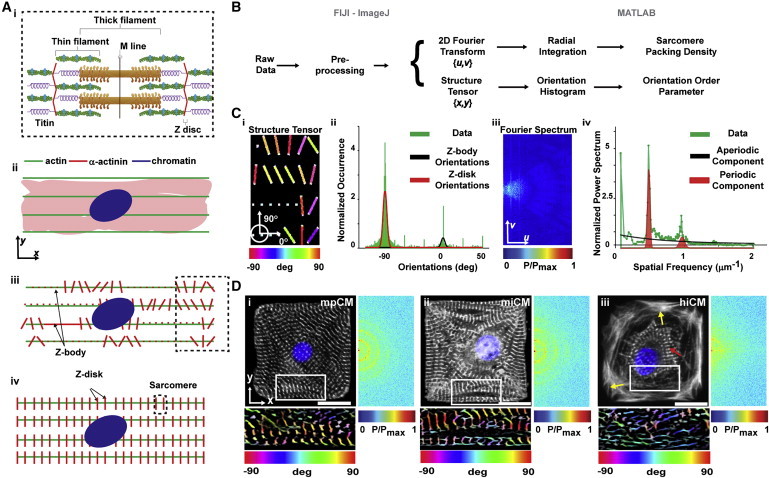
Metrics of Contractile Architecture to Characterize the Progression of Myofibrillogenesis

(A) Schematic representation of a sarcomere (i) and of the distribution of α-actinin (red) during myofibrillogenesis: in the cytoplasm (ii), along the actin (green) filament in the form of Z-bodies (iii), and incorporated into the Z-disks (iv).

(B) Algorithmic detection of the orientation and periodic registration of α-actinin-positive structures using the image spatial (coordinates x,y) and Fourier (coordinates u,v) domains.

(C) Color-coded orientations (i, from the inset of synthetic image Figure 1Bii) displayed into a histogram (ii) can be fitted to identify orientations belonging to Z-disks (red) and Z-bodies (black). In parallel, the 2D Fourier power spectrum (iii) was integrated into a 1D curve (iv) and fitted to identify the contribution of periodically spaced Z-disks (red) and aperiodic Z-bodies (black).

(D) α-actinin immunostains (white) of mononucleated (DAPI, blue) murine primary (mpCM, i) and murine (miCM, ii) or human (hiCM, iii) induced pluripotent stem cell-derived cardiomyocytes. The color-coded representation of the α-actinin orientation in the inset is reported below the image. The positive semiplane for the Fourier transform is reported on the right of each image.

Scale bar represent 20 μm. See also Figures S2 and S3.

Quantitative Analysis of the Contractile Cytoskeleton in Murine Primary and Stem Cell-Derived Single Cardiomyocytes

To test our analysis tool, we asked whether we could quantify the ability of human and murine-induced pluripotent stem cell-derived cardiomyocytes (hiCMs and miCMs, respectively) to replicate the contractile cytoskeletal architecture observed in murine primary cardiomyocytes (mpCMs) in vitro (Parker et al., 2008). Qualitatively, we observed that mpCMs (Figure 1Di) and miCMs (Figure 1Dii) 3 days after seeding on square fibronectin islands showed mature myofibrillar architecture, characterized by uniformly distributed sarcomeric α-actinin-rich striations. Conversely, hiCMs (Figure 1Diii) exhibited sparse Z-disks solely in the perinuclear region and arranged in ring-like myofibrils (red arrow in Figure 1Diii). In addition, close to the hiCM membrane, the actin and sarcomeric α-actinin signals were diffuse (yellow arrows) and resembled the cortical architecture observed in immature and/or migratory cells (Parker et al., 2008; Sheehy et al., 2012). Quantitatively, while local regions of aligned Z-disks could be detected (color-coded insets below the panels in Figure 1D), the Fourier analysis clearly demonstrated a globally reduced periodicity in the sarcomere distribution of hiCMs than observed in miCMs and mpCMs (insets on the right of the panels in Figure 1D). Consistently, the SPDs measured in mpCMs and miCMs were two times higher than in hiCMs (Figure S3). Notably, all myocytes considered in this study were positive for sarcomeric α-actinin, suggesting that they would have been clustered in the same group by traditional assays detecting the presence of this protein or its transcript (Cahan et al. 2014; Mummery et al., 2012).

Quantitative Analysis of the Maturity of the Contractile Cytoskeleton in Human Stem Cell-Derived Cardiomyocytes

We and others have previously shown that extending time in culture (Lundy et al., 2013; McCain et al., 2014a) could be beneficial for obtaining hiCMs with a more mature phenotype than we observed here. However, evaluating the quality of mass-produced stem cell-derived myocytes requires an extensive structure-function characterization and a direct comparison against myocytes exhibiting a postnatal phenotype (Sheehy et al., 2014). We reasoned that since the process of myofibrillogenesis is highly conserved across species (Sissman, 1970) we could design a prescreening tool that estimates the effectiveness of maturation strategies by integrating our metrics of myofibrillar architecture with machine-learning algorithms for structural phenotyping. While available platforms require a user-selected training set, a set of images that an “expert” assigns to all phenotypic classes (Eliceiri et al., 2012), we took advantage of our ability to recapitulate myofibrillogenesis in vitro using primary cardiomyocytes from neonate rats (rpCMs) (Agarwal et al., 2013; Parker et al., 2008) to create such a training set. First, we cultured rpCMs and hiCMs as engineered tissues that mimic the native architecture of the myocardium (Sheehy et al., 2014) (Figures 2A and S4). Second, we assigned the sets of features (Figure S1; Table 1) extracted from images collected at 6 (Figure 2Ai), 24 (Figure 2Aii), and 48 hr (Figure 2Aiii) after seeding to the classes of differentiated, immature, and mature myocytes, respectively. We collected digital images from more than 100 cells (insets in Figure 2A and Figure S4A–B) in each condition. Third, we utilized the automatically annotated dataset to train a simple naive Bayes classifier as well as two more advanced supervised learning strategies based on neural networks and tree bagging (Figure S4C). We selected three machine-learning strategies that operate under various assumptions (Table 2) to demonstrate that our classification was not biased (Eliceiri et al., 2012) by the choice of one specific algorithm. Finally, we asked the three classifiers to confirm whether or not hiCMs (Figure 2Aiv) possess a mature structural architecture.

Figure 2.

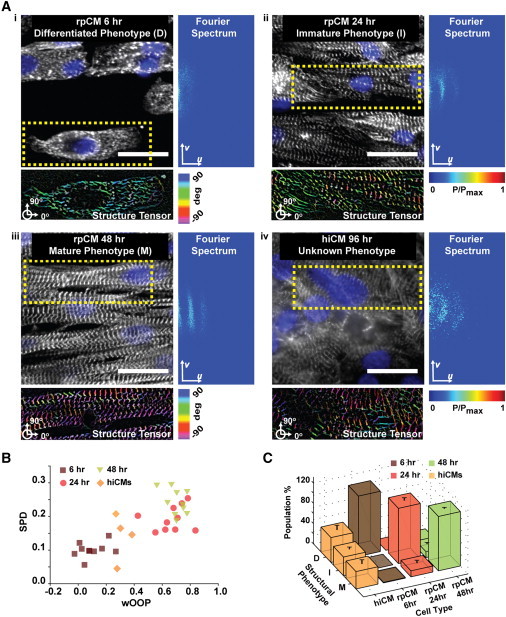
Structural Phenotyping of Stem Cell-Derived Cardiomyocytes

(A) α-actinin (white) and chromatin (blue) images of rpCMs at 6 (i), 24 (ii), and 48 hr (iii) as well as hiCMs at 72 hr (iv) after seeding with color-coded orientations and Fourier representations. Scale bar represents 25 μm.

(B) Scatter plot showing how our metrics of myofibrillar architecture quantitatively captured the progression of myofibrillogenesis in rpCM tissues from differentiated (6 hr, brown squares) to immature (24 hr, red circles) and finally mature (48 hr, green triangles) myocytes. In contrast, the hiCM tissues (orange diamonds) exhibited a relatively immature myofibrillar organization.

(C) A dataset comprising ∼120 sarcomeric α-actinin images per conditions (insets in Ai–Aiv) was acquired, and the features extracted from this dataset were utilized to train several classifiers to distinguish the classes of differentiated (D), immature (I), and mature (M) myocytes. The classifiers assigned only ∼29% of the 118 hiCM images to the class of myocytes with a mature structural phenotype, with the rest showing differentiated or immature contractile architectures.

Results are shown as mean ± SEM. See also Figure S4.

Table 2.

Machine Learning Algorithms Adopted for the Analysis of the Myofibrillogenesis Dataset

Classifier Number	Classifier Name	Pros	Cons
1	naive Bayes	One of the simplest classifiers, based on intuitive probability models, and it is computationally very treatable.	It simplistically assumes that all the features are statistically independent, which may not be true for sarcomeres whose structure, during myofibrillogenesis, becomes more periodic and well-aligned.
2	neural network (NN)	A popular machine learning algorithm for structural phenotyping. Extensive literature shows how a NN classifier can always be constructed, providing that one has a good enough dataset.	The data model is not intuitive. The neural network optimization is not trivial and requires considerations for the dataset size as well as the stochastic initialization.
3	tree bagging	A popular machine-learning algorithm for structural phenotyping. The data model is more intuitive than NN.	Optimization of the tree bagging algorithm is not trivial and requires careful consideration of the sample and tree sizes.

See Figure S4.

At the tissue level, as rpCMs in culture underwent myofibrillogenesis, we observed that weighted OOP (wOOP) and SPD increased as expected (Figure 2B). In comparison, hiCMs scored values consistent with their immature myofibrillar organization. Further, all classifiers trained on the rpCMs dataset failed to recognize a mature myofibrillar architecture in the majority of hiCMs images (Figure S4D). Specifically, ∼70% of the 118 hiCM images were not classified as mature by the naive Bayes classifier, ∼71% by the neural network classifier, and ∼77% by the tree bagging classifier. For example, the neural network classified ∼40% of hiCMs as differentiated myocytes and ∼31% as immature myocytes (Figure 2C). Interestingly, 29% of the cells embedded in anisotropic hiCM tissues did display mature myofibrillar architectures, suggesting a pool of hiCM with enhanced myogenic potential may exist (Hartjes et al., 2014). Thus, we (1) provided quantitative metrics for the organization of the contractile cytoskeleton of primary and stem cell-derived cardiomyocytes and (2) utilized this information to unbiasedly and robustly quantify their maturation.

Discussion

Quantitative methods to characterize the contractile cytoskeleton of striated muscle cells have been previously proposed. For example, the analysis of the orientation of intracellular elements has been conducted adopting mean orientations (Rao et al., 2013). Unfortunately, the specific circular statistics tests (Berens, 2009) required to compare and contrast these mean orientations are only rarely adopted. By using the OOP values in the range of 0–1, we were able to employ classical statistical tools, such as ANOVA (Figure S3). Additionally, approaches based on nonlinear fitting of multiple Von Mises distributions have been proposed (Rezakhaniha et al., 2012); in the context of fluorescence bioimaging though, these methods may suffer from overfitting issues, given the large numbers of parameters that are needed to identify multiple distributions. Here we restricted ourselves to only two distributions, centered on the two biophysically relevant principal directions of Z-disks and Z-bodies that are orthogonal to one another. We were thus able to limit the number of fitting parameters, largely reducing the risk of overfitting. Fourier analysis has also been previously considered in the estimation of sarcomere length (Lundy et al., 2013; Wei et al., 2010). Our automatic approach offers significant advantages in that the contractile cytoskeleton within the entire cell is considered, reducing the user bias (Eliceiri et al., 2012) introduced by manual selections in the spatial (Lundy et al., 2013) or Fourier (Wei et al., 2010) domains. Moreover, our algorithm not only yields an estimate of the sarcomere length across the entire spatial extension of the cell/tissue, but also reveals the relative presence of well-formed sarcomeres irrespectively from the direction of their alignment. When the myofibrils are highly aligned (Figure 2Aiii), the Fourier spectrum exhibits peaks along one principal direction; conversely, when sarcomeres are well organized along many directions (Figure 1Di), the Fourier spectrum shows a circular pattern. By integrating across all directions in the Fourier domain, we are able to quantify the sarcomeres translational periodicity across all directions in the spatial domain.

Finally, the method proposed here for the calculation of the SPD significantly improves our previous efforts (McCain et al., 2014b; Wang et al., 2014). By normalizing the energy of the periodic component to the total energy of the sarcomeric α-actinin image, we estimate a signal-to-noise ratio that is bound in the unit interval, a desirable property for many machine-learning algorithms (Shamir et al., 2010).

In conclusion, we have developed 11 metrics to characterize the structural phenotype of primary and stem cell-derived cardiomyocytes in a way that is biophysically related to their functional proficiency (Feinberg et al., 2012). Moreover, by engineering myocyte shape and tissue architecture, we were able to generate a myofibrillogenesis dataset that allows structural phenotyping of stem cell-derived cardiomyocytes in an unbiased fashion and that is largely robust to the choice of a specific machine-learning strategy. Finally, while assessing the quality of human pluripotent stem cell-derived myocytes remains critical, to date, their maturation has been suboptimally estimated (Mummery et al., 2012; Sheehy et al., 2014), as healthy human myocytes are not readily available. Since myofibrillogenesis is an extremely well-conserved physiological process (Sissman, 1970), our method allows for a quantitative characterization of myocytes maturation that naturally overcomes this limitation.

Experimental Procedures

Substrate Engineering

Photolithographic masks bearing desired features were drawn in AUTOCAD (Autodesk). UV light was shone through the mask into a silicon wafer (Wafer World), previously spin coated with SU-8 3005 photoresist (MicroChem). The wafer was then developed in propylene glycol methyl ether acetate (Sigma) and utilized to cast polydimethylsiloxane (PDMS, Sylgard 184; Dow Corning; 10:1 ratio) stamps. Glass coverslips were also coated with PDMS and treated for 8 min in the UV ozone cleaner before coming into contact with PDMS stamps inked with fibronectin (50 μg/ml; BD Biosciences).

Alternatively, coverslips were coated with polyacrylamide hydrogels (streptavidin-acrylamide/bis ratio 7.5/0.3%). To transfer fibronectin islands, the hydrogel was dried (37°C, 10 min), brought into contact with stamps inked with biotinylated fibronectin (Pierce), and finally sterilized with UV exposure (15 min).

Primary Harvest

Ventricular myocytes were isolated from day 2 neonate Balb/c mice and Sprague Dawley rats according to procedures approved by the Harvard University institutional animal care and use committees. Isolated ventricles were incubated in cold (4°C) 0.1% (w/v) trypsin (USB) solution for approximately 12 hr. Ventricular tissue was further exposed to serial treatments (2 min each) of 0.1% (w/v) warm (37°C) collagenase type II (Worthington Biochemical) solution. Isolated rat and mouse cardiomyocytes were seeded onto engineered substrates at a density of 10,000 and 20,000 cells/cm², respectively. Culture medium consisted of Medium 199 (Invitrogen) supplemented with 10% (v/v) heat-inactivated fetal bovine serum (FBS), 10 mM HEPES, 20 mM glucose, 2 mM L-glutamine, 1.5 μl vitamin B12, and 50 U/ml penicillin for the first 48 hr. The FBS concentration was then reduced to 2%.

Stem Cell Culture

hiCM and miCMs were kindly provided by Cellular Dynamics and Axiogenesis (CorAt-iPS), respectively. Cells were cultured as per manufacturers’ recommendations: hiCMs were seeded in the presence of vendor-provided plating medium; miCMs were positively selected after plating onto 10 mg/ml fibronectin coated flasks. After 72 hr, both cell types were dissociated with 0.05% trypsin-EDTA solution (Invitrogen, 25200-072) and seeded onto the engineered substrates at a density of 10,000 cells/cm².

Immunocytochemistry and Imaging

At room temperature (RT), cells were treated with 4% paraformaldehyde and 0.05% Triton X-100 in PBS (v/v) for 10 min and incubated with anti-sarcomeric α-actinin (A7811; Sigma) and anti-fibronectin antibodies (F3648; Sigma) for 1 hr (1:200 dilution). Samples were further treated with DAPI (Invitrogen), Alexa Fluor 633-conjugated phalloidin (A22284, Invitrogen), and Alexa Fluor 488-conjugated goat anti-mouse IgG and Alexa Fluor 546-conjugated goat anti-rabbit IgG secondary antibodies (Invitrogen) for 2 hr at RT. Samples were imaged with a Zeiss LSM confocal microscope (Carl Zeiss Microscopy) equipped with the EC Plan-Neofluar 40×/1.30 oil DIC M27 objective; 1024 × 1024 pixels per image were acquired for a final pixel size of 160 nm.

Image Processing and Future Extraction

Preprocessing was performed with ImageJ/FIJI (Schindelin et al., 2012). The tubeness (Sato et al., 1998) and OrientationJ (Rezakhaniha et al., 2012) plugins were used to highlight the filamentous structure and calculate the orientations of foreground pixels, respectively. MATLAB (Mathworks) was adopted for feature extraction.

Orientational Order Parameter

The structure tensor method generated orientations {ϑ₁,ϑ₂,…,ϑ_N} whose frequency of occurrence we plotted in a histogram, such as in Figures 1Ci, 1Cii, and S3. The OOP was calculated using the mean resultant vector from circular statistics (Berens, 2009)

$$OOP=\frac{1}{N}\left|{\sum }_{j=1}^N{e}^{i{\vartheta }_j}\right|,$$ (Equation 1)

where $i=\sqrt{-1}$ is the complex unit, e is Euler’s number (∼2.71), and ϑ_j is the jth orientation in {ϑ₁,ϑ₂,…,ϑ_N}. The sum of unit vectors in Equation 1 is bound by 0 (for a set of randomly oriented vectors) and 1 (for a set of perfectly aligned vectors). Further, we fitted the orientation histogram with the following linear mix of Von Mises Distributions

$$f\left(\theta ;{\mu }_1,{\delta }_1,{\mu }_2,{\delta }_2,\gamma \right)=\gamma \frac{\exp \left[{\delta }_1\cos \left(\vartheta -{\mu }_1\right)\right]}{2\pi I_0\left({\delta }_1\right)}+\left(1-\gamma \right)\frac{\exp \left[{\delta }_2\cos \left(\vartheta -{\mu }_2\right)\right]}{2\pi I_0\left({\delta }_2\right)},$$ (Equation 2)

where μ_1,2 and δ_1,2 represent the localization and spread parameters for the Z-disks and Z-bodies peak, respectively, γ indicates the fraction of orientations allocated into the Z-disk peak, and I₀ is the modified Bessel function of order 0. We then sampled 1,000 orientations from the two fitted Von Mises probability density distributions and calculated OOP₁ and OOP₂ for the Z-disk and Z-body peaks, respectively. In addition, we introduced a weighted version of the OOP: wOOP = γ ∗ OOP₁ that quantifies both the presence (γ) and the alignment (OOP₁) of the Z-disks in the image.

Sarcomeric Packing Density

To calculate the degree of spatial organization of sarcomeres, we first considered the Fourier power spectrum P(u,v) of the preprocessed sarcomeric α-actinin image I(x,y)

$$\{\begin{array}{c}P\left(u,v\right)={\left|F\left(u,v\right)\right|}^2\\ F\left(u,v\right)={\iint }_{{\mathbb{R}}^2}I\left(x,y\right)\exp \left[i2\pi \left(xu+yv\right)\right]dxdy\end{array}.$$ (Equation 3)

Equation 3 uses the Fast Fourier Transform algorithm to establish a correspondence between the spatial domain of the image I(x,y) and the Fourier domain where the power spectrum P(u,v) is defined. The signal energy (E_TOT) was sampled and integrated along 1,024 directions to obtain a 1D representation (Γ(ω)) that exhibits periodic peaks (subscript p), in correspondence of spatial frequencies that are integer multiple of ω₀, modulated by an aperiodic noise term (subscript ap).

$$E_{TOT}={\iint }_{{\mathbb{R}}^2}P\left(u,v\right)dudv={\int }_0^{\infty }\left[\omega {\int }_{-90}^{90}P\left(\omega ,\vartheta \right)d\vartheta \right]d\omega ={\int }_0^{\infty }\left[\text{Γ}\left(\omega \right)\right]d\omega .$$ (Equation 4)

Equation 4 states that the total energy in the image can be expressed integrating the 2D power spectrum P(u,v) or, alternatively, through the integration of its 1D representation Γ(ω). To approximate this 1D function, we chose the relationships in Equation 5, where ${\widehat{\text{Γ}}}_{ap}$ is a decaying exponential and ${\widehat{\text{Γ}}}_p$ is the sum of three Gaussian peaks.

$$\{\begin{array}{c}\widehat{\text{Γ}}\left(\omega ;\xi \right)={\widehat{\text{Γ}}}_p\left(\omega ;{\xi }_p\right)+{\widehat{\text{Γ}}}_{ap}\left(\omega ;{\xi }_{ap}\right)\\ {\widehat{\text{Γ}}}_{ap}\left(\omega ;{\xi }_{ap}\right)=a\exp \left(-\omega /b\right);{\xi }_{ap}=\left\{a,b\right\}\\ {\widehat{\text{Γ}}}_p\left(\omega ;{\xi }_p\right)={\sum }_{k=1}^3{a}_k\exp \left[-{\left(\omega -k{\omega }_0\right)}^2/b_k\right];{\xi }_p={\left\{a_k,b_k,{\omega }_0\right\}}_{k=\mathrm{1,2,3}}\end{array}.$$ (Equation 5)

We fitted the function to the data using Matlab “lsqnonlin” function that uses the Trust Region Reflective algorithm (Coleman and Li, 1996). With this approach, we were able to calculate (see Equation 6) the sarcomere length the area under the periodic component E_p (or sarcomeric energy), as well as its ratio with the total area (total energy), a quantity we named sarcomeric packing density (SPD):

$$\{\begin{array}{c}{E}_p={\int }_D{\widehat{\text{Γ}}}_p\left(\omega ;{\xi }_p\right)d\omega \\ SPD=E_p/E_{TOT}\\ SL={\omega }_0^{-1}\end{array}.$$ (Equation 6)

Machine Learning

The naive Bayes, neural network, and tree bagging classifiers were implemented using Matlab built-in functions (see also Supplemental Information). Ten random iterations were seeded to ensure that the results were stochastically robust. For the naive Bayes and tree bagging classifiers, training was performed with a 10-fold cross-validation test. For the neural network, we used 70%, 15%, and 15% of the rpCMs dataset for the training, validation, and testing phases, respectively.

Downloadable Content

The myofibrillogenesis dataset and the ImageJ code utilized in this paper can be downloaded from the Disease Biophysics Group website: http://diseasebiophysics.seas.harvard.edu/.