Abstract
Motivation: Identifying disease associated taxa and constructing networks for bacteria interactions are two important tasks usually studied separately. In reality, differentiation of disease associated taxa and correlation among taxa may affect each other. One genus can be differentiated because it is highly correlated with another highly differentiated one. In addition, network structures may vary under different clinical conditions. Permutation tests are commonly used to detect differences between networks in distinct phenotypes, and they are time-consuming.
Results: In this manuscript, we propose a multilevel regularized regression method to simultaneously identify taxa and construct networks. We also extend the framework to allow construction of a common network and differentiated network together. An efficient algorithm with dual formulation is developed to deal with the large-scale n ≪ m problem with a large number of taxa (m) and a small number of samples (n) efficiently. The proposed method is regularized with a general Lp () penalty and models the effects of taxa abundance differentiation and correlation jointly. We demonstrate that it can identify both true and biologically significant genera and network structures.
Availability and implementation: Software MLRR in MATLAB is available at http://biostatistics.csmc.edu/mlrr/.
Contact: liuzx@cshs.org
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Massive 16S rRNA and whole-metagenomic shortgun sequencing data have been generated due to advances in next-generation sequencing technologies. The goals of metagenomic research are to investigate the host–microbiota associations and bacteria interactions, and examine how changes in microbiota may affect metabolic functions and human disease. Two crucial research problems, disease associated taxa (genera, operational taxonomic units [OTUs]) selection and correlation network constructions, are usually studied separately. Both filter and model-based approaches have been proposed to detect differences in bacteria composition and relative abundance. Filter-based statistical tests select disease-associated bacteria features one at a time (Alekseyenko et al., 2013; White et al., 2009) and suffer from multiple comparisons problem. Model-based approaches, on the other hand, identify disease-associated taxa through building a sparse prediction model (Liu et al., 2011; Tanaseichuk et al., 2013), and are efficient for explicitly evaluating the predictive power of multiple taxa. However, these methods mainly focus on differences in abundance without considering the interactions among taxa.
Biological and taxa association networks have been constructed with various methods (Horvath and Dong, 2008; Krämer et al., 2009; Ruan et al., 2006; Xia et al., 2013). Such networks investigate the interactions and causality among group of genes systematically. Metabolic networks have also been proven to be powerful tools for studying the physiological and biochemical characteristics of various functional and evolutionary properties of a cell (Guimera and Nunes Amaral, 2005; Kreimer et al., 2008). A local Poisson graphical (log-linear) model and a Bayesian generalized graphical model have been proposed recently for constructing association networks based on RNA-seq data (Allen and Liu, 2013; Zhang and Mallick, 2013). Among all the methods, various graphical models with L1 regularization are perhaps the most common approach for graphical structure estimation (Banerjee et al., 2008; Liu and Ihler, 2011; Meinshausen and Bühlmann, 2006; Peng et al., 2009; Yuan and Lin, 2007). L1 regularized approaches are based on neighborhood selection for each variable (gene) i. They build a L1-based sparse regression model for each , with the remaining variables , and determine the sparse graphical model with the collected regression coefficients. They have also been extended to dependency network construction with sparse Bayesian network structure learning (Xiang and Kim, 2013). L1-based approaches automatically identify a number of dependent genes and are computationally efficient for large-scale network construction, but these approaches construct the network without considering differentiation of the genes across different clinical conditions. In addition, parameters estimated from L1 penalized regression are asymptotically biased and L1 does not always identify the true model consistently (Zou, 2006). Therefore, elastic net with (), which is equivalent to Lp (), was proposed for choosing highly correlated genes (Zou and Hastie, 2005), and Lp () penalized regression was proposed for reducing the biases of estimates (Liu et al., 2010b; Mazumder et al., 2011).
In this article, we develop sparse multilevel models for simultaneous gene selection and network construction, and simultaneous common and differentiated network construction under different clinical conditions. An efficient algorithm with duality and a general Lp () penalty is also developed to deal with the n ≪ m problem efficiently. We also propose a novel criteria entitled mean parameter difference (MPD) for and p selection. Our methods will be evaluated with simulated and real metagenomic count data. Since the variance of metagenomic counts depends on the mean count, the data are first transformed to a normal distribution using the arcsin and log-ratio variance-stability methods (Friedman and Alm, 2012; Liu et al., 2011). We demonstrate that the proposed approaches successfully identify true and biological important taxa and network structures associated with the disease.
2 Methods
Given n samples with phenotype , our goal is to identify phenotype associated taxa and simultaneously detect the network structure of those species. We are also interested in detecting network differences associated with distinct clinical conditions. For each sample, we have multiple metagenomic count features including the number of 16S rRNA clones assigned to a specific taxon, or the number of shotgun reads mapped to a specific biological pathway or subsystem. The data structure can be represented as:
where X is the metegenomic count matrix with n samples and m features, xkj denotes the total number of reads of feature j in sample k, and is a binary vector that indicates clinical conditions. A multi-class will be encoded with the one-versus-rest or one-versus-one scheme. There are two standard approaches to model metagenomic count data. One is to model the sequencing counts directly with zero-inflated Poisson or negative binomial regression (Greene, 1994; Lambert, 1992; Mullahy, 1986). However, this approach is computationally intensive especially for high-dimensional data. Building a network of decent size requires hours or even days. In addition, the joint likelihood is hard to estimate, so many likelihood-based variable selection criteria such as cross-validation and AIC cannot be applied. We, therefore, will adapt the computationally more efficient approach by first normalizing data through transformation, and then applying the machine learning or statistical tools. Data transformation has also been proposed for analyzing similar RNA-seq count data (Zwiener et al., 2014). To adjust for the read-depth differences in sequencing, the metagenomic count matrix X is first transformed into a proportion matrix , where and . To overcome variance heterogeneity with compositional data, the proportion matrix P is then converted into a normally distributed matrix with the arcsine or log-ratio transformation. (Liu et al., 2011; Sherbecoe and Studebaker, 2004). For the log-ratio transformation, there may be zeros in the proportion matrix. Therefore, we first replace
where is a small imputed value for pkj. Then the log-ratio transformation yields
where pkm is the value in the last column of the P matrix (Neocleous et al., 2011). Usually, the values in the last column are the number of sequences that were not assigned to any known taxon with the RDP classifier (rdp.cme.msu.edu), or the sum of sequencing counts in OTU clusters where the total number of counts is below a given threshold.
2.1 Multilevel regularized methods
Given normalized and binary clinical output , the task is to identify taxa that are different between clinical conditions, and identify correlation structures among taxa. We propose multilevel neighborhood selection methods that incorporate both Z and . Three different levels of distributions under different conditions are proposed:
for and is an element-wise multiplication. For each taxon i, is the conditional probabilities given a different set of variables. Assuming is a Gaussian distribution, the conditional probabilities in Models (I)–(III) can be inferred by different linear regression models, where each is a linear combination of Qi.
| (1) |
| (2) |
| (3) |
Equation (3) is the most general model conditional on the rest of the taxa , phenotype and their interactions. Equation (3) reduces to Equation (2) and Equation (1), and Model (III) becomes Models (II) and (I), respectively, when setting ai = 0 or . In the rest of this article, we will explore algorithms only for Equation (3). The same computational approach can be used for Equations (2) and (1). In Model (3), the parameter ai represents the associations between and , indicates that taxon is differentiated under different clinical conditions (). The value of measures the direct dependency between taxon and the remaining taxa, and shows there is a correlation between and given all other variables. In addition, determines correlation changes across different clinical conditions, and suggests that there is a differentiation in correlation between case and control. Therefore, depending on the problem under study, we can simultaneously identify the differentiated taxa and construct a common and a differentiated network using ai, bij and cij, respectively. Because it is common that n ≪ m in genomic and metagenomic data, learning the local graphical structure is usually based on L1. More generally Lp ()-based regularized regression for each to minimize the following error function:
| (4) |
This will yield a sparse solution with a small number of nonzero parameters when . With the ordinary lasso (p = 1), the error function E will be convex. An unique solution can be found for a given , but the estimation is biased toward zero. On the other hand, the solution will have the attractive oracle property with p < 1. Lp regression selects the correct models by producing nearly unbiased estimates for the non-zero parameters while forcing the other parameters to zero. However, the error function E is not convex when p < 1. Even though there are efficient algorithms with L1 for high-dimensional data, efficient algorithms with general Lp penalized regression are less well developed. Based on our previous work for survival analysis (Liu et al., 2010b), we propose an expectation maximization (EM)-like algorithm to deal with the high-dimensional problem.
2.2 Efficient EM-like algorithm for Lp penalized regression
Let
. We drop the sub-index i in and Qi for simplicity. An EM-like algorithm for a generic and can be developed as follows. Given the parameters , where , and , the error function to minimize is
| (5) |
where is the penalty term and n ≪ m. By introducing an auxiliary vector , we may rewrite Equation (4) as
| (6) |
With Equation (5), we can estimate the M step by first minimizing (maximizing ) by taking the first order derivative and setting it to zero.
where indicates element-wise division. So
Instead of finding the high-dimensional () primal parameters directly, we introduce n-dimensional dual variables , so we have
| (7) |
where
| (8) |
and
| (9) |
By substituting the primal variables into Equation (9), we have
| (10) |
where
Ku is a much smaller n × n symmetric matrix and is predetermined as long as is given. The dual variables can be calculated in matrix form as follows:
| (11) |
The primal variables can then be updated explicitly with a simple matrix computation.
| (12) |
The expectation step is simply . Therefore, we have the EM algorithm for each and Qi with the local graphical model:
EM-like Algorithm.
Given a , small numbers ϵ and ε, and training data ,
Initializing ,
While ,
E-step:
M-step:
END
.
The EM algorithm is highly efficient when n ≪ m, because it uses the inverse of matrix instead of the inverse of , as in ordinary regression. Compared with one with dimension of ten-thousands, inverting a matrix with hundreds of dimensions is very fast. As discussed earlier, this algorithm will converge to a global optimum with a p = 1, because the error function is convex. A local minimum is guaranteed with p < 1. Computational experiences with Lp suggest that it converges to a unique solution for , when the error function is nearly convex. To construct a local graphical network, we run the EM-like algorithm m times for each . The non-zero s indicate a dependency between taxa i and j. Models for each node can be estimated independently and in parallel using appropriate computational power.
Negative correlations between genes are difficult to confirm and seemingly less ‘biologically relevant’ (Lee et al., 2004). Negative correlation can be introduced when count data are transformed into proportions. For example, transforming two random samples with zero correlation into proportions will lead to a perfect r = –1 negative correlation, which does not seem biologically sensible. Our approach can be adapted to study positive dependency only by setting in the M-step of EM algorithm.
2.2.1 Determination of and p
Both and p determine the sparsity of the model. is partitioned into 100 equal intervals in a log scale, and p is chosen from in this article for simplicity. The regularization parameter and p are determined through cross-validation. We build regression models with 100 different s and 20 different ps, the optimal and p are then selected with either the minimal mean squared error (MSE) of the test data or the most stable parameter (edge) estimation with k-fold cross-validation. Other criteria such as AIC and BIC can also be used to find the optimal and p. Although cross-validation with MSE is straightforward, stability selection chooses an optimal with the minimal mean difference of the estimated parameters. Mathematically, we first estimate k sets of parameters with k-fold cross-validation, and the MPD for given and p is defined as
MPD is similar to the stability selection (StARS) approach which identifies the most stable set of parameters with cross-validation (Liu et al., 2010a). Because MSE is known as a loose criteria for L1, and MPD is a more conservative measure tending to select less variables, the optimal p chosen with MPD is usually larger than 1, whereas the optimal p with MSE is less than 1. In addition, a node (taxon) will be dropped out when the test MSE is larger than a predetermined threshold.
3 Results
3.1Simulation data
Count data for simulation are generated with Poisson distributions and known correlation structure (Zhang and Mallick, 2013). The count xij has a Poisson distribution with mean τij, and has normal distribution with mean μ and covariance Σ. An adjacency matrix can be measured by . We simulated data with two groups, with the number of nodes (variables) of m = 200, and sample size n = 20, 40 and 60 for each group, respectively. The mean μi (i = 0, 1) for each group is and , respectively, so the generated data only have the first five features differentiated. Therefore, we have a binary class problem with , where if sample group 0 and yk = 1 for sample group 1. Three different network structures were incorporated in the data: (i) a common network structure A, where A is a band matrix with bandwidth 1 and each node only connects to its neighborhood nodes, (ii) a common network structure A, where A is a band matrix with bandwidth 2 and (iii) different network structures with A0 being an adjacency matrix of bandwidth 1 for class 0, and A1 being an adjacency matrix of bandwidth 2 for class 1. After we generated the count matrix X with known network structure A and class information , Equation (1) was used to detect differentiated features and the common network structure simultaneously with the first two datasets. We simulated these data 100 times. The generated count data were then transformed with proportion and arcsin transformations. The log-ratio transformation yields similar performance, so only results with proportion and arcsin transformations are reported in this article. Five-fold cross-validation was used to determine the optimal parameters and p. The area under ROC curves (AUC) was used to evaluate the performance of detecting proposed network structures, where the sensitivity for a network is the proportion of edges that are correctly identified, whereas the specificity for a network measures the proportion of no-edges that are correctly detected. The ROC curve and AUC were then calculated accordingly. Moreover, the performance of feature selection is defined as the number of times that the first five features are correctly identified. AUC for validating the network structures and the number of times that the first five true features are selected are reported in Tables 1 and 2, respectively.
Table 1.
Predicted AUCs with different network structures and parameters
| Sample size |
Band 1 network |
Band 2 network |
||
|---|---|---|---|---|
| n | ||||
| 20 | ||||
| 40 | ||||
| 60 | ||||
Notes: Data were simulated with m = 200, and n = 20, 40 and 60, respectively.
Table 2.
Frequencies of correctly identified features and average false-discovery rate over 100 simulations
| Feature | Band 1 network (n) |
Band 2 network (n) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||||||
| 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | 20 | 40 | 60 | |
| 1 | 51 | 81 | 90 | 83 | 93 | 100 | 53 | 79 | 100 | 100 | 100 | 100 |
| 2 | 42 | 60 | 73 | 80 | 93 | 94 | 49 | 67 | 85 | 90 | 100 | 98 |
| 3 | 40 | 46 | 70 | 84 | 91 | 92 | 35 | 48 | 93 | 82 | 91 | 96 |
| 4 | 59 | 62 | 75 | 70 | 93 | 97 | 30 | 56 | 78 | 94 | 96 | 96 |
| 5 | 80 | 94 | 99 | 93 | 95 | 99 | 40 | 58 | 91 | 89 | 96 | 95 |
| AFPR (%) | 2.7 | 1.7 | 1.4 | 0.36 | 0.03 | 0 | 3.5 | 2.7 | 2.1 | 3.8 | 3.5 | 2.8 |
Notes: Only the first five features are truly differentiated.
Our methods identified the true differentiated features and network structures as shown in Tables 1 and 2. Overall, the predicted AUCs become larger when the sample size increases. In addition, minimizing MPD performs better than minimizing test MSE. Compared with the average AUCs of 0.83, 0.94 and 0.97 with MSE for band 1 network, the corresponding AUCs with MPD are 0.89, 0.97 and 0.99 for n = 20, 40 and 60, respectively. Similar results were achieved for band 2 network with different sample sizes and optimal parameters. With n = 20, 40 and 60, respectively, out of 100 simulations for band 1 network, more than 40, 46 and 70 times of five differentiated features were appropriately identified with MSE, whereas more than 70, 91 and 92 times of the five features were correctly selected with MPD. MSE identified at least 30, 48 and 78 times of five differentiated features correctly for band 2 network, whereas MPD accurately selected the five features at least 82, 91 and 95 times, indicating that MPD is more accurate. The accuracy of feature identification increases with sample size. Five features were identified correctly over 92 and 95 times with MPD and the sample size of 60 for band 1 and 2 networks, respectively, whereas the average false-positive rates (AFPR) were all under 5%. The comparison between our approach and Student’s t-test with the same data is reported in Supplementary Appendix S1. Student’s t-test leads to high FPRs and fails to identify the true features even with the conservative Bonferroni correction. Feature selection with network correction is important, and the proposed approach provides an efficient way to accomplish it.
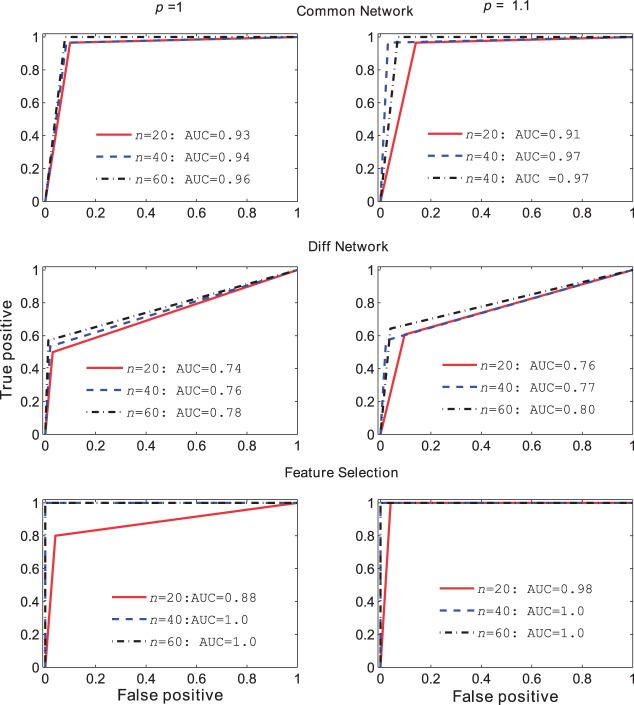
Differentiated features, and common and differentiated network structures can also be identified simultaneously with Equation (3). Simulated data were generated with the Poisson distribution with known means and network structures. Data for class 0 is again generated with mean μ0 and a band 1 network and for class 1 is generated with μ1 and a band 2 network, respectively. So the class output is defined similarly as the previous simulations, and the common network to detect is the band 1 network the differentiated network to identify is the differential structure between band 1 and 2 networks. Equation (3) is used to evaluate the performance. Predictive performance of proposed method is shown in Figure 1: Differentiated features, and the structures of common and differentiated networks were detected with high accuracy. Because MSE usually has the best performance when p < 1, and MPD has the best performance when p > 1, we define a new integrated performance measure that chooses the optimal in roman> for variable selection. AUC for differentiated features (bottom panel Fig. 1) can be identified perfectly (AUC = 1) with a larger sample size (n = 40) for each group. The common network structure (top panel of Fig. 1) can be detected with over 0.91 AUC, while distinguishing the differentiated structure is more difficult with the test AUC of over 0.74. In addition, AUCs increase as the sample size becomes larger. Finally, the performances with L1 and penalties are quite similar with the integrated measure, indicating that it is possible to achieve a good performance with L1 regularized regression with an appropriate measure.
Fig. 1.
Performance base on AUC for common and differentiated networks and differentiated features with P =1 and 1.1, respectively. Top panel: AUC for common network detection, middle panel: AUC for differentiated networks and bottom panel: AUC for feature selection
3.2 Benchmark metagenomic data
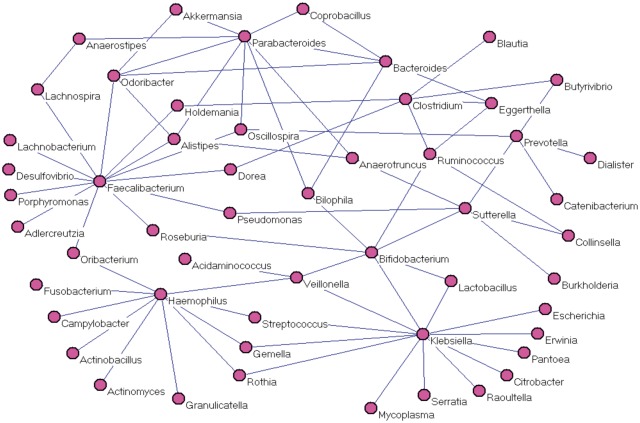
A metagenomic dataset was generated from research findings in our own group (Tong et al., 2013). A recent analysis of microbial co-occurrence in the HMP cohort revealed significant relationships across many body compartments, including 3005 edges and 67 edges among microbiota of all body sites and the gut (fecal compartment), respectively. The differences (if any) may be due to healthy only subjects, different cohorts and fecal (versus mucosal wash compartments). There are in total 299 samples with 76 inflammatory bowel disease (IBD) subjects including Crohn’s disease (CD) and ulcerative colitis (UC), and 223 non-IBD subjects. Out of 299 samples, 285 (72 IBDs and 213 controls) have metagenomic count data available. There were a total of 5648 OTUs available. We merged OTUs at the genus level. Then genera with high abundances were selected for further study after discarding those genera with less than five reads on average. Data were then normalized with the proportion and arcsin transformation. The class is a binary vector with yk = 0 for non-IBD, and yk = 1 for IBD samples or vice versa. The input Z is the normalized taxa matrix. To identify differentiated genera and positive correlations in whole, IBD and non-IBD populations, we run the program for Equation (3) two times with 0/1 values flipped. Five-fold cross-validation and MPD were used to find optimal . Our program (mlrr) identified the optimal parameter pair and determined the best model automatically. Genes with higher abundance in IBD and non-IBD are reported in Table 3. Eight identified genera have higher abundance in IBD, whereas 20 have higher abundance in non-IBD, indicating less bacterial diversity in IBD patients. Common and differentiated networks are shown in Figures 2 and 3, respectively. Several important findings are demonstrated with Table 3, Figures 2 and 3 together. Genera Klebsiella has higher abundance in IBD with the largest estimated parameter (0.0626). It also has the highest degrees of 13 and 7 in common and control network, respectively. Klebsiella is probably harmful, because it loses its connections (co-occurrences) with other genera and has higher abundance in IBD. Disease status is determined by both the relative abundance of Klebsiella and its co-occurrence patterns with other genera. In fact, Klebsiella is a well-studied IBD-associated bacteria. It is a likely triggering factor associated with the initiation and development of IBD (Rashid et al., 2013; Sanchez et al., 2013). On the other hand, genera Faecalibacterium has higher abundance in non-IBD (lower abundance in IBD) with the largest parameter 0.0319. It also has the largest degree of 13 in the common network, and is connected to Ruminococcus in the IBD network. This may indicate that Faecalibacterium is a protective genera and its lack may contribute to IBD. The fact that Ruminococcus and Faecalibacterium link to each other and both have lower abundance in IBD suggests that the co-abundance of Ruminococcus and Faecalibacterium may be useful for IBD diagnosis. The association between Faecalibacterium and IBD has been an active topic of research recently in the literature (Lopez-Siles et al. 2014; Machiels et al., 2013). Investigators have shown that Faecalibacterium is relevant to the etiology and pathogenesis of IBD both in clinical and laboratory investigations. However, the role of Ruminococcus and its co-abundance with Faecalibacterium in IBD has not been well studied. Another genera Haemophilus may also be important for IBD. It has the degree of 9 and 4 in common and non-IBD network, respectively, and has higher abundance in non-IBD. It loses its co-abundance with several other genera in IBD. The other genera such as Fusobacterium, Bacteroides, Veillonella, Lactobacillus and Escherichia with high abundance in IBD may be potential gut pathogens and associated with IBD. On the other hand, the 20 identified genera with higher abundance in non-IBD may be protective bacteria that are negatively associated with IBD. Moreover, genera such as Bifidobacterium could be an important target for IBD, even if its relative abundance does not vary between case and control. Bifidobacterium has interactions with other genera in both common and non-IBD networks, but does not have any connections in the IBD network. The variation in co-occurrence networks may have biological and clinical implications. Finally, less bacteria diversity and interactions in IBD have been observed as shown in the genera list and IBD network. Therefore, it is important to study variations of relative abundance, and common (background) and differentiated networks systematically. Our approach can identify IBD associated bacteria and provide potential targets for further investigations.
Table 3.
Identified Genera that are differentiated in relative abundances across different clinical conditions
| IBD |
non-IBD |
||
|---|---|---|---|
| Genera | Parameters | Genera | Parameters |
| Acidaminococcus | 0.0078 | Bilophila | 0.0020 |
| Bacteroides | 0.0091 | Blautia | 0.0011 |
| Escherichia | 0.0022 | Clostridium | 0.0014 |
| Fusobacterium | 0.0105 | Collinsella | 0.0010 |
| Klebsiella | 0.0626 | Coprococcus | 0.0057 |
| Lactobacillus | 0.0051 | Desulfovibrio | 0.0034 |
| Mycoplasma | 0.0022 | Dorea | 0.0013 |
| Veillonella | 0.0081 | Eubacterium | 0.0013 |
| Faecalibacterium | 0.0319 | ||
| Haemophilus | 0.0029 | ||
| Holdemania | 0.0012 | ||
| Lachnobacterium | 0.0013 | ||
| Lachnospira | 0.0040 | ||
| Oscillospira | 0.0028 | ||
| Phascolarctobacterium | 0.0021 | ||
| Prevotella | 0.0113 | ||
| Pseudomonas | 0.0013 | ||
| Roseburia | 0.0033 | ||
| Ruminococcus | 0.0042 | ||
| Sutterella | 0.0058 | ||
Notes: The estimated parameters are reported in columns 2 and 4, respectively. The larger the parameter value, the more differentiated the genera.
Fig. 2.
Common network constructed across clinical conditions
Fig. 3.
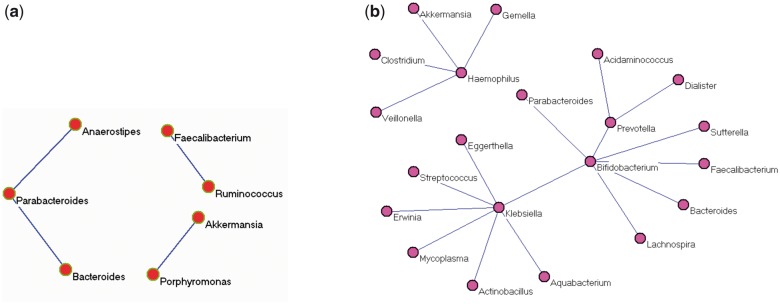
Differentiated networks: a) network solely for IBD and b) network solely for non-IBD control
4 Conclusions
We proposed a multilevel penalized regression method for simultaneous genera selection and network construction. We also developed an efficient EM-like algorithm with dual-formulation for solving a general Lp, regularized problem. The proposed algorithm includes L1 and elastic net penalties as special cases, and efficiently deals with high-dimensional n ≪ m problem. The elastic net penalty is equivalent to a Lp with . We compared the performance of the proposed method with different p values. Different optimal ps can be selected from different performance measures. A usually has the best performance with a loose MSE measure, while a p > 1 will lead to the best performance with a more conservative MPD criteria. LASSO achieves the best performance with the average of optimal s from test MSE and MPD. We tested our method with simulated and real rRNA 16S sequencing data. Comparing with available methods for network construction and feature selection in the literature, the proposed approach identifies true features and biologically important genera, and constructs common and differentiated networks jointly with high accuracy. It provides a novel tool for studying correlation and differentiation together, and is computational efficient for high-dimensional metagenomic data. Recent work has greatly expanded the cohort size co-analyzed for microbial community structure in new-onset IBD (PMID: 24629344). The present methodology offers a new perspective on disease association and community structure that would be particularly valuable in tackling such extensive datasets. The proposed approach can also be applied to most RNA-seq data directly provided they are normalized.
Funding
This work was partially supported by grants from National Science Foundation [DMAC: ADT-1220747 to Z.L.], Crohn’s and Colitis Foundation of America [to J.B.], National Institutes of Health [DK46763 to J.B. and D.P.B.M.], National Institutes of Health NCRR and NCATS [UL1TR000124 to J.B.].
Conflict of Interest: none declared.
Supplementary Material
References
- Alekseyenko A.V., et al. (2013) Community differentiation of the cutaneous microbiota in psoriasis. Microbiome,1, 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen G.I., Liu Z. (2013) A local Poisson graphical model for inferring networks from sequencing data. IEEE Trans. Nanobiosci., 12, 189–198. [DOI] [PubMed] [Google Scholar]
- Banerjee O., et al. (2008) Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data. JMLR, 9, 485–516. [Google Scholar]
- Greene W.H. (1994) Some accounting for excess zeros and sample selection in Poisson and negative binomial regression models. Working Paper EC-94-10, Department of Economics, New York University. [Google Scholar]
- Guimera R., Nunes Amaral L.A. (2005) Functional cartography of complex metabolic networks. Nature, 433, 895–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., Alm E.J. (2012) Inferring correlation networks from genomic survey data. PLoS Comput. Biol., 8, e1002687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horvath S., Dong J. (2008) Geometric interpretation of gene coexpression network analysis. PLoS Comput. Biol., 4, e1000117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krämer N., et al. (2009) Regularized estimation of large-scale gene association networks using graphical Gaussian models. BMC Bioinformatics, 10, 384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreimer A., et al. (2008) The evolution of modularity in bacterial metabolic networks. Proc. Natl Acad. Sci. U. S. A., 105, 6976–6981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert D. (1992) Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics, 34, 1–14. [Google Scholar]
- Lee H.K., et al. (2004) Coexpression analysis of human genes across many microarray data sets. Genome Res., 14, 1085–1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H., et al. (2010a) Stability approach to regularization selection for high dimensional graphical models. Adv. Neural Inform. Process. Syst., 24, 1432–1440. [PMC free article] [PubMed] [Google Scholar]
- Liu Q., Ihler A. (2011) Learning Scale Free Networks by Reweighted L1 Regularization. AISTATS. JMLR Workshop and Conference Proceedings Volume 15. [Google Scholar]
- Liu Z., et al. (2010b) Kernel based methods for accelerated failure time model with ultra-high dimensional data. BMC Bioinformatics, 11, 606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z., et al. (2011) Sparse distance-based learning for simultaneous multiclass classification and feature selection of metagenomic data. Bioinformatics, 27, 3242–3249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Siles M., et al. (2014) Mucosa-associated Faecalibacterium prausnitzii and Escherichia coli co-abundance can distinguish Irritable Bowel Syndrome and Inflammatory Bowel Disease phenotypes. Int. J. Med. Microbiol., 304, 464–475. [DOI] [PubMed] [Google Scholar]
- Machiels K., et al. (2013) A decrease of the butyrate-producing species Roseburia hominis and Faecalibacterium prausnitzii defines dysbiosis in patients with ulcerative colitis. Gut, 63, 1275–1283. [DOI] [PubMed] [Google Scholar]
- Mullahy J. (1986) Specification and testing of some modified count data models. J. Econometrics, 33, 341–365. [Google Scholar]
- Mazumder R., et al. (2011) SparseNet: Coordinate descent with non-convex penalties. JASA, 106, 1125–1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinshausen N., Bühlmann P., (2006) High-dimensional graphs and variable selection with the lasso. Ann. Statist., 34, 1436–1462. [Google Scholar]
- Neocleous T., et al. (2011) Transformations for compositional data with zeros with an application to forensic evidence evaluation. Chemom. Intell. Lab. Syst., 109, 77–85. [Google Scholar]
- Peng J., et al. (2009) Partial correlation estimation by joint sparse regression models. JASA, 104, 735–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rashid T., et al. (2013) The role of Klebsiella in Crohn’s disease with a potential for the use of antimicrobial measures. Int. J. Rheumatol., 2013, 610393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruan Q., et al. (2006) Local similarity analysis reveals unique associations among marine bacterioplankton species and environmental factors. Bioinformatics, 22, 2532–2538. [DOI] [PubMed] [Google Scholar]
- Sanchez E., et al. (2013) Duodenal-mucosal bacteria associated with celiac disease in children. Appl. Environ. Microbiol., 79, 5472–5479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherbecoe R.L., Studebaker G.A. (2004) Supplementary formulas and tables for calculating and interconverting speech recognition scores in transformed arcsine units. Int. J. Audiol., 43, 442–448. [DOI] [PubMed] [Google Scholar]
- Tanaseichuk O., et al. (2013) Phylogeny-based classification of microbial communities. Bioinformatics, 30, 449–456. [DOI] [PubMed] [Google Scholar]
- Tong M., et al. (2013) A modular organization of the human intestinal mucosal microbiota and its association with inflammatory bowel disease. PLoS One, 8, e80702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White J., et al. (2009) Statistical methods for detecting differentially abundant features in clinical metagenomic samples. PLoS Comput. Biol., 5, 1000352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia L.C., et al. (2013) Efficient statistical significance approximation for local similarity analysis of high-throughput time series data. Bioinformatics, 29, 230–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang J., Kim S. (2013) A* Lasso for learning a sparse Bayesian network structure for continuous variables. Adv. Neural Inform. Process. Syst., 26, (NIPS 2013) pp. 2418–2426. [Google Scholar]
- Yuan M., Lin Y. (2007) Model selection and estimation in the Gaussian graphical model. Biometrika, 94, 19–35. [Google Scholar]
- Zhang L., Mallick B.K. (2013) Inferring gene networks from discrete expression data. Biostatistics, 14, 708–722. [DOI] [PubMed] [Google Scholar]
- Zou H. (2006) The adaptive lasso and its oracle properties. J. Am. Stat. Assoc., 101, 1418–1429. [Google Scholar]
- Zou H., Hastie T. (2005) Regularization and variable selection via the elastic net. J. R. Stat. Soc. B, 67, 301–320. [Google Scholar]
- Zwiener I., et al. (2014) Transforming RNA-Seq data to improve the performance of prognostic gene signatures. PLoS One, 9, e85150. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.