Abstract
Ions surround nucleic acids in what is referred to as an ion atmosphere. As a result, the folding and dynamics of RNA and DNA and their complexes with proteins and with each other cannot be understood without a reasonably sophisticated appreciation of these ions’ electrostatic interactions. However, the underlying behavior of the ion atmosphere follows physical rules that are distinct from the rules of site binding that biochemists are most familiar and comfortable with. The main goal of this review is to familiarize nucleic acid experimentalists with the physical concepts that underlie nucleic acid–ion interactions. Throughout, we provide practical strategies for interpreting and analyzing nucleic acid experiments that avoid pitfalls from oversimplified or incorrect models. We briefly review the status of theories that predict or simulate nucleic acid–ion interactions and experiments that test these theories. Finally, we describe opportunities for going beyond phenomenological fits to a next-generation, truly predictive understanding of nucleic acid–ion interactions.
Keywords: ions, RNA/DNA, electrostatics, Poisson–Boltzmann, Manning condensation, Hill equation, free energy
INTRODUCTION
Nucleic acids are central to the storage, transmission, processing, and regulation of genetic information, serving as carriers of the genetic code, catalysts, and mechanochemical switches. Although the importance of ions for the structure, folding, and function of DNA and RNA, and for their interactions with proteins has long been appreciated, the physical properties and energetics of ion–nucleic acid interactions are often not intuitive. Misconceptions remain common.
Nucleic acid–ion interactions provide large interaction energies. Thus, these interactions are a critical component of a complete description of the folding of functional DNAs and RNAs, of interactions of nucleic acids with ligands and macromolecule partners, and of the function of RNAs and RNA–protein complexes and machines. These processes include viral packaging and function and the assembly and function of the ribosome, spliceosome, signal recognition particle, telomerase, chromosomes, and chromatin (1–6). Quantitative description of these interactions is a grand challenge that needs to be met to fully understand biological function and regulation involving nucleic acids and to rationally manipulate and engineer nucleic acids and their complexes.
On the surface, understanding nucleic acid–ion interactions would seem no more complex than any receptor–ligand interaction. However, the vast majority of ion–nucleic acid interactions involve the so-called ion atmosphere, a loosely associated sheath of ions surrounding the nucleic acid polyelectrolyte, and even site-bound metal ions are influenced by the ion atmosphere. Because this ion atmosphere is highly mobile, involves many ions, and varies with ionic conditions, it is not easily appreciated and explained.
Several treatments have laid out thermodynamic and mathematical frameworks of ion–nucleic acid interactions (e.g., References 7–13). However, these treatments are often steeped in thermodynamic language unfamiliar to most biochemists and molecular biologists. Recent experimental breakthroughs now provide an opportunity to present a more intuitive and empirically grounded description of the important properties of the ion atmosphere and its influence on nucleic acids and their interactions. Drawing both on theoretical models of the ion atmosphere and on the latest experimental findings, this review aims to lay out a conceptual framework to guide thinking about ion–nucleic acid interactions and aid the nucleic acid experimental practitioner. We also hope that this conceptual treatment helps clarify and focus the considerable future challenges in this area.
THE BASICS
Electrostatic Effects in Nucleic Acids: How Important Are They?
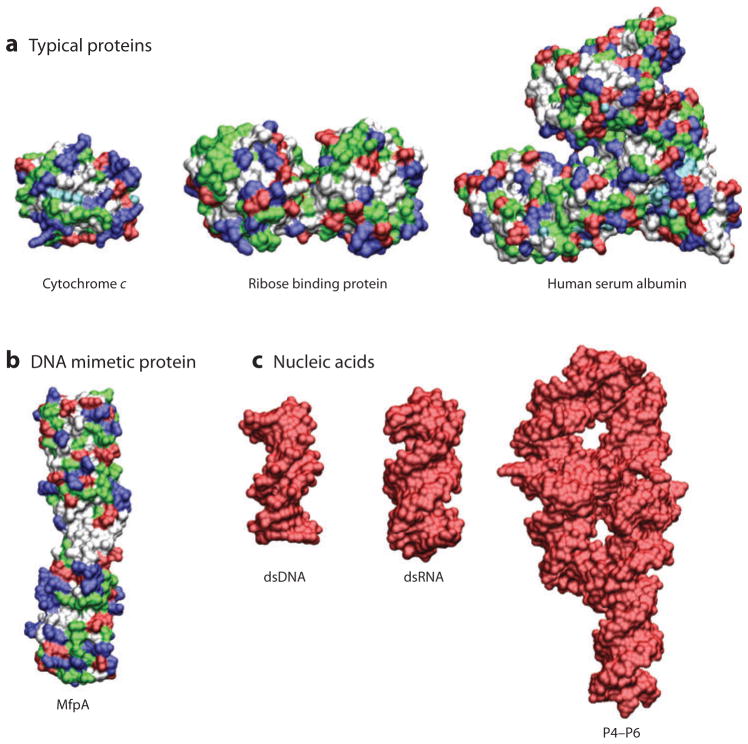
Although electrostatic interactions are important for all biological macromolecules, their energetic consequences are enormous for nucleic acids. Consider that only 5 of the 20 amino acids that make up proteins are charged at physiological pH, and as there are both positively and negatively charged amino acids, the net charge on most proteins tends to be small (Figure 1) (14, 15). In contrast, the phosphate backbone of nucleic acids carries one negative charge per residue. As a result, nucleic acids are highly charged (Figure 1) (16). Bringing these charges in close proximity during RNA folding or DNA compaction requires overcoming an enormous electrostatic energy barrier (9, 17). For example, in the absence of counterions, the electrostatic repulsion encountered in the folding of the 400-nt Tetrahymena self-splicing intron RNA would correspond to ~600 kcal/mol, approximately a thousand times the thermal energy kBT (0.62 kcal/mol at 37°C) (17).
Figure 1.
Structures of (a) three typical proteins, (b) the DNA mimetic pentapeptide repeat protein MfpA, and (c) three nucleic acids. Nucleic acids are highly negatively charged compared with proteins. Negatively charged residues are shown in red, positively charged residues in blue, polar residues in green, and nonpolar residues in white. The proteins shown are cytochrome c [Protein Data Bank (PDB) identifier 1CRC (188), 105 residues, and total estimated charge +9e], ribose binding protein [PDB 1URP (189), 271 residues, total charge −2e], and human serum albumin [PDB 1E7H (190), 585 residues, total charge −15e]. (b) The pentapeptide repeat protein MfpA [PDB 2BM4 (191), 186 residues, total charge −5e] inhibits gyrase by binding as a DNA mimetic (191, 192) despite having only a modest overall negative charge. (c) The nucleic acids shown are double-stranded DNA (dsDNA) [PDB 2BNA (193), 24 residues, total charge −22e], double-stranded RNA (dsRNA) [adapted from PDB 3CIY (194), 30 residues, total charge −28e], and the P4–P6 domain from the Tetrahymena group I intron ribozyme [PDB 1GID (21), 158 residues, total charge −157e].
Counterions reduce the electrostatic repulsion, which is referred to as screening. The concentration and charge of the cation(s) present greatly affect the extent of charge screening and thus whether an RNA molecule will fold or whether a protein will bind a stretch of DNA. Most functional RNA molecules will not fold under low salt conditions (18) and, indeed, addition of Mg2+ continues to be the most common way to induce folding in RNA biochemical experiments. Conversely, favorable electrostatic interactions due to formation of DNA–protein and RNA–protein complexes are reduced at higher salt concentrations.
Why Are the Effects of Screening Ions So Difficult to Experimentally Dissect?
The fluctuating nature of the ion atmosphere around nucleic acids has made quantitative experimental studies challenging. In particular, the ion atmosphere is (mostly) invisible to traditional structural biology techniques, such as X-ray crystallography, NMR, or (cryo–) electron microscopy. Furthermore, folding events or conformational transitions induced by changing the ion atmosphere also involve other physical phenomena, such as tertiary structure formation and ion binding, so that the specific effects of the atmosphere typically cannot be readily isolated, quantified, and understood.
Can the ion atmosphere be identified though X-ray crystallography?
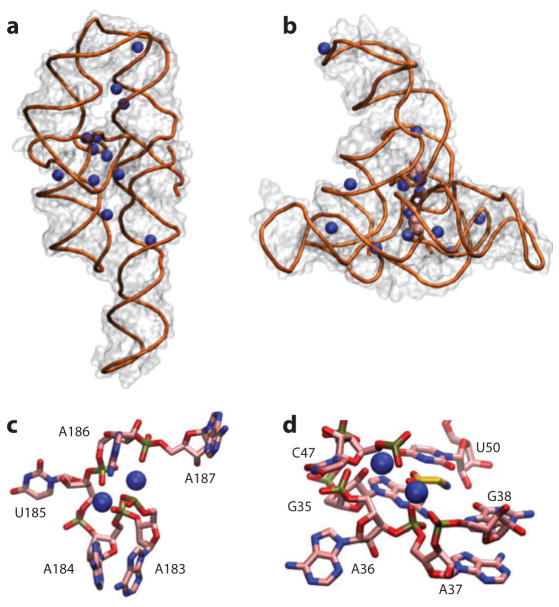
X-ray crystallography is a powerful tool to study the specific contacts made by ions and nucleic acids. RNA crystal structures often reveal bound ions that can be assigned in the crystallographic electron density map (19–29). The crystallographically resolved ions are typically bound to specific sites on the RNA molecule, where they are at least partially dehydrated and often in close proximity to one or several phosphoryl groups (Figure 2) (19, 20, 23, 25, 30). However, although high-resolution RNA structures have provided invaluable details about local RNA–ion interactions, they do not describe the ion atmosphere. Using the very simple rule of overall charge neutralization (see the section below titled Are There Any Universal Principles Governing Nucleic Acid–Ion Interactions?), one can see that cations identified in X-ray structures account for only a small fraction of the positive charge that is present; there must be other ions in the ion atmosphere (Figures 2 and 3). Apparently these ions form a fluctuating and extended layer around the DNA or RNA that cannot be captured by crystallography (1, 2, 10, 31–33). It is also worth noting that crystallization conditions can affect the position and occupancy of metal ions. For example, the same position can be occupied by different ions in different crystal structures of the same RNA (19, 34–37), and ion occupancy in solution may be different from that in the crystal structure.
Figure 2.
Crystal structures reveal details of ion–nucleic acid interactions but fail to give a complete picture of the ion atmosphere. (a) Crystal structure of the P4–P6 domain of the Tetrahymena group I intron ribozyme [Protein Data Bank (PDB) identifier 1GID] (21). Twelve crystallographically resolved Mg2+ ions are shown as blue spheres. (b) Crystal structure of the tandem aptamer of a glycine riboswitch from Fusobacterium nucleatum (PDB 3P49) (195). The two glycine molecules bound to the tandem aptamer are shown in pink. Thirteen crystallographically resolved Mg2+ ions are shown as blue spheres. (c) Close-up of the metal ion core of the P4–P6 RNA. Metal ions (spheres) interact with the adenine (A)-rich bulge, making a number of contacts and organizing the RNA residues. (d) Detailed rendering of the glycine binding pocket of aptamer I of the structure in panel b. The two crystallographically resolved Mg2+ ions (spheres) coordinate a series of backbone residues in the binding pocket as well as the ligand glycine. These RNAs have 158 and 169 residues, corresponding to total charges of the RNAs of −157 and −168, respectively. The structures resolve 12 and 13 Mg2+, respectively, which means that only ~15% of the ion atmosphere required for charge neutrality is accounted for by the explicitly resolved ions. In addition, the crystallographically resolved ions can be replaced by ions of other identities; both RNAs can undergo partial folding in high concentrations of monovalent ions (62, 83). Docking of the P5abc metal ion core in the P4–P6 RNA (c) and glycine binding (d) and folding to the native state for the tandem aptamer riboswitch require divalent ions, however, with limited specificity between different divalent species (52, 62, 103).
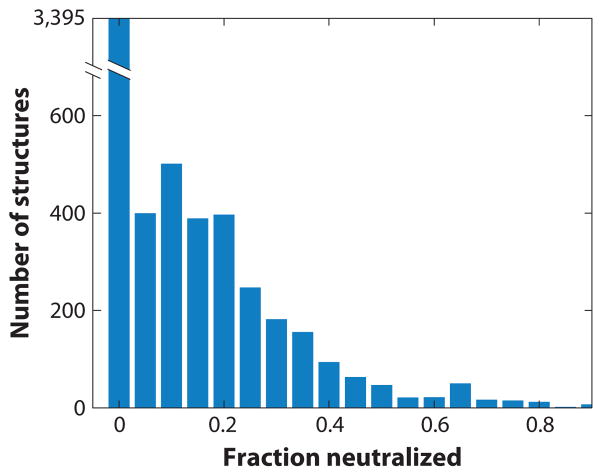
Figure 3.
Statistical analysis of ions in nucleic acid crystal structures. Distribution of the fraction of nucleic acid charges that are neutralized by ions resolved in the crystal structures of 6,238 nucleic acids obtained from the nucleic acid data base (http://ndbserver.rutgers.edu/). Nucleic acid charges were estimated by counting atoms of type P (phosphorus); ion charges were estimated by counting all elemental ions of the first and second groups as well as Mn2+, Fe2+, Co2+, Ni2+, Cu2+, and Zn2+. The “fraction neutralized” is defined as the total positive charge due to the ions divided by the total negative charge of the nucleic acid. More than half of all crystal structures of nucleic acids do not resolve any ions, and in the structures that do report ions, the total charge of the crystallographically resolved ions, on average, accounts for only ~20% of the total nucleic acid charge.
Why Are the Effects of Screening Ions So Difficult to Model?
Positive ions are attracted to nucleic acids due to their negative charge, and negative ions are repelled. As a consequence, the local environment of a nucleic acid in solution has a higher concentration of positive ions than the unperturbed bulk ion concentration far away from the nucleic acid (counterion accumulation) and a lower local concentration of negatively charged ions (coion depletion). At this level, electrostatic interactions are simple.
But despite a seemingly simple basis in charge repulsion and attraction, modeling nucleic acid–ion interactions presents a formidable theoretical challenge. There are a very large number of ions, and they can occupy many different positions. Furthermore, interaction with each of the other ions must be considered in addition to interactions with the nucleic acid. In modeling approaches, this complexity is exacerbated by the long-range nature of electrostatic interactions (38) given by Coulomb’s law (Equation 1): The electrostatic interaction energy, U1,2, between two charges, q1 and q2, falls off only as 1/r, where r is the distance between the charges, in contrast to charge–dipole and dipole–dipole interaction energies, which fall off more steeply with separation (e.g., dipole–dipole interactions fall off with a 1/r3 dependence; ε0 and ε are the electric permittivity of vacuum and the dielectric constant, respectively):
| 1 |
For a sense of scale, the dielectric constant is 80 in water, and the repulsive energy of two phosphoryl groups, each with charge −1e at the distance typical of nearest-neighbor nucleotides (7 Å), is 0.6 kcal/mol. This value—for just a single pair of nucleic acid groups—is already close to the thermal energy kBT, so that removing it (by screening) or doubling it would have a nonnegligible effect on the energetic balance between nucleic acid conformations. When summed over all pairs of phosphoryl groups, counterions, and coions in an RNA or DNA system, the total electrostatic interaction energies are enormous. Further complicating the analysis of nucleic acid–ion behaviors and energetics is the presence of large ensembles of conformations of the nucleic acids of interest. Thus, in addition to determining the nucleic acid–ion energetics of one nucleic acid conformation, any modeling effort must repeat this calculation many times, for each of the nucleic acid conformations that represent the overall ensemble of conformers present (39–43).
Finally, consideration of the ions themselves is highly complex. Whereas some of the ions remain solvated essentially as present in a normal salt solution, others closely approach the nucleic acid, resulting in polarization and solvation changes; and some of the closest approaching ions become partially desolvated and occasionally fully or nearly fully desolvated (1, 19, 20, 23). Situations like these are not well approximated by a simple continuum dielectric constant as in Equation 1, and state-of-the-art simulations do not reproduce the polarization effects of ions or water molecules (44–48). Additional discussion of modeling issues appears below.
Are There Any Universal Principles Governing Nucleic Acid–Ion Interactions?
As described above, the interactions of ions and nucleic acids can be extraordinarily complicated to experimentally dissect or to model. Fortunately, there is one powerful concept that universally holds and can guide our efforts to understand these electrostatic interactions: charge neutrality. The sum of all positive and negative charges in solution must equal to zero (1, 8, 33, 49). Even small deviations from charge neutrality give rise to very large Coulomb forces that strongly attract charged species such that neutrality is restored at equilibrium. (Recall that charge separation across membranes is used by cells to store and transduce energy and can be the predominant component of the proton-motive force used to synthesize ATP.) Applied to nucleic acids, charge neutrality means that overall counterion accumulation and coion depletion exactly balance the charges on the nucleic acid; in other words, the sum of all charges from the nucleic acid and its ion atmosphere is zero. This turns out to be a strong and nontrivial constraint. (Analogous constraints do not exist for the association of neutral metabolites to macromolecules.) However, taking advantage of the principle of charge neutrality requires looking at all charged objects in a system: the negatively charged nucleic acid, the positively charged counterions, and even the negatively charged coions (see the section below titled What Is in the Ion Atmosphere?).
VISUALIZING THE ION ATMOSPHERE
What Is in the Ion Atmosphere?
If X-ray crystallography cannot define the ion atmosphere’s contents, how can we determine them? The ion atmosphere extends in all directions from a nucleic acid until ion concentrations become equal to those in the bulk solution (Figure 4a). From the principle of charge neutrality, one can think of the ion atmosphere as the integration of all ions and charges in the space surrounding the nucleic acid until the total charge of the ion atmosphere is equal and opposite to that of the nucleic acid and the total combined charge of the nucleic acid and ion atmosphere becomes zero (Figure 4b). Although this is the cleanest definition of the ion atmosphere, it poses several challenges. As ions are distributed at varying distances from the nucleic acid and thus have different behaviors, how does one assay them? For example, 23Na NMR relaxation approaches assess Na+ ions that closely approach the nucleic acid (50) but will not count the ions that are in the atmosphere but are too distant to collide with the nucleic acid over the specified time period of the relaxation measurement.
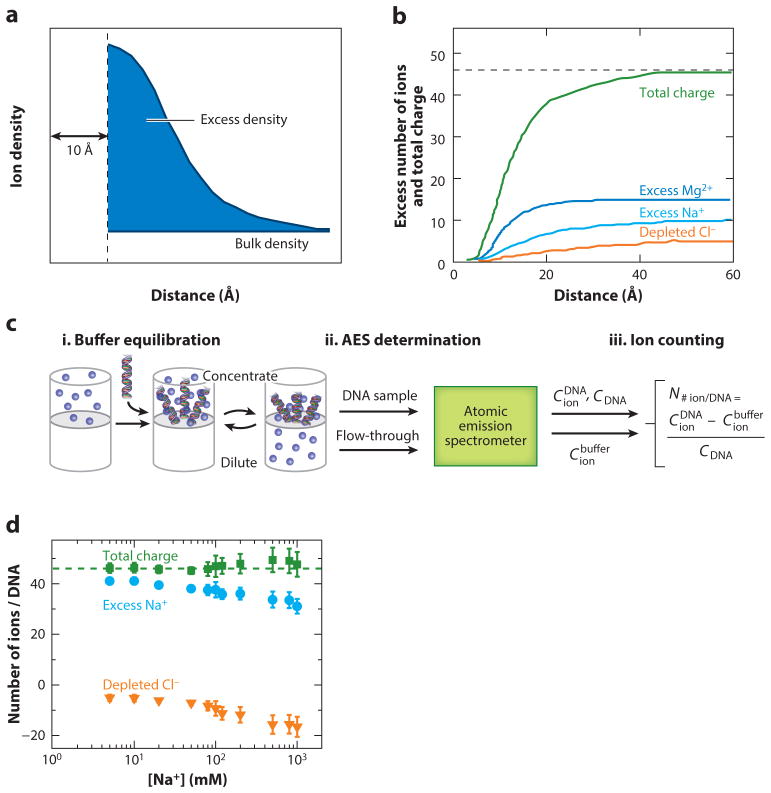
Figure 4.
Quantifying the total composition of the ion atmosphere. (a) Excess ion density as a function of distance from a nucleic acid, approximated here as a cylinder of radius 10 Å, determined from Poisson–Boltzmann theory. The ion atmosphere does not penetrate into the cylinder; the ion density is highest close to the nucleic acid and equals the bulk concentration far away from the nucleic acid. (b) The excess numbers of ions determined from a molecular dynamics simulation and the total charge of these ions around a 24-bp DNA duplex. The total charge of the ion atmosphere is equal and opposite to the charge of the DNA of −46e (dashed line). The example shown is for 5 mM MgCl2 and 40 mM NaCl. Data were taken from Reference 183. (c) Scheme of the buffer equilibration–atomic emission spectroscopy (BE-AES) approach that enables complete quantification of the total ion atmosphere (51, 53). (d) The number of associated excess Na+ ions (blue circles), depleted Cl− ions (orange triangles), and their total charge (green squares) around a 24-bp DNA duplex determined by BE-AES. The total charge of the ion atmosphere is equal, to within experimental error, to the inverse of the DNA charge (dashed line). Data are from Reference 51.
Recent experiments enable an accounting of the full content of the ion atmosphere. The approach involves buffer equilibration–atomic emission spectroscopy (BE-AES) (Figure 4c) and is commonly referred to as “ion counting” (51–53). BE-AES relies on carefully equilibrating the buffer around a nucleic acid sample and on quantifying the elemental composition of the solution using atomic emission spectroscopy (51, 53), that is, counting how much of each element is present in solution. By comparing the ion concentration in the nucleic acid containing sample with the flow-through, buffer-only sample, it is possible to count the total number of excess ions that are present in the ion atmosphere (Figure 4c). This approach is able to achieve high precision because all ions are quantified from a single sample (via their separate atomic emission lines), and each sample can be normalized by the amount of nucleic acid present by quantifying the phosphorus atoms.
Most fundamentally, BE-AES has experimentally confirmed overall charge neutrality (Figure 4d) (51). In addition, as described below, it has been used to characterize properties of the ion atmosphere and to test predictions from electrostatic theories. Other counting approaches, utilizing ion-specific fluorescent dyes, have been used to count specific ions present in the ion atmosphere and how they vary with conditions and conformational transitions but cannot assess the atmosphere in its entirety (33, 52–56).
Does Cation Accumulation Fully Account for the Nucleic Acid–Ion Atmosphere?
We emphasize above that the ion atmosphere achieves charge neutrality. Naïvely one might have expected then that the sum of charges from the cations in the atmosphere is equal to the charge on the nucleic acid that it surrounds. However, this is not the case for a simple reason: In addition to accumulating cations in the atmosphere, there is “negative binding” of anions (also called coions), or preferential exclusion of anions from the atmosphere. This exclusion makes physical sense in that negatively charged coions are repelled from the negatively charged nucleic acid in solution. Thus, the total charge of the accumulated cations does not match the full charge of the nucleic acid.
What is harder to predict is the scale of this coion exclusion effect. For weakly charged objects (such as most proteins) in monovalent salt, simple theories predict that the number of coions excluded from the object is equal to the number of counterions brought in to screen the charge. However, nucleic acids are highly charged, and most theories about so-called polyelectrolytes predict that the number of counterions brought into the resulting atmosphere exceeds the number of excluded coions because of the strong attraction to the polyelectrolyte. In qualitative agreement with this intuition, BE-AES experiments indicate measurable exclusion of anions but much less than the accumulation of cations of the same valency (Figure 4d, shown schematically in Figure 5) (51).
Figure 5.
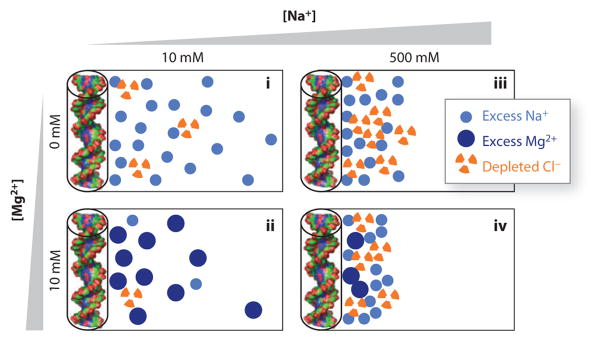
Schematic of the ion atmosphere surrounding nucleic acids under different solution conditions. The circles represent excess counterions and depleted coions in the ion atmosphere, respectively, compared with a buffer-only sample. The number of accumulated and depleted ions shown schematically corresponds (approximately) to the results of buffer equilibration–atomic emission spectroscopy ion counting measurements for 24-bp DNA duplexes (represented by cylinders and molecular renderings on the left of each panel) (51), with each symbol representing two ions. The schematically rendered ion atmospheres depict several experimentally observed trends: (i) Higher total ionic concentration increases coion depletion compared to counterion accumulation, which is partly due to excluded volume effects (see Reference 196 for details); (ii) an atmosphere predominantly of divalent cations leads to a tighter spatial association of the ions around the nucleic acid; (iii) at approximately equal concentrations of mono- and divalent ions, the ion atmosphere is dominated by divalent ions; and (iv) even in a large excess of monovalent ions, some divalent ions are expected to remain close to the nucleic acid.
What Is the Shape of the Ion Atmosphere?
Names like ion atmosphere, ion cloud, or ion sheath used here and in the literature denote a group of ions that is fluctuating but localized near the surface of the nucleic acid. Most theories predict that a region of high counterion density is localized to approximately ~10 Å around the nucleic acid at typical ion concentrations. This corresponds to 1–10 M cation concentrations to achieve charge neutrality (57). Although the BE-AES experiments above have confirmed overall charge neutrality and other basic expectations (51), those experiments do not give information about the spatial distribution and location of ions.
Anomalous small-angle X-ray scattering (ASAXS) can probe the shape and spatial extent of the ion atmosphere. It uses the differential scattering properties of individual atomic species at different X-ray energies and thus can determine the ion–nucleic acid scattering for the probed (or isolated) ion. The anomalous scattering signal is related to the sum of the scattering from all pairs of atoms of the probed ion and the nucleic acid. ASAXS has revealed several basic properties of the ion atmosphere. There is a tighter distribution of divalent cations than monovalent cations around a nucleic acid (58, 59). This difference is predicted based on the stronger attractive forces for the divalent cations (see the next section). The overall scattering signals revealed about half as many ions for an atmosphere made up of divalent cations than for an atmosphere made up of monovalent cations, as expected based on the amount of charge needed to achieve charge neutrality (58, 60).
What Is the Relative Screening from Divalent and Monovalent Cations?
Most biochemical experiments in in vitro, cellular, or viral contexts have mixtures of divalent and monovalent cations. Biochemists are accustomed to maintaining a constant ionic strength, I, to maintain constant charge screening, using the simple relationship of the sum of each ion’s concentration weighted by the square of its valency [e.g., I [Na+]·(+1)2 + [Mg2+]·(+2)2 + [Cl−]·(−2)2]. Ionic strength is related to how sharply the electric field is screened as a function of distance from a weakly charged point source. However, nucleic acids are strongly charged. For these systems the approximation of a point charge does not hold, and equal ionic strength does not correspond to equal screening by their atmospheres; there is no universal relationship for the degree of screening as a function of ion concentrations. Nevertheless, certain qualitative statements can be made, as elaborated in the following section.
What Is the Relative Ion Atmosphere Occupancy by Divalent and Monovalent Cations?
In terms of balance of monovalent and divalent ions present within the atmosphere, simple polyelectrolyte theories predict—and BE-AES experiments have confirmed—that divalent ions constitute a larger fraction of the ion atmosphere than would be predicted from the simple mole fraction present in bulk (Figure 5). For example, in a background of 20 mM Na+, only ~0.5 mM Mg2+ is needed to replace half of the Na+ ions in the ion atmosphere of a simple DNA duplex (51). As a consequence, nearly all of the accumulated counterions are divalent if mono- and divalent ions are present in approximately equal concentrations (Figure 5). A rough empirical rule of thumb is that ~10 mM Mg2+ gives similar behavior to ~1 M Na+, for example, in RNA folding in cases without specific ion binding (61, 62) or for DNA duplex stability (63–65), but this is far from exact and presumably depends on the properties and charge density of the particular nucleic acid or nucleic acid conformation.
The exact composition of a nucleic acid’s ion atmosphere and the relative energetics of different nucleic acid conformations depend on the bulk concentrations of all ions. These properties cannot yet be accurately predicted from theory.
ENERGETIC EFFECTS OF THE ION ATMOSPHERE
How Strong Is the Electrostatic Interaction Between Nucleic Acid Helices?
In the absence of counterions, the strength of electrostatic interactions is large, even between two phosphate groups. At the level of nucleic acid helices, the repulsive energy between two 10-bp double helices with their point of closest contact within 10 Å would be ~60 kcal/mol (~100 times the thermal energy) in the absence of an ion atmosphere. This is substantially larger than the scale of energies from RNA or DNA base pairing and stacking (1–3 kcal/mol). The ion atmosphere reduces this electrostatic repulsion. Theoretical calculations (see the section below titled Can We Compute Ion Atmosphere Properties and Energetics from Poisson–Boltzmann Theory?) indicate that this repulsion is decreased enormously (very roughly 10-fold to ~6 kcal/mol) in 150 mM monovalent salt, and even further in millimolar concentrations of divalent ions.
The energetic estimates above come from theoretical calculations that have been difficult to test in the context of nucleic acid folding events. Important work in DNA liquid crystals has successfully measured the energies versus the distance between long helices but in the context of a complex, condensed phase (66–69). To isolate electrostatic energetics, we used a simple model system: two DNA duplexes tethered by a short polyethylene glycol (PEG) linker (Figure 6a,b) (17, 40). The preformed helices have known structures and greatly reduced the number of conformations present, and the use of a PEG instead of nucleic acid linker removed the potentially complicating features of linker electrostatics, stacking, and hydrogen bonding. We followed the conformational ensemble of states by small-angle X-ray scattering (SAXS); compared the SAXS results with predictions from PB electrostatic calculations for each ionic condition used; and coupled that with the conformational entropy from the PEG tether, determined by extensive molecular dynamics (MD) simulations. (As the PEG tether has only rotatable C–C and C–O bonds, it represents the simplest challenge for MD, much simpler than with proteins and nucleic acids.)
Figure 6.
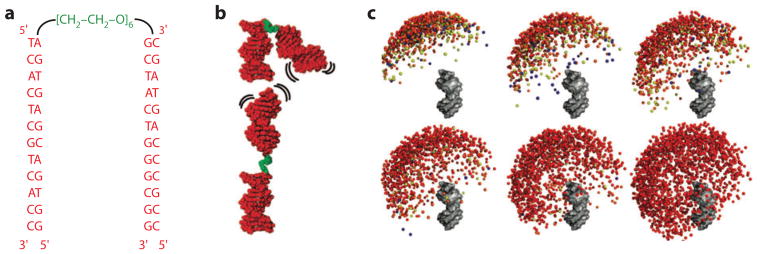
The interplay of nucleic acid structural ensembles and ion interactions. The tethered duplex system has been used as a model system to study how ion interactions modulate the conformational ensemble of nucleic acids (17, 40, 41). (a,b) Sequence and schematic of the tethered duplex system. The system consists of two 12-bp DNA duplexes (red) joined by a flexible polyethylene glycol tether (green). (c) Visualization of the computationally derived ensemble of the tethered duplex system at various ionic conditions, from left to right and top to bottom: 0.02, 0.06, 0.17, 0.3, 2.0 M monovalent ions; the last image (bottom right) shows the ensemble in the absence of electrostatics (i.e., steric effects only). One duplex is rendered in gray, and the colored balls represent the distal end of the other duplex. Colors represent the energetic difference between the conformer and the minimum-energy conformer observed in the ensemble, from red (<1 kBT) to blue (>3 kBT). At a low salt concentration, electrostatic repulsion leads to repulsion between the duplexes; at a higher salt concentration, the repulsion is reduced, and a larger conformational ensemble is explored. Adapted with permission from Reference 40. Copyright 2008, American Chemical Society.
With an increasing concentration of salt, the tethered duplex relaxed from a highly repelled state (Figure 6c). Quantitative comparisons were made to SAXS profiles predicted from the PB-MD modeling. [A strength of SAXS is that experimental scattering profiles can be directly predicted from a given structure (70, 71).] These comparisons revealed similar behavior as predicted from PB theory for monovalent ions, although with modest differences for monovalent cations of various sizes. There were substantial deviations for divalent metal ions: The concentration of Mg2+ required to induce electrostatic relaxation was ~30-fold lower than predicted from PB modeling (40). Nevertheless, there was no evidence for collapse to a compact state due to the Mg2+-induced attraction predicted by some theories—even at Mg2+ concentrations up to 600 mM (17). Overall, these and other comparisons suggest that the energetic predictions of PB theory can be reasonable approximations to reality in monovalent salts in the absence of other complicating features, such as specific ion effects. For experimental conditions with Mg2+, the repulsive energy is likely to be more screened than predicted by PB, and still more complications arise from specific binding effects. Improving theories for nucleic acid–ion energetics is an important frontier (see the section below titled The State of Theory).
Can RNA Folding Energies Be Estimated from Mg2+ Titrations?
A quantitative description of how an RNA folds requires estimating the transition’s folding free energy (ΔG) and how it changes with mutations (ΔΔG values). ΔG is related to the ratio of folded and unfolded molecules. But in typical experiments that explore RNA catalysis or function, RNAs are well folded, and the unfolded population cannot be easily isolated or measured. Fortunately, RNAs often attain their functional tertiary structures upon addition of Mg2+ (72–77). Analogous to estimating protein ΔG values through temperature or chemical denaturant titrations, RNA ΔG values can, in principle, be estimated from precisely characterizing folding fractions near Mg2+-folding midpoints and extrapolating to the standard solution conditions used for functional experiments. Using Mg2+ is a particularly convenient choice for RNA because, unlike temperature or denaturant, Mg2+ titrations often isolate RNA tertiary structure formation events with limited or no change in RNA secondary structure. Unfortunately, there remains substantial confusion in interpreting and analyzing RNA Mg2+ titrations, with many complexities arising from effects of the ion atmosphere, as elaborated below.1
Experimental data monitoring the ion-dependent folding or function of RNA molecules [e.g., chemical footprinting data, the radius of gyration, or activity as a function of [Mg2+] (72–77, 80–84)] are often well described by a Hill equation (85) in the form of Equation 2,
| 2 |
and Equation 3,
| 3 |
where fF is the fraction folded at a given Mg2+ concentration, Kmid is the Mg2+ midpoint, and n is the Hill coefficient. With integer coefficients, the Hill model corresponds to a two-state equilibrium in which one state has n more ligands bound than the other. Consequently, fits to Equation 2 have been described in terms of n Mg2+ ions binding to the RNA, the equilibrium represented by Equation 3. But this interpretation can be misleading. First, as mentioned above, ion–RNA interactions are governed by charge neutrality of the ion atmosphere. Thus, there are many more ions associated with the RNA than the n ions implicated from Equation 2, although the Hill coefficient n does read out the average difference in ions of the type being varied between the folded and unfolded state at the Mg2+ midpoint (8–10, 56, 86, 87).2 At an extreme, n can be a small fraction of unity, but the actual RNA molecule binds hundreds of Mg2+ ions in both the unfolded and folded states. In addition, and also because of charge neutrality, other ions are released for every Mg2+ ion that associates with RNA as it folds. Such an exchange process upon RNA folding is conceptually distinct from a typical ligand-binding event. Finally, observation of Mg2+-induced RNA folding generally does not imply that the Mg2+ binds to a specific site on the folded RNA; the folding can be (and is often) due to the additional screening from atmospheric Mg2+. For example, the formation of a tetraloop–receptor tertiary contact in the Tetrahymena ribozyme and in isolated systems has been extensively studied via Mg2+ titration. However, there is no evidence for site binding to this RNA, and the same interaction forms stably in the presence of sufficiently high monovalent ion concentrations (61, 78, 88).
Beyond conceptual confusion, serious problems arise when using Hill fits to estimate folding free energies, ΔG, and free-energy differences, ΔΔG, between mutants. The Hill coefficient is often assumed to be a constant independent of [Mg2+]. This assumption a priori seems to be the simplest choice but, in fact, holds only in a few RNA systems. The number of Mg2+ ions, even around a single nucleic acid structure, changes with ion concentration (Figure 5), and because the Hill coefficient reads out the difference of such Mg2+ numbers between unfolded and folded states, this difference is likely to vary with the bulk ion concentrations. Changes of structure within each state (e.g., upon electrostatic relaxation of an unfolded state) (Figure 6) provide additional sources for Hill coefficient variation. Beyond these theoretical issues, there are the experimental observations: For example, RNA mutants that require higher Mg2+ concentrations to fold also often are fitted to apparent Hill coefficients that differ from the wild type (75, 80–82).
If the Hill coefficient is not constant, how then can one extrapolate ΔG from the midpoint of a Mg2+ titration up to the Mg2+ concentration used for functional experiments? How can one compare ΔΔG between mutants if they give different Hill coefficients? First of all, ΔG should not be extrapolated outside the range of the actual measurements. For example, it is dangerous to use a standard state of 1 M Mg2+ when folding fractions can only be measured precisely at low millimolar Mg2+ concentrations. Such extrapolations amplify errors in Hill slopes to produce quantitatively or qualitatively wrong conclusions about energetic effects of mutations. Instead, an experimenter can use a thermodynamic model with a varying Hill coefficient that matches the observed Hill coefficient for the measured mutants and assumes a ΔΔG that is independent of Mg2+ concentrations. For example, if the value of n obtained from each mutant varies linearly with each mutant’s midpoint, a simple expression can be applied as an approximation in Equation 4 (79, 87, 89):
| 4 |
where nWT and nmutant are the apparent Hill coefficients measured at the folding midpoints KWT and Kmutant for the wild-type and mutant RNAs, respectively. The assumptions behind this and other models are given in Reference 79. If the apparent Hill coefficient n does not vary smoothly in the experiments, or if independent information indicates that ΔΔG may vary strongly with [Mg2+], then the experimenter must find simplifying solution conditions (see the below section titled Can We Get Rid of the Ion Atmosphere?) or use methods that permit measurement of ΔG for all the mutants under identical experimental conditions. For the latter route, it is now feasible to use single-molecule approaches to measure unfolded fractions of ~10−2 and thus make unambiguous comparisons for RNA variants with folding free-energy differences of up to kBT · ln(10−2) ~ 3 kcal/mol (90, 91).
Can Direct Binding of Mg2+ Be Separated from the Effects of Atmospheric Mg2+?
The direct or specific binding of RNA with divalent metal ions, as opposed to its association with a fluctuating ion atmosphere, has been difficult conceptually and problematic experimentally. On the one hand, the vast majority of Mg2+ titrations following RNA folding or function have used simple site-binding models described by the Hill equation (see the previous section). On the other hand, it has been stated that specific metal ion binding to RNA in inner sphere complexes is extremely rare because the cost of ion desolvation is so high. Both misrepresent the physical and energetic nature of these binding and association events.
When metal ions site-specifically bind to small molecules, proteins, or nucleic acids, one or more water molecules that solvate the metal ion are lost but are replaced by ligands in the binding site. Although it is true that there is an enormous cost to stripping a solvating inner-sphere water molecule from a metal ion in solution, there is a similar enormous “payout” in replacing that water molecule with a functional group from the receptor molecule. Consider that Mg2+ ions lose their solvating water molecules to bind ethylenediaminetetraacetic acid (EDTA), yet bind with nanomolar affinity. Many factors are involved in determining the position and affinity of a bound metal ion, including the ligand type and charge, as well as whether there are nearby ligands positioned or easily rearranged to provide a multidentate binding. There are well-documented cases of site-specific binding of metal ions to RNA (24, 92–98). Strong positive evidence for functionally important binding of Mg2+ to a specific RNA site can be obtained from experiments involving thio or amine substitution for oxygen ligands to weaken the binding of Mg2+ and allow rescue of function with “soft” metal ions like Mn2+ (99–101). Inconsistent thermodynamic or kinetic frameworks have caused widespread confusion in the metal ion rescue literature, but quantitative modeling—with error analysis—can now be achieved to expose and eliminate such problems and limitations (79; also see the above section titled Can RNA Folding Energies Be Estimated from Mg2+ Titrations?).
Can We Get Rid of the Ion Atmosphere?
Given the complexities introduced by the ion atmosphere of understanding nucleic acid energetics, it would seem desirable to find conditions in which the atmosphere is simply removed, so that a nucleic acid can be studied independent of its complicating effects. However, in accord with the principle of charge neutrality, “disappearing” the atmosphere is not possible. The net charge around a negatively charged nucleic acid must total zero, and only ions can accomplish this. In particular, dialysis into deionized water of nucleic acid samples, such as RNA purified from cells or viruses, does not strip away ions associated with the nucleic acids. Instead, such dialysis can result in the opposite of what is desired. The most strongly charged counterions, polyamines, basic peptides, or, worse, unknown species associate with the nucleic acid to keep it neutral. A better strategy to purify nucleic acid samples is to dialyze into buffers that contain known concentrations of known salts. Similarly, experimental conditions or discussions that refer only to having MgCl2 present or titrating in Mg2+ ignore the preexisting ion atmosphere and the inability of the classical site binding and Hill analysis to describe ion effects with nucleic acids (see the above section titled Can RNA Folding Energies Be Estimated from Mg2+ Titrations?).
Although the ion atmosphere around a nucleic acid can never be removed, the atmosphere’s effects can be minimized through a counterintuitive strategy: using conditions with very high concentrations of monovalent salt, such as 2 M NaCl, to “swamp” the atmosphere. Under such conditions, the atmosphere composition is dominated by the monovalent ions. As a further simplification, the atmosphere gives efficient screening between phosphate groups, so that electrostatic forces between nucleic acid segments can, to a first approximation, be neglected. Under these conditions, if titration of Mg2+ leads to a structural change, that transition would most likely correspond to specific binding of an Mg2+ ion; the alternative, better electrostatic screening of the folded state by atmospheric Mg2+, is unlikely due to the dominance of monovalent ions in the atmosphere. In high monovalent salt conditions, Mg2+ titrations become conceptually closer to standard ligand binding. Indeed, spectroscopic and biochemical identification of site-bound divalent ions, Hill fits that can be simply interpreted as the number of site-bound metal ions, and high-precision ion counting of those ions become feasible (52, 62, 97, 102, 103). A current, unmet challenge is to connect these unambiguous structural insights and energetic measurements under artificially high monovalent salt backgrounds to more standard conditions (79).
THE STATE OF THEORY
Because the fluctuating, volatile nature of the ion atmosphere makes visualization and experimental dissection difficult, its predominant description has come from theoretical models. Importantly, any assessment of the thermodynamic consequences of the ion atmosphere, such as for RNA folding or protein–nucleic acid binding, requires a quantitative theoretical description of nucleic acid–ion interactions. An adequate theoretical description should make quantitative and nontrivial predictions, and, in turn, there is a need for experimental benchmarks against which to test theoretical predictions. Here, we discuss commonly used models of the ion atmosphere and evaluate them against the available experimental benchmarks.
Does Manning Theory Account for Ion Atmosphere Effects?
A simple and yet influential model for DNA–ion interactions was proposed by Manning decades ago (104–106). Manning calculated that DNA and other polyelectrolytes with sufficiently high charge density induce a condensation of cations at the polyelectrolyte surface until its effective charge is reduced below a critical value. According to these simple electrostatic calculations, this condensed or bound layer is predicted to effectively neutralize ~60–70% of the DNA backbone charge.
The strength (and, at the same time, the limitation) of Manning or so-called counterion condensation (CC) theory is its simplicity. Its consistency with a number of experiments that can be interpreted by assigning an effective charge suggests that it captures an important property of polyelectrolyte interactions (80, 107–114), but as with any simplified approach, there are also aspects of the actual system that are sacrificed. For example, atomic-level properties and interactions of the ions, solvent molecules, and hydration of the polyelectrolyte are not included. The theory also can imply a seemingly rigid distinction between a condensed layer and the rest of the ion atmosphere, whereas these together are responsible for full charge neutralization and form a continuum. On a practical level, the notion that full neutralization occurs in solution is often not realized by researchers who are aware of the predicted ~0.7 neutralization by the condensed layer but lack a full understanding of this theory. Moving forward, concepts from Manning’s theory are being used in next-generation and more detailed theories (4, 11, 115, 116), and other approaches are also under development, as outlined in the following sections.
Can We Compute Ion Atmosphere Properties and Energetics from Poisson–Boltzmann Theory?
Poisson–Boltzmann (PB) theory is widely used to describe the ion atmosphere associated with nucleic acids and proteins (1, 12, 31, 33, 114). This theory has been used to quantitatively predict the composition and shape of the ion atmosphere around nucleic acids and has provided insight into the electrostatic component of the free-energy landscape governing RNA folding. Because PB theory has been the predominant ion atmosphere theory, we first introduce how PB theory models the ion atmosphere, then discuss its approximations and shortcomings, and finally evaluate its validity in light of recent rigorous experimental tests.
Poisson–Boltzmann theory background and equation
PB theory describes the interaction of mobile ions with fixed charges in solution (1, 33, 117–122). The fixed charge density, denoted ρfixed (r⃗), is typically defined by the structure of the protein or nucleic acid of interest. PB theory considers the situation where the charged molecule is surrounded by solvent, approximated as a continuum, with a dielectric constant ε(r⃗) and mobile ions of charge zi that interact with fixed charge density and with the average potential of all ions. This average potential of all ions is determined by their Boltzmann factor (hence the Boltzmann in PB), the exponential term in Equation 5 below. The index i enumerates all ion species present in the solution. The charge zi can be positive or negative; for instance, zi = +2 if i = Mg2+, and zi = −1 if i = Cl−. The PB equation is a differential equation for the electrostatic potential Φ(r⃗), derived from the Poisson equation that governs the electrostatic potential around charges (hence the name Poisson in PB) (12, 123, 124):
| 5 |
where e is the elementary charge, kB is the Boltzmann constant, and T is the absolute temperature. The term cibulk is the bulk concentration of ion species, i, namely the concentration far from the charged macromolecule. The term λ(r⃗) is an accessibility factor that defines the regions in space that are accessible to ions (where λ = 1) or inaccessible to ions (e.g., inside the macromolecule, where λ = 0). The exponential function from the Boltzmann factor (the last term in Equation 5) makes the equation nonlinear; consequently, Equation 5 is referred to as the nonlinear PB equation. For computational simplicity, a linearized version of the equation, referred to as the Debye–Hückel theory (125), is sometimes used but is not adequate for poly-electrolytes. The general approach is to compute Φ(r⃗) by numerically solving Equation 5.
From the solution of the PB equation and Φ(r⃗), all other quantities of interest can be determined. Most importantly, knowing the electrostatic potential at all points in space [i.e., Φ(r⃗)] allows the electrostatic contributions to free energies to be calculated for any process of interest, including association events, folding, and conformational changes. PB also allows calculation of the number of associated ions, and, as described below, this provides a powerful link to experiment.
Software packages for Poisson–Boltzmann calculations
A number of freely available software packages have been developed to solve the PB equation (Equation 5) numerically and have enabled widespread application of PB theory to macromolecular systems of interest. Examples of PB software packages include Del-Phi (118, 126, 127), APBS (122, 128, 129) [with the useful PDB2PQR (130) interface], MEAD (131), and AQUASOL [employing the Langevin dipole PB approach, a scheme extending the PB framework by representing the solvent as self-orienting dipoles of variable density (44, 132–135)].
Limitations of the Poisson–Boltzmann theory
PB theory makes several simplifying approximations in its treatment of the ion atmosphere. First, it does not consider the ions as discrete objects but treats their interactions in an averaged or mean-field theory fashion. Thus, ion–ion correlations are neglected. Second, in the PB framework, ions do not have a discrete size and are only characterized by their valency or charge. The mean-field nature of PB theory also prevents other atomic-level properties, including ion polarizability and desolvation, from being considered. Similarly, it treats the aqueous environment and the interior of the nucleic acid as media with uniform dielectric constants, ε(r⃗), neglecting their discrete nature and polarizability. Despite these limitations, PB theory has been widely applied to nucleic acid systems, in part because of its relative ease of implementation.
Experimental tests of Poisson–Boltzmann theory
Although PB theory introduced the concept of the ion atmosphere to many and provides a means to calculate electrostatic interaction energies, its use as a quantitative, predictive tool required testing. Incisive tests of any theory require experimental systems that are simple enough to avoid extraneous features, as these can complicate relating experiment to theory and introduce factors that can inadvertently serve as free fitting parameters. For example, early tests of tRNA folding demonstrated that PB models could account for Mg2+-dependent folding but also incorporated assumptions about the nature of the unfolded state and included an adjustable parameter for the folding contribution from the formation of tertiary interactions (39, 55, 56, 62, 136–138). Similarly, folding assays for group I ribozymes revealed that folding is much more efficiently induced by divalent than monovalent cations, as predicted by PB theory and other polyelectrolyte theories (32, 80, 139, 140), but the complexity of large RNAs precludes rigorous evaluation of the PB model. We therefore turned to simplified experimental systems. Much of this work has been reviewed, so we briefly describe it and refer readers to the prior review and the original papers (17, 33, 40–42, 51, 53, 141).
As noted above, BE-AES, or ion counting, provides a powerful window into the ion atmosphere. For PB theory, ion counting could test the effect of ion identity (e.g., size), as well as the competition of the monovalent and divalent cations for occupancy of the ion atmosphere. Simple DNA duplexes could be used to minimize accompanying folding events or conformational rearrangements. As the valency of ions is the only property taken into account in PB, all ions of the same valency, such as Li+, Na+, K+, and Rb+, are predicted to behave identically. Experimentally, the smaller ions modestly out-compete, by two- to threefold, the larger ions for ion atmosphere occupancy (33, 51). Some differences can be accounted for by incorporating additional terms into the PB free-energy functional, but a fully successful treatment is not yet available and may not be possible (141, 142). In addition, careful studies with more complex RNA systems reveal different effects from different monovalent cations, with trends that do not match the preferential ion atmosphere occupancy order for the simple helix, and these ion-specific effects differ from system to system (e.g., References 24, 143, and 144). These observations suggest that more specific interactions, even with monovalent cations, need to be taken into account to fully understand the ion atmosphere and RNA energetics.
For the physiologically important divalent ions, ion counting experiments with simple DNA helices demonstrate that the preferential divalent ion association occurs at two- to threefold smaller divalent ion concentrations than predicted from PB theory (51). In addition, SAXS-based experiments with the simple tethered two-helix model system, referred to above (Figure 6), revealed discrepancies in the divalent ion concentration dependences of conformational relaxation from charge screening of more than an order of magnitude, relative to PB predictions (33, 40). In contrast, the deviations from PB theory for relaxation induced by monovalent cations were modest. The stronger deviations for divalent cations are consistent with ion–ion correlation effects, as higher valency (and higher charge density) is expected to increase correlations in the positions of the ions with respect to one another (16, 57, 145, 146).
Overall, these and other results (58, 59, 114, 147, 148) suggest that PB theory provides a good guide for the general expected behavior of the ion atmosphere. However, it does not provide a quantitative description of the contents or energetics of that atmosphere. Deviations appear to arise from the fundamental limitations of the mean-field approximation, specifically that ions in PB theory lack size, relevant atomic or solvation properties, and spatial correlations with one another.
Can Expansions of Poisson–Boltzmann Fix Its Problems with Divalent Ions?
There are a number of approaches to modeling ion–nucleic acid interactions that go beyond PB theory and try to overcome its limitations. Some theoretical treatments stay close to the PB framework and enhance it by adding size-dependent terms (141, 142, 149–152) or an improved treatment of the solvent (44, 133–135, 153). Other approaches employ Monte Carlo schemes with an explicit treatment of (part of) the ions (13, 154–157). Such approaches are clearly necessary given the known failures for PB theory, in particular the lack of ion–ion correlations, for divalent and higher-valency ions. Currently, none of these models can be readily applied to a range of systems, and none have been subjected to stringent experimental tests. The development of a tractable theory that can accurately predict the properties of the divalent and higher-valency ions in the atmosphere remains an important outstanding challenge.
Can the Ion Atmosphere Do More Than Screen Repulsion?
Counterintuitive effects and striking deviations from PB theory arise in the related phenomena of overcharging, charge inversion, and ion-mediated attraction. These terms describe situations in which a highly charged solute (e.g., double-stranded DNA) is surrounded by so many counterions that the apparent net charge seen from some distance changes sign (i.e., becomes positive for DNA). Under these circumstances the charged solute is said to have undergone charge inversion and has become overcharged. These phenomena have been observed experimentally for trivalent and higher-valency ions (158–164) but do not appear to occur for divalent or monovalent ions under physiological hydration and pH conditions (163, 165). Theoretical descriptions of charge inversion and like-charge attraction emphasize the critical role of ion–ion correlations and spatial ordering of the multivalent ions (16, 154, 166–169). Although it is also clear experimentally that there can be attractive forces that bring nucleic acids together, especially in the presence of trivalent and higher-valency cations, tests of the scale of such factors with helices of the length typical in folded RNAs even with very high concentrations of Mg2+ revealed no significant attractive forces; instead, the observed effects could be fully explained by simpler charge screening effects (17).
Can We Predict Specific Metal Ion Binding Sites?
Understanding the energetics of metal ion binding requires modeling not only the electrostatic interaction between the metal ion and the RNA moieties but also water desolvation, RNA–metal interactions mediated by discrete water molecules, electronic polarization of these moieties, and the effects of the other ions in the atmospheric background. The ability to predict these interactions remains limited. Currently, the simplest and best-defined metal ion prediction puzzle involves taking the exact atomic coordinates of an RNA from its crystal structure and predicting the locations of crystallographically observed metal ion sites. Even here, only ~50% of the crystallographic sites can be recovered by current knowledge-based algorithms (27, 170, 171). Predicting the number and location of site-bound metal ions in nucleic acids of unknown structure or in solution versus crystals is still more difficult and remains an unmet challenge. Experimental methods can, in favorable cases, identify bound metal ions and their binding sites, but care and caution are needed in carrying out and interpreting these experiments (79, 99, 101).
Can Molecular Dynamics Just Simulate the Ion Atmosphere?
In contrast to PB theory, MD simulations can treat the solvent explicitly by representing both water molecules and ions as discrete particles (172, 173). In addition, MD simulations naturally treat the macromolecule as flexible; in other words, the positions of the atoms that make up the protein or nucleic acid are updated in the simulation, whereas PB-type approaches consider mostly a static macromolecular structure and require calculations for a series of discrete structures. As a consequence, MD simulations can potentially be more accurate than PB theory and related approaches.
However, several issues require careful consideration. First, the added detail (explicit solvent, flexible macromolecule) makes MD much more computationally costly than PB methods. Second, for realistic simulations, it is important to have a sufficiently large simulation volume (174) and number of explicit ions such that the ions far from the nucleic acid in the simulation have bulk-like properties regarding concentrations, fluctuations, and ion relaxation (175, 176). In particular, it is insufficient to only include just enough counterions to make the overall simulated system charge neutral (176, 177). For example, Pappu and coworkers (177) found that they had to include 800 ion pairs (and 55,000 water molecules) in addition to 30 neutralizing counterions in their simulation of the 32-residue Tar-Tar* RNA kissing loop motif.
MD simulations also, by necessity, involve a large number of parameters that describe the interactions (van der Waals, electrostatics, etc.) between different kinds of atoms. Several authors have recently pointed out that some of the popular choices of parameter sets used for ion simulations may be flawed and produce unphysical artifacts, such as the formation of salt clusters at concentrations well below the concentration limit (178–180) or unphysical attraction and clustering of DNA (180). But changing parameters to prevent such artifactual behavior does not ensure an ability to predict other behaviors. Physically realistic ion parameters are a prerequisite to correctly addressing more challenging problems, such as ion interactions with nucleic acids and nucleic acid–protein complexes. Recent efforts have been aimed at improving parameters for MD simulations by comparison with experimental results, such as osmotic pressures (180), crystal phase parameters (179, 181), Raman spectroscopy (182), and BE-AES data (183).
Most basically, any computational approach requires rigorous experimental tests and predictions of nontrivial properties to evaluate the theory, and the need for computation in a truly unbiased fashion is becoming more and more apparent. The Critical Assessment of Protein Structure Prediction consortium (CASP) revealed, through blind predictions of previously unknown protein structures, much greater limits in our ability to predict protein structures than previously recognized; multiple structure prediction algorithms, developed using previously determined structures with portions of these data set aside for testing and validation, failed in the face of truly blind predictions (184, 185). Other communities, including the RNA structure community, are following the example set by CASP and are developing their own blind prediction tests (186, 187).
For nucleic acid electrostatics, we have an emerging suite of experimental tools that can provide benchmarks for further developing computational approaches and, ultimately, rigorous tests of new predictions from those approaches. We anticipate a continued and highly integrated feedback loop of computation and experiment using ion counting, ASAXS, and energetic tests with simple nucleic acid systems that will greatly advance our understanding of and ability to predict the properties, behavior, and structural and energetic consequences of ions and the ion atmosphere.
SUMMARY POINTS.
Nucleic acid folding, structure, and interactions are central to biology and cannot be understood without a deep appreciation of electrostatics.
Nucleic acids and other polyelectrolytes are surrounded by an ion atmosphere. Its properties are distinct from standard site binding, and it is extremely challenging to study and understand.
As many biochemists and molecular biologists are unfamiliar with the underlying physics and manifestations of the ion atmosphere, we have attempted to provide a basic conceptual and practical guide, discussing both current experimental and theoretical approaches used to probe and describe the ion atmosphere.
Theoretical descriptions of the ion atmosphere, including the Hill model, Manning condensation, PB theory, and Monte Carlo and MD approaches, have been used to explain the ion atmosphere and ion–nucleic acid interactions. Of these, the most common, the Hill model, is the most limited, and there is currently no theory that quantitatively accounts for all aspects of nucleic acid–ion interactions.
The principle of charge neutrality is a powerful concept. It serves as a guide for the interpretation of experiments and development of intuition about ion atmosphere behavior.
Ion counting and other experimental tools, using simple nucleic acid systems, have been critical in testing electrostatic theories and provide benchmarks for the future development of electrostatic theories and computational approaches for nucleic acid electrostatics.
Development of quantitative descriptions of nucleic electrostatics and energetics will require a tight experimental–computational feedback loop with rigorous evaluation of blind and nontrivial predictions.
Understanding of the ion atmosphere and its energetic manifestations is fundamental to understanding the functions and interactions of nucleic acids in biology and to developing an ability to engineer nucleic acids for use in cellular regulation and other processes.
FUTURE ISSUES.
A strength of the BE-AES ion counting method is that all ions in essentially arbitrary samples can be quantified. Extensions of BE-AES to complex folded RNAs and to nucleic acid–protein complexes have the potential to dissect the ion atmosphere and help understand its energetic consequences in these more complex settings.
The adequate treatment of ions in MD simulations remains a challenge, and further tests are needed. Unanswered questions are how well classical simulation protocols based on fixed charges can correctly capture ion behavior in solution and what properties will ultimately require polarizable force fields or quantum mechanical treatments.
Development and rigorous testing of MD force fields for nucleic acid–ion interactions are needed to ultimately provide a predictive and complete understanding of RNA and DNA folding and interactions.
Investigators need to develop quantitative, first-principles models for specific ion binding to nucleic acids. To date, only simplified systems using very high monovalent cation concentrations to effectively saturate the ion atmosphere have yielded direct, quantitative information about site-binding stoichiometry. Future challenges are to carry out such analyses under physiological salt conditions and to account for the site interaction energies.
Understanding the effect of the ion atmosphere and ion binding on nucleic acid dynamics is lacking. In addition, we do not know the response time of the ion atmosphere to the dynamics of the nucleic acid and its binding partners, or to what extent that response time influences nucleic acid kinetic, dynamic, and binding properties. Also needed is an understanding of whether specific metal ion interactions help nucleate RNA structures, and whether establishment of these interactions can be rate limiting.
The overall goal is to develop a quantitative and predictive understanding of nucleic acid folding and structure, alone or with other interaction partners.
A critical aspect of this grand challenge is determining whether ion atmosphere effects can be treated as independent energetic contributors that can then be combined in an additive fashion with contributions from, for example, tertiary motif interactions, conformational preferences of helix junctions, and protein binding.
Acknowledgments
We thank Aleksei Aksimentiev, David Garcia, Serge Lemay, and the members of the Doniach and Herschlag labs for useful discussions. We acknowledge the enormous amount of research in this area by many groups and regret, owing to space and scope limitations, that it was not possible to cite a large amount of fascinating and high-quality work. We received funding from the Netherlands Organisation for Scientific Research (NWO), the Burroughs Wellcome Fund (Career Award at the Scientific Interface), and National Institutes of Health grant PO1 GM066275.
Glossary
- Ion atmosphere
the set of ions that interact with a charged solute, such as a macromolecule, in solution
- Polyelectrolyte
a macromolecule that is highly charged in aqueous solution; DNA and RNA are negatively charged polyelectrolytes
- Screening
reduction of long-range electrostatic interactions between charged objects in the presence of an ion atmosphere
- Bulk ion concentration
the concentration of ions far away from the nucleic acids, which can be experimentally set (by dialysis) or measured
- Counterion accumulation
increased local concentration of positive ions around a negatively charged solute due to electrostatic attraction
- Coion depletion
decreased local concentration of negative ions around a negatively charged solute due to electrostatic repulsion
- BE-AES
buffer equilibration–atomic emission spectroscopy
- ASAXS
anomalous small-angle X-ray scattering
- SAXS
small-angle X-ray scattering
- MD
molecular dynamics
- Poisson–Boltzmann (PB) theory
a differential equation describing the average (i.e., mean-field) electrostatic interactions of ions with a charged solute in solution
- Electrostatic potential
related to the strength of the electrical field and used to calculate electrostatic energies for charged particles
- Mean-field theory
a theory that considers interactions of ions with an effective, approximate potential representing the averaged effect of all other ions
- Ion–ion correlations
the repositioning of ions due to the presence of other ions; spacing of like-charged ions beyond that expected from the average ion concentration
- Overcharging
a phenomenon whereby a highly charged molecule (e.g., negatively charged DNA) attracts so many counterions that its overall charge changes sign
Footnotes
A major complication that occurs independently of the ion atmosphere (and, indeed, occurs widely for protein systems) is the possibility of multiple folding transitions that are mistakenly lumped together by a low-resolution experimental observable (non-two-state behavior). For example, native gel electrophoresis or X-ray scattering can detect the compaction of RNAs as a function of Mg2+ but can miss folding of subdomains, leading to inconsistencies in thermodynamic models. Information-rich folding readouts, such as chemical footprinting, can resolve folding transitions and give self-consistent thermodynamic models; for an example, see Reference 73.
Measuring the Hill coefficient also involves addition of coions (e.g., chloride in the case of MgCl2), so there can be a contribution from the difference in the numbers of coions excluded from the folded versus the unfolded state. This contribution is negligible if there is already a sufficiently high background concentration of the coion (e.g., in NaCl), and we ignore it here for simplicity of language.
DISCLOSURE STATEMENT
The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
Contributor Information
Jan Lipfert, Email: Jan.Lipfert@lmu.de.
Sebastian Doniach, Email: sxdwc@slac.stanford.edu.
Rhiju Das, Email: rhiju@stanford.edu.
Daniel Herschlag, Email: herschla@stanford.edu.
LITERATURE CITED
- 1.Draper DE, Grilley D, Soto AM. Ions and RNA folding. Annu Rev Biophys Biomol Struct. 2005;34:221–43. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 2.Draper DE. RNA folding: thermodynamic and molecular descriptions of the roles of ions. Biophys J. 2008;95:5489–95. doi: 10.1529/biophysj.108.131813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Knobler CM, Gelbart WM. Physical chemistry of DNA viruses. Annu Rev Phys Chem. 2009;60:367–83. doi: 10.1146/annurev.physchem.59.032607.093728. [DOI] [PubMed] [Google Scholar]
- 4.Chen SJ. RNA folding: conformational statistics, folding kinetics, and ion electrostatics. Annu Rev Biophys. 2008;37:197–214. doi: 10.1146/annurev.biophys.37.032807.125957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jiang T, Wang ZG, Wu J. Electrostatic regulation of genome packaging in human hepatitis B virus. Biophys J. 2009;96:3065–73. doi: 10.1016/j.bpj.2009.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wong GC, Pollack L. Electrostatics of strongly charged biological polymers: ion-mediated interactions and self-organization in nucleic acids and proteins. Annu Rev Phys Chem. 2010;61:171–89. doi: 10.1146/annurev.physchem.58.032806.104436. [DOI] [PubMed] [Google Scholar]
- 7.Chin K, Sharp KA, Honig B, Pyle AM. Calculating the electrostatic properties of RNA provides new insights into molecular interactions and function. Nat Struct Biol. 1999;6:1055–61. doi: 10.1038/14940. [DOI] [PubMed] [Google Scholar]
- 8.Misra VK, Draper DE. The interpretation of Mg2+ binding isotherms for nucleic acids using Poisson–Boltzmann theory. J Mol Biol. 1999;294:1135–47. doi: 10.1006/jmbi.1999.3334. [DOI] [PubMed] [Google Scholar]
- 9.Misra VK, Draper DE. Mg2+ binding to tRNA revisited: the nonlinear Poisson–Boltzmann model. J Mol Biol. 2000;299:813–25. doi: 10.1006/jmbi.2000.3769. [DOI] [PubMed] [Google Scholar]
- 10.Draper DE. A guide to ions and RNA structure. RNA. 2004;10:335–43. doi: 10.1261/rna.5205404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tan ZJ, Chen SJ. Electrostatic correlations and fluctuations for ion binding to a finite length polyelectrolyte. J Chem Phys. 2005;122:44903. doi: 10.1063/1.1842059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Grochowski P, Trylska J. Continuum molecular electrostatics, salt effects, and counterion binding—a review of the Poisson–Boltzmann theory and its modifications. Biopolymers. 2008;89:93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 13.Tan ZJ, Chen SJ. Predicting ion binding properties for RNA tertiary structures. Biophys J. 2010;99:1565–76. doi: 10.1016/j.bpj.2010.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kantardjieff KA, Rupp B. Protein isoelectric point as a predictor for increased crystallization screening efficiency. Bioinformatics. 2004;20:2162–68. doi: 10.1093/bioinformatics/bth066. [DOI] [PubMed] [Google Scholar]
- 15.Kiraga J, Mackiewicz P, Mackiewicz D, Kowalczuk M, Biecek P, et al. The relationships between the isoelectric point and: length of proteins, taxonomy and ecology of organisms. BMC Genomics. 2007;8:163. doi: 10.1186/1471-2164-8-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grosberg AY, Nguyen TT, Shklovskii BI. Colloquium: the physics of charge inversion in chemical and biological systems. Rev Mod Phys. 2002;74:329–45. [Google Scholar]
- 17.Bai Y, Das R, Millett IS, Herschlag D, Doniach S. Probing counterion modulated repulsion and attraction between nucleic acid duplexes in solution. Proc Natl Acad Sci USA. 2005;102:1035–40. doi: 10.1073/pnas.0404448102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Brion P, Westhof E. Hierarchy and dynamics of RNA folding. Annu Rev Biophys Biomol Struct. 1997;26:113–37. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
- 19.Jack A, Ladner JE, Rhodes D, Brown RS, Klug A. A crystallographic study of metal-binding to yeast phenylalanine transfer RNA. J Mol Biol. 1977;111:315–28. doi: 10.1016/s0022-2836(77)80054-5. [DOI] [PubMed] [Google Scholar]
- 20.Quigley GJ, Teeter MM, Rich A. Structural analysis of spermine and magnesium ion binding to yeast phenylalanine transfer RNA. Proc Natl Acad Sci USA. 1978;75:64–68. doi: 10.1073/pnas.75.1.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cate JH, Gooding AR, Podell E, Zhou K, Golden BL, et al. Crystal structure of a group I ribozyme domain: principles of RNA packing. Science. 1996;273:1678–85. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- 22.Cate JH, Doudna JA. Metal-binding sites in the major groove of a large ribozyme domain. Structure. 1996;4:1221–29. doi: 10.1016/s0969-2126(96)00129-3. [DOI] [PubMed] [Google Scholar]
- 23.Cate JH, Hanna RL, Doudna JA. A magnesium ion core at the heart of a ribozyme domain. Nat Struct Biol. 1997;4:553–58. doi: 10.1038/nsb0797-553. [DOI] [PubMed] [Google Scholar]
- 24.Basu S, Rambo RP, Strauss-Soukup J, Cate JH, Ferre-D’Amare AR, et al. A specific monovalent metal ion integral to the AA platform of the RNA tetraloop receptor. Nat Struct Biol. 1998;5:986–92. doi: 10.1038/2960. [DOI] [PubMed] [Google Scholar]
- 25.Conn GL, Gittis AG, Lattman EE, Misra VK, Draper DE. A compact RNA tertiary structure contains a buried backbone–K+ complex. J Mol Biol. 2002;318:963–73. doi: 10.1016/S0022-2836(02)00147-X. [DOI] [PubMed] [Google Scholar]
- 26.Ennifar E, Walter P, Dumas P. A crystallographic study of the binding of 13 metal ions to two related RNA duplexes. Nucleic Acids Res. 2003;31:2671–82. doi: 10.1093/nar/gkg350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Banatao DR, Altman RB, Klein TE. Microenvironment analysis and identification of magnesium binding sites in RNA. Nucleic Acids Res. 2003;31:4450–60. doi: 10.1093/nar/gkg471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Stefan LR, Zhang R, Levitan AG, Hendrix DK, Brenner SE, Holbrook SR. MeRNA: a database of metal ion binding sites in RNA structures. Nucleic Acids Res. 2006;34:D131–34. doi: 10.1093/nar/gkj058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Robertson MP, Scott WG. The structural basis of ribozyme-catalyzed RNA assembly. Science. 2007;315:1549–53. doi: 10.1126/science.1136231. [DOI] [PubMed] [Google Scholar]
- 30.Correll CC, Freeborn B, Moore PB, Steitz TA. Metals, motifs, and recognition in the crystal structure of a 5S rRNA domain. Cell. 1997;91:705–12. doi: 10.1016/s0092-8674(00)80457-2. [DOI] [PubMed] [Google Scholar]
- 31.Sharp KA, Honig B. Salt effects on nucleic acids. Curr Opin Struct Biol. 1995;5:323–28. doi: 10.1016/0959-440x(95)80093-x. [DOI] [PubMed] [Google Scholar]
- 32.Woodson SA. Metal ions and RNA folding: a highly charged topic with a dynamic future. Curr Opin Chem Biol. 2005;9:104–9. doi: 10.1016/j.cbpa.2005.02.004. [DOI] [PubMed] [Google Scholar]
- 33.Chu VB, Bai Y, Lipfert J, Herschlag D, Doniach S. A repulsive field: advances in the electrostatics of the ion atmosphere. Curr Opin Chem Biol. 2008;12:619–25. doi: 10.1016/j.cbpa.2008.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Scott WG, Finch JT, Klug A. The crystal structure of an all-RNA hammerhead ribozyme: a proposed mechanism for RNA catalytic cleavage. Cell. 1995;81:991–1002. doi: 10.1016/s0092-8674(05)80004-2. [DOI] [PubMed] [Google Scholar]
- 35.Scott WG, Murray JB, Arnold JR, Stoddard BL, Klug A. Capturing the structure of a catalytic RNA intermediate: the hammerhead ribozyme. Science. 1996;274:2065–69. doi: 10.1126/science.274.5295.2065. [DOI] [PubMed] [Google Scholar]
- 36.Blount KF, Uhlenbeck OC. The structure-function dilemma of the hammerhead ribozyme. Annu Rev Biophys Biomol Struct. 2005;34:415–40. doi: 10.1146/annurev.biophys.34.122004.184428. [DOI] [PubMed] [Google Scholar]
- 37.Shi H, Moore PB. The crystal structure of yeast phenylalanine tRNA at 1.93 Å resolution: a classic structure revisited. RNA. 2000;6:1091–105. doi: 10.1017/s1355838200000364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Leach AR. Molecular Modeling: Principles and Applications. Harlow, UK/New York: Prentice Hall; 2001. [Google Scholar]
- 39.Grilley D, Misra V, Caliskan G, Draper DE. Importance of partially unfolded conformations for Mg2+-induced folding of RNA tertiary structure: structural models and free energies of Mg2+ interactions. Biochemistry. 2007;46:10266–78. doi: 10.1021/bi062284r. [DOI] [PubMed] [Google Scholar]
- 40.Bai Y, Chu VB, Lipfert J, Pande VS, Herschlag D, Doniach S. Critical assessment of nucleic acid electrostatics via experimental and computational investigation of an unfolded state ensemble. J Am Chem Soc. 2008;130:12334–41. doi: 10.1021/ja800854u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chu VB, Lipfert J, Bai Y, Pande VS, Doniach S, Herschlag D. Do conformational biases of simple helical junctions influence RNA folding stability and specificity? RNA. 2009;15:2195–205. doi: 10.1261/rna.1747509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Anthony PC, Sim AY, Chu VB, Doniach S, Block SM, Herschlag D. Electrostatics of nucleic acid folding under conformational constraint. J Am Chem Soc. 2012;134:4607–14. doi: 10.1021/ja208466h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dupuis NF, Holmstrom ED, Nesbitt DJ. Single-molecule kinetics reveal cation-promoted DNA duplex formation through ordering of single-stranded helices. Biophys J. 2013;105:756–66. doi: 10.1016/j.bpj.2013.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Azuara C, Orland H, Bon M, Koehl P, Delarue M. Incorporating dipolar solvents with variable density in Poisson–Boltzmann electrostatics. Biophys J. 2008;95:5587–605. doi: 10.1529/biophysj.108.131649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ben-Yaakov D, Andelman D, Podgornik R. Dielectric decrement as a source of ion-specific effects. J Chem Phys. 2011;134:074705. doi: 10.1063/1.3549915. [DOI] [PubMed] [Google Scholar]
- 46.Demery V, Dean DS, Podgornik R. Electrostatic interactions mediated by polarizable counterions: weak and strong coupling limits. J Chem Phys. 2012;137:174903. doi: 10.1063/1.4763986. [DOI] [PubMed] [Google Scholar]
- 47.Senn HM, Thiel W. QM/MM methods for biomolecular systems. Angew Chem Int Ed Engl. 2009;48:1198–229. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- 48.Schworer M, Breitenfeld B, Troster P, Bauer S, Lorenzen K, et al. Coupling density functional theory to polarizable force fields for efficient and accurate Hamiltonian molecular dynamics simulations. J Chem Phys. 2013;138:244103. doi: 10.1063/1.4811292. [DOI] [PubMed] [Google Scholar]
- 49.Record MT, Jr, Anderson CF, Lohman TM. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Q Rev Biophys. 1978;11:103–78. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- 50.Bleam ML, Anderson CF, Record MT. Relative binding affinities of monovalent cations for double-stranded DNA. Proc Natl Acad Sci USA. 1980;77:3085–89. doi: 10.1073/pnas.77.6.3085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bai Y, Greenfeld M, Travers KJ, Chu VB, Lipfert J, et al. Quantitative and comprehensive decomposition of the ion atmosphere around nucleic acids. J Am Chem Soc. 2007;129:14981–88. doi: 10.1021/ja075020g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Das R, Travers KJ, Bai Y, Herschlag D. Determining the Mg2+ stoichiometry for folding an RNA metal ion core. J Am Chem Soc. 2005;127:8272–73. doi: 10.1021/ja051422h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Greenfeld M, Herschlag D. Probing nucleic acid–ion interactions with buffer exchange–atomic emission spectroscopy. Methods Enzymol. 2009;469:375–89. doi: 10.1016/S0076-6879(09)69018-2. [DOI] [PubMed] [Google Scholar]
- 54.Grilley D, Soto AM, Draper DE. Direct quantitation of Mg2+–RNA interactions by use of a fluorescent dye. Methods Enzymol. 2009;455:71–94. doi: 10.1016/S0076-6879(08)04203-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Soto AM, Misra V, Draper DE. Tertiary structure of an RNA pseudoknot is stabilized by “diffuse” Mg2+ ions. Biochemistry. 2007;46:2973–83. doi: 10.1021/bi0616753. [DOI] [PubMed] [Google Scholar]
- 56.Grilley D, Soto AM, Draper DE. Mg2+–RNA interaction free energies and their relationship to the folding of RNA tertiary structures. Proc Natl Acad Sci USA. 2006;103:14003–8. doi: 10.1073/pnas.0606409103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Eisenberg B. Interacting ions in biophysics: Real is not ideal. Biophys J. 2013;104:1849–66. doi: 10.1016/j.bpj.2013.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Das R, Mills TT, Kwok LW, Maskel GS, Millett IS, et al. Counterion distribution around DNA probed by solution X-ray scattering. Phys Rev Lett. 2003;90:188103. doi: 10.1103/PhysRevLett.90.188103. [DOI] [PubMed] [Google Scholar]
- 59.Andresen K, Das R, Park HY, Smith H, Kwok LW, et al. Spatial distribution of competing ions around DNA in solution. Phys Rev Lett. 2004;93:248103. doi: 10.1103/PhysRevLett.93.248103. [DOI] [PubMed] [Google Scholar]
- 60.Pabit SA, Meisburger SP, Li L, Blose JM, Jones CD, Pollack L. Counting ions around DNA with anomalous small-angle X-ray scattering. J Am Chem Soc. 2010;132:16334–36. doi: 10.1021/ja107259y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Takamoto K, Das R, He Q, Doniach S, Brenowitz M, et al. Principles of RNA compaction: insights from the equilibrium folding pathway of the P4–P6 RNA domain in monovalent cations. J Mol Biol. 2004;343:1195–206. doi: 10.1016/j.jmb.2004.08.080. [DOI] [PubMed] [Google Scholar]
- 62.Lipfert J, Sim AY, Herschlag D, Doniach S. Dissecting electrostatic screening, specific ion binding, and ligand binding in an energetic model for glycine riboswitch folding. RNA. 2010;16:708–19. doi: 10.1261/rna.1985110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Thomas R. Research on the denaturation of desoxyribonucleic acids. Biochim Biophys Acta. 1954;14:231–40. doi: 10.1016/0006-3002(54)90163-8. [DOI] [PubMed] [Google Scholar]
- 64.Williams AP, Longfellow CE, Freier SM, Kierzek R, Turner DH. Laser temperature-jump, spectroscopic, and thermodynamic study of salt effects on duplex formation by dGCATGC. Biochemistry. 1989;28:4283–91. doi: 10.1021/bi00436a025. [DOI] [PubMed] [Google Scholar]
- 65.Nakano S, Fujimoto M, Hara H, Sugimoto N. Nucleic acid duplex stability: influence of base composition on cation effects. Nucleic Acids Res. 1999;27:2957–65. doi: 10.1093/nar/27.14.2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Rau DC, Lee B, Parsegian VA. Measurement of the repulsive force between polyelectrolyte molecules in ionic solution: hydration forces between parallel DNA double helices. Proc Natl Acad Sci USA. 1984;81:2621–25. doi: 10.1073/pnas.81.9.2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Rau DC, Parsegian VA. Direct measurement of the intermolecular forces between counterion-condensed DNA double helices. Evidence for long range attractive hydration forces. Biophys J. 1992;61:246–59. doi: 10.1016/S0006-3495(92)81831-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Podgornik R, Rau DC, Parsegian VA. Parametrization of direct and soft steric-undulatory forces between DNA double helical polyelectrolytes in solutions of several different anions and cations. Biophys J. 1994;66:962–71. doi: 10.1016/S0006-3495(94)80877-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Korolev N, Lyubartsev AP, Rupprecht A, Nordenskiöld L. Competitive binding of Mg2+, Ca2+, Na+, and K+ ions to DNA in oriented DNA fibers: experimental and Monte Carlo simulation results. Biophys J. 1999;77:2736–49. doi: 10.1016/s0006-3495(99)77107-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Koch MH, Vachette P, Svergun DI. Small-angle scattering: a view on the properties, structures and structural changes of biological macromolecules in solution. Q Rev Biophys. 2003;36:147–227. doi: 10.1017/s0033583503003871. [DOI] [PubMed] [Google Scholar]
- 71.Lipfert J, Doniach S. Small-angle X-ray scattering from RNA, proteins, and protein complexes. Annu Rev Biophys Biomol Struct. 2007;36:307–27. doi: 10.1146/annurev.biophys.36.040306.132655. [DOI] [PubMed] [Google Scholar]
- 72.Fang X, Pan T, Sosnick TR. A thermodynamic framework and cooperativity in the tertiary folding of a Mg2+-dependent ribozyme. Biochemistry. 1999;38:16840–46. doi: 10.1021/bi991700n. [DOI] [PubMed] [Google Scholar]
- 73.Fang X, Littrell K, Yang XJ, Henderson SJ, Siefert S, et al. Mg2+-dependent compaction and folding of yeast tRNAPhe and the catalytic domain of the B. subtilis RNase P RNA determined by small-angle X-ray scattering. Biochemistry. 2000;39:11107–13. doi: 10.1021/bi000724n. [DOI] [PubMed] [Google Scholar]
- 74.Russell R, Millett IS, Doniach S, Herschlag D. Small angle X-ray scattering reveals a compact intermediate in RNA folding. Nat Struct Biol. 2000;7:367–70. doi: 10.1038/75132. [DOI] [PubMed] [Google Scholar]
- 75.Fang XW, Golden BL, Littrell K, Shelton V, Thiyagarajan P, et al. The thermodynamic origin of the stability of a thermophilic ribozyme. Proc Natl Acad Sci USA. 2001;98:4355–60. doi: 10.1073/pnas.071050698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Russell R, Zhuang X, Babcock HP, Millett IS, Doniach S, et al. Exploring the folding landscape of a structured RNA. Proc Natl Acad Sci USA. 2002;99:155–60. doi: 10.1073/pnas.221593598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Lipfert J, Das R, Chu VB, Kudaravalli M, Boyd N, et al. Structural transitions and thermodynamics of a glycine-dependent riboswitch from Vibrio cholerae. J Mol Biol. 2007;365:1393–406. doi: 10.1016/j.jmb.2006.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Silverman SK, Deras ML, Woodson SA, Scaringe SA, Cech TR. Multiple folding pathways for the P4–P6 RNA domain. Biochemistry. 2000;39:12465–75. doi: 10.1021/bi000828y. [DOI] [PubMed] [Google Scholar]
- 79.Frederiksen JK, Li NS, Das R, Herschlag D, Piccirilli JA. Metal-ion rescue revisited: biochemical detection of site-bound metal ions important for RNA folding. RNA. 2012;18:1123–41. doi: 10.1261/rna.028738.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Heilman-Miller SL, Thirumalai D, Woodson SA. Role of counterion condensation in folding of the Tetrahymena ribozyme. I Equilibrium stabilization by cations. J Mol Biol. 2001;306:1157–66. doi: 10.1006/jmbi.2001.4437. [DOI] [PubMed] [Google Scholar]
- 81.Doherty EA, Batey RT, Masquida B, Doudna JA. A universal mode of helix packing in RNA. Nat Struct Biol. 2001;8:339–43. doi: 10.1038/86221. [DOI] [PubMed] [Google Scholar]
- 82.Chauhan S, Caliskan G, Briber RM, Perez-Salas U, Rangan P, et al. RNA tertiary interactions mediate native collapse of a bacterial group I ribozyme. J Mol Biol. 2005;353:1199–209. doi: 10.1016/j.jmb.2005.09.015. [DOI] [PubMed] [Google Scholar]
- 83.Koculi E, Hyeon C, Thirumalai D, Woodson SA. Charge density of divalent metal cations determines RNA stability. J Am Chem Soc. 2007;129:2676–82. doi: 10.1021/ja068027r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Moghaddam S, Caliskan G, Chauhan S, Hyeon C, Briber RM, et al. Metal ion dependence of cooperative collapse transitions in RNA. J Mol Biol. 2009;393:753–64. doi: 10.1016/j.jmb.2009.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its oxygen dissociation curve. J Physiol. 1910;40:4–7. [Google Scholar]
- 86.Misra VK, Draper DE. A thermodynamic framework for Mg2+ binding to RNA. Proc Natl Acad Sci USA. 2001;98:12456–61. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Leipply D, Draper DE. Dependence of RNA tertiary structural stability on Mg2+ concentration: interpretation of the Hill equation and coefficient. Biochemistry. 2010;49:1843–53. doi: 10.1021/bi902036j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Takamoto K, He Q, Morris S, Chance MR, Brenowitz M. Monovalent cations mediate formation of native tertiary structure of the Tetrahymena thermophila ribozyme. Nat Struct Biol. 2002;9:928–33. doi: 10.1038/nsb871. [DOI] [PubMed] [Google Scholar]
- 89.Das R, Karanicolas J, Baker D. Atomic accuracy in predicting and designing noncanonical RNA structure. Nat Methods. 2010;7:291–94. doi: 10.1038/nmeth.1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Sattin BD, Zhao W, Travers K, Chu S, Herschlag D. Direct measurement of tertiary contact cooperativity in RNA folding. J Am Chem Soc. 2008;130:6085–87. doi: 10.1021/ja800919q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Solomatin SV, Greenfeld M, Chu S, Herschlag D. Multiple native states reveal persistent ruggedness of an RNA folding landscape. Nature. 2010;463:681–84. doi: 10.1038/nature08717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Dahm SC, Uhlenbeck OC. Role of divalent metal ions in the hammerhead RNA cleavage reaction. Biochemistry. 1991;30:9464–69. doi: 10.1021/bi00103a011. [DOI] [PubMed] [Google Scholar]
- 93.Wang S, Karbstein K, Peracchi A, Beigelman L, Herschlag D. Identification of the hammer-head ribozyme metal ion binding site responsible for rescue of the deleterious effect of a cleavage site phosphorothioate. Biochemistry. 1999;38:14363–78. doi: 10.1021/bi9913202. [DOI] [PubMed] [Google Scholar]
- 94.Sigel RK, Vaidya A, Pyle AM. Metal ion binding sites in a group II intron core. Nat Struct Biol. 2000;7:1111–16. doi: 10.1038/81958. [DOI] [PubMed] [Google Scholar]
- 95.Maderia M, Hunsicker LM, DeRose VJ. Metal-phosphate interactions in the hammerhead ribozyme observed by 31P NMR and phosphorothioate substitutions. Biochemistry. 2000;39:12113–20. doi: 10.1021/bi001249w. [DOI] [PubMed] [Google Scholar]
- 96.Pyle A. Metal ions in the structure and function of RNA. J Biol Inorg Chem. 2002;7:679–90. doi: 10.1007/s00775-002-0387-6. [DOI] [PubMed] [Google Scholar]
- 97.DeRose VJ. Metal ion binding to catalytic RNA molecules. Curr Opin Struct Biol. 2003;13:317–24. doi: 10.1016/s0959-440x(03)00077-0. [DOI] [PubMed] [Google Scholar]
- 98.Nakano S, Cerrone AL, Bevilacqua PC. Mechanistic characterization of the HDV genomic ribozyme: classifying the catalytic and structural metal ion sites within a multichannel reaction mechanism. Biochemistry. 2003;42:2982–94. doi: 10.1021/bi026815x. [DOI] [PubMed] [Google Scholar]
- 99.Christian EL. Identification and characterization of metal ion binding by thiophilic metal ion rescue. In: Hartmann RK, Bindereif A, Schön A, Westhof E, editors. Handbook of RNA Biochemistry. Weinheim, Ger: Wiley-VCH; 2005. pp. 319–44. [Google Scholar]
- 100.Basu S, Strobel SA. Thiophilic metal ion rescue of phosphorothioate interference within the Tetrahymena ribozyme P4–P6 domain. RNA. 1999;5:1399–407. doi: 10.1017/s135583829999115x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Hougland JL, Piccirilli JA, Forconi M, Lee J, Herschlag D. How the group I intron works: a case study of RNA structure and function. Cold Spring Harb Monogr Arch. 2006;43:133–205. [Google Scholar]
- 102.Nakano S, Proctor DJ, Bevilacqua PC. Mechanistic characterization of the HDV genomic ribozyme: assessing the catalytic and structural contributions of divalent metal ions within a multichannel reaction mechanism. Biochemistry. 2001;40:12022–38. doi: 10.1021/bi011253n. [DOI] [PubMed] [Google Scholar]
- 103.Travers KJ, Boyd N, Herschlag D. Low specificity of metal ion binding in the metal ion core of a folded RNA. RNA. 2007;13:1205–13. doi: 10.1261/rna.566007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Manning GS. Limiting laws and counterion condensation in polyelectrolyte solutions I. Colligative properties. J Chem Phys. 1969;51:924–33. [Google Scholar]
- 105.Manning GS. Limiting laws and counterion condensation in polyelectrolyte solutions. IV The approach to the limit and the extraordinary stability of the charge fraction. Biophys Chem. 1977;7:95–102. doi: 10.1016/0301-4622(77)80002-1. [DOI] [PubMed] [Google Scholar]
- 106.Manning GS. Molecular theory of polyelectrolyte solutions with applications to electrostatic properties of polynucleotides. Q Rev Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 107.Keyser UF, Koeleman BN, Van Dorp S, Krapf D, Smeets RMM, et al. Direct force measurements on DNA in a solid-state nanopore. Nat Phys. 2006;2:473–77. [Google Scholar]
- 108.Bayer J, Radler JO. DNA microelectrophoresis using double focus fluorescence correlation spectroscopy. Electrophoresis. 2006;27:3952–63. doi: 10.1002/elps.200500947. [DOI] [PubMed] [Google Scholar]
- 109.Ghosal S. Electrokinetic-flow-induced viscous drag on a tethered DNA inside a nanopore. Phys Rev E. 2007;76:061916. doi: 10.1103/PhysRevE.76.061916. [DOI] [PubMed] [Google Scholar]
- 110.Maffeo C, Schopflin R, Brutzer H, Stehr R, Aksimentiev A, et al. DNA–DNA interactions in tight supercoils are described by a small effective charge density. Phys Rev Lett. 2010;105:158101. doi: 10.1103/PhysRevLett.105.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Vuletic T, Babic SD, Grgicin D, Aumiler D, Radler J, et al. Manning free counterion fraction for a rodlike polyion: aqueous solutions of short DNA fragments in presence of very low added salt. Phys Rev E. 2011;83:041803. doi: 10.1103/PhysRevE.83.041803. [DOI] [PubMed] [Google Scholar]
- 112.Cherstvy AG. DNA cyclization: suppression or enhancement by electrostatic repulsions? J Phys Chem B. 2011;115:4286–94. doi: 10.1021/jp2003479. [DOI] [PubMed] [Google Scholar]
- 113.McIntosh DB, Saleh OA. Salt species-dependent electrostatic effects on ssDNA elasticity. Macromolecules. 2011;44:2328–33. [Google Scholar]
- 114.Hecht JL, Honig B, Shin YK, Hubbell WL. Electrostatic potentials near-the-surface of DNA: comparing theory and experiment. J Phys Chem. 1995;99:7782–86. [Google Scholar]
- 115.Hansen PL, Podgornik R, Parsegian VA. Osmotic properties of DNA: critical evaluation of counterion condensation theory. Phys Rev E. 2001;64(2 Part 1):021907. doi: 10.1103/PhysRevE.64.021907. [DOI] [PubMed] [Google Scholar]
- 116.Tan ZJ, Chen SJ. Ion-mediated nucleic acid helix-helix interactions. Biophys J. 2006;91:518–36. doi: 10.1529/biophysj.106.084285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Anderson CF, Record MT. Polyelectrolyte theories and their applications to DNA. Annu Rev Phys Chem. 1982;33:191–222. [Google Scholar]
- 118.Honig B, Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268:1144–49. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 119.Jayaram B, Sharp KA, Honig B. The electrostatic potential of B-DNA. Biopolymers. 1989;28:975–93. doi: 10.1002/bip.360280506. [DOI] [PubMed] [Google Scholar]
- 120.Yang AS, Gunner MR, Sampogna R, Sharp K, Honig B. On the calculations of pKas in proteins. Proteins. 1993;15:252–65. doi: 10.1002/prot.340150304. [DOI] [PubMed] [Google Scholar]
- 121.Sharp KA, Honig B. Calculating total electrostatic energies with the non-linear Poisson–Boltzmann equation. J Phys Chem. 1990;94:7684–92. [Google Scholar]
- 122.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc Natl Acad Sci USA. 2001;98:10037–41. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Holm C, Kekicheff P, Podgornik R. Electrostatic Effects in Soft Matter and Biophysics. Dordrecht, Neth: Kluwer Acad; 2001. [Google Scholar]
- 124.Dong F, Olsen B, Baker NA. Computational methods for biomolecular electrostatics. Methods Cell Biol. 2008;84:843–70. doi: 10.1016/S0091-679X(07)84026-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Debye P, Hückel E. The theory of electrolytes. I The lowering of the freezing point and related occurrences. Phys Z. 1923;24:185–206. [Google Scholar]
- 126.Nicholls A, Honig B. A rapid finite-difference algorithm, utilizing successive over-relaxation to solve the Poisson–Boltzmann equation. J Comput Chem. 1991;12:435–45. [Google Scholar]
- 127.Honig B, Rocchia W, Alexov E. Extending the applicability of the nonlinear Poisson–Boltzmann equation: multiple dielectric constants and multivalent ions. J Phys Chem B. 2001;105:6507–14. [Google Scholar]
- 128.Holst MJ, Saied F. Numerical solution of the nonlinear Poisson–Boltzmann equation: developing more robust and efficient methods. J Comput Chem. 1995;16:337–64. [Google Scholar]
- 129.Holst MJ, Saied F. Numerical solution of the nonlinear Poisson–Boltzmann equation: developing more robust and efficient methods. J Comput Chem. 1995;16:337–64. [Google Scholar]
- 130.Dolinsky TJ, Czodrowski P, Li H, Nielsen JE, Jensen JH, et al. PDB2PQR: expanding and upgrading automated preparation of biomolecular structures for molecular simulations. Nucleic Acids Res. 2007;35:W522–25. doi: 10.1093/nar/gkm276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Bashford D, Gerwert K. Electrostatic calculations of the pKa values of ionizable groups in bacte-riorhodopsin. J Mol Biol. 1992;224:473–86. doi: 10.1016/0022-2836(92)91009-e. [DOI] [PubMed] [Google Scholar]
- 132.Koehl P, Delarue M. AQUASOL: an efficient solver for the dipolar Poisson–Boltzmann–Langevin equation. J Chem Phys. 2010;132:064101. doi: 10.1063/1.3298862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Koehl P, Orland H, Delarue M. Beyond the Poisson–Boltzmann model: modeling biomolecule–water and water–water interactions. Phys Rev Lett. 2009;102:087801. doi: 10.1103/PhysRevLett.102.087801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Koehl P, Orland H, Delarue M. Computing ion solvation free energies using the dipolar Poisson model. J Phys Chem B. 2009;113:5694–97. doi: 10.1021/jp9010907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Azuara C, Lindahl E, Koehl P, Orland H, Delarue M. PDB_hydro: incorporating dipolar solvents with variable density in the Poisson–Boltzmann treatment of macromolecule electrostatics. Nucleic Acids Res. 2006;34:W38–42. doi: 10.1093/nar/gkl072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Misra VK, Draper DE. The linkage between magnesium binding and RNA folding. J Mol Biol. 2002;317:507–21. doi: 10.1006/jmbi.2002.5422. [DOI] [PubMed] [Google Scholar]
- 137.Misra VK, Shiman R, Draper DE. A thermodynamic framework for the magnesium-dependent folding of RNA. Biopolymers. 2003;69:118–36. doi: 10.1002/bip.10353. [DOI] [PubMed] [Google Scholar]
- 138.Lipfert J, Chu VB, Bai Y, Herschlag D, Doniach S. Low-resolution models for nucleic acids from small-angle X-ray scattering with applications to electrostatic modeling. J Appl Crystallogr. 2007;40:S229–34. [Google Scholar]
- 139.Perez-Salas UA, Rangan P, Krueger S, Briber RM, Thirumalai D, Woodson SA. Compaction of a bacterial group I ribozyme coincides with the assembly of core helices. Biochemistry. 2004;43:1746–53. doi: 10.1021/bi035642o. [DOI] [PubMed] [Google Scholar]
- 140.Heilman-Miller SL, Pan J, Thirumalai D, Woodson SA. Role of counterion condensation in folding of the Tetrahymena ribozyme. II Counterion-dependence of folding kinetics. J Mol Biol. 2001;309:57–68. doi: 10.1006/jmbi.2001.4660. [DOI] [PubMed] [Google Scholar]
- 141.Chu VB, Bai Y, Lipfert J, Herschlag D, Doniach S. Evaluation of ion binding to DNA duplexes using a size-modified Poisson–Boltzmann theory. Biophys J. 2007;93:3202–9. doi: 10.1529/biophysj.106.099168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Borukhov I, Andelman D, Orland H. Steric effects in electrolytes: a modified Poisson–Boltzmann equation. Phys Rev Lett. 1997;79:435–38. [Google Scholar]
- 143.Shiman R, Draper DE. Stabilization of RNA tertiary structure by monovalent cations. J Mol Biol. 2000;302:79–91. doi: 10.1006/jmbi.2000.4031. [DOI] [PubMed] [Google Scholar]
- 144.Lambert D, Leipply D, Shiman R, Draper DE. The influence of monovalent cation size on the stability of RNA tertiary structures. J Mol Biol. 2009;390:791–804. doi: 10.1016/j.jmb.2009.04.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Shklovskii BI. Screening of a macroion by multivalent ions: correlation-induced inversion of charge. Phys Rev E. 1999;60:5802–11. doi: 10.1103/physreve.60.5802. [DOI] [PubMed] [Google Scholar]
- 146.Shapovalov VL, Brezesinski G. Breakdown of the Gouy–Chapman model for highly charged Langmuir monolayers: counterion size effect. J Phys Chem B. 2006;110:10032–40. doi: 10.1021/jp056801b. [DOI] [PubMed] [Google Scholar]
- 147.Pabit SA, Qiu X, Lamb JS, Li L, Meisburger SP, Pollack L. Both helix topology and counterion distribution contribute to the more effective charge screening in dsRNA compared with dsDNA. Nucleic Acids Res. 2009;37:3887–96. doi: 10.1093/nar/gkp257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Pollack L. SAXS studies of ion–nucleic acid interactions. Annu Rev Biophys. 2011;40:225–42. doi: 10.1146/annurev-biophys-042910-155349. [DOI] [PubMed] [Google Scholar]
- 149.Rouzina I, Bloomfield VA. Influence of ligand spatial organization on competitive electrostatic binding to DNA. J Phys Chem. 1996;100:4305–13. [Google Scholar]
- 150.Antypov D, Barbosa MC, Holm C. Incorporation of excluded-volume correlations into Poisson–Boltzmann theory. Phys Rev E. 2005;71:061106. doi: 10.1103/PhysRevE.71.061106. [DOI] [PubMed] [Google Scholar]
- 151.Gavryushov S. Mediating role of multivalent cations in DNA electrostatics: an epsilon-modified Poisson–Boltzmann study of B-DNA–B-DNA interactions in mixture of NaCl and MgCl2 solutions. J Phys Chem B. 2009;113:2160–69. doi: 10.1021/jp809245a. [DOI] [PubMed] [Google Scholar]
- 152.Gavryushov S. Electrostatics of B-DNA in NaCl and CaCl2 solutions: ion size, interionic correlation, and solvent dielectric saturation effects. J Phys Chem B. 2008;112:8955–65. doi: 10.1021/jp711339d. [DOI] [PubMed] [Google Scholar]
- 153.Poitevin F, Orland H, Doniach S, Koehl P, Delarue M. AquaSAXS: a web server for computation and fitting of SAXS profiles with non-uniformally hydrated atomic models. Nucleic Acids Res. 2011;39:W184–89. doi: 10.1093/nar/gkr430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Grønbech-Jensen N, Mashl RJ, Bruinsma RF, Gelbart WM. Counterion-induced attraction between rigid polyelectrolytes. Phys Rev Lett. 1997;78:2477–80. [Google Scholar]
- 155.Nishio T, Minakata A. Effects of ion size and valence on ion distribution in mixed counterion systems of rodlike polyelectrolyte solution. I Mixed-size counterion systems with same valence. J Chem Phys. 2000;113:10784–92. [Google Scholar]
- 156.Abbondanzieri EA, Greenleaf WJ, Shaevitz JW, Landick R, Block SM. Direct observation of base-pair stepping by RNA polymerase. Nature. 2005;438:460–65. doi: 10.1038/nature04268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.He Z, Chen S-J. Quantifying Coulombic and solvent polarization-mediated forces between DNA helices. J Phys Chem B. 2013;117:7221–27. doi: 10.1021/jp4010955. [DOI] [PubMed] [Google Scholar]
- 158.Wilson RW, Bloomfield VA. Counterion-induced condensation of deoxyribonucleic acid. A light-scattering study. Biochemistry. 1979;18:2192–96. doi: 10.1021/bi00578a009. [DOI] [PubMed] [Google Scholar]
- 159.Bloomfield VA. DNA condensation by multivalent cations. Biopolymers. 1997;44:269–82. doi: 10.1002/(SICI)1097-0282(1997)44:3<269::AID-BIP6>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 160.Angelini TE, Liang H, Wriggers W, Wong GC. Like-charge attraction between polyelectrolytes induced by counterion charge density waves. Proc Natl Acad Sci USA. 2003;100:8634–37. doi: 10.1073/pnas.1533355100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Besteman K, Zevenbergen MA, Heering HA, Lemay SG. Direct observation of charge inversion by multivalent ions as a universal electrostatic phenomenon. Phys Rev Lett. 2004;93:170802. doi: 10.1103/PhysRevLett.93.170802. [DOI] [PubMed] [Google Scholar]
- 162.van der Heyden FH, Stein D, Besteman K, Lemay SG, Dekker C. Charge inversion at high ionic strength studied by streaming currents. Phys Rev Lett. 2006;96:224502. doi: 10.1103/PhysRevLett.96.224502. [DOI] [PubMed] [Google Scholar]
- 163.Besteman K, Van Eijk K, Lemay SG. Charge inversion accompanies DNA condensation by multivalent ions. Nat Phys. 2007;3:641–44. [Google Scholar]
- 164.Andresen K, Qiu X, Pabit SA, Lamb JS, Park HY, et al. Mono- and trivalent ions around DNA: a small-angle scattering study of competition and interactions. Biophys J. 2008;95:287–95. doi: 10.1529/biophysj.107.123174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Besteman K, Hage S, Dekker NH, Lemay SG. Role of tension and twist in single-molecule DNA condensation. Phys Rev Lett. 2007;98:058103. doi: 10.1103/PhysRevLett.98.058103. [DOI] [PubMed] [Google Scholar]
- 166.Rouzina I, Bloomfield VA. Macroion attraction due to electrostatic correlation between screening counterions. 1 Mobile surface-adsorbed ions and diffuse ion cloud. J Phys Chem. 1996;100:9977–89. [Google Scholar]
- 167.Nguyen TT, Grosberg AY, Shklovskii BI. Macroions in salty water with multivalent ions: giant inversion of charge. Phys Rev Lett. 2000;85:1568–71. doi: 10.1103/PhysRevLett.85.1568. [DOI] [PubMed] [Google Scholar]
- 168.Jiménez-Ángeles F, Lozada-Cassou M. A model macroion solution next to a charged wall: over-charging, charge reversal, and charge inversion by macroions. J Phys Chem B. 2004;108:7286–96. [Google Scholar]
- 169.Kanduc M, Naji A, Podgornik R. Counterion-mediated weak and strong coupling electrostatic interaction between like-charged cylindrical dielectrics. J Chem Phys. 2010;132:224703. doi: 10.1063/1.3430744. [DOI] [PubMed] [Google Scholar]
- 170.Burkhardt C, Zacharias M. Modelling ion binding to AA platform motifs in RNA: a continuum solvent study including conformational adaptation. Nucleic Acids Res. 2001;29:3910–18. doi: 10.1093/nar/29.19.3910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Philips A, Milanowska K, Lach G, Boniecki M, Rother K, Bujnicki JM. MetalionRNA: computational predictor of metal-binding sites in RNA structures. Bioinformatics. 2012;28:198–205. doi: 10.1093/bioinformatics/btr636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Cheatham TE, III, Kollman PA. Molecular dynamics simulation of nucleic acids. Annu Rev Phys Chem. 2000;51:435–71. doi: 10.1146/annurev.physchem.51.1.435. [DOI] [PubMed] [Google Scholar]
- 173.Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide. New York: Springer; 2002. [Google Scholar]
- 174.Mackerell AD, Jr, Nilsson L. Molecular dynamics simulations of nucleic acid–protein complexes. Curr Opin Struct Biol. 2008;18:194–99. doi: 10.1016/j.sbi.2007.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Cheatham TE, III, Young MA. Molecular dynamics simulation of nucleic acids: successes, limitations, and promise. Biopolymers. 2000;56:232–56. doi: 10.1002/1097-0282(2000)56:4<232::AID-BIP10037>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 176.Chen AA, Marucho M, Baker NA, Pappu RV. Simulations of RNA interactions with monovalent ions. Methods Enzymol. 2009;469:411–32. doi: 10.1016/S0076-6879(09)69020-0. [DOI] [PubMed] [Google Scholar]
- 177.Chen AA, Draper DE, Pappu RV. Molecular simulation studies of monovalent counterion-mediated interactions in a model RNA kissing loop. J Mol Biol. 2009;390:805–19. doi: 10.1016/j.jmb.2009.05.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178.Auffinger P, Cheatham TE, III, Vaiana AC. Spontaneous formation of KCl aggregates in biomolecular simulations: a force field issue? J Chem Theory Comput. 2007;3:1851–59. doi: 10.1021/ct700143s. [DOI] [PubMed] [Google Scholar]
- 179.Joung IS, Cheatham TE., III Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J Phys Chem B. 2008;112:9020–41. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Yoo J, Aksimentiev A. Improved parametrization of Li+, Na+, K+, and Mg2+ ions for all-atom molecular dynamics simulations of nucleic acid systems. J Phys Chem Lett. 2011;3:45–50. [Google Scholar]
- 181.Hart K, Foloppe N, Baker CM, Denning EJ, Nilsson L, Mackerell AD., Jr Optimization of the CHARMM additive force field for DNA: improved treatment of the BI/BII conformational equilibrium. J Chem Theory Comput. 2012;8:348–62. doi: 10.1021/ct200723y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Callahan KM, Casillas-Ituarte NN, Roeselova M, Allen HC, Tobias DJ. Solvation of magnesium dication: molecular dynamics simulation and vibrational spectroscopic study of magnesium chloride in aqueous solutions. J Phys Chem A. 2010;114:5141–48. doi: 10.1021/jp909132a. [DOI] [PubMed] [Google Scholar]
- 183.Yoo J, Aksimentiev A. Competitive binding of cations to duplex DNA revealed through molecular dynamics simulations. J Phys Chem B. 2012;116:12946–54. doi: 10.1021/jp306598y. [DOI] [PubMed] [Google Scholar]
- 184.Moult J, Pedersen JT, Judson R, Fidelis K. A large-scale experiment to assess protein structure prediction methods. Proteins. 1995;23:ii–v. doi: 10.1002/prot.340230303. [DOI] [PubMed] [Google Scholar]
- 185.Moult J. A decade of CASP: progress, bottlenecks and prognosis in protein structure prediction. Curr Opin Struct Biol. 2005;15:285–89. doi: 10.1016/j.sbi.2005.05.011. [DOI] [PubMed] [Google Scholar]
- 186.Sripakdeevong P, Beauchamp K, Das R. Why can’t we predict RNA structure at atomic resolution? In: Leontis N, Westhof E, editors. RNA 3D Structure Analysis and Prediction. Heidelberg, Ger: Springer; 2012. pp. 43–65. [Google Scholar]
- 187.Cruz JA, Blanchet MF, Boniecki M, Bujnicki JM, Chen SJ, et al. RNA-puzzles: a CASP-like evaluation of RNA three-dimensional structure prediction. RNA. 2012;18:610–25. doi: 10.1261/rna.031054.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Sanishvili R, Volz KW, Westbrook EM, Margoliash E. The low ionic strength crystal structure of horse cytochrome c at 2.1 Å resolution and comparison with its high ionic strength counterpart. Structure. 1995;3:707–16. doi: 10.1016/s0969-2126(01)00205-2. [DOI] [PubMed] [Google Scholar]
- 189.Bjorkman AJ, Mowbray SL. Multiple open forms of ribose-binding protein trace the path of its conformational change. J Mol Biol. 1998;279:651–64. doi: 10.1006/jmbi.1998.1785. [DOI] [PubMed] [Google Scholar]
- 190.Bhattacharya AA, Grune T, Curry S. Crystallographic analysis reveals common modes of binding of medium and long-chain fatty acids to human serum albumin. J Mol Biol. 2000;303:721–32. doi: 10.1006/jmbi.2000.4158. [DOI] [PubMed] [Google Scholar]
- 191.Hegde SS, Vetting MW, Roderick SL, Mitchenall LA, Maxwell A, et al. A fluoroquinolone resistance protein from Mycobacterium tuberculosis that mimics DNA. Science. 2005;308:1480–83. doi: 10.1126/science.1110699. [DOI] [PubMed] [Google Scholar]
- 192.Khrapunov S, Cheng H, Hegde S, Blanchard J, Brenowitz M. Solution structure and refolding of the Mycobacterium tuberculosis pentapeptide repeat protein MfpA. J Biol Chem. 2008;283:36290–99. doi: 10.1074/jbc.M804702200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Drew HR, Samson S, Dickerson RE. Structure of a B-DNA dodecamer at 16 K. Proc Natl Acad Sci USA. 1982;79:4040–44. doi: 10.1073/pnas.79.13.4040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Liu L, Botos I, Wang Y, Leonard JN, Shiloach J, et al. Structural basis of Toll-like receptor 3 signaling with double-stranded RNA. Science. 2008;320:379–81. doi: 10.1126/science.1155406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Butler EB, Xiong Y, Wang J, Strobel SA. Structural basis of cooperative ligand binding by the glycine riboswitch. Chem Biol. 2011;18:293–98. doi: 10.1016/j.chembiol.2011.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Giambaşu GM, Luchko T, Herschlag D, York DM, Case DA. Ion counting from explicit solvent simulations and 3D-RISM. Biophys J. 2014;106:883–94. doi: 10.1016/j.bpj.2014.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]