Pattern formation by vascular mesenchymal cells

Abstract

In embryogenesis, immature mesenchymal cells aggregate and organize into patterned tissues. Later in life, a pathological recapitulation of this process takes place in atherosclerotic lesions, when vascular mesenchymal cells organize into trabecular bone tissue within the artery wall. Here we show that multipotential adult vascular mesenchymal cells self-organize in vitro into patterns that are predicted by a mathematical model based on molecular morphogens interacting in a reaction-diffusion process. We identify activator and inhibitor morphogens for stripe, spot, and labyrinthine patterns and confirm the model predictions in vitro. Thus, reaction-diffusion principles may play a significant role in morphogenetic processes in adult mesenchymal cells.

In embryonic development, mesenchymal stem cells organize into condensations of varying sizes and shapes to form patterned tissues, such as ribs, vertebrae, and honeycombed trabeculae in long bones. In adult disease, such as atherosclerosis and aortic valvular stenosis, these embryonic events recur, as multipotential vascular mesenchymal cells (VMCs) differentiate into osteoblasts and other cell types (1). Fully formed bone arises in the artery wall and in cardiac valves, under the control of developmental genes (2, 3). This ectopic tissue forms focal and nodular patterns in a patchy distribution throughout the vasculature. We investigated the pattern formation mechanisms in these cells.

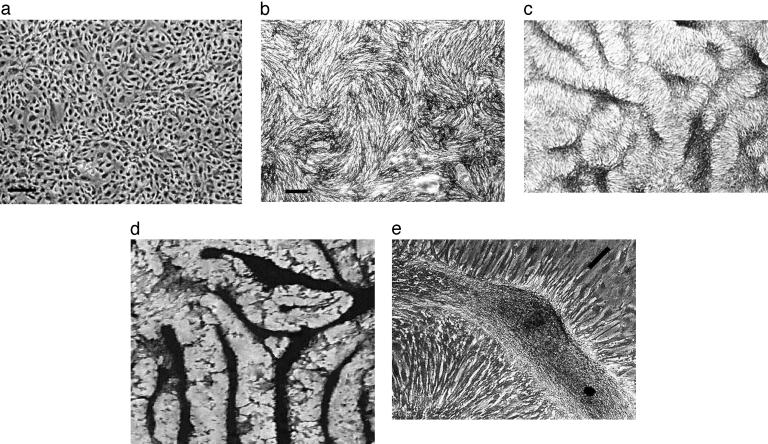
When cultures of VMCs are enzymatically dissociated and plated homogeneously in tissue culture, they first form uniform monolayers, with no apparent pattern. But over ≈20 days, the cells proliferate and organize into a sequence of distinct patterns. At day 1, the VMCs show no preferred alignment (Fig. 1a). By day 4, cells begin to align with their neighbors (Fig. 1b, “swirls”). By day 10, the cells aggregate into regularly spaced, stripe-like ridges of high cell density, ≈40 μm in width (Fig. 1c). Over the next several days, these high-density ridges gradually interconnect into labyrinthine patterns, with a preferred spacing, ≈100 μm (Fig. 1d). Cells in the center of the ridge then calcify, forming the bone mineral hydroxylapatite (2). At higher magnification, individual monolayer cells can be seen to orient perpendicular to the edges of the multicellular ridge (Fig. 1e), suggesting chemotactic migration.

Fig. 1.

Pattern formation in cultured VMCs in vitro. Over 20 days, VMCs plated in vitro develop from a monolayer of randomly oriented cells of nearly uniform density (approximately day 1; stage 1) (a), to local alignment of cells into regions (“swirls”) of nearly uniform size (approximately day 4; stage 2) (b), to ridges of high cell density (dark areas) (approximately day 10; stage 3) (c), to connected ridges forming a labyrinthine pattern (approximately day 16; stage 4) (von Kossa stain) (d). (e)At ×3 higher magnification, a phase-contrast image of an unstained ridge shows the perpendicular orientation of cells in the monolayer relative to the edges of the multicellular ridge. [Bar = 250 μm(a and b); c and d are at the same magnification as b; bar in e shows the approximate size, shape, and orientation of a single cell.]

As first proposed by Turing (4), pattern formation in biology can often be modeled mathematically by postulating “morphogens” that react chemically and diffuse. He showed that a highly simplified reaction-diffusion partial differential equation could indeed exhibit pattern formation emerging from a homogeneous state (4). Reaction-diffusion equations, modeling the interactions of activators and their inhibitors, have since been used to analyze pattern formation in many chemical and biological systems (5–9). Pattern formation modeling in biology began with mathematical models of the chemotaxis of single-celled organisms (10); more sophisticated models for chemotaxis have since been developed for Dictyostelium and Salmonella (11–14).

The pattern formation paradigm has been extended into vertebrate cell types (15) and to fundamental physiological processes such as angiogenesis (16). Some important morphogens have also been identified, including members of the transforming growth factor β and Hedgehog families as well as retinoic acid (17–20). Mathematical models have been developed for a number of additional pattern-formation processes, including angiogenesis, blood coagulation, and the appearance of periodic structures in bone and tooth formation (21–23).

A frequent obstacle to extending pattern-formation work into vertebrate physiology has been the difficulty in identifying the specific morphogens creating the pattern. But in these VMC cultures, we can identify the probable inhibitor and activator, allowing specific predictions from the mathematical model to be tested experimentally. It is known that VMCs express a powerful morphogen, bone morphogenetic protein 2 (BMP-2) (2, 24), a member of the transforming growth factor β superfamily. BMP-2 is a known chemoattractant (24) and morphogen (17, 25, 26). Its Drosophila homolog, decapentaplegic, is also a recognized morphogen (27).

In Turing-type activator-inhibitor models, the inhibitor must diffuse more rapidly than the activator, to limit and sculpt the domain. The VMCs also produce matrix carboxyglutamic acid protein (MGP), which has been shown to inhibit BMP-2 effects (28, 29) and, with its unusually small size (≈10 kDa), is likely to diffuse more rapidly than BMP-2. We therefore hypothesized that MGP acts as the inhibitor for a reaction-diffusion process forming these patterns.

Thus, identification of the activator was based on the requirements that it: (i) is a known chemoattractant, (ii) is a known morphogen, (iii) has a known inhibitor, and (iv) is expected to diffuse more slowly than its inhibitor. Although other protein pairs may satisfy one or some of these criteria, the combination of BMP-2 and MGP stands out as satisfying all four criteria.

Mathematical Model

We constructed a simplifying mathematical model of the VMC pattern formation process, consisting of a system of partial differential equations. Activator and inhibitor concentrations were modeled as continuously distributed over a 2D domain. Our reaction kinetics were based on the known interactions of BMP-2 with MGP in our experimental preparation. These kinetic mechanisms led us to build on a model of Gierer and Meinhardt (5, 30). The effective concentrations of activator and inhibitor are represented as U(x, y) and V(x, y). Our initial state consisted of uniform distributions of U and V with small (2%) random perturbations. U and V then evolve according to the following equations, which we write in dimensionless variables:

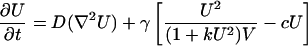[1]

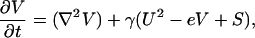[2]

where D = D_U/D_V is the ratio of the diffusion coefficients of activator and inhibitor, respectively, and γ is a factor that relates the chemical kinetics, the spatial domain size, and the diffusion rates. [If γ^* is the dimensional value (t^-1) of this scaling parameter, then γ = γ^* L²D_v^-1, where L is the linear dimension of the domain.] In Eq. 1, the activator U spurs its own production autocatalytically. It is known that this autocatalysis saturates (31) (see also Fig. 5, which is published as supporting information on the PNAS web site), hence we chose the sigmoidal form U²/(1+ kU²). (The parameter k governs the saturation level of the autocatalytic reaction.) The inhibition of U by V is modeled by the V term in the denominator. There is also first-order degradation of U at a rate c. In Eq. 2, the term U² is used to represent the observation that MGP expression is induced by BMP-2 in a greater-than-linear manner by BMP-2 at the level of MGP that is inhibitory for BMP-2 (32). The eV term represents first-order degradation of the inhibitor at a rate e. S represents an exogenous source of inhibitor. Parameter selection, sensitivity, and other details of the model are addressed in Supporting Text.

We simulated this mathematical model numerically and compared the results to the four stages seen in culture. In the early stages of the simulation, the distribution of activator peaks was evenly scattered (Fig. 2a). In the next stage, the gradient (grad U) of activator activity shows a similar pattern of local alignment as observed in the cell culture (Fig. 2b). In the third stage of the simulation, a stripe pattern emerges (Fig. 2c), and this develops into a labyrinthine pattern with a preferred spacing length (Fig. 2d). At this stage, a detail of the gradient (grad U) of the activator activity shows perpendicular orientation at the edges of the stripes (gray arrows, Fig. 2e).

Fig. 2.

Numerical solutions of the mathematical model corresponding to each of the stages from Fig. 1. Model results are displayed as levels of U with black for high and white for low levels. (a) Initially, the model shows a diffuse distribution of activity peaks (maxima of U). (b) Later, local alignment patterns develop, as shown by the direction field of the activator gradient, grad U (arrows), which would correspond with cell orientation and direction of migration in the culture. (c and d) This is followed by development of stripe-like concentrations of U (c) then formation of a labyrinthine pattern (d). (e) At higher detail (≈×3), gray arrows depict the direction field of grad U, which corresponds to the perpendicular orientation of cells in culture. Model parameter values: γ = 15,000, D = D₁/D₂, D₁ = 0.01, D₂ = 2.0, c = 0.01, k = 0.65, S = 0, e = 0.02. The basis for parameter selection and robustness of the model is discussed in Supporting Text, which is published as supporting information on the PNAS web site. These images are regions of the overall simulation that correspond in spatial scale with the culture images, which are subregions of the overall plate.

From Stripes to Spots

The mathematical model also provided two predictions. The first is that addition of exogenous inhibitor will convert the stripe pattern to a spot pattern (Movie 1, which is published as supporting information on the PNAS web site). This is because an increase of V (due to the exogenous source) will lessen activator growth, so that activator diffusion and decay dominate over activator production far from regions of high activator concentration. The prediction of stripe-to-spot conversion was then confirmed in the experimental culture: when exogenous MGP was added to the preparation, cultures developed a spot-like, instead of a stripe-like, pattern of high cell density regions (Fig. 3).

Fig. 3.

From stripes to spots: in vitro patterns after addition of exogenous inhibitor, compared with predictions of the mathematical model. (a) After treatment with 40 nM exogenous MGP, cells aggregated into a spot-like pattern instead of the stripe pattern shown in Fig. 1 c and d. (b) Addition of a source term to the mathematical model, to simulate treatment with exogenous inhibitor, also yielded a spot-like pattern. (c) Higher-power photomicrograph of the in vitro spot-like pattern showing radial orientation of cells at the edges of the rounded aggregate. (d) Simulation corresponding to c showing the direction field of grad U as gray arrows. Regions of high activator concentration are shown in black. Cells were cytochemically stained for alkaline phosphatase in a and c. Model parameter values are the same as for Fig. 2, except for addition of a dimensionless source term (S = 0.006) in Eq. 2 as a pulse.

Stripe Doubling

The second prediction from the model is that the pattern would change in response to the drug warfarin, which partially blocks the inhibitory action of MGP on BMP-2. Warfarin inhibits regeneration of vitamin K1 epoxide and thereby blocks vitamin K-dependent γ-carboxylation of the glutamic acid residues in MGP (33, 34). These modified residues are required for MGP function (35). There are several possible mechanisms by which warfarin may alter this system: It may alter MGP charge, size, and shape (hence its diffusion coefficient); its binding to extracellular matrix; the functional domain surface area; the interaction between the two morphogens; and/or the expression level of a morphogen. Warfarin also may act on other proteins, even ones that are not vitamin K-dependent (36).

In the cell cultures, warfarin treatment resulted in a characteristic refinement of the labyrinthine pattern [Fig. 4: control (a and e); treated (c and g)]. The density of ridges doubled as new ridges formed. In the model, increases in γ alone (but not k) produced corresponding stripe doubling [Movie 2, which is published as supporting information on the PNAS web site; Fig. 4: original (b and f); increased γ (d and h)]. “Stripe doubling” has been described in mathematical models of epithelial pigmentation (6) and in more general mathematical models (37, 38).

Fig. 4.

Mode doubling with warfarin: in vitro pattern after addition of exogenous inhibitor of MGP compared with control (a, c, e, and g) and with corresponding predictions of the mathematical model (b, d, f, and h). (a and b) Early pattern formation in vitro (a) and in the mathematical model (b). (c) With addition of warfarin (4 nM), the spatial frequency of ridges doubled. (d) The mathematical model shows a corresponding pattern. (e–h) Higher power of a–d, illustrating mode splitting. Model parameters are the same as for Fig. 2, except that midway through the simulation, the initial value of γ = 15,000 was increased to 30,000 to represent the addition of warfarin (d and h). Cultures in a, c, e, and g are stained by the von Kossa method.

The mathematical model is also consistent with experiments showing that overexpression of BMP-2 in developing chick limbs increases the size of high-density cartilage condensations (25). Overexpression was incorporated into the mathematical model by increasing the production of activator, which increased the size of the regions of high U value (results not shown), corresponding to increased size of regions of high cell density.

These findings suggest that vascular mesenchymal cells selforganize following the predictions of a reaction-diffusion mathematical model. This model did not require a separate equation for cell movement; the effect of the chemotactic response of the cells on U (more cells leading to increased activator production) (24) is incorporated in the positive feedback term of Eq. 1. Thus, the results generated by the model represent a “chemical prepattern” (7, 39). We cannot exclude the possibility that other models with different kinetics (see, for example, Fig. 6, which is published as supporting information on the PNAS web site) may predict similar patterns.

Importantly, the pattern formed governs not only the aggregation of cells but also their ultimate differentiation and mineralization, which occur only within the stripes and spots of the pattern. Moreover, the patterns of mineralization induced by morphogens in these vascular cells may have a role in atherosclerotic vascular calcification (2, 35, 36) and suggest possible mechanisms for the teratogenic effects of warfarin on the skeleton.