Abstract
We propose a model for membrane-cortex adhesion that couples membrane deformations, hydrodynamics, and kinetics of membrane-cortex ligands. In its simplest form, the model gives explicit predictions for the critical pressure for membrane detachment and for the value of adhesion energy. We show that these quantities exhibit a significant dependence on the active acto-myosin stresses. The model provides a simple framework to access quantitative information on cortical activity by means of micropipette experiments. We also extend the model to incorporate fluctuations and show that detailed information on the stability of membrane-cortex coupling can be obtained by a combination of micropipette aspiration and fluctuation spectroscopy measurements.
Introduction
In many cells, a thin layer of cytoskeleton called “cortex” underlies the plasma membrane. While the cellular membrane serves as a barrier for the cell and a mechanism to communicate with the extracellular media, the cortex, made mostly of actin cross-linked filaments and myosin II, provides rigidity and allows for active remodeling of the cell boundaries, essential for instance for cell motility. The control of membrane-cortex adhesion is crucial to many cellular processes. Indeed, membrane-cortex detachment and the formation of cellular blebs, spherical protrusions of the unbound plasma membrane, is often a sign of apoptosis (1,2). Membrane blebbing is also used for motility by several cell types, including amoebae and possibly cancer cells (3–6).
It is acknowledged that membrane-cortex adhesion is obtained via specific interactions between large numbers of ligand and receptor molecules (7), such as Talin (8) and ezrin/radixin/moesin proteins (9). Spontaneous membrane detachment, also known as blebbing, has been associated with myosin activity within the cortex (10,11). Externally induced perturbations using micropipette aspiration or osmotic shocks show that a sufficiently large drop of external pressure can induce membrane detachment (12). Consequently the links between the membrane and cortex are constantly under stress, which origin is ultimately related to acto-myosin cortical tension and osmotic pressure.
In this article, we present a model for adhesion based on the kinetics of the membrane-cortex ligands (13–16). We describe the stability of adhesion by coupling the kinetics of the ligands to the stress exerted on them and to physical properties of the membrane. In its simplest form, the model establishes the mechanical equilibrium of the cell considering both the pressure drop across the membrane and the prestressed state of the cortex, and predicts the outcome of a micropipette aspiration experiment in terms of physical parameters. These predictions are then compared to experiments from the literature. We also discuss extensions of the model to include spatial modulations of the membrane and different scenarios of hydrodynamic interactions, depending on the porosity of the cortex and its actual distance to the membrane. In particular, we obtain analytical expressions for the structure factor and fluctuation spectrum of the membrane in certain limits, and show how these results may be used to obtain additional information on the density of ligands by means of fluctuation spectroscopy experiments on eukaryotic cells.
Materials and Methods
The adhesion of a flexible membrane on a substrate by means of discrete linkers has been extensively studied in the past (18–23), mostly using computer simulations. It is a highly nontrivial problem due to the multiplicity of energy scales (membrane rigidity and tension, linker stiffness, and binding energy) and timescales (membrane and cytosol fluidity, linker’s diffusion, and binding kinetics). In particular, the role of fluctuations on the unbinding transition of a membrane possessing metastable bound and unbound states has been characterized numerically (19), but the unbinding of a membrane subjected to a constant pressure has, to our knowledge, not been systematically investigated. Our primary goal here is to assess the role of cortical prestress on membrane-cortex detachment.
To this aim, we first adopt a highly simplified model, where we assume a nearly planar membrane subject to a normal external stress σ and attached to the cortex by a density of linkers ρb, which is necessarily smaller than a maximal value ρ0 (Fig. 1). The cortex is assumed to be flat and immobile, so that the model is only valid at length scales below the correlation length for cortex undulations. For a constant normal stress σ, an equilibrium state may exist with a planar membrane at position u where a uniform density ρb of bound springlike linkers with elastic constant k balances the external force. To find the conditions for the existence and stability of such an equilibrium state, we may write dynamical equations assuming spatial uniformity, where u and ρb are only time-dependent,
| (1) |
| (2) |
where η is an effective viscosity per unit length, and u = 0 corresponds to the position for which the bound linkers are not stretched. For small membrane displacements, the relevant contribution to dissipation is due to cytosol flow through the cortex meshwork, and the effective parameter η can be estimated as η ∼ ηch/ξ2 (see Section S1 in the Supporting Material for details), where ξ ∼ 30 nm is the scale of the cortex mesh size (24), h ∼ 500 nm is the thickness of the cortex, and η ∼ 3 × 10−3 – 2 × 10−1 Pa s is the cytosol viscosity (10).
Figure 1.
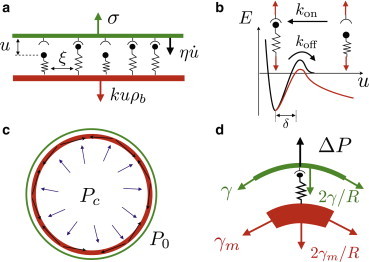
Sketch of the system. (a) The ligands are modeled as springs that link the cortex (red) and the membrane (green). (b) Kinetic rates kon and koff of the ligands. The value koff depends on the load (17). (c) Forces involved in the cell at steady state: internal pressure, Pc, and external pressure, P0, exert a normal force on the membrane and cortex, which is compensated by the membrane and cortex tension. (d) The normal projection of the acto-myosin tension in the cortex is transmitted to the membrane through proteins that link the cortex and the membrane. To see this figure in color, go online.
The linker kinetics is defined by the attachment and detachment rates kon and koff (Fig. 1), and is assumed to be much faster than the typical timescale of membrane shape relaxation. The force-dependent kinetics of the linkers then imposes a strong nonlinear coupling between the kinetics and the position of the membrane. The detachment rate is assumed to follow a Kramer’s-like kinetics (25) appropriate to thermally induced processes,
| (3) |
where δ is a characteristic bond length in the nanometric scale (17). For simplicity, we assume linker attachment to be an active process occurring at a constant rate kon. Therefore, detailed balance is not obeyed, as previously considered in membrane adhesion problems (18). This assumption allows us to disregard membrane fluctuations between attachment points, and yields a simple analytical form for the unbinding transition. However, it does not capture binding cooperativity occurring due to the smoothing of membrane fluctuations near attachment points (19–23).
Two relevant dimensionless quantities characterize the mechanics of the linkers: the kinetic ratio, χ, and the ratio of the force on the membrane to an intrinsic force scale of the linkers, α, with
| (4) |
Equilibrium solutions to Eqs. 1 and 2 exist only for α < α∗, where the latter is defined by
| (5) |
Taking χ ∼ 10−3 (26) and δ ∼ 1 nm, the critical force per link is σ∗/ρ0 ∼ 18 pN, corresponding to ∼4.5 times the thermal force per link kBT/δ. This fixes the condition for the detachment of the membrane from the cortex, which occurs for stresses that surpass the critical stress σ∗ = ρ0α∗(χ)kBT/δ.
The adhesion energy w per unit area may be defined as the work necessary to bring the stress of the linkers from its rest value to the critical value for detachment in a quasi-static fashion, that is,
| (6) |
where σ(u) is the equilibrium stress for each u. Note that the adhesion energy depends on the actual state of the cell ueq, which is generically unknown and incorporates the prestress state of the cell due to cortical tension.
Within our simplified model, the average density of bound linkers ρb,eq, the critical stress σ∗, and the adhesion energy w all scale linearly with the density of available linkers ρ0. This scaling results from our assumption of a constant binding rate. A different scaling is expected if the binding rate depends on the average position and fluctuations of the free membrane between anchoring points. If the on-rate obeys detailed balance, one expects ρb,eq ∼ ρ02 in the absence of a pressure difference (20,21). As discussed in the following sections, the results of micropipette experiments are consistent with a linear scaling σ∗ ∼ ρ0.
Results and Discussion
The simplified stochastic model of adhesion outlined in the previous section is used below to analyze two different kinds of experiments that can probe membrane-cortex interaction. First, we analyze micropipette experiments where the critical suction pressure required to unbind the cell membrane from the cortex was measured in different cellular contexts, where the density of adhesion molecules and of cortical motors have been altered. Second, we derive the effect of membrane-cortex interaction on the membrane fluctuation spectrum. There is as of yet no experimental data that can be directly confronted to the latter derivation. We hope this article will foster experimental spectroscopy studies that will couple membrane fluctuation analysis with cell micromanipulation, along the lines described below.
Mechanical equilibrium of the cell
Force balance at the membrane involves the difference of pressure across the membrane, ΔP, and the normal projection of the cortex and membrane tension, γm and γ, respectively,
where R is the radius of the cell, assumed spherical. At equilibrium, the links sustain the stress needed to maintain the cortex and the membrane adhered, σeq = 2γm/R, which accounts for the difference between the pressure and the membrane tension stresses, ΔP − 2γ/R. Whenever the equilibrium stress exceeds the critical value σ∗, we expect the cell membrane to detach spontaneously.
Micropipette aspiration (12,16,27–29), among other techniques (11,30,31), allows us to apply pressure perturbations of controlled intensity and area. Pressure perturbations can be supplemented with perturbations on relevant cell parameters such as myosin activity and link or cortex density, by genetics (27–29) or direct drug treatment (10,11,31). Tether pulling experiments have also been used to probe membrane-cortex adhesion (32), but their interpretation is rather nontrivial (33). In the following, we restrict ourselves to a quantitative interpretation of micropipette aspiration experiments.
Micropipette aspiration
During a micropipette experiment, a pressure drop is applied on a small region of the membrane defined by the micropipette radius Rp. A new equilibrium state in the micropipette requires an increase of the stress exerted on the links with respect to σeq,
| (7) |
where ΔP ≡ P0 – Pp is the difference between the extracellular media and the aspiration pressure, and R is the radius of the cell after deformation. Characteristic bounds for membrane tension γ ≲ 10−4 N/m and radius of cell R ∼ 10 μm and pipette Rp ∼ 5 μm allow membrane tension to compensate for a pressure of ∼20 Pa, which is small compared to the range of experimental pressures ∼100–1000 Pa. As a consequence, we will neglect the membrane tension contribution in the following. The last term in the right-hand side accounts for the cortical stress, or prestressed state of the cell σeq. In general, force balance does not need to be satisfied and the cell will eventually be entirely sucked inside the pipette if the suction pressure ΔPp is too large (16). Here we focus on the case where the cortex is able in principle to compensate for the pipette pressure.
Using our previous analysis for the membrane-cortex adhesion, we can relate the critical stress for the links, σ∗, with the critical aspiration pressure needed to unbind the membrane via Eq. 7:
| (8) |
The critical aspiration pressure has two contributions: the pressure needed to detach a certain number of relaxed links, given by the density of ligands and the critical force per link (first term); and the contribution from the presence of acto-myosin tension in the cortex, which sets a nonzero stress on the links at equilibrium, hence reducing the amount of pressure needed to reach the critical stress (second term, Fig. 2 a).
Figure 2.
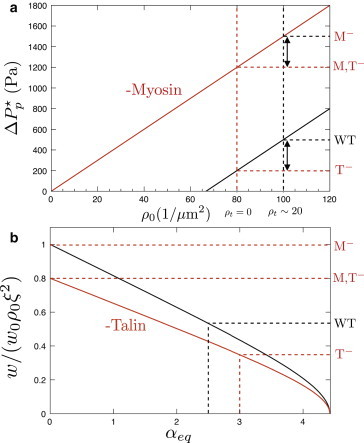
Theoretical predictions for the critical aspiration pressure and adhesion energy in a micropipette experiment. (a) Critical pressure as a function of the density of linkers ρ0 according to Eq. 8. (Solid black and red lines) Cells with and without myosin II, respectively. (Horizontal dashed lines) Experimentally measured value of the critical detachment pressure (28) for wild-type cells (WT), mutants lacking myosin (M−), mutants lacking talin (T−), and double mutants (M, T−). The slope and height of the two theoretical curves is entirely determined by these critical pressures (see text). (b) Effective adhesion energy as a function of the equilibrium cortical tension in the cell according to Eq. 9. (Solid black and red lines) Cells with and without talin, respectively. To see this figure in color, go online.
As in determining the critical aspiration pressure, we find that the adhesion energy per unit area measured when detaching the membrane (Eq. 6) depends on the level of cortical rest tension, σeq = 2γm/R, which ultimately determines the effective number of ligands to be broken:
| (9) |
Here, w0 ≡ (kBT/δ)2/(kξ2) is an upper bound for the adhesion energy, that corresponds to nonprestressed ligands, and for clarity we have used rescaled quantities for the stretching, z ≡ u/u0 with u0 ≡ kBT/(kδ), and ligand density . The adhesion energy per unit area depends linearly on the saturation density of links, , but contains a correction factor that includes the prestressed state of the cell. In the presence of cortical tension in the cell, there is both a reduction of the number of effective bound links, and an increase of stress per link. Consequently, close to the unbinding transition, the adhesion energy is reduced in a strongly nonlinear way by increasing the cortex prestress (Fig. 2 b).
Discussion of micropipette experiments
Our model allows us to directly relate the critical perturbation pressure needed to detach the membrane from the cortex to two physiologically relevant quantities: the density of membrane-cortex ligands, and the myosin-driven cortical tension (Eq. 8). This relationship provides not only a rational explanation for the membrane unbinding for a variety of cell phenotypes where either the density of ligands or myosin activity is altered, but also a method to directly probe cortex activity by measuring the critical pressure needed to unbind the membrane.
We refer to previous experimental results concerning the abrupt unbinding induced by micropipette suction to assess the validity of our model (12,28). To test the relationship among critical pressure, ligand density, and cortical tension, we would ideally need to measure the critical pressure for cells whose phenotype has been quantitatively altered. Merkel et al. (28) considered four phenotypes of the amoebae Dictyostelium: wild-type, myosin-inhibited, talin-inhibited (a membrane-cortex linker), and double mutants. These four phenotypes are sufficient to qualitatively test our model and obtain values for all the relevant parameters.
Mutations that perturbed ligand density and cortex activity should be independent within our model. Accordingly, the difference of unbinding pressure for two values of ligand density must be the same independently of the value of cortical activity (Fig. 2 a). In Merkel et al. (28), the decrease of critical pressure between the wild-type and talin-inhibited amoebae is comparable to the corresponding decrease between the myosin-inhibited and double-inhibited mutants (∼150–200 Pa and ∼150–500 Pa, respectively), even though the actual values of the cortical tension with and without myosin differ by a factor of 5 due to cortical prestress. This suggests that the critical pressure scales linearly with the density of available bounds: ΔPp∗ ∼ ρ0, as predicted by our simple model (Eq. 8). Comparing the critical pressures in both wild-type and myosin-null cells for a fixed link density (Figs. 3b and 4b in Merkel et al. (28)), we can estimate the myosin-driven cortical stress in the wild-type amoeba,
This is at least two orders-of-magnitude higher than the typical membrane tension of a vesicle, γ, and contributes to the 60% of the ∼1600 Pa needed to unbind the membrane. This estimate of the cortical tension agrees well with direct experimental measurements in Dictyostelium (27). Finally, introducing the obtained value of γm into the rest stress σeq = 2γm/R, and using the stationary state solution of Eqs. 1 and 2, , the equilibrium stretching of the linkers can be found, ueq ∼ 100 nm, as well as that roughly all the linkers are connected in equilibrium conditions for the wild-type cells, ρb,eq/ρ0 = αeq/zeq ∼ 1.
For myosin-inhibited amoebae, the micropipette pressure is directly related to the available density of links (Eq. 8). Using the results from Merkel et al. (28), we can estimate the relative concentration of talin with respect to the saturation link concentration:
Assuming the saturation density to be ρ0 ∼ 100 links/μm2, talin density should be roughly ρt ∼ 20 links/μm2. The asymmetric distribution of this small density of talin links seems to be enough to drive directed motion in amoebae (28). Similar observations are reported for zebrafish cells (31). For completeness, assuming a ligand length δ ∼ 1 nm, we find
and the critical force per link σ∗/ρ0 ∼ 16 pN is four times the thermal force of the link kBT/δ, which is close to our initial estimate (∼18 pN). This quantity is independent of the cell phenotype and only depends on the kinetic rate ratio χ. In fact, from the experimental estimate of α∗, we can derive the kinetic ratio of on- and off-rates of the membrane-cortex linkers, χ ∼ 10−3, in agreement with Rognoni et al. (26). Moreover, using the stationary solution of our model, a critical stretching u∗ ∼ 200 nm and a critical fraction of bound linkers ρb∗/ρ0 ∼ 0.9 are found. Our results show that the rest stress σeq = 2γm/R is ∼60% of the critical unbinding value σ∗ for wild-type cells, while it is ∼75% in talin-null cells. This is consistent with the observation that spontaneous blebbing of migratory Dictyostelium is more frequent for talin-null mutants than for wild-type cells (34).
Finally, our model gives a prediction for the adhesion energy as a function of the ligand density and cortical activity (Eq. 9). In the case of the four phenotypes discussed above, the maximum adhesion energy is w0ρ0ξ2 ∼ 2 × 10−5 J/m2, and corresponds to the mutant lacking myosin (a nonprestressed cell, αeq = 0). For a mutant lacking Talin and myosin II, the adhesion energy is reduced by ∼10–30% due to the decrease in ρ0. For a wild-type cell and a mutant lacking talin, the adhesion energies are further reduced, by 50% and 65%, respectively, due to cortical prestress (Fig. 2 b). The dramatic increase in the adhesion energy for a cell lacking myosin activity, which can be ∼200%, illustrates the importance of cortex activity in the cell in determining the experimental measurements of adhesion energy and detachment pressures. Table 1 recapitulates the numerical values used for the parameters of the model. These parameters may vary significantly depending on cell lines and experimental conditions, so this choice is somewhat arbitrary. However, we emphasize that both the cortical tension γm and the fraction of bonds associated with Talin ρt/ρ0 do not depend on this choice and can be directly determined by confronting Eq. 8 with the experimental results.
Table 1.
Estimates for model parameters
| Symbol | Description | Estimate (Ref.) |
|---|---|---|
| ξ | cortex mesh size | 30 nm (24) |
| h | cortex thickness | 500 nm (10) |
| ηc | cytosol viscosity | 10−2 Pa s (10) |
| kon | linker attachment rate | 104 s−1 (26) |
| free linker detachment rate | 10 s−1 (26) | |
| δ | linker bond length | 1 nm (17) |
| k | linker stiffness | 10−4 N/m (text) |
| ρ0 | density of available linkers | 1014 m−2 (text) |
| R | cell radius | 10 μm (28) |
| γ | membrane surface tension | 5 × 10–5 N/m (11) |
| κ | membrane bending ridigity | 10−19 J (30) |
| γm | cortical tension | 5 × 10–3 N/m (this work) |
Membrane undulations
The model for membrane-cortex adhesion discussed so far considers a flat membrane, disregarding possible membrane undulations. In this section, we address the linear dynamics of long-wavelength perturbations around the flat membrane state:
| (10) |
The coarse-grained interface Hamiltonian includes the elastic energy of bound linkers and contributions from the membrane bending rigidity and tension (35),
| (11) |
where κ is the bending modulus and σ = ρb,eqkueq. As before, the restoring elastic forces exerted by the linkers are treated within a continuous approximation, and membrane fluctuations between bound linkers are not accounted for. This description is appropriate for length scales larger than the average spacing between linkers ρ0−1/2 ∼ 100 nm.
Membrane deformations induce Stokes flows in the surrounding fluid. These flows mediate long-range hydrodynamic interactions in the membrane, leading to a nonlocal membrane dynamics that is better treated in Fourier space. The full dynamical problem requires a proper treatment of cytosol permeation through the porous cortex and the (less) porous lipid membrane at all length scales (36,37). For simplicity, we restrict ourselves to a simplified treatment, where cytosol permeation through the cortex is only included for the lowest Fourier mode q = 0. The other modes are treated below neglecting the effect of the cortex on hydrodynamics, as is appropriate for sufficiently large membrane-cortex distances and/or large cortex mesh size. The effect of finite cortex permeation is studied in Section S4 in the Supporting Material. Using standard results of membrane hydrodynamics (38) together with Eq. 11, the dynamics of long-wavelength membrane deformations read
| (12) |
| (13) |
where is the wave-vector. Within our approximation, the relaxation dynamics of the mode q = 0 (Eq. 12) is decoupled from the other modes (Eq. 13) at the linear level of perturbations. Equation 12 can be seen as a linearized version of Eq. 2 when transformed back to real space.
In turn, the dynamics of the long-wavelength perturbations of the density of bonds reads
| (14) |
Equations 12–14 completely specify the dynamics of linear perturbations around the flat membrane state, both for the membrane displacement u and the density of bonds ρb. However, in the limit of long wavelengths, membrane deformations proceed much more slowly than linker kinetics. In general, membrane dynamics is slower than linker kinetics at length scales above a cross-over wavelength λcross, which is determined from an analysis of the eigenvalues and eigenvectors of the dynamical system in Eqs. 13 and 14. With the parameters given in Table 1, this crossover occurs in the bending-dominated regime, for which λcross ≃ 2π(κ/(4ηckon))1/3 ∼ 0.4 μm. For larger length scales, the kinetics of the linkers shown in Eq. 14 is always essentially equilibrated and an adiabatic approximation may be used. The system can then be described in terms of only the slow variable δu:
| (15) |
Under the adiabatic approximation, the dispersion relation of membrane dynamics ω(q) = −(κq4 + γq2 + ρb,eqk)/(4ηcq) features a maximum due to membrane-cortex adhesion (see Section S2.1 in the Supporting Material for details). This maximum naturally defines a correlation length for shape fluctuations, λc, below which the membrane can be seen as essentially rigid. This correlation length depends on a combination of both mechanical properties of the membrane and of the linkers:
| (16) |
With the values given in Table 1, we find λc ∼ 0.6 μm for an unperturbed cell (ρb,eq ≃ ρ0). This value is larger than both the cross-over wavelength of the free membrane undulations, μm, and the spacing between linkers, ρ0−1/2 ∼ 0.1 μm. The computed correlation length is slightly smaller than the pipette radius, so the approximation of a rigid membrane is only marginally valid in that case. However, it becomes more accurate near the unbinding transition because the correlation length λc increases with decreasing density of bonds ρb (see Section S3 of the Supporting Material for details). In the general case, including all hydrodynamic effects of the cortex, the value of λc may differ from Eq. 16 or, for low cortex porosity and short membrane-cortex distances, it may not even be well defined (see Section S4 in the Supporting Material for details).
Finally, at the mean-field level, the critical stress σ∗ at which the membrane detaches from the cortex is not affected by membrane undulations because the q = 0 mode is the first one to become unstable in the framework of Eqs. 12–14. Fluctuations of the membrane shape may, however, create regions of locally low linker density and high linker stress, thereby widening the unbinding transition boundary.
Fluctuation spectroscopy
The formulation of an adhesion model accounting for membrane undulations provides an appropriate framework to extract additional information about membrane-cortex adhesion from the statistics of membrane fluctuations. For instance, applying the energy equipartition theorem to Eq. 11 one obtains, under the adiabatic approximation, a membrane structure factor of
| (17) |
where ρb,eq is the equilibrium value of the density of bound linkers (see Section S2.2 of the Supporting Material for details). This result is consistent with the situation of a membrane confined in a harmonic potential (39–41). Here, the confinement contribution explicitly arises from the attachment kinetics of the linkers via the adiabatic approximation. This fact allows us to experimentally determine the density of bound linkers, ρb,eq, from measurements of the static structure factor of the cell membrane (42). Specifically, the long-wavelength limit q → 0 needs to be measured in fluctuation microscopy experiments in order to determine ρb,eq from Eq. 17. Transforming Eq. 17 to real space, the mean-square amplitude of membrane undulations reads (see Section S2.3 of the Supporting Material for details):
| (18) |
Finally, the model in the previous section also provides dynamical information on membrane undulations. Specifically, the power spectral density of membrane fluctuations can be shown to take the form (43,44)
| (19) |
where qmin and qmax are the cutoff values of the wave-vector q. In our model, either the perimeter of the cell, the correlation length of cortex undulations, or the radius of the pipette in the experimental setup proposed in Fig. 3 a sets the large-wavelength cutoff, qmin ∼ 1/R, and the short-wavelength cutoff is set by the spacing of the linkers: qmax = 2π/ρ0−1/2. In fluctuation spectroscopy experiments, the laser focal diameter sets the limitation for the latter (43,44).
Figure 3.
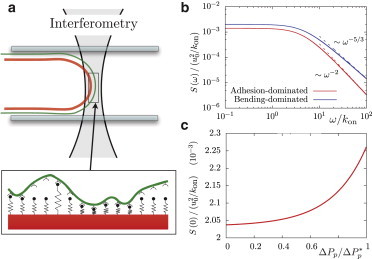
Density of membrane-cortex bonds from fluctuation spectroscopy experiments. (a) Illustration of a combined spectroscopy and micropipette experiment that could probe the density of membrane-cortex bonds. (b) Power spectral density calculated from Eq. 19 in the limit of vanishing surface tension (γ = 0), both for adhesion-dominated and bending-dominated membrane fluctuations. (Dashed lines) Known high-frequency limits. The rescaling length u0 is defined as u0 ≡ kBT/(kδ). Parameters are taken from Table 1, with ρb,eq = ρ0, and the power spectrum is integrated from qmin = 1/R to qmax = 2π/d, with d = 0.5 μm the focal diameter of the optical trap (44). (c) Low-frequency plateau of the power spectrum for adhesion-dominated fluctuations (Eq. 21) as a function of the pressure on the membrane. To see this figure in color, go online.
Membrane-cortex detachment induced by micropipette aspiration is a rather invasive procedure to assess the stability of the membrane-cortex cellular interface. An alternative approach could be to monitor membrane fluctuations for different aspiration pressures using fluctuation spectroscopy, as sketched in Fig. 3 a. Fig. 3 b shows the power spectrum density (Eq. 19) in the limit γ → 0 both for bending-dominated and adhesion-dominated membrane fluctuations. The high-frequency limits were previously obtained:
for λcqmax ≫ 1, and
otherwise (43–45) (see more details in Section S2.4 of the Supporting Material). However, our model gives an analytical expression for the full power spectrum in the adhesion-dominated regime (qmax < [ρb,eqk/κ]1/4):
| (20) |
The density of membrane-cortex bonds ρb,eq can be extracted by fitting this expression to experimental measurements. In particular, if adhesion dominates membrane fluctuations, ρb,eq can be simply obtained from the plateau of the power spectrum at low frequencies:
| (21) |
The value of this plateau is plotted in Fig. 3 c as a function of the pressure on the membrane, ΔP, which modifies the density of bound linkers. Experimentally, the pressure on the membrane can be varied, either decreasing cortical tension by inhibiting myosin activity or via micropipette suction. Hence, we propose combined spectroscopy and micropipette experiments, as illustrated in Fig. 3 a, to test the predictions in Fig. 3 and estimate the density of membrane-cortex bonds. Note that the tip of the aspirated membrane is not flat, but is on average hemispherical with a radius of curvature matching the pipette radius. A rigorous analysis of the fluctuation spectrum should be done using spherical harmonics rather than Fourier transform. Furthermore, Eq. 19 does not account for the hard-wall repulsion introduced by the pipette walls. As discussed in Betz and Sykes (44), this introduces differences in the low frequency limit of the power spectrum. However, this should not affect the pressure dependence of the zero-frequency power spectrum shown in Fig. 3 c. The correction to Eq. 20 due to a finite average membrane curvature can be reduced by increasing the radius of the micropipette, or by tuning myosin activity rather than using a micropipette to modify the average density of bond linkers.
The measurement of the density of membrane-cortex linkers from fluctuation spectroscopy is complementary to the quantitative determination of the cortical activity and adhesion energy from micropipette experiments, as discussed above. Indeed, data on fluctuation spectra of generic eukaryotic cells other than red blood cells are still lacking. Peukes and Betz (46) have recently obtained such spectra in blebs during their growth stage, while the cortex is still reforming and, thus, weak. However, information about the full cortex could only be extracted from experiments probing the fluctuations of strongly adhered membranes instead of blebs. Peukes and Betz (46) analyze the fluctuation spectra as that of isolated membranes, with the effect of the cortex only incorporated into an effective tension of the membrane. In contrast, our model accounts for the effect of the adhesion to the cortex via the kinetics of the linkers, thus providing a theoretical framework in which to consistently interpret fluctuation spectroscopy experiments on strongly adhered cell membranes.
As a final comment, it is worth stressing that, in this article, we have only addressed passive fluctuations of thermal origin. In general, different active processes could potentially modify the presented scenario. Typically, active processes are quantitatively most pronounced at low frequencies. At high enough frequencies it has been shown that the role of active fluctuations can be incorporated through an increased effective temperature of the membrane (39,47,48). A detailed analysis of this point is beyond the scope of this work and is deferred to future work.
Conclusions
We have described a model for membrane-cortex adhesion that relates the unbinding pressure and adhesion energy measured in micropipette experiments to two cellular parameters, the membrane-cortex ligand density and the myosin-driven cortical activity. The validity of the model is qualitatively discussed, although a complete set of experiments will be required for a complete validation. The proposed relationship between unbinding pressure and cortical activity provides a method to measure the cortical activity by means of micropipette aspiration experiments. Accounting for membrane undulations allows us to relate the fluctuation spectrum of the membrane to the density of bound membrane-cortex bonds, thus providing a method for measuring this quantity in fluctuation spectroscopy experiments. Together, these experiments could give access to quantitative information about membrane-cortex adhesion in the framework of our model.
Acknowledgments
R.A. acknowledges support from Fundació “la Caixa”, J.C. acknowledges financial support of the Ministerio de Economa y Competitividad under projects No. FIS2010-21924-C02-02 and No. FIS2013-41144-P and the Generalitat de Catalunya under projects No. 2009 SGR 14 and No. 2009 SGR 878, and P.S. acknowledges support from the Human Frontier Science Program under grant No. RGP0058/2011.
Footnotes
Pierre Sens’s present address is Physico-Chimie Curie, CNRS UMR 168, Institut Curie, 11 rue Pierre et Maris Curie, Paris, France.
Contributor Information
Jan Brugués, Email: brugues@mpi-cbg.de.
Pierre Sens, Email: pierre.sens@curie.fr.
Supporting Material
Supporting Citations
References (49–54) appear in the Supporting Material.
References
- 1.Coleman M.L., Sahai E.A., Olson M.F. Membrane blebbing during apoptosis results from caspase-mediated activation of ROCK I. Nat. Cell Biol. 2001;3:339–345. doi: 10.1038/35070009. [DOI] [PubMed] [Google Scholar]
- 2.Vermeulen K., van Bockstaele D.R., Berneman Z.N. Apoptosis: mechanisms and relevance in cancer. Ann. Hematol. 2005;84:627–639. doi: 10.1007/s00277-005-1065-x. [DOI] [PubMed] [Google Scholar]
- 3.Blaser H., Reichman-Fried M., Raz E. Migration of zebrafish primordial germ cells: a role for myosin contraction and cytoplasmic flow. Dev. Cell. 2006;11:613–627. doi: 10.1016/j.devcel.2006.09.023. [DOI] [PubMed] [Google Scholar]
- 4.Yoshida K., Soldati T. Dissection of amoeboid movement into two mechanically distinct modes. J. Cell Sci. 2006;119:3833–3844. doi: 10.1242/jcs.03152. [DOI] [PubMed] [Google Scholar]
- 5.Fackler O.T., Grosse R. Cell motility through plasma membrane blebbing. J. Cell Biol. 2008;181:879–884. doi: 10.1083/jcb.200802081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Charras G., Paluch E. Blebs lead the way: how to migrate without lamellipodia. Nat. Rev. Mol. Cell Biol. 2008;9:730–736. doi: 10.1038/nrm2453. [DOI] [PubMed] [Google Scholar]
- 7.Sheetz M.P. Cell control by membrane-cytoskeleton adhesion. Nat. Rev. Mol. Cell Biol. 2001;2:392–396. doi: 10.1038/35073095. [DOI] [PubMed] [Google Scholar]
- 8.Tsujioka M., Yumura S., Yonemura S. Talin couples the actomyosin cortex to the plasma membrane during rear retraction and cytokinesis. Proc. Natl. Acad. Sci. USA. 2012;109:12992–12997. doi: 10.1073/pnas.1208296109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tsukita S., Yonemura S. Cortical actin organization: lessons from ERM (ezrin/radixin/moesin) proteins. J. Biol. Chem. 1999;274:34507–34510. doi: 10.1074/jbc.274.49.34507. [DOI] [PubMed] [Google Scholar]
- 10.Charras G.T., Coughlin M., Mahadevan L. Life and times of a cellular bleb. Biophys. J. 2008;94:1836–1853. doi: 10.1529/biophysj.107.113605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tinevez J.-Y., Schulze U., Paluch E. Role of cortical tension in bleb growth. Proc. Natl. Acad. Sci. USA. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rentsch P.S., Keller H. Suction pressure can induce uncoupling of the plasma membrane from cortical actin. Eur. J. Cell Biol. 2000;79:975–981. doi: 10.1078/0171-9335-00124. [DOI] [PubMed] [Google Scholar]
- 13.Seifert U. Rupture of multiple parallel molecular bonds under dynamic loading. Phys. Rev. Lett. 2000;84:2750–2753. doi: 10.1103/PhysRevLett.84.2750. [DOI] [PubMed] [Google Scholar]
- 14.Erdmann T., Schwarz U.S. Stability of adhesion clusters under constant force. Phys. Rev. Lett. 2004;92:108102. doi: 10.1103/PhysRevLett.92.108102. [DOI] [PubMed] [Google Scholar]
- 15.Erdmann T., Pierrat S., Schwarz U.S. Dynamic force spectroscopy on multiple bonds: experiments and model. Europhys. Lett. 2008;81:48001. [Google Scholar]
- 16.Brugués J., Maugis B., Sens P. Dynamical organization of the cytoskeletal cortex probed by micropipette aspiration. Proc. Natl. Acad. Sci. USA. 2010;107:15415–15420. doi: 10.1073/pnas.0913669107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Evans E. Probing the relation between force—lifetime—and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 2001;30:105–128. doi: 10.1146/annurev.biophys.30.1.105. [DOI] [PubMed] [Google Scholar]
- 18.Rózycki B., Lipowsky R., Weikl T.R. Adhesion of membranes with active stickers. Phys. Rev. Lett. 2006;96:048101. doi: 10.1103/PhysRevLett.96.048101. [DOI] [PubMed] [Google Scholar]
- 19.Reister-Gottfried E., Sengupta K., Smith A.-S. Dynamics of specific vesicle-substrate adhesion: from local events to global dynamics. Phys. Rev. Lett. 2008;101:208103. doi: 10.1103/PhysRevLett.101.208103. [DOI] [PubMed] [Google Scholar]
- 20.Krobath H., Różycki B., Weikl T.R. Binding cooperativity of membrane adhesion receptors. Soft Matter. 2009;5:3354. [Google Scholar]
- 21.Weikl T.R., Asfaw M., Lipowsky R. Adhesion of membranes via receptor-ligand complexes: domain formation, binding cooperativity, and active processes. Soft Matter. 2009;5:3213. [Google Scholar]
- 22.Reister E., Bihr T., Smith A.-S. Two intertwined facets of adherent membranes: membrane roughness and correlations between ligand-receptors bonds. New J. Phys. 2011;13:025003. [Google Scholar]
- 23.Hu J., Lipowsky R., Weikl T.R. Binding constants of membrane-anchored receptors and ligands depend strongly on the nanoscale roughness of membranes. Proc. Natl. Acad. Sci. USA. 2013;110:15283–15288. doi: 10.1073/pnas.1305766110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bovellan M., Romeo Y., Charras G. Cellular control of cortical actin nucleation. Curr. Biol. 2014;24:1628–1635. doi: 10.1016/j.cub.2014.05.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kramers H. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 26.Rognoni L., Stigler J., Rief M. Dynamic force sensing of filamin revealed in single-molecule experiments. Proc. Natl. Acad. Sci. USA. 2012;109:19679–19684. doi: 10.1073/pnas.1211274109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dai J., Ting-Beall H.P., Titus M.A. Myosin I contributes to the generation of resting cortical tension. Biophys. J. 1999;77:1168–1176. doi: 10.1016/s0006-3495(99)76968-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Merkel R., Simson R., Sackmann E. A micromechanic study of cell polarity and plasma membrane cell body coupling in Dictyostelium. Biophys. J. 2000;79:707–719. doi: 10.1016/S0006-3495(00)76329-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Campillo C., Jerber J., Sykes C. Mechanics of membrane-cytoskeleton attachment in Paramecium. New J. Phys. 2012;14:125016. [Google Scholar]
- 30.Dai J., Sheetz M.P. Membrane tether formation from blebbing cells. Biophys. J. 1999;77:3363–3370. doi: 10.1016/S0006-3495(99)77168-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Diz-Muñoz A., Krieg M., Heisenberg C.-P. Control of directed cell migration in vivo by membrane-to-cortex attachment. PLoS Biol. 2010;8:e1000544. doi: 10.1371/journal.pbio.1000544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Borghi N., Brochard-Wyart F. Tether extrusion from red blood cells: integral proteins unbinding from cytoskeleton. Biophys. J. 2007;93:1369–1379. doi: 10.1529/biophysj.106.087908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schumacher K.R., Popel A.S., Spector A.A. Computational analysis of the tether-pulling experiment to probe plasma membrane-cytoskeleton interaction in cells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:041905. doi: 10.1103/PhysRevE.80.041905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zatulovskiy E., Tyson R., Kay R.R. Bleb-driven chemotaxis of Dictyostelium cells. J. Cell Biol. 2014;204:1027–1044. doi: 10.1083/jcb.201306147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Boal D. Cambridge University Press; Cambridge, UK: 2002. Mechanics of the Cell. [Google Scholar]
- 36.Gov N., Zilman A.G., Safran S. Hydrodynamics of confined membranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:011104. doi: 10.1103/PhysRevE.70.011104. [DOI] [PubMed] [Google Scholar]
- 37.Strychalski W., Guy R.D. A computational model of bleb formation. Math. Med. Biol. 2013;30:115–130. doi: 10.1093/imammb/dqr030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Seifert U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997;46:13–137. [Google Scholar]
- 39.Gov N., Zilman A.G., Safran S. Cytoskeleton confinement and tension of red blood cell membranes. Phys. Rev. Lett. 2003;90:228101. doi: 10.1103/PhysRevLett.90.228101. [DOI] [PubMed] [Google Scholar]
- 40.Fournier J.-B., Lacoste D., Raphaël E. Fluctuation spectrum of fluid membranes coupled to an elastic meshwork: jump of the effective surface tension at the mesh size. Phys. Rev. Lett. 2004;92:018102. doi: 10.1103/PhysRevLett.92.018102. [DOI] [PubMed] [Google Scholar]
- 41.Merath R.-J., Seifert U. Nonmonotonic fluctuation spectra of membranes pinned or tethered discretely to a substrate. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;73:010401. doi: 10.1103/PhysRevE.73.010401. [DOI] [PubMed] [Google Scholar]
- 42.Popescu G., Ikeda T., Feld M.S. Optical measurement of cell membrane tension. Phys. Rev. Lett. 2006;97:218101. doi: 10.1103/PhysRevLett.97.218101. [DOI] [PubMed] [Google Scholar]
- 43.Betz T., Lenz M., Sykes C. ATP-dependent mechanics of red blood cells. Proc. Natl. Acad. Sci. USA. 2009;106:15320–15325. doi: 10.1073/pnas.0904614106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Betz T., Sykes C. Time resolved membrane fluctuation spectroscopy. Soft Matter. 2012;8:5317. [Google Scholar]
- 45.Helfer E., Harlepp S., Chatenay D. Viscoelastic properties of actin-coated membranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;63:021904. doi: 10.1103/PhysRevE.63.021904. [DOI] [PubMed] [Google Scholar]
- 46.Peukes J., Betz T. Direct measurement of the cortical tension during the growth of membrane blebs. Biophys. J. 2014;107:1810–1820. doi: 10.1016/j.bpj.2014.07.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Manneville J.-B., Bassereau P., Prost J. Activity of transmembrane proteins induces magnification of shape fluctuations of lipid membranes. Phys. Rev. Lett. 1999;82:4356–4359. [Google Scholar]
- 48.Manneville J.-B., Bassereau P., Prost J. Active membrane fluctuations studied by micropipet aspiration. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;64:021908. doi: 10.1103/PhysRevE.64.021908. [DOI] [PubMed] [Google Scholar]
- 49.Guyon E., Hulin J.-P., Mitescu C.D. Oxford University Press; New York: 2001. Physical Hydrodynamics. [Google Scholar]
- 50.Lin L.C., Brown F.L. Dynamic simulations of membranes with cytoskeletal interactions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:011910. doi: 10.1103/PhysRevE.72.011910. [DOI] [PubMed] [Google Scholar]
- 51.de Gennes P.G., Taupin C. Microemulsions and the flexibility of oil/water interfaces. J. Phys. Chem. 1982;86:2294–2304. [Google Scholar]
- 52.Gov N., Safran S.A. Pinning of fluid membranes by periodic harmonic potentials. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;69:011101. doi: 10.1103/PhysRevE.69.011101. [DOI] [PubMed] [Google Scholar]
- 53.Safran S.A. Addison-Wesley; Boston, MA: 1994. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. [Google Scholar]
- 54.Ranft J., Prost J., Joanny J.-F. Tissue dynamics with permeation. Eur. Phys. J. E Soft Matter. 2012;35:46. doi: 10.1140/epje/i2012-12046-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


