Abstract
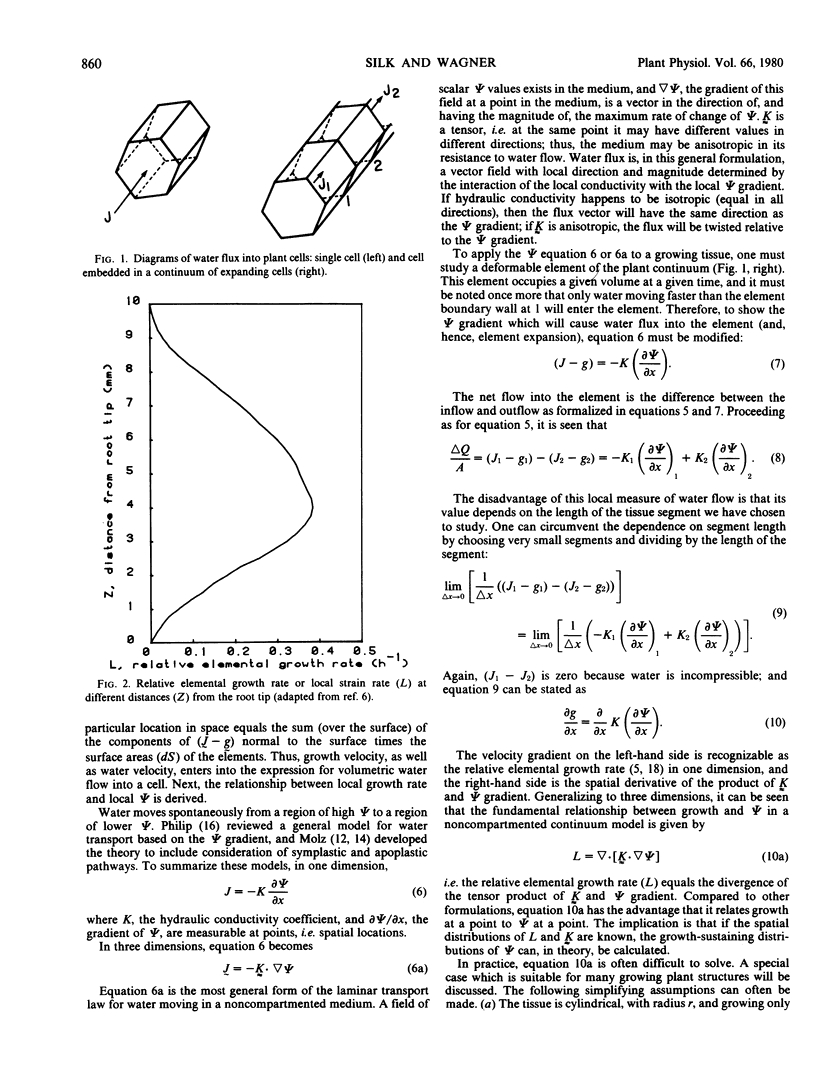
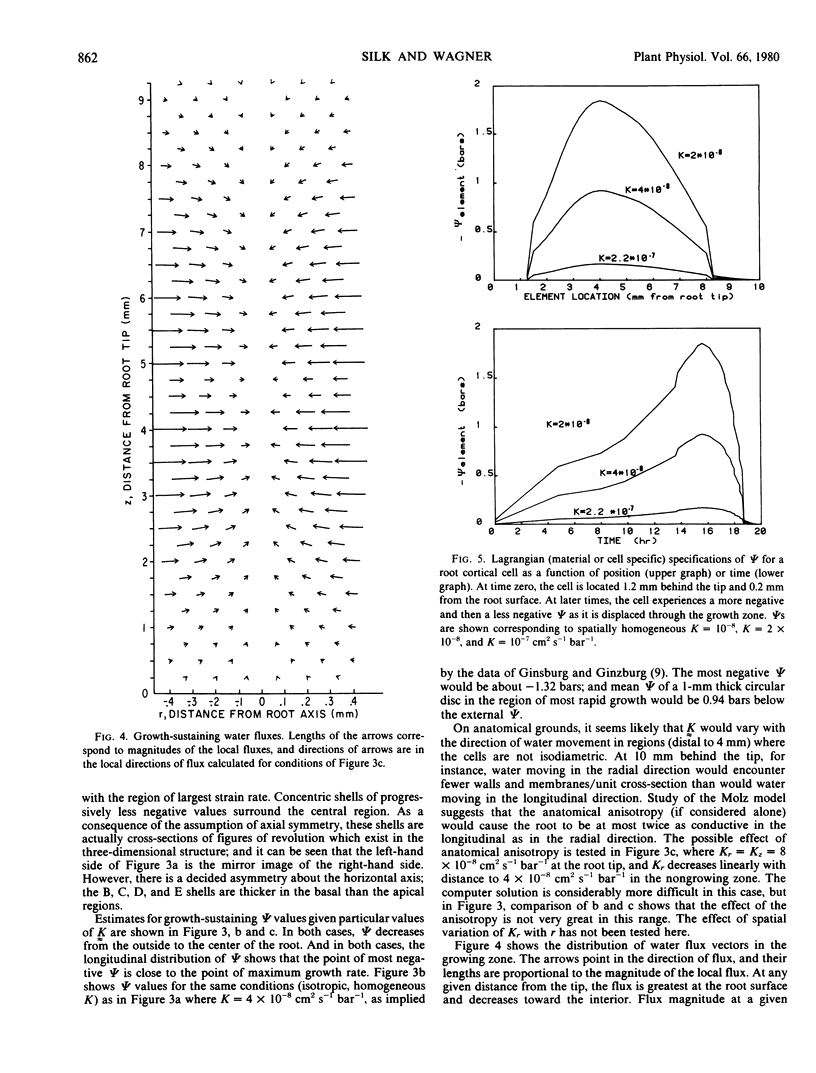
An equation is derived from transport theory to relate local growth rate to local water potential in an expanding tissue. For a noncompartmented continuum model, the relative elemental growth rate (L) equals the divergence of the tensor product of hydraulic conductivity (K̰) and the gradient of water potential, ψ, i.e. L = ▽ • [K̰ · ▽ ψ]. This equation is solved numerically using published values of L and K̰ to show the water potential distribution which can sustain the observed growth pattern in the primary root of Zea mays L. The water potential required to sustain growth decreases from the outside to the inside of the root, and the longitudinal profile shows most negative values near the location of the highest growth rate. A cell originally located near the apex experiences a loss and then a gain in water potential as it is displaced through the growth zone.
The approach differs from previous formulations in two respects: the assumption of spatial heterogeneity in growth rate, and the solution for spatial (site-specific) rather than material (cell-specific) values of water potential. The role of air spaces and of components (wall and possibly cytoplasm) of the water-conducting pathway which do not accumulate water remains to be clarified; and, as in earlier work, the most uncertain aspects of the analysis are probably the values for hydraulic conductivity.
Full text
PDF


Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- ERICKSON R. O., GODDARD D. R. An analysis of root growth in cellular and biochemical terms. Growth. 1951;(Suppl 10):89–116. [PubMed] [Google Scholar]
- Fiscus E. L., Kramer P. J. General model for osmotic and pressure-induced flow in plant roots. Proc Natl Acad Sci U S A. 1975 Aug;72(8):3114–3118. doi: 10.1073/pnas.72.8.3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hüsken D., Steudle E., Zimmermann U. Pressure probe technique for measuring water relations of cells in higher plants. Plant Physiol. 1978 Feb;61(2):158–163. doi: 10.1104/pp.61.2.158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molz F. J. Growth-induced Water Potentials in Plant Cells and Tissues. Plant Physiol. 1978 Sep;62(3):423–429. doi: 10.1104/pp.62.3.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molz F. J. Water transport through plant tissue: the apoplasm and symplasm pathways. J Theor Biol. 1976 Jul 7;59(2):277–292. doi: 10.1016/0022-5193(76)90170-3. [DOI] [PubMed] [Google Scholar]
- Philip J. R. Propagation of Turgor and Other Properties Through Cell Aggregations. Plant Physiol. 1958 Jul;33(4):271–274. doi: 10.1104/pp.33.4.271. [DOI] [PMC free article] [PubMed] [Google Scholar]



