Abstract
Motivation: Alignment-based sequence similarity searches, while accurate for some type of sequences, can produce incorrect results when used on more divergent but functionally related sequences that have undergone the sequence rearrangements observed in many bacterial and viral genomes. Here, we propose a classification model that exploits the complementary nature of alignment-based and alignment-free similarity measures with the aim to improve the accuracy with which DNA and protein sequences are characterized.
Results: Our model classifies sequences using a combined sequence similarity score calculated by adaptively weighting the contribution of different sequence similarity measures. Weights are determined independently for each sequence in the test set and reflect the discriminatory ability of individual similarity measures in the training set. Because the similarity between some sequences is determined more accurately with one type of measure rather than another, our classifier allows different sets of weights to be associated with different sequences. Using five different similarity measures, we show that our model significantly improves the classification accuracy over the current composition- and alignment-based models, when predicting the taxonomic lineage for both short viral sequence fragments and complete viral sequences. We also show that our model can be used effectively for the classification of reads from a real metagenome dataset as well as protein sequences.
Availability and implementation: All the datasets and the code used in this study are freely available at https://collaborators.oicr.on.ca/vferretti/borozan_csss/csss.html.
Contact: ivan.borozan@gmail.com
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Sequence comparison of genetic material between known and unknown organisms plays a crucial role in metagenomic and phylogenetic analysis. Sequence similarity search is a method of sequence analysis that is extensively used for characterizing unannotated sequences (Altschul et al., 1997). It consists of aligning a query sequence to a sequence database with the aim of determining those sequences that have statistically significant matches to that of the query. In this way, for example, a known biological function or taxonomic category of the closest match can be assigned to the query for its characterization.
Alignment-based methods, however, can produce incorrect results when applied to more divergent but functionally related sequences that have undergone sequence rearrangements. Sequence rearrangements such as genetic recombination and shuffling or horizontal gene transfer are observed in a variety of organisms including viruses and bacteria (Delviks-Frankenberry et al., 2011; Domazet-Loo and Haubold, 2011; Shackelton and Holmes, 2004). These processes, which produce alternating blocks of sequence material, are at odds with the alignment-based sequence comparison, which assumes conservation of contiguity between homologous segments (Vinga and Almeida, 2003). Another weakness of the alignment-based approach is in the use of different methods for scoring pairwise protein sequence alignments, as reported in Vinga and Almeida (2003).
In addition to sequence rearrangements, viral genomes exhibit gene gain and loss, gene duplication and high sequence mutation rates (Duffy et al., 2008; Shackelton and Holmes, 2004). The cumulative effect of these changes make viral genomes among the most variable in nature. Because of this high sequence divergence and the often small number of genes, viral genomes present a greater challenge to phylogenetic classification and taxonomic analysis when these are based on sequence comparison by alignment only. Improving the results of such studies is important for better understanding viruses and their involvement in human diseases, including cancer (zur Hausen, 2007).
Because of these shortcomings, active research has been conducted into alignment-free measures to overcome the above limitations. A number of alignment-free measures have been proposed in recent years as reported in two comprehensive reviews (Vinga, 2014; Vinga and Almeida, 2003).
In this study, we propose a new classification model that combines similarity scores obtained from alignment-free and alignment-based similarity measures with the aim to exploit the complementary nature of these measures to improve the classification accuracy. In our model, the classification of sequences is performed by using a combined sequence similarity score (CSSS) that is calculated based on the weighted contribution of similarity scores, where weights reflect the discriminatory ability of individual measures in the training set. One unique feature of our model is based on the observation that the similarity between some sequences is determined more accurately with one type of similarity measure rather than another, hence in our model, different sets of weights can be associated with different sequences (i.e. sequences to be classified). Furthermore, we provide a mathematical framework that can include any number of additional similarity measures and show that our model (i) is applicable to both nucleotide and amino acid sequences (ii) improves the classification accuracy over a purely alignment-based sequence comparison approach and (iii) improves the classification accuracy for metagenomic analysis of short reads produced by next-generation sequencing technologies.
Recently, a number of methods for metagenomic analysis have been proposed (Brady and Salzberg, 2009; Huson and Xie, 2014; Huson et al., 2007; Nalbantoglu et al., 2011; Patil et al., 2011; Rosen et al., 2011; Wood and Salzberg, 2014). Of these seven methods, PhymmBL (Brady and Salzberg, 2009) is the method closest in approach to the method presented in this study, since it classifies reads (or contigs) using an integrated score obtained by combining the interpolated Markov models (IMM) score (an alignment-free/composition-based similarity measure) with the BLAST (Altschul et al., 1997) score. PhymmBL (Brady and Salzberg, 2009) has been shown to outperform MEGAN (Huson et al., 2007) for longer contigs, while for shorter ones, the results of comparison are misleading at best since MEGAN produces results in a form that cannot be directly compared to those of PhymmBL (Brady and Salzberg, 2009, 2011) and the model proposed in this study. We believe that improving the classification accuracy for shorter reads (100–1000 bp) is critical, since such metagenomic analysis does not require the assembly of raw sequenced reads prior to classification. For these reasons and to address the objective (iii) in the previous paragraph, we chose to compare the classification results obtained with the model presented in this study to four primarily composition-based models [PhymmBL (Brady and Salzberg, 2009), NBC (Rosen et al., 2011), PhyloPythiaS (Patil et al., 2011) and RAIphy (Nalbantoglu et al., 2011)] and the two most recently published methods for the classification of metagenomic sequences, Kraken (Wood and Salzberg, 2014) based on the exact alignment of k-mers and PAUDA (Huson and Xie, 2014) an alignment-based method.
2 Materials and Methods
2.1 Sequence similarity measures
In this section, we describe the five sequence similarity measures that we chose to use in our classification model. Three of them are alignment-free sequence similarity measures and two of them are alignment-based sequence similarity measures.
2.1.1 Alignment-free sequence similarity measures
The choice of the three alignment-free sequence similarity measures (see below) is based on the notion of complementarity between these measures and the two alignment-based similarity measures that we chose to use in this study. Specifically, similarity measures based on k-mer frequencies [the Euclidean Distance (ED) and Jensen–Shannon divergence (JSD)] do not depend on any assumption of the contiguity of conserved segments, as the alignment-based measures do. They do, however, depend on the choice of the k-mer size (Wu et al., 2005). In contrast, the compression-based (CB) measure (Li et al., 2001) built upon the concept of Kolmogorov complexity is both independent of the k-mer size (since it is not based on k-mer counts) and the assumption of the contiguity of conserved segments.
The ED and JSD measures both require the number of all possible k-mers to be counted for any given sequence, where n is the alphabet size (i.e. n = 4 for DNA sequences and n = 20 for protein sequences) and k is the length of the k-mer sequence. To count the number of k-mers in DNA sequences, we use the JELLYFISH (Marais and Kingsford, 2011) algorithm and for protein sequences, we use a Python script from Gupta et al. (2008). The raw counts are used to form a vector of all possible k-mers of length k,
| (1) |
raw counts in Equation (1) are then normalized to form a probability distribution vector
| (2) |
giving the relative abundance of each k-mer.
1. The ED
The similarity score between two sequences X and Y is the ED between their nk dimensional probability distribution vectors and as defined in Equation (3)
| (3) |
| (4) |
where Equation (4) ensures that each vector is normalized and has length 1 in the nk dimensional space. The choice for this metric is based on its simplicity, well defined mathematical properties and its demonstrated effectiveness as an alternative to the alignment method (Vinga and Almeida, 2003). The ED defined in Equation (3) has values that range between 0 and 1, with lower values indicating increasing similarity and higher values decreasing similarity.
2. The JSD
This is an information theoretic non-symmetric divergence measure of two probability distributions. The JSD between two sequences X and Y is calculated between their nk dimensional probability distribution vectors and as shown below
| (5) |
where Mi = , i = and KL is the Kullback–Leibler divergence defined below
| (6) |
Provided that the base 2 logarithm is used in Equation (6), JSD has values that range between 0 and 1, with lower values indicating increasing similarity and higher values decreasing similarity. The choice for this similarity measure is based on its ability to successfully reconstruct phylogenies using whole-genome sequences as reported in Sims et al. (2009).
3. The CB measure
This similarity measure is based on the concept of Kolmogorov complexity. Conditional Kolmogorov complexity (or algorithmic entropy) of sequence X given sequence Y is defined as the length of the shortest program computing X on input Y. In this way, measures the randomness of X given Y. The Kolmogorov complexity K(X) of a sequence X is defined as where e is an empty string. We note that Kolmogorov complexity K(X) of a sequence X is non-computable and that in practice K(X) is approximated by the length of the compressed sequence X, obtained using compression algorithms such as Lempel-Ziv-Markov chain algorithm (LZMA) or GenCompress (Chen et al., 1999). Our choice for this measure is based on the following two properties (i) CB is not affected by sequence rearrangements and (ii) since CB is not a frequency-based measure, it is not affected by the choice of the k-mer size. To calculate the CB distance between two sequences X and Y, we chose to use the normalized compression distance (NCD) (Cilibrasi and Vitányi, 2005) as defined below:
| (7) |
where
| (8) |
where denotes the length of a compressed sequence using a particular compression algorithm and where XY denotes the concatenation of sequence X with sequence Y. Note that the NCD in Equation (8) is an empirical approximation of the normalized information distance, which is defined as a metric in Cilibrasi and Vitányi (2005). The distance calculated using Equation (7) takes values between 0 and 1, with lower values indicating increasing sequence similarity and higher values decreasing sequence similarity. The compression algorithm used in this study is plzip (http://www.nongnu.org/lzip/plzip.html) a multi-threaded, lossless data compressor based on the lzlib compression library that implements a simplified version of the LZMA algorithm. All sequences in this study were compressed using plzip with the compression level parameter set to 4, with matched length and dictionary size set to their default values.
2.1.2 Alignment-based sequence similarity measures
4. The BLAST-based measure
For the classification of DNA sequences, the distance between the query sequence X and subject Y is expressed in terms of the BLAST bit scores calculated using the BLAST algorithm (Altschul et al., 1997) (blastall version 2.2.18, blastall -p blastn), with default parameter value settings.
5. The Smith–Waterman (SW)-based measure
For the classification of protein sequences, similarity scores expressed in terms of P values calculated using the SW algorithm were taken from Liao and Noble (2003).
2.2 Classification model
As mentioned in Section 1, we propose to exploit the complementary properties of the five individual similarity measures described above to improve the accuracy with which nucleotide or amino acid sequences are characterized. Our aim is to propose a CSSS that will improve upon the limitations of the individual sequence similarity scores (as described in Section 1) and lead to an improved classification performance.
The CSSS model rests on three assumptions (i) that similarity measures are complementary in nature (as described in the previous section), (ii) that some sequences are better characterized with one type of similarity measure than another and (iii) that their individual values are in the range between 0 and 1.
Among many machine learning algorithms that are available today, the nearest neighbour (NN) algorithm is one of the simplest and most intuitive classification algorithms. For this reason, the NN algorithm is often used as the reference classifier in comparative studies. The k-NN algorithm performs the classification by identifying the k-NNs that are the closest in terms of a distance/similarity measure to a query (or test sample). It then assigns to the query the class that occurs the most often among the k-NNs. In the case where k = 1, the query is assigned the class of the closest single NN. Because of these properties, we find the 1-NN algorithm to be a natural choice for the classifier in our approach, as described below.
Let = < > be an n dimensional vector of sequence similarities/distance scores between the sequence X in the test set and the ith sequence in the training set, calculated using jth sequence similarity measure.
For each sequence X in the test set, we can now define the n dimensional vector of combined sequence similarity/distance scores, to be the linear combination of vectors across j = similarity measures as shown below
| (9) |
where wj is the weight of the jth sequence similarity measure calculated as the ratio of the between group variability () to the within group variability () (i.e. the F-test statistics) for each vector as shown in Equation (10).
| (10) |
Note that the combination of scores obtained using different similarity measures shown in Equation (9) is performed independently for each sequence X in the test set.
The between group variability in Equation (10) is defined as
| (11) |
where CL denotes the total number of classes (or groups) in the training set, denotes the mean of similarity/distance scores in the clth class for the measure j, and ncl is the number of observations (or similarity/distance scores) in the clth class.
The within group variability in Equation (10) is defined as
| (12) |
where is the lth similarity/distance score in the clth out of CL classes of for the measure j and N is the total number of sequences (or samples) in the training set.
Thus, if X represents an unknown sequence in the test set, the k-NN algorithm will find the k nearest examples in the n dimensional vector = < >, where n is the total number of examples with known labels in the training set and is the combined similarity/distance score between the sequence X in the test set and the ith sequence in the training set.
Prior to combining alignment-based scores (such as the ones obtained with SW or BLAST algorithms) with those obtained using alignment-free similarity measures, the n dimensional vector of sequence similarities/distance scores = < >, is first transformed into normalized scores as shown in Equations (13) and (14), so that their values range between 0 and 1,
| (13) |
| (14) |
with lower values indicating increasing sequence similarity and higher values decreasing sequence similarity.
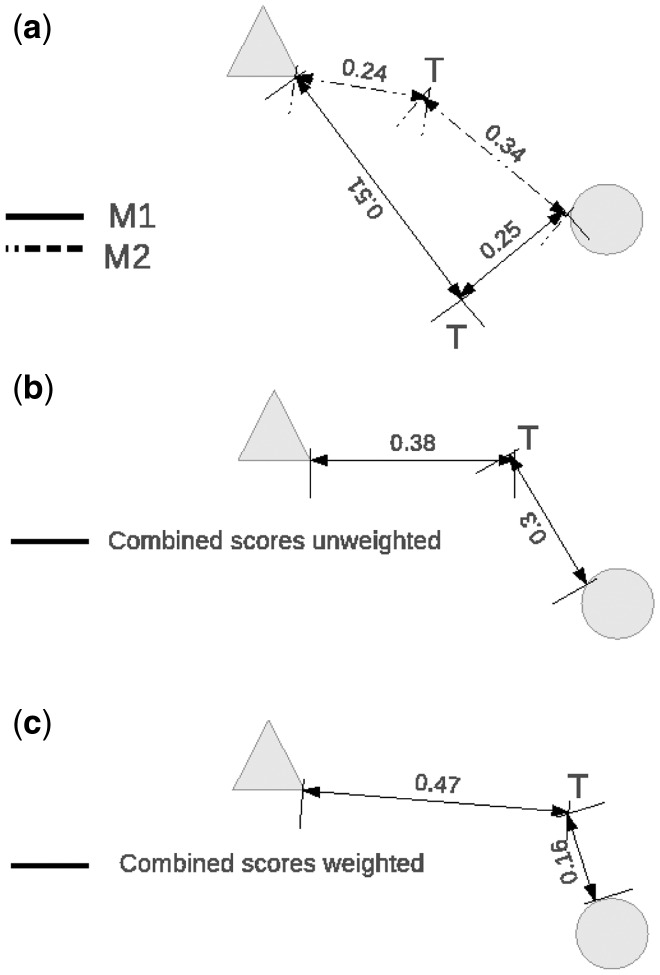
In Figure 1, we illustrate how the combination of sequence similarity scores proposed in this study, and a 1-NN classifier can improve the classification accuracy of a given test sample. Let M1 and M2 be two similarity measures, and T a test sample that can be assigned either one of the two classes in the training set (either a ‘circle’ or a ‘triangle’) based on a single NN closest in distance to T. Let also assume that T is known to belong to the class ‘circle’. As shown in Figure 1a, according to the M1 measure, the test sample T is assigned the correct class (i.e. ‘circle’), while according to the M2 measure T is assigned the incorrect class (i.e. a ‘triangle’). In Figure 1b, we show how by doing a simple arithmetic mean of distances/scores (i.e. M1 and M2 have same weights) the bias of M2 can be corrected by the M1 measure. Moreover, in Figure 1c, we show how a properly weighted arithmetic mean (in this example, M1 was assigned a weight of 10 and M2 a weight of 2) can even further improve the classification accuracy of T. We also see from this simple example that 1-NN is the simplest and the most intuitive choice for the classifier for our model since its assigns T to the class based on the single nearest (in terms of a distance) neighbour in the training set.
Fig. 1.
A graphical representation of how the CSSS model can improve the classification accuracy of a given test sample. M1 and M2 are two similarity measures and T is a test sample that can be assigned either a class ‘circle’ or a class ‘triangle’ that are present in the training set. In (a) according to M1, T is assigned the correct class (i.e. ‘circle’), whereas according to M2, T is assigned the incorrect class (i.e. a ‘triangle’). In (b), we show the classification according to the combined unweighted score. In (c), we show the classification according to the combined weighted score
In Section 3, we demonstrate how the choice of different measures (see the previous section) and the weighting scheme proposed in Equation (10) leads to an improved classification accuracy on the three different datasets used in this study.
2.2.1 Selection of similarity measures prior to classification
To remove similarity measures from Equation (9) with low predictive power (for more details see Section 4) the selection of similarity measure prior to classification of test samples is performed as follows:
The training set is split into two sets, set A and set B, using 2/3, 1/3 splits.
The classification performance of each similarity measure is evaluated on the set B using set A as the training set.
Only similarity measures with prediction accuracy greater or equal to 10% are selected.
2.2.2 Selection of the k-mer size
The k-mer size necessary to calculate similarity measures in Equations (3) and (5) is a free parameter in our model and its upper bound needs to satisfy the inequality given in Equation (15)
| (15) |
where n is the alphabet size and L is the length of the smallest genome in either the training or test sets. The inequality in Equation (15) avoids calculations with k-mer sizes that are so large they produce erroneous and artificial differences between genomes that ultimately correlate with genome lengths rather than genome content as described in Akhter et al. (2013). Thus to compare genomes (or protein sequences) based on similarity measures [see Equations (3) and (5)] that use frequency distribution vectors [see Equation (2)] the k-mer size should be chosen in such a way to satisfy the inequality shown in Equation (15).
2.3 Datasets
We evaluate the ability of our model to classify different types of biological sequences using three datasets, one containing viral nucleotide sequences, a second consisting of longueur nucleotide reads (with an average of 759 bp in length) from a real metagenome and a third consisting of protein sequences.
2.3.1 Dataset I
Because of their considerable variability, viral genomes are expected to pose a greater challenge to phylogenetic classification than genomes from other organisms. In this regard, we evaluate the classification performance of the CSSS model using a dataset composed of 1066 complete viral genomes downloaded from the NCBI RefSeq database. The classification of viral genomes into genera was performed in three steps:
Step 1: the 1066 viral sequences across 147 different genera were divided into training and test sets in such a way that for each genus the test set consisted of viral genomes that were not represented in the training set. The relative sizes of the training and test sets were respectively set to 3/4 and 1/4.
Step 2: selection of similarity measures prior to the classification of test examples selected in step 1 was performed as described in Section 2 (see Section 2.2.1) using the training set from step 1
Step 3: Prediction of viral genera in the test set selected in step 1 is performed using the training set selected in step 1 and CSSSs calculated using the formula shown in Equation (9) with similarity measures selected in step 2. Note that the training set in this step consists only of complete viral genomes.
The complete evaluation of the classification performance was carried out using test samples generated in step 1 composed of complete viral genomes and viral sequence fragments of 1000 bp, 500 bp and 100 bp in length, viral fragments were sampled at random from each complete viral genome in the test set obtained in step 1. Note that for viral fragments the set B in step 2 (see also Section 2.2.1) contains sequences that are of the same fragment length as those in the test set of step 1. To evaluate the variability of results, training and test sets were sampled randomly from the entire dataset (see step 1), 10 times.
2.3.2 Dataset II
Next-generation sequencing promises to expand the scope of metagenomic projects by significantly increasing the number of organisms that can be sequenced from any given sample. One challenge for metagenomic analysis is the accuracy with which short reads are classified into groups representing the same or similar taxa. Improving the classification accuracy in such studies should lead to more reliable estimates of biological diversity in sequenced sample. For this reason, we evaluate the ability of our model to classify reads using a real Acid Mine Drainage metagenome (Tyson et al., 2004). This dataset is known to contain three dominant populations; the archaeon Ferroplasma acidarmanus and two groups of bacteria, Leptospirillum sp. groups II and III. Reads that aligned with high confidence to draft genomes of these three micro-organisms were first identified using the MUMmer algorithm (Delcher et al., 2003) (with the minimum length of a match set to 70% of the full read length). A total of 20 907 of these reads were found (with an average of 759 bp in length), of these 18 579 aligned to Leptospirillum sp. groups II and III genomes and 2328 to the Ferroplasma acidarmanus genome. The classification performance was evaluated at the phylum level using a training set composed of complete bacterial and archaeal genomes across 15 different phyla and 86 sequences downloaded from the NCBI RefSeq database. The 15 phyla include both the Euryarchaeota and Nitrospirae phyla to which Ferroplasma acidarmanus and Leptospirillum sp. groups II and III belong to. The three draft reference genomes were not used as part of the training set. Selection of similarity measures prior to classification of the test examples was conducted as described in Section 2 (see Section 2.2.1). Set A in this case consisted of complete bacterial and archaeal genomes as described above, while set B consisted of sequences of 1000 bp in length that were sampled at random from complete bacterial and archaeal genomes in the training set in such a way that for each phylum, set B consisted of genomes that were not present in set A.
2.3.3 Dataset III
One of the objectives of protein sequence analysis is the inference of structure or function of unannotated protein sequences encoded in the genome. We test the ability of the CSSS model to correctly classify previously unseen protein families drawn from the Structural Classification of Proteins database (Murzin et al., 1995). The protein dataset consists of 4352 distinct protein sequences (ranging from 20 to 994 amino acids in length) grouped into 54 families and 23 superfamilies (Liao and Noble, 2003). The protein sequences of the 54 families were divided into test and training sets in such a way that proteins within the family are considered positive test examples while proteins outside the family but within the same superfamily are considered as a positive training examples (Liao and Noble, 2003). We note that the original dataset includes negative examples, which we did not use in our evaluation. Selection of similarity measures prior to classification of the test examples was conducted as described in Section 2. In this case, the training set consisted of 1779 proteins belonging to the positive training examples, which were then split into set A and set B as described in Section 2 (see Section 2.2.1).
3 Results
The evaluation of the classification performance on Datasets I and II was carried out using the accuracy classification score defined in Equation (16) shown below,
| (16) |
where is the predicted value of the ith sample, yi is the corresponding true value, nts is the total number of test samples and 1(x) is the indicator function having a value of 1 when and 0 when .
As explained in Section 1, we decided to compare the results obtained in this study on Datasets I and II to six other composition- and alignment-based models that were developed for the classification of metagenomic data with reads (or fragments) as short as 100 bp in length. Of these six models, PhymmBL (Brady and Salzberg, 2009) is the method closest in approach to ours since it combines scores from IMMs with those of BLAST resulting in a combined score that achieves higher accuracy than BLAST scores alone.
3.1 Dataset I—Taxonomic classification of viral sequences
We evaluate the classification performance of the CSSS model [see Equation (9)] by predicting genera of viral DNA sequences in Dataset I (see Section 2). The training and test sets are generated as described in Section 2—Dataset I. The classification of test examples is then performed using the NN algorithm (1-NN) with the CSSSs calculated as given in Equation (9). For this dataset, the combined score in Equation (9) is calculated based on scores obtained with the three alignment-free measures [see Section 2, Equations (3, 5 and 7)] and the normalized BLAST score [see Equation (13)]. The value for the k-mer size is varied between 2 and 5, and the classification performance of the individual similarity measures is determined for each training and test sets as described in Dataset I, step 2 (see Section 2). The optimum value for the k-mer size is then selected based on the following two conditions (i) best classification performance and (ii) k-mer size has to satisfy the inequality given in Equation (15). Note that the optimum k-mer sizes were estimated separately for complete viral genomes and for each of the three different viral fragment lengths (see Section 2.3.1).
In Table 1, we compare the classification performance of the CSSS model to five other models, PAUDA (Huson and Xie, 2014), NBC (Rosen et al., 2011), Kraken (Wood and Salzberg, 2014), PhymmBL (Brady and Salzberg, 2009) and RAIphy (Nalbantoglu et al., 2011). We note that for this dataset, we could not compare the results obtained with the CSSS model to those of PhyloPythiaS (Patil et al., 2011) for two reasons (i) PhyloPythiaS requires at-least 100 kb of sequence for each genus and (ii) our training set, composed of 147 different genera, exceeds the file limit size of 10 MB imposed by the PhyloPythiaS web server. We also note that PhymmBL has been shown to perform better (see Brady and Salzberg, 2011) for shorter read lengths (100–800 bp) than both PhyloPythiaS and RAIphy. The results presented in Table 1 were obtained using identical training and test sets.
Table 1.
The classification accuracy [see Equation (16)] for Dataset I obtained with the CSSS (1-NN classifier) and the five other models: PhymmBL (Brady and Salzberg, 2009), NBC (Rosen et al., 2011), Kraken (Wood and Salzberg, 2014), RAIphy (Nalbantoglu et al., 2011) and PAUDA (Huson and Xie, 2014) when predicting 147 different viral genera across 266 viral DNA sequences as a function of the viral fragment length
| Classifier | Full-length genomes accuracy (%) | Viral fragment length 1000-bp accuracy (%) | 500-bp accuracy (%) | 100-bp accuracy (%) |
|---|---|---|---|---|
| CSSS | 91.43 ± 0.99 | 70.02 ± 2.01 | 63.02 ± 1.49 | 35.94 ± 3.31 |
| PhymmBL | 86.56 ± 2.19 | 68.90 ± 1.78 | 57.28 ± 2.09 | 29.79 ± 1.66 |
| NBC | 74.67 ± 0.64 | 59.06 ± 1.49 | 50.39 ± 2.77 | 34.04 ± 1.53 |
| Kraken | 48.47 ± 1.85 | 26.66 ± 1.94 | 23.07 ± 2.19 | 16.26 ± 1.40 |
| RAIphy | 42.03 ± 1.56 | 30.72 ± 1.66 | 23.97 ± 1.66 | 14.06 ± 1.17 |
| PAUDA | 0.10 ± 0.15 | 6.73 ± 1.40 | 21.22 ± 1.32 | 31.89 ± 2.42 |
Table 1 presents that the CSSS model and PhymmBL significantly outperform other classification methods for short viral fragments (500–1000 bp) and complete viral genomes. Furthermore, significant improvement in classification accuracy is obtained when using the CSSS model over that of PhymmBL for 100–500 bp viral fragments and complete viral genomes. We found no significant difference between the CSSS model and PhymmBL for 1000 bp fragments (P value = 0.23, using the two sample t-test). Also no significant difference was found between the CSSS model and NBC (Rosen et al., 2011) for very short 100-bp viral fragments (P value = 0.13, using the two sample t-test). We refer the reader to Section 4 for the explanation of these two results. Because CSSS and PhymmBL are both hybrid models that combine the alignment-based and the alignment-free/composition-based approaches, in Supplementary Table S4 in Supplementary Data we compare the performance of the CSSS model to that of PhymmBL when BLAST scores are used for classification alone. Both models achieve higher accuracy than BLAST scores alone (except for the CSSS model with short 100 bp fragments). From Supplementary Table S4 in Supplementary Data, we also note that higher accuracy is achieved when classification is performed using BLAST scores alone with CSSS rather than PhymmBL, we explain the reason for this discrepancy in Section 4.
3.2 Dataset II—Classification of reads from a real metagenome dataset
For this dataset, the k-mer size was set to 4 to satisfy the inequality in Equation (15) with L = 1000 bp. The classification performance of the CSSS model was evaluated using the training and test sets as described in Dataset II (see Section 2). The combined score in Equation (9) was calculated based on scores calculated with the three alignment-free measures (see Section 2, Equations (3, 5 and 7)] and the normalized BLAST score [see Equation (9)]. In Table 2, we compare the classification performance of the CSSS method to that of six other models on Dataset II (see Section 2). Dataset II is composed of 20 907 reads (with an average of 759 bp in read length) that are known to align to three genomes as described in Section 2—Dataset II. Both CSSS and PhymmBL achieve higher level of accuracy than any other model, followed by PhyloPythiaS. PhymmBL achieves a slightly higher accuracy than CSSS for reads that align to Leptospirillum sp. groups II and III genomes (Nitrospirae phylum), while the CSSS model performs better at classifying reads that align to the Ferroplasma acidarmanus genome (Euryarchaeota phylum). Again we show in Supplementary Table S5 in Supplementary Data that the performance based solely on BLAST scores for the two best models (CSSS and PhymmBL) is superior for the CSSS model than PhymmBL.
Table 2.
The classification accuracy [see Equation (16)] for Dataset II obtained with the CSSS (1-NN classifier) and the six other models: PhymmBL (Brady and Salzberg, 2009), PhyloPythiaS (Patil et al., 2011), NBC (Rosen et al., 2011), Kraken (Wood and Salzberg, 2014), RAIphy (Nalbantoglu et al., 2011) and PAUDA (Huson and Xie, 2014) when predicting the phyla for 20 907 reads belonging to Leptospirillum sp. groups II and III genomes (18 579 reads) and Ferroplasma acidarmanus genome (2328 reads)
| Classifier | Euryarchaeota accuracy (%) | Nitrospirae accuracy (%) |
|---|---|---|
| CSSS | 87.03 | 96.66 |
| PhymmBL | 81.14 | 97.67 |
| PhyloPythiaS | 72.76 | 95.42 |
| NBC | 16.15 | 82.07 |
| Kraken | 0.26 | 77.14 |
| RAIphy | 1.03 | 66.99 |
| PAUDA | 4.38 | 8.41 |
3.3 Dataset III—Classification of protein sequences
Next, we evaluated the ability of the CSSS model to classify protein sequences in Dataset III (see Section 2). Dataset III was originally created to evaluate methods for detecting distant sequence similarities among protein sequences as described in (Liao and Noble, 2003). The results obtained with the CSSS model are compared with those presented in Kocsor et al. (2006), where the performance of the combined similarity measure Lempel-Ziv-Welch (LZW)-BLAST (obtained by combining CB LZW and BLAST scores) was compared with that of the SW algorithm and two hidden Markov model-based algorithms using two types of classifiers the NNs (1-NN) algorithm and the support vector machine (SVM). Instead of calculating BLAST scores, the evaluation of the CSSS model on this protein dataset was performed using SW P values, taken from Liao and Noble (2003). The k-mer size for this dataset was set to 1 since the much larger alphabet size for protein sequences (n = 20) requires sequences of length L ≥ 400 for the k-mer size of 2 [see Equation (15)] a value that is much larger then the length of many of the protein sequences in Dataset III. The combined score in Equation (9) is calculated based on scores obtained using the three alignment-free measures [see Section 2, Equations (3, 5 and 7)] and normalized SW P values [see Equation (14)]. For the purpose of comparison with results presented in Kocsor et al. (2006) the classification results of the CSSS model are expressed as the integral of the AUC curve shown in Supplementary Figure S2 in Supplementary Data (note that since Dataset III contains 54 families the maximum value for this integral is 54).
In Table 3, we present that the CSSS method achieves a slightly better performance than the SW P value similarity/distance measure (using either the SVN or the 1-NN classifier) as reported in Kocsor et al. (2006) and performs much better than the combined LZW-BLAST similarity measure with the 1-NN classifier also reported in Kocsor et al. (2006).
Table 3.
The classification performance on protein domain sequences for the CSSS model (1-NN classifier) with the k-mer size=1 (see Section 3), expressed as the integral of the AUC curve shown in Supplementary Figure S2 in Supplementary Data
| Similarity/distance measure | Classification method |
|
|---|---|---|
| SVM | 1-NN | |
| SW P valuea | 48.66 | 50.22 |
| LZW-BLASTa | 49.0 | 37.18 |
| CSSS | NA | 50.64 |
Since Dataset III contains 54 protein families, the maximum value for the integral of the AUC curve is 54, which correspond to all 54 protein families being classified without error.
aSimilarity/distance measures presented in Kocsor et al. (2006).
4 Discussion
Sequence comparison is at the core of many bioinformatics applications such as metagenomic classification, protein sequence and function characterization and phylogenetic studies to name a few. In many of these applications, the alignment-based sequence comparison is widely used, but this does not come without some limitations. One important limitation is that the alignment-based similarity measure might give erroneous information when used with sequences that have undergone some type of sequence rearrangement. Alignment-free similarity measures offer an alternative to the alignment-based ones in that they are unaffected by such genetic processes.
In this study, we propose a model that combines similarity scores obtained with alignment-based and alignment-free sequence similarity measures [see Equation (9)] to gain additional discriminatory information about sequences and to improve their characterization.
In Tables 1 and 2, we present that our approach performs better than most of the other methods used in this study when predicting genera of unknown viral sequences (i.e. sequences that are not part of the training set as described in Dataset I) or when predicting phyla of metagenomic sequences. The main conceptual difference between the CSSS model and the other classification methods used in this study, at the exception of PhymmBL, is that the CSSS model combines similarity scores obtained with both the alignment-based and the alignment-free sequence similarity measures, while the other models rely on either one of these two approaches. Thus, NBC (Rosen et al., 2011), RAIphy (Nalbantoglu et al., 2011) and PhyloPythiaS (Patil et al., 2011) rely on the alignment-free composition-based approaches (using k-mer frequencies or k-mer counts) and PAUDA (Huson and Xie, 2014) relies on the alignment-based approach and Kraken (Wood and Salzberg, 2014) on the exact alignment of k-mers. Although in some respects, our approach is similar to that of PhymmBL, since both methods combine scores calculated using different types of similarity measures [PhymmBL uses BLAST scores and IMMs scores (Salzberg et al., 1998)], there are two main differences that can explain the results obtained with Dataset I shown in Table 1.
First, the CSSS model uses four different similarity measures, so that if sufficiently independent one from another, their combined additive effect could confer a greater discriminatory power than the two similarity scores combined by PhymmBL. In Supplementary Table S6 in Supplementary Data, we show the classification accuracy of individual similarity measures used by CSSS and PhymmBL models as a function of the viral fragment length.
Although the classification performance of the ED [see Equation (3)] and JSD [see Equation (5)] measures are very similar, the classification performance of the CB [see Equation (7)] measure drops rapidly below 10% as the length of viral fragments decreases. If, however, we perform the classification on full length viral genomes (see Section 2.3.1) we find that the CB measure improves the performance by as much as 5.79% when combined with the other three measures (ED, JSD and BLAST). This shows that the CB measure contains significant additional information, only for sequences that are similar in length to those in the training set, that is complementary to the information contained by the other three measures. This drop in performance of the CB measure as a function of the fragment length, relative to the length of the genomes in the training set, explains also the smaller difference in performances observed between the CSSS and PhymmBL models when classifying longueur reads in Dataset II (see Section 2) shown in Table 2.
Since the ED and JSD measures show similar classification performances, we investigated the degree of independence of these two measures by performing a principal components analysis (PCA) of the similarity scores obtained using viral genomes from Dataset I. We found that the first component (i.e. PCA1) is strongly associated with the ED measure in test samples, while the second component (i.e. PCA2) is strongly associated with the JSD measure, a result that is independent of the viral fragment length as shown in Supplementary Figure S3 in Supplementary Data. These results indicate that these two measures can be considered as orthogonal and thus not correlated, with the ED measure accounting for most of the variation across viral genomes in test samples. To further determine the effect of these two measures on the classification performance, we removed each measure from the model one at the time and then recalculated the accuracy scores. We found that for full viral genomes, the effect of removing the ED measure reduced the classification performance significantly by 5%, while removing the JSD measure reduced it only slightly (0.25%). However, in the case of shorter viral fragments, dropping either one of these two measures from the model did not produce any significant change to the performance, while removing both produced a significant drop in performance (up to 3% for 1000 bp reads). In the light of these results, we conclude that both of these measures contain complementary information that is useful for characterizing viral sequences.
The second important difference between our model and PhymmBL is in the weighting scheme used. In the PhymmBL model, the weights assigned to each similarity measure (i.e. combined score = IMM + 1.2(4 - log(E)), where IMM is the score of the best matching IMM and E the smallest E-value returned by BLAST) have the same value for all test examples, in the CSSS model weights are determined independently for each test example based on the discriminatory ability of each measure using the training set [see Equation (9)]. Having different sets of weights for different test, samples (i.e. test sequences) should improve the classification performance since some sequences will be better characterized with one type of similarity measure than another. Another important difference between these two methods is in the classification performance using BLAST results alone. As shown in Supplementary Tables S4–S6 in Supplementary Data, we found that a significant improvement in classification is obtained when the BLASTN algorithm is used instead of mega-BLAST, the algorithm used by PhymmBL. BLASTN is more sensitive than mega-BLAST because it uses a shorter word size (default value of 11) that makes it better at finding-related nucleotide sequences between more divergent biologically sequences since the initial exact match can be shorter.
We found that for very short viral fragments (100 bp in length), the CSSS model performs better than PhymmBL and achieves slightly better accuracy (but not significant P value = 0.13, using the two sample t-test) than the NBC model, as shown in Table 1. By examining the individual performance of the sequence similarity measures used by the CSSS model, we found that the composition-based and CB similarity measures are more affected by the shorter fragment size than the alignment based one, as shown in Supplementary Table S6 in Supplementary Data. Despite this drop in performance (of the composition-based and the CB similarity measures) for short 100 bp viral fragments, by virtue of combining different similarity measures the CSSS model still achieves better performance than the alignment-based method PAUDA (P value = 0.008, using the two sample t-test) or the hybrid PhymmBL (Phymm + BLAST) (P value = 0.0001, using the two sample t-test) and performs equally well as the best composition-based model used in this study, namely NBC.
In Section 3, we have shown that our approach can also be used effectively for protein sequence classification. In Table 3, we show that our model outperforms a similar but simpler LZW-BLAST 1-NN model (Kocsor et al., 2006). The main differences between these two approaches are the number of similarity measures used [frequency-based measures such as those given in Equations (3) and (5) were not used in Kocsor et al., 2006], a different method with which similarity measures are combined and SW scores (P values) instead of BLAST scores. Without using a weighting scheme, the LZW-BLAST method uses a simple multiplication rule to combine the LZW and BLAST scores (Kocsor et al., 2006). We found that the multiplication rule used in Kocsor et al. (2006) performs significantly better in combination with an SVM rather than a NN classifier. The model proposed in this study performs better than the SVM (LZW-BLAST) model reported in Kocsor et al., (2006) and slightly better than the 1-NN (SW P value) as shown in Table 3. We attribute this smaller gain in classification performance to the short protein sequences in Dataset III, which pose a greater challenge to the three alignment-free similarity measures examined in this study.
As shown in Equation (9), our model combines similarity scores using a linear combination of vectors (equivalent to calculating a weighed arithmetic mean of scores obtained with each individual similarity measure). We did explore combining similarity scores using a different multiplicative model which we found to significantly under-perform (in combination with the NN classifier) when used on datasets presented in this study.
Finally, our approach can be easily extended to any number of additional similarity measures (such as the IMMs used by PhymmBL) that might produce additional gain in discriminatory information about sequences and thus improve the overall classification performance. Therefore, future work will include assessing the performance of additional similarity measures that could be integrated into our model.
Funding
This work was conducted with the support of the Ontario Institute for Cancer Research through funding provided by the government of Ontario to the authors.
Conflict of Interest: none declared.
Supplementary Material
References
- Akhter S., et al. (2013) Applying Shannon’s information theory to bacterial and phage genomes and metagenomes. Sci. Rep. , 3, 1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F., et al. (1997) Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. , 25, 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady A., Salzberg S.L. (2009) Phymm and PhymmBL: metagenomic phylogenetic classification with interpolated Markov models. Nat. Methods , 6, 673–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady A., Salzberg S. (2011) PhymmBL expanded: confidence scores, custom databases, parallelization and more. Nat. Methods , 8, 367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., et al. (1999) A compression algorithm for DNA sequences and its applications in genome comparison. Genome Inform. Ser. Workshop Genome Inform. , 10, 51–61. [PubMed] [Google Scholar]
- Cilibrasi R., Vitányi P.M. (2005) Clustering by compression. IEEE Trans. Inf. Theory , 51, 1523–1545. [Google Scholar]
- Delcher A.L., et al. (2003) Using MUMmer to identify similar regions in large sequence sets. Curr. Protoc. Bioinformatics , Chapter 10, Unit 10.3. [DOI] [PubMed] [Google Scholar]
- Delviks-Frankenberry K., et al. (2011) Mechanisms and factors that influence high frequency retroviral recombination. Viruses , 3, 1650–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domazet-Loo M., Haubold B. (2011) Alignment-free detection of horizontal gene transfer between closely related bacterial genomes. Mob. Genet. Elements , 1, 230–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy S., et al. (2008) Rates of evolutionary change in viruses: patterns and determinants. Nat. Rev. Genet. , 9, 267–276. [DOI] [PubMed] [Google Scholar]
- Gupta S., et al. (2008) Predicting human nucleosome occupancy from primary sequence. PLoS Comput. Biol. , 4, e1000134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huson D.H., Xie C. (2014) A poor man’s blastx–high-throughput metagenomic protein database search using pauda. Bioinformatics , 30, 38–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huson D.H., et al. (2007) MEGAN analysis of metagenomic data. Genome Res. , 17, 377–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kocsor A., et al. (2006) Application of compression-based distance measures to protein sequence classification: a methodological study. Bioinformatics , 22, 407–412. [DOI] [PubMed] [Google Scholar]
- Li M., et al. (2001) An information-based sequence distance and its application to whole mitochondrial genome phylogeny. Bioinformatics , 17, 149–154. [DOI] [PubMed] [Google Scholar]
- Liao L., Noble W.S. (2003) Combining pairwise sequence similarity and support vector machines for detecting remote protein evolutionary and structural relationships. J. Comput. Biol. , 10, 857–868. [DOI] [PubMed] [Google Scholar]
- Marais G., Kingsford C. (2011) A fast, lock-free approach for efficient parallel counting of occurrences of k-mers. Bioinformatics , 27, 764–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murzin A.G., et al. (1995) SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. , 247, 536–540. [DOI] [PubMed] [Google Scholar]
- Nalbantoglu O.U., et al. (2011) RAIphy: phylogenetic classification of metagenomics samples using iterative refinement of relative abundance index profiles. BMC Bioinformatics , 12, 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patil K.R., et al. (2011) Taxonomic metagenome sequence assignment with structured output models. Nat. Methods , 8, 191–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen G.L., et al. (2011) Nbc: the naive Bayes classification tool webserver for taxonomic classification of metagenomic reads. Bioinformatics , 27, 127–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salzberg S.L., et al. (1998) Microbial gene identification using interpolated Markov models. Nucleic Acids Res. , 26, 544–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shackelton L.A., Holmes E.C. (2004) The evolution of large DNA viruses: combining genomic information of viruses and their hosts. Trends Microbiol. , 12, 458–465. [DOI] [PubMed] [Google Scholar]
- Sims G.E., et al. (2009) Alignment-free genome comparison with feature frequency profiles (FFP) and optimal resolutions. Proc. Natl Acad. Sci. U S A , 106, 2677–2682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson G.W., et al. (2004) Community structure and metabolism through reconstruction of microbial genomes from the environment. Nature , 428, 37–43. [DOI] [PubMed] [Google Scholar]
- Vinga S. (2014) Editorial: Alignment-free methods in computational biology. Brief Bioinform. , 15, 341–342. [DOI] [PubMed] [Google Scholar]
- Vinga S., Almeida J. (2003) Alignment-free sequence comparison-a review. Bioinformatics , 19, 513–523. [DOI] [PubMed] [Google Scholar]
- Wood D.E., Salzberg S.L. (2014) Kraken: ultrafast metagenomic sequence classification using exact alignments. Genome Biol. , 15, R46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T.J., et al. (2005) Optimal word sizes for dissimilarity measures and estimation of the degree of dissimilarity between DNA sequences. Bioinformatics , 21, 4125–4132. [DOI] [PubMed] [Google Scholar]
- zur Hausen H. (2007) Infections Causing Human Cancer . Wiley-VCH Verlag GmbH & Co; KGaA., Weinheim. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.