Mechanochemical Symmetry Breaking in Hydra Aggregates

Abstract

Tissue morphogenesis comprises the self-organized creation of various patterns and shapes. Although detailed underlying mechanisms are still elusive in many cases, an increasing amount of experimental data suggests that chemical morphogen and mechanical processes are strongly coupled. Here, we develop and test a minimal model of the axis-defining step (i.e., symmetry breaking) in aggregates of the Hydra polyp. Based on previous findings, we combine osmotically driven shape oscillations with tissue mechanics and morphogen dynamics. We show that the model incorporating a simple feedback loop between morphogen patterning and tissue stretch reproduces a wide range of experimental data. Finally, we compare different hypothetical morphogen patterning mechanisms (Turing, tissue-curvature, and self-organized criticality). Our results suggest the experimental investigation of bigger (i.e., multiple head) aggregates as a key step for a deeper understanding of mechanochemical symmetry breaking in Hydra.

Introduction

During embryogenesis the organism develops from a single cell to a complex entity composed of tissues showing different types of patterns (1). Chemical patterns are patterns of diffusing signaling molecules involved in tissue development, called morphogens (2–4). In contrast, mechanical patterns are related to shape/geometry and (visco-)elastic properties of cells or tissues, which are expressed in terms of geometry, strain, stress, or stiffness (5,6). During many developmental steps, chemical and mechanical patterns appear simultaneously, and it is frequently difficult to distinguish cause from effect.

However, the traditional view of morphogenesis is dominated by a purely chemical approach, where mechanical patterns are regarded as simple consequences of chemical prepatterns (7). According to this theory, morphogenesis is a hierarchical sequence of chemical patterning processes, where each pattern depends critically on the previous one.

Increasing amounts of experimental data show that mechanical or geometric cues can actively influence morphogenetic processes and cell differentiation (for review, see Chanet and Martin (8) and Farge (9)). This suggests that the interplay between chemical and mechanical processes could lead to pattern formation in many cases (10,11). Moreover, purely chemical models propose the existence of morphogens behaving in a certain way (e.g., long-range inhibitors for Turing (4) or the Gierer-Meinhardt (12) models), but these morphogens have not been identified after several decades of research (13). Finally, at least some developmental processes do not critically depend on the existence of chemical prepatterning; from lower animals (14) to organs of mammals (15,16), it has been shown that they may evolve from dissociated and randomly aggregated cells.

For these reasons, the need for fresh modeling approaches, integrating mechanical and chemical processes during development, has been recently stressed (17). Although the number of mechanical models of morphogenesis has strongly increased during the last decade (18), approaches considering mechanochemical processes during tissue development are still in the early stages (10,19,20).

To study the mechanochemistry of development, the Hydra polyp is a suitable organism. Hydra is an established biological model organism for morphogenesis (21,22) and it has been traditionally used to apply purely chemical pattern formation models—such as in the seminal article of Alan Turing (4) and in related approaches (3,12,23,24). Hitherto, several morphogens involved in early pattern formation (i.e., axis formation) have been identified in Hydra: Members of the Wnt signaling pathway are locally expressed during early head formation, with Wnt3 constituting the earliest marker of this signal cascade (25,26). Furthermore, production of the permanently expressed Ks1 morphogen appears to be upregulated in response to early signals of head formation (27,28) whereas its graded expression inversely correlates with the head-forming potential in adult Hydra polyps (29).

However, these molecules are not good candidates for morphogens in Turing-type models; note that the long-range inhibitors are still elusive in Hydra (13,30,31). It has also been recently shown that in this organism, tissue mechanics is indispensable during early pattern formation (19), suggesting that purely chemical models are insufficient.

Hydra is attractive from a modeling point of view. It has a simple body plan and the complexity can be reduced by studying the so-called Hydra aggregates (14). Here, de novo pattern formation and regeneration of polyps can be observed from a bulk of randomly mixed and aggregated cells. Initially, these cells form a hollow tissue sphere, which exhibits osmotically driven shape oscillations: Due to water influx, the tissue sphere swells until tissue rupture takes place, which is followed by a rapid collapse and tissue healing; then the process starts again (32). After several oscillations (phase I), aggregates suddenly change their homogeneous structure to a chemically and mechanically inhomogeneous system (phase II), which defines the first axis-defining step in Hydra called symmetry breaking (19,25,32). In contrast to recent findings in yeast (33), the location of tissue rupture in Hydra aggregates does not seem to determine the final body axis: Before symmetry breaking, the rupture point of each cycle occurs at a different location (19).

In some systems, there is evidence that pattern formation is driven by motile cells (34), which can explain why corresponding molecular species are not found. However, experimental observations exclude such a mechanism in Hydra. Cellular patterning requires a range of cell populations with distinct properties (34). In contrast, pattern formation and symmetry breaking in Hydra can be achieved in aggregates with varying cell composition (14) and axis formation can be induced by purely chemical cues (35).

Thus, in this article, we investigate possible mechanochemical processes underlying symmetry breaking in Hydra aggregates. We propose a model combining osmotically driven shape oscillations (19,36) and morphogen dynamics and test its ability to reproduce recent experimental results. Furthermore, we compare previously proposed models for symmetry breaking, such as diffusion-driven instability (the Turing model (12,19)), self-organized criticality (i.e., SOC (27,37)), and curvature-increasing mechanisms (10) with respect to their predictions of dynamics of this process. Our results are discussed in the context of morphogens associated with symmetry breaking and head formation, such as Ks1 and Wnt (25,26,28).

Materials and Methods

Model

In this section, based on experimental data, we develop an osmomechanochemical (OMC) model for symmetry breaking in early Hydra aggregates. This model combines osmotic processes with tissue mechanics and morphogen dynamics. Because the exact mechanism of morphogen clustering during body axis formation in Hydra is unknown, we focus on the activator-inhibitor model exhibiting Turing instability. However, we consider and compare different alternative mechanisms proposed previously in the literature (such as SOC and curvature-increasing models), which we investigate for simplicity on spheres of fixed radius without tissue mechanics.

The osmomechanochemical model

The OMC model describes dynamics of two interacting and diffusing morphogen species in an elastically deforming tissue surface which undergoes osmosis-driven shape oscillations.

Dynamics of tissue deformations are based on a gradient flow minimizing the free energy, accounting for osmotic pressure, tissue stretching, bending, and local morphogen concentrations. Together with Turing-type morphogen dynamics, we obtain a model in the form of coupled nonlinear partial differential equations of fourth-order.

Most importantly, we propose the following feedback loop between morphogens and tissue mechanics (see Fig. 1): There exists a morphogen that locally lowers the resistance to lateral tissue stretch (MC1), and patterning of this morphogen critically depends on lateral tissue stretch (MC2).

Figure 1.

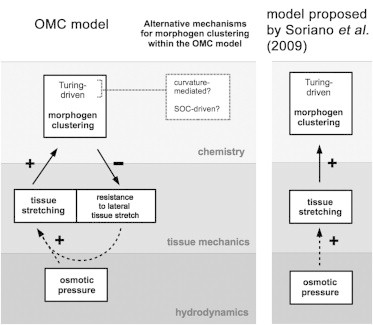
Proposed interactions among morphogens, tissue mechanics, and osmotic processes during symmetry breaking in Hydra aggregates. (Left-hand side) OMC model (presented within this study); (right-hand side) model of Soriano et al. (19). (Continuous arrows) Experimentally motivated model assumptions; (dotted arrows) physical relationships.

These assumptions on the mechanochemical coupling are based on the observation that symmetry breaking in Hydra spheres involves formation of an early head, having a head-organizer in the center (13). The early head can be characterized in different ways: mechanically as a weak spot in the tissue (19,25,27) (i.e., a lower resistance to lateral tissue stretching), or chemically as the local expression of characteristic morphogens, such as multiple Wnt (25,26) or Ks1 (28) molecules. Furthermore, mechanochemical symmetry breaking requires the shape oscillations mentioned above, leading to periodic tissue stretch (19).

The OMC model constitutes an extension of the reaction-diffusion model proposed by Soriano et al. (19) for Hydra symmetry breaking, but differs in the following points (Fig. 1).

• 1.Soriano et al. (19) consider influence of tissue stretch on morphogen patterning instead of a feedback loop.
• 2.We explicitly model tissue deformations, whereas Soriano et al. (19) incorporates the shape oscillations more phenomenologically.
• 3.In contrast to Soriano et al. (19), the OMC model does not require the assumption of viscoelasticity to reproduce experimental results.

Mathematical modeling framework

To describe mathematically the dynamics of a Hydra aggregate, we use a continuous approach, which is justified by the large number of cells (≈10⁴) in the system (19). The cell bilayer forming a hollow tissue sphere is at any time t approximated by a closed two-dimensional surface Γ(t), embedded in three-dimensional space. The evolution of Γ(t) is given by a diffeomorphic time-dependent representation $\overrightarrow{X}$, parameterized over the unit sphere S² ⊂ ℝ³. Thus, Γ(t) is the image of $\overrightarrow{X}\left(\cdot ,t\right)$ with $\overrightarrow{X}\left(\overrightarrow{s},t\right):S^2\times \left[0,T\right]\to {\mathrm{ℝ}}^3$ for a T ∈ ℝ_>0.

Local concentrations of the morphogens A and B at time t are given by continuous functions Φ_A, Φ_B on the deforming tissue surface Γ(t), defined as morphogen concentrations per cell volume, Φ_i(t): Γ(t)→ ℝ_≥0, i ∈ {A,B}. In order to achieve a consistent formulation with chemical processes being defined on S² rather than on Γ, we redefine Φ_i accordingly. This can be done by using the fact that we can identify material points $\overrightarrow{X}\left(\overrightarrow{s},t\right)$ on Γ(t) with $\overrightarrow{s}\in S^2$, because $\overrightarrow{X}$ is smooth and bijective. Thus, for each $\overrightarrow{s}\in S^2$, t ∈ [0,T], and i ∈ {A,B}, we define the function ϕ_i: $S^2\times \left[0,T\right]\to {\mathrm{ℝ}}_{\ge 0}\mathrm{by}{\varphi }_i\left(\overrightarrow{s},t\right)={\Phi }_i\left(\overrightarrow{X}\left(\overrightarrow{s},t\right)\right).$

Energy terms describing elastic behavior

In this study we treat the tissue as purely elastic and not viscoelastic. Although corresponding timescales are within the range of viscoelastic processes, previous studies showed that purely elastic models reproduce Hydra tissue behavior (e.g., Krahe et al. (38), Mombach et al. (39), and Kücken et al. (36)) and can be used as an approximation. Furthermore, we will show that effects that have been previously ascribed to viscoelastic properties of Hydra can be explained by elastic tissue behavior.

Elastic tissue deformations are based on minimization of free energy $\mathcal{F}$, composed of energy terms related to tissue bending, stretching, and osmotic pressure. Free energy formulations are expressed in terms of surface integrals, ${\int }_{\Gamma }\dots d\overrightarrow{S}$, or volume integrals, ${\int }_{\Omega }\dots d\overrightarrow{V}$, where Ω is the domain inside, i.e., Γ = ∂Ω. We will abbreviate Γ = Γ(t) and Ω = Ω (t). In the parametric formulation, due to the divergence theorem, these time-dependent integrals are given by ${\int }_{\Gamma }\dots d\overrightarrow{S}={\int }_{S^2}\dots \sqrt{g}d\overrightarrow{s}$ and ${\int }_{\Omega }d\overrightarrow{V}=\left(1/3\right){\int }_{S^2}\overrightarrow{X}\cdot \overrightarrow{n}\sqrt{g}d\overrightarrow{s}$, respectively. Here, $\overrightarrow{n}$ is the outer unit normal vector and $\sqrt{g}$ is a surface measure, the latter representing the local area of the tissue and depending on the parametric function $\overrightarrow{X}$.

Osmotic processes and pressure

It has been previously shown that early Hydra aggregates undergo osmotically induced shape oscillations, consisting of repeated tissue swelling, rupture/collapse, and healing cycles (32,36). These oscillations appear to be required for symmetry breaking (19). To integrate this aspect, we follow the approach of Fütterer et al. (32), assuming a Darcy-type law for the temporal development of the total water volume V(t) inside the tissue shell. This is (in the absence of elastic resistance) given by

$$d_{t}V=-{\mathcal{A}}_0\alpha \left(C_{\text{out}}-C_{\text{in}}\right),$$ (1)

Here, ${\mathcal{A}}_0={\int }_{S^2}\sqrt{g(t=0)}d\overrightarrow{s}$ is the initial (unstressed) total tissue area, α is a constant depending on temperature and water permeability, and (C_in – C_out) is the difference in ion concentrations per unit of volume from the inside to the outside of the Hydra shell (36). Although C_in depends on time, it has been shown that it does not change appreciably after an initial equilibration (36). Hence, for the sake of simplicity, we use a constant for effective ion concentration difference between the inside and the outside of the aggregate, ΔC_eff := C_out(t >> 0) – C_tn(t >> 0). With Eq. 1, it follows for the preferred aggregate volume that

$$V\left(t\right)=-{\mathcal{A}}_0\alpha \Delta C_{\text{eff}}t+\underset{\Omega \left(t=0\right)}{\int }d\overrightarrow{V}.$$ (2)

We include Eq. 2 in an energy term elastically penalizing a possible overpressure in the interior of the aggregate, the latter quantified by deviations of this volume ${\int }_{\Omega }d\overrightarrow{V}$ from the preferred value V(t). This energy is given by

$${\mathcal{F}}_{\text{osm}}=\frac{{\kappa }_1}{2}{\left(\underset{\Omega }{\int }d\overrightarrow{V}-V\left(t\right)\right)}^2,$$ (3)

where κ₁ balances osmotic pressure with elastic tissue resistance. Furthermore, Eq. 3 is only valid if the tissue sphere is intact. For consideration of tissue rupture and pressure release, we refer to the next subsection.

Tissue stretching, rupture, and healing

Lateral tissue stretching is assumed to play a major role during symmetry breaking in Hydra spheres (19). Hence, unlike in the previous approaches (10,40), we consider a locally compressible surface. We introduce the energy term

$${\mathcal{F}}_{\text{comp}}=\underset{\Gamma }{\int }\frac{{\kappa }_2}{2}\frac{{\left(\sqrt{g}-\sqrt{g_0}\right)}^2}{\sqrt{g_0}\sqrt{g}}d\overrightarrow{S},$$ (4)

which is a generalization of the Hook energy for a spring (41). Deviations of the local tissue area $\sqrt{g}$ from the initial (relaxed) value $\sqrt{g_0}=\sqrt{g\left(t=0\right)}$ are elastically penalized, weighted by the stretch rigidity κ₂.

The osmotically induced swelling of the Hydra tissue shell Γ ends due to local tissue rupture, where pressure is released from a small hole until healing takes place, and the swelling process starts again (19,27,32). Because topological changes of Γ are difficult to handle mathematically (and are not the primary aim of this study), we introduce the effect of tissue rupture and healing on a more phenomenological level: If local tissue stretch exceeds a certain threshold β, i.e., $\sqrt{g}/\sqrt{g_0}>\beta$, we set the osmotic pressure to zero by setting $V\left(t\right)={\int }_{\Omega \left(t=0\right)}d\overrightarrow{V}$ for a certain time period t ∈ [t_rupt, t_heal[, and

$$V\left(t\right)=-{\mathcal{A}}_0\alpha \Delta C_{\text{eff}}\left(t-t_{\text{heal}}\right)+\underset{\Omega \left(t=0\right)}{\int }d\overrightarrow{V}$$

afterwards. Hence, we obtain a pressure release in the moment of tissue rupture t_rupt, and a pressure regeneration starting from the moment of completed tissue healing t_heal. In the following, we have set β = (1.25)², which matches the experimental observation that rupture occurs, if, for the relative radius R = (r – r₀)/r₀, it holds R > 0.25, where r₀ is the initial and r this aggregate radius (36).

To account for point (MC1) of the mechanochemical coupling, we set κ₂ = κ₂(Φ_A, Φ_B), i.e., we assume that the resistance to stretching depends on local morphogen concentrations. However, a simple linear relationship between tissue stiffness and morphogen concentrations would be unrealistic, because we expect saturation for high morphogen concentrations. We set

$${\kappa }_2={\kappa }_2\left({\Phi }_A\right)=-\lambda \text{tanh}\left({\Phi }_A-2\right)+\xi ,$$ (5)

where Φ_A has been chosen over Φ_B for simplicity. The interpretation of Eq. 5 is that the stretch rigidity κ₂ decreases with increasing morphogen concentration Φ_A and then shows a saturation, i.e., κ₂ → (ξ − λ) for Φ_A → ∞. Using the parameter values in the Supporting Material, we obtain a maximum effective reduction of κ₂ due to Φ_A by a factor of ∼0.4, which could be achieved in vivo by locally lowering the cell-cell-contacts.

Bending

To describe the resistance of the tissue surface to bending, we use the Helfrich free energy (42), which is given by

$${\mathcal{F}}_{\text{bend}}=\underset{\Gamma }{\int }\frac{{\kappa }_3}{2}{H}^{2}d\overrightarrow{S}.$$ (6)

Here, H is the mean curvature and κ₃ is the bending rigidity (40). Because tissue curvature effects are assumed to play a minor role within this model, we neglect modifications of $\mathcal{F}$_bend due to tissue compressibility, which would include changes in bending stiffness κ₃ due to local stretching or compression.

Evolution equations for the deforming tissue surface

The total energy $\mathcal{F}$ = $\mathcal{F}$_bend + $\mathcal{F}$_comp + $\mathcal{F}$_osm of the Hydra tissue shell is given as sum of the energy terms Eqs. 3, 4, and 6. Within this study, we assume that κ₁ >> κ₂,κ₃, because the swelling rate appears to have only a weak dependence on the elasticity of the Hydra shell (36). However, the energy terms for bending and stretching are not negligible even for high values of κ₁ (the latter leading to a global volume constraint), because κ₂ and κ₃ are connected to local curvatures and stretches, which are not uniquely determined by a prescribed volume.

Evolution of the deforming Hydra shell up to time T > 0 is now given by the L²-gradient flow of the total energy

$$d_t\left(\overrightarrow{X}\cdot \overrightarrow{n}\right)=-L\frac{{\delta }^{\perp }}{\delta \overrightarrow{X}}\left(\mathcal{F}\left(\overrightarrow{X},{\Phi }_A,{\Phi }_B\right)\right),$$ (7)

where d_t(.) is the total time derivative, L is a kinetic coefficient, $\overrightarrow{n}$ is the surface normal vector, and $\left({\delta }^{\perp }/\delta \overrightarrow{X}\right)(.)$ denotes the strong formulation of the variation perpendicular to the deformed surface Γ. Thus, we simplify our system considering only normal surface deformations. This is motivated by the fact that the main deforming force resulting from osmotic pressure acts purely normally. The gradient flow Eq. 7 leads to the minimization of the free energy $\mathcal{F}$, hence to the mechanical equilibrium. However, gradient flows may also describe realistic dynamics of deforming surfaces when we consider overdamped systems, e.g., biological surfaces embedded in a fluid (40,43–45). For more details in corresponding definitions, further information on the calculation of gradient flows, detailed calculation of variations, and technical remarks, we refer to the Supporting Material and to Mercker et al. (40).

Morphogen dynamics

Instead of using gradient flows of $\mathcal{F}$ to derive dynamics of chemicals (10), the evolution of morphogens is assumed to be independent of $\mathcal{F}$. This is motivated by the fact that morphogen molecules are not part of the mechanical surface itself, but only may indirectly influence tissue mechanics. Hence, morphogen dynamics do not, per se, depend on $\mathcal{F}$.

For the chemical patterning during symmetry breaking in Hydra aggregates, we follow the ideas of Soriano et al. (19) using a reaction-diffusion equation for morphogen patterning. In particular, we modify the minimum model of Koch and Meinhardt (46), considering pattern formation of an activator Φ_A and an inhibitor Φ_B on a deformed sphere, given by the equations

$$d_t{\Phi }_A=D_A{\Delta }^{\Gamma }\left({\Phi }_A\right)+C_A\left({\Phi }_A^2/{\Phi }_B-{\Phi }_A\right),$$ (8)

$$d_t{\Phi }_B=D_B{\Delta }^{\Gamma }\left({\Phi }_B\right)+C_B\left({\Phi }_A^2-{\Phi }_B\right).$$ (9)

Here, D_A and D_B are diffusion rates; ${\Delta }^{\Gamma }(.)$ is the surface Laplace operator; and C_A and C_B are reaction rates, comprising production and removal. Equations 8 and 9 are strongly related to those presented by Plaza et al. (47), because we also incorporate tissue curvature and advection, where the latter is in our case naturally given due to the Lagrangian description of Γ (10). However, we additionally consider tissue stretch instead of growth processes.

To include point (MC2) of the mechanochemical coupling, according to Soriano et al. (19), we assume that diffusion rates depend on lateral tissue stretch. We set

$$D_B=D_A+{\tilde{D}}_B\text{log}\left(\sqrt{g}/\sqrt{g_0}\right),$$ (10)

i.e., diffusion of the inhibitor Φ_B is accelerated if the tissue is laterally stretched, but shows a saturation effect. Alternatively, one could reduce activator diffusion as a response to tissue stretch (19). Using the parameter values as presented within the Supporting Material, local tissue stretch leads to a maximal effective increase of D_B by a factor of ∼100. In vivo, underlying mechanisms could be selective channels, which close and open depending on tissue stretch (19).

Possible morphogen patterning mechanisms

The mechanochemical coupling (i.e., the mutual coupling of morphogen dynamics with tissue stretch) is the most important part of the OMC model. We emphasize that the choice of a Turing mechanism for morphogen pattern formation is somewhat arbitrary within this model, because we primarily focus on the mechanochemical aspects of Hydra symmetry breaking, with less attention to the exact chemical mechanism. Thus, Eqs. 8 and 9 could be replaced by alternative mechanisms (Fig. 2).

Figure 2.

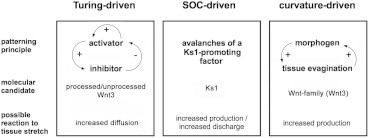
Three alternative mechanisms for morphogen patterning within the context of the OMC model, i.e., coupled to tissue stretch and leading to symmetry breaking in Hydra.

To shed more light on the underlying chemical patterning mechanisms, we compare Turing models with two alternatives (SOC and curvature-increasing models) that have been also proposed to explain symmetry breaking in Hydra-aggregates (4,37,40). In particular, we concentrate on the dependence of the symmetry breaking time t_SB on the initial aggregate radius r₀. To reduce complexity, at this stage we do not couple those models with tissue deformations.

Turing patterning

Turing models have been used to explain morphogen pattern formation and axis development in Hydra for more than 60 years (4,19,23,48), and have been numerically studied on different tissue geometries including spheres (47,49). We investigated if these models are able to reproduce different experimental data. A Turing model is a nonlinear reaction-diffusion system with diffusion-driven instability (DDI), in which the system admits a spatially homogeneous steady state u_s that is 1) stable with respect to spatially homogeneous perturbations, but 2) unstable with respect to spatially nonhomogeneous perturbations.

Considering the nonlinear system on spheres of radius r₀ for initial conditions being a small perturbation of u_s, the solution is well approximated by the solution of the linearized system, whose maximum grows like $c_{\ell }{e}^{{\lambda }_{\ell }t}$. Here, ${\lambda }_{\ell }$ is the largest eigenvalue of the linearized system and $c_{\ell }$ is a coefficient depending on the initial condition. We observed that for the same initial condition, $c_{\ell }$ grows linearly with the radius r₀.

Defining the symmetry breaking time as the moment where a certain threshold $\overline{u}$ is exceeded, we obtain $t_{SB}\left(r_0\right)=\text{log}\left(\overline{u}/c_{\ell }\left(r_0\right)\right)/{\lambda }_{\ell }\left(r_0\right).$

Tissue curvature-driven patterning

Recently, an alternative to Turing models has been proposed, where the patterning of only one diffusing morphogen type is driven by a simple positive feedback loop between tissue curvature and morphogen production (40). The morphogen is assumed to drive tissue bending in one direction (e.g., outward curving by apical constriction), and tissue curvatures are assumed to drive local morphogen production in turn. Thus, the interplay between morphogen production and actively generated and passively adapting tissue curvatures leads to pattern formation without reliance on molecular long-range inhibitors (40). Although there is so far no experimental evidence for this mechanism in Hydra, mechanisms using mechanical cues as long-range inhibitors might explain why the identification of appropriate molecular (Turing-) inhibitors still fails. Hence, we investigated if the model of Mercker et al. (40) reproduces the experimental data for the symmetry-breaking time t_SB. For details concerning the tested parameter space and the definition of t_SB in this context, we refer the reader to Computational Methods.

SOC-driven patterning

The morphogen Ks1 has been shown to be a molecular marker for early head formation in Hydra (28). Further studies have documented that fractal expression patterns of Ks1 in Hydra aggregates show behavior of SOC. Based on these observations, Gamba et al. (37) proposed a certain SOC mechanism for Ks1 expression, originally used in the modeling of earthquakes (50). Here, Ks1 patterning is based on nearest-neighbor interactions of cells. Gamba et al. (37) demonstrated that this model reproduces different experimental observations, such as fractal appearance and size-distribution of Ks1-positive cell clusters and their localization depending on temperature gradients. Thus, we investigated whether the temporal behavior of this model can also reproduce different experimental data. For further details regarding corresponding techniques and the definition of t_SB, we refer the reader to the next subsection.

Computational methods

In this subsection, we present computational methods for the investigation of the models. For details concerning the parameterization, we refer to the Supporting Material.

General computation schemes

For simulations of the OMC model and the curvature-increasing model, we used the finite-element library GASCOIGNE 3D (51), approximating the fourth-order partial differential equations in a mixed formulation. For spatial discretization, we used biquadratic elements with ≥8659 grid points; for time discretization, a semi-implicit Euler scheme. For further details of the computation scheme we refer to Mercker et al. (10,40). Computations of the SOC model and of the inverse eigenvalue functions related to the Turing pattern are carried out in C++ and MATLAB 7.11 (The MathWorks, Natick, MA), respectively.

Data analysis of the OMC model

Most of the following definitions are based on the experimental methods as described in Soriano et al. (19). The radius r of (deformed) simulated aggregates Γ = ∂Ω is defined as r = (A/(4π))^1/2, with tissue surface area $\mathcal{A}={\int }_{\Gamma }d\overrightarrow{S}$. Changes in aggregate shape symmetry are quantified by the factor b/a with minor and major inner aggregate axis b and a, respectively. Here, a is defined as the radius of the smallest possible sphere B_a with B_a ⊃ Ω, and b as the radius of the largest possible sphere B_b with B_b ⊂ Ω and the same center as B_a. The symmetry breaking time t_SB is defined as the moment at which the system geometry initially reaches a certain asymmetry, namely if b/a < 0.95 holds. Swelling rate s has been determined by linear regression of r(t) for t ∈ [0,t_rupt[, where t_rupt is the moment of first tissue rupture, averaged over the first three cycles.

Data analysis of the Turing model

We consider a linear reaction-diffusion system ∂_tu = DΔu + Ju on a sphere $S_{r_0}$ of radius r₀. Here, u is a vector of two or three components, D is the diagonal matrix of the diffusion coefficients, and J is the Jacobian of the kinetic system evaluated at the homogeneous steady state. DDI occurs if 1) J has only eigenvalues with negative real parts, and 2) there is a value $\ell \ge 1$ such that the matrix $J_{\ell }\left(r_0\right):=J-\left(\ell \left(\ell +1\right)/r_0^2\right)D$ has an eigenvalue with positive real part. Using the Routh-Hurwitz theorem (Gantmacher (52)), we see that these conditions require a sufficient spread of the diffusion coefficients and that J is not s-stable (compare to Satnoianu et al. (53) for the general definition and the Supporting Material for systems of two and three equations).

We use the method of least-squares under nonlinear constraints to find parameters (entries of D and J) such that there is a minimal deviation between the experimentally given symmetry breaking time and $\text{log}\left(\overline{u}/c_{\ell }\left(r_0\right)\right)/{\lambda }_1\left(r_0\right)$, where λ₁(r₀) is the largest eigenvalue of J₁(r₀).

The initial guess for fitting involves randomly generated matrices D⁰ and J⁰, where D⁰ is diagonal with nonnegative ordered entries and J⁰ is in the Turing space (compare to the Supporting Material).

Data analysis of the curvature increasing model

In Mercker et al. (40), it has been shown that the parameter space of the curvature-increasing model can be reduced to three independent constants $\tilde{\gamma }$, $\tilde{\zeta }$, and $L_{X_c}$. Here, $L_{X_c}$ influences only the timescale, $\tilde{\gamma }$ controls the size of appearing morphogen patches (and scales with the system size), and $\tilde{\zeta }$ influences the distance between these patches and does not depend on system size (40). Within this model, we define the symmetry breaking time t_SB as the time at which a certain morphogen concentration Φ is exceeded, namely if $\text{max}\left\{\Phi \left(\overrightarrow{s}\right)|\overrightarrow{s}\in S^2\right\}>0.1$. To fit the model-based curve of t_SB(r₀) to experimental data, for each value $\tilde{\zeta }$, we varied the temporal (i.e., $L_{X_c}$) and spatial scaling of the curvature-increasing model such that a minimum of the deviation between model and experimental data has been achieved. Because system size itself has been varied, $\tilde{\gamma }$ has been always set to a constant.

Data analysis of the SOC model

We used the SOC model and parameters as proposed in Gamba et al. (37). The only difference is a square lattice instead of a hexagonal lattice, as originally proposed by Olami et al. (50). We numerically verified that our square lattice model qualitatively reproduces the behavior of the hexagonal model, such as size distribution of Ks1-positive expression domains at different time-steps, including criticality (results not shown). Knowing that an aggregate of size r₀ = 138 μm corresponds to a network of c = 10⁴ cells (19), we deduce the relation c = 10⁴r₀²/138² to convert the network size into the initial radius r₀ of a Hydra shell.

As proposed by Gamba et al. (37), we assume that the axis of the Hydra aggregate is locked at the moment where a certain Ks1-positive cluster size is exceeded, i.e., the symmetry breaking moment t_SB. Alternatively, we define t_SB as the moment when Ks1 expression becomes scale free, which appears to experimentally coincide with symmetry breaking (27).

To compare the behavior of t_SB(r₀) between the SOC model and the experiments, we varied the temporal scaling of the SOC model as to minimize the deviations between numerical and experimental data.

Temperature gradients

In experiments with Hydra aggregates it has been shown that temperature gradients direct the orientation of the body axis and the localization of the head, which has been reproduced by simulations of the corresponding SOC model (27,37). To investigate the influence of temperature on the outcome of the curvature-increasing and Turing models, we introduce linear gradients along the z axis in each reaction or diffusion constant k within the corresponding model. Especially, we consider the values k + dT k at the upper end and k − dT k at the lower end of the aggregate. We performed for each model and each dT ∈ {0.0, 0.2, 0.5} a total of 20 simulations. Head orientation has been subsequently evaluated by calculating the angle θ between the center of the first appearing morphogen patch and 0°, the latter defining the coldest part of the aggregate. We always use projections of the three-dimensional sphere on the z,x plane.

Results and Discussion

Behavior of the OMC model

In the following, we use simulations of the OMC model to investigate osmomechanochemical mechanisms leading to symmetry breaking in Hydra aggregates.

Shape oscillations

To begin, we investigate osmotically induced shape oscillations of an aggregate before symmetry breaking by simulating the OMC model for short times, which minimizes the influence of chemical processes on the system. We show that shape oscillations generated by the OMC model agree with corresponding experimental data. We consider the oscillations of a system with initial radius r₀ = 138 μm within different osmotic milieus, the latter given by ΔC_eff. Corresponding simulation results fit the experimental data: Evolution of the radius r follows a sawtooth time pattern with a nearly linear swelling and frequency increasing with higher inner ion concentration (Fig. 3, A and D). Furthermore, averaging the swelling rate s over the first three cycles reveals that s depends linearly on the ion concentration difference ΔC_eff (Fig. 3, B and E). Finally, changing the initial system size r₀ but keeping the ion concentrations constant reveals (similarly to experiments) an almost linear dependence of s on the radius r₀ in the range of 100–200 μm (Fig. 3, C and F). However, especially for larger systems, simulation results reveal a saturation effect of s(r₀). In summary, numerical results suggest that our system reproduces the experimentally observed shape oscillations qualitatively and quantitatively.

Figure 3.

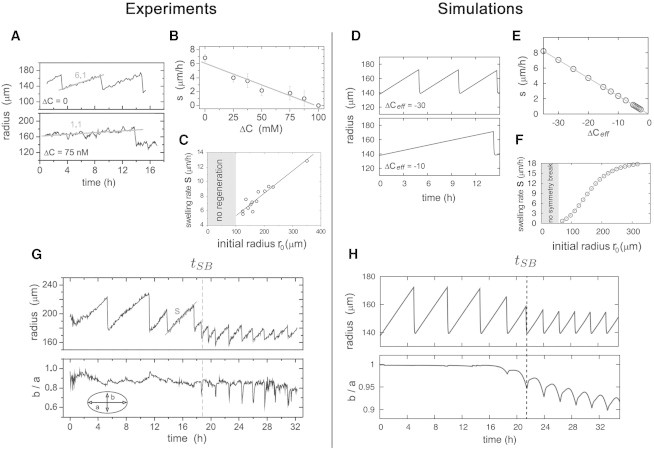
Numerical simulations and comparison with experiments considering osmotically driven shape oscillations. (A–F) Frequency and slope of sawtooth-like shape oscillations depend on both ion concentration and aggregate size. (G and H) Evolution of radius r and ratio between the minor and major inner axes b/a. Symmetry breaking time t_SB coincides with low values of b/a. (A, B, and G are taken with permission from Soriano et al. (19) and C from Kücken et al. (36).) For (D) and (E), we used a system of initial size r₀ = 138 μm.

Based on this, in the following, we investigate the OMC model for times sufficient for the system to pass from phase I (before symmetry breaking) to phase II (after symmetry breaking) to allow chemical processes play a noticeable role. In agreement with experiments (19,32), we observe in our simulations a relatively abrupt change in the mechanochemical properties of the system: At t_SB, the sawteeth are smaller (see Fig. 3, G and H, upper panel) and the previously constant value b/a ≈ 1 starts to peak at lower values (see Fig. 3, G and H, lower panel), with the latter indicating the loss of symmetry. Furthermore, an important observation is that the times at which b/a reaches minima coincide with moments of tissue collapse in both experiments and simulations.

With the change in mechanical symmetry, the sphere also develops a chemical asymmetry at t_SB: Whereas morphogens appear equally distributed before symmetry breaking (Fig. 4 A), after t_SB, a distinct morphogen patch becomes apparent (Fig. 4 C). Due to the proposed feedback loop, this patch causes a local weakening of the tissue leading to both the mechanical system asymmetry (i.e., low values of b/a) and earlier tissue rupture reducing the sawteeth size. This local tissue weakening probably causes an effect shared by simulations and experimental observations (19): In phase I, tissue rupture occurs at random places whereas in phase II, rupture only occurs at the center of the morphogen patch, representing an early organizer (results not shown). Finally, simulations also show instances of anisotropic inflation-deflation in phase II, as described for aggregates by Soriano et al. (19) (Fig. 4 C, right-hand side). Interestingly, the difference with respect to experimental data is that here, an opposed motion is only restricted to one side of the aggregate. In contrast, the data of Soriano et al. (19) show this behavior at two opposite points.

Figure 4.

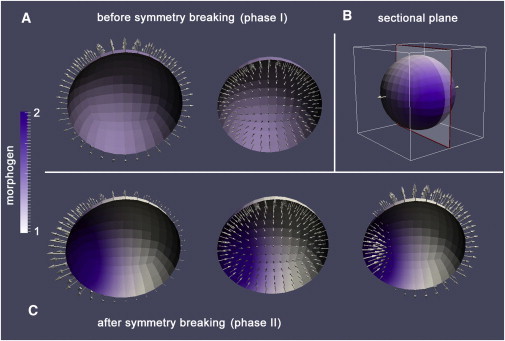
Snapshots of numerical simulations before and after symmetry breaking. (A) Symmetrical behavior before symmetry breaking changes to an asymmetrical shape and chemical patterning after symmetry breaking (C). (B) Sectional plane used for (A) and (C). (Open arrows) Direction of tissue motion; (purple color) high levels of activator morphogen Φ_A. Please note that there are moments of anisotropic inflation-deflation after symmetry breaking (lower panel, right-hand side). All simulations consider the OMC model of initial size r₀ = 138 μm. To see this figure in color, go online.

Symmetry breaking time

To further investigate our model, we compared simulations to experimental dependence of t_SB on swelling rate s, ion concentration difference ΔC_eff, and system size r₀. Unexpectedly, simulations also reproduce the experimentally observed nonlinear dependence of t_SB on swelling rate and ion concentration difference, respectively. This behavior has been previously ascribed to viscoelastic cell properties (19) and was not expected in a purely elastic system. Because the simulation results reproduce experiment strikingly well (Fig. 5, B and C), this behavior must be linked to shape oscillations rather than to rheological cell properties.

Figure 5.

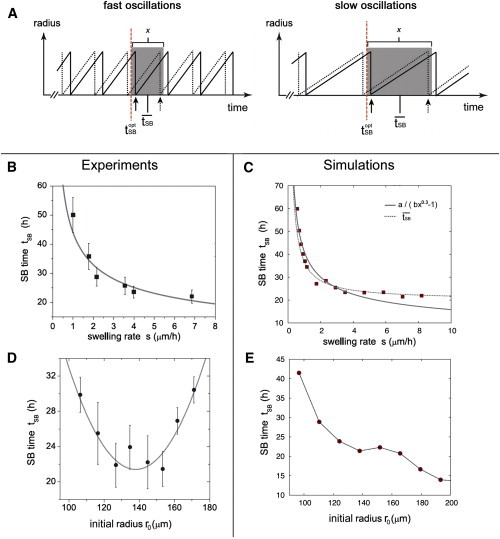
Scheme, simulations, and experiments considering symmetry breaking time t_SB. (A) Schematic dependence of t_SB on shape oscillations. The molecular mechanism of symmetry breaking allows t_SB to occur earliest at $t_{SB}^{\text{opt}}$. Solid (dashed) lines represent sawteeth with t_SB close to (away from) $t_{SB}^{\text{opt}}$ (solid and dashed arrows indicate corresponding moments of t_SB, respectively). Delays of t_SB are caused by the fact that t_SB always coincides with the moment of largest tissue stretch (upper tip of sawteeth). Thus, t_SB happens always within a certain interval (shaded in dark gray) with length x and mean value $\overline{t_{SB}}$, the latter depending on $t_{SB}^{\text{opt}}$, swelling rate s, and radius r. (C and D) The t_SB value depending on swelling rate s in experiments (B) and our simulations (C). The curve $\overline{t_{SB}}$ (dashed line in C) fits t_SB(s) better than the function a/(bx^0.3 – 1) (solid lines in B and C), the latter previously ascribed to viscoelastic cell properties (19). (D and E) Experimentally determined dependence of t_SB on system radius r differs distinctly between experiments (D) and numerical data (E), the latter based on Turing-like patterning. (B) and (D) are taken with permission from Soriano et al. (19).) To see this figure in color, go online.

We propose that, instead, a simple delaying impact of shape oscillations on symmetry breaking time t_SB is the cause for this behavior (see Fig. 5 A): As we see in Fig. 3, G and H, t_SB coincides with moments of maximal tissue stretch, i.e., tissue rupture at upper tip of a sawtooth. This means that even if the system could establish symmetry breaking at time $t_{SB}^{\text{opt}}$, the actual symmetry breaking time t_SB is delayed, depending on the moment when the next tissue rupture occurs for a $t_{\text{rupt}}\ge t_{\text{SB}}^{\text{opt}}$. Hence, t_SB occurs within the interval $\left[t_{\text{SB}}^{\text{opt}},t_{\text{SB}}^{\text{opt}}+x\right[$, where x is the time of an oscillation (see Fig. 5 A). The exact location of $t_{SB}\in \left[t_{SB}^{\text{opt}},t_{SB}^{\text{opt}}+x\right[$ may differ for different aggregates due to individual differences; however, the mean value is given by $\overline{t_{SB}}$. Trigonometry provides that $\overline{t_{SB}}=t_{SB}^{\text{opt}}+\omega /s$, where ω = r_rupt – r₀, r_rupt is the radius at time t_rupt and s is the swelling rate. Based on Fig. 5 C, we roughly estimate $t_{SB}^{\text{opt}}\approx 20\text{h}$ considering s → ∞. As we can see in Fig. 5 C, $\overline{t_{SB}}$ (dashed line) approximates t_SB(s) better than the function a/(bx^0.3 − 1) previously proposed in Soriano et al. (19) (solid lines in Fig. 5, B and C). Hence, a purely elastic tissue model appears to be sufficient to describe the main aspects of Hydra tissue behavior.

Which morphogen patterning mechanism is involved?

So far, all presented simulation results are partly independent of the chemical aspect of symmetry breaking and pattern formation: Until now only the fact that tissue stretch causes morphogen patterning was required, but not what this dependence and the patterning mechanism looks like in detail.

To understand the role of chemistry in the process of symmetry breaking, we considered the dependence of t_SB on the initial aggregate radius r₀. Here, the simulation results for the OMC model strongly differ from the experimental results (Fig. 5, D and E). As a next step, we compared experimental data (Fig. 5 D) to the results for the Turing-, SOC-, and curvature-increasing models. These purely chemical models have been investigated in systems without shape oscillations. In contrast, the experimental results depicted in Fig. 5 D are the result of both chemical and mechanical effects influencing t_SB. This means that, in a direct comparison, we assume 1) that the delaying impact of shape oscillations is negligible in the considered range of r₀; and that 2) parameters depending on periodic tissue stretch can be represented by constant values, i.e., we assume that a tissue constantly stretched at a medium level behaves approximately like the oscillating system.

The first assumption can be easily justified by pointing out that the above-mentioned delaying effect is only visible for swelling rates x ≤ 4 μm/h (Fig. 5, B and C), which corresponds (within the ion concentration regime used for Fig. 5 D) to aggregate sizes <100 μm (see Fig. 3 G), i.e., below the range considered in in Fig. 5 D. Regarding the second assumption, we cannot exclude that the oscillating system produces (beside the delaying impact) other effects we cannot describe using constant parameters. One possibility: finite size synchronization effects between oscillating mechanical and chemical processes (54) that may cause fluctuations in Ks1-expression depend on the sphere size in a nontrivial way. Nevertheless, we assume that the following studies present the main characteristics of the three investigated pattern formation models, and we postpone coupling them to shape oscillations to future research.

Turing patterning

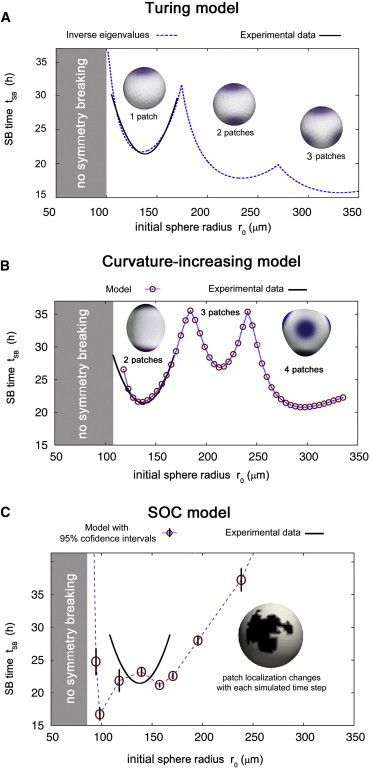
Although we found several different sets of parameters for Turing systems of two and three equations approximating the experimental data provided in Fig. 5 D, they were all indistinguishable to the naked eye. One example is given in Fig. 6 A. As we can see, the Turing mechanism fits experimental data quite well, including the loss of symmetry breaking below sizes of r₀ < 100 μm. For larger systems, our numerical data predict an acceleration of symmetry breaking with characteristic upward peaks of t_SB at each system size where an additional morphogen patch appears. However, to our knowledge, corresponding experimental data are not available so far. Hence, the experimental investigation of t_SB for larger (multiple head) aggregates could serve as a key step to validate an underlying DDI mechanism in Hydra aggregates. In contrast to experimental observations (27), simulations of the Turing model do not show dependence of axis orientation on temperature gradients (Fig. 7).

Figure 6.

Different models considering symmetry breaking time t_SB depending on system size. (A) Turing model. (B) Curvature-increasing model. (C) SOC model. (Black solid lines) Approximated experimental data taken from Soriano et al. (19). (Dashed blue lines and red points) Model data. (Gray shaded) Regions without symmetry breaking. To see this figure in color, go online.

Figure 7.

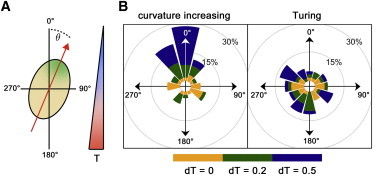
Angular orientation of the Hydra aggregate head orientation within a temperature gradient, simulated for different patterning mechanisms. (A) Schematic view. (B) Rosette-diagram of the curvature-increasing versus the Turing model. 0° corresponds to the cold side. To see this figure in color, go online.

The morphogen Wnt3 fulfills properties of the activator molecule: It appears early during head formation (26); is strongly restricted to the organizer region (25); and its regulation contains elements for an autoregulatory feedback (via the molecules Tcf and β-catenin) and a repressor (31)—as required within Eq. 8. However, a possible molecular candidate for the long-range inhibitor is still missing, and for both Wnt3-activator and -inhibitor molecules, various binding sites have been identified (31). Furthermore, it has been recently proposed that Wnt molecules may act as both activators and, after processing, inhibitors (24).

Tissue curvature-driven patterning

As depicted in Fig. 6 B, the curvature-increasing mechanism fits experimental data, including the loss of symmetry breaking for small aggregates. However, the behavior of t_SB for larger aggregates differs distinctly from that of a Turing-driven mechanism: Above r₀ ≈ 110 μm, symmetry breaking occurs, starting with two patches for 110 μm ⪅ r₀ ⪅ 180 μm, three patches for 180 μm ⪅ r₀ ⪅ 240 μm, and four patches for r₀ ⪆ 240 μm. Hence, in this model, the smallest possible number of morphogen patches is 2, in contrast to one organizer appearing experimentally in small aggregates. However, two patches still define one body axis. Additional mechanisms are required leading to the selection and dominance of one organizer. In accordance with experimental data (27,37), simulations of the curvature-increasing model reveal that the orientation of the body axis depends critically on temperature gradients: Defining the first of the two (40) appearing morphogen patches as the head, we find that weak temperature gradients (dT = 0.2) result in preferred head formation at the cold (θ ≈ 0°) or the warm (θ ≈ 180°) site, while stronger gradients (dT = 0.5) lead to heads only at the cold side (Fig. 7 B).

Wnt3 molecules appear early during head formation and are restricted to outwardly curved tissue regions, such as head and budding zones (25,26). Thus, one of the various binding sites regulating Wnt3-expression (31) could be influenced by local tissue deformations, finally stimulating Wnt3-expression in evaginated tissue regions. In turn, it has been experimentally shown that Wnt-signaling induces local tissue evaginations in Hydra (35), which could constitute the other part of the curvature-driven feedback loop. In contrast to Turing models, we do not need the existence of a molecular long-range inhibitor, because this role is played by regions where the tissue is not outwardly curved (40).

To obtain a more complete model, such curvature-driven morphogen patterning might need additional coupling to osmomechanical processes, as assumed for Turing-driven patterning within the OMC model (Fig. 1). The morphogen could again lower the resistance to lateral tissue stretch if the production of this morphogen depends on tissue curvature as well as tissue stretch (Fig. 2). Thus, tissue curvature and stress could jointly influence morphogen patterning, leading to symmetry breaking only in case of periodic shape oscillations. Numerical investigation of such a coupling is postponed to future research.

SOC-driven patterning

We tested different possible mechanisms defining symmetry breaking in the context of the SOC model. Assuming that the exceedance of a critical (relative) Ks1-positive cluster size, $N_{\text{crit}}^{\text{rel}}$, locks the head localization, the dependence of t_SB on system size shows neither a parabolic shape nor a loss of symmetry breaking for small systems, but changes monotonously. The same holds true if we define the moment of scale-free Ks1 expression as the moment of symmetry breaking (results not shown). However, if we assume that a critical absolute Ks1-positive cluster size $N_{\text{crit}}^{\text{abs}}$ defines the axis, the shape of t_SB(r₀) is qualitatively similar to experimental results: for small aggregates, we do not observe symmetry breaking whereas for larger systems, t_SB shows an almost parabolic shape (Fig. 6 C). In contrast to the Turing and the curvature-induced mechanism (Fig. 6, A and B), here, t_SB increases monotonously for larger systems with 150 μm ⪅ r₀ ⪅ 350 μm. We find the best match to experimental data for $N_{\text{crit}}^{\text{abs}}=2250$, which is of the same order as the critical sizes estimated in Gamba et al. (37). Although the agreement of these simulations with experimental data is not as good as in the case of the Turing or the curvature-increasing model, the exact shape of t_SB(r₀) could be influenced by other parameters of the SOC model, such as neighbor numbers or production rates, which have not been varied in our studies.

As mentioned above, the SOC mechanism reproduces the dependence of head localization on weak and strong temperature gradients, as previously shown in Soriano et al. (27) and Gamba et al. (37).

Assuming that Ks1-patterning defines the head localization, it might act upstream of morphogen expression patterns related to the organizer, such as Wnt3 (25,26). Although a direct interaction between Ks1 and Wnt3-regulatory elements probably does not take place (31), interestingly, regulatory elements of Ks1 and Wnt3 were both identified to specifically bind the same type of molecules—nuclear proteins from the basal tissue (29,31).

Similarly to the Turing- or the curvature-driven patterning, a complete model of symmetry breaking might involve the coupling of the SOC mechanism to OMC shape oscillations of the Hydra aggregate (Fig. 1). A natural coupling involves Ks1-expressing cells lowering the resistance to lateral tissue stretch, and in turn, tissue stretch accelerating protein production and/or discharge processes (Fig. 2).

Conclusions

In this article we model interplay among osmotic, chemical, and mechanical processes leading to symmetry breaking in Hydra aggregates. Simulations demonstrate that a simple feedback loop between tissue mechanics and morphogen patterning can qualitatively and quantitatively reproduce a wide range of experimental data. In particular, we assume that tissue stretch induces morphogen clustering, and morphogen lowers the resistance to lateral stretching. To elucidate the chemical part of this mechanochemical interplay, we compared previously proposed morphogen patterning models, namely the Turing, SOC, and curvature-increasing models. Comparison to experimental data neither strongly supports nor excludes any of these mechanisms. We showed that the dependence of symmetry breaking time t_SB on system size r₀ distinctly differs among these three mechanisms for aggregates with r₀ ⪆ 180 μm. Thus, we suggest experimental investigations of larger aggregates as a key step to gain further insights into the molecular mechanisms of Hydra symmetry breaking.

Author Contributions

M.M., A.K., and A.M.-C. designed research; M.M. developed mathematical models; M.M. and A.K. performed research, developed numerical tools, and analyzed data; and M.M., A.M.-C., and A.K. wrote the article.

Editor: Rong Li.

Supporting Citations

References (55,56) appear in the Supporting Material.