Abstract
Gibbons are believed to have diverged from the larger great apes ∼16.8 MYA and today reside in the rainforests of Southeast Asia. Based on their diploid chromosome number, the family Hylobatidae is divided into four genera, Nomascus, Symphalangus, Hoolock, and Hylobates. Genetic studies attempting to elucidate the phylogenetic relationships among gibbons using karyotypes, mitochondrial DNA (mtDNA), the Y chromosome, and short autosomal sequences have been inconclusive . To examine the relationships among gibbon genera in more depth, we performed second-generation whole genome sequencing (WGS) to a mean of ∼15× coverage in two individuals from each genus. We developed a coalescent-based approximate Bayesian computation (ABC) method incorporating a model of sequencing error generated by high coverage exome validation to infer the branching order, divergence times, and effective population sizes of gibbon taxa. Although Hoolock and Symphalangus are likely sister taxa, we could not confidently resolve a single bifurcating tree despite the large amount of data analyzed. Instead, our results support the hypothesis that all four gibbon genera diverged at approximately the same time. Assuming an autosomal mutation rate of 1 × 10−9/site/year this speciation process occurred ∼5 MYA during a period in the Early Pliocene characterized by climatic shifts and fragmentation of the Sunda shelf forests. Whole genome sequencing of additional individuals will be vital for inferring the extent of gene flow among species after the separation of the gibbon genera.
Keywords: approximate Bayesian computation, gibbon species, rapid radiation, whole genome sequences
THE family Hylobatidae, commonly known as gibbons, is believed to have diverged from the larger great apes ∼16.8 MYA (Carbone et al. 2014). Sometimes known as small apes, gibbons demonstrate substantial morphological differentiation from the great apes; their much smaller bodies are highly adapted to an arboreal mode of locomotion in the rainforests of Southeast Asia. They also demonstrate very little sexual dimorphism that may, in part, be related to their generally monogamous mating patterns (Fuentes 2000) (although some gibbon species develop differences in coat color at sexual maturity).
Each species demonstrates distinct “call” and “song” types (Geissmann 2002); however, attempts to classify gibbon species and genera based solely on morphological features have been problematic (Mootnick 2006). Primarily on the basis of their karyotypes, gibbons are now divided into four major genera, with Nomascus, Symphalangus, Hylobates, and Hoolock each possessing 52, 50, 44, and 38 diploid chromosomes, respectively. While many genetic studies have been performed, including a number based on karyotypes (Müller et al. 2003), mitochondrial DNA (mtDNA) (Hayashi et al. 1995; Takacs et al. 2005; Monda et al. 2007; Whittaker et al. 2007; Matsudaira and Ishida 2010; Van Ngoc et al. 2010), Y chromosomes (Chan et al. 2012), Arthrobacter luteus (ALU) repeats (Meyer et al. 2012), and short stretches of autosomal sequence (Kim et al. 2011; Wall et al. 2013), the phylogenetic relationships among the four gibbon genera remain unresolved, with at least seven different topologies being supported by different data.
A recent study examined ∼1.5 Mb of orthologous autosomal sequence generated by second-generation sequencing from one individual representing each of the four genera (Wall et al. 2013). This study, too, was inconclusive and suggested that the gibbon genealogy demonstrates substantial incomplete lineage sorting (ILS). However, the experimental design was limited by the lack of a suitable reference genome (short reads were aligned to highly divergent human hg19 assembly). To examine the species tree relationships among gibbons, as well as estimate key demographic parameters such as the time when the various gibbon genera diverged, we generate whole genome sequence data from eight individuals representing all four gibbon genera and utilize the newly released gibbon (nomLeu1) reference genome (Carbone et al. 2014) for mapping and variant calling. Then we apply a coalescent-based ABC approach that can handle large amounts of sequence data and that corrects for potential sequencing error and reference genome mapping bias.
Materials and Methods
Second-generation sequencing
Blood and tissues were obtained in agreement with protocols reviewed and approved by the Gibbon Conservation Center. More details on all aspects of the methods are provided in Supporting Information. DNA was extracted from blood or cell lines, and paired-end libraries were prepared with the Illumina TruSeq chemistry. Libraries were shotgun sequenced on the HiSeq 2000 platform, generating 2 × 100-bp reads. Multiple runs were performed to generate a minimum of 10× mean coverage on each sample after all postprocessing. Mean coverage ranged from 11.5× to 19.5×. Exome capture using the TruSeq Exome Enrichment kit (Illumina) was also performed on one N. leucogenys (NLE) sample (Vok, 116× coverage) and one species syndactylus (SSY) sample (Monty, 64× coverage)
Read mapping and variant calling
Trimmed reads from the shotgun sequencing were aligned to nomLeu1 with Stampy (v. 1.0.17) (Lunter and Goodson 2011). For the two NLE samples, Stampy was used in its “hybrid mode” where alignment with Burrows-Wheeler Aligner (BWA) (v. 0.5.9) (Li and Durbin 2009) is attempted first. A substitution rate of 0.001 was specified, along with BWA minimum seed length of 2, fraction of missing alignments 0.0001, and quality threshold 10. For the non-NLE samples, Stampy was used with a substitution rate of 0.015 (Kim et al. 2011). Local realignment at indel sites was performed with the Genome Analysis Toolkit (GATK, v. 1.4-37) (McKenna et al. 2010; Depristo et al. 2011). PCR duplicates were removed with samtools. GATK UnifiedGenotyper was run separately on the two samples from each genus and single nucleotide variants (SNVs) and indels with a quality score of at least 50 were retained to create a mask of variant sites to be excluded from base quality score recalibration. The GATK indel realignment tool was run again to standardize alignment of indels across all samples. UnifiedGenotyper from GATK version 2.1-11 (to allow multiallelic calling) was used to produce a final set of SNVs and indels. Each site was annotated with the consensus quality score of the nomLeu1 reference sequence. Exome sequencing data were processed separately from the shotgun data but using the same bioinformatic pipeline (more details can be found in Supporting Information).
Masking of the gibbon reference genome for downstream analysis
The nomLeu1 genome is composed of 17,968 contigs, ranging in size from 2496 bases to ∼74 Mb. As small loci may be compressed and represent duplications in the gibbon genome that have not been properly separated during the assembly process, we masked out all scaffolds <1Mb in length, yielding 273 scaffolds that span ∼2.73 Gb. University of California Santa Cruz (UCSC)’s gibbon–human pairwise alignments were used to identify nonautosomal sequence. Specifically, gibbon loci that aligned to human X, Y, or M in UCSC’s “net” alignments (Kent et al. 2003) were masked, along with locations in the gibbon genome that were not primary alignments to locations in the human genome. Further, locations where the gibbon reference quality was below a phred quality of 50 repeats [identified by Tandem Repeat Finder (Benson 1999) or by RepeatMasker (Smit et al. 1996)], LAVA elements identified in Carbone et al. (2014), copy number variants (CNV) with an estimated ploidy >2.5 in any sample (also identified in Carbone et al. 2014), infinite site violations, positions where any sample has less than <7× coverage, or more than their 95th percentile read depth, and bases within 3 bp of any indel called were excluded, unless otherwise specified, from downstream analysis.
Profiling of sequencing errors
As our WGS coverage is ∼15× per sample, it is likely that some observed genotype calls will not reflect the true underlying genotypes, either because of a combination of low coverage and errors in the sequencing reads or as a result of choices in the bioinformatic processing (e.g., variant quality score thresholds). Therefore, we compared genotype calls between the WGS and whole exome sequencing (WES) data at the same genomic positions to profile errors present in our medium coverage WGS, assuming high coverage WES reflects a “truth set.” Separate profiles were constructed for Vok and Monty. These profiles were then used (a) as training data to find a set of high confidence SNPs variable across all eight gibbon samples using machine learning (ML) methods, and (b) to stochastically model error processes in our subsequent ABC analysis.
Our profiling and modeling of errors made the following simplifying assumptions: (1) after masking, any WES site with 30× ≤ coverage ≤ 200× is called without error and reflects the truth dataset and all other bases are ignored, (2) per site read depth and mapping bias (which we naively model by noting whether the sample belongs to the same taxon as the reference or not) account for all genotyping errors observed, and (3) all false negatives (i.e., SNPs present in the WES, but not present in the whole genome data) are singletons. We profiled errors between the WES truth set and WGS for a given target sample (Vok or Monty) via two categories: errors involving singleton polymorphisms (defined with respect to the nomLeu1 reference), and genotyping errors when the polymorphism is segregating with a nonreference allele present in two or more chromosomes.
For the former category, we recorded the number of singleton calls in our WGS data vs. the number in the WES truth set. For a site to be considered a singleton, a single nonreference allele must be present in either the WGS, the WES truth set, or both for the target sample, and it must not have been observed in any other sample. Singleton sites that agree and disagree between the WGS and WES truth sets are considered as “correct” and “incorrect,” respectively.
For the latter category (i.e., any site that is segregating in either the WGS, the WES truth set, or both, but is not defined as a singleton as described above) we created 3 × 3 confusion matrices over the set of genotype calls (reference homozygous, heterozygous, alternative homozygous) to describe all nine possible WGS vs. WES truth set genotype calls for the target sample. The diagonals of these confusion matrices reflect sites with concordant calls between the WGS vs. WES truth set (i.e., they are correct) and off-diagonals represent discordance, and thus potential errors (i.e., incorrect). For example, the sum of the middle column will represent all heterozygous sites in the WES truth set. The middle element of this column represents sites that were also called heterozygous in the WGS data (i.e., correctly called sites). The top (bottom) element represents a genotyping error in the WGS data where the site is truly heterozygous but was called homozygous reference (alternate).
Finding accurately called segregating sites
ML classification techniques, such as variant quality score recalibration, have been successfully used to find a subset of sites that are predicted to be truly segregating in a sample. However, the authors know of no technique that has been used to predict whether or not individual genotypes have been correctly called, and as such downstream methods that presume that the genotypes are correct when they are in fact incorrect may suffer accordingly. To this end we developed an ML classification protocol to find a set of segregating sites where every genotype within is predicted to be correct for use in our principal components analysis. Broadly, this protocol uses the comparison of the WGS and WES truth set to train several largely disparate classifiers. The classifiers are then used to predict the accuracy of individual genotypes across the genome. We note that this protocol may introduce some level of bias with respect to the agglomerative properties of sites (owing to the increased difficulty in calling heterozygous vs. homozygous genotypes) as opposed to individual genotypes, and as such this approach would be undesirable for evaluating, say, the site frequency spectrum.
More specifically, the ML suite Weka version 3.6.8 (Hall et al. 2008) was used to classify the WGS genotype data at all called segregating sites, with the aim of finding a subset of very high quality sites. Using the definition of correct from our profiling of errors, we collected the set of all genotypes that were incorrectly called in the genome, and a random and equally sized sampling of genotypes that were called correctly for both our NLE and our non-NLE (SSY) sample. A variety of features from the GATK output (see Supporting Information for the entire list) as well as whether the call is from the NLE or the non-NLE sample, and the combined P-value of the distribution of read depths observed at the site were used in the ML analysis. Using the various features, we generated a training set and evaluated the performance of a variety of classifiers using 10-fold cross-validation. Four techniques—multilayer perceptron, ridor, rotation forest, and classification by regression—showed reasonable performance (75–85% accuracy). After various optimization procedures, we classified a genotype call as correct if all four classifiers predicted that the genotype was correct, and we classified a site as correct if all genotypes at a site were classified as correct. Principle Components Analysis (PCA) was performed using smartpca (Patterson et al. 2006) and visualized using R.
ABC analysis
Our ABC framework was designed to (a) identify the most likely species topology for the four gibbon genera that underwent WGS and (b) estimate key parameters of the gibbon speciation process (specifically effective population sizes and divergence times) (more detail can be found in the Supporting Information).
Data:
ABC analysis was performed on two datasets containing independent loci of small enough length such that intra and interlocus recombination could reasonably be ignored. Set 1 included 12,413 nongenic loci consisting of 1 kb of total callable sequence across a contiguous stretch of no more than 3 kb separated by at least 50 kb and at least 50 kb from the nearest exon. Set 2 included 11,323 genic loci consisting of 200 bp of total callable sequence across a contiguous stretch of no more than 4 kb separated by at least 1 kb (this distance will likely violate our assumption of independence but increasing this distance substantially decreased the number of usable loci and thus reduced the accuracy and precision of our inference to a greater extent), with an allowance of a maximum of 100 bp of the locus lying adjacent to an exon and the rest lying in the exon (Figure S1). In addition to the masks and coverage filters described above, we also masked CpG consistent sites as well as conserved phastCons (Siepel et al. 2005) elements inferred from primate genomes with a further 100 bp padding either side of the element. Variant sites were polarized against the aligned human reference genome, hg19.
Phylogeny models and parameter priors:
We treated all possible phylogenetic relationships among the four gibbon genera as distinct models (including, where applicable, the true polytomy model). The models are described by two classes of parameters, mean population nucleotide diversity, θ, and branch lengths, τ, in units of expected number of substitutions (thus mutation rates per site per generation do not need to be explicitly stated during the analysis). Priors ranged between 0.0001 and 0.03 for all θ and τ parameters (a justification for these prior ranges is given in Supporting Information). Unless otherwise stated, all prior distributions for all demographic parameters (θ and τ) are all uniformly distributed on a log10 (×) scale.
Simulations:
Coalescent simulations of demographic models and parameters were performed using a version of ms (Hudson 2002) modified for Python that allowed fast parallel processing to allow us to efficiently simulate the thousands of loci seen in our observed data. To account for mutation rate heterogeneity among loci, we estimated relative sequence divergence for all loci, taking the average sequence divergence for each of the eight gibbon individuals from hg19. These individual locus estimates were then normalized around a mean of 1, allowing us to follow the approach of Rannala and Yang (2003) and scale θ for each individual locus in our demographic simulations.
Stochastic error modeling:
We used the error profiles for the singleton and nonsingleton categories described above in Vok and Monty to construct an error model E = <S, M> for a particular sample that could transform perfectly correct data generated by coalescent simulations into data reflective of the error processes that are likely to have occurred during whole genome sequencing and postprocessing. We found that with our bioinformatic pipeline, the total number of observed singletons was always less than or equal to the true number. Therefore S was calculated as the proportion of missing singletons, or the probability of not calling a true singleton in the WGS data. During a coalescent simulation of genetic data, S reflects the rate at which true singletons will be hidden or dropped and the genotype called as homozygous reference. To construct M, we took the 3 × 3 confusion matrix generated for nonsingletons and divided the number in each element of the matrix by the sum of all elements within their respective columns. During a simulation of genetic data, for any site not classed as a true singleton but still segregating, the values within a particular column of M reflect the probabilities of a multinomial distribution that determines the rate that a true genotype of a particular type will be transformed to one of the two other genotypes or stay the same.
To apply our error correction to (a) nonexome regions in the two target samples, and (b) nonexome regions in the other six samples for which there was no WES, we constructed separate E models for each read depth ≥7× (i.e., we constructed Ei, the estimated error rate at a particular read-depth i). This allowed us to construct an overall E model for a particular sample, regardless of whether it was one of the two target samples or not, by taking a weighted average of Ei, with weights determined by the empirical distribution of read depths at the specific regions of interest. The Ei models for Vok and Monty were used for NLE and non-NLE samples, respectively, to take into account any potential mapping biases.
Ancestral state misidentification adjustment:
The 2% ancestral state misidentification was incorporated into simulations by calculating the expected number of sites to experience a mutation along the hg19 lineage for each locus (1000 bp × 2% = 20 sites). The number of sites to actually “flip” (i.e., assign the wrong ancestral state) for each locus during a simulation is drawn from a Poisson distribution with this mean. These sites are then randomly assigned to a position along the locus with equiprobability, though only positions that are found to segregate among the gibbon chromosomes need to be flipped computationally.
Summary statistics:
We computed the following summary statistics to describe the observed and simulated data for every pair of populations across all loci: mean number of shared derived polymorphisms, mean number of private derived polymorphisms in each population, and the mean number of private fixed sites in each population. We also explored including the variance of these summary statistics across all loci but found they added little to our ability to infer parameters in the model while contributing more noise to the partial least squares (PLS) transformation and reduced the proportion of correctly inferred simulated topologies using simulated pseudo-observed data.
Inference:
We used the logistic regression (LR) method previously described (Fagundes et al. 2007) to perform model choice. When estimating model parameters, we utilized ABCtoolbox (Wegmann et al. 2010), which implements a general linear model (GLM) adjustment (Leuenberger and Wegmann 2010) on retained simulations. Before ABC analysis for parameter inference, the full set of summary statistics was transformed into PLS components (Wegmann et al. 2009) and we used the change in root mean square error (RMSE) to guide the choice of number of components. The 1% of simulations closest to the observed data were retained for the GLM (parameter estimation) and LR (model choice) adjustments.
G-PhoCS analysis
The Markov chain Monte Carlo (MCMC) Bayesian coalescent-based method described by Gronau et al. (2011) was performed using the software G-PhoCS to estimate θ and τ values for a bifurcating tree (we ignored the effect of migration). On this occasion, we included a human haploid sequence (hg19) as an outgroup for the overall gibbon phylogeny (rather than just to infer the ancestral state as in the ABC analysis). The same 12,431 1-kb loci and the bifurcating species tree with the highest posterior probability from the ABC analysis described above were utilized and the mutation rate was fixed individually for each locus as above using the normalized divergence values. The gamma prior for θ was set to be relatively broad and the same for all present and ancestral populations with shape, α = 2 and rate, β = 1000. Gamma priors for τ were also set to be relatively broad, with the α value always 2. However, either (a) β was set as 200 for all τ-values or (b) individual β-values were set for each τ such that the mean value reflected rough estimates from the ABC analysis or the human/gibbon split time from Carbone et al. (2014) (Table S1). We ran three independent MCMC chains for both prior settings a and b. We allowed 10,000 samples as burn-in followed by 100,000 samples for estimating parameters. The Markov chain converged to stationarity much quicker than the utilized burn-in period, and all six runs converged to the same stationary distribution. Results were processed using the software Tracer (http://tree.bio.ed.ac.uk/software/tracer/).
Results
Second generation sequencing and validation
We performed second generation WGS on two individuals (one male and one female) from each of the four gibbon genera (Table 1). For our Nomascus samples, represented by the species leucogenys (NLE, the northern white-cheeked gibbon), the two individuals examined differed from the (NCBI Project 13975 GCA_000146795.1) nomLeu1 reference genome. For our Hylobates samples (the most diverse genus with ∼13 species), we examined one individual each from the H. moloch (HMO, Javan gibbon) and H. pileatus (HPI, pileated gibbon). Our Symphalangus sample is represented by two individuals from the species syndactylus (SSY, Siamang gibbon). It is important to point out that the two Hoolock samples from the leuconedys species (HLE, Eastern hoolock gibbon) represent the only wild-born individuals present in the study, whereas all other individuals were captive born (i.e., offspring of individuals living in zoos). We also mention that matings between different gibbon species (and even different genera) are known to result in viable offspring in captivity (Myers and Shafer 1979; Mootnick 2006; Hirai et al. 2007). If any of the individuals in our sample are indeed hybrids between different species, our analysis may be affected in unexpected ways.
Table 1. Gibbon samples undergoing second generation sequencing.
| Chr no. | Genus | Species | Common name | Code | Sex | Origin | Mean coverage |
|---|---|---|---|---|---|---|---|
| 52 | Nomascus | Nomascus leucogenys | Northern white-cheeked | NLE | M | Parents WB | 13.78 |
| F | Parents WB | 11.50 | |||||
| 50 | Symphalangus | Symphalangus syndactylus | Siamang | SSY | M | Sire WB, dam CB | 12.80 |
| F | parents CB | 19.53 | |||||
| 38 | Hoolock | Hoolock leuconedys | Eastern hoolock gibbon | HLE | M | WB | 19.15 |
| F | WB | 14.36 | |||||
| 44 | Hylobates | Hylobates pileatus | Pileated gibbon | HPI | M | Parents WB | 14.33 |
| 44 | Hylobates | Hylobates moloch | Javan gibbon | HMO | F | Sire WB, dam CB | 12.96 |
WB, wild born; CB, born in captivity.
After postprocessing the sequence data, we obtained a mean coverage of 15× (min = 11.5×, max = 19.5×) (Figure S2). As previous work has indicated a relatively high divergence between gibbon genera, we attempted to incorporate potential reference bias into our postprocessing by utilizing a higher substitution rate (1.5%) when mapping sequence reads for non-NLE samples, and by using a hybrid mapper, Stampy (Lunter and Goodson 2011) to increase sensitivity. To validate our variant calling, we performed high coverage WES on one NLE individual and one non-NLE sample (the male SSY sample). Mean coverage for WES data were 116× (compared with 14× for WGS data) and 64× (compared with 13× for WGS data), respectively. Human-based exome capture has been shown to be effective in primates as diverged from humans as macaques (Jin et al. 2012). Utilizing only exome calls with coverage between 30× and 200× we found slightly greater concordance between the WGS and WES data for the NLE (99.6%) vs. non-NLE samples (99.4%) (Table S2). Noticeably when only examining singleton variants, calling was markedly better in the reference taxa (∼99% of exome-called sites identified in the WGS data) than in the nonreference taxa (∼96%), suggesting reference biases may still exist in our data for rare variants in nonreference taxa.
Genetic diversity among gibbon genera
Within genera diversity, assessed for this dataset by Carbone et al. (2014), demonstrated that NLE samples had the highest level of nucleotide diversity (π ∼ 2.2 × 10−3), while values as low as ∼7.3 × 10−4 were observed in the HPI sample. Nucleotide diversity for the HMO sample was also relatively high at ∼1.7 × 10−3, followed by SSY (∼1.4 × 10−3), and then the two wild-born HLE (∼8 × 10−3). By way of comparison, π ranges from ∼0.5–1.0 × 10−3 in humans, 1.8 × 10−3 in western lowland gorillas, and 2.3 × 10−3 in Sumatran orangutans (Prado-Martinez et al. 2013). To examine the relative levels of genetic differentiation among the gibbon genera we performed PCA on the individual samples. For this analysis we examined diallelic SNPs called in all individuals. High-quality SNPs were identified by using concordance with the WES data to train a ML algorithm to predict highly confident genotype calls across the whole genome and in samples that did not undergo WES. In addition, to ensure independence of SNPs, we randomly selected sites that were separated by at least 100 kb when on the same scaffold. This resulted in a dataset of 25,531 high-quality genome-wide independent SNPs. The first four principal components accounted for 40.2, 31.2, 24.6, and 3.5% of the variation, respectively (Figure S3, A and B). The four genera showed substantial genetic differentiation and were clearly separated in the PCA plot in the first two components, though no clear intergenera phylogenetic relationship emerged. Individuals from the same species showed high similarity suggesting limited intergenera hybridization or contamination. The two Hylobates species could be clearly distinguished in PC4. We were also able to reproduce the same patterns when only using a random subset of ∼200 SNPs (Figure S3, C and D), suggesting it may be possible to perform relatively low coverage shotgun sequencing from a number of different gibbon species and use a similar approach to this in order to identify a small yet powerful set of species-specific SNPs. This could be particularly important for management of gibbons in zoos when it can often be difficult to distinguish different species or even genera based on fur alone, sometimes leading to accidental hybrids.
A coalescent-based ABC analysis of the gibbon phylogeny
Unless species branch lengths are several orders of magnitude larger than the expected time to the most recent common ancestor of sequences within a species, it is important to model stochasticity in the distribution of gene trees across loci when inferring an underlying species tree (Rosenberg and Nordborg 2002). Current Bayesian coalescent-based methods such as BEAST (Drummond and Rambaut 2007) that explicitly take into account sequence and population divergence simultaneously to infer species trees are generally computationally intractable for large datasets (Bryant et al. 2012). Therefore, to infer the species topology for gibbon genera we developed an ABC (Beaumont et al. 2002) method for inference of a species tree with four taxa. The method can also infer species divergence times and effective population sizes for a given topology, can handle large amounts of sequence data, is not dependent on haplotype phase, and incorporates information derived from our modeling of errors from comparing WGS with high coverage WES data.
Analogous to the Bayesian approach of Gronau et al. (2011), which uses an analytical derivation to determine the likelihood of the full data given typical population genetic parameters, the data required for this ABC method are short, independent loci as we assume no intralocus recombination and free recombination between loci. The latter is a necessary convenience given that no recombination map is currently available for gibbons. Thus, we assembled a set of independent “nongenic” sequences that mapped at least 50 kb away from genes (∼12,000 1-kb loci) and that excluded CpG consistent sites as well as evolutionarily conserved elements (Siepel et al. 2005) (Figure S1). Mutations detected in these loci are expected to represent neutral variation and to evolve at a relatively constant rate. To reduce reference-mapping bias, we also assembled an analogous set of independent “genic” loci that span exons (∼11,000 200-bp loci) and that should have lower diversity, recognizing that these loci may have been subjected to natural selection, which may bias any parameter estimates.
Analysis of pseudo-observed data generated by simulations demonstrated that we were able to detect the correct topology from randomly drawn datasets using our method 88.4% of the time, with the correct model among the three highest posterior probabilities 99% of the time (Figure S4). Analysis of a more targeted set of pseudo-observed data demonstrated that the method is only likely to fail when an internal branch is extremely small (almost instantaneous in evolutionary terms) or when the total height of the tree in units of expected number of substitutions is on the order of 0.001 (equivalent to ∼1 million years for apes) (Figure S5), which is unrealistic for gibbons.
As most ABC analyses are based on performing simulations to approximate an otherwise analytically intractable likelihood function, we also attempted to stochastically model sequence errors (missing singletons and incorrect genotype calls at other segregating sites) that are likely to have occurred in the real second generation sequencing data. Errors were introduced into coalescent simulations by an E model constructed by comparing the WGS with the high coverage WES data. By incorporating this E model we found through simulated pseudo-observed data that we could infer more accurate estimates of θ and τ under very simple demographic scenarios (one population with a constant size θ through time and two populations of constant size that diverged at some time, τ, in the past) (Figure S6). A full description of the above validation of our ABC framework using pseudo-observed data are given in Supporting Information.
Prior to the ABC analysis of the real data we examined the one-dimensional distribution for each individual summary statistic from 10,000 random simulations from the θ and τ parameter space and found a good fit to our nongenic and genic observed data, while a PCA also demonstrated a good multidimensional fit (Figure S7).
Table 2 shows the posterior probabilities from the ABC analysis for all phylogenetic models for the observed data for both the nongenic and genic loci using the corrected (with stochastic errors introduced via the E model) and uncorrected coalescent simulations (a total of four analyses). No topology dominates the analysis, with three to four topologies having posterior probabilities >10% in the corrected simulations. The best topology using nongenic and genic loci for the corrected simulations differ, and both still maintain relatively low posterior probabilities of ≤19%. Two topologies appear most prominent with posterior probabilities >10% in all four analyses and the highest means across all four analyses and both (genic and nongenic) corrected analyses. One is the most frequently observed topology in the sequence divergence analysis (((SSY, HLE), NLE),(HPI, HMO)) of Carbone et al. (2014) and the other is a related topology where (HPI, HMO) and NLE are swapped as the most external groups with HLE and SSY remaining as sister taxa. Together the posterior probability for both these related topologies sum to 30–32%. However, in general the posterior probabilities are lower than typically observed in our pseudo-observed datasets, suggesting that we have little confidence in the true topology. This is consistent with the hypothesis of a rapid radiation of gibbon species from a large ancestral population.
Table 2. Posterior probabilities for the 15 possible four-population topologies for nongenic and genic loci.
| Nongenic | Genic | |||
|---|---|---|---|---|
| Topology | Corrected | Uncorrected | Corrected | Uncorrected |
| (((SSY,HLE)NLE)(HPI,HMO)) | 0.16 | 0.15 | 0.19 | 0.15 |
| ((((HPI,HMO)NLE)SSY)HLE) | 0.19 | 0.14 | 0.11 | 0.08 |
| (((SSY,HLE)(HPI,HMO))NLE) | 0.14 | 0.23 | 0.13 | 0.19 |
| ((((HPI,HMO)NLE)HLE)SSY) | 0.13 | 0.11 | 0.06 | 0.05 |
| (((NLE,HLE)SSY)(HPI,HMO)) | 0.06 | 0.05 | 0.10 | 0.08 |
| ((((HPI,HMO)SSY)NLE)HLE) | 0.07 | 0.06 | 0.08 | 0.07 |
| ((((HPI,HMO)SSY)HLE)NLE) | 0.05 | 0.07 | 0.07 | 0.14 |
| (((HPI,HMO)NLE)(SSY,HLE)) | 0.05 | 0.04 | 0.05 | 0.03 |
| (((NLE,SSY)HLE)(HPI,HMO)) | 0.03 | 0.03 | 0.06 | 0.04 |
| (((NLE,HLE)(HPI,HMO))SSY) | 0.04 | 0.03 | 0.04 | 0.04 |
| (((NLE,SSY)(HPI,HMO))HLE) | 0.03 | 0.03 | 0.03 | 0.02 |
| ((((HPI,HMO)HLE)SSY)NLE) | 0.02 | 0.04 | 0.03 | 0.06 |
| ((((HPI,HMO)HLE)NLE)SSY) | 0.02 | 0.02 | 0.02 | 0.02 |
| (((HPI,HMO)SSY)(NLE,HLE)) | 0.01 | 0.01 | 0.03 | 0.02 |
| (((HPI,HMO)HLE)(NLE,SSY)) | 0.01 | 0.01 | 0.01 | 0.00 |
Boldface type indicates the topology identified using sequence divergence in Carbone et al. (2014).
The simplest phylogenetic description of this process would be a four-way hard polytomy. Therefore we constructed an additional model with all four genera diverging at the same time and analyzed this scenario within the same ABC framework as the previously examined 15 bifurcating topologies (i.e., we examined 16 different models in total). This did not affect our ability to infer the correct model using pseudo-observed datasets. As with considering only strictly bifurcating topologies, we were able to detect the correct topology from randomly drawn datasets from all 16 models 87.3% of the time. Of the 16 individual models, the instantaneous model was the one with the lowest proportion of correctly predicted pseudo-observed datasets but was still high at 82.4%.
Despite having the lowest predictive value, when we examined the real data the posterior probability for the instantaneous model ranged from 87–90% for both the nongenic and genic loci and for the corrected and uncorrected simulations (Table 3). The posterior probabilities of the 15 bifurcating topologies after the addition of the instantaneous model were necessarily much lower but still highly correlated with the previous values with r2 ranging between 0.91 and 0.98. Thus, our ABC analysis strongly supports a relatively instantaneous hard polytomy for the divergence of the four gibbon genera over that of a particular bifurcating topology. Evidence for this can also be seen visually by examining a PCA of the summary statistics for 1000 random datasets from each of the 16 models, with the instantaneous model lying within the center of the cloud of all models and the observed data found firmly within this part of the cloud (Figure S8). Other polytomy combinations may also fit the data (for example a model with the initial divergence of three lineages, followed by a later Hoolock and Symphalangus divergence) but our ability to reliably discriminate such additional intermediate models is likely to further worsen given our instantaneous model already shows reduced predictive ability compared to the other fully bifurcating models.
Table 3. Posterior probabilities for the 15 possible four-population topologies as well as a instantaneous four-way hard polytomy for nongenic and genic loci.
| Nongenic | Genic | |||
|---|---|---|---|---|
| Topology | Corrected | Uncorrected | Corrected | Uncorrected |
| Instant | 0.874 | 0.859 | 0.902 | 0.899 |
| (((SSY,HLE)NLE)(HPI,HMO)) | 0.024 | 0.023 | 0.018 | 0.017 |
| ((((HPI,HMO)NLE)SSY)HLE) | 0.024 | 0.023 | 0.011 | 0.011 |
| (((SSY,HLE)(HPI,HMO))NLE) | 0.023 | 0.037 | 0.016 | 0.018 |
| ((((HPI,HMO)NLE)HLE)SSY) | 0.015 | 0.016 | 0.007 | 0.008 |
| ((((HPI,HMO)SSY)NLE)HLE) | 0.008 | 0.007 | 0.010 | 0.007 |
| (((HPI,HMO)NLE)(SSY,HLE)) | 0.007 | 0.006 | 0.005 | 0.002 |
| (((NLE,HLE)SSY)(HPI,HMO)) | 0.007 | 0.007 | 0.009 | 0.008 |
| ((((HPI,HMO)SSY)HLE)NLE) | 0.005 | 0.008 | 0.007 | 0.013 |
| (((NLE,HLE)(HPI,HMO))SSY) | 0.003 | 0.003 | 0.004 | 0.005 |
| (((NLE,SSY)HLE)(HPI,HMO)) | 0.002 | 0.002 | 0.002 | 0.003 |
| ((((HPI,HMO)HLE)NLE)SSY) | 0.002 | 0.002 | 0.002 | 0.002 |
| (((NLE,SSY)(HPI,HMO))HLE) | 0.002 | 0.002 | 0.001 | 0.001 |
| ((((HPI,HMO)HLE)SSY)NLE) | 0.002 | 0.004 | 0.002 | 0.003 |
| (((HPI,HMO)SSY)(NLE,HLE)) | 0.001 | 0.001 | 0.003 | 0.002 |
| (((HPI,HMO)HLE)(NLE,SSY)) | 0.001 | 0.000 | 0.000 | 0.000 |
Estimation of parameters describing gibbon demography
To estimate when this rapid radiation may have taken place, we constructed a model where all four genera diverge simultaneously with the addition of a subsequent divergence of the two Hylobates species. This resulted in a model with seven θ and two τ parameters. The summary statistics from the nongenic loci were transformed into PLS components to infer these parameters. Parameter estimates and posterior distributions are shown in Table S3 and Figure S9. These results are based on 15 PLS components, the value at which the largest reduction in the RMSE was observed across all parameters, Figure S10, and for which the C.I. values for τ were considered relatively reliable based on how often the true value fell within the estimated 95% C.I. using 1000 pseudo-observed datasets (Veeramah et al. 2012).
Observed values of π described above were within the 95% C.I. for the θ values estimated by the ABC analysis for present-day species and showed the same relative pattern with the highest value in the NLE and lowest value in the HPI sample. The divergence time, τ1, for the two Hylobates samples was ∼50% less than that for the divergence time of the four gibbon genera, τ2, which is consistent with the relative difference in sequence divergence of ∼50% seen in Carbone et al. (2014). Because the priors were log10 scaled, the associated 95% C.I. values potentially could be larger in absolute values (i.e., 10^val) than if the observed posterior distribution had been shifted toward a smaller branch length. Therefore, we reran the ABC analysis using unscaled flat priors for the two τ values, which resulted in highly similar median values but much narrower 95% C.I.’s (Table 4, Table S4, Figure S11). We note that these C.I.’s were somewhat anticonservative as assessed by pseudo-observed datasets (see column “HDPI 95% fit” of Table 4 and Table S4). When we assume a μ of 1 × 10−9 per site per year * 3/4 (to take into account that we excluded CpG sites) (Hodgkinson and Eyre-Walker 2011) this results in an estimate for the time of the gibbon radiation of 1.6 + 3.5 = 5.1 MYA (τ1–τ2 combined limits of 95% C.I. 2.5–7.7 MYA) and a split time of 1.6 MYA (95% C.I. 0.6–2.9 MYA) for the two Hylobates samples. In addition, assuming 10 years per generation for gibbons (Harvey et al. 1987) and thus a μ of 7.5 × 10−9 per generation, Ne for extant species varies from 57,000 (NLE) to 7500 (HPI). Interestingly, the ancestral gibbon Ne is estimated to be much larger at 132,000 (107,000–162,000) (Figure 1A) as would be expected if substantial ILS was observed. It should be noted that the estimate of the ancestral Hylobates population size (based on θT1) may be somewhat unreliable as the regressed posterior distribution shows a major shift from the raw retained posterior distribution (Figure S11) while this was also the θ value for which the largest number of PLS components was needed to obtain a reasonable reduction in the RMSE (Figure S12).
Table 4. Posterior estimates for an instantaneous speciation model for gibbon genera using a flat prior for τ.
| Posterior estimationb | |||||
|---|---|---|---|---|---|
| HDPI 95 | |||||
| Parameter | HDPI 95% fita | Mode | Median | Lower | Upper |
| θNLE | 0.930 | 1.71E-03 | 1.72E-03 | 1.07E-03 | 2.73E-03 |
| θSSY | 0.936 | 9.25E-04 | 9.24E-04 | 5.97E-04 | 1.43E-03 |
| θHLE | 0.937 | 4.17E-04 | 4.17E-04 | 2.63E-04 | 6.58E-04 |
| θHPI | 0.968 | 2.24E-04 | 2.25E-04 | 1.30E-04 | 3.92E-04 |
| θHMO | 0.974 | 8.29E-04 | 8.32E-04 | 4.13E-04 | 1.68E-03 |
| θT1 | 0.958 | 3.54E-03 | 3.80E-03 | 7.69E-04 | 1.90E-02 |
| θTanc | 0.964 | 3.97E-03 | 3.97E-03 | 3.23E-03 | 4.86E-03 |
| τ1 | 0.905 | 1.05E-03 | 1.23E-03 | 5.01E-04 | 2.18E-03 |
| τ2 | 0.911 | 2.69E-03 | 2.59E-03 | 1.41E-03 | 3.63E-03 |
A metric demonstrating how often known simulated values (n = 1,000) fell within the calculated 95% C.I., which gives a guide to the reliability of these C.I.’s for real data.
Calculated using 15 PLS components, 1,000,000 simulations, and retaining 1%. All priors ranged from 0.0001 to 0.03 when log10 scaled.
Figure 1.
Parameter estimates for the instantaneous radiation (A) and bifurcating speciation (B) model for gibbon genera. μ = 7.5 × 10−9/site/generation, 10 years per generation. θT2- and θT3-based Ne values are not to scale.
One potential source of error in estimating parameters is ancestral state misidentification due to back mutations along the human lineage, which was used as an outgroup (Hernandez et al. 2007). Our simulated data assumed an infinites sites model. Assuming a human–gibbon split time of 16.8 MYA and μ of 1 × 10−9 per site per year, each site has ∼98% chance [(1-1 × 10−9)^16,800,000] of not experiencing a substitution along the human branch. Therefore, we conducted the ABC parameter estimation on a set of 105 simulations where we incorporated a 2% rate of random ancestral allele misidentification. Though this binary model of back mutation is highly simplistic (e.g., it does not take into account mutations to another base-pair type or trinucleotide context), we found it had only minimal impact on our 95% C.I.’s compared with the same number of simulations that did not incorporate some ancestral state misidentification error (Table S5). This suggests that our divergence time estimates may be only slightly underestimated by not accounting for this error.
To investigate the effect of imposing a model of instantaneous speciation rather than bifurcating species divergence on our parameter inference, we also modeled the five gibbon species assuming the best sequence phylogeny from Carbone et al. (2014) and that was also suggested by our ABC model choice analysis, [(((SSY, HLE)NLE)(HPI,HMO))] (Table S6, Figure 1B, Figure S13, Figure S14). The median estimates of the posterior distributions for the seven θ parameters common to both the bifurcating and instantaneous models (five extant population values as well θT1 and θanc) were similar, while the 95% C.I. for θT1 and θT2 were broad and uninformative. Consistent with the rapid speciation hypothesis (even when allowing bifurcating speciation), τ2+ τ3+ τ4 was roughly equivalent to τ2 for the instantaneous speciation model, with τ3 and τ4 being an order of magnitude smaller (i.e., very short internal branch lengths).
We also applied the 1 kb data to the method of Gronau et al. (2011) as this approach is based on a similar model (i.e., the coalescent with population divergence) as our bifurcating ABC analysis; however, it should be more accurate for parameter estimation as it is based on an exact model likelihood rather than an approximation (although it does not currently incorporate the possibility of sequence error). While the implementation for estimating divergence times is slightly different (e.g., our ABC approach uses time intervals between divergence events rather than absolute divergence times from the present), the results are very similar: very short internal branch lengths among gibbon genera and a total gibbon genera divergence time of ∼5–6 MYA. However, as expected when using the full data rather than an approximation of it (Csilléry et al. 2010), the 95% C.I.’s estimated by G-PhoCS (Table S1) were substantially narrower than those estimated by ABC, which are likely inflated because of a loss of information through the use of insufficient summary statistics.
Allele sharing and D-statistic analysis
Because of the small sample sizes and large divergence times, it is not expected that we would have the ability to infer gene flow if added as an additional parameter (whether an instantaneous pulse or continuous migration after divergence) in our ABC analysis. Although intergenera hybrids have been observed in captivity, they are almost certainly infertile as a result of the complicated patterns of homology that would disrupt meiotic pairing. Moreover, such matings have never been observed in the wild, even for sympatric species (Hirai et al. 2007). Therefore, it is unlikely that gene flow would continue for long after divergence as is typically modeled using isolation with migration approaches. Of course, this assumption depends on the rate of karyotypic change, which is thought to have occurred relatively soon after divergence and to have contributed to the speciation process (Carbone et al. 2014). Thus, accounting for biologically meaningful gene flow would increase the complexity of the model beyond what can likely be reliably inferred using ABC for this dataset.
However, a fairly simply measure that can help to infer admixture events (although not necessarily help to reveal the mode, timing, or extent of admixture) is the D-statistic (Durand et al. 2011). We first examined patterns of allele sharing across the whole genome by tallying the state of each genus at variable sites by (a) choosing sites that met certain quality criteria (as determined by our masks) and that were homozygous for the same allele in both individuals from a genus (filt1), (b) randomly sampling one allele from the two genotypes from a genus for sites that met the same quality criteria as a (filt2), or (c) randomly sampling one read from both individuals in a genus at a site (filt3) (Table S7a). We also repeated this at the species level, using only the highest coverage sample from each species (in this case filt1 reflects homozygous allele sharing) (Table S7c). Results were not qualitatively different using these different filtering criteria.
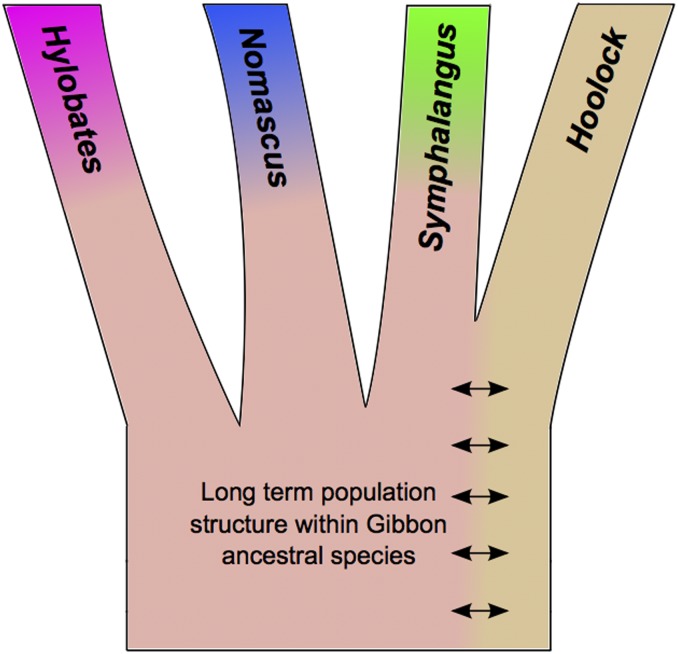
Consistent with our ABC analysis and Wall et al. (2013), SSY and HLE share the largest number of alleles. Interestingly, while NLE and the two Hylobates samples share a fairly low number of alleles compared with other pairwise comparisons, they both share more alleles with SSY than HLE. We performed a D-statistic analysis that demonstrated this excess sharing was statistically significant (Table S7, b and d). Under the assumption that SSY and HLE diverged last among the four genera as indicated in our ABC analysis, such a pattern is consistent with a model involving two independent gene flow events into SSY from both NLE and Hylobates after they diverged from HLE. An alternative model that does not invoke postdivergence gene flow involves the maintenance of long-term population structure between the ancestors of HLE and the ancestral population giving rise to the other gibbon genera (Figure 2). We attempted to incorporate population structure into our ABC framework but found via simulations that we could not distinguish between these models, especially given a parameter space consisting of short internal branch lengths as observed in this dataset (data not shown).
Figure 2.
Cartoon of proposed model of ancestral population structure among gibbon genera.
We also used the D-statistic to examine whether there was any evidence of unbalanced allele sharing between the two Hylobates species. While the D-statistic slightly favored more allele sharing between HMO and the other three genera, the values were generally quite low and the Z-scores were only greater than |2| under filtering scheme 2.
Discussion
Previous attempts to resolve the phylogenetic relationships among the four gibbon genera based on different genetic systems (karyotypes changes, mtDNA, the Y chromosome, and short autosomal sequences, and ALU repeats) resulted in widely discordant phylogenies. All samples utilized in this study were also analyzed as part of the Gibbon Genome Project (Carbone et al. 2014) where the best supported overall consensus tree based on genome-wide sequence divergence was found to be (((SSY, HLE), NLE),(HPI, HMO)). However, all four gibbon genera demonstrated a narrow range for sequence divergence (1.08–1.12%; mean 1.10%). Here, we developed a potentially powerful species tree analysis framework for four taxa that made use of genome-wide second generation sequencing data and took into account discordant gene trees and applied them to the problem of the phylogenetic relationships of the four gibbon genera. Despite the availability of whole genome sequence data and the methodology demonstrating success with most simulated pseudo-observed datasets, we could not confidently resolve the phylogenetic relationships between Nomascus, Symphalangus, Hylobates, and Hoolock, although Symphalangus and Hoolock may represent the most recently diverged genera. This latter result is consistent with the best consensus gene tree identified by Carbone et al. (2014) and Wall et al. (2013).
The most well-supported bifurcating phylogeny is characterized by long external branch lengths and very short internal branch lengths, pointing to a rapid radiation of the four gibbon genera from a large ancestral effective population of ∼105 individuals. Indeed, when we included an additional model representing a four-way hard polytomy in our ABC analyses we found substantial support for this scenario of instantaneous divergence over any of the individual bifurcating topologies (at least at the level of resolution of branch lengths afforded by the data). This demographic scenario would explain previous observations of genome-wide ILS (Wall et al. 2013) and discordant phylogenies across smaller datasets. However, we note that an alternative explanation is that the ancestral gibbon population already exhibited structure prior to the divergence of the four gibbon genera.
It is possible that such a stark restructuring of the gibbon population during this proposed radiation event was driven by some major climatic or geological shift. This is particularly likely as gibbons reside predominantly on the relatively shallow Sunda continental shelf of Southeast Asia. At various times, sea level changes and volcanic activity significantly altered the amount of habitable land (i.e., above sea level) in this region. As gibbons live a highly arboreal lifestyle, any reduction or fragmentation of their native forest habitats could have led to extreme genetic isolation between geographically dispersed populations. This, coupled with a rapid evolution of karyotype differences, could have driven the speciation process among these gibbon taxa.
Uncertainty in timing of the gibbon radiation
It is important to note that associating the timing of speciation with the geological or climatological record is complicated by uncertainty in how we calibrate our estimates of τ (i.e., our choice of mutation rate). A phylogenetic estimate of μ for great apes that is often used is ∼1 × 10−9 per site per year, an estimate based on calibrating sequence divergence with the fossil record (Takahata and Satta 1997; Nachman and Crowell 2000). This would place the radiation of gibbon genera within the early Pliocene ∼5 MYA. Interestingly, it has been proposed that the Sunda shelf was largely one land mass up to 5 MYA (Outlaw and Voelker 2008), after which sea levels began to rise until ∼3 MYA (Cichon et al. 2004) leading to the fragmenting of the region. There is evidence for an increased rate of divergence in other plants and animals during this early Pliocene window (Gorog et al. 2004; Outlaw and Voelker 2008; Akula et al. 2010; López-Guillermo et al. 2010) and thus, it is possible that gibbon divergence may have been driven by the same process.
On the other hand, a value of μ = 0.5 × 10−9 per site per year has recently been estimated using direct observation of mutations in human trios and quartets (Roach et al. 2010; Kong et al. 2012). Scally and Durbin (2012) attempted to reconcile the phylogenetic and direct pedigree estimates with the fossil record (which itself is used to calibrate the phylogenetic estimate) by invoking the hominid slowdown hypothesis. Under this hypothesis, the increased body size of great apes correlates with a decrease in generation time and a reduction in the annual mutation rate after their divergence from Old World monkeys. Evidence for this comes from evolutionary comparisons of Great Apes to Old World monkeys (e.g., humans have a 30% slower evolutionary rate as compared to baboons) (Kim et al. 2006). While generally bigger than Old World monkeys, the largest gibbons, from the genus Symphalangus, are approximately half the size of the smallest great ape, Pan paniscus. Thus, given that gibbons have smaller body sizes (and shorter generation times) than other apes, it is not clear to what extent the hominid slowdown hypothesis would apply.
Decreasing the mutation rate would lead to a Late Miocene speciation time of up to ∼10 MYA, thus encompassing previous estimates of divergence at ∼6–8 MYA based on mtDNA (Chan et al. 2010; Matsudaira and Ishida 2010; Van Ngoc et al. 2010). However, fossil calibration-based estimates such as used in these studies are subject to their own biases (Lukoschek et al. 2012), while estimates of demography from a single locus (especially a nonrecombining region of the genome, no matter how well resolved the gene tree) are subject to large evolutionary stochasticity (Rosenberg and Nordborg 2002). It is noteworthy that the Y chromosome estimate differs from the mtDNA estimate substantially (5 and 9 MYA, respectively) despite application of the same calibration procedures (Chan et al. 2012).
Our results do appear to rule out the hypothesis of Chivers (1977), which suggests a Late Pleistocene divergence of gibbon genera. Despite this, the constant formation and destruction of land bridges during the Pleistocene that drives the Pleistocene pump hypothesis (Gorog et al. 2004; Akula et al. 2010) may have contributed to divergence of the several species within each gibbon genus (for example the pileatus/moloch split we observe ∼1.6 MYA). Though the exact numbers are the subject of some debate, it is generally accepted that there are at least 7, 6, and 2 different Hylobates, Nomascus, and Hoolock species, respectively (Van Ngoc et al. 2010; Mittermeier et al. 2013; Rowe and Myers 2015). Movement during these periods likely explains the current distribution of Hylobates species both on the mainland and the islands of Sumatra, Borneo, and Java, especially when one considers that gibbons probably cannot swim. Today neighboring gibbon species are largely isolated from each other by rivers. Further whole genome sequencing of multiple individuals from additional species, along with the application of powerful genomic methods to infer gene flow or admixture between species, will provide invaluable information for inferring the relationships among gibbon species across Southeast Asia. In addition, while it is well recognized that land bridges certainly formed during the Pleistocene, there is still great uncertainty as to whether these would have involved forest canopy or more savannah-like vegetation (Bird et al. 2005). Analysis of patterns of historic gene flow among the tree dwelling gibbons may help shed light on this process. Recent work using small amounts of autosomal sequence data (∼11 kb) has already found evidence of asymmetrical gene flow between Hylobates species currently located on different islands (Chan et al. 2013) while a basic D-statistic analysis in this article also hinted at the possibility of introgression between genera after divergence.
Challenges in the use of whole genome sequence data for estimating demographic parameters:
Despite the fact that we generated whole genome sequences, it is important to appreciate that the explicit ABC modeling performed here utilized only a small amount of the total available data. A pairwise sequentially Markovian coalescent (PSMC) (Li and Durbin 2011) analysis presented in Carbone et al. (2014) takes a different approach to utilizing genome-scale sequence data. By incorporating patterns of genetic diversity across individual genome sequences, important insights can be gained into changing Ne through time. To summarize these findings in the context the ABC demographic analysis presented here, both the NLE and HMO populations show major fluctuations in effective population size during the time frame after gibbon genera diverged, when Pleistocene geological and climate shifts were taking place.
Composite likelihood methods that evaluate the entire allele frequency spectrum (AFS) across many populations may also prove useful for inference in situations such as the one presented here (Gutenkunst et al. 2009). These methods are likely to be particularly effective for estimating additional parameters such as recent size changes and migration when many individuals are sampled from multiple species compared to our approach, which uses only a summary of the AFS, though demographic events on the order of millions of years ago may still not be tractable regardless of sample size (Robinson et al. 2014). These approaches can also take advantage of recent methods that allow relatively unbiased estimation of the AFS from even low coverage second generation sequencing data (though this currently must be done for each population separately). There have also been advances in extending these AFS-based approaches to many (more than three) populations and testing alternative scenarios even when using nonnested models and composite rather than full likelihoods (Excoffier et al. 2013), though whether these can reliably be used for contrasting many different models simultaneously in a phylogenetic context has yet to be explored. One notable limitation of these approaches is that they assume independence of sites and ignore linkage, and thus inference of migration and admixture is potentially underpowered (Sousa and Hey 2013).
However, to fully exploit whole genome data for demographic inference using coalescent methods, it will be vital to construct genetic maps in gibbons, preferably separately for each genus, such that recombination can be appropriately incorporated into any population genetic analysis. In addition, despite applying a correction factor in our analysis, reference bias toward Nomascus genomes was evident in our data, and it is likely that even more reference bias exists than we actually observe due to the variable karyotypes across genera. It seems unlikely that further large-scale Sanger sequencing will be used to link up scaffolds or generate reference genomes for the other three non-Nomascus genera, while short-read Illumina data are not suited for this task. However, the application of new sequencing technologies with long reads such as the PacBio (English et al. 2012) and nanopore (Schneider and Dekker 2012) technologies may provide useful and relatively low cost alternatives to assemble more robust reference genomes. This should lead to more powerful demographic and evolutionary analyses of gibbons in the future.
Using ABC in phylogenetics
There is currently one published generalized ABC phylogenetic approach (ST-ABC) (Fan and Kubatko 2011). This method relies on having accurately phased sequence as it treats frequencies of gene tree topologies across loci as the data rather than summary statistics, and has only been tested and applied to relatively small datasets. However, it has also been questioned whether ST-ABC can accurately approximate the posterior distribution, as it relies on expectations of the distribution of gene trees rather than random simulations that incorporate sampling variability (Buzbas 2012). Our ABC approach does not have these limitations. While it could not reliably infer a particular bifurcating gibbon genera topology with any confidence because of the extremely short internal branch lengths (as we showed with our additional analysis of an instantaneous speciation model, a bifurcating topology may not actually exist in this case of gibbons), simulations suggest our ABC approach should allow us to infer the correct species topology for four taxa in most reasonable cases.
However, it is important to appreciate that the framework applied here is tailored for this particular dataset involving unphased genome-wide data from a few individuals per taxa that diverged within the last 10 million years or so. How it would scale up with regard to speed with increasing numbers of samples, and how much accuracy and precision would be lost with fewer loci requires further investigation. It is possible that adding variance in the number of shared sites across loci as a summary statistic may prove useful in this case. In addition, increasing the number of taxa considered (even by one) could prove problematic due to a rapid increase in the parameter space (i.e., a large increase in the number of possible topologies) and an increase in the numbers of summary statistics needed to capture the phylogenetic structure (i.e., the potential impact of the “curse of dimensionality”). Combining more efficient ways of traversing tree space (Bryant et al. 2012) may help with regard to the former issue, while choosing a more efficient set of summary statistics (e.g., via PLS) may improve the latter; however, there are still likely to be limits to how well the data can be summarized in just a few summary statistics for large phylogenies. Another potential issue of our approach that would place limits on the possible time depth for the phylogeny considered is the assumption of an infinite sites mutation model. It would be trivial to incorporate more complex substitution models, although this would also increase the computational burden.
With these improvements in mind, the ABC family of methods has the potential to provide a useful and flexible phylogenetic tool that balances the need to incorporate large genomic datasets while taking into account gene tree uncertainty and variation in a coalescent framework. Genomic data are being generated at a rapid pace for a diverse set of species and it is clear that phylogenetic methods are required that can accommodate such data. ABC provides one approach to do this.
Supplementary Material
Acknowledgments
We thank Ryan Sprissler and the University of Arizona Genetics Core for assistance with sequencing and Ryan Gutenkunst for computing resources. Support for this work was provided by the National Institutes of Health to J.D.W. and M.F.H. (R01_HG005226) and an European Research Council Starting Grant (260372) and Ministerio de Ciencia e Innovación (Spain) BFU2011-28549 to T.M.-B.
Footnotes
Supporting information is available online at http://www.genetics.org/lookup/suppl/doi:10.1534/genetics.115.174425/-/DC1.
Communicating editor: M. A. Beaumont
Literature Cited
- Akula N., Cabanero M., Cardona I., Corona W., 2010. Speciation dynamics in the SE Asian tropics: Putting a time perspective on the phylogeny and biogeography of Sundaland tree squirrels, Sundasciurus. Mol. Phylogenet. Evol. 55: 711–720. [DOI] [PubMed] [Google Scholar]
- Beaumont M. A., Zhang W., Balding D. J., 2002. Approximate Bayesian computation in population genetics. Genetics 162: 2025–2035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson G., 1999. Tandem repeats finder: a program to analyze DNA sequences. Nucleic Acids Res. 27: 573–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bird M. I., Taylor D., Hunt C., 2005. Palaeoenvironments of insular Southeast Asia during the Last Glacial Period: a savanna corridor in Sundaland? Quat. Sci. Rev. 24: 2228–2242. [Google Scholar]
- Bryant D., Bouckaert R., Felsenstein J., Rosenberg N. A, RoyChoudhury A., 2012. Inferring species trees directly from biallelic genetic markers: bypassing gene trees in a full coalescent analysis. Mol. Biol. Evol. 29: 1917–1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzbas E. O., 2012. On the article titled “Estimating species trees using approximate Bayesian computation”(Fan and Kubatko, Molecular Phylogenetics and Evolution 59: 354–363). Mol. Phylogenet. Evol. 65: 1014–1016. [DOI] [PubMed] [Google Scholar]
- Carbone L., Harris R. A., Gnerre S., Veeramah K. R., B. Lorente-Galdos et al, 2014. Gibbon genome and the fast karyotype evolution of small apes. Nature 513: 195–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan Y.-C., Roos C., Inoue-Murayama M., Inoue E., Shih C.-C., et al. , 2010. Mitochondrial genome sequences effectively reveal the phylogeny of Hylobates gibbons. PLoS ONE 5: e14419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan Y.-C., Roos C., Inoue-Murayama M., Inoue E., Shih C.-C., et al. , 2012. A comparative analysis of Y chromosome and mtDNA phylogenies of the Hylobates gibbons. BMC Evol. Biol. 12: 150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan Y.-C., Roos C., Inoue-Murayama M., Inoue E., Shih C.-C., et al. , 2013. Inferring the evolutionary histories of divergences in Hylobates and Nomascus gibbons through multilocus sequence data. BMC Evol. Biol. 13: 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chivers D. J., 1977. The lesser apes, pp. 539–598 in Primate Conservation, edited by Monaco P. R. I. O., Bourne H. G. Academic Press, New York. [Google Scholar]
- Csilléry K., M. Blum, O. E. Gaggiotti, and O. François, 2010 Approximate Bayesian computation (ABC) in practice. Trends in Ecology & Evolution. 25: 410–418. [DOI] [PubMed]
- Depristo M. A., Banks E., Poplin R., Garimella K. V., Maguire J. R., et al. , 2011. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat. Genet. 43: 491–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A. J., Rambaut A., 2007. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol. Biol. 7: 214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand E. Y., Patterson N., Reich D., Slatkin M., 2011. Testing for Ancient Admixture between Closely Related Populations. Mol. Biol. Evol. 28: 2239–2252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- English, A. C., S. Richards, Y. Han, M. Wang, V. Vee et al., 2012 Mind the gap: upgrading genomes with Pacific Biosciences RS long-read sequencing technology PLoS ONE 7: e47768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier, L., I. Dupanloup, E. Huerta-Sanchez, V. C. Sousa, and M. Foll, 2013 Robust demographic inference from genomic and SNP data. PLoS Genet 9: e1003905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagundes N. J. R., Ray N., Beaumont M., Neuenschwander S., Salzano F. M., et al. , 2007. Statistical evaluation of alternative models of human evolution. Proc. Natl. Acad. Sci. USA 104: 17614–17619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan H. H., Kubatko L. S., 2011. Estimating species trees using approximate Bayesian computation. Mol. Phylogenet. Evol. 59: 354–363. [DOI] [PubMed] [Google Scholar]
- Fuentes A., 2000. Hylobatid communities: changing views on pair bonding and social organization in hominoids. Am. J. Phys. Anthropol. 113: 33–60. [DOI] [PubMed] [Google Scholar]
- Geissmann T., 2002. Duet-splitting and the evolution of gibbon songs. Biol. Rev. Camb. Philos. Soc. 77: 57–76. [DOI] [PubMed] [Google Scholar]
- Gorog A. J., Sinaga M. H., et al. , 2004. Vicariance or dispersal? Historical biogeography of three Sunda shelf murine rodents (Maxomys surifer, Leopoldamys sabanus and Maxomys whiteheadi). Biological Journal of the. [Google Scholar]
- Gronau I., Hubisz M. J., Gulko B., Danko C. G., Siepel A., 2011. Bayesian inference of ancient human demography from individual genome sequences. Nat. Genet. 43: 1031–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst, R. N., R. D. Hernandez, S. H. Williamson, and C. D. Bustamante, 2009 Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet 5: e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall M., Frank E., Holmes G., Pfahringer B., Reutemann P., et al. , 2008. The WEKA data mining software: an update. ACM SIGKDD Explorations 11: 10–18. [Google Scholar]
- Harvey, P. H., R. D. Martin, and T. H. Clutton-Brock, 1987 Life Histories In Comparative Perspective, University of Chicago Press, Chicago. [Google Scholar]
- Hayashi S., Hayasaka K., Takenaka O., Horai S., 1995. Molecular phylogeny of gibbons inferred from mitochondrial DNA sequences: preliminary report. J. Mol. Evol. 41: 359–365. [DOI] [PubMed] [Google Scholar]
- Hernandez R. D., Williamson S. H., Bustamante C. D., 2007. Context dependence, ancestral misidentification, and spurious signatures of natural selection. Mol. Biol. Evol. 24: 1792–1800. [DOI] [PubMed] [Google Scholar]
- Hirai H., Hirai Y., Domae H., Kirihara Y., 2007. A most distant intergeneric hybrid offspring (Larcon) of lesser apes, Nomascus leucogenys and Hylobates lar. Hum. Genet. 122: 477–483. [DOI] [PubMed] [Google Scholar]
- Hodgkinson A., Eyre-Walker A., 2011. Variation in the mutation rate across mammalian genomes. Nat. Rev. Genet. 12: 756–766. [DOI] [PubMed] [Google Scholar]
- Hudson R. R., 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. [DOI] [PubMed] [Google Scholar]
- Jin X., He M., Ferguson B., Meng Y., Ouyang L., et al. , 2012. An effort to use human-based exome capture methods to analyze chimpanzee and macaque exomes. PLoS ONE 7: e40637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent W. J., Baertsch R., Hinrichs A., Miller W., Haussler D., 2003. Evolution’s cauldron: duplication, deletion, and rearrangement in the mouse and human genomes. Proc. Natl. Acad. Sci. USA 100: 11484–11489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S. K., Carbone L., Becquet C., Mootnick A. R., Li D. J., et al. , 2011. Patterns of genetic variation within and between gibbon species. Mol. Biol. Evol. 28: 2211–2218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.-H., Elango N., Warden C., Vigoda E., Yi S. V., 2006. Heterogeneous genomic molecular clocks in primates. PLoS Genet. 2: e163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong A., Frigge M. L., Masson G., Besenbacher S., Sulem P., et al. , 2012. Rate of de novo mutations and the importance of father’s age to disease risk. Nature 488: 471–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leuenberger C., Wegmann D., 2010. Bayesian Computation and Model Selection Without Likelihoods. Genetics 184: 243–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R., 2009. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25: 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R., 2011. Inference of human population history from individual whole-genome sequences. Nature 475: 493–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Guillermo A., Campo E., Xue Z. Y., Yarnall D. P., Briley J. D., et al. , 2010. Elucidating the evolutionary history of the Southeast Asian, holoparasitic, giant-flowered Rafflesiaceae: Pliocene vicariance, morphological convergence and character displacement. Mol. Phylogenet. Evol. 57: 620–633. [DOI] [PubMed] [Google Scholar]
- Lukoschek V., Scott Keogh J., Avise J. C., 2012. Evaluating fossil calibrations for dating phylogenies in light of rates of molecular evolution: a comparison of three approaches. Syst. Biol. 61: 22–43. [DOI] [PubMed] [Google Scholar]
- Lunter G., Goodson M., 2011. Stampy: a statistical algorithm for sensitive and fast mapping of Illumina sequence reads. Genome Res. 21: 936–939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsudaira K., Ishida T., 2010. Phylogenetic relationships and divergence dates of the whole mitochondrial genome sequences among three gibbon genera. Mol. Phylogenet. Evol. 55: 454–459. [DOI] [PubMed] [Google Scholar]
- McKenna A., Hanna M., Banks E., Sivachenko A., Cibulskis K., et al. , 2010. The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 20: 1297–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer T. J., McLain A. T., Oldenburg J. M., Faulk C., Bourgeois M. G., et al. , 2012. An Alu-based phylogeny of gibbons (hylobatidae). Mol. Biol. Evol. 29: 3441–3450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittermeier, R. A., D. E. Wilson, and A. B. Rylands, 2013 Handbook of the Mammals of the World, Lynx Edicions, Barcelona. [Google Scholar]
- Monda K., Simmons R. E., Kressirer P., Su B., Woodruff D. S., 2007. Mitochondrial DNA hypervariable region‐1 sequence variation and phylogeny of the concolor gibbons. Nomascus. Am. J. Primatol. 69: 1285–1306. [DOI] [PubMed] [Google Scholar]
- Mootnick A. R., 2006. Gibbon (Hylobatidae) species identification recommended for rescue or breeding centers. Primate Conservation 21: 103–138. [Google Scholar]
- Müller S., Hollatz M., Wienberg J., 2003. Chromosomal phylogeny and evolution of gibbons (Hylobatidae). Hum. Genet. 113: 493–501. [DOI] [PubMed] [Google Scholar]
- Myers R. H., Shafer D. A., 1979. Hybrid ape offspring of a mating of gibbon and siamang. Science 205: 308–310. [DOI] [PubMed] [Google Scholar]
- Nachman M. W., Crowell S. L., 2000. Estimate of the mutation rate per nucleotide in humans. Genetics 156: 297–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Outlaw D. C., Voelker G., 2008. Pliocene climatic change in insular Southeast Asia as an engine of diversification in Ficedula flycatchers. J. Biogeogr. 35: 739–752. [Google Scholar]
- Patterson N., Price A. L., Reich D., 2006. Population structure and eigenanalysis. PLoS Genet. 2: e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prado-Martinez J., Sudmant P. H., Kidd J. M., Li H., Kelley J. L., et al. , 2013. Great ape genetic diversity and population history. Nature 499: 471–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B., Yang Z., 2003. Bayes estimation of species divergence times and ancestral population sizes using DNA sequences from multiple loci. Genetics 164: 1645–1656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roach J. C., Glusman G., Smit A. F. A., Huff C. D., Hubley R., et al. , 2010. Analysis of genetic inheritance in a family quartet by whole-genome sequencing. Science 328: 636–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson J. D., Coffman A. J., Hickerson M. J., Gutenkunst R. N., 2014 Sampling strategies for frequency spectrum-based population genomic inference. BMC Evol. Biol. 14: 254. [DOI] [PMC free article] [PubMed]
- Rosenberg N. A., Nordborg M., 2002. Genealogical trees, coalescent theory and the analysis of genetic polymorphisms. Nat. Rev. Genet. 3: 380–390. [DOI] [PubMed] [Google Scholar]
- Rowe N., Myers M. (Editors), 2015. All the World’s Primates. Available at: http://alltheworldsprimates.org/Home.aspx. Accessed: 2015. [Google Scholar]
- Scally A., Durbin R., 2012. Revising the human mutation rate: implications for understanding human evolution. Nat. Rev. Genet. 13: 745–753. [DOI] [PubMed] [Google Scholar]
- Schneider G. F., Dekker C., 2012. DNA sequencing with nanopores. Nat. Biotechnol. 30: 326–328. [DOI] [PubMed] [Google Scholar]
- Siepel A., Bejerano G., Pedersen J. S., Hinrichs A. S., Hou M., et al. , 2005. Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes. Genome Res. 15: 1034–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smit A. F. A., Hubley R., Green P., 1996 RepeatMasker Open. Available at: http://www.repeatmasker.org. Accessed: April 25, 2013
- Sousa V. C., Hey J., 2013. Understanding the origin of species with genome-scale data: modelling gene flow. Nature Publishing Group 14: 404–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takacs Z., Morales J. C., Geissmann T., Melnick D. J., 2005. A complete species-level phylogeny of the Hylobatidae based on mitochondrial ND3–ND4 gene sequences. Mol. Phylogenet. Evol. 36: 456–467. [DOI] [PubMed] [Google Scholar]
- Takahata N., Satta Y., 1997. Evolution of the primate lineage leading to modern humans: phylogenetic and demographic inferences from DNA sequences. Proc. Natl. Acad. Sci. USA 94: 4811–4815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Ngoc T., Mootnick A. R., Geissmann T., Li M., Ziegler T., et al. , 2010. Mitochondrial evidence for multiple radiations in the evolutionary history of small apes. BMC Evol. Biol. 10: 74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veeramah K. R., Wegmann D., Woerner A., Mendez F. L., Watkins J. C., et al. , 2012. An early divergence of KhoeSan ancestors from those of other modern humans is supported by an ABC-based analysis of autosomal resequencing data. Mol. Biol. Evol. 29: 617–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall J. D., Kim S. K., Luca F., Carbone L., Mootnick A. R., et al. , 2013. Incomplete lineage sorting is common in extant gibbon genera. PLoS ONE 8: e53682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wegmann D., Leuenberger C., Excoffier L., 2009. Efficient approximate Bayesian computation coupled with Markov chain Monte Carlo without likelihood. Genetics 182: 1207–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wegmann D., Leuenberger C., Neuenschwander S., Excoffier L., 2010. ABCtoolbox: a versatile toolkit for approximate Bayesian computations. BMC Bioinformatics 11: 116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittaker D. J., Morales J. C., Melnick D. J., 2007. Resolution of the Hylobates phylogeny: Congruence of mitochondrial D-loop sequences with molecular, behavioral, and morphological data sets. Mol. Phylogenet. Evol. 45: 620–628. [DOI] [PubMed] [Google Scholar]
- Zhong G., Geng J., Wong H. K., Ma Z., Wu N., 2004. A semi-quantitative method for the reconstruction of eustatic sea level history from seismic profiles and its application to the southern South China Sea. Earth Planet. Sci. Lett. 223: 443–459. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.