Topology-function conservation in protein–protein interaction networks

Abstract

Motivation: Proteins underlay the functioning of a cell and the wiring of proteins in protein–protein interaction network (PIN) relates to their biological functions. Proteins with similar wiring in the PIN (topology around them) have been shown to have similar functions. This property has been successfully exploited for predicting protein functions. Topological similarity is also used to guide network alignment algorithms that find similarly wired proteins between PINs of different species; these similarities are used to transfer annotation across PINs, e.g. from model organisms to human. To refine these functional predictions and annotation transfers, we need to gain insight into the variability of the topology-function relationships. For example, a function may be significantly associated with specific topologies, while another function may be weakly associated with several different topologies. Also, the topology-function relationships may differ between different species.

Results: To improve our understanding of topology-function relationships and of their conservation among species, we develop a statistical framework that is built upon canonical correlation analysis. Using the graphlet degrees to represent the wiring around proteins in PINs and gene ontology (GO) annotations to describe their functions, our framework: (i) characterizes statistically significant topology-function relationships in a given species, and (ii) uncovers the functions that have conserved topology in PINs of different species, which we term topologically orthologous functions. We apply our framework to PINs of yeast and human, identifying seven biological process and two cellular component GO terms to be topologically orthologous for the two organisms.

Availability and implementation: http://bio-nets.doc.ic.ac.uk/goCCA.zip

Contact: natasha@imperial.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Proteins carry out specific tasks in a cell by binding to each other. New proteins are getting identified due to recent advances in genome sequencing technologies, and annotating their biological functions is receiving increasing interest (Radivojac et al., 2013). Similarly wired proteins in the protein–protein interaction networks (PINs) are shown to carry out similar functions and that fact has been exploited for transferring functional annotations between proteins (Milenković and Pržulj, 2008; Nabieva et al., 2005; Samanta and Liang, 2003; Vazquez et al., 2003). A protein’s function can be described at different levels of detail, from its molecular functions to the phenotypes that it affects. Identifying a unified descriptor for protein function is a challenging task due to the inter-dependencies and unclear separation between these levels. Gene ontology (GO) is a well-established way of handling these issues (Ashburner et al., 2000). A GO term represents either a biological process (BP), a molecular function, or a cellular component (CC) phenomenon and the ontology containing these terms describe their dependencies. A protein can be associated with multiple GO terms, each representing a different functional characteristic of the protein.

One of the important properties of a network is density: density is the proportion of the node pairs in a network that are connected with edges and it measures how tightly the network is wired. Apart from density, many different standard network properties, such as degree distribution, clustering coefficient, betweenness centrality and closeness centrality, can be used for trying to understand the information contained in the wiring of a protein in the PIN (Newman, 2010). Graphlets have been shown to be particularly useful in capturing different aspects of the wiring around a node; graphlets are small, connected, non-isomorphic, induced subnetworks of a large network (Pržulj et al., 2004). Nodes within each graphlet are said to belong same automorphism orbit, if they can be mapped to each other by an automorphism (Pržulj, 2007). The thirty 2- to 5-node graphlets and their 73 automorphism orbits are illustrated in Figure 1A. The wiring around a node can be described by generalizing the notion of node degree to graphlet degree (Milenković and Pržulj, 2008): the graphlet degree vector of node n, denoted by GDV_n, is a 73-dimensional vector where its ith coordinate, GDV _n[i], is the number of graphlets that node n touches at orbit i (Fig. 1B). The GDV captures the wiring patterns around a node for all possible subnetworks with up to five nodes.

Fig. 1.

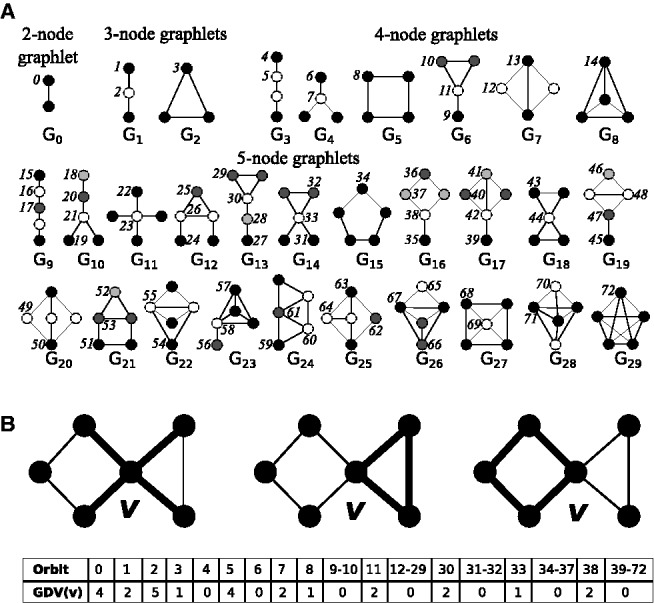
Graphlets. (A) The thirty 2- to 5-node graphlets, denoted by G₀,…,G₂₉ and their 73 automorphism orbits, denoted by 0,1,…,72 (Pržulj, 2007). (B) An illustration of the GDV of node v, e.g. node v is touched by four edges (orbit 0—illustrated in the left panel), one triangle (orbit 3—illustrated in the middle panel) and one four-node cycle (orbit 8—illustrated in the right panel). In this way, GDV quantifies the wiring of a node in the network (Milenković and Pržulj, 2008)

Because proteins almost never perform their function alone, but interact with each other to carry out their function, analysing their interaction patterns can give valuable insights into their function inside a cell (Sharan et al., 2007). It has been shown that proteins with similar functions and cellular locations tend to cluster together in the PIN of yeast (Chua et al., 2006) and 70–80% of interacting protein pairs share at least one function (Vazquez et al., 2003).

Several graph-theoretic approaches were proposed to predict the functions of proteins based on their shared neighbourhoods (Samanta and Liang, 2003; Vazquez et al., 2003) or on their closeness in the PINs (Nabieva et al., 2005). However, it was shown that the functional similarities between proteins do not necessarily depend on them being in the same local neighbourhoods, but on the similarities of their interaction patterns independent of the network location (Milenković and Pržulj, 2008). Another group of methods aligns PINs of two or more species to identify the evolutionary conserved parts of the PINs and use the resulting node-to-node mappings to transfer the functional annotations of proteins across species (Clark and Kalita, 2014). These graph-theoretic approaches show that the topological characteristics of proteins complement their sequence and structural characteristics and enable transfer of their functional annotation (Sharan and Ideker, 2006; Yook et al., 2004).

Although the link between topology and function has been widely studied, all of these studies assume that, for each function, the wiring patterns of the annotated proteins are similar. However, evolution might have varying effects on different parts of the PINs. For this reason, while some essential functions might carry the topological similarity constraint, other functions that are linked with more species-specific processes may not have such topological similarity constraints and therefore, their topological characteristics can vary.

Unlike the previous studies that aim to predict the functions of proteins from their wiring patterns in PINs, we aim to identify the most prominent wiring patterns of biological functions and to characterize their conservation across species. Our new method utilizes the canonical correlation analysis (CCA) method (Hotelling, 1936) to identify significant topology-function relationships, with the topology being represented by the graphlet degrees of proteins and their functions by GO annotations. To identify the evolutionarily conserved topology-function relationships, we separately apply our CCA-based methodology on different species and integrate the obtained results. We illustrate our method on yeast and human PINs, as they are the most complete to date, and we uncover consistent topology-function relationships for seven BP and two CC terms. These functions reveal the regions of the PINs that are evolutionarily the most conserved, which we term topologically orthologous. Furthermore, we perform three case studies on the identified patterns of ‘DNA-dependent Transcription Initiation’, ‘Cellular Localization’ and ‘Proteasome Complex’ GO annotations and show that our results are coherent with the underlying topology.

2 Materials and methods

2.1 Our new methodology

We uncover the species-specific and evolutionarily conserved (cross-species) relationships between wiring patterns and functional annotations of proteins with the following three step approach.

Step 1: identifying topology-function relationships.

For each species, the associations between topological characteristics and biological functions are defined based on their common change patterns (also called shared variance). CCA (Dillon and Goldstein, 1984; Hotelling, 1936) is a method for finding linear relationships between two sets of variables. CCA has been applied in bioinformatics context for linking gene expression data with sequence motifs (Rhee et al., 2009), identifying binding and functional sites in protein sequences (Gonzalez et al., 2012), and identifying correlated gene expressions and network characteristics (Vert and Kanehisa, 2003). Here, we utilize it to link topological descriptors with functional annotations.

For identifying the topology-function relationships, the first variable set, ${\mathbb{R}}^t$, is defined to represent topological information based on the GDVs of the proteins in the PIN. For both human and yeast, we obtain the PINs and compute the GDVs of all nodes in the PINs. We rescale the graphlet degrees to log-scale [i.e. replacing each graphlet degree x with log(x + 1)] to suppress extreme values (Milenković and Pržulj, 2008). Because low degree nodes are likely to be located in the incomplete parts of the PIN (Wang and Wu, 2013), we exclude the proteins with degree less than 4 from the CCA after which, 8 192 proteins remain for human, and 4 740 proteins remain for yeast in their respective PINs. This threshold is chosen so that all proteins can touch to graphlets at any of the graphlet orbits (a detailed discussion on the degree threshold is provided in Supplementary Section S.1). Note that the GDVs are computed before this filtering, so the exclusion has no effect on the GDVs, but only on the number of proteins that are analysed by the CCA. The second variable set of CCA, ${\mathbb{R}}^f$, is defined to represent the functional information based on the GO term annotations of the proteins. For each protein in the PIN, we encode its GO annotations as binary variables: 1 if the protein is annotated with the GO term, and 0 otherwise. We only include the GO terms that have at least five annotated proteins for both yeast and human, as we would like to identify consistent patterns in the two species and reliable patterns are unlikely to be found with fewer than five example cases. Given n pairs of variable vectors from ${\mathbb{R}}^t\times {\mathbb{R}}^f$ for n proteins, CCA finds weight vectors so as to maximize the Pearson’s correlation between the weighted sums of ${\mathbb{R}}^t$ and ${\mathbb{R}}^f$, i.e. between canonical variates. After finding the first set of such weights, CCA iterates min{t,f} times to find more weight vectors, such that the resulting canonical variates are not correlated with any of the previous canonical variates. The weight matrices, W₁ and W₂, are constructed by combining all of the identified weight vectors.

The association matrix that encodes the pairwise relations between the two sets of features is then constructed as $W_1\times S\times W_2^{+}$, where S is a diagonal matrix of canonical correlations (i.e. Pearson’s correlations among canonical variates) that weights the variates according to their correlation strength, and $W_2^{+}$ is the Moore–Penrose pseudoinverse of W₂ (detailed in Supplementary Section S.2). The association matrix combines all topology-function relationships identified by CCA and it is able to transform a GDV to a vector of real-valued topology-based annotations (illustrated in Fig. 2A and additionally explained in the figure’s legend).

Fig. 2.

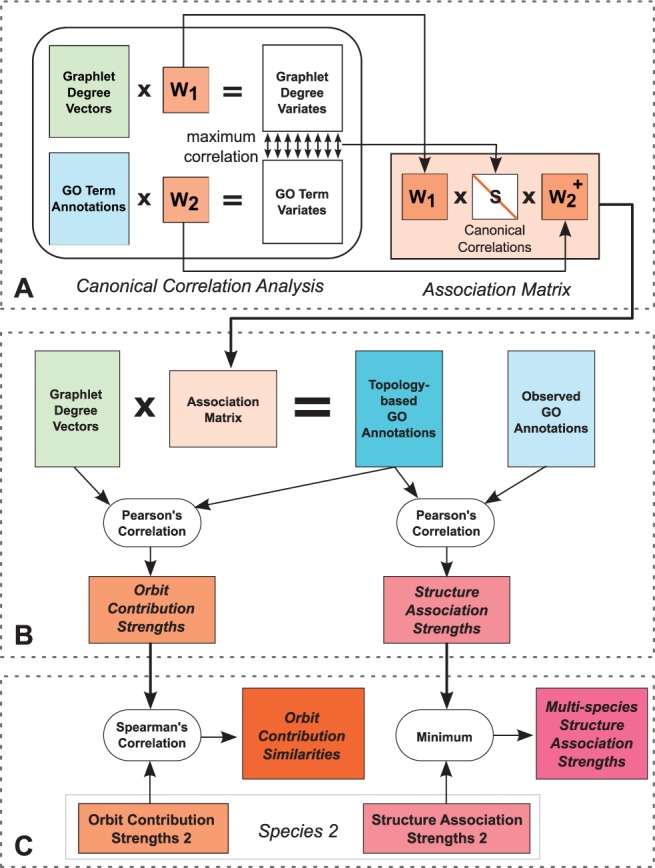
Our method for identifying the species-consistent relationships between network topology and biological function. Panel A illustrates the association matrix construction from CCA. CCA identifies weight matrices W₁ and W₂ that maximize the Pearson’s Correlation between the resulting canonical variates. These weight matrices are used for defining an association matrix that transforms GDVs to topology-based GO annotations. Panel B shows the process of identifying and characterizing single-species topology-function associations. The association matrix is used for computing the topology-based GO annotations that explain how strongly each GO term is associated with a given GDV. The Pearson’s Correlation between the topology-based GO annotations and observed GO annotations give the structure association strengths that indicate the extent to which each GO term is associated with network structure. The Pearson’s Correlation between the GDVs and the topology-based GO annotations give the orbit contribution strengths that explain the involvement of each orbit in the topology-function association per GO-term. Panel C illustrates the identification of orthologous topology-function associations. For a pair of species, the multi-species structure association strength can be computed by taking the minimum of the two per-species structure association strengths. Orbit contribution similarities for the GO terms can be quantified via the Spearman’s Correlation of the per-species orbit contribution strengths

Step 2: quantifying the topology-function relationship strengths.

There are two questions that we would like to answer using the information encoded in the association matrix: (i) which GO terms are significantly associated with a specific topological pattern in the PIN, and (ii) which graphlet orbits are significantly important for the topological pattern of a specific GO term. Although the canonical variates and their correlations with the input variables can be analysed directly in this respect, such an approach would be insufficient for uncovering the conserved patterns across species because the dimensions of the two CCA runs on yeast and human are different, and the obtained canonical variates are not comparable. To overcome this issue, we develop a method that elegantly summarizes the information encoded in the association matrix. Our method first computes the topology-based GO term annotations by multiplying the GDVs with the association matrix and then uses the obtained topology-based annotations to derive two measures that answer the two questions (Fig. 2B).

Our first measure, the structure association strength, identifies the GO terms that are strongly linked with a specific topological pattern by quantifying the linear dependence between the topology-based GO annotations and the observed GO annotations [obtained from NCBI FTP Server (Maglott et al., 2013)] using the Pearson’s correlation (Fig. 2B). The high structure association strength indicates that there is a strong correspondence between topology and function.

Our second measure, orbit contribution strength, identifies the most important orbits for the topological pattern of a GO term by quantifying the linear dependencies between graphlet degrees of each orbit and topology-based GO annotations using the Pearson’s correlations (Fig. 2B). For each GO term, the orbits with the highest absolute orbit contribution strengths characterize the local topology associated with the function described by the GO term. A discussion on choosing the topology-based annotations rather than the observed annotations for computing this measure is provided in Supplementary Section S.3.

Step 3: identifying orthologous topology-function relationships.

We can effectively find the topology-function relationships for each species by analysing their structure association strengths and orbit contribution strengths. The remaining question that we would like to answer is: which of the identified topology-function relationships are conserved across different species? To identify orthologous topological patterns, we first compute the structure association strengths and orbit contribution strengths for each species by applying the first two steps of the method. Each GO term will then have a structure association strength and a 73-dimensional orbit contribution strength vector for each species. We compare these statistics to assess the conservation, as explained in Figure 2C.

Consistently strong topology-function correspondences for two species can be identified by taking the minimum of each GO term’s per-species structure association strengths, which we term multi-species structure association strengths. Taking the minimum when combining the scores guarantees that the worst topology-function correspondence is taken into account for each GO term. High multi-species structure association strengths mean that the annotations for the GO term can be accurately inferred from the local topology for both species.

To determine whether a GO term is associated with similar topologies across two species, we compute the orbit contribution similarities by taking Spearman’s correlation between the two orbit contribution strength vectors of the GO term. The Spearman’s correlation tests the similarity of the rank ordering of the orbits, and therefore assesses whether the best and worst orbit associations are consistent for the two species.

The statistical significance of the two strength measures and of the cross-species topology-function similarities are computed using permutation tests (Supplementary Section S.4 for details). We adjust the estimated P-values using Benjamini–Hochberg correction for the statistical errors caused by multiple hypotheses testing.

2.2 Datasets

2.2.1 Protein–protein interaction networks

We obtain the PINs of S. cerevisiae (baker’s yeast) and H. sapiens (human) from BioGRID database (version 3.2.106—November 2013) (Stark et al., 2006). We include all physical interactions that are identified by any of the relevant experimental evidence codes, while excluding interactions that are annotated only as genetic interactions. We remove the ubiquitin proteins from the PINs of both species (i.e. UBC from human and UBI4 from yeast), because these proteins can bind to almost all proteins in the PIN, hiding the topological characteristics of functional interactions and generating noisy topological patterns. The resulting human PIN contains 13 410 proteins (nodes) and 116 552 interactions (edges), while the yeast PIN contains 77 360 interactions among 5 831 proteins.

2.2.2 Gene ontology (GO) annotations

We obtain GO term annotations for the human and yeast proteins from the NCBI FTP Server (ftp://ftp.ncbi.nlm.nih.gov/gene/DATA/gene2go.gz) (downloaded on June 11, 2013) (Maglott et al., 2013). GO annotations from all GO evidence codes are included in the dataset, but annotations with qualifiers (e.g. NOT, colocalizes-with) are excluded. GO terms labelled by an alternate ID are remapped to the unique ID for the term. We use the full GO hierarchy (http://www.geneontology.org/ontology/obo_format_1_2/) and infer parent GO annotations from ‘is-a’ relationships.

3 Results and discussion

We apply our methodology to identify the orthologous topology-function associations between yeast and human. Although our methodology can be applied on the datasets of any species, due to the limited availability of protein–protein interaction and GO annotation data, we study these two organisms for which the available datasets are more complete. Yeast is a model organism that is widely used to infer the molecular basis of BPs in. For this reason, determining the functions that are performed in similar ways is important and this motivates us to study these two organisms. We summarize our main observations on the two organisms (Section 3.1) and perform case studies on three GO terms that show consistent patterns for the two species (Sections 3.2 and Supplementary Section S.9).

3.1 Summary of observed topology-function patterns

For both yeast and human datasets, we first apply CCA to obtain all existing linear dependencies across the wiring patterns and GO term annotations of proteins. The highest canonical correlations identified by this analysis is within the range of the 0.239–0.433. Further discussions on the raw CCA results are provided in Supplementary Section S.5.

For identifying the statistically significant relationships between GO terms and graphlet orbits, we compute the structure association strengths and orbit contribution strengths of the GO terms that are annotated with at least five proteins in both species. The GO term annotation threshold of five is chosen so that the GO annotations provide sufficient variance for CCA analysis, while as many GO terms as possible are considered (a detailed discussion on the GO term annotation threshold is provided in Supplementary Section S.1). The topology-function relationship of a GO term is accepted to be significant if the following conditions hold: (i) the structure association strength of the GO term has an adjusted P-value $\le 0.05$, and (ii) at least one of the orbit contribution strengths of the GO term has an adjusted P-value $\le 0.05$. To avoid reporting results on high-level GO terms, which annotate too many proteins and hence are not specific enough for interpretation, we only report the significant patterns of the GO terms that annotate fewer than 5% of the proteins in the PINs (i.e. 291 proteins in yeast and 670 proteins in human). Supplementary Table S.1 reports the number of GO terms that have significant topology-function relationships along with the total number of evaluated GO terms.

Next, we focus on identifying the subset of these patterns that are conserved between yeast and human. We identify the GO terms with consistent topology-function relationships across yeast and human by utilizing orbit contribution similarities and multi-species structure association strengths. A GO term is accepted to have a significantly conserved topology-function relationship if the following conditions hold: (i) the multi-species structure association strength of the GO term has an adjusted P-value $\le 0.05$, and (ii) the orbit contribution similarity of the GO term has an adjusted P-value $\le 0.05$. Based on these conditions, we show that 15 BP terms and nine CC terms have significantly conserved topology-function relationships, while no molecular function terms have such patterns. Note that these patterns provide further evidence of the link between network topology and biological function, since it is not possible to obtain such large numbers of significant topology-function relationships from meaningless randomized networks, as explained in Supplementary Section S.6. We say that two GO terms are ‘redundant’ if they annotate similar sets of proteins and have similar meanings. When we group the identified GO terms based on their redundancies, we obtain seven BP and two CC terms that are non-redundant (Supplementary Section S.7). For interpreting their consistent topological patterns, we compute their orbit contribution strength profiles by averaging the two orbit contribution strength vectors obtained from yeast and human. Figure 3 summarizes the orbit contribution strength profiles of the non-redundant conserved topology-function relationships. Detailed results for each statistically significant GO term are provided in the Supplementary Figure S.10.

Fig. 3.

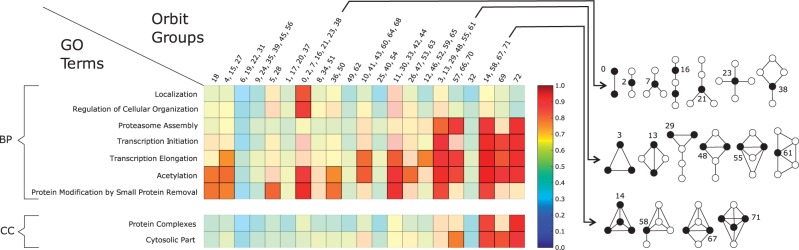
The orbit contribution strength profiles of non-redundant terms that have significantly conserved topology-function relationships. The heatmap at the top summarizes the significant patterns for the non-redundant BP terms, and the heatmap at the bottom summarizes the significant patterns for the non-redundant CC terms. Each heatmap row corresponds to the average orbit contribution strength profile of the GO term that represent the redundant group. Each heatmap cell represents the maximum orbit contribution strength in the relevant orbit group (Fig. 1A for illustrations of orbits 0,1,…,72). For illustrative purposes, graphlet orbits are grouped based on the similarity of their graphlet degrees following the methodology of Yaveroğlu et al. (2014) (explained in Supplementary Section S.8). The orbit groups that do not have any significantly high orbit contribution strengths are coloured semi-transparently. Note that cells plotted with solid colours do not mean that all orbits in the relevant group have significant relationships with the GO term, but it means that at least one of the orbits has a significant relationship (for the exact list of significant orbits; Supplementary Data S1). Black nodes of the graphlets on the right denote the orbits of the corresponding column in the heatmap

Our analysis shows that ‘localization’ and ‘regulation of cellular organization’ processes are significantly linked with orbit group {0,2,7,16,21,23,28}. These orbits correspond to ‘broker’ roles (i.e. topological positions) in sparse graphlets, where the ‘broker’ orbit mediates the connection between two nodes that are not directly connected (illustrated in Fig. 3). A case study that investigates the brokerage role of the proteins that are annotated with ‘Cellular Localization’ (GO:0051641) term is provided in Section 3.2.

A different set of topological patterns, consisting of orbit groups {3,13,29,48,55,61}, {14,58,67,71}, {72} (illustrated in Fig. 3), is linked with ‘Proteasome Assembly’, ‘Transcription Initiation’ and ‘Transcription Elongation’ processes. The first orbit group is linked with nodes located on triangles or nodes that connect multiple triangles. The second and third orbit groups represent dense network regions (e.g. orbits 14, 67, 71) and mediators between a dense network region and a ‘hanging off’ (sparsely linked) node, such as orbit 58. In addition to the three orbit groups, ‘Proteasome Assembly’ process is also linked with orbit group {57, 66, 70}, which represents non-central positions on dense subgraphs. Transcription-related processes are also linked with orbit 69, which has a role similar to orbits {3,13,29,48,55,61}. ‘Transcription Elongation’ is further linked with orbit groups {4, 15, 27}, {10,41,43,60,64,68}, {11,30,33,42,44} and {12,46,52,59,65} that represent peripheral and semi-peripheral orbits on sparser graphlets. As a case study about this group of topological patterns, we analyse the ‘DNA-dependent Transcription, Initiation’ (GO:0006352) in Section 3.2.

In contrast to the previously listed GO terms that are linked with certain topological characteristics, ‘Acetylation’ and ‘Protein Modification by Small Protein Removal’ terms are significantly linked with multiple topological characteristics. The interesting point about their topological patterns is that cyclic patterns, such as graphlets G₅ and G₁₅, are never statistically significantly linked with these processes. This might indicate that these processes tend not to appear in topological patterns that are easily destructible, since it is easy to disrupt a cycle simply by disrupting a single node, e.g. removal of orbit 8 in G₅ increases the distances between its nodes.

The consistency of these patterns for yeast and human indicates that the regulation of cellular organization, transcription and acetylation mechanisms are topologically well-preserved during evolution. This might be because these processes are essential, and hence, they need to be similarly carried out for all species, and therefore, being conserved through evolution and showing similar wiring patterns in different organisms.

The CC terms that have significant topology-function relationships fall into two groups: (i) protein complexes and (ii) cytosolic part. Both of these CC groups are linked with orbit groups {14,58,67,71} and {72}, that reside in densely connected regions of the PINs. In addition, cytosolic part is also linked with orbit groups {57, 66, 70} and {69} that again reside in dense network regions, the first group representing non-central roles in these regions, and the second group representing the role connecting four triangles. To investigate a pattern from this group of topology-function relationships, we provide a case study on the ‘Proteasome Complex’ (GO:0000502) term in Supplementary Section S.9.

3.2 Case studies

A systematic validation of the results presented in Section 3.1 is not possible, because there does not exist a gold-standard topology-function mapping. For this reason, we perform three case studies to find biological validation for the observed wiring patterns of the topologically orthologous functions (also see Supplementary Section S.9 for the proteasome complex case).

3.2.1 DNA-dependent transcription initiation

DNA-dependent transcription initiation term captures any BP that is involved in the assembly of RNA polymerase preinitiation complex (PIC) at the core promoter region of a DNA template, resulting in the subsequent synthesis of RNA from that promoter (Borukhov and Nudler, 2008). Our analysis shows that this process is consistently linked with densely connected regions of the PIN, i.e. orbits 3, 13, 14, 58, 61, 67, 69, 71 and 72 (Supplementary Fig. S.10). Two hundred twelve proteins in human PIN and 32 proteins in yeast PIN are annotated with this term. When we check the GO term enrichments of these proteins to understand their common characteristics, we observe that many of these proteins appear in the nucleus (135 proteins for human and 31 proteins for yeast), where the protein–protein interactions are more clustered and denser than the other parts of the cell (Supplementary Table S.2). On the other hand, many of these proteins form protein complexes (122 proteins for human and 29 proteins for yeast). Protein complexes tend to appear in densely connected patterns, which is also similar to the topological patterns of DNA-dependent transcription initiation. There are two major protein complexes that are consistently associated with the annotated proteins of both species: (i) RNA Polymerase II and (ii) mediator coactivator complex. RNA Polymerase II is an enzyme that catalyses the transcription of DNA to synthesize precursors of mRNA (Kornberg, 1999), and therefore, has a principal role in the gene expression and regulation for all organisms (Borukhov and Nudler, 2008). Mediator coactivator complex serves as a bridge between the activator and basal transcription machinery of RNA Polymerase II and the general transcription factors (Biddick and Young, 2005) and acts as a docking site for transcription elongation factors (Takahashi et al., 2011). It has been shown that most protein complexes tend to be densely connected in PINs and RNA Polymerase II and mediator coactivator complex are no exceptions (Gagneur et al., 2004). Apart from the densely connected patterns that are associated with orbits 14 and 72, observing that orbits 13, 58, 61, 67, 69 and 71 are also significantly associated with the GO term highlights the bridging role of the Mediator complex in these dense subnetworks (illustrated in Fig. 4). It is shown that significant homology exists between RNA polymerases over organisms, which suggests that the existence of an evolutionarily conserved mechanism of RNA synthesis (Sims et al., 2004). Similarly, mammalian Mediator complex is also shown to share structural and functional properties with yeast Mediator subunits (Tomomori-Sato et al., 2004), and it is known to be evolutionarily conserved (Malik and Roeder, 2010). These studies validate our observations on the conserved topological patterns of DNA-dependent transcription initiation. Our observations provide further evidence on the conservation of this process in the wiring of the PINs, complementing the sequence-similarity based evidences.

Fig. 4.

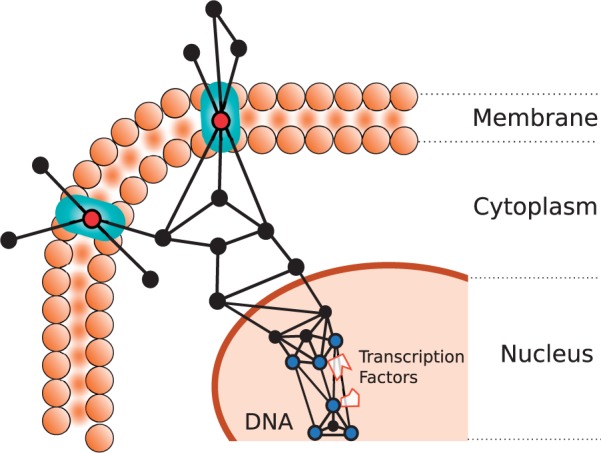
Illustration of the identified topological characteristics in case studies 1 and 2. The small circles represent proteins and the lines connecting them represent edges. The cellular localization term is identified to be significantly linked with mediator positions in sparse graphlets; i.e. graphlet orbits 0, 2, 7, 11, 16, 21, 23, 33, 42 and 44. We illustrate such connectivity patterns for the proteins of this function on the cell membrane, over the green membrane pores (circles filled with red). The DNA-dependent transcription initiation term is identified to be significantly linked with dense connections and clique-like patterns; i.e. 3, 13, 14, 58, 61, 67, 69, 71 and 72. We illustrate such connectivity patterns inside the nucleus, over the transcription factors and DNA (circles filled with blue)

3.2.2 Cellular localization

Cellular localization term captures any cellular process in which a substance, or a cellular entity (e.g. a protein complex or organelle) is transported to, or maintained in a specific position within the membrane of a cell. Our analysis on this process shows that this process is consistently linked with broker positions on sparse graphlets, which mediate the connection between two disconnected nodes, or connect a node to a well-connected group of proteins, i.e. orbits 0, 2, 7, 11, 16, 21, 23, 33, 42 and 44 (Supplementary Fig. S.10). Two hundred eighty-three proteins in human PIN and 205 proteins in yeast PIN are annotated with cellular localization term. When we check the other GO term enrichments of these proteins to understand their common characteristics, we observe that many of them are located at the membrane (147 proteins for human and 67 proteins for yeast), and cytoplasm (121 proteins for human and 99 proteins for yeast). Proteins are more loosely connected in these CCs than in nucleus (Supplementary Table S.2), and this supports the observation on the sparsity of the graphlets that are significantly linked with this GO term. In addition, many of these proteins are linked with transport process (131 proteins for human and 114 proteins for yeast) and response to stimulus process (176 proteins for human and 46 proteins for yeast). Proteins that are involved in these processes act as ‘universal adapters’ by binding to multiple ligands and connecting otherwise disconnected ligands to each other. For example, when the human proteins are ranked based on the similarity of their wiring patterns to the topological profile identified for cellular localization, the two highest ranking proteins, PLXNA2 and RAMP3, are transmembrane proteins (McLatchie et al., 1998; Pasterkamp, 2012). Transmembrane proteins tend to interact with many different cytoplasmic proteins as well as with their extra-cellular ligands, while they rarely interact with each other as illustrated in Figure 4 (Pinkert et al., 2010). Similarly, the highest ranked proteins of yeast, YEL1 and AFI1, act as polarization-specific docking domains for AFR3 protein that regulate the budding mechanisms in yeast. These proteins function in different steps in regulating the localization of ARF3 to the plasma membrane (Tsai et al., 2008). AFI1 is also involved in intra-golgi and golgi-endoplasmic reticulum trafficking. When performing their functions, these proteins bind to ligands at different cellular localizations, or at different time points, and hence, they form the observed brokerage patterns.

4 Conclusion

We propose a three-step method that is able to find topology-function relationships that persist across the PINs of different species, even if these topological patterns are not formed by the same sets of proteins. With our method, we identify that seven BP and two CC GO terms have non-redundant topology-function relationships for yeast and human. Our case studies on the patterns of ‘DNA-dependent Transcription Initiation’, ‘Cellular Localization’ and ‘Proteasome Complex’ validate that our results are in agreement with the underlying biological mechanisms.

Our analysis uncovers conserved topology-function relationships on a relatively small number of high-level GO terms. This is due to the fact that GO terms that are annotated with small sets of proteins are less likely to appear as significant. Furthermore, while we mainly focus on conserved topology-function relationships, our method also uncovers many species-specific ones. For example, a highly specific GO term, ‘Maturation of SSU-rRNA’, is linked with the orbits of dense graphlets (i.e. orbits 3, 14, 58, 67, 69, 70, 71, 72) in yeast while the same patterns are not observed in human. Analysis of such species-specific topology-function relationships can shed light on the wiring patterns of a wider range of functions and raise interesting questions about the underlying reasons for different wiring patterns of proteins annotated with the same GO terms in different species. This could further improve our understanding of the evolution of those functions.

Although the association matrix can be used for predicting the GO term annotations of the proteins from their wiring patterns in PINs, our results show that not all topology-function relationships are conserved across species, which is likely to negatively impact the quality of predictions. However, if prediction is the objective, graphlet degree statistics can be further supported with other types of features (e.g. protein sequence, or structure). Our methodology can easily accommodate such additional features to derive more accurate linear transformations for predicting biological function.

Our method is applicable to any number of species, although the incompleteness of the PINs limits it to yeast and human for the time being. When more complete protein–protein interaction datasets become available, we will be able to apply our method without modification. By replacing the functional annotations with other biological information about proteins, our method would further uncover conserved wiring patterns in different phenomena, including those in disease or KEGG pathway annotations of proteins.

Funding

This work is supported by the European Research Council (ERC) Starting Independent Researcher Grant [278212], National Science Foundation (NSF) Cyber-Enabled Discovery and Innovation (CDI) [OIA-1028394], ARRS project [J1-5454], the Serbian Ministry of Education and Science Project [III44006] and the intramural programme of US National Library of Medicine.

Conflict of Interest: none declared.