Nanoscale protein domain motion and long-range allostery in signaling proteins—a view from neutron spin echo spectroscopy

Abstract

Many cellular proteins are multi-domain proteins. Coupled domain–domain interactions in these multidomain proteins are important for the allosteric relay of signals in the cellular signaling networks. We have initiated the application of neutron spin echo spectroscopy to the study of nanoscale protein domain motions on submicrosecond time scales and on nanometer length scale. Our NSE experiments reveal the activation of protein domain motions over a long distance of over more than 100 Å in a multidomain scaffolding protein NHERF1 upon binding to another protein, Ezrin. Such activation of nanoscale protein domain motions is correlated with the allosteric assembly of multi-protein complexes by NHERF1 and Ezrin. Here, we summarize the theoretical framework that we have developed, which uses simple concepts from nonequilibrium statistical mechanics to interpret the NSE data, and employs a mobility tensor to describe nanoscale protein domain motion. Extracting nanoscale protein domain motion from the NSE does not require elaborate molecular dynamics simulations, nor complex fits to rotational motion, nor elastic network models. The approach is thus more robust than multiparameter techniques that require untestable assumptions. We also demonstrate that an experimental scheme of selective deuteration of a protein subunit in a complex can highlight and amplify specific domain dynamics from the abundant global translational and rotational motions in a protein. We expect NSE to provide a unique tool to determine nanoscale protein dynamics for the understanding of protein functions, such as how signals are propagated in a protein over a long distance to a distal domain.

Prolegomena

The phenomenon of long-range allostery is au fond intramolecular signaling: information arising from ligand-binding is communicated to a distal site in a protein. Allostery occurs in numerous biological processes. Long ago, it was proposed that protein dynamics can propagate allosteric signals between distinct binding sites (Cooper and Dryden 1984). It is now increasingly believed that protein motion is a common mechanism for driving allosteric communication (Popovych et al. 2006), enzymatic catalysis (Goodey and Benkovic 2008), and for molecular recognition (Boehr et al. 2009; Bhattacharya et al. 2013). Cellular proteins are typically composed of multiple domains that are connected by apparently unstructured linkers. A powerful theme in cell signaling is that these multi-domain proteins relay signals allosterically via cellular signaling pathways and networks (Nussinov et al. 2013; Ma et al. 2011). Learning how proteins move on nano-length scales will provide important insights into how multi-domain proteins coordinate domain–domain coupling and propagate allosteric signals in the cell signaling network.

Protein motions are hierarchical, occurring on time scales ranging from femtoseconds to longer than seconds, and on length scales from angstroms to micrometers (Frauenfelder et al. 1991; Daniel et al. 2003; Zaccai 2000; Mukhopadhyay et al. 2007; Palmer 2004; Ha et al. 1999). Protein motions on picosecond to nanosecond timescales, and conformational transitions on millisecond time scales can typically be characterized by nuclear magnetic resonance (NMR) at atomic resolution (Palmer 2001). Single molecule biophysics has allowed the dynamics of biological macromolecules to be observed on timescales from milliseconds to seconds (Deniz et al. 2008; English et al. 2006; Greenleaf et al. 2007). However, nanoscale protein motions on nanosecond-to-microsecond timescales and on nanometer length scales are at best difficult to access by existing experimental biophysical techniques. Currently there is a spatial-temporal dynamic gap, on nanosecond-to-microsecond timescales and on nanometer length scales, where we cannot determine the dynamics of proteins and protein complexes.

Advances in biophysical experiments are beginning to overcome this important limitation. For example, a recent single molecule imaging study, with improved 100 microsecond time resolution, suggests that the tilting and wobbling thermal fluctuations in the motor protein myosin, likely occurring on nanosecond-to-microsecond timescale, facilitate myosin in finding its next stepping site on an F-actin filament (Beausang et al. 2013). As a commentary article on Beausang et al. (2013) points out, “while millisecond timescale detection reveals changes in position or orientation between stable conformations of the protein, important dynamic information during the transitions between these states, which occur on the nanosecond-to-microsecond timescale, are lost” (Berger 2013). Thus, it is increasingly recognized that nanoscale motions in proteins or in large protein complexes can dictate protein function. Hereafter, we refer to nanosecond-to-microsecond timescales and nanometer length scales as nanoscale protein motions.

Neutron spin echo spectroscopy (NSE) emerges as the candidate technique to study nanoscale protein motions (Bu et al. 2005; Farago et al. 2010; Hong et al. 2014a, b; Biehl and Richter 2014; Stadler et al. 2014). We have applied NSE to study the changes in nanoscale protein motions in multi-domain proteins (Bu et al. 2005; Farago et al. 2010; Bu and Callaway 2011; Callaway et al. 2013). We have shown that, when the multi-PDZ scaffolding protein NHERF1 is bound to another adapter protein, Ezrin, the PDZ domains, located more than 120 Å from the Ezrin-binding site, become activated to bind to membrane proteins, which correlates with long-range allostery regulation observed in this set of multi-domain cell signaling proteins (Li et al. 2005; Li et al. 2009).

The utility of NSE in deciphering the internal telegraph of long-range allostery is not obvious, and requires an excursion into non-equilibrium statistical mechanics. Moreover, NSE is unfamiliar to most practitioners of biophysics, for there are only few instruments extant capable of performing these experiments, and their use requires specialized abilities. We have developed a combined theoretical and experimental formalism aimed at reducing the hurdles to the application of NSE to protein nanoscale motions. Here, we first review some background information, making an excursion onto a small skerry, before addressing the main continent.

Brownian dynamics and low Reynolds number: mass without mass

Protein dynamics manifests itself in a world guided by a set of laws that are counterintuitive at best. First, we must remember that Reynolds number is very small. Reynolds number, commonly abbreviated as Re, is estimated by Re ~ Lv/ν where L is a characteristic length scale of the system, v a characteristic velocity, and ν the kinematic viscosity of the solvent (where for water ν ~ 10⁵ Å²/ns). Note that Re is an imprecise concept, used to argue that certain terms in the Navier–Stokes equations of fluid dynamics can safely be neglected. Re is a dimensionless ratio of the relative importance of inertial forces (involving mass) to massless, diffusive, viscous (Brownian) forces. When Re is less than a few thousand, we are said to be at low Re, and diffusive forces are dominant. For typical proteins (Howard 2001) Re < < 0.1 so that we are well within the mass-independent low Re domain when studying protein dynamics. Protein dynamics thus has much more in common with playing badminton at the bottom of a swimming pool filled with molasses than with an aircraft carrier crossing the ocean.

How does low Re affect dynamics? Consider the coordinate x(t) describing the a particle undergoing motion in a fluctuating external Brownian force F(t) via the Langevin equation:

$$m\ddot{x}\left(t\right)+\mathrm{\zeta }\dot{\mathrm{x}}\left(t\right)+kx\left(t\right)=F\left(t\right)$$

where the superscript dot denotes differentiation with respect to time, m mass, ζ the friction constant and k is the spring constant (Howard 2001; Doi and Edwards 1986). Solutions of the homogeneous (F = 0) equation are linear combinations of expressions of the form

$$x(t)=x(0)\exp \left(\text{ω}t\right)$$

where ω satisfies the quadratic equation mω² + ζω + k = 0. At low Re, inertial effects can typically be neglected, so m can be safely taken to zero. The coordinate x(t) then undergoes overdamped motion x(t) ~ exp(−kt/ζ). However, this simple m → 0 result is invalidated when the discriminant of the quadratic equation is negative:

$${\mathrm{\zeta }}^2-4\mathit{km}<0$$

which occurs when the spring constant k is sufficiently large. In that case, the motion includes underdamped oscillatory dynamics, and phenomena such as sound waves can occur. Thus, the assumption of mass-independent overdamped motion (where sound waves are absent) is correct for rigid bodies or rigid bodies connected by soft spring linkers. Stiff bodies (where k is large) exhibit underdamped motion and require special consideration. It is thus the overdamped regime that dictates nanoscale protein motions.

Thus, we see that the simplest description of protein dynamics does not manifestly obey Newton’s laws. For instance, a body at rest will not remain at rest when acted upon by a fluctuating Brownian force F(t), but will rather require work to keep it in place. Forces are not proportional to mass times acceleration, as mass is absent. Rather, they are proportional to velocity, incorporating the concept of a mobility tensor which we discuss in detail below. Essential formulae must be independent of mass—for instance, we now have a center of friction rather than a center of mass. The diffusion of deuterated proteins will be the same as their hydrogenated counterparts, despite the mass difference.

Neutron spin echo spectroscopy

Because NSE is an emerging biophysical technique, we give a brief introduction of how it works. NSE is a quasielastic neutron scattering technique that measures the difference in velocities between the incident and the scattered neutrons (Bee 1988; Higgins and Benoit 1994). NSE employs the Larmor precession of neutron spins in a magnetic guide field as a clock to measure extremely small changes in velocities of scattering neutrons (Mezei 1980; Mezei et al. 2003), allowing the detection of very small energy changes in the scattering neutrons of δE ~10³–10⁻² μeV, corresponding to picosecond-to-microsecond dynamics. Note that, unlike NMR spin echo, producing “neutron spin echo” is only for the purpose of measuring the difference in velocities between the incident and scattering neutrons (Mezei et al. 2003).

The dynamic information obtained by NSE can thus be understood by extending the principles that we have learned from the elementary technique of dynamic light scattering (DLS) (Berne and Pecora 1976; Pecora 1985), While both DLS and NSE measure the space-time correlation function of fluctuations, DLS measures I(Q,t) on micron or longer length scales because of the long wavelength of visible light. DLS measure the intensity correlation g²(Q,t) while NSE measures the field correlation g¹(q,t). In DLS, the Siegert relation is used to obtain in g¹(q,t). A protein or a protein complex has a typical size of 10–500 Å. DLS thus only “sees” a protein as a point object, and can only determine the diffusion constant, which is independent of Q. Because of the shorter wavelength of neutrons, NSE measures I(Q,t) on nanometer to submicron length scales, and can reveal the nanoscale internal fluctuations in a protein or a protein complex. NSE can determine macromolecular motions on nanometer to micron length-scales and on nanosecond to microsecond time scales. Nevertheless, until recently, NSE has been mainly applied to study the dynamics of synthetic polymers in solution and melt, and other types of soft matter (Mezei 1980; Farago 2003; Ewen and Richter 1997).

Nonequilibrium statistical mechanics and the mobility tensor

The framework that we developed emerges as an extension, albeit more complex (Bu et al. 2005; Farago et al. 2010; Bu and Callaway 2011; Callaway et al. 2013), of ideas developed for polymer dynamics (Doi and Edwards 1986; Berne and Pecora 1976). We summarize the basic approach here. We begin by considering the dynamics information obtained via an NSE experiment. NSE measures the intermediate scattering function I(Q,t), which is the spatial Fourier transformation of the space–time van Hove correlation function G(r,t) (Mezei 1980),

$$I\left(Q,t\right)={\displaystyle \underset{V}{\int }G\left(r,t\right)exp\left(-iQ\cdot r\right)dr}$$

with Q the magnitude of the scattering vector, t the time, and r the position of a scattering center. The designation “intermediate” arises precisely because only one of the variables of G(r,t) is Fourier transformed. Like the static small angle neutron scattering, in the low Q region, I(Q,t) is dominated by coherent scattering that corresponds to the cross-correlation G(r,t), i.e., the probability of finding a nucleus at position r_i at time t = 0 and finding another nucleus at position r_j at time t. For a protein in solution, I(Q,t) can typically be fit to a single exponential in time (and is difficult to fit to more exponentials) at a given Q. A natural way to interpret the NSE data is to examine the effective diffusion constant D_eff(Q) as a function of Q, which is determined by the normalized intermediate scattering function I(Q,t)/I(Q,0):

$$\begin{array}{l}\mathrm{\Gamma }\left(Q\right)=-\underset{t\to 0}{lim}\frac{\partial }{\partial t}ln\left[I\left(Q,t\right)/I\left(Q,0\right)\right]\\ D_{\mathit{eff}}\left(Q\right)=\frac{\mathrm{\Gamma }\left(Q\right)}{Q^2}\end{array}$$ 1

where I(Q,0) is the static form factor.

In order to describe the dynamics of a protein in solution, we utilize the remarkable Akcasu–Gurol approach originally developed to describe the dynamics of random coil polymers (Akcasu and Gurol 1976), generalized to include rotational motion (Bu et al. 2005):

$$D_{\mathit{eff}}\left(Q\right)=\frac{k_{B}T}{Q^2}\frac{{\displaystyle \sum _{jl}〈b_j{b}_l\left(Q\cdot {H_{jl}}^T\cdot Q\mathit{+}{L}_j\cdot {H_{jl}}^R\cdot L_l\right)e^{iQ\cdot \left(r_j-r_l\right)}〉}}{{\displaystyle \sum _{jl}〈b_j{b}_l{e}^{iQ\cdot \left(r_j-r_l\right)}〉}}$$ 2

where b_j is the coherent scattering length of a subunit j, H^T is the translational mobility tensor, H^R is the rotational mobility tensor, and k_BT is the usual temperature factor. The structural coordinates of the macromolecule, taken relative to the center of friction of the protein, are given by r_j (note that Σ r_j = 0). In practice, the structural coordinates can be atoms, protein domains in a multi-domain protein, or subunits in a multimeric protein complex, and may be obtained from high-resolution crystallography or NMR, or from low-resolution electron microscopy and small angle X-ray and neutron scattering. In Eq. 2, L_j = r_j × Q is the torque vector for each coordinate. The brackets < > denote an orientational average over the vector Q, so that

$$<Q_a{Q}_b\mathit{exp}\left(iQr\right)>Q^{-2}=\left(1/3\right){\mathrm{\delta }}_{\mathit{ab}}{j}_0\left(Qr\right)+\left[\left(1/3\right){\mathrm{\delta }}_{\mathit{ab}}-\left(r_a{r}_b/r^2\right)\right]j_2\left(Qr\right)$$

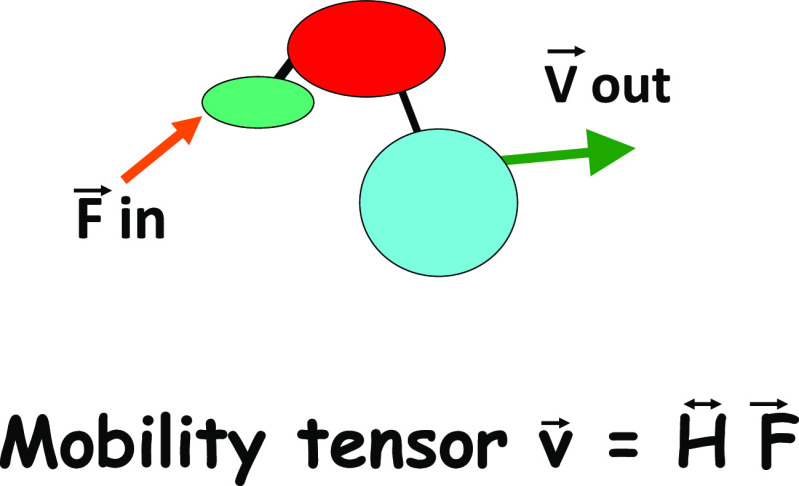
can be expressed in terms of the spherical Bessel functions j. The translational mobility tensor H^T in Eq. 2 is defined by the velocity response v = H^T F to an applied force F. The rotational mobility tensor H^R is defined by the angular velocity response ω = H^Rτ to an applied torque τ. The relationship between force, velocity and the translational mobility tensor is illustrated in Fig. 1.

Fig. 1.

The relationship between force and the mobility tensor. The translational mobility tensor gives the velocity response (speed and direction) of a given protein domain to a force applied to itself or to another domain

The mobility tensor provides a direct indication of the existence of internal degrees of freedom

As discussed above, Eq. 2 is valid for either rigid bodies or rigid-body subunits connected by soft spring linkers (Bu et al. 2005). For a completely flexible body, the rotational diffusion term (involving H^R) is absent. The rotational mobility tensor arises from the consideration of rigid body constraints, introduced via Lagrange multipliers or by generalized coordinates (Doi and Edwards 1986). For a rigid body composed of N identical beads, the translational mobility tensor H^T is a matrix with N² identical 3 × 3 elements since H^T yields the same velocity response of e.g., subunits B and C to a force applied to subunit A. For an object with internal flexibility, the elements of the mobility tensor will not be equal, so forces applied to a given bead would result in different velocities for other beads and the body would not remain rigid. Comparing models of the mobility tensor from Eq. 2 to experimental D_eff(Q) from NSE experiments allows one to extract the internal dynamics of a protein or protein complex. Thus, the key point of Eq. 2 is that the effective diffusion constant D_eff(Q) can be calculated if we know the structural coordinates of the protein, and have proposed a model for the mobility tensor. NSE therefore allows us to test models of the mobility tensor, and thereby determine and characterize internal dynamic modes in the protein. We stress that the mobility tensor does not explicitly depend upon mechanical forces like spring constants, and is rather an eidolon generated by protein motion (much as the motion of the surrounding fluid could be described by Navier–Stokes hydrodynamics for a larger body).

We now evaluate the rotational mobility tensor H ^R for a rigid body. In this case, both the rotational and translational mobility tensors are 3 × 3 matrices, equal for each subunit. The angular velocity vector of the rigid object is ω = H^R τ, with the torque τ = Σ_n r_n x F_n. The velocity is separated into center of friction and rotational contributions v_n = V + (ω x r_n) = N H^T F_n. Thus, for an arbitrary 3-component vector ω

$$\text{ω}=H^R{\mathrm{\Sigma }}_n{r}_n\times {\left(N{H}^T\right)}^{-1}(V+\text{ω}\times r_n)$$ 3

We note that Σ r_j = 0 (so the term involving V drops out). Then, Eq. 3 is of the form ω = Mω for an arbitrary vector ω, and thus M is the identity matrix. This can be simplified further by the substitution ω = H^T Q, leading to useful general results like D_eff(Q → ∞) = 2 D_eff (Q = 0) for a uniform rigid body (Bu et al. 2005; Farago et al. 2010; Bu and Callaway 2011). Equation 3 shows that the 3 × 3 matrix H^R can be evaluated from the 3 × 3 matrix H^T and bead subunit coordinates r_{n .} The rotational mobility tensor is thus entirely determined by the translational mobility tensor and the coordinates of the protein. We adopt the simplifying assumption that all three principal spatial components of the translational mobility tensor for each subunit are equal to D₀/(k_BT) = 1/ζ with ζ the friction constant of a subunit, and D₀ the measured diffusion constant of the protein. Then, a compact formula of H^R is given (Bu et al. 2005; Farago et al. 2010; Bu and Callaway 2011):

$${H^R}_{\mathrm{\alpha }\mathrm{\beta }}=N\left(D_0/k_{B}T\right){\left[{\mathrm{\Sigma }}_n\left({\mathrm{\delta }}_{\mathrm{\alpha }\mathrm{\beta }}{r^2}_n–r_{r\mathrm{\alpha }}{r}_{n\mathrm{\beta }}\right)\right]}^{-1}$$ 4

where D₀ is the diffusion constant of the protein or protein complex at Q = 0, which can be measured experimentally by pulsed field gradient NMR (PFG NMR) or dynamic light scattering, and N is the number of structural coordinates of the protein, relative to its center of friction (note that Σ_n r_n = 0). We use Greek indices (α, β) for spatial coordinates (x,y,z) and Roman symbols (m,n) to number bead subunits. With Eqs. 2–4, an estimate of D_eff (Q) for a rigid-body can be made by simply using only the coordinates and diffusion constant D₀. Our simple approach does not require complicated molecular dynamics simulations, elastic network models, fits to rotational expansions in spherical harmonics, or Navier–Stokes hydrodynamics. We do not have to fit NSE data, but can directly predict the outcome of an NSE experiment from other experiments to test models of the mobility tensor. We now adumbrate this point.

Note that PFGNMR measures the self-diffusion coefficient, while DLS measures the mutual diffusion coefficient. For DLS, it is necessary to measure the diffusion at several protein concentrations and extrapolate to zero concentration. Nevertheless, the extrapolated diffusion constant may not reflect the D₀ at the high protein concentration measured by NSE. Thus, PFGNMR is more reliable than DLS to estimate D₀ at the same protein concentration as measured by NSE.

For an object with internal domain motion, comparing the calculated D_eff(Q) with experimental NSE data allows one to extract the relative degree of dynamic coupling between the various components of the system. This dynamic coupling is defined by the mobility tensor. For example, a rigid two-domain system is described by a translational mobility tensor (spatial indices are ignored)

$$H=H_0\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)$$ 5a

with all elements of the tensor equal, and yields (via Eq. 2) the simple result that the translational contribution to the effective diffusion constant is given by D^T _eff(Q) = k_BT H₀, independent of Q. By contrast, a two-domain system with internal motion will possess a translational mobility tensor

$$H=\left(\begin{array}{cc}{H}_1& 0\\ 0& H_2\end{array}\right)$$ 5b

in principal coordinates. Thus, the application of equal forces to the two domains will result in their having different velocities, revealing internal motion. For the case where there is one internal translational mode between subunits 1 and 2 with D₁ = k_BTH₁ and D₂ = k_BTH₂ (Bu et al. 2005), the translational contribution to the effective diffusion constant is:

$${D^T}_{\mathit{eff}}\left(Q\right)=\frac{D_1{S}_1\left(Q\right)+D_2{S}_2\left(Q\right)}{S\left(Q\right)}$$ 5c

Here, S₁(Q) and S₂(Q) are the form factors of the separate individual protein domains, while S(Q) is the form factor of the entire protein. Orientational averages are performed, so that, e.g., S(Q) = Σ j₀ (Qr), and S(Q) is normalized so that S(0) = N². D₁ and D₂ are the diffusion constants of individual domains. Thus, the Q dependence of the effective diffusion constant D _eff (Q) reveals the existence of internal motion. We stress that Eq. 5c is only the translational contribution to the effective diffusion constant, and that real comparisons with experiment require that the rotational contributions also be included. The point of presenting Eq. 5c is to show that the form of the mobility tensor is directly reflected in the Q dependence of the effective diffusion constant.

To summarize, the calculations that we have presented consist of rigid-body motion (including both translational and rotational motion), and an internal mode. We stress that, in principle, it is possible to include the effects of arbitrary translational and rotational internal motion in the calculation (Bu et al. 2005). The combination of NSE and first cumulant analysis allows one to test complex models of the mobility tensors of the system, and extract dynamical information about the internal motions of the protein.

Activation of long-range allostery in a multidomain scaffolding protein revealed by NSE

The virtue of the above simple approach can be seen by comparing our calculations with the experimental NSE results from a cell signaling scaffolding protein called NHERF1 (Farago et al. 2010). NHERF1 plays essential roles in modulating the intracellular trafficking and assembly of a number of receptors and ion transport proteins. NHERF1 is a multi-domain protein that has two modular domains, PDZ1 and PDZ2, and a disordered but compact C-terminal domain, with three domains connected by unstructured linkers (Li et al. 2005; Li et al. 2007; Bhattacharya et al. 2010). The C-terminal domain binds to the FERM domain of Ezrin with high affinity, K_d = 19 nM (Reczek et al. 1997). We have shown that binding to FERM to the C-terminal domain of NHERF1 allosterically increases the binding affinity of both PDZ1 and PDZ2 domains of NHERF1 for the cytoplasmic tail of CFTR (Li et al. 2005; Li et al. 2009). The PDZ1 and PDZ2 domains are 110 and 80 Å, respectively, from the FERM binding site in the CT domain. The NHERF1∙FERM complex thus suggests long-range allosteric transmission of binding signals on nanometer length scales (Li et al. 2009). Our NSE experiments revealed the activation of inter-domain motions of the PDZ domains in NHERF1 on submicrosecond time scales upon binding to FERM. A dynamic protein can recognize more binding partner proteins and bind to one partner more tightly than a rigid homolog (Bhattacharya et al. 2013). We thus correlate the activated domain motions with the increased binding capabilities of the PDZ domains in the complex, and thus the propagation of allosteric signals from the Ezrin-binding site to the remote PDZ domains that are located as far as 110 Å distant.

For NHERF1 alone in solution, the calculated rigid body D_eff(Q) agrees with the NSE experimental data quite well (see Fig. 2). The rigid-body calculation uses as input only the translational diffusion coefficient D₀ of NHERF1 obtained from PFG NMR and the “dummy atom” structural coordinates (Svergun 1999) reconstructed from solution small angle X-ray and neutron scattering (SAXS and SANS) (Li et al. 2009, 2007).

Fig. 2.

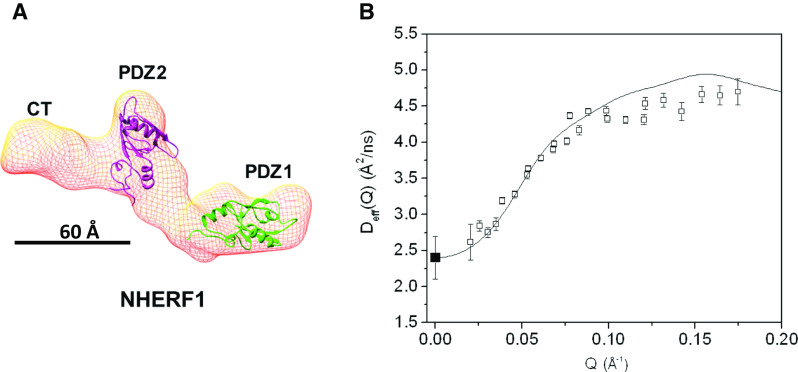
NHERF1 alone behaves as a rigid-body in solution as shown from NSE experiments. a The 3-D shape of NHERF1 reconstructed from SAXS (Li et al. 2009) using the ab initio program DAMMIN (Svergun 1999). The known high-resolution structures of the PDZ1 (PDB code: 1I92) and PDZ2 (PDB code: 2KJD) domains are docked into the 3-D shape, using UCSF chimera (Pettersen et al. 2004). EBD, which overlaps with the last 13 amino acid residues that interact with PDZ2 is not marked in the graph. b Comparing the experimental D_eff (Q) of NHERF1 (black open square) with the rigid-body calculation (black solid line). The overall translational diffusion constant D_o (filled black square) at Q = 0 Å⁻¹ is D_o = 2.4 Å²/ns from PFG NMR measurements

We have compared our calculations with the NSE experimental results on two types of complexes of NHERF1 bound to FERM (see Fig. 3). One complex is the hydrogenated NHERF1 in complex with the hydrogenated FERM (NHERF1∙^hFERM), and the other complex is hydrogenated NHERF1 bound to deuterium-labeled FERM (NHERF1∙^dFERM). As we have pointed out, at low Reynolds number the dynamics of a protein as seen by NSE should not depend upon its mass, but rather upon its size. In our calculations, we thus always impose the constraint that the dynamics, and therefore the mobility tensors of the hydrogenated and deuterated components are the same. When calculating D_eff(Q) for the NHERF1·^dFERM complex, the scattering from the deuterated component is treated as “invisible” in Eq. 2 because of contrast matching, i.e., the neutron scattering length density of the deuterated component contrast matches that of the D₂O buffer background. We used D₀ of the deuterated complex or the hydrogenated complex obtained from PGF NMR or from dynamic light scattering and the structural coordinates obtained from SANS.

Fig. 3.

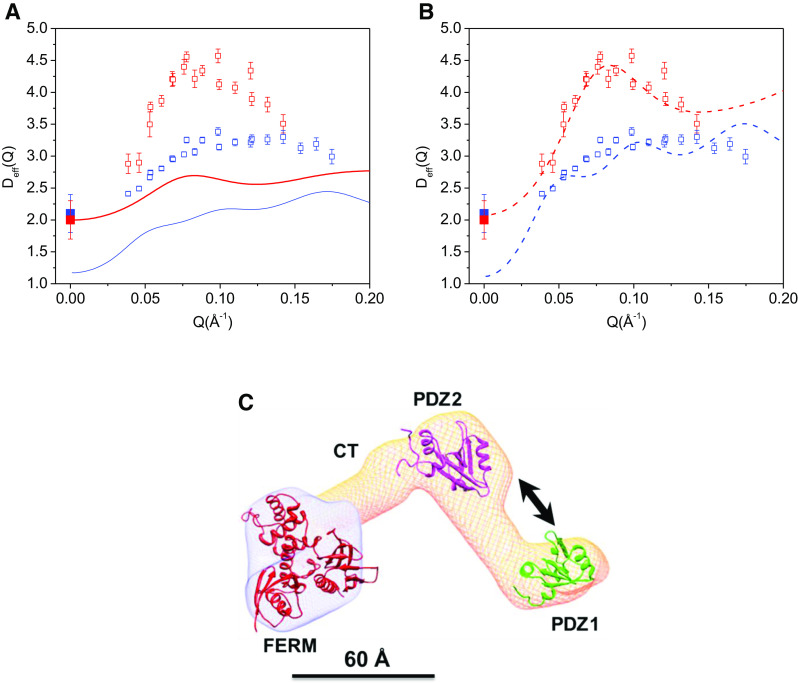
Activation of inter-domain motion in NHERF1 upon binding to the FERM domain of Ezrin. a Comparing experimental D_eff(Q) of NHERF1∙^dFERM and NHERF1∙^hFERM with rigid-body calculations. Open red squares are the NSE data from NHERF1∙^dFERM. Open blue squares are the NSE data from NHERF1∙^hFERM. Solid red and blue squares are the self-diffusion constants D_o of NHERF1∙^dFERM and NHERF1∙^hFERM obtained from PFG NMR, respectively. The solid red line is from rigid-body model calculations of the NHERF1∙^dFERM complex. The solid blue line is from rigid-body model calculations of the NHERF1∙^hFERM complex. b Comparing experimental D_eff(Q) of deuterated complex NHERF1∙^dFERM and hydrogenated complex NHERF1∙^hFERM with calculations incorporating interdomain motion between PDZ1 and PDZ2. The symbols for the experimental data are the same as in (a). The dashed red curve is calculated from model incorporating domain motion between PDZ1 and PDZ2 for the NHERF1∙^dFERM complex. The dashed blue curve is calculated from model incorporating domain motion between PDZ1 and PDZ2 for the NHERF1∙^hFERM complex. The comparisons in (a) and (b) show that deuteration of the FERM domain amplifies the effects of protein internal motions detected by NSE. c A model representing domain motion between PDZ1 and PDZ2 in the complex. The 3-D shape of the complex is reconstructed from SANS (Bajpai et al. 2009). The known high-resolution structure fragments of PDZ1, PDZ2, and the FERM domain (PDB code: 1NI2) are docked into the envelope using UCSF chimera (Pettersen et al. 2004). The arrows represent translational motion between PDZ1 and PDZ2. A length-scale bar of 60 Å is shown

As shown in Fig. 3a, the agreement between the experimental NSE data and rigid-body calculations is poor for both the NHERF1∙^dFERM and the NHERF1∙^hFERM complexes. We have then incorporated domain motions in our calculations, with the mobility tensor with an internal mode between the PDZ1 and PDZ2 domains (Fig. 3b). The calculated D_eff(Q) with internal motion agrees quite well with the NSE results for the NHERF1∙^dFERM complex. Nevertheless, for the NHERF1∙^hFERM complex, the computed D₀ at Q = 0 is not close to the experimental values from PFG NMR measurements. We attribute this discrepancy to large conformational variations in NHERF1 by the unfolding of the CT domain upon binding to FERM. Such complications are minimal in the NHERF1∙^dFERM complex because the deuterated ^dFERM is “invisible” to neutrons.

A simple four-point model describes domain motion

The simple calculations we presented above require only the structural coordinates and a single constraint, the diffusion constant at Q = 0 Å⁻¹ for the deuterated complex, which can be measured by PFG NMR, to generate the computed D_eff(Q). We further introduce an even more simplified model that yields the same effect, and serves to explain the D _eff (Q) observed by NSE experiments. The simplified model is taken by extracting four points that represent the coordinates of the center-of-friction of domains obtained from the SANS data of the NHERF1∙FERM complex. These points form a triangle, as shown in Fig. 4a, with the distances FERM–PDZ2 = 80 Å, PDZ2–PDZ1 = 59 Å, and FERM–PDZ1 = 110 Å. The CT domain is taken as being halfway between the FERM and PDZ2 domains. We include the point representing the FERM domain with a weight factor of 3 to account for its larger size relative to the other domains. Because it is possible to obtain the center-of-friction distances between the domains with confidence even with low resolution SAXS or SANS data, this model possesses fewer uncertainties than a model based upon the molecular shape. More details of the four-point calculations have been described previously (Farago et al. 2010).

Fig. 4.

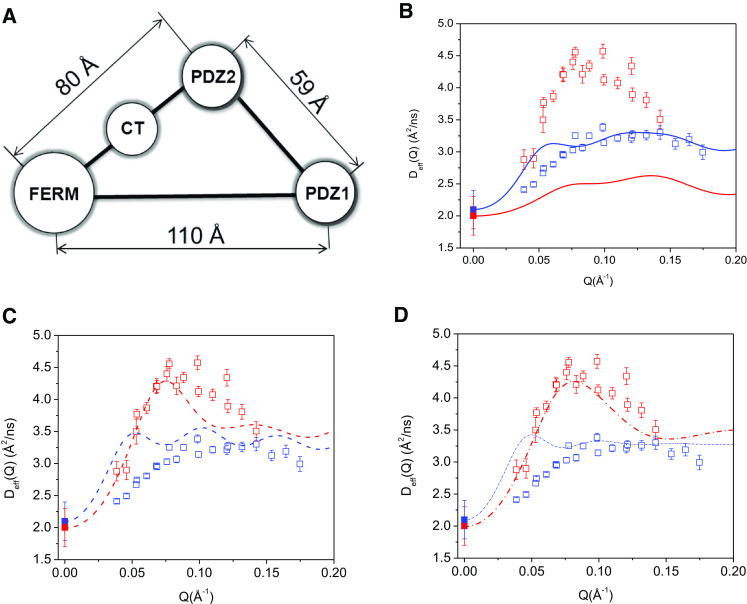
A simple four-point model can well describe domain motion in the complex. a The four-point model represents the NHERF1∙FERM complex, with the centers of PDZ1, PDZ2, CT, and FERM domain taken from Fig. 3a. b Comparing the experimental NSE data with the four-point rigid-body calculations for NHERF1∙^hFERM (blue open squares are the experimental data and blue solid line is the calculated data) and for NHERF1∙^dFERM (red open squares are experimental data and red solid line is the calculated data). D_o of NHERF1∙^dFERM (solid red squares) and NHERF1∙^dFERM (solid blue squares) from PFG NMR are shown. c Comparing the experimental data with calculations assuming inter-domain motion between PDZ1 and PDZ2 in NHERF1∙^dFERM (red dash line) and NHERF1∙^hFERM (blue dash line). The experimental symbols are the same as in (b). d Comparing the experimental data with calculations incorporating inter-domain motion between PDZ1 and PDZ2, as well as assuming finite size form factor of spheres of 20 Å radius for the FERM domain and for both PDZ domains in NHERF1∙^dFERM (red dash dot line) and in NHERF1·^hFERM (blue dash dot line)

Figure 4b is the D_eff(Q) of the four-point rigid-body model, without incorporating internal domain motion between PDZ1 and the rest of the complex. Figure 4c is the D_eff(Q) of the four-point model incorporating internal domain motion between PDZ1 and the rest of the complex. After incorporating internal motion, the overall D_eff(Q) from the four-point model agrees well with the experimental data for both the partially deuterated and the hydrogenated complexes. The comparison between calculation and experimental data improves after including the form factor of a 20 Å radius sphere for the FERM domain and both PDZ domains in the calculation (Fig. 4d). Thus, the NSE data are better represented by the four-point model that includes PDZ1–PDZ2 interdomain motion than by a model that assumes the complex is a rigid body. Further improvement likely requires the use of methods of evaluating the mobility tensors for proteins with high accuracy.

Moreover, from the four-point model calculations, we note that D_eff(Q) for the hydrogenated rigid complex and the hydrogenated complex with internal motion are nearly indistinguishable (Fig. 5a). For the deuterated complex, D_eff(Q) obtained from the inter-domain motion model is significantly different from that of the rigid-body model (Fig. 5b). This can be explained as due to the relatively large contribution to Eq. 2 of the effects of rotational diffusion of the overall object, which dominates and obscures the effects of internal motion when no deuteration is performed. For the partially deuterated complex, both the docked domain calculation (Fig. 3b) and the four-point model (Fig. 5b) show that D_eff(Q) of the rigid-body complex is significantly different from that of the complex with internal domain motion. Thus, deuteration of a domain or subunit in a protein complex can amplify the effects of internal protein dynamics as detected by NSE.

Fig. 5.

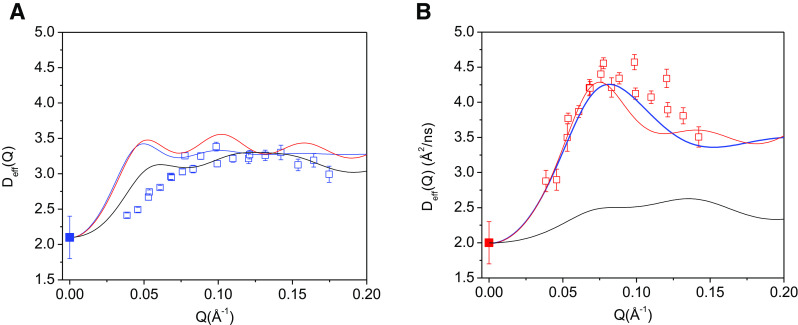
For the hydrogenated NHERF1∙^hFERM complex, the difference in D_eff(Q) between the rigid-body model and domain-motion models is very small, but is significantly increased in the deuterated complex. a Comparing the rigid-body calculation with the domain-motion calculation in the four-point model in the hydrogenated NHERF1∙^hFERM complex. NSE data from the NHERF1∙^hFERM (blue open squares), the four-point rigid-body model (black line), four-point model incorporating domain motion between PDZ1 and PDZ2 (red line), four-point model incorporating domain motion between PDZ1 and PDZ2 and finite size form factor of 20 Å radius for the FERM domain, PDZ1 and PDZ2 (blue line). D₀ at Q = 0 Å⁻¹ as measured from PFG NMR is shown in blue solid square. b Comparing the rigid-body calculation with the domain-motion calculation in the four-point model in the deuterated NHERF1∙^dFERM complex. NSE data from the NHERF1∙^dFERM (red open squares), the four-point rigid-body model (black line), four-point model incorporating domain motion between PDZ1 and PDZ2 (red line), four point model incorporating domain motion between PDZ1 and PDZ2 and finite size form factor of 20 Å radius for the FERM domain, PDZ1 and PDZ2 (blue line). D₀ at Q = 0 Å⁻¹ as measured from PFG NMR is shown in red solid square

Perspectives and challenges for the future

Clearly, we are only beginning to understand nanoscale protein motions. Much is to be learned about the nature of nanoscale protein motions and their roles in protein function. The structure of a multidomain protein is heterogeneous, and is comprised of structured modular domains and disordered linkers and tails. How do nanoscale motions differ in different segments in a multidomain protein? Are the nanoscale protein domain motions coupled, and how do the coupled domain motions change in response to protein complex formation? How does post-translational modification such as phosphorylation affect nanoscale protein motions and protein complex formation? For multi-domain protein interactions, it is of particular interest to know how target-binding triggers the propagation of nanoscale protein fluctuations in different segments in the same protein, or in different protein binding partners. Determining the changes in nanoscale motions in protein binding partners will provide a means to further our understanding of the mechanisms of how signals are propagated in multi-protein complexes, which affect hierarchical cellular signaling pathways and networks (Nussinov et al. 2013; Nussinov 2012). Combining NSE experiments with our new theoretical and experimental strategies will allow us to address these questions.