Testing for genetic associations in arbitrarily structured populations

Abstract

We present a new statistical test of association between a trait and genetic markers, which we theoretically and practically prove to be robust to arbitrarily complex population structure. The statistical test involves a set of parameters that can be directly estimated from large-scale genotyping data, such as that measured in genome-wide association studies (GWAS). We also derive a new set of methodologies, called a genotype-conditional association test (GCAT), shown to provide accurate association tests in populations with complex structures, manifested in both the genetic and environmental contributions to the trait. We demonstrate the proposed method on a large simulation study and on the Northern Finland Birth Cohort study. In the Finland study, we identify several new significant loci that other methods do not detect. Our proposed framework provides a substantially different approach to the problem from existing methods, such as the linear mixed model and principal component approaches.

INTRODUCTION

Performing genome-wide tests of association between a trait and genetic markers is one of the most important research efforts in modern genetics [1–3]. However, a major problem to overcome is how to test for associations in the presence of population structure [4]. Human populations are often structured in the sense that the genotype frequencies at a particular locus are not homogeneous throughout the population. Rather, there is heterogeneity in the genotype frequencies among individuals (correlated with variables such as geography or ancestry). At the same time, there may be other loci and non-genetic factors that also correlate with this genotype frequency heterogeneity, which in turn are correlated with the trait of interest. When this occurs, genetic markers become spuriously statistically associated with the trait of interest despite the fact that there is no biological connection.

The importance of addressing association testing in structured populations is evidenced by the existence of a large literature of methods proposed for this problem [5, 6]. The well-established methods all take a similar strategy in that the trait is modeled in terms of the genetic markers of interest, while attempting to adjust for genetic structure. Two popular approaches are to correct population structure by including principal components of genotypes as adjustment variables [7, 8] or by fitting a linear mixed effects model involving an estimated kinship or covariance matrix from the individuals’ genotypes [9, 10]. Previous work investigating the limitations of these two methods includes Wang, et al. (2013) [11]. These two approaches have been shown to be based on a common model that make differing assumptions about how the kinship or covariance matrices are utilized in the model [5]. This common model does not allow for non-genetic (e.g., environmental) contributions to the trait to be dependent with population structure. The linear mixed effects model requires that the genetic component is composed of small effects that additively are well-approximated by the Normal distribution. The model itself is therefore an approximation, and it is not yet possible to theoretically prove that a test based on this model is robust to structure for the more general class of relevant models that we investigate.

By taking a substantially different approach that essentially reverses the placement of the trait and genotype in the model, we formulate and provide a theoretical solution to the problem of association testing in structured populations for both quantitative and binary traits under general assumptions about the complexity of the population structure and its relationship to the trait through both genetic and non-genetic factors. This theoretical solution directly leads to a method for addressing the problem in practice that differs in key ways from the mixed model and principal component approaches. The method is straightforward: a model of structure is first estimated from the genotypes, and then a logistic regression is performed where the SNP genotypes are logistically regressed on the trait plus an adjustment based on the fitted structure model. The coefficient corresponding to the trait is then tested for statistical significance.

This association-testing framework is robust to general forms of population genetic structure, as well as to non-genetic effects that are dependent or correlated with population genetic structure (for example, lifestyle and environment may be correlated with ancestry) and with heteroskedasticity that is dependent on structure. We introduce an implementation of this test, called “genotype conditional association test” (GCAT). We show the proposed method corrects for structure on simulated data with a quantitative trait and compares favorably to existing methods. We also apply the method to the Northern Finland Birth Cohort data [12] and identify several new associated loci that have not been identified by existing methods. For example, the proposed method is the only one to identify a SNP (rs2814982) associated with height, which we note is linked to another SNP (rs2814993) that has been associated with skeletal frame size [13]. We discuss the advantages and disadvantages of the proposed framework with existing approaches, and we conclude that the proposed framework will be useful in future studies as sample sizes and the complexity of structure increase.

RESULTS

Simulation Studies

We performed an extensive set of simulations to demonstrate that the proposed test is robust to population structure and to assess its power to detect true associations (full technical details in Online Methods and Supplementary Note). We compared the proposed test to its Oracle version (where model (3) from Online Methods and test-statistic (6) from Supplementary Note are used with the true individual-specific allele frequency values imputed). We also included in the simulation studies three important and popular methods: (i) the method of adjusting the trait and genotypes by principal components computed from the full set of genotypes [8] and (ii) two implementations of the linear mixed effects model (LMM) approach [9, 10], specifically EMMAX by Kang et al. (2010) [10] and GEMMA by Zhou and Stephens (2012) [15]. The methods are abbreviated as “PCA,” “LMM-EMMAX,” and “LMM-GEMMA.”

For each of 33 simulation configurations, we simulated and analyzed 100 GWAS data sets from a quantitative trait model (equation (1) from Online Methods), for a grand total of 3300 simulated data sets. Each simulation scenario involved m = 100,000 simulated SNPs on n individuals, where n ranged from 940 to 5000 depending on the scenario. For a given simulated study, we therefore obtained a set of 100,000 p-values, one per SNP. So-called “spurious associations” occur when the p-values corresponding to null (non-associated) SNPs are artificially small. For a given p-value threshold t, we expect there to be m₀ × t false positives among the m₀ p-values corresponding to null SNPs, where m₀ = 100,000–10 in our case. At the same time, we can calculate the observed number of false positive simply by counting how many of the null SNP p-values are less than or equal to t. The excess observed false positives are spurious associations. A method properly accounts for structure when the average difference is zero. The best one can do on a study-by-study basis is captured by the Oracle method, which according to our theory is immune to structure and provides the correct null distribution.

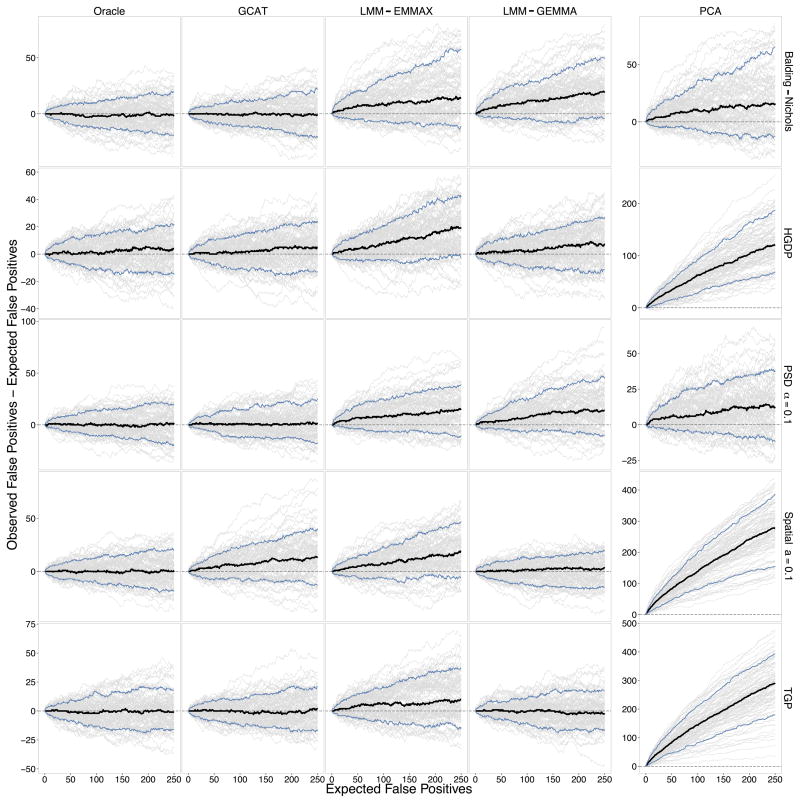
Fig. 2 shows the excess in observed false positives vs. the expected number of false positives for the Oracle, GCAT (proposed), PCA, and both implementations of LMM under five configurations of structure for a quantitative trait variation apportionment corresponding to genetic=5%, non-genetic=5%, and noise=90%. It can be seen that the proposed GCAT method performs similarly to the Oracle test, whereas PCA tends to suffer from an excess of spurious associations.

Figure 2.

Performance of association testing methods. One-hundred quantitative trait GWAS studies were simulated in each of the Balding-Nichols, HGDP, TGP, PSD (α =0.1), and Spatial (a =0.1) simulation scenarios (see Online Methods for definitions of each) to compare the Oracle, GCAT (proposed), LMM-EMMAX, LMM-GEMMA, and PCA testing methods. The variance contributions to the trait are genetic=5%, non-genetic=5%, and noise=90%. The difference between the observed number of false positives and expected number of false positives is plotted against the expected number of false positives under the null hypothesis of no association for each simulated study (grey lines), the average of those differences (black line), and the middle 90% (blue lines). All simulations involved m =100,000 SNPs, so the range of the x-axis corresponds to choosing a significance threshold of up to p-value ≤ 0.0025. The difference on the y-axis is the number of “spurious associations.” PCA is shown on a separate y-axis since it usually has a much larger maximum than the other methods. The Oracle method is where the true population structure parameters are inputted into the proposed test (see Results), which we have theoretically proven always corrects for structure (see Supplementary Note).

We found from using the distributed binary executable EMMAX software and our own implementation that EMMAX required a 10-fold increase in computational time over the proposed method and PCA when analyzing n = 5000 individuals. Therefore, it was not reasonable to apply EMMAX to all 3300 simulated GWAS data sets. We limited comparisons with EMMAX to five representative structure configurations. GEMMA was computationally more efficient, though still significantly slower than GCAT or our implementation of PCA.

Supplementary Figs. 1–8 show results from the remaining set of simulations from all 33 simulation configurations. Due to the computational constraints mentioned above for EMMAX, the additional simulations feature only results from GEMMA for LMM methods.

In comparing the statistical power among the methods (Supplementary Figs. 9–17), we found that the Oracle, GCAT, and PCA performed similarly well, while the two LMM methods sometimes showed a loss or gain in power depending on the scenario. We also carried out analogous simulations on binary traits simulated (from trait model equation (2) in Online Methods) and we found that all methods performed similarly well in terms of producing correct p-values that were robust to structure. This result agrees with the comparisons made between PCA and a linear mixed effects model in Astle and Balding (2009) [5].

Analysis of the Northern Finland Birth Cohort Data

We applied the proposed method to the Northern Finland Birth Cohort (NFBC) genome-wide association study data [12], which includes several metabolic traits and height (Supplementary Figure 18). This study has also been analyzed by the LMM and PCA methods, as well as a standard analysis uncorrected for structure [10]. We carried out association analyses with the proposed method on the 10 traits that were also analyzed using the other methods (Table 1). After processing the data, including filtering for missing data, minor allele frequencies, and departures from Hardy-Weinberg equilibrium, the data were composed of m = 324,160 SNPs and n = 5027 individuals (Supplementary Note). The LFA model of population structure was estimated from a subset of the data where markers were at least 200 kbp apart.

Table 1.

Number of significant loci at genome-wide significance (p-value < 7.2×10⁻⁸) for each of the 10 traits from the Northern Finland Birth Cohort data. Each method was performed with a subsequent genomic control inflation factor correction applied (denoted by +GC). The counts for LMM+GC, PCA+GC, and Uncorr+GC were obtained from Table 2 in Kang et al. (2010). In this case LMM is EMMAX-LMM.

Trait	Abbreviation	GCAT+GC	LMM+GC	PCA+GC	Uncorr+GC
Body Mass Index	BMI	0	0	0	0
C-reactive Protein	CRP	2†	2	2	2
Diastolic blood pressure	DBP	0	0	0	0
Glucose	GLU	3	2	2	2
HDL Cholesterol	HDL	4	4	2	4
Height	Height	1	0	0	0
Insulin	INS	0	0	0	0
LDL Cholesterol	LDL	4	3	3	3
Systolic blood pressure	SBP	0	0	0	0
Triglycerides	TG	2	3	2	2
	Total	16	14	11	13

^†Result when the Box-Cox transformation was not applied to the CRP trait. The result is 1 when the transformation is applied.

Most traits showed only approximate Normal distributions, so we applied a Box-Cox Normal transformation to all traits so that they satisfy the model assumptions. We noted that C-reactive Protein (CRP) and Triglycerides (TG) traits followed an exponential distribution more closely, so it was unnecessary to transform these two traits. The developed theory can be extended to exponential distributed quantitative traits as well.

The 20 most significant SNPs for each of the 10 traits are shown in Supplementary Table 1. Kang et al. (2010) utilized a genome-wide significance threshold of p-value < 7.2×10⁻⁸ as proposed in ref. [16], so we also utilized this threshold for comparative purposes. The numbers of loci found to be significant for each method are shown in Table 1. Whereas our proposed method identifies 16 significant loci, the other methods identify 11 to 14 loci.

We identified three new loci that were not identified by the other methods. None of the other methods identified any significant associations for the height trait. However, we identified rs2814982 on chromosome 6 as being statistically associated with height (Supplementary Table 1). This SNP is located ~70kbp from another SNP, rs2814993, which has been associated with skeletal frame size in a previous study [13]. Additionally, rs2814993 was the fifth most significant SNP for height. For the LDL cholesterol trait, we identified a significant association with rs11668477, which was significantly associated with LDL cholesterol in a different study [17]. Finally, there were significant associations between the glucose (GLU) trait and a cluster of SNPs (rs3847554, rs1387153, rs1447352, rs7121092) proximal to the MTNR1B locus; variation at this locus has been associated with glucose in a previous study [18].

As described in Sabatti et al. (2009) [12], the NFBC data show modest levels of inflation due to population structure as measured by the genomic control inflation factor (GCIF) [19] of test statistics from an uncorrected analysis. The population structure present among these individuals may be subtler and manifested on a finer scale than other settings. Noting that the GCAT approach does not attempt to adjust for a polygenic background, the GCIF values calculated for the proposed method (Supplementary Table 2) were found to be in line with what is expected for polygenic traits where no structure is present [20], providing evidence that the proposed method adequately accounts for structure.

DISCUSSION

We considered models of quantitative and binary traits involving genetic effects and non-genetic effects in the presence of arbitrarily complex population structure. We allowed for the non-genetic effects to be confounded with population genetic structure since structure, ancestry, geography, lifestyle, and environment – all factors potentially involved in complex traits – may be highly dependent with one another. A mathematical argument showed that under these models, it is most reasonable to account for this confounding in the genotypes, but it is not tractable to do so in the non-genetic effects. This follows because we have many instances of genotypes that can be jointly modeled to provide reliable estimates of structure, but the non-genetic effects are never directly observed and we do not have repeated instances of them. In general it is not possible to estimate a latent variable that accounts for the confounding between structure and non-genetic effects.

These observations led us to propose an inverse regression approach to testing for associations, where the association is tested by modeling genotype variation in terms of the trait plus model terms accounting for structure. In this model, the terms accounting for structure were based on the logistic factor analysis (LFA) approach that we have proposed [14], although the general form of the association test can incorporate other methods that estimate population structure. We mathematically proved under general assumptions that the trait term in the model is non-zero only when the genetic marker is truly associated with the trait, regardless of the population structure. We demonstrated that the implemented test properly accounts for structure in a large body of simulated studies that included a wide range of population structures. We also applied the method to 10 traits from the Northern Finland Birth Cohort genome-wide association study. The proposed method identified three new loci associated with the traits, including being the only method among those we considered that identifies a locus associated with the height trait. Overall, we showed that the proposed method compares favorably to existing methods and we also noted that it has favorable computational requirements compared to existing methods.

As GWAS increase in sample size and levels of complexity of population structure, it is important to develop methods that properly account for structure and that scale well with sample size. Whereas we found that the popular principal components adjustment does not properly account for structure, we also found that the mixed model approach performs reasonably well. However, the mixed model approach involves estimating a n × n kinship matrix (where n is the number of individuals in the study) and its current implementation does not scale well with sample size. The kinship matrix quickly becomes computationally unwieldy when n grows large, and the possibility of the estimated kinship matrix becoming overwhelmed by noise is a concern [21]. In the Northern Finland Birth Cohort data, the mixed model approach required us to estimate 12 million parameters, whereas the proposed method involved estimating 25-thousand parameters, a ~500-fold decrease. A study involving n = 10,000 individuals with the same complexity of structure requires estimating about 50-million parameters in the mixed model kinship matrix, whereas the proposed method requires estimating 50-thousand parameters, a ~1000-fold decrease. In addition, estimating the structure in the proposed method primarily uses singular value decomposition, for which a rich literature of computational techniques exists. We utilized a Lanczos bidiagonalization algorithm [22], which scales approximately linearly with respect to n for d ≪ n, where is d the number of latent variables used in the LFA model of population structure (Online Methods). The proposed method is well equipped to scale to massive GWAS and can take advantage of future advances for computing singular value decomposition.

The key assumption to verify in utilizing the proposed GCAT approach is that population structure observed in the SNP genotypes is adequately modeled and estimated. One can test for associations among SNPs that show convincing empirical evidence that the model of structure is reasonably well-behaved; this can be directly tested on the genotype data as previously demonstrated in our logistic factor analysis (LFA) model of structure [14]. For example, on the Northern Finland Birth Cohort Study, we empirically verified that utilizing the LFA model with dimension d = 6 accounted for structure reasonably well for the great majority of SNPs. The linear mixed effects model (LMM) approach and principal components (PCA) approach make trait model assumptions that may be difficult to verify in practice (Online Methods and Supplementary Note). In cases where the probabilistic model that we assume is not validated on the data, a different model should be utilized. For example, our probabilistic model does not account for closely related individuals.

We anticipate that the proposed genotype conditional association test (GCAT) will be useful for future studies. The framework we have developed should facilitate its extension to traits modeled according to distributions not considered here while maintaining our theoretical proof that the test accounts for population structure in the presence of non-genetic effects also confounded with structure.

ONLINE METHODS

Population Structure Model

Suppose that there are n individuals, each with m measured SNP genotypes. The genotype for SNP i in individual j is denoted by x_ij ∈ {0,1,2}, i = 1,2, …, m, j = 1,2, …, n. We collected these SNP genotypes into an m × n matrix X, where the (i, j) entry is x_ij. We denote the genotypes for individual j by x^j = (x_1j, x_2j, …, x_mj)^T.

We utilize our recently developed framework that flexibly models complex population structures for diallelic loci [14]. As described in Results, z is an unobserved latent variable that is assumed to capture heterogeneity in allele frequencies among individuals and can be interpreted as capturing the effect of population structure. (Note that, as described in Results, z also captures information on non-genetic contributions to the trait, such as those related to lifestyle and environment.) For a SNP i, the allele frequency π_i can be viewed as being a function of z, π_i(z). For a random sample of n individuals, we therefore have implicitly sampled unobserved z₁, z₂, …, z_n with resulting allele frequencies π_i(z₁), π_i(z₂), …, π_i(z_n) for SNP i. In Hao et al. (2013) [14], we formulate and estimate a model for m SNPs simultaneously while providing a flexible parameterization of the form of π_i(z).

For shorthand, π_ij ≡ π_i(z_j) is the allele frequency for SNP i conditioned on the ancestry state of individual j. The π_ij values may be called “individual-specific allele frequencies” [14]. These allele frequencies can be collected into an m × n matrix F, where the (i,j) entry is π_ij. Note that E[x_ij/2|z_j] = π_ij, and when Hardy-Weinberg equilibrium holds, x_ij|z_j ~ Binomial(2, π_ij). We utilize the framework from Hao et al. (2013) [14], called “logistic factor analysis” (LFA), that allows the simultaneous estimation of all π_ij from a given genotype data set X. Specifically, it provides estimates of latent variables that form a linear basis of the $\text{logit}({\pi }_{ij})=log\left(\frac{{\pi }_{ij}}{1-{\pi }_{ij}}\right)$ quantities, which turns out is the most convenient scale on which to estimate a model of structure for the proposed testing framework. It should be noted that other well-behaved estimates of π_ij may be utilized as well. Further details are provided in Supplementary Note.

Trait Models

We assume a trait (either quantitative or binary) has been measured on each individual, which we denote by y_j, j = 1,2, …, n. We consider the following models of quantitative and binary traits. We write the trait models in terms of additive genetic effects, but the framework can be extended to account for dominance models and interactions, and the models can also incorporate adjustment variables that capture known sources of trait variation.

The quantitative trait model is

$$y_j=\alpha +\sum _{i=1}^m{\beta }_i{x}_{ij}+{\lambda }_j+{\epsilon }_j$$ (1)

where β_i is the genetic effect of SNP i on the trait, λ_j is the random non-genetic effect, and ε_j is the random noise variation. To allow the interdependence of structure, lifestyle, and environment, we assume that x^j = (x_1j, …, x_m,j)^T, λ_j, and ${\sigma }_j^2$ may all be functions of z_j. We assume that $\mathrm{E}[{\epsilon }_j\mid {\mathit{z}}_j]~\text{Normal}(0,{\sigma }_j^2({\mathit{z}}_j))$, which allows for heteroskedasticity of the random noise variation. The distribution of λ_j can remain unspecified, although we assume that λ_j and z_j may be dependent random variables. The population genetic model summarized shows how the distribution of ${(x_{ij})}_{i=1}^m$, depends on z_j. Without having observed z_j, it follows that ${(x_{ij})}_{i=1}^m$, λ_j, and ε_j are dependent random variables; however, we assume that conditional on z_j, these random variables are independent.

The binary trait model is

$$log\left(\frac{Pr(y_j=1)}{Pr(y_j=0)}\right)=\alpha +\sum _{i=1}^m{\beta }_i{x}_{ij}+{\lambda }_j$$ (2)

where again β_i is the genetic effect of SNP i on the trait, λ_j is the non-genetic effect, and we allow for the case that x^j and λ_j may be dependent due to the common confounding latent variable z_j as described for the quantitative trait model.

We have shown that the linear mixed effects model and principal components approaches involve more restrictive assumptions about the trait models utilized in testing for associations (Supplementary Note).

Association Test Immune to Population Structure

We have derived a statistical hypothesis test of association that is equivalent to testing whether β_i = 0 for each SNP i in the above trait models (1) and (2), and whose null distribution does not depend on structure or the non-genetic effects correlated with structure, making it immune to spurious associations due to structure (Supplementary Note). Specifically, the test allows for general levels of complexity in structure because the test is based on adjusting for structure according to individual-specific allele frequencies.

We have proved a theorem (Supplementary Note) that shows that β_i = 0 in models (1) and (2) implies that b_i = 0 in the following model:

$$\begin{array}{c}{x}_{ij}\mid y_j,{\mathit{z}}_j~\text{Binomial}(2,{\text{logit}}^{-1}(a_i+b_i{y}_j+\text{logit}({\pi }_{ij})))\\ \text{logit}\left(\frac{\mathrm{E}[x_{ij}\mid y_j,{\mathit{z}}_j]}{2}\right)=a_i+b_i{y}_j+\text{logit}({\pi }_{ij})\end{array}$$ (3)

for all j = 1,2, …, n. This establishes a model that can be used to test for associations in place of models (1) and (2). Note that the non-genetic effects, heteroskedasticity, and polygenic background do not appear in the above model used to test for associations. This is important because under our general assumptions, these terms can be difficult or even impossible to estimate in practice. Furthermore, testing for association under this model means that the test will have a valid null distribution regardless of the form of the non-genetic effects, heteroskedasticity, and polygenic background.

As fully detailed in Supplementary Note, an association statistic whose null distribution is known can be constructed by testing whether b_i = 0 in the above model, which we have shown is a valid test if β_i = 0 in traits models (1) and (2). Briefly, the testing procedure works as follows:

1. Formulate and estimate a model of population structure that provides well-behaved estimates of the logit(π_ij) values. We specifically use the logistic factor analysis (LFA) approach of ref. [14], which has been shown to provide a accurate linear basis of the logit(π_ij) values.

2. For each SNP i, perform a logistic regression of the SNP genotypes on the trait values plus the model terms that estimate the ${\{\text{logit}({\pi }_{ij})\}}_{j=1}^n$ values. Also, perform a logistic regression of the SNP genotypes on only the model terms that estimate ${\{\text{logit}({\pi }_{ij})\}}_{j=1}^n$, where the trait is now excluded from the fit. These two model fits are compared via a likelihood ratio statistic, where the larger the statistic, the more evidence there is that b_i ≠ 0.

3. Calculate a p-value for each SNP, which is done based on our result that when the null hypothesis of no association is true, β_i = 0 in models (1) and (2), then the above statistic follows a ${\chi }_1^2$ distribution for large sample sizes.

In our implementation, d estimated logistic factors (from LFA [14]) are included as covariates, which serve as the model terms that estimate the ${\{\text{logit}({\pi }_{ij})\}}_{j=1}^n$ values.

We call our proposed test the “genotype-conditional association test” (GCAT). As a general concept, such an approach is sometimes called an inverse regression model because the trait and genotype are reversed in the regression.

Simulated Data

The complete simulation study on quantitative traits involved population structure constructed in 11 different ways for each of three different apportionments of variance among genetic effects, non-genetic effects, and random variation that all contribute to variation in the trait. Therefore, each configuration involved a constructed allele frequency matrix F and values assigned to variances $\text{Var}\left({\sum }_{i=1}^n{\beta }_i{x}_{ij}\right),\text{Var}\left({\sum }_{j=1}^n{\lambda }_j\right)$, and Var(ε_j) from model (1). For each of these 33 =11×3 configurations, we simulated 100 GWAS data sets, for a grand total of 3300 studies.

We simulated allele frequencies: (i) from the Balding-Nichols model [23] based on allele-frequency and F_ST estimates calculated on the HapMap data set (Balding-Nichols); (ii) subject to structure estimated from two real data sets: the Human Genome Diversity Project (HGDP) and the 1000 Genomes Project (TGP); (iii) at four different levels of admixture by varying the parameter α (defined in Supplementary Note) in the Pritchard-Stephens-Donnelly (PSD) model [24], which is an extension of the Balding-Nichols model; and (iv) for four different types of spatially defined structure (Spatial) by varying the parameter a (defined in Supplementary Note). We intentionally simulated challenging population structures, having in mind that future GWAS such as the forthcoming “Genotype Tissue Expression” program (GTEx) data may involve particularly challenging forms of structure.

In order to provide an extra challenge to the proposed test, we simulated the allele frequencies from a model that differs from the LFA model (equation 4 in Supplementary Note). We generated allele frequencies parameterized by F = ΓS, where F is the matrix of π_ij values, G is an m × d matrix and S is the d × n matrix that encapsulates the structure (with d = 3). This model captures as special cases the Balding-Nichols model and the PSD model [14]. It was also intended to provide an advantage to the PCA and LMM methods because the structure is manifested on the observed genotype scale [14], which is the same scale on which both methods estimate structure.

We simulated 10 truly associated SNPs whose effect sizes are distributed according to a Normal distribution. All genotypes were simulated to be in linkage equilibrium so that true and false positives are unambiguous. We set the variances $\text{Var}\left({\sum }_{i=1}^n{\beta }_i{x}_{ij}\right),\text{Var}\left({\sum }_{j=1}^n{\lambda }_j\right)$, and Var(ε_j) to be: (5%, 5%, 90%), (10%, 0%, 90%), and (10%, 20%, 70%). Setting these variances enforced a certain overall level of genetic contribution to the trait; therefore our simulation study results were minimally affected by the choice of 10 truly associated SNPs and the Normal distribution on their effect sizes. In each simulation scenario, we simulated data for m = 100,000 SNPs and n = 5000 individuals, except HGDP necessarily restricted us to n = 940 individuals and TGP to n = 1500 individuals. The dimension of the structure was set to d = 3, although we carried out the same simulations for d = 6 and the results were quantitatively very similar and qualitatively equivalent.

Additional details on the simulations can be found in Supplementary Note.

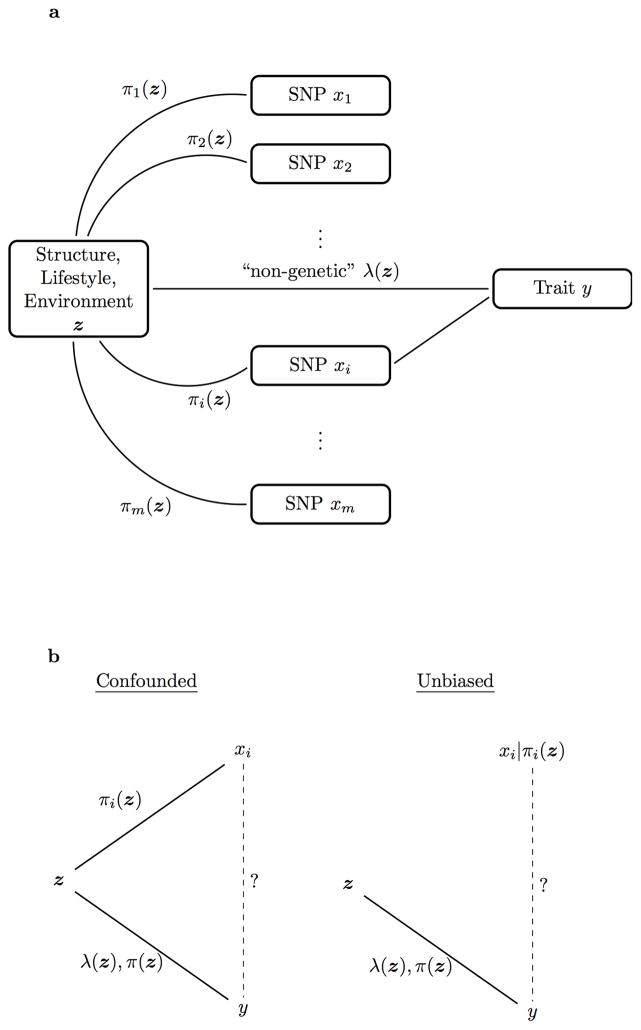
Figure 1.

Rationale for the proposed test of association. (a) A graphical model describing population structure and its effects on a trait of interest. Population structure is captured by a common latent variable z among a set of loci x_i (i =1,2, …, m), via the allele frequencies π_i(z). When one locus has a causal effect on the trait, this induces spurious associations with other loci affected by population structure. At the same time, population structure may be correlated with lifestyle and environment as these are all possibly related to ancestry and geography. (b) Accounting for confounding due to latent population structure. Left panel: A test for association between the i^th SNP x_i and trait y without taking into account z will produce a spurious association due to the fact that both x_i and y are confounded with z. Right panel: A test for association between x_i|π_i(z) and y will be an unbiased because conditioning on π_i(z) breaks the relationship between z and x_i.