Significance
There are certainly few remaining unsolved physics problems as simple and as fundamental as the magnetoelastic buckling phenomenon. In fact, it is just a little more complex than the Euler instability that describes the buckling transition of an axially compressed rod. Here, the bending energy is provided by the magnetization of the system and is balanced by the mechanical energy that hinders the deformation. It is fundamental in the respect that this mechanism could be realized at many different scales with many types of magnetic materials as soon as they offer the suitable combinations of parameters, mainly involving the magnetic susceptibility and the bending modulus. It could find many applications such as the magnetic remote control of nano- or microcantilevers.
Keywords: magnetoelasticity, buckling, nanoparticles, instability, magnetic
Abstract
In its simplest form the magnetoelastic buckling instability refers to the sudden bending transition of an elastic rod experiencing a uniform induction field applied at a normal angle with respect to its long axis. This fundamental physics phenomenon was initially documented in 1968, and, surprisingly, despite many refinements, a gap has always remained between the observations and the theoretical expectations. Here, we first renew the theory with a simple model based on the assumption that the magnetization follows the rod axis as soon as it bends. We demonstrate that the magnetoelastic buckling corresponds to a classical Landau second-order transition. Our model yields a solution for the critical field as well as the shape of the deformed rods which we compare with experiments on flexible ferromagnetic nickel rods at the centimeter scale. We also report this instability at the micrometer scale with specially designed rods made of nanoparticles. We characterized our samples by determining all of the relevant parameters (radius, length, Young modulus, magnetic susceptibility) and, using these values, we found that the theory fits extremely well the experimental results for both systems without any adjustable parameter. The superparamagnetic feature of the microrods also highlights the fact that ferromagnetic systems break the symmetry before the buckling. We propose a magnetic “stick–slip” model to explain this peculiar feature, which was visible in past reports but never detailed.
In the past decade there has been an emerging field of research on new magnetic and elastic soft materials whose shape can be remotely controlled by application of an external magnetic field (1–3). Indeed, at many scales and in various domains, magnetic filaments (4, 5), gels (6), and so on (7) show great promise in numerous domains of application (8). With the progress in the design of these materials, their magnetic susceptibility increases, and brings them closer to the behavior of the more conventional magnetic alloys. Thus, they can benefit a more ancient domain of research that described their magnetoelastic properties. Magnetoelasticity generally describes various phenomena that couple magnetization and mechanical deformation of solid-state objects (9). Excluding magnetostriction, the domain splits into two categories depending on whether the system is driven by free macroscopic currents or only by bound currents. In this latter case, the system may be studied only for its equilibrium configuration, or for its dynamic behavior (10). The complexity of the solution of the magnetic field in the general case justifies that a comprehensive description of the phenomenon is restricted to some trivial geometries such as rods of large aspect ratios (11). The main contribution to the field was made in 1968 with an elegant work (12) that paved the way both for experiments and theory but whose measures showed a critical field twice lower than expected. Further studies (13, 14) reduced the gap down to by considering the edge effect on the magnetic field. This effect could be avoided in the cylindrical geometry, which was experimentally tested only once (15). Another approach consisted of minimizing an energy functional (16, 17) and yielded similar values for the buckling threshold.
In many aspects, we bring original contributions to the field: theoretically, we show the most commonly used model was only suitable for rods of weak magnetic susceptibility. We alternatively propose the “axial model” to describe rods of higher susceptibility and we show for the first time, to our knowledge, that both models display a Landau second-order transition. We also report experiments, first, with pure nickel rods more flexible than the specimens used previously and suitable to analyze their bent shape: they proved the axial model to be excellent. Second, we report the magnetoelastic buckling of recently designed microrods made out of nanoparticles (18) for which the shapes and the threshold values also matched our theoretical expectations. The transition of this paramagnetic system happens when the rod is strictly orthogonal to the field in contrast with ferromagnetic rods which can buckle after an initial deflection. We interpret this observation with a “magnetic stick–slip” model whose simulations reconcile our theory with past and present experiments on ferromagnetic systems.
Theory
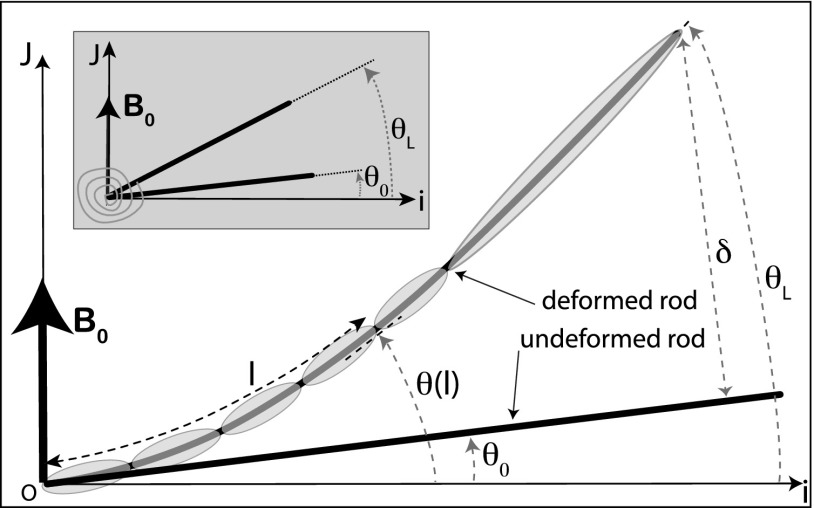
We consider a cylindrical rod with length L and radius (Fig. 1), straight at rest. We suppose it is a Hookean solid, homogeneous, with Young's modulus E and bending modulus . The magnetic susceptibility of the material (not supposed to be linear) is defined by . The cylindrical geometry brings two advantages: the Poisson ratio is not involved in the bending modulus (19) and the absence of edge avoids any magnetic point effects. Except for those induced by the field, we neglect any external force such as gravity which did not interfere in the experiments (Material and Methods). We are not considering twist in the problem, which therefore reduces to two dimensions, the third being omitted in the forthcoming. The shape of the rod is parametrized by the coordinates in the coordinate system , where is the unitary vector oriented with the uniform induction field and l is the curvilinear abscissa. We define . For the sake of simplicity we will only consider the cantilevered rod clamped at and free at . We note [and for the heuristic model described below] and . is the distance between the tip of the deformed rod and its projection on the undeformed rod. The symbols and applied to any vector (, …), respectively, designate their axial and orthogonal projections on the rod local tangent.
Fig. 1.
Diagram and notations. Schema for a magnetized bent rod modeled by a chain of ellipsoids. (Inset) Schema for the heuristic model.
The physics principles which determine the bending shape of a magnetoelastic rod are rather simple: locally the magnetic torque due to the angle between the internal magnetization and the external field must balance the mechanical torque associated with the bending. Considerations on the magnetization of a large aspect ratio ellipsoid (SI Text, section 1A and Fig. S1A), for which the infinite cylinder appears to be a limit, enlighten the buckling mechanism: for an isotropic and paramagnetic material of such a shape, the magnetization is uniform and the strong demagnetizing field in the transverse direction tends to orient the magnetization in the axial direction (SI Text, section 1B and Fig. S1B). So, for a rod, the magnetization is transverse only when the field is strictly orthogonal to it. Therefore, a cantilevered rod submitted to a strictly orthogonal field remains undeformed as long as the energy cost of bending dominates the magnetic energy term. But, once the field reaches a critical value the balance is in favor of the magnetic term : while bending, the magnetization becomes mostly axial and increases suddenly. In a first approach, this mechanism ensures that the paramagnetic feature of the model presented below will describe the experiments correctly even if they are performed with ferromagnetic materials. These latter are primarily demagnetized and, because the deformations during an increase of the external field yield a monotonic increase of the magnetization, this latter follows a first magnetization curve, thus mimicking a paramagnetic material.
The determination of the magnetic field requires solving the Maxwell equations with the appropriate boundary conditions, which clearly prevents an analytic treatment for the case of the bent cylinder. The first historical way around this problem (12) consisted of establishing the expression for the field in an infinite straight slab to which the bending modes were added as perturbations. Alternatively, a so-called “energy method” (17) (renamed here the “independent model” for reasons explained below) yielded the same critical threshold in the limit of low susceptibility and large aspect ratio geometry.
The Independent Versus the Axial Model.
It is common to write the energy functional of magnetic rods (5, 16, 17) as , where is the local bending energy per unit length (19) and is the free magnetic enthalpy per unit volume at abscissa l along the rod (20). In SI Text, section 1C, we show that even if the material is magnetically nonlinear, differentiation of the functional leads to the local torque balance equation: for , and the boundary condition at the free extremity: [we define (SI Text, section 1); for , because ]. The value of fixes the other boundary condition. However, this result implicitly supposes that the local magnetization depends only on the local orientation of the rod with respect to the external field (according to equations of SI Text, section 1A), disregarding the magnetization in the rest of the rod: in fact, this model consists of approximating the rod by a series of independent ellipsoids (Fig. 1). But, are they truly magnetically independent from each other? We checked this approximation by estimating , the field in a small section of the rod induced by the magnetization everywhere else in the sample. The result (SI Text, section 1C and Fig. S1C) is that for an excitation along the rod axis, . This is to be compared with , the field in the local section if it were not under influence of other parts. For materials with , the independent model is therefore inaccurate.
Thus, considering the magnetization is mostly axial in an infinite cylinder (SI Text, section 1B and Fig. S1B), and using a “mean-field” approximation, we propose the axial model based on the following two assumptions: (i) the magnetization mostly orients along the rod axis (if not strictly orthogonal to the field) and its longitudinal component is constant, and (ii) the magnetization is determined by its maximum value, i.e., by the part of the rod which most aligns with the external field (the free tip for the cantilever rod). The shape of a bent rod is indeed almost entirely determined by the axial magnetization: the transverse magnetization is not only weak, it also induces a very small torque when . Finally, the magnetization may arise from the external field (condition ii) or from a permanent moment. The free magnetic enthalpy per unit length of the rod is now and the new torque balance is for . Both models may be solved by the same method: introducing the characteristic length scales for the independent model and for the axial model, and integrating the torque balance equations yields the Euler equations: and , respectively. Interestingly, when , is a valid solution in both cases. The Euler equations yield the respective rod shapes (and thus the deflection at ): and ; and .
In each configuration the solutions require , implicitly provided by for the independent model. In the axial model, we need to transcript assumption (ii) to specify , with . Thus, defining ultimately , the solution for now depends on . In both cases, these equations always admit a solution when . It means that no instability exists when the field is not strictly perpendicular to the straight rod. On the contrary, for , a solution for requires for the independent model and for the axial model. These conditions yield the buckling fields for each model: and , about lower than . These theoretical results are plotted in Fig. S2 and in comparison with the experiments (Figs. 2 and 3).
Fig. 2.
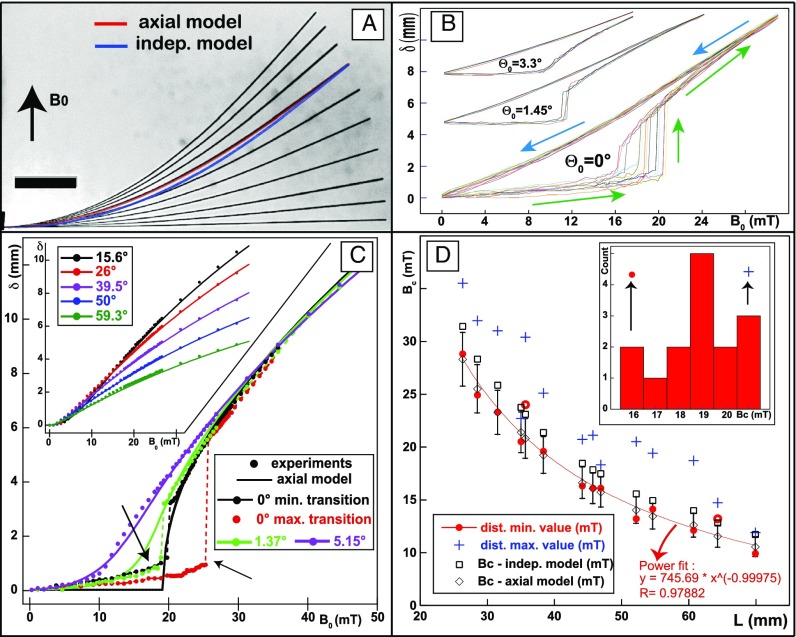
Experiments with nickel rods. (A) Montage of 10 superposed pictures of the same 60.7-mm rod with increasing values of from 0 to 39.6 mT by increment of 4.4 mT ( = 1°). The bar represents 1 cm. On the 26.6-mT rod are superposed the theoretical curve from the independent model (blue, mean difference with the experimental shape = 15%) and the axial model (red, mean difference: 2.4% < 165 m). Analysis for this rod yields = 35.8°, = 36.4 mm, = 464 mT, = 21.6 mT, = 29.8. Angle of with the rod axis at the free end = 1.32°, at l = 0 = 5.33 mT (max value). (B) Repeated magnetization cycles (field increased: green arrow, decreased: blue arrow) showing the absolute value of rod tip deflections. For = 0, L = 44.1 mm (10 out of 15 paths occurred in the field direction). For = 1.45° and = 3.3°, L = 39 mm, the y axis does not apply. (C) Theoretical (axial model) and measures of rod tip deflections for a 38.1-mm rod at various incidences and as a function of . The inset and the main figures correspond to the same graph split in two for clarity. Dots: experimental measures. Solid lines: axial model using the measured parameters of the rod [ adjusted at 18.9 mT while the theoretical value was = (19.2 1.7) mT] and taking into account the variation of with H. Dashed lines are simple links between dots to highlight the transition. For = 0 the two cycles correspond to the lowest (black) and largest (red) threshold out of a distribution of 15 cycles. The two arrows point at the most striking divergence between the theory and the experiments. (D) Buckling threshold of 14 rods for various lengths at = 0. (Inset) Example of histogram of measures of for 1 rod. We analyzed 7 to 20 repeated cycles (mean = 14) for each rod. Main figure: minimum value (red dots, precision: 0.11 mT) and max value (blue cross) of for 14 rods made out of 8 different pieces of wire (some are recut) as a function of L. The error bars for theoretical values of [derived from the uncertainty on C (10%), (6.3%), and L (0.6%)] are shown only for the axial model (lozenges) but also apply to the independent model (squares). All minimum measured thresholds [except for two rods originating from the same wire (red and white dots)] differ by less than this uncertainty from the axial model (from −4% to 6.5%, mean = 0.7%). The red curve is a power fit of the minimum transition showing an exponent of −1.
Fig. 3.
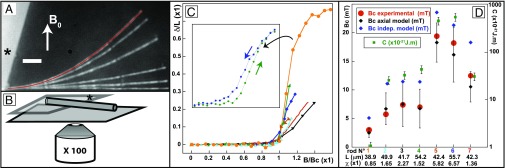
Experiments with microrods. (A) Montage of six superposed micrographs (back-scattered light) of a microrod [L = (42.3 0.05)m, r = (0.3 0.01)m, C = (30.3 5.7)10−21 Jm, = 1.35 0.2] deformed by a magnetic field applied at = 0 and varying from 10 to 20 mT with a regular increment of 2 mT. On the 20-mT rod, the theoretical shape from the axial model is superposed in red (mean difference 0.16m, max 0.5m, whereas the max divergence of the undeformed rod from a straight line is 0.13m. The pictures for 0–10 mT are indistinguishable. White bar = 5m. The mark (*) indicates the coverslip onto which the rod sticks as sketched on B. (C) Deflection of the tip of seven rods while the orthogonal magnetic field is increased. (Inset) An entire cycle of field increase and decrease is shown for rod one, and shows a weak hysteresis (due to plastic deformation). (D) Comparison between the theoretical critical field from the axial model (black lozenges), the independent model (blue lozenges), and the measured buckling field (red dots) referring to the left y axis. The error bars on the theoretical values originate from the uncertainty on the measured properties of the rod (L, r, C, and ) and the errors on the measured field are on the order of the size of the dots. All observed buckling fields are compatible with the axial model (average difference: 3%, range −20–20%). Rod length (L) and the susceptibility are written under the rod number (same color as on graph C), whereas their bending modulus (C) is plotted (green squares) with the log scale on the right axis.
The Heuristic Model.
A basic qualitative description of the buckling may be obtained by modeling the flexible rod by an infinitely rigid one of the same size anchored at and subject to a restoring torque (Fig. 1A, Inset). The corresponding torque balance equation for this system is . Considering solely the longitudinal magnetization such as in the axial model yields the same equation where is replaced by . The numerical solution shows that the system indeed behaves qualitatively like the axial and independent models (Fig. S2). In particular for only, a critical transition is observed for . An energy equation of the system is obtained by integrating the torque: . It corresponds to a classical second-order Landau development, thus predicting the usual critical exponents, also obtained in the independent and axial models (SI Text, section 3 and Fig. S3). This simplistic model still contains the relevant physics of the buckling. It was used to demonstrate that the magnetic nonlinearity has no impact on and to investigate how ferromagnetic permanent moments influence the paramagnetic models (Discussion and Analysis and SI Text, section 6).
Experimental Results
Nickel Rods: Magnetic Susceptibility Derived from Shape Analysis.
Before running the magnetization experiments on nickel rods (see Material and Methods and Fig. S4 for the setup), we measured all their relevant parameters [r = 46 3 m, L = 20–80 mm, C=(5.1 0.5)10−8 Jm; Material and Methods]. To measure the magnetic susceptibility , we performed vibrating sample magnetometry (VSM) on a bundle of rods. We then compared the experimental shape of the magnetized rods with the theoretical models, for various incidences of the field [ and were derived from the deflections of the rod measured at the tip . It yielded and for any l] (Fig. 2A). For all tested shapes , the difference with the axial model was below , whereas the independent model underestimates the axial magnetization and the curvature of the rod at the vicinity of its anchor (differences ). The axial model does not depend on the origin of the magnetization, and accordingly, the excellent accuracy between experiments and the theory did not depend on whether the rod was demagnetized or not. The axial model was therefore used to derive the magnetic susceptibility from measures of the tip deflections [ and yield and , and then ]. To obtain the magnetization curve on a large range of values, we performed, after demagnetization, measures of the deflections of the tip for various fields from 0 to 44 mT for three different rods (, 55, and 63 mm) exposed at various angles to the induction field ( ranging from 1 to 80°). We found that a Langevin law fitted well the first-magnetization data, which yielded a value for for the three rods in agreement with the VSM data (Fig. S4D). Consistent with the measure of the magnetic susceptibility, when taking its variation into account, Fig. 2C shows that the axial model provides almost always the correct value for the rod deflection at any incidence of the field without adjustable parameters because only the measured values of the parameters (L, r, C, ) were used [the dependence of with H was taken into account by writing , where , is the Langevin function (SI Text, section 1), and are derived from the fit of the magnetization curve (Fig. S4D)]. As discussed below, the model also matches the minimum observed buckling threshold when . However, it describes neither the initial deflection at this incidence, nor the surprising transition which occurs at nonorthogonal incidence as described below.
Nickel Rods: Buckling Experiments.
Experimental study of the buckling threshold was performed over 20 different nickel rods prepared as described in Material and Methods. A typical deflection experiment consisted of running an automatic sequence of 80–150 measures during which the field was incremented from 0 to 44 mT and then decreased again back to 0 (Movie S1). Still pictures of the equilibrium were taken typically 2 s after each new value of the external field. A first initial run consisted of increasing the field by steps of 0.9 mT to obtain an estimation of the buckling transition. All subsequent runs were designed to approach more specifically this zone at the best precision allowed by the generator (0.22 mT). After this “precision zone” of typically 5–15 mT, the step was set back to 0.9 mT for the rest of the ascent and the descent. Before each run, we demagnetized the sample (Material and Methods). At 0 mT the rods recovered their straight shape, showing that no plastic deformation had occurred. Each equilibrium image was analyzed by our software to obtain the shape of the rod, which also provided the deflection of the tip as a function of the field intensity (Fig. 2B). Most importantly, we always observed a first initial deflection that increased linearly with the field (typically 1 mm for a 44-mm rod) and during which small vibrations could be seen. This initial deflection and the subsequent jump occurred either toward the field direction or opposite to it. The initial symmetry breaking was very surprising and, suspecting a misalignment, we varied the field incidences. But, we observed instabilities up to an angle of (Fig. 2 B and C and Movie S2), always in the direction of the tilt. At any incidence, the greater the value of the threshold, the larger the gap of the transition. We interpreted this as a simple consequence of the increase of the postbuckling deflection with the field intensity. After the maximum value of the external field was reached, the portion of the curve corresponding to the decrease of the field followed a different path reflecting magnetic hysteresis. If a subsequent run was performed without demagnetization, the deflection followed up the same downward part of the curve.
Another striking feature of these experiments is the nonreproducibility of the threshold (Fig. 2B). For all of the rods we tested, although we took great care in reproducing exactly the same procedure (same demagnetization, same repositioning of the rod, same automatic magnetization) we found the value of the threshold varies from one run to another, without correlation with the sequence order. The absolute dispersion was on average of the mean value of the threshold (range 3.7% for the largest rods to for the smallest). We suspected a cause of this discrepancy was that our measures were done out of equilibrium. So, we performed various experiments to test this hypothesis (increasing the waiting time, slightly vibrating the sample, etc.) but in fact, the only sensitive step was the demagnetizing procedure: when submitted to a demagnetizing field parallel to its axis, almost one out of two rods did not buckle, whereas this happened only very sparsely when the demagnetization was transverse. After a buckling transition, the deflection paths resumed a very reproducible trajectory whatever the position of the threshold (Fig. 2B).
Fig. 2D shows comparison between theoretical and experimental values of the threshold for various rod sizes as permitted by the size of our inducting coils and the power of the generator. For each rod analyzed we compared the minimum, the mean, and the maximum value of the threshold distribution with the theoretical values. We also took into account the dependence of with H by measuring on the last configuration before buckling, from which we deduced and . We also estimated that the transverse field always remained below 1 mT, yielding . We finally found that the maximum measured values of the threshold were on average higher than those derived from the independent model, and higher than the values from the axial model. By contrast, 12 out of the 14 values of the minimum threshold of each distribution were found to differ by less than the uncertainty from the value yielded by the axial model, with a mean difference of (magnetostriction accounts for a mean increase of Bic by 0.1%). The power fit yields the expected slope of −1 for the dependence with the length. By contrast, only four minimum measures are compatible with the independent model.
Microrods.
Experiments analogous to those on nickel rods were also performed with micrometer-sized (L50 m, r150–200 nm) superparamagnetic ( 1–10), soft (E 1–100 GPa) rods made of iron oxide nanoparticles (ø 10–16 nm, volume fraction 5–20%) complexed with opposite charge polymers (Material and Methods and Fig. S5). Here also, we measured all relevant parameters to calculate the buckling threshold. In particular, C(10−19–10−21) Jm was measured from the analysis of the thermal fluctuations (details will be published elsewhere), and was obtained through magnetic bending experiments for = 35° similarly to the measure of for nickel rods. [These measures show that magnetostriction does not impact significantly the measures presented here.]
The making process yields broad distributions for these parameters and about 200 trials were done before 7 rods presented the suitable combination of values to observe a buckling transition (Fig. 3 and Movie S3) with a critical field below the maximum intensity delivered by our apparatus (30 mT). A further difficulty was that these rods undergo plastic deformation when deformed. Although this did not prevent us from observing the buckling transition, large deflections permanently deformed the rod and, except for two rods, the transition could be observed only once. Observations were done in a quasistatic equilibrium after a waiting time ( 500 ms) large before the elastic time scale ( 1–100 ms, where is the water viscosity) but during which some plastic deformations occurred. Several features contrasted with the experiments on nickel rods: first, the transition occurred only when the field was strictly orthogonal to the rod, otherwise only a continuous bending occurred. Second, in two examples (as permitted by little plastic deformation) the deflection path during the decrease of the field exhibited small hysteresis (Fig. 3C), reflecting the absence of ferromagnetism. Third, when possible, the repeated observations of the buckling yielded a reproducible value. Like for nickel rods, comparison with the axial model proved the theoretical bending shape to be accurate (Fig. 3A) at any angle of the field, and, using the measured parameters, the expected values of the threshold were found equal to those observed (Fig. 3D). By contrast, only two measures were compatible with the independent model.
Discussion and Analysis
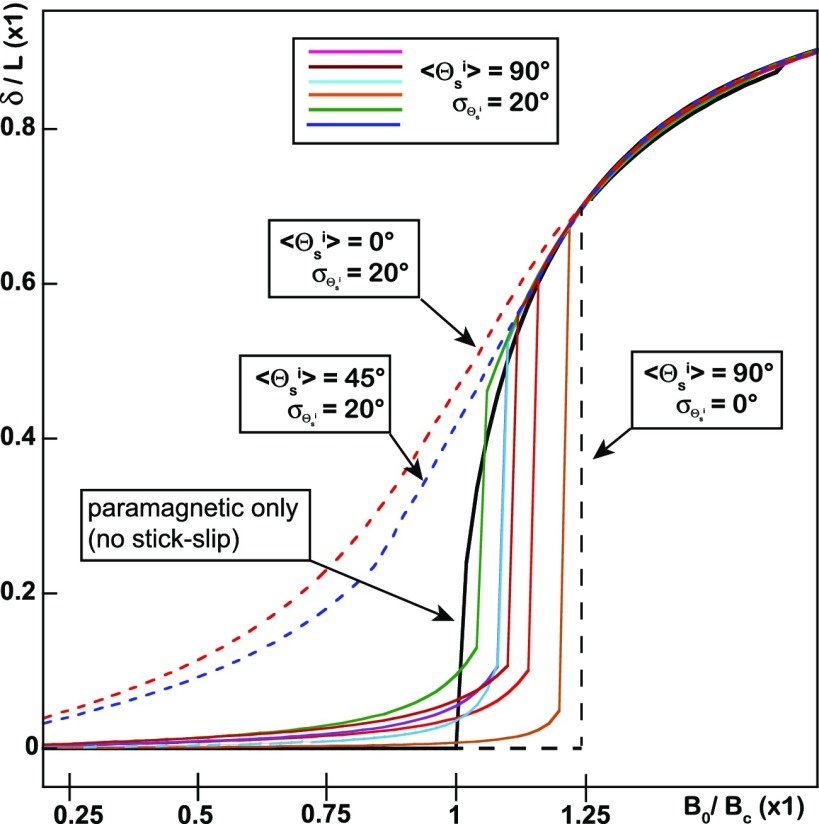
The main idea of this paper is that the magnetization of a bent rod with experiencing a uniform induction field is constant and essentially follows its main axis. Indeed, this simple assumption yields the correct shape of the rods (the difference with the experiments being of the order of the rod radius), and the correct value of the threshold when the system is paramagnetic. Better calibrated rods (the radius must be measured with a precision below ) will be required for challenging this model again. Using recently designed superparamagnetic microrods, we demonstrate the possibility to realize a buckling instability at low fields (2–25 mT), whereas foregoing experiments on alloys were done at hundreds of mT or so. Most importantly, they show that a paramagnetic system behaves consistently with the axial model. By contrast, it highlights the divergences observed with ferromagnetic rods: (i) these latter bend before the transition; (ii) surprisingly, the theory matches (within on average) the observed threshold with the lowest––not largest––value observed among a broad distribution. In fact, most previous works (12–15) contain plots of deflection which show a bending anterior to the buckling. In general the highest value of the transition was retained (21) and the question of how a transition may occur once the symmetry is broken has almost (22) never been raised. We first excluded the role of the nonconstant susceptibility in this matter (SI Text, section 6). Instead, we propose to explain this feature by considering a microscopic ferromagnetic aspect of the material. The first clue for our interpretation is that the initial bending must be the consequence of some (nontransverse) permanent moments. [This is supported by our measure of the initial bend to be , whereas an error on the field incidence would yield (from the heuristic model; SI Text, section 6).] Our working hypothesis was that after demagnetization, some Weiss domains remain stuck in fixed directions and induce randomly distributed permanent moments in the rod. The Barkhausen effect accounts for these domains which perturb the first magnetization curve which is paramagnetic on average but exhibits some hysteresis in the detail. These “stuck” domains must follow a “rotational stick–slip” mechanism: they comply with the external field excitation and merge with the internal paramagnetic field when this latter gets too high. Before this happens, a small but finite contribution of the permanent moment may bend the rod even if the field is orthogonal to its axis. This interpretation is supported by our numerical simulations based on the heuristic model complemented by a distribution of permanent moments (SI Text, section 6). The results (Fig. 4 and Movies S4–S6) reproduce all qualitative features of the observed ferromagnetic transitions (Fig. 2B), and show that the bending depends strongly on how the permanent moments are initially distributed. After a transverse demagnetization, they are expected to be on average orthogonal to the rod , but with a small angular dispersion . The simulations show that the initial randomization of their directions along the same distribution accounts for a variety of deflections as observed in the experiments. The quickest buckling occurs for the most initially deflected rods in which most stuck domains “slip” during this initial bending: at the threshold, the entire rod is paramagnetic and the experiment matches the theory. On the opposite, the most delayed transition happens when . In this case, there is almost no initial deflection, no domain slips before the buckling, and less available parametric material contributes to the transition which requires a greater field to happen. From the width of the experimental threshold dispersion, we may estimate the proportion of stuck domains to be . In any case, all domains ultimately slip when the internal field has increased sufficiently (close to saturation) and all deflections converge to the same path, as in the experiments. Simulations also indicate that a transition is possible for : in this case, the stuck domains hinder the bending and, at the transition, all of the stuck domains suddenly slip when the paramagnetic magnetization has increased sufficiently (Movie S6).
Fig. 4.
Stick–slip simulations of progressively magnetized ferromagnetic rods. Simulation of deflections of increasingly magnetized ferromagnetic rods at orthogonal incidence of the field ( = 0), using the stick–slip heuristic model (SI Text, section 6). If no domain is stuck (the system is entirely paramagnetic) the transition occurs at the critical field (black solid line). For all other curves, 20% of the potential maximum (saturated) magnetization is initially (i.e., at = 0) assigned to permanent moments pointing in random directions (with respect to the rod main axis). The latter are randomly drawn along a Gaussian distribution whose moments are displayed for each curve. For the strict condition ( = 90° and = 0°) the buckling occurs at the max value (black dashed line). When 90° and 20°, a variety of deflected paths is observed before the transition is reached (colored solid lines). Transitions are rarer when 0 (red and blue dashed lines).
Conclusion
This magnetic stick–slip model provides a global understanding of the magnetoelastic buckling transition in ferromagnetic materials. It explains why a transition may occur after an initial bend and highlights the match of the axial theory with the lowest value of the threshold distribution. It suggests that, in ferromagnetic rods, the prebuckling equilibrium is stabilized by ferromagnetic permanent moments. Altogether, this work encompasses a renewed theory consistent with new detailed experiments at two length scales on the magnetoelastic buckling instability. Little work will be required to adapt the theory to other boundary conditions and the experiments to other materials. Our model should also yield new insights on magnetoelastic dynamics. We hope that this work will trigger a global interest in this magnetic instability which may serve in many applications.
Material and Methods
Nickel Rods.
Nickel rod samples (20–80 mm long) were prepared by melting, under tension, a piece of pure nickel wire (ø = 50 m, Weber). Their bending modulus was measured by analyzing their deflection under their own weight. We found repeatedly C = (5.1 0.5)10−8 Jm for eight samples. The wire diameter was checked by conventional optical microscopy after their preparation and was found to be 46 3 m, corresponding to a Young's modulus of E = 230 70 GPa. Before each magnetic measurement the rods were demagnetized in the axial and/or orthogonal direction with a 50-Hz alternative field first increased to saturation and then slowly decreased to zero. To study their deformation upon magnetization, the rods were laid horizontally at the center of induction coils in the Helmholtz configuration (ø = 70 cm, L = 7 mH, R = 0.2; SI Text, section 4). To prevent vertical bending under their own weight, rods were eventually coated with a thin layer of vegetable oil so they would float on a water-filled dish installed between the coils. The sample holder could be rotated horizontally to allow various field incidences. The solenoids were powered by a 3-kW dc generator (SM30-100D, Delta Electronika). The magnetic field was initially calibrated using a Hall effect Gaussmeter (LakeShore 410, Cryotronics) and the field gradient was less than 10−4 T/m over 10 cm in both axes at the center. A CCD camera (PLA623C PixelLink) was fixed between the two coils to monitor the sample from above. The precision on the rod shape was 50 m, yielding a precision of 5 × 10−3 rad on its angle relative to the field. At this resolution, the samples were found to be perfectly linear. Both generator and camera were controlled by a home-made plugin for ImageJ. We developed another plugin to automatically recognize the shape of the rods with the same precision.
Microrods.
Microrods consisted of iron oxide nanoparticles (ø = 10–16 nm) slowly complexed with opposite-charged polymer [poly(diallyldimethylammonium chloride) MW < 100,000, Sigma-Aldrich] while being submitted to a magnetic field (50–250 mT) (18). Nanoparticles, synthesized by the Massart procedure (23), were kindly provided by Olivier Sandre, Laboratoire de Chimie des Polymères Organiques, Université de Bordeaux, Bordeaux, France. After preparation, rods (length distribution 1–100 m) were diluted 100× before being flowed into a home-made flow cell in which we arranged a hang-over by using coverslips of various thicknesses. We used a magnet to force the rods to sediment on the hang-over edge and orient perpendicularly to it, so that a part would stick on the glass and sufficient length remained free of solid contact (Fig. 2B). The sample was sealed using a UV-cured polymer solution. The back-scattered image of the rods was observed with a DMIRB inverted Leica microscope equipped with an apoplan 100× N.A. 1.3 objective and a Photometrics fx-Coolsnap camera. We developed a magnetic setup to apply a magnetic field (SI5) which varied by less than 0.25% over the size of a rod ( 100 m) in the plane of the rod deformation. In the other direction, the vertical gradient (0.6 T/m) was sufficiently weak to prevent the rod from bending but was the principal source of uncertainty on the field intensity due to the uncertainty on the rod vertical position 10 m. As for nickel rod experiments, we developed ImageJ plugins to control the setup and recognize the rod shapes at a precision below 10nm.
Supplementary Material
Acknowledgments
The authors thank Olivier Sandre for providing the nanoparticles, Andrejs Cēbers for constructive discussions, Loïc Auvray for his trust in this project and financial support, and Pascal Monceau and Laurent Limat for their final reading of the manuscript. F.G. warmly thanks Didier Bouscary for his unconditional support.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1422534112/-/DCSupplemental.
References
- 1.Wilhelm C, Cebers A, Bacri JC, Gazeau F. Deformation of intracellular endosomes under a magnetic field. Eur Biophys J Biophys Lett. 2003;32(7):655–660. doi: 10.1007/s00249-003-0312-0. [DOI] [PubMed] [Google Scholar]
- 2.Oukhaled G, Cebers A, Bacri JC, Di Meglio JM, Py C. Twisting and buckling: A new undulation mechanism for artificial swimmers. Eur Phys J E Soft Matter. 2012;35(11):121. doi: 10.1140/epje/i2012-12121-y. [DOI] [PubMed] [Google Scholar]
- 3.Danas SK, Kankanala SV, Triantafyllidis N. Experiments and modeling of iron-particle-filled magnetorheological elastomers. J Mech Phys Solids. 2012;60(1):120–138. [Google Scholar]
- 4.Goubault C, et al. Flexible magnetic filaments as micromechanical sensors. Phys Rev Lett. 2003;91(26 Pt 1):260802. doi: 10.1103/PhysRevLett.91.260802. [DOI] [PubMed] [Google Scholar]
- 5.Cēbers A, Cīrulis T. Magnetic elastica. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(3 Pt 1):031504. doi: 10.1103/PhysRevE.76.031504. [DOI] [PubMed] [Google Scholar]
- 6.Nguyen VQ, Ahmed AS, Ramanujan RV. Morphing soft magnetic composites. Advanced Materials. 2012;24(30):4041–4054. doi: 10.1002/adma.201104994. [DOI] [PubMed] [Google Scholar]
- 7.Jamin T, Py C, Falcon E. Instability of the origami of a ferrofluid drop in a magnetic field. Phys Rev Lett. 2011;107(20):204503. doi: 10.1103/PhysRevLett.107.204503. [DOI] [PubMed] [Google Scholar]
- 8.Fayol D, et al. Use of magnetic forces to promote stem cell aggregation during differentiation, and cartilage tissue modeling. Advanced Materials. 2013;25(18):2611–2616. doi: 10.1002/adma.201300342. [DOI] [PubMed] [Google Scholar]
- 9.Moon F. Magneto-Solid Mechanics. Wiley; New York: 1984. [Google Scholar]
- 10.Moon F, Pao YH. Vibration and dynamic instability of a beam-plate in a transverse magnetic field. J Appl Mech. 1969;36(1):92–100. [Google Scholar]
- 11.Kankanala S, Triantafyllidis N. Magnetoelastic buckling of a rectangular block in plane strain. J Mech Phys Solids. 2008;56(4):1147–1169. [Google Scholar]
- 12.Moon F, Pao YH. Magnetoelastic buckling of a thin plate. J Appl Mech. 1968;35(1):53–58. [Google Scholar]
- 13.Wallerstein D, Peach M. Magnetostatic buckling of beams and thin plates of magnetically soft material. J Appl Mech. 1972;35(2):451–475. [Google Scholar]
- 14.Miya K, Hara K, Someya K. Experimental and theoretical-study on magnetoelastic buckling of a ferromagnetic cantilevered beam-plate. J Appl Mech. 1978;45(2):355–360. [Google Scholar]
- 15.Moon F, Hara K. Buckling induced stresses in martensitic stainless steels for magnetic fusion reactors. Nucl Eng Des. 1982;71:27–31. [Google Scholar]
- 16.Moon F. 1978. Problems in magneto-solid mechanics. Mechanics Today (Pergamon Press, New York), Vol 4, pp 333–338.
- 17.Yang W, Pan H, Zheng D, Cai Q. An energy method for analyzing magnetoelastic buckling and bending of ferromagnetic plates in static magnetic fields. J Appl Mech. 1999;66(4):913–917. [Google Scholar]
- 18.Yan M, Fresnais J, Sekar S, Chapel JP, Berret JF. Magnetic nanowires generated via the waterborne desalting transition pathway. ACS Appl Mater Interfaces. 2011;3(4):1049–1054. doi: 10.1021/am101188y. [DOI] [PubMed] [Google Scholar]
- 19.Landau LD. Théorie de l’élasticité. MIR; Moscow: 1990. pp. 95–100. [Google Scholar]
- 20.Landau LD. Physique théorique. VIII, Électrodynamique des milieux continus. MIR; Moscow: 1969. pp. 169–172. [Google Scholar]
- 21.Dalrymple J, Peach M, Viegelah GL. Magnetoelastic buckling of thin magnetically soft plates in cylindrical mode. J Appl Mech. 1974;41(1):145–150. [Google Scholar]
- 22.Popelar CH, Bast CO. Exp Mech. 1972;12(12):537–542. [Google Scholar]
- 23.Massart R, Dubois E, Cabuil V, Hasmonay E. Preparation and properties of monodisperse magnetic fluids. J Magn Magn Mater. 1995;149(1-2):1–5. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.