Direct Cytoskeleton Forces Cause Membrane Softening in Red Blood Cells

Abstract

Erythrocytes are flexible cells specialized in the systemic transport of oxygen in vertebrates. This physiological function is connected to their outstanding ability to deform in passing through narrow capillaries. In recent years, there has been an influx of experimental evidence of enhanced cell-shape fluctuations related to metabolically driven activity of the erythroid membrane skeleton. However, no direct observation of the active cytoskeleton forces has yet been reported to our knowledge. Here, we show experimental evidence of the presence of temporally correlated forces superposed over the thermal fluctuations of the erythrocyte membrane. These forces are ATP-dependent and drive enhanced flickering motions in human erythrocytes. Theoretical analyses provide support for a direct force exerted on the membrane by the cytoskeleton nodes as pulses of well-defined average duration. In addition, such metabolically regulated active forces cause global membrane softening, a mechanical attribute related to the functional erythroid deformability.

Introduction

Although it was discovered some time ago that ATP is a critical factor in the maintenance of the global shape of red blood cells (RBCs) (1–3), the metabolic regulation of red cell deformability was clearly pointed out only recently (4–7). The elastic properties of RBCs are dominated by the interaction between the lipid bilayer and the underlying spectrin cytoskeleton (8,9), which is a dynamical meshwork mainly consisting of spectrin filaments linked by reconfigurable junctional complexes (5,6). The transient binding capacity of these complexes depends on their phosphorylation state (10–12). This structural network endows the spectrin skeleton with the basic role of globally imparting structural rigidity to the cell membrane (13) and locally regulating its flexibility through reversible phosphorylation at the anchoring nodes (6,14). Indeed, the ability of RBCs to undergo reversible large deformations cannot be rationalized on the basis of a fixed connectivity of the cytoskeleton, but instead requires a model that attributes metabolically driven forces to active remodeling of the RBC cytoskeleton (6,14). Therefore, RBC dynamics has been postulated to be metabolically regulated by continuous remodeling of the junctional nodes of the spectrin skeleton (6–8,14). Under the optical microscope, normal RBCs experience large membrane undulations at the equatorial emplacement, a phenomenon originally referred to as the RBC flicker (15,16). This was initially interpreted as the manifestation of metabolic activity (17,18), although several works treated the fluctuations as purely thermal (19–21). Recently, the RBC flickering phenomenon has been revisited (6,7,22–24), providing an accurate catalog of static-averaged mechanical properties measured at different physiological conditions. The renewed interest in its metabolic causes and the possible functional consequences for RBC dynamics have motivated theoretical efforts hypothesizing the existence of ATP-dependent cytoskeleton forces (14,25–27). An adequate understanding of this hypothesis requires that a distinction be made between the active contribution of the cytoskeleton and passive thermal fluctuations, a problem that awaits definite experimentation. Likewise, no clear experimental evidence of the primary forces involved in this activity has been reported yet, and their temporal and spatial characteristics remain a matter of debate. Experimental approaches to the flickering phenomenon suffer from restricted time resolution and the limited spatial discrimination of membrane motions in the submicron scale. The use of ultrafast optical microscopy (28) renders the classical flickering method (29,30) capable of tracking cell contour fluctuations at very high sampling rates with subpixel resolution, thus allowing noninvasive detection of signal correlations over broad timescales. Normal RBCs have a characteristic biconcave or discocyte shape, a symmetry property that facilitates the detection, in Fourier space, of the active contributions to the normal modes of membrane motion at the equatorial rim. Here, using ultrafast flickering analysis at the cell equator, we show direct evidence of ATP-dependent forces exerted on the RBC membrane, which are detected as correlated pulses with a well-defined average duration that cause a characteristic nonthermal signal in the membrane fluctuation spectra.

Materials and Methods

Chemicals

Unless stated otherwise, all materials were purchased at Sigma-Aldrich (Madrid, Spain).

Preparation of red blood cells

Human RBCs were obtained from blood of healthy donors freshly extracted by venipuncture. When necessary, blood samples were stored in EDTA-containing tubes to avoid coagulation before the erythrocyte concentrate was obtained. The latter is obtained after centrifugation (5000 × g for 10 min at 4°C). The RBC concentrate was rinsed three times with phosphate-buffered saline (PBS) (RBCs/PBS, 1:5 v/v). A blood aliquot (20 μL) was diluted in PBS (250 μL) containing phosphate buffer (130 mM NaCl, 20 mM Na₃PO₄, 10 mM glucose, and 1 mg/mL bovine serum albumin (hereinafter PBS(+) buffer). This buffer does not contain exogenously added ATP but is able to induce the production of ATP through glycolysis. RBC suspensions were rinsed three times (10 min at 2300 × g) in PBS(+). Thereafter, the RBC pellet was resuspended (1:15) in PBS(+). Aliquots (10 μL) of this RBC suspension were transferred to the observation chamber (37°C), which was immediately sealed with a coverglass to avoid evaporation and osmotic stress.

Cytoskeleton inactivation

To study the effect of inactivating the cytoskeleton, we tested RBCs under ATP-depletion and protein-cross-linking conditions. The ATP depletion was performed by incubating cells for 2 h at 37°C in the PBS(−) solution, which is the PBS(+) buffer devoid of glucose and containing 6 mM iodoacetamide and 10 mM inosine, as previously described (7,17). Iodoacetamide is an alkylating drug that blocks the essential active site -SH group in both glyceraldehyde-3-phosphate dehydrogenase and hexokinase (and hence inhibits glycolysis and ATP generation) (31). Inosine is a substrate for human RBC metabolism, and it becomes phosphorylated via purine nucleoside phosphorylase. In the presence of inosine, inorganic phosphate is depleted if it is in short supply, and this starves the phosphorylation of glyceraldehyde-3-phosphate via glyceraldehyde-3-phosphate dehydrogenase, thus inhibiting ADP phosphorylation further down the glycolytic pathway. The result of combining inosine and iodoacetamide is an effective inhibition of cytoskeletal phosphorylation. Drugged cells were maintained in the ATP-depleted medium during experiments. Cells were fixed with glutaraldehyde, which quickly cross-links proteins (32). RBCs were fixed for 30 min at 37°C with a solution of glutaraldehyde (0.2% final) diluted in PBS(−) (18). Glutaraldehyde is known to solidify the hemoglobin in RBCs and cross-link the cytoskeleton (33). Although both treatments somewhat rigidify the RBCs and both inhibit ATP production, stiffening is expected to be weaker for iodoacetamide-treated RBCs than for fixed RBCs treated with cross-linking agent. Passivation experiments by enolase inhibition were performed by adding potassium fluoride (KF, 150 mM) dissolved in PBS(−) buffer. The F⁻ anion inhibits glycolysis (in concentrations >3 mM), and thus, extensive ATP-metabolic depletion is expected (34).

Flickering spectroscopy

Membrane fluctuations were tracked at the equatorial plane of RBCs using an inverted Nikon 80i microscope (Tokyo, Japan) in the bright-field mode (PlanApo objective 100×, zoom 2×) equipped with an ultrafast complementary metal oxide silicon camera (FastCAM SA3, Photron, Tokyo, Japan; 200 kfps maximal rate, 1 Mpixel; 12 Gbytes RAM). Instantaneous fluctuations are decomposed as a discrete series of Fourier modes, h(t) = Σ_(q)h_q(t) exp(iq_mx), where q_m = m/R is the equatorial projection of the fluctuation wavevector (with R the radius and m = 2,3,4,…∞ the azimuthal number) (15). RBC dynamics is experimentally probed through the autocorrelation function, defined as ACF_q(t) = 〈h_q(t − t′)h_q(t′)〉, where the angled brackets indicate an average over the time series obtained from a given fluctuation sequence. The first mode (m = 1), which corresponds to the motion of the center of mass, is completely separated from the flickering per se modes (m ≥ 2). Consequently, contributions from translational motion are adequately eliminated from the experimental records. Good statistics was achieved only when time averaging was performed over long time series (typically 5 s at 20 kHz sampling; n ≈ 10⁴ frames). The ultrafast method described here is able to track fluctuations over very long time periods, thus allowing for coherent detection of different components that appear to be correlated over very different timescales. This technical goal cannot be achieved with classical flickering studies involving much slower videomicroscopy (16,22).

Results and Discussion

Equatorial fluctuations: time series and probability distribution function

In real space, the RBC-equatorial fluctuations, namely h(x,t) = R(x,t) − R₀, are measured as local deviations of the equatorial radius, R(x,t), from an average value, R₀, calculated with respect to the center of mass of the discoidal profile (29,30). Fig. 1 shows flickering time traces tracked during 5 s at a high rate (up to 5 kHz) and minimal exposure time (0.2 ms), a set of observational conditions adequate to enable efficient exploration of the accessible membrane configurations. Healthy RBCs, or healthy dyscocytes (dys_h), were studied in PBS(+) buffer, a medium that supports metabolic production of ATP by glycolysis. Healthy RBCs undergo large fluctuations characterized by long-lived excursions far away from the equilibrium position (Fig. 1 A). The statistical distribution of membrane fluctuations is found to be broad and nearly symmetric (Fig. 1 A). On average (calculated over a statistically significant population of single cells), the membrane fluctuations follow a normal distribution characterized by a large RMSD value, Δh(dys_h) = 32.2 nm (±10%; N = 40), which is consistent with the literature (7,20,22). An adequate account of active cytoskeleton components requires comparison with discoid RBCs in an ATP-depletion medium (dys_d). We incubated RBCs for 2 h in PBS(−) buffer, which led to energy depletion of the cell (31). We found that a 2 h incubation was sufficient for the drugs to inactivate the cytoskeleton; most of the RBCs in the sample became rigid in the echinocyte shape (see Fig. 1 B, left), and the remaining discocytes (dys_d) exhibited significantly reduced fluctuations (Fig. 1 B). Such drugged discoid erythrocytes (dys_d) were used to define the passive skeleton state (7,17). In comparison with healthy RBCs (dys_h), the drugged specimens (dys_d) exhibit weaker fluctuations, as shown by the time trace in Fig. 1 B (center) The average displacements registered in ATP-depleted cells Δh(dys_d) = 11.2 nm (±6%; N = 32) were found to be significantly smaller than for healthy cells. An additional control was performed with rigid erythrocytes obtained after treatment with glutaraldehyde, a potent protein cross-linker that induces solidification of both the cytoplasm hemoglobin and the membrane cytoskeleton (32). Under this experimental condition, we had practically motionless specimens, herein informally called fixed erythrocytes (dys_f), which still maintained the discocyte shape (Fig. 1 C). We observed weaker fluctuations characterized by slender distributions (Δh(dys_f) = 7.8 nm (±5%; N = 25); see Fig. 1 C) typical for rigid specimens with a null metabolism. In treated erythrocytes, only fast local fluctuations are observed (passive cases in Fig. 1, B and C (dys_d and dys_f, respectively), which are different from the slow large-scale undulations detected in healthy specimens (Fig. 1 A, dys_h). This distinctive feature assigns to the healthy flicker cells a richer long-time dynamics compared to that of passive cells, as identified by other authors (6,7,17,18). The presence of these long-scale and ATP-dependent motions enables us to explore the cytoskeleton activity in two ways, 1) by determining its impact on the global mechanical properties of the RBC membrane, and 2) by testing for signatures of active forces on the dynamical correlations of the membrane motions.

Figure 1.

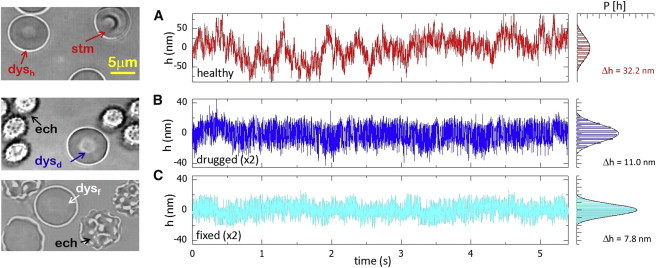
Characteristic membrane-fluctuation time traces tracked at an arbitrary (real-space) point in the equatorial profile of RBCs (both global variations in the cell radius (cell swelling) and net displacements of the cell center (cell translation) have been subtracted from the data). The data correspond to RBCs with a discocyte shape (dys) at different activity states, as shown in the micrographs (left). (A) A healthy flicker (dys_h) upon cytoskeleton activity. (B and C) Passive cases (h-scale magnified by a factor of 2 with respect to (A)) included drugged RBCs (dys_d) after ATP depletion in PBS(−) buffer (B) and cells fixed with glutaraldehyde (dys_f) (C). Although most RBCs in the passive conditions appeared as nonfluctuating speckled echinocytes, some retained their discocyte shape and continued to fluctuate (dys_d and dys_f). The normalized histograms at right represent the probability distributions of the membrane displacements averaged over all the points in the equatorial profile (σ_h is the standard deviation). The line envelopes correspond to the normal distribution. To see this figure in color, go online.

RBC mechanical properties: membrane rigidities and effective temperature

To get further insight into the spatial and dynamic characteristics of active forces involved in the RBC flicker requires a precise account of the mechanical properties of both the passive lipid membrane and the underlying cytoskeleton. In the classical treatment of the fluctuation spectrum by Brochard and Lennon, only the fluid lipid bilayer is considered, which is assumed to have an elasticity determined by bending (κ) and tension (σ) rigidities (16). Using the Milner-Safran (MS) framework to describe membrane fluctuations in the quasispherical geometry, the bending/tension modes are viewed as linear combinations of the spherical harmonics, Y_lm(ϕ, θ) (35). However, in the flickering experiment, we can only obtain information from the focal plane, which is adjusted at the equatorial site where the sharpest image can be focused. Several authors have clarified how the MS analysis can be adapted to the case where the equatorial contour of an axisymmetric membrane is tracked by time-resolved microscopy (29,30). In this case, the equatorial undulations correspond to the discrete sequence of circular eigenmodes with the wavevector determined by the azimuthal number, q = m/R (m = 2,3,4…∞ and R₀ is the spherical radius). Every equatorial MS mode is expressed as a sum of the azimuthal projection of the spherical harmonics Y_lm(ϕ, θ = π/2) over the possible states of polar orientations compatible with the equatorial undulation, i.e., where l ≥ m (combining Eq. S1.9 with Eq. S1.4 in the Supporting Material for t = 0; also see Eq. S.12), this sum is

$$P_m\left(q=m/R\right)=\frac{\langle h_m^2\rangle }{R^2}=\frac{k_{\text{B}}T}{\kappa }\sum _{l=m}^{l_{\max }}{\left\{\left(l+1\right)\left(l-1\right)\left[l\left(l+1\right)+{\Sigma }_{\text{eff}}\right]\right\}}^{-1},$$ (1)

where Σ_eff = σR²/κ + 4c₀R − 2(c₀R)² accounts for the apparent membrane tension (σ), which is corrected by the local spontaneous curvature (c₀R = −2.4 for RBCs at the equator (36); see Section SI1 in the Supporting Material for details).

In RBCs, a spectrin-based cytoskeleton is linked underneath to the lipid bilayer, and thus, two additional components must be taken into account in the elastic free energy: 1), the intrinsic shear rigidity of the spectrin network (37), and 2) the confinement coupling between the membrane and the cytoskeleton (13). In this case, the MS description remains valid for a q-dependent renormalized value of the bending modulus (in Eq. 1), which includes both additional contributions (14,25):

$$\kappa \Rightarrow {\kappa }_{\text{eff}}\left(q\right)=\kappa +\frac{9k_{\text{B}}T}{16\pi \kappa }\mu q^{-2}+\gamma q^{-4},$$ (2)

where μ is the shear modulus and γ is a spring constant accounting for the confinement energy involved in constraining large membrane excursions from the cytoskeleton. At high q, both cytoskeleton contributions vanish and the effective bending modulus, κ_eff, renormalizes to the bare value, κ.

Fig. 2 A shows the fluctuation spectra experimentally obtained for RBCs under the different conditions considered in this work. On the one hand, for passive cells (dys_d in PBS(−) buffer and dys_f in PBS(−) with glutaraldehyde), the fits of the experimental data to the MS spectrum characterize the passive component of the RBC membrane as a rigid material (see Table 1), in contrast to the high flexibility of typical fluid bilayers (κ ≈ 10k_BT, μ ≡ 0). On the other hand, the fluctuation spectrum of normal RBCs (in the presence of ATP) shows amplitudes higher than those found for the former passive cells (more than one order of magnitude higher at low q; see Fig. 2 A). Any extra rigidity component, i.e., other than those considered for the passive fluctuations, should contribute to the reduction of the global fluctuations. Consequently, this dynamic enhancement can be interpreted either as 1) effective softening, leading to lower effective elastic constants; or 2) higher effective temperature, accounting for internal active forces, e.g., the cytoskeletal kicking force hypothesized previously (7,14,38).

Figure 2.

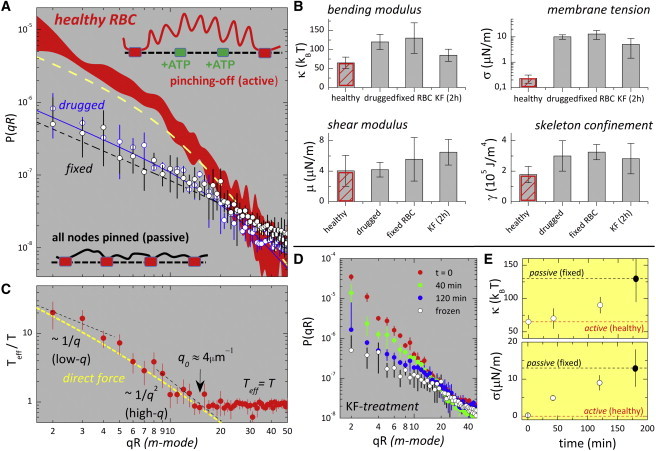
(A) Experimental static spectra calculated from the time-averaged amplitudes of the equatorial modes, P(qR) = <h_q²>, of discocytes at different states (see Materials and Methods). In the active case (red), the variance band represents data obtained over different healthy cells (N = 40). In passive cases, blue- and black-outlined circles represent the average spectra measured for drugged and fixed discocytes, respectively. Lines represent the fits to the MS spectrum using Eqs. 1 and 2, with bending modulus κ_eff as defined in Eq. 2. For the healthy RBCs (dashed yellow line), in the low-q region dominated by membrane tension, the MS spectrum predicts smaller fluctuations than can be registered experimentally. (B) Statistics for the mechanical parameters as obtained from the fits to the P(qR) spectra (see Table 1 for numerical data). (C) Effective temperature, defined as T_eff/T = P_h/P_d (from the data in A) and plotted as a function of the fluctuation wavenumber, m = qR. The dashed yellow line represents the trend expected for a direct force (the black dashed line indicates limiting behavior, T_eff ∼ 1/q at low q and T_eff ∼ 1/q² at high q (at γ ≠ 0); see Gov (38)). (D) Inactivation kinetics for RBCs treated with KF. The different curves correspond to the P(qR) spectra recorded at increasing KF incubation times. (E) Time dependence of the mechanical parameters along the inactivation process in (D) (open circles); the solid circles correspond to a passive limit represented by the mechanical parameters of the fixed discocytes with a cross-linked cytoskeleton after treatment with glutaraldehyde. To see this figure in color, go online.

Table 1.

Mechanical characteristics of the RBC discocytes

Discocyte	N	κ (10−19J)	σ (μN/m)	μ (μN/m)	γ (105 J/m4)
Healthy	40	2.7 ± 0.6	0.23 ± 0.1	4.0 ± 1.0	1.7 ± 0.5
Drugged	32	5.0 ± 0.8	10.0 ± 0.6	4.2 ± 1.0	1.0 ± 0.2
Fixed	25	5.4 ± 1.5	13 ± 4	5.6 ± 1.5	1.5 ± 0.5
KF-treated	6	3.5 ± 0.7	5 ± 2	6.5 ± 1.5	1.0 ± 0.2

Errors indicate N-populational standard deviations.

For healthy cells, the values of the elastic parameters obtained from the analysis of the high-q regime (where thermal noise dominates) in terms of thermal fluctuations and an effective elasticity (with Eqs. 1 and 2; see data in Table 1 and Fig. 2 B), are found to be in agreement with literature data obtained by a similar analysis (6,7,22). Remarkably, the effective membrane tension is found to be significantly smaller in healthy RBCs (σ_h = 0.23 ± 0.1 μN/m) than in passive cells, in particular when data are compared to those for fixed cells obtained after cytoskeleton cross-linking with glutaraldehyde (σ_f = 13 ± 4 μN/m). In view of the large excess area available in the discocyte shape, the low-tension state of normal RBCs could be perceived as a loose interaction between the flexible membrane and the rigid cytoskeleton, in contrast with the permanent anchoring in the passive cases (see cartoon in Fig. 2 A). In addition, the bending stiffness is found to be significantly lower in normal RBCs than in the passive cases (κ_act ≈ κ_pass/2, see Table 1 and Fig. 2 B). Such mechanical softening, observed under cytoskeleton phosphorylation, can be understood as a dynamical effect related to the reversibility of cytoskeleton anchoring; the mechanical effects are much more flexible and floppy healthy RBCs, compared to stiffer passive cells. However, no significant changes are detected in the shear modulus (μ) or in the confinement constant (γ), the two mechanical parameters reporting global cytoskeleton connectivity (see Table 1 and Fig. 2 B). Consequently, we cannot eliminate the possibility of dynamic coupling with targeted energy transfer at different scales as an explanation of the effective membrane-softening characteristic of healthy cells with a reversibly connected cytoskeleton. A crude analysis of the spatial distribution of the effective softening can be made in terms of effective temperatures calculated from the comparison between the experimental spectra of the normal and passive cells, after taking into account the overall changes in the elastic moduli, i.e., T_eff/T ≡ P_h/P_d (Fig. 2 C). (Drugged, instead of fixed, cells were taken as the reference passive state. The reason for this choice is that the possible additional bulk rigidity appeared in fixed cells as a consequence of hemoglobin cross-linking in the cytoplasm.) A high effective temperature is observed at low q (T_eff/T ≈ 20 at qR ≈ 2), indicating the global activity of the RBC. Before thermal effects become dominant (T_eff ≈ T), the active effects decrease first as T_eff ∼ q⁻¹ at low wavenumbers (m < 4) and then renormalize to T_eff ∼ q⁻² for intermediate values (4 < m < 15). This behavior is a clear signature of an active direct force (38), in contrast to active curvature-inducing forces, for which one expects an increase in T_eff with increasing q (38). Finally, active effects become negligible compared to the thermal contribution at wavevectors above a mesoscopic cutoff, q₀ ≈ 4 μm⁻¹ (m > m₀ ≈ 15), where T_eff/T ≈ 1. This cutoff corresponds to the smallest membrane patch for which global activity is detected (where active motion is dominant over thermal fluctuations), λ₀ = 2π/q₀ ≈ 1500 nm, a distance well above the characteristic mesh size of the cytoskeleton network. Because the cytoskeleton unit element is actually smaller (39), a ≤ 100 nm << λ₀, if λ₀ indicates the length scale of the active patch, then the probability of a given cytoskeleton node being active at a given moment might be small, as suggested for the detailed model of the active membrane (26,27). Indeed, if many cytoskeletal nodes became detached simultaneously, a catastrophic decrease of the shear modulus would be detected at rest conditions, similar to the fluidization transition experimentally observed in healthy cells stressed at high rates (40). Since no such sharp decrease of the in-plane rigidity is observed (the shear modulus being essentially constant in the different realizations), we conclude that most of the cross-linking nodes of the spectrin skeleton are pinned to the plasma membrane, and that detachment events, which occur upon phosphorylation, are rather rare and sparsely distributed in space and time (14). This argument also applies for the averaged membrane confinement, which is essentially preserved with a dynamically interacting cytoskeleton. The detection of enhanced (active) amplitudes supports the hypothesis of the existence of metabolically regulated motions that are measurable over large spatial scales (q << q₀ = 2π/λ₀). Further evidence of the metabolic softening of healthy RBCs is provided by additional experiments in which potassium fluoride was added to the PBS(−) buffer (KF 150 mM final). In that case, enolase was blocked by fluoride anion during glycolysis, which inhibited the main metabolic source of ATP (41). A progressive decrease of the flickering activity is observed in the experiments presented here (see Fig. 2 D), especially at low q, where the spectral amplitudes are dominated by the active component and restrained by membrane tension. A quantitative analysis of the effective mechanical constants indicates a progressive stiffening upon ATP inhibition. This is detected as an increase of the bending modulus (Fig. 2 E, upper) and the membrane tension (Fig. 2 E, lower) from their low effective levels, corresponding to healthy RBCs, to maximal values, corresponding to the bare mechanical response of the passive cells. Note that membrane stiffening is observed after both the increase of permanent connection with the spectrin network and the reduction of active forces due to ATP inhibition.

Time-autocorrelation function: thermal modes plus ATP-dependent force

In the simplest description, the dynamics of the active membrane fluctuations is given in the Langevin form (14,27),

$$\frac{\partial h_q}{\partial t}+{\omega }_{\text{q}}{h}_q={\text{Λ}}_q\left[f_{\text{th}}\left(t\right)+f_{\text{act}}\left(t\right)\right],$$ (3)

where ω_q is the damping coefficient of the membrane response that arises from the balance of the thermal (f_th) and active (f_act) excitation forces with the elastic restoring forces and viscous friction, which ultimately determine the relaxation timescale. The latter is described by the Oseen interaction kernel; for a free membrane, Λ_q ≈ (4ηq)⁻¹, where η is the effective viscosity of the RBC cytoplasm (see Section SI2 in the Supporting Material for details). The thermal force is an uncorrelated Gaussian noise, 〈f_th(t)f_th(t′)〉_q = 2k_BTΛ_q⁻¹δ(t−t′), producing Brownian motion with exponentially decaying time correlations when convoluted with viscous friction. The active force introduces additional correlations in the form of a characteristic timescale describing the pulse duration. If one considers stochastic pulse lengths, τ, with a Poissonian distribution P(τ), the correlations of the direct forces take a shot-noise form, that is, 〈f_act(t)f_act(0)〉_q = (n_m/2) F² exp(−t/τ). To describe such an active component (27,34), the model implements a direct force of amplitude, ±f₀, and duration, τ, produced by kicking motors randomly distributed on the membrane with an areal density, n_m. This results in an effective force, F (∼p_onf₀, where p_on is the probability of an individual motor being on), globally exerted by the active motors on the membrane, which consequently moves at a velocity proportional to F/η (η is the bulk viscosity). To discriminate active forces from regular thermal motions in the RBC flicker considered here, we analyze time autocorrelation in the equatorial fluctuation modes, which actually arise from a combination of spherical harmonics projected on the azimuthal plane (see Sections SI1 and SI2 in the Supporting Material for a detailed discussion). Fig. 3 shows the experimental height-to-height temporal autocorrelation functions, ACF_q(t) = 〈h_q(t)h_q(0)〉, measured for the equatorial eigenmodes of discocytes (q = m/R). A pure-thermal relaxation is expected in the passive case of a viscous membrane (Fig. 3 A, left), where the relaxation profile is described by an exponential decay modified by the special function exponential integral, E_a(x) (see Eq. S2.15c in the Supporting Material),

$$AC{F}_q^{\left(\text{th}\right)}\left(q,t;\alpha \right)\approx e^{-{\omega }_{\mathit{q}}t}-\left({\omega }_{\mathit{q}}t\right){\mathrm{E}}_{3/\left(2+\alpha \right)}\left({\omega }_{\mathit{q}}t\right),$$ (4)

with a shape parameterized by α, a renormalization parameter that varies in the interval comprised between α = 1 (regular fluid membrane) and α = 0 (viscous membrane) (see Section SI2 in the Supporting Material for details). The decay rate, ω_q, is essentially determined by the relaxation rate of the fundamental spherical harmonic, l = m (see Eq. S1.10a),

$${\omega }_q\left(l=m=qR\right)=\frac{{\kappa }_{\text{eff}}}{{\eta }_{\text{eff}}{R}^3}\frac{l\left(l+1\right)+{\Sigma }_{\text{eff}}}{Z\left(l\right)},$$ (5)

where Z(l) = (2l + 1)(2l²+2l−1)/l(l + 1)(l + 2)(l−1). In the high-q limit, Z(l) ≈ 4/l, so Eq. 5. converts to the usual dispersion equation for the planar membrane model in a bulk fluid of effective viscosity η_eff, i.e., ω_q ≈ (κq⁴ + σq² + γ)/4η_effq. If the membrane has an intrinsic surface viscosity μ_m, the bulk viscosity takes a q-dependent effective value, η_eff = η(1 + μ_mq/2η) (42). This can be rewritten in terms of a characteristic length, L_C = μ_m/2η, that determines the crossover between bulk- and membrane-dominated frictional regimes, that is, η_eff = η(1 + qL_C) (for details, see Eqs. S2.13 and S2.14 in the Supporting Material).

Figure 3.

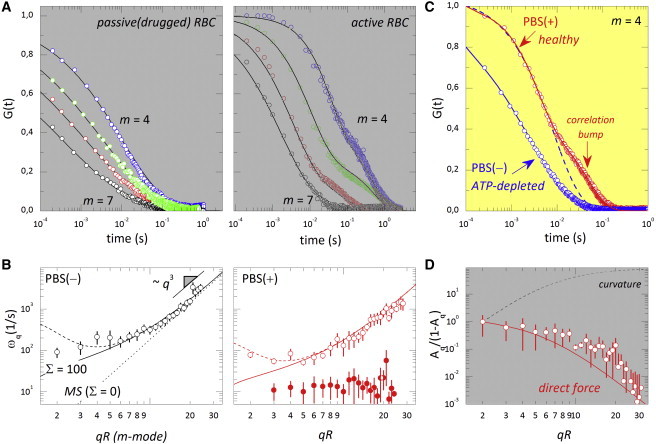
(A) Experimental autocorrelation functions of the RBC flicker in the passive (drugged, left) and active (healthy, right) cases; wave numbers m = qR = 4 (blue), 5 (green), 6 (red), and 7 (black). Solid lines correspond to fits of the experimental data to the stretched exponential model in Eq. 4 for the thermal modes in passive cells (left) and to the bimodal function in Eq. 6 for the healthy cells (right). (B) Relaxation rates in the passive (left) and active (right) cases, with open circles corresponding to thermal modes, ω_q, and solid circles to the active component, ω_act. MS frequencies were fitted using Eq. 5 with η = 6 cP and κ_eff from Eq. 2, taking values from Table 1 (dotted line, tensionless membrane, Σ = 0; solid line, tensioned membrane, Σ > 0; dashed line: tensioned and viscous membrane, Σ > 0, γ > 0, with L_C = 260 ± 80 nm). (C) Comparison between autocorrelation (m = 4) in passive cells with Eq. 4 (blue) and in healthy cells with Eq. 6 (red). (D) Relative amplitudes of the active component decaying according to the direct-force model (red line, Eq. 7) and the curvature-force model (black dashed line). To see this figure in color, go online.

We first probed for relaxation rates of the low-q modes in drugged cells (Fig. 3 A, left), where a single relaxation corresponding to the thermal fluctuations is indeed observed. In this case, data can be accurately described by the modified exponential profile in Eq. 4. As expected, the fitted values of the relaxation rates, ω_q (Fig. 3 B, left), follow the theoretical prediction in Eq. 5 for thermal modes in a quasispherical membrane subjected to cytoskeleton confinement. Taking the experimental values of Table 1, c₀R = −2.4 (36) and η = 6 cP (43), one gets L_C = 260 ± 80 nm (best fit value). Below this characteristic length (q > L_C⁻¹), which is compatible with the mesh size of the cytoskeleton, frictional dissipation is controlled by the intrinsic viscosity of the membrane; from the current experiments, μ_m = 2ηL_C ≈ 3 × 10⁻⁹ kg/s, in agreement with previous estimations (42).

Once the passive realization was found to be consistent with the regular dynamics of the thermal motions in a viscous membrane, the dynamics of the RBC flicker was tested in the PBS(+) medium containing glucose, thus enabling glycolysis and therefore the production of ATP (Fig. 3 A, right). The presence of ATP in the active case makes relaxation significantly slower than in the former passive case (compare the two curves in Fig. 3 C), which suggests a dynamical softening caused by the cell activity. Furthermore, a correlation bump is systematically observed in the long-time tail of the relaxation functions obtained for healthy cells (Fig. 3 A, right), a feature absent in drugged cells (Fig. 3 A, left). The observation of this extra contribution to the mechanical relaxation of the healthy RBC flicker–in addition to the primary thermal component—is the main experimental result of this study and demonstrates the presence of temporally correlated forces in the stress field driving the membrane fluctuations. A similar correlated component was recently identified to be a direct consequence of nonequilibrium molecular activity in a model system with artificially reconstituted membrane motors (44). The active component observed in RBCs is ATP-dependent and emerges at a timescale that is clearly distinguished from the relaxation of the thermal mode, which indicates additionally correlated membrane motion caused by direct forces with a similar duration. Consequently, if this active force is assumed to be uncorrelated with the thermal forces in Eq. S3.3, the autocorrelation function ACF(t) takes the bimodal form

$$AC{F}_q^{\left(\text{act}\right)}\left(t\right)=\left(1-A_q\right)AC{F}_q^{\left(\text{th}\right)}\left(t\right)+A_q\exp \left(-{\omega }_{\text{act}}t\right),$$ (6)

where the first term is the regular thermal component and the second term accounts for the additional correlations that appear at timescale τ (= 1/ω_act) as a result of metabolic activity (Fig. 3 B, right). From the fits, both the relaxation rates and the relative amplitudes of the two modes are obtained, the faster due to the properties of the thermal fluctuations and the slower to metabolic activity. When timescales are compared, the presence of ATP (Fig. 3 B, right) makes the whole relaxation significantly slower than in the former passive case (Fig. 3 B, left). This slowing-down effect suggests a dynamic softening in healthy cells, compatible with the effective decrease of elasticity moduli deduced from the static data in Fig. 2, i.e., ω_q(normal)/ω_q(ATP-depleted) = κ_h/κ_d ≈ 1/2. Indeed, from the comparison of the relaxation rates of the thermal modes, assuming an effective bending-like regime in the high-q limit (Fig. 3 B), we estimate ω_q(healthy)/ω_q(drugged) ≈ κ_h/κ_d ≈ 0.5, showing that the relaxation rate of the mechanical response is affected by the cytoskeletal activity, an intrinsic property of the equation of motion (Eq. 3) and in agreement with the values presented in Table 1.

Thereafter, we analyzed the correlation bump that occurs in healthy cells. We observed that in drugged cells, it disappeared as a consequence of ATP synthesis inhibition. Surprisingly, such a slower, and ATP-dependent, component is found with a near-constant relaxation rate, ω_act ≈ 10 s⁻¹, regardless of the probed wavevector (Fig. 3 B, right). With respect to its amplitudes, at low wavevector, the active component is found to be comparable to the thermal bending mode (A_q ≈ 0.5 at qR ≤ 4); however, its relative amplitude decreases with increasing q, indicating a larger dominance of the thermal mode at higher q (Fig. 3 D). The two characteristics that support an active nature (see Section SI3 in the Supporting Material) are 1) a single-exponential decay, ACF^(act) ∼ exp(−t/τ), compatible with shot-noise correlations; and 2) a nondispersive q-dependence, τ ≈ ω_act⁻¹ ∼ q⁰, indicative of a direct force (26,27) with a given characteristic timescale independent of the spatial scale probed. These features could represent the dynamical signature of the reaction cycle of a metabolic process producing nonequilibrium membrane forces of average duration τ. The observed correlation bump may be related to a force applied by kicking active elements on the membrane, similar to the correlation effect of pumping activity described in Bouvrais et al. (44). This active force should be pulsed, as it is applied during a short time,τ ≈ ω_act⁻¹ ≈ 100 ms, which may be related to the quick metabolic remodeling of the cytoskeleton (14,26). The model in Ben-Isaac et al. (27) and Gov (38) can be used to predict the relative amplitude of the active mode; for a direct force of amplitude F (see Eqs. S3.2 and S3.3 in the Supporting Material), one gets

$$\frac{A_q}{1-A_q}\propto \frac{n_m{\left(F{\text{Λ}}_q\right)}^2}{2k_{\text{B}}T{\Lambda }_q}\frac{{\omega }_{\mathit{q}}}{\left|{\omega }_q^2-{\omega }_{\text{act}}^2\right|}.$$ (7)

Taking the values n_m(F/4η)² = 2.5 10⁵ nm²/s² and ω_act = τ⁻¹ = 10 s⁻¹, this expression predicts the active mode driven by a direct force with a relative amplitude that compares well with the observation (Fig. 3 D). In the tension-dominated regime, this ratio is expected to decay as ∼1/q⁴ when ω_q >> ω_act and as ∼1/q⁰ for ω_q ≈ ω_act, in agreement with experimental results. We also note that the active-component amplitude in Eq. 7 is predicted to diverge (in the linear model) when ω_act = ω_q, but in the healthy RBC, we are everywhere far from this resonance, ω_act < ω_q (Fig. 3 B, right). An alternative case corresponds to active forces that induce membrane curvature. In this case, the force is coupled to the local membrane curvature, ∇²h (instead of h), so we get F → F(qr)² in Eq. 7 (with r being the spontaneous radius of curvature associated with the active conformational change) (38). Consequently, the effect of curvature-inducing forces increases with increasing q, which is the opposite of what was observed, thus ruling out this force mode (Fig. 3 D). As a proof of consistency, we analyzed the mutual correspondence between the characteristic time of the cytoskeletal motions and the spatial scale where membrane activity dominates (T_eff > T at q < q₀; see Fig. 2 C). From the theoretical model of an active membrane pumped by direct forces (38), in the tension-dominated regime, one expects a renormalization between two limiting regimes at a crossover wavevector, q_c ≈ 2ητ⁻¹/γ, which determines the boundary between an active force-dominated regime (q < q_c) and a kinematic regime governed by membrane tension (q > q_c). Assuming τ ≈ 0.1 s, one estimates that q_c ≈ 1 μm⁻¹, so that m_c = q_c × R ≈ 4–5, in agreement with experimental crossover behavior (see Fig. 2 C).

Power spectra: Brownian flicker versus cytoskeleton forces

To better characterize the chromatic characteristics of the flickering noise, the power spectral densities (PSDs) were computed by Fourier transform of the fluctuations: PSD(ω) = ‖∫h(t)e^iωtdt‖². Fig. 4 shows the results from experiments under different conditions. Membrane motion is found to have much larger spectral densities in healthy RBCs than in ATP-depleted cells (Fig. 4 A). The spectral density of healthy cells is found to be enhanced at low frequencies compared to that in the passive cases, indicating that active cells have more energy in the slower motions, even more than expected for the mechanically soft Brownian flicker (with mechanical constants given in Table 1 for healthy RBCs). We attribute the extra fluctuations to active forces (Fig. 4). Our model of active RBC flicker considers membrane-driving forces superposed on passive thermal motions (27,38); in the ideal tensionless case (see Eq. S3.4 in the Supporting Material),

$$\text{PSD}\left(\omega \right)\approx {\text{PSD}}_{\text{th}}\left(\omega \right)+{\left(\frac{F}{4\eta }\right)}^2\frac{n_m\tau }{{\omega }^2\left(1+{\omega }^2{\tau }^2\right)}.$$ (8)

Figure 4.

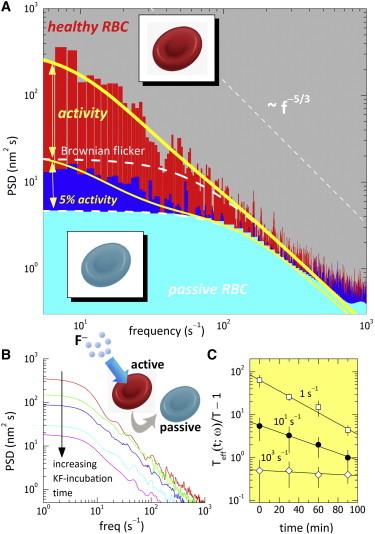
(A) PSDs of the RBC flickers using the fast-Fourier transform (FFT) algorithm, PSD(ω) = {FFT[h(t)]}², for healthy cells (dys_h) (red region), drugged cells (dys_d) (blue region), and fixed cells (cyan region). Vertical bars correspond to experimental data; lines indicate theoretical predictions (see Eqs. S3.3 and S3.4 for the pure thermal spectrum (dashed lines) and the thermal spectrum plus the active component arising from direct cytoskeletal forces (with 5% residual activity in the passive case) (solid lines)). (B) Time evolution of the experimental PSDs of RBC flickers under KF treatment. (C) KF-passivation kinetics measured as the decrease in effective temperature calculated from the data in (B) interpolated at different frequencies. To see this figure in color, go online.

No correlation between active motions and thermal fluctuations is assumed in this (simplest) approximation (25,27), and thus, we consider additive contributions to the spectral amplitudes. The first component represents passive Brownian flickering composed of the dynamic superposition of the thermal modes in a flexible membrane (16). At high frequencies, a Brownian-noise decay is expected, PSD_th(ω → ∞) ∼ ω^−5/3 (7,16). In the low-frequency regime, thermal fluctuations are dominated by the tension of the membrane (σ_eff) and the confinement term (γ), so an upper bound with a value determined by σ_eff is expected in the passive spectra, PSD_th(ω →0) ∼ k_BT/σ_eff. This is the pure thermal behavior found for the glutaraldehyde-fixed discocytes (Fig. 4 A). In addition, the second summand in Eq. 8 accounts for the spectral density corresponding to the ideal shot noise produced by active elements exerting pulsed forces on a tensionless membrane (σ → 0) (27,38). If present, the active term should contribute mainly at low frequencies, measurable as an increase of the spectral density. However, at high frequencies, where Brownian noise dominates, the active component is expected to strongly decrease as ∼ω⁻⁴. Indeed, the flickering spectrum of healthy cells is observed with the ω^−5/3 decay corresponding to thermal components at high frequencies, in agreement with previous experiments (7,25). However, at frequencies <10 Hz (≈ω_act), the healthy flicker dissipates additional power compared to the pure thermal component corresponding to the Brownian flicker (Fig. 4 A). Taking the values we fitted for Fig. 3, i.e., τ = 1/ω_act = 100 ms and n_m(F/4η)² = 2.5 × 10⁵ nm²/s², the model provides an accurate prediction of the active fluctuations in both frequency regimes (Fig. 4 A). This implies a breakdown of the equilibrium description at frequencies <10 s⁻¹, leading to a frequency-dependent dissipative component due to active motions. Such frequency dependence resembles the results of the Betz experiment with an optical trap, from which the same timescale was inferred for the active component (7). By contrast, RBCs with a passive cytoskeleton (treated with either ATP-inhibitory drugs or glutaraldehyde) are observed to dissipate significantly less power, with a comparatively lighter spectral distribution compared to that of healthy cells at low frequencies. In particular, for fixed cells, the observed PSD is compatible with pure thermal fluctuations of a rigid membrane, as deduced from the PSD ratio calculated at low frequencies, [PSD_h/PSD_f]_ω→0 ≈ (σ_f/σ_h)_eff ≈ 10², which is in accordance with data shown in Table 1. Some remaining activity is detected in drugged cells, and it is measured as additional power dissipated at low frequencies with respect to fixed cells (∼5% of the activity of healthy cells in dys_d at ω ≤ ω_act ≈ 10 s⁻¹; Fig. 4 A). The expression for the active contribution of the PSD, given in Eq. 8, is an approximation for the limit of zero tension, and therefore, it strictly applies to the high-ω regime where tension is not dominant. Numerically integrating the PSD for the active component for low ω, where the tension is dominant (27,38), gives the well-behaved function plotted in Fig. 4 A. Further evidence for the existence of active elements dissipating additional power is provided from experiments of glycolysis breakdown with fluoride anions (F⁻). Fig. 4 B shows the time evolution of the PSDs during treatment of RBCs with potassium fluoride (KF). A significant decrease of the dissipated power is observed alongside the kinetic process of enolase inhibition, especially at low frequencies. Because ATP levels progressively decrease after glycolysis inhibition, a proportional decrease of the metabolic activity is expected in accordance with the observed decrease of the mechanical power. The relative decrease of the dissipated power is plotted in Fig. 4 C as a function of time, i.e., T_eff(t)/T = PSD(t)/PSD(t→∞), taking the PSD registered after 2 h as the reference passive state (PSD(t→∞) ≈ PSD_th, for which T_eff ≈ T). The results presented in Fig. 4 C indicate a first-order kinetics for the inactivation process, T_eff(t; ω) ∼ e^−k(ω)t, characterized by a frequency-dependent inhibition rate, k, which determines how fast the mechanical activity is inhibited in the presence of KF. Indeed, the lower the frequency probed, the faster the observed rate of decrease of activity, a fact consistent with the presence of correlated effects due to cytoskeleton forces only at timescales longer than the pulse time (Fig. 4 C; k > 0 at ω < 10² s⁻¹ ≈ 1/τ).

Cytoskeleton pinning and active dynamics

We gain further insight about the spatial characteristics of the detected shot forces by discussing our results in structural terms. The RBC membrane is composed of a flexible lipid bilayer, mainly composed of phospholipids and cholesterol, which is linked to a metabolically active cytoskeletal network. The native structure of unstressed membrane RBC skeleton has been determined by transmission electron microscopy (TEM) (45,46). TEM images of intact membranes reveal a foam-like meshwork of spectrin filaments with a gradual decrease in density from the center of the cell to the equatorial edge. The ultrastructure of stretched patches of the RBC cytoskeleton reveals a network organization (see Fig. 5 A) in which spectrin filaments are the main structural component (2,3). In vivo, the characteristic length of the network is a = 46 ± 15 nm (46), indicating that on average, the size of spectrin filaments in the native membrane skeleton is a fraction of its contour length (L ≈ 190 nm) observed in membrane patches stretched on TEM grids (39). Spectrin filaments are pinned to the membrane via transmembrane- and membrane-associated proteins (47,48). To assemble the network, the distal tails of the spectrin filaments are connected at pinning nodes via junctional complexes consisting of actin, tropomyosin, protein band 4.1, and other regulatory proteins (Fig. 5 A, inset) (39,47,48). On average, at a given 4.1-based node, six spectrin ends make a reversible complex with each actin oligomer, producing an almost hexagonal network (39). Membrane attachment of the junctional nodes is provided by protein band 4.1 (49), which associates with spectrin/actin complexes, forming a high-affinity ternary complex that recognizes specific membrane pinning domains in the transmembrane protein glycophorin C (8,50,51). Ankyrin provides additional membrane linkage through spectrin association at a binding site located close to the filament midregion (52). This domain creates a tight linking association between spectrin and the cytoplasmic domain of protein band 3, the RBC anion exchanger (9). Network stability is mainly dependent on those two interactions, the one defined by the junctional complex at the distal ends of spectrin tetramers and the one defined by ankyrin (5). All the RBC cytoskeletal proteins except actin can be phosporylated by several kinases present in the erythrocyte (3–5). Regarding spectrin, an increased phosphorylation is known to decrease the mechanical stability of intact RBCs via cytoskeletal disentanglement (12). However, spectrin phosphorylation has been shown not to affect spectrin bound to ankyrin (3–5). The question then arises: how does ATP cause the dynamic remodeling of the cytoskeletal attachment? The answer should be puzzling, but some authors have plausibly argued in favor of ATP-dependent phosphorylation of the 4.1 protein (7,14), which controls the spectrin-membrane connections at the junctional nodes in the cytoskeletal network. Indeed, at a high level of phosphorylation, protein band 4.1 drastically reduces its ability to associate with spectrin, which triggers the dissociation of glycophorin C from the membrane skeleton (10,12,51,53). This phosphorylation is catalyzed by protein kinase C (PKC), which disassembles the spectrin/actin/4.1 trimer, the essential cytoskeletal complex that determines the mechanical stability of the RBC membrane (12). Indeed, PKC activation is known to lead to a decreased overall stability of the membrane skeleton (12,53,54), a structural effect that is consistent with a measurable increase of the dynamic fluctuations of the RBC membrane, as revealed by Betz et al. (7). Therefore, assuming the currently accepted mechanochemical model of the 4.1 nodes (51,53), every unpinning event bears a reaction kicking force that should be stressed on the lipid membrane upon dissociation of a spectrin filament from the junctional complex (14,26). The timescale involved in the unbinding process has not yet been determined, but our experiments suggest that the active shots last for ∼0.1 s (see Fig. 3), in agreement with the active timescale detected by Betz et al. (7). The cartoon in Fig. 5 B depicts a generic kicking event where the active element of the membrane undergoes a net displacement, δ, occurring during time τ under a reaction force of amplitude f₀, exerted after unpinning phosphorylation at a junctional complex. In this model, a single-shot event is visualized as the net displacement, δ, of a membrane, which is driven by a kicking force of amplitude f₀. In view of the experimental data presented here, if the observed overcorrelation corresponds to the collective action of single kicking events of duration τ ≈ 0.1 s, assuming the active model of Fig. 5 B, on average, every elemental membrane patch undergoes a transverse displacement of length δ ≈ Δh_h − Δh_f ≈ 25 nm, a distance compatible with the dimensions of the elemental cell of the cytoskeletal network (46).

Figure 5.

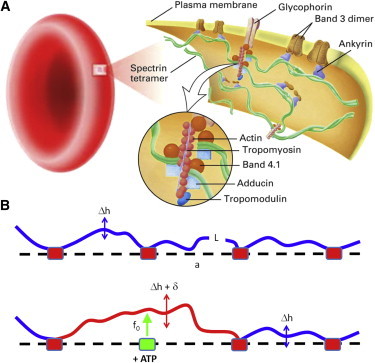
(A) Cartoon of the molecular structure of the RBC cytoskeleton in which we explain our dynamical model. A near-hexagonal spectrin network is assembled by means of multiprotein junctional complexes (see details in the text), which act as primary attachments to the plasma membrane via a specific membrane domain of band 4.1 protein that reversibly interacts with glycophorin C in an ATP-dependent manner. Secondary attachment is provided by ankyrin, which interacts with transmembrane band 3 dimers. (B) Pinning model of cytoskeleton activity at junctional nodes. Complete membrane attachment to a rigid cytoskeleton causes effective stiffening, shown as low-amplitude fluctuations, Δh (upper). Node phosphorylation causes the membrane to pinch off from the cytoskeleton, resulting in an effective kicking force of amplitude f₀ in the membrane, which undergoes a normal displacement, δ (lower). In this case, the membrane experiences larger fluctuations of average amplitude Δh + δ. To see this figure in color, go online.

Active forces driven by the RBC cytoskeleton dynamics

At every single cytoskeleton phosphorylation event, the membrane is reversibly pinched off from one pinning element, which individually exerts a kicking force of amplitude f₀ with a well-defined duration τ ≈ 0.1 s, which determines the average burst time of the active component revealed in the correlation function; ω_act = τ⁻¹ ≈ 10 s⁻¹ (Fig. 3 B). This characteristic time should define the frequency threshold to detect activity in the power spectrum. In native membranes, assuming that every skeletal unit cell contains only one potential kicker, the average surface density of active elements should be of the order n_m ≈ a⁻² ≈ 500 kickers/μm². This estimation is compatible with the numerical density of membrane anchors (3). Therefore, assuming their homogeneous distribution along the cell with an average area of A ≈ 140 μm² (2,3), a maximal density of n_m ≤ 10³ μm⁻² is calculated. It is noteworthy that the direct-force model in Eq. 8 (25,27) is able to describe the experimental PSDs of healthy cells taking the values n_m(F/4η)² = 2.5 × 10⁵ nm² s⁻² and τ = 0.1 s. If these parameters are related to the structural model, and assuming a maximal areal density of potentially active elements (kickers) of n_m ≈ 5 × 10⁻⁴ nm⁻², one gets F ≈ 5 × 10⁻⁴ pN (taking η = 6 cP). This value could become even higher if a lower density of membrane active sites is assumed at the equatorial cell site: F ≈ 2 × 10⁻³ pN assuming n_m ≈ 2.5 × 10⁻⁵ nm⁻² (for a ≈ L ≈ 200 nm). Because F ≤ 2 × 10⁻³ pN is the average force necessary to explain the additional power associated with the active motions of the healthy RBC flicker observed at large scales, only a small fraction (<10%) of spectrin-based cytoskeleton elements are required to be sparsely activated at a given time; since F = p_onf₀, assuming f₀ ≈ 5 × 10⁻³ pN, one estimates p_on ≤ 0.1, the probability for an active cytoskeletal node to be on at a given moment. For an individual kicker, the probability of being on is p_on = τ/(Δτ + τ), where Δτ is the waiting time between consecutive pulses of duration τ. Since p_on ≤ 0.1, taking τ ≈ 0.1 s, we calculate a delay of Δτ ≥ 1 s as the time necessary for a single node in the cytoskeleton to reattach the spectrin filament and to exert a new kick on the membrane. The mechanical work associated with a single shot is W_shot = f₀δ ≈ 1 pN × nm ≈ k_BT, just a fraction of the chemical energy released under the hydrolysis of one ATP molecule (ΔE_ATP ≈ 13k_BT). In healthy cells, the ATP-induced dissociation of spectrin filaments is transient and reversible. A decreased activity is expected under the ATP-depletion condition, since the waiting time, Δτ, for the forthcoming kicking event increases, thereby decreasing p_on and thus decreasing the strength of the effective force that produces the enhanced fluctuations. This is the case for drugged cells or after the use of KF. In the cross-linked cytoskeleton condition (glutaraldehyde treatment), no spectrin dissociation is possible (p_on = 0), and therefore a completely passive behavior is observed in the fixed RBCs. In healthy cells, every kicking event involves single pulses of amplitude f₀ ≈ 5 × 10⁻³ pN sparsely applied during a short time, τ ≈ 0.1 s. Each cytoskeletal element that becomes active only sporadically (p_on ≤ 0.1) is expected either to locally extend the membrane or to change curvature. To cause local membrane extension, a normal force of f_σ ≈ σδ ≈ 5 × 10⁻³ pN must be applied on its own cytoskeletal node (σ_h ≈ 0.2 μN/m). However, to produce a local change in membrane curvature, a larger force, of the order f_κ ≈ κ/δ ≈ 10 pN (where κ ≈ κ_h ≈ 65k_BT), has to be applied. Therefore, a single pulse exerting a direct force as low as f₀ ≈ 5 × 10⁻³ pN would be able only to cause local membrane dilation, not change the local curvature, as deduced from the q-dependence of the active amplitudes (see Fig. 3 D). At a global scale, the action of N_m = An_m ≈ 10⁵ kickers working sparsely at a probability as low as p_on ≈ 0.1 will produce a global force in the membrane of F_kick = N_m^1/2f₀p_on ≈ 1 pN. This force is enough to pump the breathing mode of the cytoskeleton network, F_κ ≈ κ/R ≈ 0.1 pN, and even to drive the large-wavelength tension modes involved in the global area dilation required for changing cell shape, F_σ ≈ σR ≈ 1 pN. In healthy cells, in addition to the direct forces causing out-of-equilibrium activity at global scales (observed as enhanced low-q fluctuations), we detect a global membrane softening associated with ATP-dependent cytoskeletal activity. Although this mechanical softening could be merely compositional (due to cytoskeletal reorganization), membrane detachment is sparse and transient, which suggests a dynamical coupling between active forces and passive mechanical modes of the membrane. Bouvrais and colleagues reported a similar softening associated with the activity of pumping forces reconstituted in artificial bilayers devoid of a structural cytoskeleton (44), thus supporting the hypothesis of mechanical coupling rather than a pure compositional effect.

Conclusions

The results presented here represent an experimental proof of the existence of temporally correlated active forces exerted on the RBC membrane due to metabolic activity. Furthermore, these results strongly support the notion that such forces arise within the spectrin cytoskeleton. The active force appears as sporadic pulses of weak amplitude (f₀ ≈ 5 × 10⁻³ pN) with a relatively long duration (τ ≈ 0.1 s). This kicking activity is spatially sparse over the cytoskeleton, but its dynamical correlation causes global effects on the cell membrane. This cytoskeletal force is shown to be metabolically driven (ATP-dependent) and to produce enhanced membrane fluctuations extending over large distances and relaxing over long times. Although the details of the dynamic mechanism of this activity in the RBC membrane remain unknown, our observations are compatible with the superposition of two stochastic motions that are different in nature, the active pulses due to cytoskeleton detachments and the mechanical modes driven by thermal motions. In healthy RBCs, spectrin detachment events are relatively infrequent and sparse, but sufficient to produce enhanced motions over cellular scales and overall mechanical softening. A more precise look at the constitutive relationships and the regulatory network of this cytoskeleton force will allow for a detailed description of the active flicker mechanism and therefore a better understanding of the dynamic pathways underlying the active mechanics of RBCs in physiological conditions.

Author Contributions

R.R.G. performed research, contributed analytic tools, analyzed the data, and discussed the results. I.L.M. contributed analytic tools, analyzed the data, and discussed the results. M.M. contributed analytic tools, analyzed the data, and discussed the results. G.E. discussed the results and wrote the article. N.S.G. and F.M. performed the research, contributed analytic tools, analyzed the data, discussed the results, and wrote the article.

Editor: Cecile Sykes.