Ensemble-Biased Metadynamics: A Molecular Simulation Method to Sample Experimental Distributions

Abstract

We introduce an enhanced-sampling method for molecular dynamics (MD) simulations referred to as ensemble-biased metadynamics (EBMetaD). The method biases a conventional MD simulation to sample a molecular ensemble that is consistent with one or more probability distributions known a priori, e.g., experimental intramolecular distance distributions obtained by double electron-electron resonance or other spectroscopic techniques. To this end, EBMetaD adds an adaptive biasing potential throughout the simulation that discourages sampling of configurations inconsistent with the target probability distributions. The bias introduced is the minimum necessary to fulfill the target distributions, i.e., EBMetaD satisfies the maximum-entropy principle. Unlike other methods, EBMetaD does not require multiple simulation replicas or the introduction of Lagrange multipliers, and is therefore computationally efficient and straightforward in practice. We demonstrate the performance and accuracy of the method for a model system as well as for spin-labeled T4 lysozyme in explicit water, and show how EBMetaD reproduces three double electron-electron resonance distance distributions concurrently within a few tens of nanoseconds of simulation time. EBMetaD is integrated in the open-source PLUMED plug-in (www.plumed-code.org), and can be therefore readily used with multiple MD engines.

Main Text

Biophysical techniques probing the structural dynamics of biomolecules typically yield signals that arise from an ensemble of molecular conformations, and thus it is often not straightforward to interpret the experimental data unambiguously. For example, double electron-electron resonance (DEER) spectroscopy is increasingly used to measure distances between spin-labeled cysteine residues (1), and to assess conformational mechanisms in proteins. DEER spectra, however, actually translate into distance probability distributions, which are often multimodal and interdependent, and might reflect a variety of protein conformations and rotameric states of the labels.

Molecular dynamics (MD) simulations are arguably the best computational approach to address this problem. The concept is to employ an MD simulation to construct an ensemble of molecular configurations X that is consistent with the measured probability distribution of an observable $\xi ={\xi }^f\left(\mathbf{X}\right)$, while simultaneously representing the molecular system more realistically (solvent, temperature, etc.) than in standard structural-refinement methods. In practice, this approach entails a modification of the simulation energy function, $U\left(\mathbf{X}\right)$, so that the resulting probability distribution, $\rho \left(\mathbf{X}\right)$, fulfills the experimental data with the minimum possible bias i.e., the so-called maximum-entropy principle (2,3). If the experimental data for observable ξ is binned into a histogram, a possible modification of $U\left(\mathbf{X}\right)$ is a linear perturbation, leading to (4)

$$\rho \left(\mathbf{X}\right)=\frac{\text{e}\text{x}\text{p}\left\{-\beta U\left(\mathbf{X}\right)+{\sum }_i{\lambda }_i{h}_i\left[{\xi }^f\left(\mathbf{X}\right)\right]\right\}}{\int d{\mathbf{X}}^{\mathbf{\text{'}}}\text{e}\text{x}\text{p}\left\{-\beta U\left({\mathbf{X}}^{\prime }\right)+{\sum }_i{\lambda }_i{h}_i\left[{\xi }^f\left({\mathbf{X}}^{\mathbf{\text{'}}}\right)\right]\right\}},$$ (1)

where the i index denotes each of the bins in the measured histogram of ξ, and $h_i\left[{\xi }^f\left(\mathbf{X}\right)\right]=1$ if the value of ${\xi }^f\left(\mathbf{X}\right)$ is in bin i, while $h_i\left[{\xi }^f\left(\mathbf{X}\right)\right]=0$ otherwise (and β = 1/k_BT, where k_B is the Boltzmann constant and T is the temperature). The λ_i parameters, which must be determined in each case, ensure that the time averages of $h_i\left({\xi }^f\left(\mathbf{X}\right)\right)$ are equal to the experimental probability values for each of the bins i. Practical applications of the maximum-entropy formulation in Eq. 1 have so far relied on computationally intensive approaches such as averaging over multiple system replicas simulated concurrently (4–7) or iterative optimization algorithms to determine the values of λ_i (2,3).

Here, we present an alternative, single-replica approach inspired by the metadynamics method (8,9), which is also consistent with the maximum-entropy principle. We refer to this method as ensemble-biased metadynamics (EBMetaD). Let us define ρ_exp(ξ) as the target experimental probability distribution of observable ξ and F(ξ) as the free energy,

$$F\left(\xi \right)=-\frac{1}{\beta }\text{l}\text{n}\left[\int d\mathbf{X}\text{e}\text{x}\text{p}\left\{-\beta U\left(\mathbf{X}\right)\right\}\delta \left(\xi -{\xi }^f\left(\mathbf{X}\right)\right)\right]+C,$$ (2)

where C is a constant. In the limit of infinitesimally narrow bins, Eq. 1 becomes (Appendix S1 in the Supporting Material):

$$\rho \left(\mathbf{X}\right)=\frac{\exp \left\{-\beta U\left(\mathbf{X}\right)+\ln {\rho }_{\exp }\left[{\xi }^f\left(\mathbf{X}\right)\right]+\beta F\left[{\xi }^f\left(\mathbf{X}\right)\right]\right\}}{\int d{X}^{\text{'}}\exp \left\{-\beta U\left({\mathbf{X}}^{\mathbf{\text{'}}}\right)+\ln {\rho }_{\exp }\left[{\xi }^f\left({\mathbf{X}}^{\mathbf{\text{'}}}\right)\right]+\beta F\left[{\xi }^f\left({\mathbf{X}}^{\mathbf{\text{'}}}\right)\right]\right\}}.$$ (3)

In EBMetaD, a biasing potential is added to the energy function so that the simulation samples $\rho \left(\mathbf{X}\right)$ in Eq. 3. Like in standard metadynamics, this biasing potential, denoted by $V\left({\xi }^f\left(\mathbf{X}\right),t\right)$, is constructed throughout the simulation as a cumulative sum of Gaussians, added one at a time at a frequency of 1/τ, each centered on the value of ξ at that time. In EBMetaD, however, these Gaussian functions are weighted by the target probability distribution, that is

$$V\left(\xi ,t\right)=\sum _{t^{\text{'}}=\tau ,2\tau \dots }^t\frac{w\text{e}\text{x}\text{p}\left\{-{\left[\xi -{\xi }^f\left({\mathbf{X}}_{t^{\text{'}}}\right)\right]}^2/2{\sigma }^2\right\}}{\text{e}\text{x}\text{p}\left\{S_{\rho }\right\}{\rho }_{\text{exp}}\left[{\xi }^f\left({\mathbf{X}}_{t^{\text{'}}}\right)\right]},$$ (4)

where X_t′ denotes the atomic coordinates at time t′ and σ is the Gaussians width, which sets the resolution of $F\left(\xi \right)$ and ${\rho }_{\text{exp}}\left(\xi \right)$. The quantity $S_{\rho }=-\int \text{d}\xi {\rho }_{\exp }\left(\xi \right)\ln \left[{\rho }_{\exp }\left(\xi \right)\right]$ is the differential entropy of ${\rho }_{\text{exp}}\left(\xi \right)$, i.e., $\exp \left\{S_{\rho }\right\}$ is the effective volume in ξ spanned by ${\rho }_{\text{exp}}\left(\xi \right)$, and serves a normalization factor to ensure that the mean height of the Gaussians added in the range of ${\rho }_{\text{exp}}\left(\xi \right)$ is equal to w. As in standard metadynamics, EBMetaD simulations remain close to equilibrium if w, σ, and τ in Eq. 4 are selected adequately (Appendix S2 in the Supporting Material), and a stationary condition is reached at a certain time t_e after which the biasing potential fluctuates around an average profile that converges asymptotically (10). Specifically, the change of $V\left({\xi }^f\left(\mathbf{X}\right),t\right)$ from this point forward is (11,12)

$$\dot{V}\left(\xi ,t>t_e\right)\approx \frac{C}{{\rho }_{\text{e}\text{x}\text{p}}\left(\xi \right)}\frac{\text{e}\text{x}\text{p}\left\{-\beta \left[F\left(\xi \right)+V\left(\xi ,t\right)\right]\right\}}{\int d{\xi }^{\text{'}}\text{e}\text{x}\text{p}\left\{-\beta \left[F\left({\xi }^{\text{'}}\right)+V\left({\xi }^{\text{'}},t\right)\right]\right\}}\approx C,$$ (5)

where C is a constant. Provided that the region in which ${\rho }_{\exp }\left(\xi \right)>0$ is energetically allowed by $U\left(\mathbf{X}\right)$, the implication of Eq. 5 is that the average biasing potential converges to

$$\overline{V}\left(\xi ,t>t_e\right)\approx -\frac{1}{\beta }\text{l}\text{n}{\rho }_{\text{e}\text{x}\text{p}}\left(\xi \right)-F\left(\xi \right).$$ (6)

That is, when t > t_e, the EBMetaD simulation samples the space of ξ as in the target distribution ${\rho }_{\text{exp}}\left(\xi \right)$.

It is straightforward to generalize this approach to the case of multiple observables ξ_i and probability distributions thereof, ${\rho }_{\text{exp}}\left[{\xi }_i^f\left(\mathbf{X}\right)\right]$, employing a multidimensional biasing potential analogous to that in Eq. 4:

$$V\left({\xi }_1,{\xi }_2,\dots ,t\right)=\sum _{t^{\text{'}}=\tau ,2\tau \dots }^t\sum _i\frac{w_i\text{e}\text{x}\text{p}\left\{-{\left[{\xi }_i-{\xi }_i^f\left({\mathbf{X}}_{t^{\text{'}}}\right)\right]}^2/2{\sigma }_i^2\right\}}{\text{e}\text{x}\text{p}\left\{S_{{\rho }_i}\right\}{\rho }_{\text{e}\text{x}\text{p}}\left[{\xi }_i^f\left({\mathbf{X}}_{t^{\text{'}}}\right)\right]}.$$ (7)

Owing to the scaling factors $S_{{\rho }_i}$, several distributions can be simultaneously targeted even if they have very different effective volumes. The observables ξ_i, however, ought not be a function of each other (2–4).

To test the validity of the EBMetaD method, we first considered the two-dimensional model potential $U\left(\xi ,{\xi }^{\text{'}}\right)$ shown in Fig. 1 A; the corresponding one-dimensional probability distribution ${\rho }_o\left(\xi \right)$, calculated analytically, is shown in Fig. 1 B (gray). We aim to sample instead a hypothetical experimental distribution ${\rho }_{\text{exp}}\left(\xi \right)$, also shown in Fig. 1 B (black). We thus carry out an overdamped Langevin dynamics simulation on the $U\left(\xi ,{\xi }^{\text{'}}\right)$ potential, using EB-MetaD to slowly construct the biasing potential $V\left(\xi ,t\right)$ defined in Eq. 4. As Fig. 1 B shows, the calculated histogram ${\rho }_{\text{sim}}\left(\xi \right)$ evolves gradually until it converges to the target probability distribution. Thereafter, the simulation reaches a stationary condition, and neither ${\rho }_{\text{sim}}\left(\xi \right)$ nor the average bias potential change significantly (Fig. 1 B, inset). To assess whether the ensemble sampled at convergence corresponds to that defined in Eq. 3, i.e., whether EBMetaD indeed fulfills the maximum-entropy principle, we directly compare the calculated simulation histogram ${\rho }_{\text{sim}}\left(\xi ,{\xi }^{\text{'}}\right)$ with the modified two-dimensional potential, $U\left(\xi ,{\xi }^{\text{'}}\right)-\ln {\rho }_{\exp }\left(\xi \right)-F\left(\xi \right)$, calculated analytically (k_BT = 1). As Fig. 1 C shows, these distributions match perfectly; that is, the bias introduced so as to reproduce ${\rho }_{\text{exp}}\left(\xi \right)$ does not alter $\rho (\xi \text{'})$ for any ξ-value. An extension of this test in which two hypothetical distributions ${\rho }_{\text{exp}}\left(\xi \right)$ and ${\rho }_{\text{exp}}^{\text{'}}\left({\xi }^{\text{'}}\right)$ are concurrently targeted further confirms that EBMetaD fulfills the maximum-entropy condition (see Appendix S3 and Fig. S2 in the Supporting Material).

Figure 1.

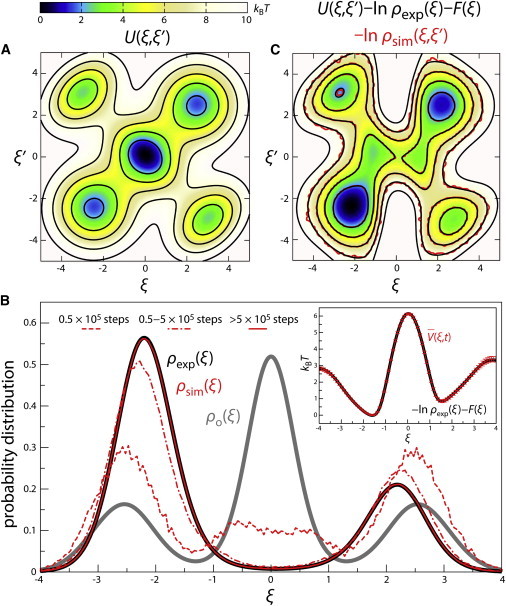
(A) Model two-dimensional potential used to test EBMetaD, via an overdamped Langevin dynamics simulation. (B) Histogram of ξ as a function of the number of simulation steps (red lines), compared with the probability distribution associated with the model potential (gray), and with the target distribution (black). (Inset) Average biasing potential, versus $-\ln {\rho }_{\exp }\left(\xi \right)-F\left(\xi \right)$ (Eq. 6), with t_e = 5 × 10⁵ steps. $F\left(\xi \right)$ was calculated analytically, as $F\left(\xi \right)=-\ln \left[\int \text{d}\xi \text{'}\exp \left\{-U\left(\xi ,{\xi }^{\text{'}}\right)\right\}\right]+C$. (C) Histogram of ξ and ξ’ from EBMetaD (red isolines), overlaid on the ensemble-corrected potential calculated analytically (black isolines) (Eq. 3). Diffusion coefficients in ξ,ξ’ were set to 10, the integration time step was 10⁻⁵, and k_BT = 1. Gaussians of height 10⁻⁴k_BT and width 0.1 were added every 10³ steps. Equivalent results were obtained for a wide range of alternative values (Fig. S1).

To test EBMetaD in a realistic application, we next considered T4 lysozyme in explicit water (Fig. 2 A, and Weaver and Matthews (13)). Following Roux and Islam (4), three methanethio-sulfonate spin-labels were attached at positions E62C, T109C, and A134C. Experimental distance distributions for each pair of nitroxide groups were obtained via electron spin resonance (ESR)/DEER spectroscopy; data were kindly provided by R. A. Stein and H. S. McHaourab (Vanderbilt University Medical Center, Nashville, TN).

Figure 2.

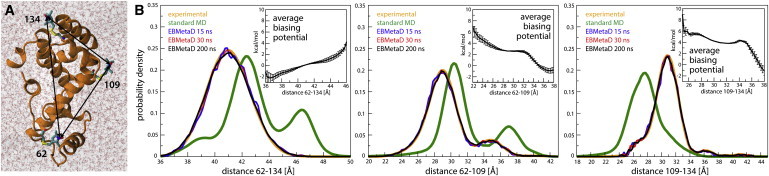
(A) Spin-labeled T4 lysozyme simulated in explicit water (PDB:2LZM (13)). The protein is enclosed in a truncated-octahedron periodic box containing 11,895 TIP3P water molecules and 10 Cl⁻ counterions that neutralize the total charge of the system. The distances between the spin-label nitroxide groups measured by ESR/DEER are indicated (solid arrows). (B) Comparison of the experimental and calculated probability distributions for each of the spin-label pairs, from either unbiased MD simulations or EBMetaD; the latter are given for different simulation times. (Insets) EBMetaD biasing potential, averaged over the simulated trajectory (t_e = 5 ns). Error bars are standard errors over three simulation fragments (see Fig. S4 for further details).

A single trajectory of ∼200 ns was then calculated with EBMetaD, using a three-dimensional biasing potential identical to that defined in Eq. 7, i.e., the three experimental distributions are targeted concurrently. For comparison, an unbiased ∼270-ns trajectory was also calculated using a standard MD. As shown in Fig. 2 B, the distance histograms derived from the unbiased trajectory fail to reproduce those obtained experimentally. By contrast, the histograms derived from the EBMetaD simulation converge to the ESR/DEER data within a few tens of nanoseconds, and preserve that agreement thereafter. To further assess the performance of the method, we compared the time-averaged biasing potential applied to each of the spin-spin distances in three fragments of the EBMetaD trajectory (excluding only the first 5 ns). As shown in Fig. 2 B (insets), the shape of the biasing potentials is largely constant in time, with fluctuations significantly larger than k_BT only in the distal, low-probability regions, thus confirming that EBMetaD reaches an approximately stationary condition (Eqs. 5 and 6). Consistent with the maximum-entropy principle, the ensemble correction introduced by EBMetaD primarily entails a population shift in the rotameric states of the spin labels (Fig. S3 A), with no significant changes in the protein backbone (Fig. S3 B); the root-mean-square deviation of the Cα-trace, relative to the starting x-ray structure, is within 2 Å in both the unbiased and EBMetaD trajectories.

In summary, we have introduced an enhanced-sampling MD simulation method to generate molecular ensembles that reproduce probability distributions for one or more independent observables. This method, referred to as ensemble-biased metadynamics, adaptively provides an ensemble correction consistent with the maximum entropy principle (2–6), without mean field approximations (4), multiple simulation replicas (4,5,7), or the iterative optimization of Lagrangian parameters (2,3). Owing to the computational efficiency and practical simplicity of the method, we posit that EBMetaD can be extremely useful in a wide range of applications, such as structure refinement, mechanistic studies based on spectroscopic data, or purely computational simulation studies. EBMetaD is integrated within the PLUMED 1.3 plug-in (14), and can be thus readily used with multiple simulation engines.

Author Contributions

F.M. and J.D.F.G. designed research and wrote the article. F.M. performed research, contributed analytical tools, and analyzed the data.

Editor: Bert de Groot.