Evolution, Energy Landscapes and the Paradoxes of Protein Folding

Abstract

Protein folding has been viewed as a difficult problem of molecular self-organization. The search problem involved in folding however has been simplified through the evolution of folding energy landscapes that are funneled. The funnel hypothesis can be quantified using energy landscape theory based on the minimal frustration principle. Strong quantitative predictions that follow from energy landscape theory have been widely confirmed both through laboratory folding experiments and from detailed simulations. Energy landscape ideas also have allowed successful protein structure prediction algorithms to be developed.

The selection constraint of having funneled folding landscapes has left its imprint on the sequences of existing protein structural families. Quantitative analysis of co-evolution patterns allows us to infer the statistical characteristics of the folding landscape. These turn out to be consistent with what has been obtained from laboratory physicochemical folding experiments signalling a beautiful confluence of genomics and chemical physics.

1. Introduction

Paradoxically, protein folding has turned out to be easy. How? Why? What’s paradoxical? This review is aimed at answering these questions, beginning with the last one [1]. Ever since Anfinsen’s groundbreaking experiments, understanding the spontaneous nature of protein folding has been widely viewed as being a difficult problem [2]. Delbrück is quoted by Gunther Stent [3] as saying about protein folding “…the reduction in dimensionality from three dimensional continuous to one dimensional discrete in the genesis of proteins is a new law of physics and one nobody could have pulled out of quantum mechanics without first seeing it in operation.” According to Stent, after saying this, Delbrück also immediately quoted Bohr as telling about a man who, upon seeing a magician saw a woman in half, shouts out “It’s all a swindle.” In a similar spirit, I think it is fair to say that a majority of people even in the last decade have looked with skepticism at claims that protein folding was becoming understood [4].

Yet today, a variety of computer algorithms can indeed translate, for the simpler systems, one dimensional sequence data into three dimensional structure albeit at moderate resolution [5,6,7]. The easiest to use algorithms rely ultimately on recoding existing biological information into the form of an energy landscape for computer simulations [5] and thus ultimately these algorithms rely on having “seen it in operation” rather than deriving their results directly from quantum mechanics. Delbrück’s demand to pull folding out of quantum mechanics, has, however, almost been satisfied by using very powerful computers to simulate fully atomistic models, the forces in which are only lightly parametrized by protein structural data [7]. So we see folding proteins really is easier than many people (including me!) thought. Nevertheless, there is something at least a bit strange, perhaps even paradoxical about this outcome, because theory has shown that protein folding indeed could have been much harder, almost as hard as Levinthal envisioned in his famous paradox in which it was pointed out that it would take a cosmological time to fold a protein by searching through all its possible structures [8].

Anfinsen’s refolding experiment itself suggests that folding can be thought of as the search for a minimum free energy arrangement in space of a heteropolymeric chain of residues. The solvent averaged interactions between amino acids depend on the residue types; some residues will interact more strongly with particular other ones than they interact with others. Thus folding is a kind of matching problem: we must find which amino acid will finally make contact with which other one in the native structure in order to reach the lowest energy three dimensional structure. The matching problem is in general NP (non-polynomial) complete [9]. To say a problem is NP complete is a mathematician’s way of saying there exist instances of such a problem (i.e. there should be certain sequences) for which no known algorithm could find the solution in a time scaling as a polynomial in the size of the problem. The exhaustive search through minima envisioned in Levinthal’s paradox scales exponentially with protein length but even an algorithm that takes a time exponentially scaling with a lower power of length (as happens in some theories based on capillarity ideas [10,11]). also would satisfy strict NP completeness so Levinthal’s estimate is certainly an exaggeration. Of course the key words in the mathematical statement are “there exist instances”. Not all instances of matching problems are expected to be equally hard. Some instances of matching problems can in fact be quite easy. A familiar biological example where search difficulty varies with the task is provided by the matching of base pairs in nucleic acid double helices as they assemble. The minimum energy matching is easily found if the two strands are exactly complementary, as in most nuclear DNA giving rise to the standard rules of replication. Finding a match is also easy if only a small fraction of the bases are not conjugate to their partners just as happens when we try to fish out functionally related sequences using primers or use modified primers for site directed mutagenesis via PCR. Comparing two divergent sequences for homology is easy, the difficulty scaling only with a polynomial in the chain length [12]. Most functional RNA sequences have easy matches also, if no pseudo-knots are formed in forming their secondary structures, but in principle the problem of pairing the bases in an arbitrary nucleic acid strand with itself can be quite difficult. This difficulty is also reflected in the cell where some messenger RNA’s turn out actually to be metastable [13]–they first find an active conformation transiently but later rearrange to an inactive but more stable form after sufficient protein has been translated by the mRNA so that the messenger is no longer needed. In contrast, it appears from the Anfinsen experiment, along with its thousands of descendants, that monomeric protein folding is usually thermodynamically controlled, with functional metastability being the exception [14] rather than the rule.

Are the easy instances of matching an amino acid sequence to itself in order to fold into a three-dimensional structure exceptional or are the tough cases the weird examples? This, of course, may depend on the details of the interactions, but the simplest arguments suggest that for a sufficiently long chain, among those chosen at random, the easy examples should be the rarities. Bryngelson and Wolynes suggested that the energy landscape of a typical random amino acid sequence would be rough, riddled with deep metastable minima of widely differing structures and resemble the rugged landscape of a glass [15,16]. They analyzed this situation with the random energy model [17]. The idea was that in a sufficiently long random sequence conflicts between different choices of the favorable interactions would inevitably arise, a phenomenon known as frustration [18]. The low energy states of such a system are all highly compromised, satisfying some interactions very stably, perhaps, but with other interactions remaining unsatisfied and in conflict giving rise to many near degenerate configurations. The mathematical validity of this idea that the energy landscape of a completely random heteropolymer would be rugged, has been buttressed both by more sophisticated statistical mechanics using the replica method [19,20] and by numerous computer simulation studies on highly simplified models that capture the essential features of self-matching chains [21,22,23].

So proteins seem to be the rare, easy instances of energy minimization. What is it that makes folding protein-like sequences easy? What is it that allows proteins to pair residues properly through Brownian motion in order to find their lowest free energy states without the molecule getting trapped in metastable states of wildly different structure as sometimes happens with RNA? The answer is that natural proteins correspond with those special sequences that have been selected to have more consistently stabilizing interactions throughout the natively structured molecule than does a typical sequence which inevitably makes many compromises in its low energy structures. Proteins are not so “frustrated” as a usual heteropolymer sequence is– we say they are “minimally frustrated” [15].

Bryngelson and Wolynes showed that, in contrast to random sequences, such unusual, easy-to-fold minimally frustrated sequences have two potential structural thermodynamic phase transitions. One of the transitions is the folding transition to a well-organized highly stable structure with perhaps some defects. Nevertheless if this correct folding would be prevented from happening, a protein still would settle down to an ensemble of structurally disparate low energy states when cooled below a characteristic temperature Tg. We would find these misfolded states in the low energy trapped ensemble to have similar energies to each other, but to be structurally quite distinct from each other. Finding one given energy minimum by a simulated annealing protocol would yield a structural prediction for that sequence, but that prediction would be quite unreliable until all the low energy arrangements of the chain were found and examined individually. Which structure out of this wide ranging ensemble prevails for a particular molecule would depend on the history of the protein synthesis and annealing, i.e. the protein folding outcome would be kinetically controlled not thermodynamically controlled. This situation is much like what happens for a liquid which becomes a glass when it is cooled if the liquid fails to crystalize [24]. The detailed atomic structure of the resulting glass varies from sample to sample but the macroscopically averaged properties of the glass, like its energy, are nearly the same from sample to sample.

For easy folding sequences, i.e. minimally frustrated sequences, the folding transition at T_F resembles a crystallization transition while the history dependent transition at Tg for poor folders is like the glass transition for a liquid. Protein folding in this picture resembles nucleation of a crystal from a small fluid drop. The kinetics of nucleation is impeded by the multiplicity of trapped states that become prominent near the glass transition temperature of the fluid, Tg. The driving force to the native structure is impeded in its effectiveness by the energetic ruggedness reflected in Tg [16,20,21].

Nucleation, folding and self assembly differ from the more familiar multi-step chemical transformations of organic synthesis or intermediary metabolism in that collective self assembly has a multiplicity of possible mechanisms–no specific sequence of steps is absolutely needed in order to achieve successful folding. Nevertheless a dominant small set of pathways can emerge as the most important ways a particular sequence assembles under some thermodynamic conditions [25,26]. The dominant routes, as well as the activation barrier determining the folding rate, depend on the way in which the loss of entropy upon ordering the chain is compensated by the additional stabilization energy that properly assembled parts of the chain achieve when the energy is compared with the weaker stabilization that occurs when the chain transiently samples improperly folded states [27]. The landscapes for protein folding or for crystallization can be described as rugged funnels [28]. See Figure 1.

Fig 1. The Funnel Diagram.

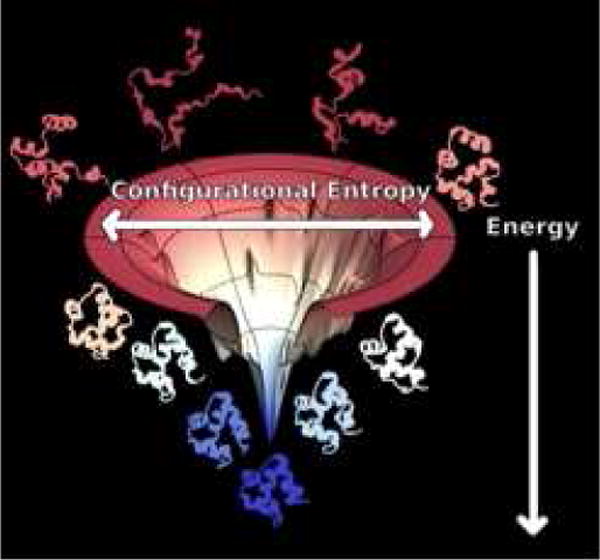
A schematic diagram of the energy landscape of a protein, here illustrated with the PDZ domain whose native structure is shown at the bottom of the funnel. The energy landscape exists in a very high dimensional space. The diagram can only give a sense of this through its representation of two dimensions. The radial coordinate measures the configurational entropy which decreases as the protein takes on a more fully folded structure. The energy of individual configurations is represented by the vertical axis. The values of the energy indicated on this axis are strongly correlated with the fraction of native structures that has formed which is often measured by the fraction of correct native-like contacts called Q. Q also typically increases as the structures descend in the funnel. The energy and entropy oppose each other so that at high temperature the protein is found in an ensemble of states near the top of the funnel. Structures of denatured configurations thus are shown near the top of the funnel. At low temperature, in contrast, an ensemble clustered around the native structures becomes thermally occupied at the bottom of the funnel. The imperfect matching of entropy and energy leads typically to a free energy barrier that separates these two ensembles of states. Surmounting this barrier limits the folding rate.

The small mini-funnels on the sides of the funnel represent trap states. These traps typically possess some native structure but also they contain energetically favorable alternative non-native contacts. Because the non-native contacts are not consistent with each other, rarely are such mini-funnels competitive in an energetic sense with the native basin. The stability of non-native interactions in any one of these traps is an unusual rare accident while the interactions that are formed in native structure have evolved in order for the individual natively folded structure to be especially stable.

The rate of attempting to escape from misfolded traps decreases as the stability of these traps increase and thus the kinetics of search depends on the glass transition temperature Tg. Easy-to-fold sequences can fold without getting trapped because they have a high T_F to Tg ratio. This ratio, in turn, depends on the comparison of the energy of the fully folded state E_F and the typical stabilization energy of a trap E_g which monotonically increases as Tg increases [29].

The minimal frustration or “funnel” [21,28] scenario as the explanation for the ease of protein folding has been confirmed, in concept, by numerous computer studies that simulate stylized stripped down models of self-associating polymers. The most comprehensive such studies simulate heteropolymers on lattices [30,31] where the exact enumeration of possibilities ensures that a complete survey of the landscape can be made so that even for bad folders the ground state can be found and certified as being correct. Other models that realistically describe the protein backbone geometry so that they give structures more easily recognized as being real proteins concur in supporting the idea that it is the magnitude of the T_F/T_G ratio determines the ease of folding to a first approximation [32,33,34]. A discussion of these studies can be found in many early reviews [21,22,35]. Yet the funnel story has seemed too simple to many people [36,37,38]. They ask “Could that really be all there is to it?” Some of the skepticism is perhaps justified because the success of the funnel landscape picture raises other questions: How does the energy landscape theory apply to real proteins (in a quantitative sense)? Exactly how easy is it to fold the proteins of Nature? These questions form the impetus for much of the last two decades’ work on protein folding theory.

In this paper I plan to first touch on the experimental evidence that proteins are indeed minimally frustrated polymers, i.e. that the energy landscape of naturally occurring proteins is actually a rugged funnel as hypothesized. The evidence for the funnel idea is actually quite overwhelming in volume. It is much too extensive to do justice to it here. I therefore refer the the reader to an earlier comprehensive review on the experimental survey of protein folding landscapes [21] using the tools of protein engineering, fast kinetics, theory and simulation. That review documents the usefulness of the rugged funnel model in understanding the kinetics of a range of systems. Atomistic simulations done recently [7] also support the funneled energy landscape picture for a large number of examples, as I will describe below.

Having achieved minimal frustration is the “swindle” (to use Bohr’s term) behind the ease of protein folding. Minimal frustration has apparently come about as the result of evolution and is encoded in existing protein structures and sequences. The mathematical instantiation of the minimal frustration principle via the T_f/T_g ratio can therefore be used as a learning tool for inferring the nature of forces within and between protein molecules– “reverse engineering” the folding problem [29,39,40,41,42]. This strategy has led to predictive algorithms for determining protein tertiary structure from sequence alone. Again the topic of protein structure prediction algorithms based on energy landscape theory has also recently been reviewed by us [5], so I will just touch on this question here. These practical successes, in my view, also should buttress our confidence in the main ideas of folding energy landscape theory.

The bulk of this review will focus on understanding precisely how easily do proteins fold–that is, what have we learned through trying to quantify the smoothness of the landscape by comparing the strength of the guiding forces to the ruggedness of the landscape. To a first approximation this quantification may be summarized in a single number, again, the T_F/T_G ratio. Several estimates of T_F/T_G have been made in different ways over the years, using laboratory data on the thermodynamics and kinetics of folding as well as experimental observations on the reconfigurational motions and residual structure in molten globules as input [43,44,45]. I will review those arguments.

As I have mentioned, the ease of protein folding must ultimately be the result of evolution. The “swindle” of easy protein folding was set up by natural history. Can we also check the idea of the evolutionary origin of minimal frustration in a quantitative sense? Is there a sign in the sequence data alone that landscapes have been funneled through natural selection? Recently it has become possible to determine the degree of funneling of entire protein families as measured by their typical T_f/T_g ratio by carrying out information theoretic analyses of large families of protein sequences and comparing the detectable coevolutionary patterns to the sequence patterns that would be expected based on the physics contained in energy landscape derived transferable force fields that are able successfully to predict tertiary folds from individual protein sequences [46]. I will review the resulting confluence of the evolutionary genomic and the physics perspectives on the energy landscape. One finds a picture of the folding energy landscape from the genomic data alone that matches pretty well with what has been previously deduced from purely physico-chemical ideas and experiments. Finally I will return to the paradoxes of easy protein folding commenting on my current view of them.

2. General Evidence that Folding Landscapes are Funneled

The experimental study of protein structure and folding mechanism has yielded many general sorts of observations about the ways proteins fold. These patterns suggest protein energy landscapes, in the main, are funneled and that proteins are minimally frustrated heteropolymers. In addition, the details of the folding mechanisms of many specific proteins have been reproduced using highly idealized models of protein energy landscapes that have no frustration at all: so called “structure based” [47,48] or Gō models [49]. These models ignore any possibility of stabilizing misfolding interactions that would lead to kinetic traps nevertheless they give solid and surprisingly accurate predictions. The landscapes of such structure based models can be thought of as being “perfect funnels”. Like the perfect gas model in elementary chemistry, the perfect funnel model, while working reasonably well, does not always have quantitative perfection. Major qualitative deviations from perfect funnel predictions are, however, quite unusual. Apparent failures of the funnel model have sometimes led us to think outside the box and to our delight have turned out to confirm that funneling is still preserved for the greater part of the folding process [50]. Many seeming exceptions to perfect funnel prediction can be accounted for by using models that have small perturbations from perfectly funneled landscapes. These models take into account weak trapping owing to residual frustration [51] or energetic heterogeneity [52] or other sources of landscape degeneracy such as the symmetry of designed protein sequences [53] or the symmetry intrinsic to oligomerization through domain swapping [54]. The success of the general predictions about folding that have come from funneled, minimally frustrated landscapes along with the multitude of detailed specific successes on many systems should give us a lot of confidence that the minimal frustration principle has more than a core of truth. The fact that we can understand and quantify deviations from the model itself is also very encouraging that we have begun to understand protein folding.

What general observations support the minimal frustration hypothesis? The first observation is the well-known robustness of protein structure to changes in sequence. Single mutations, and even sometimes dramatic overall changes in sequence like those found in “twilight zone” homologues still give remarkably similar folded native structures [55]. It is commonplace now for protein engineers to assume that making only a single mutation in a protein will leave its structure intact, once that protein has successfully folded, under the right solvent conditions. This robustness is not what would be expected for folding on a typical highly frustrated rugged landscape where an ensemble of structurally disparate competing low energy structures is the norm. Yes, a single mutation sometimes does cause a protein to unfold but this unfolding reflects an “unfair” competition between one single folded structure against myriads of unfolded alternatives, not the competition between specific structured individual alternatives. Only recently have sequences been found that adopt fixed structures but that also change drastically their structure when individual mutations are made [56]. These examples typically involve also changing of the oligomeric state of the proteins, however. Such sequences might be “missing links” in protein evolution.

For a minimally frustrated protein, the overall stability typically does not come from just a few residues but rather is spread throughout the structure. Owing to this delocalized character of the guiding forces to the native state, proteins with widely different sequences not only have similar final structures but often follow the same basic folding mechanism and sometimes have even quantitatively similar rates when tuned to the same stability [57,58]. This generalization that “topology” controls the folding mechanism (as well as its exceptions) has been documented for several protein families notably by Jane Clarke [59] but also by numerous others [60].

The most general powerful consequence of proteins having minimally frustrated landscapes is that folding kinetics almost always changes smoothly and monotonically as protein stability is changed. Studying the effect of such changes on the kinetics is the basis of modern systematic mechanistic folding studies [26,61]. The stability can be changed by changing temperature (up or down!), changing solvent conditions or by making site mutations. The smooth variation of rate with stability is expected for landscapes that are dominated by forming successively the contacts found finally in the native structure [62]. In contrast such a smooth variation is quite unexpected if wildly different structures involving specific non-native structures were to play a significant role in the folding mechanism as would be expected to happen for typical random sequences. Such unexpected variations do sometimes appear. The ROP dimer system seemingly violates the funnel concept because mutations were found that changed both the folding and unfolding rates without changing the protein stability [63]. To accommodate this anomaly, energy landscape thinking however led us to suggest the structure of the dimer had, in fact, been changed upon mutation [50]. It was later confirmed by single molecule FRET experiments that the ROP dimer indeed had, owing to its high symmetry, two different but similarly stable 4 helix bundle structures sharing a common set of interactions [64,65]. One form is dominant for the original protein but the other form dominates for the mutant. In the absence of the symmetry of the dimer system, only a few proteins show any evidence at all of degenerate trap states in which nonnative contacts play a role in the key intermediates, as we would find for a random sequence. The most notorious of these strong exceptions to the perfect funnel model is the folding of Im7, a molecule that functions by binding a toxin [66]. It turns out to be “the exception that proves the rule.” Computational analysis of the Im7 landscape shows that this rather small protein possesses a large region that is frustrated in the monomer but that takes part in the binding function of the molecule where the additional interactions with its target form that are finally favorable and the frustration is relieved upon binding [51]. This frustrated part of the molecule leads to a repacking in an intermediate when Im7 is required to fold on its own without having a partner present [67].

A more detailed test of the ideal funnel model comes from making quantitative predictions using perfectly funneled landscape calculations and comparing them with accurate experimental measurements of kinetic changes on a residue by residue basis [68,69,70,71,72]. The ideal funnel models allow us to predict the fraction of the native stability change that becomes translated into the rate change–the so-called Φ value analysis. The Φ value essentially gives the fraction of the time that a residue participates energetically in the crucial transition states for folding [62]. Very good agreement between predictions of perfect funnel models and experiment has been found in several cases for extensive sets of Φ-values measured for many systems. These include the Φ values for the folding of azurin, UIA, λ repressor and very large lactose repressor module [73].

Fully atomistic simulations also converge on confirming the validity of the funnel concept for the folding of natural proteins at least when correctly tuned all-atom force fields are used. Many early simulation studies did find some evidence for non-native intermediates in natural proteins [74,75,76]. It was suggested that these non-native traps simply had been missed by experimenters. Certainly some misfolded intermediates may be real and probably do exist in the laboratory but a poor force field also typically leads to transient misfolding (since the protein did not evolve with that man-made force field!) and this seems to be the problem in many of the early simulations of folding. In any event the importance of misfolded intermediates in the laboratory would be a quantitative question. Non-native traps may also be relatively more important in the smaller protein systems that first became accessible to simulation than they are in the more typical large proteins. In large, more slowly folding proteins, non-native traps would give bigger barriers and thus they would interfere much more dramatically with folding in vivo. This suggests that selection against misfolds should be stronger for longer proteins than shorter ones. As force fields used in the simulations have improved and the computational capabilities have also advanced so that the bigger systems can be studied [7], it has now become clear that the finally formed native contacts do, in fact, generally provide the dominant interactions in guiding the folding process [77,78]. Other non-native contacts may help collapse and also provide an overall frictional influence on the rate as expected by landscape theory [16] but they do not greatly modify the sequence of events. Eaton et al. have analyzed the heroic simulations of the Shaw group on a large number of systems. Their analysis shows that only for the artificial designed protein αD3 can one find evidence for specific non-native interactions playing any significant role in the dominant folding paths. Indeed even for αD3 the non-native interactions that form correspond to a simple sliding of helices upon each other. Such symmetrically related interactions would not be immediately apparent to the casual observer.

So proteins, in the main are minimally frustrated. Quantitatively, how much frustration is there?

3. How Rugged is the Folding Landscape – Physicochemical Approach

The first attempt to quantify the energy landscape of real proteins through the T_f/T_g ratio was made by Onuchic et al. [43]. Their goal was to see whether the then existing toy model simulations of protein folding using simplified lattice models could be used to think about real proteins. The earlier lattice calculations already had dovetailed with the analytical energy landscape ideas of Bryngelson and Wolynes [15,16] that looked at the folding process of a small protein as a random walk of an order parameter that measures the native-like character of a polymer configuration. Folding is a biased random walk because entropy favors the myriad of polymer configurations unconstrained by similarity to the native state while energy, on the other hand, favors more native-like configurations. Energy and entropy combine to give a free energy that depends on the order parameter. The gradient of the free energy then describes the bias of the walk towards folding or unfolding and depends on the temperature. The diffusion rate for the order parameter depends on the energetic ruggedness, slow rates of diffusion corresponding to rugged glassy landscapes, fast rates to smoother landscapes. The resulting description via a Kramers-like diffusion equation was shown to describe the kinetics of lattice models quite well [16,79]. In recent years the biased diffusion model has also been shown to describe the dynamics of more realistic off-lattice models [80] and has been used directly to interpret experimental data [81,82,83].

As we see, the first key quantity needed to make the connection between landscape theory and real proteins is the entropy change of the polymer when it unfolds. Calorimetry is unfortunately only of modest help in getting that the part of the entropy change relevant to the polymer chain alone because the surrounding water is structured by hydrophobic side chains in the unfolded state. We cannot easily separate out the entropy change of the water environment from the overall calorimetric change. This solvent entropy change is a non-trivial phenomenon, ultimately being the origin of cold denaturation. The folding temperature itself is directly observable so we know the energy loss must exactly compensate the configurational entropy change so T_FΔS = δE. While many folding processes occur directly from a random coil state, the collapsed but disordered state of the protein is not too far away. Apparently proteins are near a triple point between the native, compact globule and random coil phases. The entropy of the collapsed molten globule state is key because ruggedness can, in any event, only arise to a significant extent in the collapsed ensemble. Searching through collapsed states can be slow but searching through the expanded states with few stabilizing contacts is not. Collapsed state ruggedness is what could make reconfigurational search difficult.

Onuchic et al. [43] estimated the configurational entropy of the collapsed, molten globule by noting that its helical content is quite high. Both collapse and helix formation lower the molten globule entropy. The helical entropy loss can be quantitatively estimated by considering the ease of nucleation in the uncollapsed phase as measured by the σ and s parameters of the helix coil transition for uncollapsed peptides. Luthey-Schulten et al. showed how to couple the quasi-one dimensional phase transition of helix formation with the three dimensional collapse transition to relate both the entropy of the globule and its helix content to the hydrogen bond strength [84]. This theory combined with experimental data on the structural content of molten globules gives a configurational entropy of about 0.6 k_B per amino acid in the molten globule. This estimate is based on the observation that molten globules typically have about 65% α helical structure. This is quite a bit less than the 2.3 k_B per monomer unit estimated for free chains and indeed is even smaller than the 1.0 k_B per unit of the toy model lattice polymers.

Saven et al. arrive at similar numbers when the propensity of particular sequences to form helices of peptides or the thermodynamics of signals to start or stop helices is used as input to a theory of the collapsed globule [85].

According to this estimate, entropically a 60 amino acid helical protein maps pretty well on to the popular cubic lattice model of proteins that has 27 beads [43].

While the entropy of the collapsed ensemble follows from the study of residual structure in collapsed states, estimating the ruggedness of the collapsed ensemble requires knowing about the dynamics within molten globules. In 1995 Onuchic et al. [43] used the millisecond time scale value for the reconfiguration time τ_R that could be inferred from existing NMR measurements on molten globules [86] to estimate the ruggedness. Surprisingly it is still not easy to come by better values for molten globule dynamics in the laboratory. According to the Bryngelson-Wolynes random energy model estimate, τ_r is related to the ruggedness described by an energy variance ΔE² and a microscopic reconfiguration time τ₀:

$${\tau }_R={\tau }_0{e}^{\Delta E^2/2T^2}$$ (1)

Onuchic et al. took a rather short time for τ₀ ≈ 10⁻⁹ sec, so that millisecond rates in the globule give ΔE²/2T² ≈ 15.

The ruggedness ΔE² also determines the temperature of the glass transition which occurs when the temperature is low enough so that only deepest energy states out of the e^Sc/kB possible ones are thermally sampled. This condition on the entropy gives the relation

$$k_B{T}_g=\sqrt{\Delta E^2/N}/\sqrt{2S_c/N}$$ (2)

where N is the chain length.

Onuchic et al. thus arrived at a value for the glass transition temperature which is much lower than the folding temperature T_g ≈ .6T_F. This low value is consistent with a moderately strongly funneled landscape corresponding to a roughly three letter protein folding code.

The random energy model also gives an estimate for the energy of the deepest traps that would be thermally sampled at T_g. This competitive trap energy is $E_g=\sqrt{\Delta E^2\mathit{Sc}}$.

The minimum frustration principle can also be formulated in terms of the condition that the energies δE_F are less than E_g. In this form then we see minimal frustration is equivalent to there being a gap in the spectrum of folded energy states, as in Fig 2. In reality of course, this gap is filled by partially folded configuration in which some of the native contacts have formed that correspond to the structures on the paths for nucleation of properly folded protein structure. Important as they are, these partially folded configurations are sufficiently small in number that they would hardly show up on the plot.

Fig 2. The Distribution of Energies on a Funneled Folding Landscape.

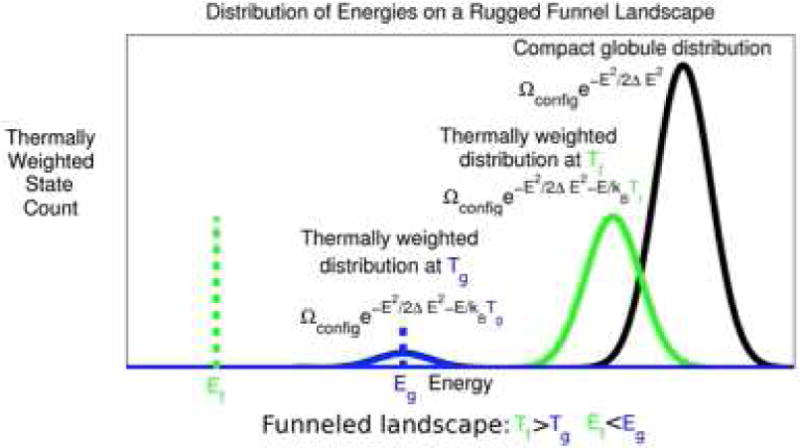
A schematic spectrum showing the density of states of a minimally frustrated protein. Compact alternative or decoy states are distributed with a nearly Gaussian distribution of energies through the random addition of conflicting contributions. At a temperature T, the thermally occupied decoys will be diminished in number but they will still have a Gaussian distribution of energies that is shifted downwards. At the glass temperature T_g only a very small number of such trap states would be thermally occupied. The energy E_g at T_g can be estimated from the width of the unbiased decoy distribution ΔE. For a minimally frustrated protein an evolved sequence fits the target structure quite well so that at a folding temperature T_F the Boltzmann weight for the target structure competes with the entire collection of states in the unfolded ensemble. For most random heteropolymers no significant gap in the spectrum exists.

As the extra stability of the target δE_F increases, relative to the width of decoy distribution ΔE, the folded structure can be more and more easily picked out from the alternatives. By maximizing δE_F/ΔE over a set of sequences one finds more and more stable “well-designed” sequences. Conversely if many sequence/structure pairs are known the parameters in the energy function can be varied so as to maximize the energy of δE_F/ΔE for the set. The resulting energy function summarizes the structural sequence correlations in the training set. In this way structural data allow us to learn transferable energy functions. Energy landscape theory provides us a theoretical “license to do bioinformatics.”

The T_F/T_G ratio of 1.6 inferred by Onuchic et al. clearly indicates the folding landscape is quite smooth. It is probably an underestimate of the smoothness. One reason the estimate may be on the low side is that the polymer chain motions in the globule are now thought to be intrinsically slower than the τ₀ estimate they used–more in the time scale of a microsecond. At the same time, escape from traps may not require rearranging the whole chain. In this regard, Plotkin et al. showed that correlations in the landscape cause only a fraction of the ruggedness to be translated into configurational slowing [87,88]. This error would go in the opposite direction, but correlations in the landscape also change the corresponding T_G estimate, so that correlations in the folding landscape turn out essentially to preserve the estimated T_F/T_G ratio at the value found for the Onuchic et al. model.

Chan has argued that the T_F/T_G ratio is actually much larger than 1.6, perhaps reaching a ratio as large as T_F/T_G ≈ 10. This very high value would correspond to a very highly funneled energy landscape. His reasoning is based on trying to match the observed high cooperativity of folding [44]. He shows that a heteropolymer model with T_F/T_G = 1.6 would give denaturation curves that are much broader than typically seen, suggesting the smoother landscape.

Clementi and Plotkin also suggest that T_F/T_G is greater than 1.6. They base their suggestion on the quantitative success that perfect funnel models have in predicting Φ-values [45]. By adding random non-native interactions, to a heterogeneous structure based model they suggest that the variance of non-native energies must be quite a bit less than what the 1.6 value for the T_F/T_G ratio would indicate; otherwise specific non-native contacts the misfolded state would greatly modify the Φ values. They suggest that T_F/T_G ratios as large as 2 or 3 would better fit the small deviations from a perfect funnel that are in fact experimentally observed.

4. Reverse Engineering the Folding Energy Landscape

The minimal frustration hypothesis provides a strategy for “reverse engineering” the folding problem–thereby energy landscape theory provides an organized way of learning the folding landscape by “having seen it in action.” The strategy which is rooted in the minimal frustration hypothesis is to tinker with the force field so as to ensure that a transferable form for the energy function, one that can be applied to any sequence, actually leads to minimally frustrated, funneled landscapes for a training set of proteins with natural sequences that we already know fold to specific known structures. If all folding landscapes are funneled and the parameters in the force field are universal and are thus transferrable, the predictive force field that results should work well for proteins not in the training set.

Testing the landscape for proper folding would be a hard reverse engineering task if it had to be done simply by trial and error. There are many parameters in even the simplest coarse-grained molecular force field. Testing even one set of parameters for the force field to see if it yields a funneled folding landscape takes quite a bit of computer time, so combinatorial search through parameter space would be prohibitively expensive. The good news is the minimum frustration principle provides a quick zeroth order check on whether a protein sequence can be folded with a given force field. All we have to do is to check that the energy of the folded state is much lower than the typical value of the energy of lowest thermal accessible misfolded state. How do we find the energy of misfolded states? The latter typical trap energy, E_G as we have seen can be estimated directly from the variance of the energy over a set of candidate decoy structures, the quantity we call the ruggedness ΔE². This variance can easily be calculated from a fixed set of representative decoys–this makes it unnecessary to find specifically the absolutely lowest energy misfolded state for a given force field. Finding the actual lowest energy misfolded would be an NP hard task. Sampling to find ΔE², however, is much easier and robust.

Taking this strategy one step further mathematically leads to an explicit optimization scheme: Maximize the ratio of δE/ΔE. This quantity is monotonically related to the T_F/T_G ratio. If the parameters in the force field enter into the energy function linearly then optimizing this ratio actually becomes a problem in linear algebra, as first noted by Goldstein et al. [29]. Even better funneled energy landscapes emerge when one employs still more elaborate nonlinear self-consistent optimization schemes in which the decoys are all iteratively re-computed by sampling misfolded structures for the already partially optimized force fields [89,90]. This strategy (illustrated in Fig 2) has over the years led to a series of ever improving force fields that now can successfully fold many globular and membrane proteins using their sequence information alone.

An historical survey of the progress made using this energy landscape theory based strategy as well as the details of its underlying mathematics have been recently presented by us [5]. Nowadays, the quality of predictions made without homology information from such force fields is almost as high as what can be achieved by tweaking the structures of known homologs. We can see the comparison of the structures predicted by the latest force field (called AWSEM, the Associative Memory Water Mediated Structure and Energy Model) to the x-ray structures for several globular proteins in Fig 3. The same strategy has even proved a successful route to developing force fields for studying membrane proteins where the funnel minimal frustration idea has been less tested. Indeed the very basis of the funnel hypothesis may be questioned for membrane proteins because of the kinetic control that may occur in vivo through the action of the translocon. Some examples of membrane protein structure prediction [91] using such a transferable force field based on energy landscape reverse engineering are shown in Fig 4. It appears that once the translocon has placed the protein in the membrane spontaneous folding à la Anfinsen ensues.

Fig 3. Predictions of Globular Protein Tertiary Structure.

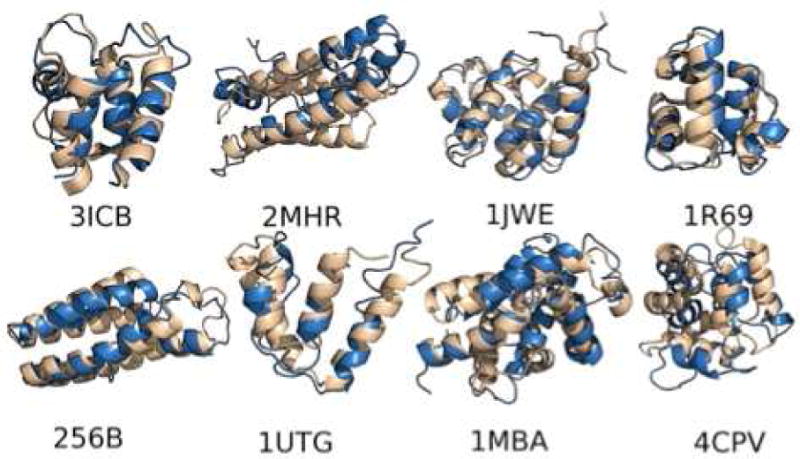
A gallery of globular protein structures predicted by the AWSEM energy landscape optimized force field are shown overlapped with the correct x-ray structures. The agreement is comparable to what can be found via homology modeling but no homology information was used in making these predictions. The examples are 3ICB: vitamin D-dependent calcium-binding protein; 2MHR: myohemerythrin; 1JWE: N-terminal domain of E. coli DNAB helicase; 1R69: aminoterminal domain of phage 434 repressor; 256bB: cytochrome B562; 1utg: uteroglobin; 1MBA: aplysia limacina myoglobin; and 4CPV: carp parvalbuminCARP. For details please see Ref 90.

Fig 4. Predictions of Membrane Protein Structures.

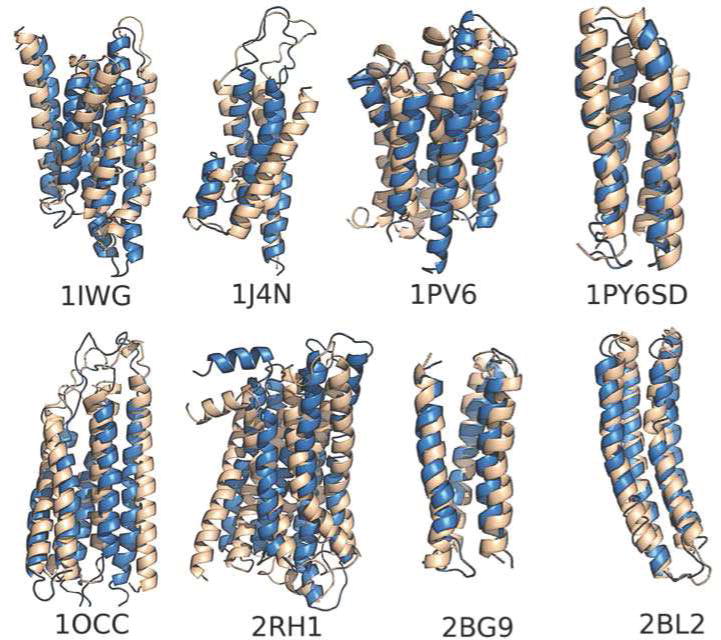
A gallery of membrane proteins structure predicted by the AWSEM-Membrane force field shown overlapped with the correct x-ray structures. The examples are 1IWG: subdomain of multidrug efux transporter; 1J4N: subdomain of aquaporin water channel AQP1; 1PV6: subdomain of lactose permease transporter; 1PY6SD: subdomain of bacteriorhodopsin; 1OCC: subdomain of cytochrome C oxidase aa3; 2RH1: 2-Adrenergic GPCR; 2BG9: subdomain of nicotinic acetylcholine receptor; and 2BL2: subdomain of V-type Na+-ATPase. For details please see Ref 91.

It is probably not an accident that these force fields which have been reverse engineered using the minimal frustrated landscape idea yield results with a resolution only comparable to what can be obtained using homology models. They are not as precise as fully determined atomistic x-ray structures. This is reasonable because the minimal frustration principle must be a result of evolution. Evolution works at the residue level not at the atomistic levels: only a limited set of side chains has been tried over the course of natural history and any new side chains beyond the standard 20 that would be needed to completely test the all-atom models haven’t been tried by Nature. This evolutionary origin of the funneled landscape can be tested in another way, which I describe in the next section.

5. The Evolutionary Landscapes of Proteins

Folding of proteins is important to their function and the proper function of proteins is needed for an organism’s survival, therefore the folding landscape is a key part of natural selection. Evolution works, however, both by selection and by random experimentation through mutation and recombination. Functional proteins in widely divergent organisms therefore have wildly different sequences. There is much evidence that structure evolves more slowly than sequence does [92]. Slow structural evolution would be expected if the folding energy landscape is funneled. Can we quantitatively relate the diversity of protein sequences all of which fold to a largely common structure to the physical energy landscapes for each of these sequences? One way to address this question is first to assume that folding to the proper structure is actually the only selection constraint on molecular evolution. The funnel hypothesis would then summarize the folding constraint by saying the energy of the folded structure E_F must be far below E_g, the typical energy of a structurally distinct trap. As we have seen the latter depends on ΔE², which itself depends foremost on the protein sequence composition (but not primarily on the order of amino acids). This suggests we can picture the evolutionary energy landscape of proteins in a way much like the folding landscape of a single protein [93]. In Fig 5 we show such a super landscape which describes how energy varies both in sequence and structure. There will be numerous funnels in the landscape corresponding to every possible structure of a protein. We can concentrate on the landscape in sequence space for evolving to a given target structure and compare it with the physical energy landscape for folding to that structure. For the sequence space landscape, the energy coordinate represents the energy that a particular sequence has when it takes on the particular target structure. One would find the most “well-designed” sequence at the bottom of the sequence space funnel. (Unfortunately many early folding theory papers used the “designed” terminology, which can be easily misinterpreted as being an endorsement of creationism!)

Fig 5. The Folding Super Landscape.

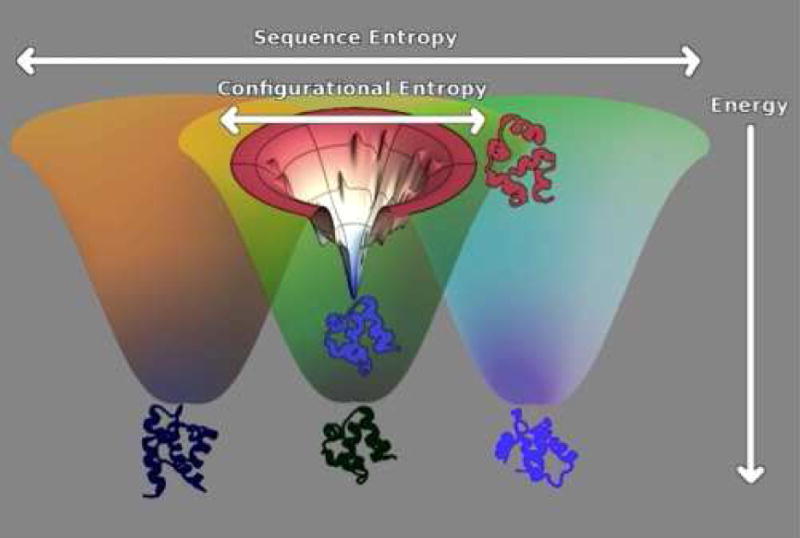
The super-energy landscape of proteins is pictured here. Ideally this would be shown as a function of both sequence and conformation simultaneously. The large funnels are pictured as a function of sequence space with the radial sizes connoting sequence entropy. Energy is again the vertical axis. Natural proteins are not necessarily the lowest energy designs. These would be found at the bottom of the super funnel. For each target the configuration space landscape is funneled, but only to an energy E_F. This structural energy landscape is, however, shown superimposed on the sequence space landscape. Disordered compact structures and sequence scrambled decoys have comparable energy statistics. They are shown near the top of the landscape. The funnels to other structures start from these same high energy states but again would finally reach energies near E_F if they have sufficiently evolved under the minimal frustration selection constraint. The energy of the traps E_G can be estimated by scrambling sequences within the native structure. This diagram shows how the evolutionary and physical configurational landscapes are related to each other. Notice that sequence space is cosmologically bigger than the structure space is as reflected by the large sequence entropy at E_F. This excess coding space allows minimally frustrated landscapes to be found through the random processes of natural selection.

It is important to remember, however, that because evolution is a random process, there is no need for selection to have given the “best designed” or most stable sequence, it is only necessary for evolution to have found a sequence that folds to a functional structure sufficiently often. To find the folded structure quickly and reliably the physical energy landscape must have a low energy E_F below some threshold for at least two reasons. One of these reasons is to avoid kinetic trapping, as we see indeed natural sequences do but also it is necessary for survival of the species to avoid being unstable against next generation mutations that would inevitably occur in a finite population of organisms [91]. The first selection constraint based on kinetic trapping would act on the organism possessing the protein itself. Kinetic trapping (if E_F would be close to E_G, the typical energy of a trap) will create long-lived misfolded proteins. Such long lived species could lead to aggregation and problems with protein trafficking. It is often thought that this is an issue in giving rise to the numerous neurodegenerative diseases. The second selection constraint really acts at the population level not at the level of the presently living individual organism. Some fraction of the offspring of a viable organism which has a protein with energy E_F will, after a mutation has occurred now become unviable. Again the closer E_F is to E_g the more this poor performance in the offspring will be a problem for the species, as a whole. Whatever is the actual origin of the selection constraint on E_F, if this energy constraint is the only constraint, we can argue that after sufficient sequence variation has occurred, one would end up with an ensemble of proteins whose sequences are random apart from their satisfying a threshold constraint on their energy in the native structure E_F. Since sequence space is cosmologically large, the selected sample would be equally well described by a Boltzmann distribution for the energy E (a_l, … a_N) of a particular sequence of amino acids (a_l … a_N) in the target structure [94,95,96,97]. This Boltzmann distribution would be characterized by an effective temperature of selection T_sel. The lower the selection temperature T_sel the lower is E_F and the more stable or “better designed” or better said minimally frustrated the sequence would be. Thus as T_sel goes down, T_F gets larger relative to the glass transition temperature T_g. If one applies a random energy model ansatz to the sequence space, just as is done for the molten globule configuration space, one ends up with an elegant relation between the evolutionary funnel characterized by E_F (and characteristic evolutionary temperature T_sel) and the physical folding funnel characterized by the same E_F (but with different physical temperatures T_F and T_g):

$$\frac{2}{T_F{T}_{\mathit{sel}}}=\frac{1}{T_g^2}+\frac{1}{T_F^2}$$ (3)

The key point is that the two “funnels” one in physical space, the other in sequence space have the same energies for native structures and also would have similar distributions of decoy energies. See Fig 6. An elementary derivation of this relation may be found in the supplementary material of Ref 46. This relation between evolutionary and physical scales was first stated in this way by Pande, Grosberg and Tanaka through more sophisticated replica arguments [97].

Fig 6. The Distributions of Energies in Sequence and Configuration Space.

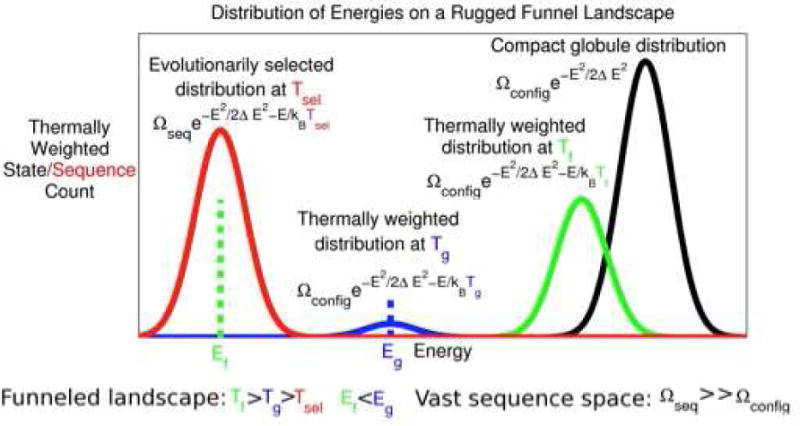
The schematic spectrum in sequence space is shown superimposed on the configurational energy spectrum. Notice that there are many sequences that fold to the same target structure because the selection temperature T_sel is greater than the sequence space glass transition temperature. This temperature in turn is lower than the structuralspace glass transition at T_g.

The assumption of a Boltzmann distribution over sequences has been taken as the basis of several new information theoretic analyses of the genomic data for protein families which maximize sequence entropy given known correlations in aligned sequences [98]. Such analyses have recently become quite useful because of the extensive genome sequencing data now available. Gene sequencing has made known to us, for many structural families, thousands of sequences all of which presumably fold to sensibly the same structure in order to retain their functions. Using the sequence data, by quantifying co-evolution at distinct sites in the protein, one can do “reverse statistical mechanics” to find the form of the energy function E_F(a_l, … a_N) that would give such a sample of sequences. Typically the information theoretic energy function is parametrized via site energies and pair interactions. One algorithm for doing reverse statistical mechanics is known as direct coupling analysis (DCA). This algorithm yields an energy function H_DCA which describes the evolutionary constraints at a given site and the coevolution of different positions in the sequence. H_DCA should be strongly correlated with the physical energy function. Indeed it has been shown that H_DCA correlates well with the energy functions developed for structure prediction. Two plots showing the correlations are found in Fig 7 and Fig 8. One of these plots shows the correlations of the in sequence space contrasting random sequences threaded on the native structure to the energies for natural sequences known to fold to the target. The other plot evaluates both the physical and evolutionary information theoretic energy for partially folded structures generated by a molecular dynamics simulation using the structure prediction force field near the folding temperature. Computing the DCA energy for differing configurations involves the inclusion only of contact pair energy terms.

Fig 7. The Correlation between Physical and Evolutionary Folding Landscapes.

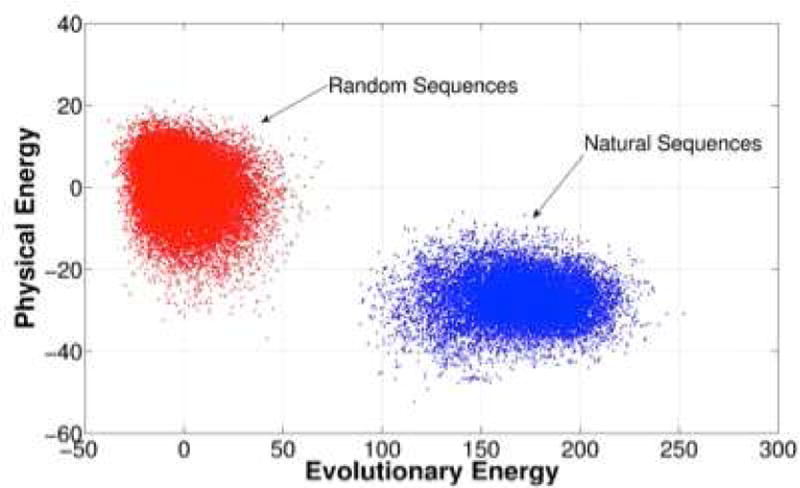
We evaluate the energies, on using the physics based AWSEM energy function, the other using the direct contact approximation genomic based energy function both for scrambled sequences and for natural sequences in the 1r69 repressor family. These pairs of energies are then plotted. We see that both the physical and evolutionary energy landscapes have sizable gaps showing the minimally frustrated nature of the proteins. For details please see Ref 46.

Fig 8. The Correlation between the Evolutionary and Physical Folding Landscape.

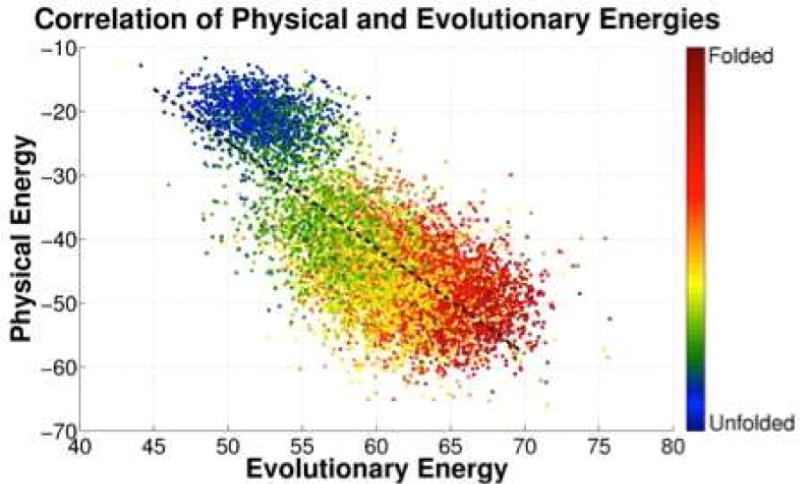
We evaluate the energies of structures using both a physical and a genomic energy function. The pairs shown in the figures correspond to partially folded protein structures generated via molecular simulation using the AWSEM energy function for the Ir69 family. Again the two landscapes turn out to be funneled and strongly correlated as would be expected from the minimal frustration principle. The colors of the points correspond to the fraction of native contacts formed in the sampled structure. For details please see Ref 46.

You can see in both plots that both energy functions generate a gap between correct sequence-structure pairs and incorrect ones: the evolutionary funnel landscape and the physical funneled landscape are highly correlated.

This analysis also allows us to access the ratio T_F/T_sel. We can then use equation (3) to find the corresponding T_F/T_g ratios. These are shown for several families in Fig 9.

Fig 9. The Smoothness of the Folding Funnel Quantified by Coevolutionary Information.

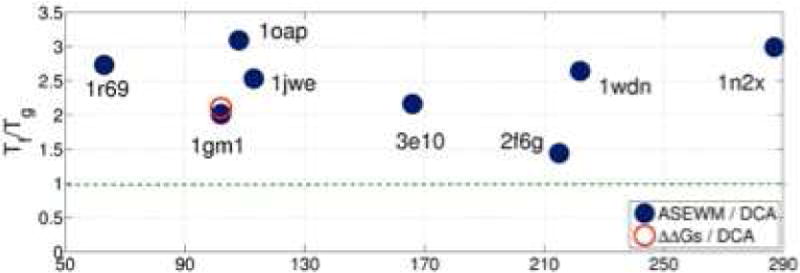
The Tf/Tg ratios for several protein families are inferred using genomics and landscape theory shown. The families are denoted by the PDB ID codes of the representative structures which are described in Ref 46. Tf/Tg measures the smoothness of a folding landscape. Higher values correspond to more ideal funnels. The red circle is an alternate way of making an estimate by comparing changes in evolutionary energies and experimentally measured stability changes. The estimated Tf/Tg ratios for all the natural protein families studied are larger than one so the folding landscape is confirmed to be a funnel. The estimates are clustered around the value of Tf/Tg = 2.5 that was estimated by Clementi and Plotkin through a comparison of measured Φ values with simulated ones. For details please see Ref 46.

It is heartening that evolutionary data give rise to estimates for T_F/T_g in the same range as those predicted by physical arguments using data from laboratory experiments. The values of the T_F/T_g ratio inferred in this way are larger than those first estimated by Onuchic et al., and are more in line with the values estimated by Clementi and Plotkin, discussed earlier.

6. Frustration and Function

Protein function requires specificity of interaction as well as sufficient stability to live in the cell and in subsequent generations of cells. In the protein world, standing there and looking pretty is not always enough, however. Proteins act as nonlinear elements in cellular networks in order to process environmental information. This nonlinearity necessitates motion and thus often an energy landscape with multiple distinct stable states. Because stability of a limited number of specific structures is so important to prevent promiscuous interactions, most of the individual interactions in proteins have evolved to give collectively strongly funneled landscapes but some strategic parts of the sequences located at specific sites in the structure have been selected to be frustrated in order to allow both motion and interaction with partners. To quantify this phenomenon requires tools for localizing the sources of frustration [18,99,100]. Localization of frustration can be detected by examining the energy changes that would occur if only the local environment of a site were to be changed through sequence mutation or allowed to change by reconfigurational physical motion. Minimally frustrated native regions will have energies in the more stable part of the distribution of local energies; regions that are unstable in comparison with the bulk of the distribution of local energies are frustrated. Checking for local frustration is relatively easy once good structures and adequate energy functions are known [99], as is now the case. It has been shown that regions where highly frustrated interactions cluster often map onto sites of allosteric change [100] or can identify binding sites [99] which then have their frustration relieved once a binding partner is found and then docked to the site. In contrast to the clustered, frustrated, functional regions, minimally frustrated interactions typically form a connected web throughout the protein that keeps subunits of the protein relatively rigid. The combination of the protein handling modules with rigidity along with specifically frustrated local regions that act as moveable elements justifies considering many large proteins as being nearly macroscopic “machines.” A key difference of these molecular machines from their fully macroscopic counterparts is that the minimally frustrated nature of most of the molecule allows the molecular protein to move by breaking or “cracking” locally and then re-assembling into a new configuration [101,102]. Local frustration analysis is easily automated and a Web server showing both the web of minimally frustrated interactions and the highly frustrated sites is available [103].

An example of the frustration patterns in an allosteric protein is shown for the RhoA oncogene in Fig 10.

Fig 10. Frustration Serves a Functional Purpose.

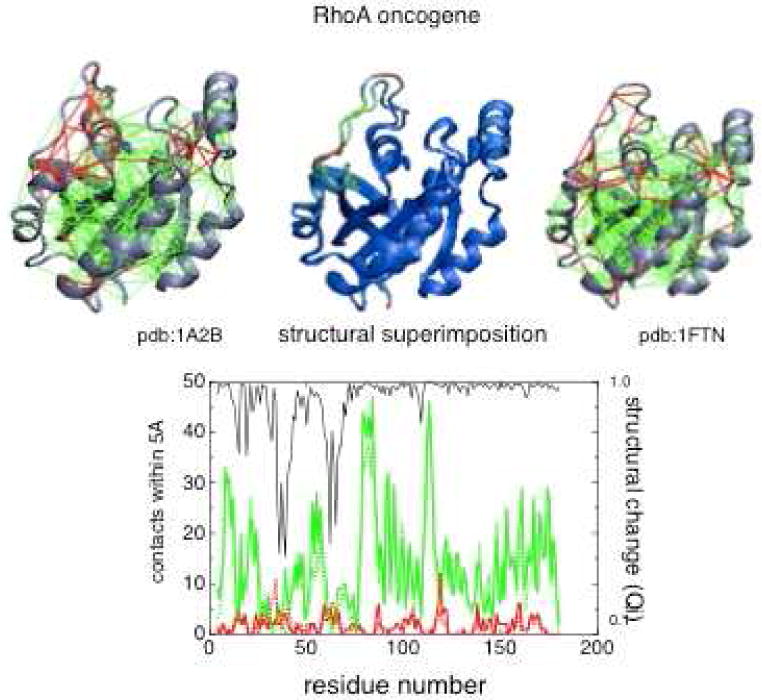
A diagram showing the minimally frustrated web of interactions in two structural forms of – RhoA an allosteric protein. This web is indicated in green. The frustrated interactions in the regions shown in red lead to alternate nearly energetically degenerate configurations that allow these regions to function as hinges. The lower panel shows the frustration levels at different sequence locations, the red line indicating the number of frustrated contacts, green the number of minimally frustrated contacts. The black line indicates the local overlap of the two interconnecting structures. Notice the regions that move (and have low Q:) correspond to the most energetically frustrated regions. For details please see Ref 103.

7. Folding Paradoxes Revisited

Protein folding has turned out to be easy and that seems paradoxical. As we have seen Levinthal’s original paradox can be avoided in several ways, the most important turning out to be that evolution has led to funneled energy landscapes. It is clear that there are other ways of simplifying the search through configuration by parsing out the configurational entropy piece meal such as capillarity effects so that only part of the chain folds at any time [10,11] or by utilizing local structural signals that increase the probability of the chain bending in the right places [85]. Nevertheless the minimal frustration hypothesis has proved to be a most fruitful tool for visualizing the folding mechanism and addressing protein design and structure prediction. The quantitative form of the minimal frustration principle has been confirmed in several ways through detailed kinetic predictions. In addition we have seen the minimal frustration principle is confirmed to be the result of natural selection and random variation through the comparison of the landscape characteristics inferred from sequence co-evolution and through folding physics. But doesn’t this resolution of the Levinthal just raise another paradox? How did the random process of evolution find the minimally frustrated sequences?

Searching sequence space would seem to be a daunting task in the same sense that the searching structure space seemed to be in the Levinthal paradox. Fred Hoyle raised just such an issue in his science fiction work “The Black Cloud” [104]. Sequence space is indeed cosmologically larger than structure space so how does evolution find minimally frustrated sequences? The answer seems to be that while minimally frustrated sequences are exponentially rare, they are dense enough in sequence space that connected paths of mutation can find minimally frustrated sequences if there is sufficient selection pressure. Indeed we can see that there is a cosmologically large number of sequences that fold even to a specific given structure. In Fig ____ we show the density of both available structural states measuring the configurational entropy and sequences at a given energy measuring the sequence entropy. The minimal frustration principle is quantitatively summarized by saying there is a gap between the folded energy and the glassy structural traps. Precisely because sequence entropy is so much larger than structural entropy the deepest most “well designed” sequence–the energy corresponding to a glass transition in sequence space will be much below the typically selected folding energy E_F. This excess of states signals the expected high connectivity of the sequence space.

As the diversity of amino acid type interactions reduces one will encounter in sequence space a glass transition that will occur now at a higher energy. Indeed it appears that such a coding crisis occurs when we are limited to 2 letter protein folding codes [105]. Finding foldable sequences for some structures becomes problematic even with 3 letter folding codes, in the computer [53]. The idea that interaction diversity is necessary to resolve the Levinthal paradox has been confirmed in the laboratory where 5 distinct amino acid types have been shown to be sufficient for design [106] but fewer numbers do not suffice.

We see that energy landscape analysis suggests that finding minimally frustrated sequences is not too hard for a random process like evolution. This has also been confirmed via simulation studies. Again when evolutionary searches are made in the computer using simplified models it has proved straightforward reach by trial and error sequences to fold into even quite complex structures [107,108,109]. Evolving for specific function at a specific locus turns out to entail evolving to fold globally as a prerequisite, according to the work of Sasai [108,109].

A rich problem, still unsolved however is how and when did the minimally frustrated sequences come into being in our world? Completely resolving this puzzle of natural history may be hard because folding appears as a phenomenon even in the earliest days of life that we can now probe through evolutionary sequence analysis. Studies of the last universal common ancestor suggest this organism had a full complement of foldable proteins [110]. So presently there is a veil over the early steps of protein biogenesis. There is hope, however, that the process of evolving foldability is still going on today. Eukaryotes encode protein with split genes. Gilbert has proposed that these exons might be themselves foldable units [111] and Gō made the case for this for hemoglobin [112]. Using energy landscape analysis Panchenko et al. showed that indeed many exons seemed to be minimally frustrated folding units. We called these units “foldons” [113,114] nearly twenty years ago. The case that foldons were exons was equivocal in 1995. The much larger amount of sequence data and better energy functions that are available today should lead to a re-examination of the foldon-exon correspondence.

There is also evidence that we can see minimal frustration evolving in real time today. During the somatic evolution of antibodies [115], Romesberg and co-workers have examined the dynamics of antibodies that have been made against fluorescent dyes. The motions of the dyes bound to the antibodies can then be probed spectroscopically. His investigations suggest that conformational substates of the antibody-dye complex disappear as the antibody evolves and that the energy landscape gets smoother and smoother as successive rounds of selection occur so that the antibody becomes a better binder. This is very much consistent with the mechanism envisioned by Sasai for evolving folding through selection pressure on specific binding at a given locus.

Thus while there is no new paradox to the trick of having evolved funneled landscapes it seems there is much more that we should be able to learn about evolution and folding in the near future. The union of energy landscape theory and modern genomics should be very fruitful.

Highlights.

• Funneled landscapes explain the paradoxes of robust protein folding.

• Energy landscape theory leads to structure prediction tools

• Comparing evolution data with landscapes quantifies the frustration of folding