Generalized Multilevel Function-on-Scalar Regression and Principal Component Analysis

Summary

This manuscript considers regression models for generalized, multilevel functional responses: functions are generalized in that they follow an exponential family distribution and multilevel in that they are clustered within groups or subjects. This data structure is increasingly common across scientific domains and is exemplified by our motivating example, in which binary curves indicating physical activity or inactivity are observed for nearly six hundred subjects over five days. We use a generalized linear model to incorporate scalar covariates into the mean structure, and decompose subject-specific and subject-day-specific deviations using multilevel functional principal components analysis. Thus, functional fixed effects are estimated while accounting for within-function and within-subject correlations, and major directions of variability within and between subjects are identified. Fixed effect coefficient functions and principal component basis functions are estimated using penalized splines; model parameters are estimated in a Bayesian framework using Stan, a programming language that implements a Hamiltonian Monte Carlo sampler. Simulations designed to mimic the application have good estimation and inferential properties with reasonable computation times for moderate datasets, in both cross-sectional and multilevel scenarios; code is publicly available. In the application we identify effects of age and BMI on the time-specific change in probability of being active over a twenty-four hour period; in addition, the principal components analysis identifies the patterns of activity that distinguish subjects and days within subjects.

1. Introduction

1.1 Motivating data

Continuous monitoring of activity using accelerometers and other wearable devices promises to revolutionize the measurement of physical activity by providing objective, unbiased observation in unprecedented minute-by-minute detail over several days or weeks. Accelerometers generally measure activity through electrical signals that are a proxy measure for acceleration (Spierer et al., 2011). “Activity counts” are devised by summarizing the voltage signals across a monitoring period known as an epoch (a one-minute epoch is common), and can be dichotomized into “active” and “inactive” epochs to study sedentary behavior. Thus, these devices give rise to generalized multilevel functional observations: generalized because both activity counts and the derived binary “active” versus “inactive” outcomes do not follow a Gaussian distribution; multilevel because each subject has several days of data; and functional in that continuous 24-hour trajectories are considered the basic unit of observation.

Accelerometers have already been deployed to explore many pressing public health contexts. Unfortunately, the analysis of accelerometer data typically reduces thousands of data points to a single summary, such as the total activity count over a 24-hour period, and few current methods utilize the richness of densely observed activity data. This immense data reduction leaves important scientific questions unaddressed. How are daily physical activity trajectories related to subject covariates, like age, gender, BMI, or socio-demographic status? To what degree do subjects differ from each other in their patterns of activity and inactivity, and to what degree do multiple days differ within one subject?

The motivation for this manuscript is to identify covariate effects and characterize residual patterns of activity in accelerometer data collected from elderly subjects enrolled in the Baltimore Longitudinal Study on Aging (Schrack et al., 2014). BLSA is a study of normative human aging with healthy, functionally-independent participants. Once enrolled, participants are followed for life and undergo extensive testing every 1-4 years depending on age. The sub-sample we consider in this paper consists of 583 men and women who wore the Actiheart, a combined heart rate and physical activity monitor adhesively placed on the chest (Brage et al., 2006). Subjects were asked to wear the device at all times other than bathing or swimming. Physical activity was measured in activity counts per minute, a cumulative summary of acceleration detected by the device within one-minute monitoring epochs (see Bai et al., 2014, for further discussion of activity counts). Throughout, we will use the term “activity” to refer to physical activity that results in measurable acceleration.

Our primary analysis focuses on binary “activity” and “inactivity” daily trajectories (see Figure 5 for example data from two subjects); analyses of the activity count trajectories appear in Appendix A.4. The goals of this work are to describe and quantify the effects of age and BMI on the time-varying probability of being active over the course of a day, and to characterize the patterns of activity that differentiate subjects from each other and days within subjects. In addition to this motivating dataset, the proposed methods will be directly relevant to existing and future accelerometer studies including the National Health and Nutrition Examination Survey (Troiano et al., 2008), the Women's Health Study (Shiroma et al., 2013), the Health ABC Study (Atkinson et al., 2007), and the Columbia Center for Children's Environmental Health birth cohort study.

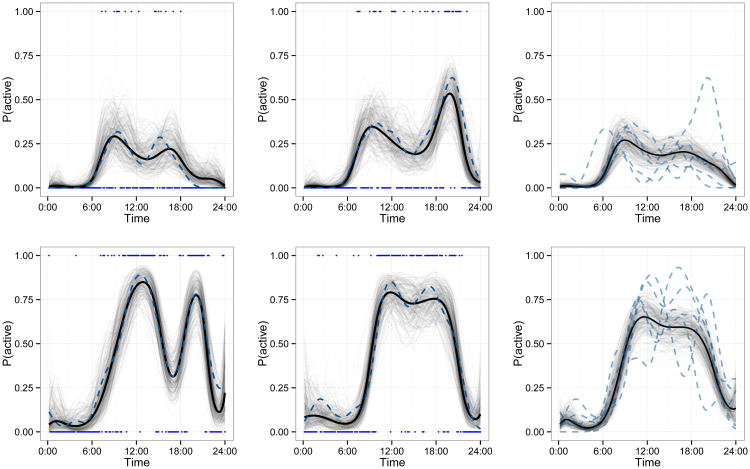
Figure 5.

Fitted values for two subjects, separately by row. In each row, the left and middle panels show observed binary values Y_ij(t) as points (separate days are shown in each panel). A Gaussian kernel smooth with IQR of 1.5 hours of the observed data is shown as a dashed curve. Estimates of subject-day-specific probability trajectories μˆ_ij(t) are shown as solid curves, and a sample from the posterior of μ_ij(t) is shown as translucent curves. In the right panel of each row, kernel smooths for each of the five observed days of the subject are shown as dashed curves. The estimated subject-specific mean trajectory μˆ_i(t) is shown as a solid curve, and a sample from the posterior of μ_i(t) is shown as translucent curves. This figure appears in color in the electronic version of this article.

1.2 Statistical framework

We observe data [Y_ij(t), x_ij] for subjects 1 ≤ i ≤ I, visits 1 ≤ j ≤ J_i and times t ∈ [0, T], where Y_ij(t) is a generalized response curve and x_ij is a length p vector of scalar covariates. For each time t, Y_ij(t) is a realization of a random variable with an exponential family distribution. We introduce the generalized multilevel function-on-scalar regression model

$$\begin{array}{c}\mathrm{E}[Y_{ij}(t)|b_i(t),{\upsilon }_{ij}(t)]={\mu }_{ij}(t)\\ g[{\mu }_{ij}(t)]={\beta }_0(t)+\sum _{k=1}^p{x}_{ij,k}{\beta }_k(t)+b_i(t)+{\upsilon }_{ij}(t)\end{array}$$ (1)

in which g(·) is a known link function, the β_k(t) are fixed effect coefficient functions corresponding to the scalar covariates x_ij, b_i(t) is a subject-specific random deviation from the fixed effect mean structure, and υ_ij(t) is a subject- and visit-specific random deviation from the subject-specific mean. The inclusion of covariate-specific random effects is a direct extension of model (1); as in traditional mixed models such “random slope functions” would allow subject-specific impacts of changing covariate levels and should be considered in future applications. As is detailed in later sections, we estimate fixed effect coefficients using a penalized spline expansion. The subject-level and subject-visit-level effects (b_i(t) and υ_ij(t), respectively) are assumed to be independent and will be decomposed using a multilevel functional principal components analysis that separates within- and between-subject directions of variability (Di et al., 2009). Principal component basis functions will be estimated using penalized splines. All model parameters – including fixed effect spline coefficients, principal component spline coefficients, and principal components scores – are jointly estimated in a Bayesian analysis.

The use of smooth functions to model activity is in accordance with the goals of our analysis. We are concerned with modeling large-scale daily activity profiles and their change as a function of age and BMI, as well as decomposing profiles into dominant patterns that distinguish subjects from each other and distinguish days within subjects. This is important for characterizing activity in an aging population, with BMI being a potential target for public health intervention. An alternative approach is to model active and inactive bouts, their duration, frequency and switches between them. All of these may be important contributors to a subject's overall health, but address questions distinct from those of interest here.

Elements of our analysis have antecedents in the statistical literature. Functional principal components analysis for cross-sectional continuous-valued curves has a long history in functional data analysis as a tool for dimension reduction and for identifying the major patterns that contribute to variation across curves; Ramsay and Silverman (2005, §8.2) has an overview, and Yao et al. (2005) describe a broadly used framework for FPCA. Goldsmith et al. (2013) noted that this standard FPCA method implicitly conditions on the estimated covariance and thus fails to account for uncertainty in estimated basis functions, meaning inference for individual curves can be poor. For multilevel functional data, Di et al. (2009) estimates both within- and between-subject covariances, and subsequently decomposes these into subject-level and visit-level principal component basis functions, with scores again estimated in a mixed model framework. van der Linde (2008) develops a Bayesian approach to FPCA using low-dimensional spline expansions for basis functions and estimating parameters through a variational approximation to the full posterior; this work is based on the probabilistic and Bayesian (non-functional) PCA methods popularized in Tipping and Bishop (1999) and Bishop (1999). Probabilistic PCA poses a factor analysis model with the additional assumption that errors follow a Gaussian distribution. It is then possible to derive maximum likelihood estimates for PCs that are equivalent to standard PCA estimates up to an arbitrary orthogonal rotation. Using probabilistic and Bayesian PCA, it is possible to rotate estimated components into principal components that span the same principal space, and thereby recover the appealing interpretation of traditional PCA.

There is an extensive literature on function-on-scalar regression with real-valued response curves. Brumback and Rice (1998) and Guo (2002) use penalized splines to model both population-level effects and curve-level deviations – the former relied on the use of fixed effects for computational convenience and the latter utilized random effect models. Several approaches have been developed that focus on population fixed effects only, treating individual curves as errors around the covariate-dependent mean; (Ramsay and Silverman, 2005, §13.4) provides an introduction. Developments in Reiss et al. (2010) and Scheipl et al. (2013) use penalized splines to model fixed effects in cross sectional and multilevel models, respectively, using cross validation or restricted maximum likelihood to select tuning parameters. A criticism of these approaches is that they make the assumption that functional errors are uncorrelated over the domain, which typically does not hold for functional data and can lead to poor inference for fixed effects. To resolve this, Reiss et al. (2010) also propose an iterative procedure, in which the fixed effects are estimated under assumed independence and then used to estimate the residual covariance. The fixed effects are then re-estimated using generalized least squares. Wavelet-based Bayesian functional mixed models are presented in Morris and Carroll (2006) with errors in the wavelet space assumed to be independent, an assumption justified by the “whitening” property of wavelet transformations. Goldsmith and Kitago (2013) developed a Bayesian penalized spline approach for multilevel function-on-scalar regression that models potential residual correlations explicitly, and showed that posterior credible intervals for fixed effects achieve nominal coverage.

In contrast to the rich literature for real-valued functional data, relatively little work exists for generalized functional responses. Hall et al. (2008) directly extend the real-valued FPCA method of Yao et al. (2005) to generalized data by positing a latent continuous process that, through a known link function, gives rise to the observed generalized outcome. The mean and covariance are estimated using observed data, and the latent mean and basis functions are obtained by inverting a linear approximation to the known link function. For binary data, Serban et al. (2013) extend this framework to allow multilevel curves with spatial correlation structures, and propose non-linear approximations to the logit link function for rare-event data. Because this approach is based on a covariance decomposition, the number of basis functions can be chosen to satisfy a percent variance explained criterion. However, methods for curve-level estimation and inference are not presented, and incorporating covariate effects in the mean is not considered. van der Linde (2009) develops a variational Bayesian algorithm for generalized FPCA that uses low-dimensional spline representations for the mean and basis functions.

With respect to the preceding literature, our methods are statistically novel in several important ways. We provide a framework for both generalized function-on-scalar regression and functional principal components analysis. From a regression standpoint, we explicitly model residual correlation to improve inference for population-level effects; at the same time, the FPCA framework describes major directions of variability. The use of fully Bayesian estimation and inference, rather than variational Bayes approximations, avoids unreasonable assumptions of posterior independence and provides joint inference that has been shown to have good numerical properties in simulations that mimic our motivating data. We consider generalized multilevel functional data, including both binary and count response curves, and develop accompanying methods; all methods can be simplified appropriately for cross-sectional data.

The remainder of the paper is organized as follows. Section 2 presents the novel methodological contributions of the manuscript, and includes subsections on the model specification, computation, and rotating estimated components to induce orthonormality. Section 3 presents simulation studies designed to mimic the motivating data and explore the estimation accuracy and inferential properties of the proposed methods. Section 4 presents the real data analysis for binary response curves. We close with a discussion in Section 5. An online appendix contains a graphical depiction of our model, additional simulations for cross-sectional data and comparing our methodology with that of Serban et al. (2013), analyses for activity counts under a Poisson distribution and log link, and details of the software implementation. All simulation code is publicly available.

2. Methods

2.1 Model

For subjects 1 ≤ i ≤ I and visits 1 ≤ j ≤ J_i, let x_ij be a length-p vector of scalar covariates and Y_ij(t) be a generalized response curve: for each t ∈ [0, 1], Y_ij(t) follows an exponential family distribution with density

$$p[Y_{ij}(t)|{\alpha }_{ij}(t)]=exp\{(Y_{ij}(t){\alpha }_{ij}(t)-b[{\alpha }_{ij}(t)])/\varphi +c[Y_{ij}(t),\varphi ]\}$$

where E[Y_ij(t)|α_ij(t)] = μ_ij(t) = b′[α_ij(t)] and Var[Y_ij(t)|α_ij(t)] = b″[α_ij(t)]ϕ. The mean is related to a linear predictor by a known link function g[μ_ij(t)] as described in model (1). In simulations and applications we use the canonical link α_ij(t) = g[μ_ij(t)], although this is not necessary for our methodology. For the binary and count response curves that are primarily discussed in the paper, the dispersion parameter ϕ is known; for other distributions (or to allow overdispersion) it may be necessary to model this parameter. The subject/visit-specific curves α_ij(t) and μ_ij(t) implicitly depend on the covariates x_ij and the random effects b_i(t) and υ_ij(t). We assume that observations on different subjects are independent; that observations on different days within a subject are conditionally independent given fixed and subject-specific parameters; and that observations at different times of the same day for the same subject are conditionally independent given fixed, subject-, and subject/day-specific parameters.

In model (1), our interest is estimating population-level fixed effects β_k(t), subject-level deviations b_i(t) from the covariate-dependent mean, and subject-visit specific deviations υ_ij(t) from the subject-specific mean. Generalizing the multilevel FPCA approach (Di et al., 2009), we expand subject-specific (level 1) and subject/day-specific (level 2) effects in terms of population basis functions and unique scores:

$$\begin{array}{c}\mathrm{E}[Y_{ij}(t)|b_i(t),{\upsilon }_{ij}(t),{\mathit{x}}_{ij}]={\mu }_{ij}(t)\\ g[{\mu }_{ij}(t)]={\beta }_0(t)+\sum _{k=1}^p{x}_{ij,k}{\beta }_k(t)+b_i(t)+{\upsilon }_{ij}(t)\\ \approx {\beta }_0(t)+\sum _{k=1}^p{x}_{ij,k}{\beta }_k(t)+\sum _{k=1}^{K^{(1)}}{c}_{ik}^{(1)}{\psi }_k^{(1)}(t)+\sum _{k=1}^{K^{(2)}}{c}_{ijk}^{(2)}{\psi }_k^{(2)}(t).\end{array}$$ (2)

The approximation in the third line stems from the use of truncated functional principal components expansions for subject-specific effects b_i(t) and subject-visit-specific effects υ_ij(t), and is implicit in all FPCA methods. Level 1 and level 2 basis functions ( ${\psi }_k^{(1)}(t)$ and ${\psi }_k^{(2)}(t)$, respectively) describe the major patterns that generate variation across subjects and across visits within subjects, and associated scores ( $c_{ik}^{(1)}$ and $c_{ijk}^{(2)}$, respectively) indicate the subject-and subject/day-specific contribution of each basis function.

In practice curves are observed on a finite grid of length D that, for notational simplicity, we assume is shared across subjects. For finite data, let Y be the (Σ_i J_i) × D matrix of row-stacked generalized functional response; X be the (Σ_i J_i) × (p + 1) fixed effects design matrix constructed by row-stacking the x_ij; β be the (p+1) × D matrix with rows containing β_k(t) evaluated on the finite grid; Z be a (Σ_i J_i) × I random intercept design matrix for the subject-specific effects; b be the I × D matrix with rows containing b_i(t) evaluated on the finite grid; and υ be the (Σ_i J_i) × D matrix with rows containing υ_ij(t) evaluated on the finite grid. Fixed effects and FPCA basis functions at both levels are expressed using a spline expansion. Let Θ denote the known D × K_Θ matrix of cubic B-spline basis functions evaluated over the finite grid on which functions are observed. Spline coefficients for the fixed effects β_k(t), the level 1 FPCA basis functions ψ⁽¹⁾(t), and the level 2 FPCA basis functions ψ⁽²⁾(t) are columns in the matrices B_X, B_ψ⁽¹⁾, and B_ψ⁽²⁾, respectively. Thus $\mathit{\beta }={\mathit{B}}_X^T{\mathbf{\Theta }}^T$ and, letting C⁽¹⁾ and C⁽²⁾ be the matrices created by row-stacking level 1 and level 2 scores for each subject and subject-visit, $\mathit{b}={\mathit{C}}^{(1)}{\mathit{B}}_{{\psi }^{(1)}}^T{\mathbf{\Theta }}^T$ and $\mathit{\upsilon }={\mathit{C}}^{(2)}{\mathit{B}}_{{\psi }^{(2)}}^T{\mathbf{\Theta }}^T$. Model (3) can now be re-expressed for finite data using

$$\begin{array}{c}\mathrm{E}[\mathit{Y}|\mathit{b},\mathit{\upsilon },\mathit{X}]=\mathit{\mu }\\ g(\mathit{\mu })=\mathit{X}\mathit{\beta }+\mathit{Z}\mathit{b}+\mathit{\upsilon }\\ =\mathit{X}{\mathit{B}}_X^T{\mathbf{\Theta }}^T+\mathit{Z}{\mathit{C}}^{(1)}{\mathit{B}}_{{\psi }^{(1)}}^T{\mathbf{\Theta }}^T+{\mathit{C}}^{(2)}{\mathit{B}}_{{\psi }^{(2)}}^T{\mathbf{\Theta }}^T.\end{array}$$ (3)

Notationally, model (4) is formulated in a similar fashion as the continuous-valued cross-sectional function-on-scalar regression models described in Ramsay and Silverman (2005, §13.4) and the continuous-valued multilevel function-on-scalar regression models described in Goldsmith and Kitago (2013). In model (4), the unknown parameters to be estimated are B_X, C⁽¹⁾,B_ψ⁽¹⁾, C⁽²⁾, and B_ψ⁽²⁾; the fixed and random effect design matrices X and Z are known, as is the B-spline basis Θ.

To ensure flexibility we use a rich B-spline basis by taking K_Θ large, but impose smoothness on resulting coefficient function estimates through the prior specification. In particular, we assume the following priors for the columns of B_X, B_ψ⁽¹⁾, and B_ψ⁽²⁾:

$$\begin{array}{c}{\mathit{B}}_{X_k}~\mathrm{N}[0,{\sigma }_{X_k}^2{P}^{-1}],\text{for}0\le k\le p,\\ {\mathit{B}}_{{\psi }_k^{(1)}}~\mathrm{N}[0,{\sigma }_{{\psi }_k^{(1)}}^2{P}^{-1}],\text{for}1\le k\le K^{(1)},\\ {\mathit{B}}_{{\psi }_k^{(2)}}~\mathrm{N}[0,{\sigma }_{{\psi }_k^{(2)}}^2{P}^{-1}],\text{for}1\le k\le K^{(2)}.\end{array}$$ (4)

In (4), P is a pre-specified K_Θ × K_Θ penalty matrix that enforces smoothness through the connection between Bayesian priors and quadratic penalization (Ruppert et al., 2003). We use P = αP₀ + (1 − α)P₂ where P₀ and P₂ are zeroth- and second-order derivative penalty matrices. Taking 0 < α ≤ 1 balances the universal shrinkage encoded in P₀ with the smoothness constraint of P₂, while ensuring P is positive definite and priors are proper. In our simulations and real data analyses we set α = .1 to predominantly enforce smoothness rather than shrinkage as is common in FDA; sensitivity analyses have indicated robustness to the choice of α in this analysis.

Completing the model specification, score vectors are assigned independent standard Normal priors ${\mathit{c}}_i^{(1)}~\mathrm{N}[0,I_{K^{(1)}}]$ and ${\mathit{c}}_i^{(2)}~\mathrm{N}[0,I_{K^{(2)}}]$, consistent with the probabilistic framework for PCA (Tipping and Bishop, 1999). Variance components ${\sigma }_{X_k}^2$, ${\sigma }_{{\psi }_k^{(1)}}^2$ and ${\sigma }_{{\psi }_k^{(2)}}^2$ are assigned IG[0.01, 0.01]. The number of level 1 and level 2 basis functions, K⁽¹⁾ and K⁽²⁾, are fixed constants chosen prior to the analysis, and sensitivity to these choices should be assessed. Simulations indicate that choosing K⁽¹⁾ and K⁽²⁾ larger than necessary does not degrade estimation or inference, but leads to increases in computation time.

2.2 Computation Using Stan

The model in Section 2.1 is implemented in Stan (Stan Development Team, 2013; Hoffman and Gelman, 2011), using an R interface for data entry and for summarizing posterior samples. Stan is an open-source, general purpose programming language for Bayesian analysis that, at the user interface level, has similarities with BUGS (Lunn et al., 2009) or JAGS (Plummer, 2003). Samples are generated using Hamiltonian Monte Carlo, an MCMC algorithm that avoids random walk behavior by using the gradient of the log-posterior (Neal, 2011). In comparison with earlier MCMC algorithms such as the Gibbs sampler, Hamiltonian Monte Carlo offers fast convergence and parameter space exploration when posteriors are highly correlated, such as in the case of the fixed, subject-specific, and subject-day-specific effects in model (3). Code for both model (3) and for an analogous cross-sectional model described in Section 3 is publicly available on the first author's website.

Computation time is a concern in all Bayesian approaches, especially for high-dimensional data such as those we consider. Here, computation times were reasonable for the moderate datasets considered in the simulations – taking several minutes for cross-sectional datasets consisting of up to 100 curves measured on grids of length 100, and taking at most a few hours for multilevel datasets with up to 100 subjects and 4 curves per subject. Real data analyses were more computationally expensive due to the higher dimensionality and increased complexity, and took several days. Details for computation time are provided in Sections 3 and 4.

2.3 Rotation

As noted in the introduction, the probabilistic PCA methods that underpin our Bayesian approach yield estimates that include an arbitrary orthogonal rotation. In this subsection we describe a method to select a specific rotation using a singular value decomposition of the estimated basis. Although this is not a necessary step for estimation, it is useful for aligning estimates across sampler iterations and for obtaining the appealing and well-established interpretation of FPCA. Here we omit notation for level 1 and level 2 basis functions: both are obtained using the same steps.

FPCA is typically posed as an expansion $b_i(t)\approx {\sum }_{k=1}^K{c}_{ik}^{\ast }{\psi }_k^{\ast }(t)$, with the ${\psi }_k^{\ast }(t)$ orthonormal basis functions and scores $c_{ik}^{\ast }$ uncorrelated zero mean random variables with non-increasing variances λ_k. Basis functions and variances are estimated using a truncated Karhunen-Loève decomposition of the covariance matrix Var(b_i(t)). Within each iteration of the sampler we estimate $\mathit{C}{\mathit{B}}_{\psi }^T{\mathbf{\Theta }}^T=\mathit{C}\mathbf{\Psi }$ where Ψ are basis functions evaluated on a finite grid, and we wish to obtain an equivalent C*Ψ* for which Ψ* is an orthonormal basis. To do so, we use the singular value decomposition of the Ψ estimated without orthonormality constraints Ψ = UDV with U, V unitary matrices and D a diagonal matrix whose entries are the singular values of Ψ in descending order. Making a substitution, we have CΨ = CUDV and define C* := CUD and Ψ* := V. Moreover, the prior assumption that Var(c_i) = I implies that for each row ${\mathit{c}}_i^{\ast }$ of C*, $\text{Var}({\mathit{c}}_i^{\ast })=\text{Var}({\mathit{c}}_i\mathit{U}\mathit{D})=\mathit{D}{\mathit{U}}^T\text{Var}({\mathit{c}}_i)\mathit{U}\mathit{D}=\mathit{D}{\mathit{U}}^T\mathit{I}\mathit{U}\mathit{D}={\mathit{D}}^2$. Thus estimates of the score variance components λ₁ ≥ λ₂ ≥ … λ_K ≥ 0 are provided by squaring the diagonal entries of D. This rotation can be conducted within each iteration of the sampler and, accounting for potential sign changes in the basis functions, provides a posterior distribution of orthonormal basis functions.

This rotation step provides a mechanism to identify the effective dimension of the basis through an examination of the λ₁ ≥ λ₂ ≥ … λ_K ≥ 0 using, for example, a scree plot as in Figure 4. Such a plot can indicate whether all estimated basis functions contribute non-negligibly to the subject- and subject/day-specific effects.

Figure 4.

Estimated MFPCA basis functions and scree plots for subject-level and subject-day-level effects (top and bottom row, respectively). Basis functions are illustrated by plotting $g^{-1}[{\beta }_0(t)\pm \sqrt{{\lambda }_k^{(L)}}{\psi }_k^{(L)}(t)]$ for basis functions k ∈ {1, 2} and levels L ∈ {1, 2}. This figure appears in color in the electronic version of this article.

3. Simulations

We demonstrate the performance of our method using a simulation in which generated data mimic the motivating application. Our focus is on assessing the estimation accuracy and inferential properties of the proposed methods. All code for the following simulations is publicly available. Additional simulations considering the cross-sectional case and comparing our proposed method to that of Serban et al. (2013) are in Appendices A.2 and A.3. Results for the cross-sectional case are similar to those presented here, and the comparison of the two approaches generally favors our method for the scenario considered.

We generate binary response curves Y_ij(t) on an equally spaced grid of length 100 according to the model

$$\begin{array}{c}\mathrm{E}[Y_{ij}(t)|b_i(t),{\upsilon }_{ij}(t),x_i]={\mu }_{ij}(t)\\ g[{\mu }_{ij}(t)]={\beta }_0(t)+x_i{\beta }_1(t)+\sum _{k=1}^2{c}_{ik}^{(1)}{\psi }_k^{(1)}(t)+\sum _{k=1}^2{c}_{ijk}^{(2)}{\psi }_k^{(2)}(t)\end{array}$$ (5)

assuming a logit link function. We let t ∈ [0, 1] represent a 24-hour period as in the motivating accelerometer study, and in the following use descriptions motivated by this context. The intercept is β₀(t) = −1.5 − sin(2tπ) − cos(2tπ), which roughly mimics a circadian rhythm over one day. The fixed effect ${\beta }_1(t)=\frac{1}{20}\varphi (\frac{t-.6}{{.15}^2})$, where ϕ(·) is the standard Normal density function, affects the probability of activity in the afternoon but not in the late evening or early morning, and we generate scalar predictors using x_i1 ∼ N(0, 25). The subject-level orthogonal basis functions are chosen to be ${\psi }_1^{(1)}(t)\propto -1.5-sin(2t\pi )-cos(2t\pi )$ and ${\psi }_2^{(1)}(t)\propto -sin(4t\pi )$, scaled such that ${\int }_0^1{[{\psi }_1^{(1)}(t)]}^2\mathit{\text{dt}}=1$ and ${\int }_0^1{[{\psi }_2^{(1)}(t)]}^2\mathit{\text{dt}}=1$. The first basis function amplifies or diminishes the circadian rhythm found in β₀(t), broadly giving higher or lower overall activity patterns, while the second affects activity probabilities in the early and later afternoon. Subject-level PC scores are generated from a mean-zero Normal distribution with variance components λ₁ = 3 and λ₂ = 1.5. Subject/day-level basis functions ${\psi }_1^{(2)}(t)\propto -1.5-sin(2t\pi )-cos(2t\pi )$ and ${\psi }_2^{(2)}(t)\propto -cos(4t\pi )$, again scaled so that squared basis functions integrate to 1. Level 2 variance components are ${\lambda }_1^{(2)}=3$ and ${\lambda }_2^{(2)}=1.5$. Setting ${\psi }_1^{(1)}(t)={\psi }_1^{(2)}(t)$ means that the dominant pattern of variability across subjects is also the dominant pattern of variability across days within a subject. This is not only scientifically plausible but also in line with our findings in the motivating example. This assumption, however, increases the difficulty of the estimation problem. For all simulations we let J_i, the number of days observed per subject, be 4.

One hundred datasets are constructed according to the preceding model for all combinations of sample size I ∈ {50, 100} and number of estimated principal components K̂⁽¹⁾= K̂⁽²⁾ ∈ {2, 5}, giving a total of four possible simulation designs. When K̂⁽¹⁾ = K̂⁽²⁾ = 5 the number of estimated PC basis functions is larger than the number of true basis functions, which is held at K = 2 throughout. Model parameters are estimated using the methodology described in Section 2. Estimation and inference is based on posterior means and quantiles of 5000 iterations from the sampler, after discarding the first 2000 as burn-in; visual inspection and diagnostics for the one simulated dataset indicate that these levels are sufficient for convergence to and exploration of the posterior distribution. We quantify estimation accuracy for fixed effects using the integrated squared error $\text{ISE}={\int }_0^1{[{\beta }_k(t)-{\widehat{\beta }}_k(t)]}^2\mathit{\text{dt}}$ and for the latent subject probability trajectories using the mean integrated squared error $\text{MISE}=\frac{1}{I}{\sum }_{i=1}^I{\int }_0^1{[{\mu }_i(t)-{\widehat{\mu }}_i(t)]}^2\mathit{\text{dt}}$. Inference is evaluated using average pointwise coverage of 95% posterior credible intervals.

Figure 1 illustrates the simulation design and results for a single dataset with I = 50 and K̂ = 5. Simulated latent probability curves μ_i(t) are shown in the left panel, and demonstrate the structure of activity trajectories as well as their variability across subjects. The true and estimated fixed effects β₀(t) and β₁(t) are plotted in the middle panels (dashed curves), along with the posterior mean (solid lines) and a posterior sample (translucent curves). Finally, the right panel shows the observed binary data Y_ij(t) for one subject on one day (points), the true latent probability curve μ_ij(t) (dashed curve), the posterior mean (solid curve) and a sample from the posterior distribution of μ_ij(t) (translucent curves).

Figure 1.

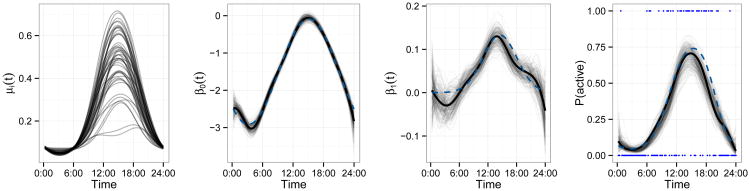
Illustration of data and results for cross-sectional simulations. The left panel shows simulated probability curves μ_i(t) for all subjects i ∈ 1, …, I. The middle panels show fixed effects β₀(t) and β₁(t) as dashed curves, with posterior mean and sample intervals in solid and translucent curves. The right panel shows observed binary responses Y_1,1(t) for subject i = 1 on day j = 1 as points; the true probability curve μ_1,1(t) as a dashed line; a sample from the posterior of μ_1,1(t) as translucent curves; and the posterior mean as a solid curve. This figure appears in color in the electronic version of this article.

Table 1 provides the average (across 100 simulated datasets) MISE for fixed effects and average MISE for latent probability trajectories, as well as average pointwise coverage and computation time. As one would expect, estimation accuracy for fixed effects improves as sample size increases. Estimation of subject effects also improves as sample size increases, although to a lesser extent than for fixed effects. In all cases, coverage for fixed effects and latent probability trajectories in near nominal levels, and the coverage of intervals for the latent subject-specific trajectories μ_i(t) and latent subject-day-specific trajectories μ_ij(t) increases as K̂ increases. Increasing K̂ does not affect estimation accuracy for β₁(t) but may negatively affect accuracy for β₀(t), either due to the flexibility in the model or because ${\psi }_1^{(1)}(t)={\psi }_1^{(2)}(t)$. Meanwhile, increasing K̂ may improve coverage for both fixed effects. Computation times are larger but not prohibitive, and generally take between one and four hours.

Table 1. Multilevel simulation results averaged across 100 datasets. Integrated mean squared errors are defined as $\mathit{\text{MISE}}={\int }_0^1{({\beta }_p(t)-{\widehat{\beta }}_p(t))}^2\mathit{\text{dt}}$ for fixed effects and $\mathit{\text{AMISE}}=\frac{1}{I}{\sum }_{i=1}^I{\int }_0^1{({\mu }_i(t)-{\widehat{\mu }}_i(t))}^2\mathit{\text{dt}}$ for probability curves. Coverage is averaged over 95% pointwise credible intervals. Computation time is reported in seconds.

		MISE				Coverage				Comp. Time
		β0(t)	β1(t)	μi(t)	μij(t)	β0(t)	β1(t)	μi(t)	μij(t)	(in sec)
I = 50;	K̂(1) = K̂(1) = 2	0.0073	0.00027	0.038	0.059	0.941	0.923	0.920	0.934	2893
	K̂(1) = K̂(2) = 5	0.0084	0.00026	0.039	0.060	0.946	0.946	0.956	0.968	5938
I = 100;	K̂(1) = K̂(2) = 2	0.0035	0.00014	0.030	0.050	0.945	0.938	0.934	0.946	6943
	K̂(1) = K̂(2) = 5	0.0040	0.00014	0.030	0.051	0.942	0.944	0.959	0.969	12290

4. Application

We now apply methods of Section 2 to the motivating data. For 583 subjects, we observe age, BMI, and minute-by-minute activity count trajectories for 5 days. Here we present results for dichotomized “active vs. inactive” response curves obtained by thresholding the observed activity counts at 10; this value is fairly conservative for defining activity in order to allow for low-intensity activity commonly observed in elderly subjects (Schrack et al., 2014). Results from the cross-sectional analysis using a Poisson distribution and log link to model activity count response curves appear in Appendix A.4. To reduce the computational burden of the analysis, data are thinned to one data point for every 10 minutes, giving 144 observations per subject per day. Our model considers age and BMI, centered at 60 and 25 respectively, as potential predictors of activity. To ensure that the value of coefficient functions at times 0:00 and 24:00 are equal we use a periodic B-spline basis. We set the size of the FPC bases K⁽¹⁾ = K⁽²⁾ = 8 and the dimension of the B-spline basis Θ is K_Θ = 10. Additional analyses using K⁽¹⁾ = K⁽²⁾ = 16 and K_Θ = 20 confirm that these choices suffice to estimate the smooth effects observed in this application. We fit model (4) using 5000 iterations of the sampler, discarding 2000 as burn-in; total computation time was 10 days.

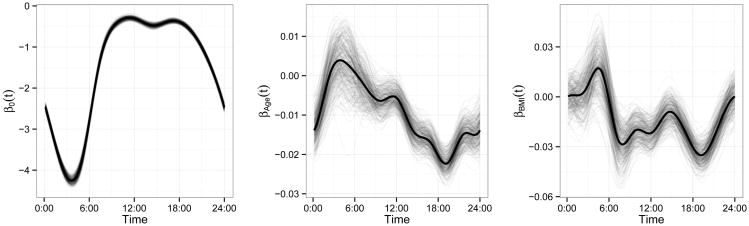
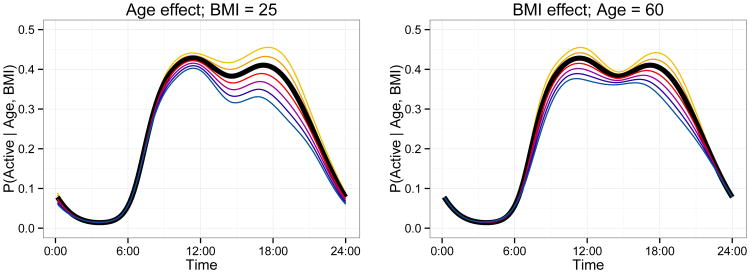
Figures 2 and 3 provide the estimated fixed effect coefficients. In Figure 2 we show the estimated effect as a solid curve and a posterior sample as translucent curves. The intercept β₀(t) gives the log odds of activity for 60 year old subject with a BMI of 25, and has an expected circadian rhythm shape. Coefficient functions β_age(t) and β_BMI(t) have a log odds ratio interpretation; for example, β_age(t) is the change in the log odds of activity for each one year increase in age, keeping BMI fixed, over a 24-hour time course. From the posterior distribution, it seems that both age and BMI have significant negative effects on the probability of being active during daytime hours. The effect of age is most pronounced in the late afternoon, perhaps as a result of increased fatigue in older subjects, while BMI is most significant in the mid-morning and mid-afternoon. Figure 3 demonstrates these effects by plotting the fitted probability of being active over a 24-hour period for several age and BMI levels.

Figure 2.

Estimated fixed effects (solid) from the real data analysis with samples from the posterior (translucent). The left panel shows the intercept β₀(t); the middle panel shows the age effect β_Age(t); the right panel shows the BMI effect β_BMI(t).

Figure 3.

The left panel shows the effect on the probability of being active of varying age in 5 year increments from 50 to 80 as a decreasing sequence of functions, while keeping BMI fixed at 25. The right panel shows the effect of varying BMI in 2.5 unit increments from 20 to 35 as a decreasing sequence of functions, while keeping age fixed at 60. In both panels, the subject- and subject-day-specific effects are set to zero. This figure appears in color in the electronic version of this article. An interactive version of this graphic appears on the first author's webpage.

In addition to fixed effects, we estimate level 1 and level 2 principal component basis functions ψ⁽¹⁾(t) and ψ⁽¹⁾(t), which have been rotated as described in 2.3. These functions model the subject- and subject-day-specific residual dependency in the 24-hour trajectories unaccounted for in the covariate-dependent mean. The top row of Figure 4 shows the directions of variation explained by the first two level 1 basis functions by plotting $g^{-1}[{\beta }_0(t)\pm \sqrt{{\lambda }_k^{(1)}}{\psi }_k^{(1)}(t)]$, k = 1, 2; the third panel shows the scree plot for the level 1 decomposition. The major directions that distinguish subjects are a general shift in the probability of being active and a contrast in the probability of being active in the daytime and non-daytime hours. Similar plots are shown for the level 2 decomposition in the second row of Figure 4. Although these figures show the basis functions using the probability of activity, the percent variance explained is calculated and the orthonormality property enforced in the log odds of activity scale. The proportion of residual (after removing fixed effects) variance explained by subject level effects, given by $\frac{{\sum }_{k=1}^{K^{(1)}}{\lambda }_k^{(1)}}{{\sum }_{k=1}^{K^{(1)}}{\lambda }_k^{(1)}+{\sum }_{k=1}^{K^{(2)}}{\lambda }_k^{(2)}}$ is 0.46 in this application, indicating moderate stability within subjects over multiple days.

Finally, we compare fitted values and observed data in Figure 5. The top row contains plots for a 85 year old subject with a BMI of 26.5. The left and middle panels show observed data for two different days as points and a moving average of the observed data as dashed lines. Subject-day-specific estimates, combining fixed effects with level 1 and level 2 FPC effects, are overlayed: the posterior mean Ŷ_ij(t) is shown as a solid curve and a posterior sample is shown as translucent curves. The right panel shows the moving average trajectory for each of the five observed days as separate dashed lines. Subject-specific estimates, combining fixed effects with only level 1 FPC effects, are again overlayed with the posterior mean Ŷ_i(t) as a solid curve and a posterior sample as translucent curves. Data for a second subject, aged 51 years with a BMI of 23.8, is shown in the bottom row of Figure 5. Our method accurately captures both large scale patterns and detailed phenomena, giving accurate estimates of the probability of being active over a 24-hour period using relatively few principal components and scores.

5. Concluding remarks

The generalized multilevel function-on-scalar regression and principal components analysis techniques developed in this manuscript are necessary tools in modern functional data analysis and are required by our application. From a methodological perspective, this work has two major motivations that have often been neglected in functional data analysis. For the problem of function-on-scalar regression, some effort is needed to account for residual correlation within functions to develop reasonable inferential procedures. Meanwhile, in functional principal components analyses, it is common to condition (implicitly or explicitly) on the estimated mean and basis functions when predicting latent subject-specific trajectories and constructing related confidence/credible intervals. Both of these issues are made more difficult in the context of generalized and multilevel functional data. Our approach has been to jointly model all parameters of interest in a Bayesian context, and in doing so we have attempted to develop a unified framework for both function-on-scalar regression and functional principal components analysis.

In the motivating real-data analysis, we confirm and quantify a scientifically plausible hypothesis: that the probability of activity decreases as individuals age and as BMI increases, and these effects are dynamic over the course of the day. Moreover, we identify the major patterns of activity that distinguish subjects from each other and that distinguish days within subjects. By focusing here on a binary activity variable we address a concern that is distinct from the intensity of activity, instead examining changes in sedentary behavior associated with changes in covariates. Meanwhile, the analysis of the changes in activity intensity appears in the Appendix with qualitatively similar results. For both outcomes, the consideration of other potentially important covariates and allowing for non-linear effects is warranted in future work.

The Bayesian procedure we develop was shown in realistic simulations to have good estimation and inferential properties. Not surprisingly, computation time can be a serious concern particularly as sample sizes, grid densities, and the number of estimated principal component basis functions grow. Another important limitation of our method is the necessity to select the dimension of the FPC bases prior to analysis. Determining whether a selection is sufficient to describe the major directions of variation can require additional confirmatory analyses with even larger values, which can impose considerable computational expense.

Future work focusing on variational Bayes or other approximations will address the computational concerns and, we suspect, will result in good estimation of model components. This will provide an important tool for choosing the dimension of the FPC bases by allowing rapid comparisons of different selections, and may also have the property of automatic relevance determination. Because such an algorithm seeks a posterior mode rather than exploring the posterior distribution, “unimportant” directions can be effectively removed by shrinking their associated variance components to zero. This decrease in computational burden may be accompanied by poorer inferential performance due to the assumptions needed for such an approximation. Balancing these priorities will depend on the particular data scenario, and both will be important.