Not Noisy, Just Wrong: The Role of Suboptimal Inference in Behavioral Variability

Abstract

Behavior varies from trial to trial even when the stimulus is maintained as constant as possible. In many models, this variability is attributed to noise in the brain. Here, we propose that there is another major source of variability: suboptimal inference. Importantly, we argue that in most tasks of interest, and particularly complex ones, suboptimal inference is likely to be the dominant component of behavioral variability. This perspective explains a variety of intriguing observations, including why variability appears to be larger on the sensory than on the motor side, and why our sensors are sometimes surprisingly unreliable.

Introduction

Even the simplest of behaviors exhibits unwanted variability. For instance, when monkeys are asked to visually track a black dot moving against a white background, the trajectory of their gaze exhibits a great deal of variability, even when the path of the dot is the same across trials (Osborne et al., 2005). Two sources of noise are commonly blamed for variability in behavior. One is internal noise; that is, noise within the nervous system (Faisal et al., 2008). This includes noise in sensors, noise in individual neurons, fluctuations in internal variables like attentional and motivational levels, and noise in motoneurons or muscle fibers. The other source of behavioral variability is external noise—noise associated with variability in the outside world. Suppose, for instance, that instead of tracking a single dot, subjects tracked a flock of birds. Here there is a true underlying direction—determined, for example, by the goal of the birds. However, because each bird deviates slightly from the true direction, there would be trial-to-trial variability in the best estimate of direction. Similar variability arises when, say, estimating the position of an object in low light: because of the small number of photons, again the best estimate of position would vary from trial to trial.

Although internal and external noise are the focus of most studies of behavioral variability, we argue here that there is a third cause: deterministic approximations in the complex computations performed by the nervous system. This cause has been largely ignored in neuroscience. However, we argue here that this is likely to be a large, if not dominant, cause of behavioral variability, particularly in complex problems like object recognition. We also discuss why deterministic approximations in complex computations have a strong influence on neural variability although not so much on single cell variability. Instead, we argue that the impact of suboptimal inference will mostly be on the correlations among neurons and, possibly, the tuning curves. These ideas have important implications for current neural models of behavior, which tend to focus on single-cell variability and internal noise as the main contributors to behavioral variability.

Although these arguments apply to any form of computation, we focus here on probabilistic inference. In this case, deterministic approximations correspond to suboptimal inference.

Internal Noise and Behavioral Variability: The Standard Approach

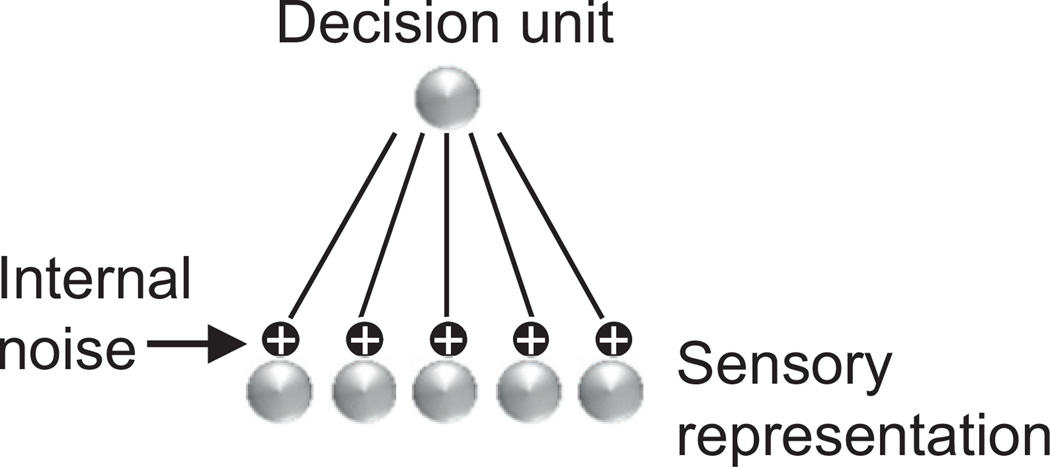
For most models in the literature, the sole cause of behavioral variability is internal noise. Many of these models focus on discrimination tasks and their architectures are variations of the simple network depicted in Figure 1. The input layer contains a population of neurons encoding a sensory variable with a population code; for instance MT neurons encoding direction of motion (Law and Gold, 2008; Shadlen et al., 1996). These neurons are assumed to be noisy, often with a variability following either a Poisson distribution or a Gaussian distribution with a variance proportional to the mean activity. Typically, the population then projects onto a single output unit whose value determines the response of the model/behavior of the animal. In mathematical psychology, the input neurons are often replaced by abstract “channels.” These channels are then corrupted by additive or multiplicative noise (Dosher and Lu, 1998; Petrov et al., 2004; Regan and Beverley, 1985).

Figure 1. Typical Neural Model of Sensory Discrimination.

The input neurons encode the sensory stimulus and projectto a single decision unit. Internal noise is injected in the response of the input units, often in the form of independent Poisson variability.

Despite these differences, the neural and psychological models are conceptually nearly identical. In particular, in both types of models behavioral performance depends critically on the level of neuronal variability, since eliminating that variability leads to perfect performance. Many models, including several by the authors of the present paper, explicitly assume that this neuronal variability is internally generated, thus blaming internal variability as the primary cause of behavioral variability (Deneve et al., 2001; Fitzpatrick et al., 1997; Kasamatsu et al., 2001; Pouget and Thorpe, 1991; Rolls and Deco, 2010; Shadlen et al., 1996; Stocker and Simoncelli, 2006; Wang, 2002). Other studies are less explicit about the origin of the variability but, particularly in the attentional (Reynolds and Heeger, 2009; Reynolds et al., 2000) and perceptual learning domains (Schoups et al., 2001; Teich and Qian, 2003), the variability is assumed to be independent of the variability of the sensory input and, as such, it functions as internal variability. For instance, it is common to assume that attention boosts the gain of tuning curves, or performs a divisive normalization of the sensory inputs. Importantly, in such models, the variability is unaffected by attention: it is assumed to follow an independent Poisson distribution (or variation thereof) both before and after attention is engaged, as if this variability came after the sensory input has been enhanced by attentive mechanisms (Reynolds and Heeger, 2009; Reynolds et al., 2000). A similar reasoning is used in models of sensory coding with population codes. Thus, several papers have argued that sharpening or amplifying tuning curves can improve neural coding. These claims are almost always based on the assumption that the distribution of the variability remains the same before and after the tuning curves have been modified (Fitzpatrick et al., 1997; Teich and Qian, 2003; Zhang and Sejnowski, 1999). This is a perfectly valid assumption if one thinks of the variability as being internally generated and added on top of the tuning curves. A common explanation of Weber’s law relies on a variation of this idea (Dehaene, 2006; Nover et al., 2005).

Given that internal variability is indeed perceived as a primary cause of behavioral variability, neuroscientists have started to investigate its origin. Several causes have been identified; two of the major ones are fluctuations in internal variables (e.g., motivational and attentional levels) (Nienborg and Cumming, 2009) and stochastic synaptic release (Stevens, 2003). Another potential cause is the chaotic dynamics of networks with balanced excitation and inhibition (Banerjee et al., 2008; London et al., 2010; van Vreeswijk and Sompolinsky, 1996). Chaotic dynamics lead to spike trains with near Poisson statistics—close to what has been reported in vivo, and close to what is used in many models.

Although it is clear that there are multiple causes of internal variability in neural circuits, the critical question is whether this internal variability has a large impact on behavioral variability, as assumed in many models. We argue below that, in complex tasks, internal variability is only a minor contributor to behavioral variability compared to the variability due to suboptimal inference. To illustrate what we mean by suboptimal inference and how it contributes to behavioral variability, we turn to a simple example inspired by politics.

How Suboptimal Inference Can Increase Behavioral Variability

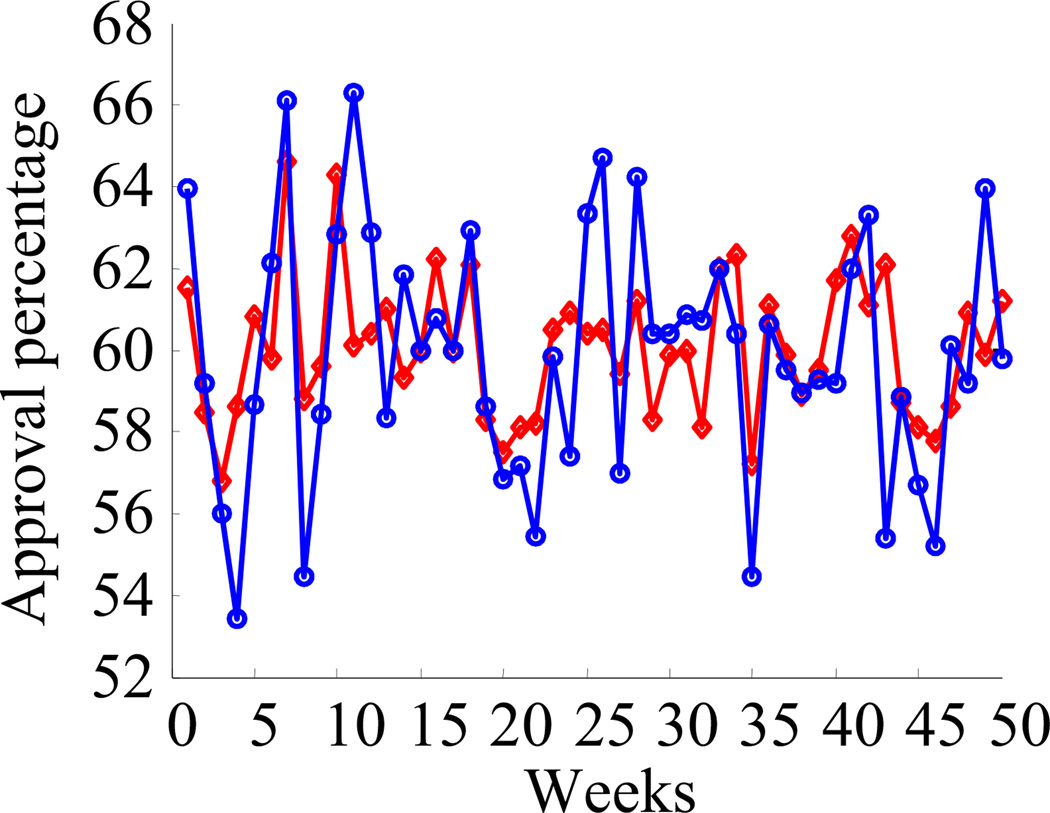
Suppose you are a politician and you would like to know your approval rating. You hire two polling companies, A and B. Every week, they give you two numbers, d_A and d_B, the percentage of people who approve of you. How should you combine these two numbers? If you knew how many people were polled by each company, it would be clear what the optimal combination is. For instance, if company A samples 900 people every week, while company B samples only 100 people, the optimal combination is d̂_opt = 0.9d_A + 0.1d_B. If you assume that the two companies use the same number of samples, the best combination is the average, d̂_av = 0.5d_A + 0.5d_B.

In Figure 2, we simulated what d_A and d_B would look like week after week, assuming 900 samples for company A and 100 for company B and assuming that the true approval ratings are constant every week at 60%. As one would expect, the estimate obtained from the optimal combination, d̂_opt, shows some variability around 60%, due to the limited sample size. The estimate obtained from the simple average, however, shows much more variability, even though it is based on the same numbers as d̂_opt, namely, d_A and d_B. This is not particularly surprising: unbiased estimates obtained from a suboptimal strategy must show more variability than those obtained from the optimal strategy. Importantly, though, the extra variability in d̂_av compared to d̂_opt is not due to the addition of noise. Instead, it is due to suboptimal inference—the deterministic, but suboptimal, computation d̂_av = 0.5d_A +0.5d_B, which was based on an incorrect assumption about the number of samples used by each company.

Figure 2. Variability Induced by Suboptimal Inference.

The plot shows the fluctuations in estimated approval ratings using two different methods. In p_opt (red), the estimate from the two different companies are combined optimally, while in p_av (blue), they are combined suboptimally. Note that the variability in p_av is greater than the variability in p_opt. This additional variability in p_av is not due to noise; it is due to suboptimal inference caused by a deterministic approximation of the assumed statistical structure of the data.

Although this simple example might seem far removed from the brain, it is in fact similar to the problem of multisensory integration: for example, d_A and d_B could correspond to an auditory and a visual cue about the position of an object in space, and d̂_av to the observer’s estimate of the position of the object.

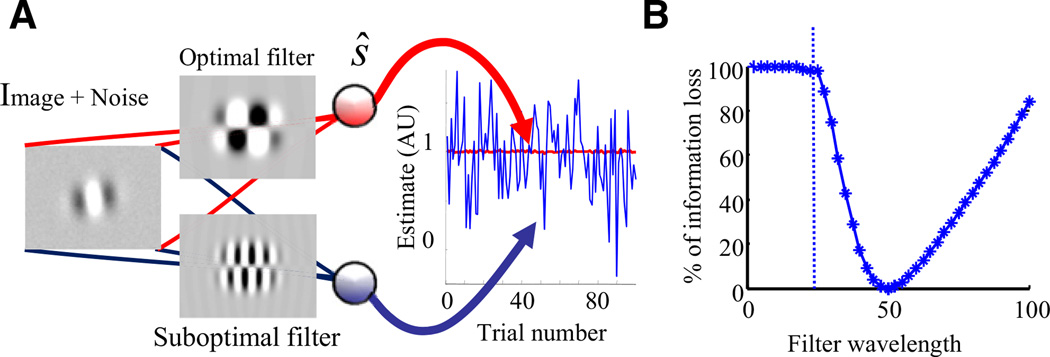
The effect of suboptimal inference can even be seen in a simple discrimination task. For instance, consider the problem of discriminating between two Gabor patches oriented at either +5° or −5°, and containing a small amount of additive noise, as shown in Figure 3A, first column. Here, the additive noise is meant to model internal noise, such as noise in the photoreceptors. Figure 3A shows two linear discriminators, whose responses are proportional to the dot product of each image with the linear filter (Figure 3A, second column) associated with each discriminator. The linear filter for the top unit in the third column of this figure was optimized to maximize its ability to discriminate between the two orientations of the Gabor patches. The linear filter of the other unit (bottom one in the third column of Figure 3A) was optimized for Gabor patches with the same Gaussian envelope but half the wavelength. The unit at the bottom thus performs suboptimal inference; it assumes the wrong statistical structure of the task, just like the politician did with d̂_av in the polling example.

Figure 3. Amplification of Noise by Suboptimal Inference.

(A) The image consists of a Gabor patch oriented at either +5° or −5°, plus small additive noise on each pixel. Both units compute the dot product of the image with a linear filter (their feedforward weights) to yield a decision of which stimulus is present. The top unit uses the filter that discriminates optimally between these two particular oriented stimuli. In contrast, the bottom unit uses a filter that is optimized for a Gabor patch with twice the frequency of the patch in the image. The plot on the right shows the activity of the two units for 100 presentations of the Gabor patches, all oriented at +5° but with different pixel noise. The filters have been normalized to ensure that the mean response is 1 in both cases. The standard deviation of the bottom unit (blue) is 54 times larger than the standard deviation of the top unit (red; although the trace looks flat, it does in fact fluctuate). In other words, more than 98% of the variability of the bottom unit is due to the use of a suboptimal filter.

(B) Percentage of Fisher information loss as a function of the wavelength of the filter. The information loss increases steeply as soon as the wavelength of the filter differs from the wavelength in the image (set to 50).

The graph in the right panel of Figure 3A shows the responses of the two units to a sequence of images with the same orientation but different noise. The responses have been normalized to ensure that the estimates are unbiased for both units. Given this normalization, greater response variability implies greater stimulus uncertainty and, therefore, greater behavioral variability. This simulation reveals two important facts. First, suboptimal inference has an amplifying effect on the internal noise. Indeed, if we set the noise to zero, the variability in both units would be zero. Second, most of the behavioral variability can be due to suboptimal inference. This can be seen by comparing the variability of the two units. For the top unit, all the variability is due to internal noise. In the bottom unit, all the extra variability is due to suboptimal inference, which in this case is 54 times the variability from the noise alone; more than 98% of the total variability.

The fraction of variability due to suboptimal inference depends, of course, on the severity of the approximation, i.e., on the discrepancy between the optimal frequency and the one assumed by the suboptimal filter. As shown in Figure 3B, the information loss grows quickly as the difference between the filter and image wavelengths grows.

The point of this example is to show that in psychophysics experiments, much of the behavioral variability might be due to suboptimal inference and not noise. This is true even in experiments in which external noise is minimized, as when the very same image is presented repeatedly across trials: suboptimal inference will amplify any internal noise (Figure 3A). In fact, we will also see that suboptimal inference can increase variability even in the absence of internal noise.

External Noise and Generative Models

In the polling and discrimination examples, we saw that suboptimal inference can amplify existing noise. In most real-world situations that the brain has to deal with, there are two distinct sources of such noise: internal and external. We have already discussed several potential sources of internal noise. With regard to external noise, it is important to point out that we do not just mean random noise injected into a stimulus, but the much more general notion of the stochastic process by which variables of interest (e.g., the direction of motion of a visual object, the identity of an object, the location of a sound source, etc) give rise to the sensory input (e.g., the images and sounds produced by an object). Here, we adopt machine learning terminology and refer to the state-of-the-world variables as latent variables and to the stochastic process that maps latent variables into sensory inputs as the generative model. For the purpose of a given task, all external variables other than the latent variables of behavioral interest are often called nuisance variables, and count as external noise.

Is Suboptimal Inference or Internal Noise More Critical for Behavioral Variability?

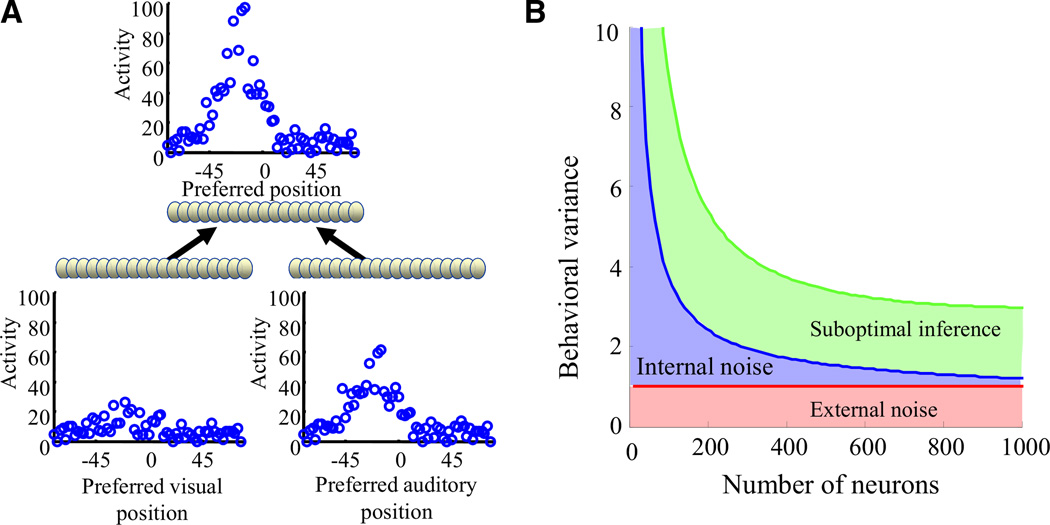
In situations in which there is both internal and external noise (i.e., a generative model), there are now three potential causes of behavioral variability: the internal noise, the external noise and suboptimal inference. Which of these causes is more critical to behavioral variability? To address this question, we consider a neural version of the polling example (Figure 2) with internal and external noise. The problem we consider is cue integration: two sensory modalities (which we take, for concreteness, to be audition and vision) provide noisy information about the position of an object, and that information must be combined such that the overall uncertainty in position is reduced. A network for this problem, which is shown in Figure 4A, contains two input populations that encode the position of an object using probabilistic population codes (Ma et al., 2006). These input populations converge onto a single output population which encodes the location of the object. Output neurons are so-called LNP (Gerstner and Kistler, 2002) neurons, whose internal state at every time step is obtained by computing a nonlinear function of a weighted sum of their inputs. This internal state is then used to determine the probability of emitting a spike on that time step. This stochastic spike generation mechanism acts as an internal source of noise, which leads to near-Poisson spike trains similar to the ones used in many neural models (Gerstner and Kistler, 2002). We take the “behavioral response” of the network to be the maximum likelihood estimate of position given the activity in the output population, and the “behavioral variance” to be the variance of this estimate. Our goal is to determine what contributes more to the behavioral variance: internal noise or approximate inference.

Figure 4. Suboptimal Inference Dominates over Internal Noise in Large Networks.

(A) Network architecture. Two inputs layers encode the position of an object based on visual and auditory information, using population codes. Typical patterns of activity on a given trial are shown above each layer. These input neurons project onto an output layer representing the position of the object based on both the visual and auditory information.

(B) Behavioral variance of the network (modeled as the variance of the maximum likelihood estimate of position based on the output layer activity) as a function of the number of neurons in the output layer. Red line: lower bound on the variance given the information available in the input layer (based on the Cramer-Rao bound). Blue curve: network with optimal connectivity. The increase in variance (compared to the red curve) is due to internal noise in the form of stochastic spike generation in the output layer. The blue curve eventually converges to the red curve, indicating that the impact of internal noise is negligible for large networks (the noise is simply averaged out). Green curve: network with suboptimal connectivity. In a suboptimal network, the information loss can be very large. Importantly, this loss cannot be reduced by adding more neurons; that is, no matter how large the network, performance will still be well above the minimum variance set by the Cramer-Rao bound (red line). As a result, for large networks, the information loss is due primarily to suboptimal inference and not to internal noise.

Figure 4B shows the behavioral variance of the network as a function of the number of neurons in the output population. The red line indicates the lower bound on this variance given the external noise (known as the “Cramer-Rao bound”; Papoulis, 1991); the variance of any network is guaranteed to be at or above this line. The blue line indicates the variance of a network that performs exact inference; that is, a network that optimally infers the object position from the input populations (see Ma et al., 2006). The reason this variance is above the minimum given by the red line is that there is internal noise, which, as mentioned above, arises from the stochastic spike generating mechanism. As is clear from Figure 4B, for large numbers of neurons, this increase is minimal. This is because for a given stimulus, each neuron generates its spikes independently of the other neurons, and, as long as there are a large number of neurons representing the quantity of interest (which is typically the case with population codes), this variability can be averaged out across neurons. This demonstrates that, for large networks, internal noise due to independent near-Poisson spike trains has only a minor impact on behavioral variability. Of course, this is unsurprising: independent variability can always be averaged out. Nonetheless, many models focus on independent Poisson noise (Deneve et al., 2001; Fitzpatrick et al., 1997; Kasamatsu et al., 2001; Pouget and Thorpe, 1991; Reynolds and Heeger, 2009; Reynolds et al., 2000; Rolls and Deco, 2010; Schoups et al., 2001; Shadlen and Newsome, 1998; Stocker and Simoncelli, 2006; Teich and Qian, 2003; Wang, 2002), and many experiments measure Fano factor and related indices (DeWeese et al., 2003; Gur et al., 1997; Gur and Snodderly, 2006; Mitchell et al., 2007; Tolhurst et al., 1983).

In contrast, the green line shows the extra impact of suboptimal inference. In this case, the connections between the input and output layers are no longer optimal: the network now over-weights the less reliable of the two populations. As a result, the behavioral variance is well above the minimal value indicated by the red line. Importantly, the gap between the red and green lines cannot be closed by increasing the number of output neurons. Therefore, for large numbers of neurons, a large fraction of the extra behavioral variability is due to the suboptimal inference, with very little contribution from the internal noise.

This example illustrates that internal noise in the form of independent Poisson spike trains has little impact on behavioral variability. This is counter to what appears to be the prevailing approach to modeling behavioral variability (Deneve et al., 2001; Fitzpatrick et al., 1997; Kasamatsu et al., 2001; Pouget and Thorpe, 1991; Reynolds and Heeger, 2009; Reynolds et al., 2000; Rolls and Deco, 2010; Schoups et al., 2001; Shadlen and Newsome, 1998; Stocker and Simoncelli, 2006; Teich and Qian, 2003; Wang, 2002). In addition, it should be clear that the more severe the approximation, the larger effect it has on behavior variability. For example, the more the network overweights the less reliable cue, the higher the green curve will be in Figure 4. This latter point is critically important because, as we argue next, severe approximations are inevitable for complex tasks.

Why Suboptimal Inference Is Inevitable

Why can’t we be optimal for complex problems? Answering this requires a closer look at what it means to be optimal. When faced with noisy sensory evidence, the ideal observer strategy utilizes Bayesian inference to optimize performance. In this strategy, the observer must compute the probability distribution over latent variables based on the sensory data on a single trial. This distribution—also called the posterior distribution—is computed using knowledge of the statistical structure of the task, which earlier we called the generative model. In the polling example, the generative model can be perfectly specified (by simply knowing how many people were sampled by each company, N_A = 900, N_B = 100), and inverted, leading to optimal performance.

For complex real-world problems, however, this is rarely possible; the generative model is just too complicated to specify exactly. For instance, consider the case of object recognition. The generative model in this case specifies how to generate an image given the identity of the objects present in the scene. Suppose that one of the objects in a scene is a car. If there existed one prototypical image of a car from which all images of cars were generated by adding noise (as was the case for the pooling example where d_A and d_B are the true approval rating plus noise due to the limited sampling), then the problem would be relatively simple. But this is not the case; cars come in many different shapes, sizes, and configurations, most of which you have never seen before. Suppose, for example, that you did not know that cars could be convertibles. If you saw one, you would not know how to classify it. After all, it would look like a car, but it would be missing something that may have previously seemed like an essential feature: a top.

In addition, even when the generative model can be specified exactly, it may not be possible to perform the inference in a reasonable amount of time. Consider the case of olfaction. Odors are made of combinations of volatile chemicals that are sensed by olfactory receptors, and olfactory scenes consist of linear combinations of these odors. This generative model is easy to specify (because it’s linear), but inverting it is hard. This is in part because of the size of the network: the olfactory system of mammals has approximately a thousand receptor types, and we can recognize tens of thousands or more odors (Wilson and Mainen, 2006). Performing inference for this problem is intractable because obtaining an exact solution requires an amount of time that is exponential in the number of behaviorally relevant odors. Importantly, olfaction is not an exception; for most inference problems of interest, the computational complexity is exponential in the total number of variables (Cooper, 1990).

Therefore, for complex problems, there is no solution but to resort to approximations. These approximations typically lead to strong departures from optimality, which generate variability in behavior. In general, one expects the variability due to the sub-optimal inference to scale with the complexity of the problem. This would predict that a large fraction of the behavioral variability for a complex task like object recognition is due to suboptimal inference (which is in deed what Tjan et al., 1995, have found experimentally), while subjects should be close to optimal for simpler tasks (as they are for instance when asked to detect a few photons in an otherwise dark room; Barlow, 1956).

In Complex Problems, Suboptimal Inference Increases Behavioral Variability Even in the Absence of Internal Noise

So far we have argued that suboptimal inference is unavoidable for complex tasks and contributes substantially to behavioral variability. In the orientation discrimination example (Figure 3), however, it would appear that internal noise, (i.e., stochasticity in the brain either at the level of the sensors or in downstream circuits) is also essential, regardless of whether the downstream inference is suboptimal. Indeed, if we set this noise to zero (which would have resulted in noiseless input patterns in Figure 3), the behavioral variability would have disappeared altogether even for the suboptimal filter. This would imply that the brain should keep the internal noise as small as possible since it is amplified by suboptimal inference. However, approximate inference does not always simply amplify internal noise. For complex problems, suboptimal inference can still be the main limitation on behavioral performance even in the absence of internal noise.

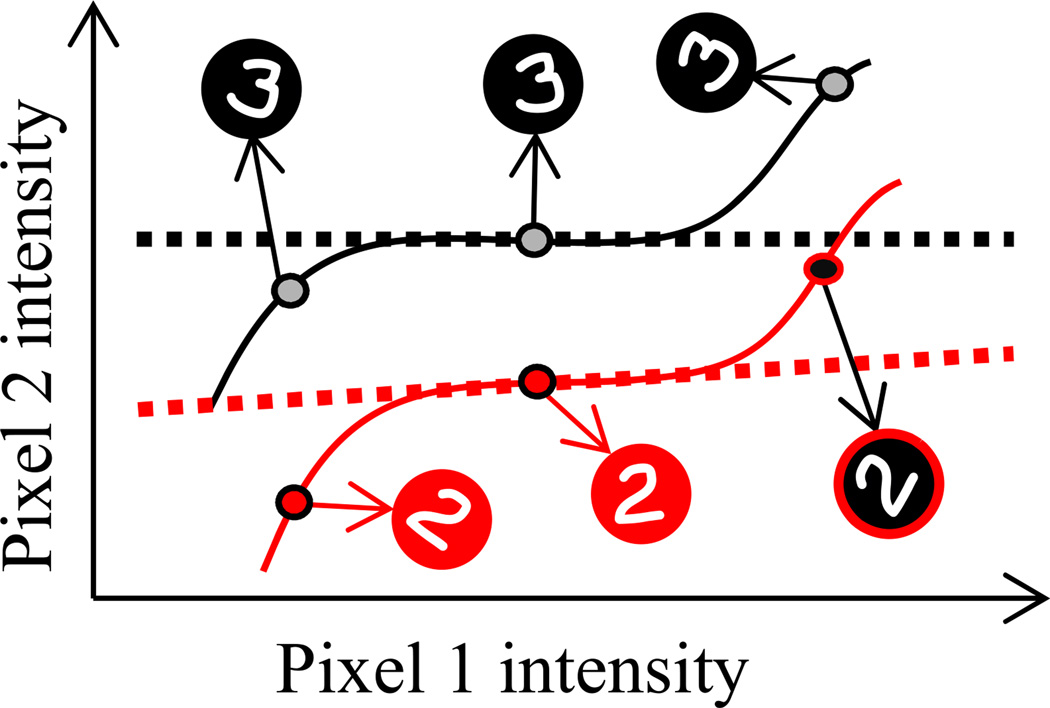
To illustrate this point, we consider the problem of recognizing handwritten digits. Each image of a particular digit can be represented as a list, or a vector, of N pixel values, where N is the number of pixels in the image. This vector corresponds to a point in an N-dimensional space in which each axis corresponds to one particular pixel. The set of all points which correspond to a particular digit, say 2, includes 2s of every possible size and orientation. This set of points makes up a smooth surface in this N-dimensional space, also known as a manifold. Figure 5 shows schematic representations of two such manifolds for the digits 2 and 3 (solid lines). According to this perspective, object recognition becomes a problem of modeling these manifolds, which is typically very difficult because of how they are curved and tangled in the high-dimensional space of possible images (DiCarlo and Cox, 2007; Simard et al., 2001). In this case, there is no alternative but to resort to severe approximations. For instance, the manifolds might be approximated by locally linear ones (dashed lines) around certain exemplars (Simard et al., 2001). New instances of a digit are then classified according to the closest linear manifold. This procedure results in misclassifying some digits when irrelevant variables (here, rotation) change the image beyond where the linear approximation is good, illustrating that this computation is suboptimal. Although here orientation and size constitute external noise because they are irrelevant to the digit classification, there is no internal noise of any kind in this example: the misclassified digits lie precisely on the corresponding manifolds. Therefore, approximate inference can have a strong impact on performance even when there is no internal noise.

Figure 5. Suboptimal Inference on Inputs without Internal Noise.

Handwritten digit recognition can be formalized as a problem of modeling manifolds in n-dimensional space, where n is the number of pixels in the image. Each point in this space corresponds to one particular image (only two dimensions are shown for clarity). We show here a schematic representation of the manifolds corresponding to rotated 2s (red solid line) and 3s (black solid line). Modeling these manifolds is typically hard and requires approximations. One common approach involves using a locally linear approximation, shown here as dashed lines. This approximation would result in misclassifying the image of the 2 shown with a black background as a 3, as it lies closer to the linear approximation of the manifold corresponding to 3. This illustrates how suboptimal inference can affect behavioral performance even when the inputs are unaffected by internal noise.

Implications for the Reliability of Sensors and Neural Hardware

We have argued that when external and internal noise are present, suboptimal inference detrimentally affects behavioral performance much more than internal noise, at least for large networks. We also argued that suboptimal inference is a greater problem in more complex tasks. Together, these two observations could shed light on the reliability of sensory organs. While some neural circuits are exquisitely finely tuned (e.g., Kawasaki et al., 1988), others exhibit surprisingly large amounts of variability, due, for instance, to stochastic release of neurotransmitters or chaotic dynamics of neural circuits. Likewise, the quality of some of our sensory organs, like proprioceptors or the ocular lens, is not particularly impressive. The optics of the eye are of remarkably poor quality and introduce a noninvertible blurring transformation which severely degrades the quality of the image. As Helmholtz once said: “If an optician wanted to sell me an instrument that had all these defects, I should think myself quite justified in blaming his carelessness in the strongest terms, and giving him his instrument back” (Cahan, 1995). Bad optics are not a source of internal noise, but they introduce bias, or systematic errors. As is well known in estimation theory, reducing bias can be done only at the cost of increasing variability (the socalled bias-variance tradeoff) and, in that sense, bad optics can contribute to behavioral variability. The key questions are as follows: why are the optics so bad, and why are there significant sources of internal noise in neural circuits? One answer to this question is that the problem of inference in vision is so complex that the loss of information due to suboptimal inference overwhelms the loss due to bad optics.

Although we have discussed perceptual problems so far, similar issues come up in motor control. Proprioception is clearly central to our ability to move. Patients who have lost proprioception are unable to move with fluidity (Rothwell et al., 1982). Yet, our ability to locate our limbs with proprioception alone is quite poor (van Beers et al., 1998) compared to, say, our ability to locate our limbs with vision (van Beers et al., 1996). If proprioception is so critical for movement, why isn’t it more precise? According to the perspective presented here, it is because the variance associated with approximations of the limb dynamics is even larger. Theories of motor control have argued that we use internal models of the limb dynamics when planning and controlling motor behaviors (Jordan and Rumelhart, 1992). However, human limbs are simply too complex to be modeled perfectly. As a result, neural circuits must necessarily settle for suboptimal models. If the models are suboptimal and the approximations are severe, the motor variability will be much larger than it would be with a perfect model. There is, then, little incentive to make proprioception very reliable, as further decreases in the variance of proprioception would only marginally increase motor performance. This could explain why proprioception is rather unreliable despite being essential to our ability to move. This would also predict that a large fraction of motor variability emerges at the planning stage, where limb dynamics have to be approximated, rather than, say, in the muscles (Hamilton et al., 2004) or proprioceptive feedback (Faisal et al., 2008). This is, indeed, consistent with recent experimental results (Churchland et al., 2006).

Suboptimal Inference and Neural Variability

How does neural processing that influences behavioral variability also influence neural variability? In particular, we ask the following question: suppose a neural circuit has performed some probabilistic inference task. How would suboptimal inference affect the neural variability in the population that represents the variables of interest? The answer, as we will see, is not straightforward. Most importantly, one should not expect single-cell variability to reflect or limit behavioral variability.

Uncertainty on a single trial is related to the variability across trials, the latter being what we call behavioral variability. For instance, if you reach for an object in nearly complete darkness, you will be very uncertain about the location of the object. This will be reflected in a lack of accuracy on any one trial, and large variability across trials. In general, behavioral variability and uncertainty should be correlated, and are equal under certain conditions (Drugowitsch et al., 2012). Here we take them as equivalent.

Uncertainty is represented by the distribution of stimuli for a given neural response, the posterior distribution p(s|r). We define neural variability quite broadly as how neural responses vary, due both to the stimulus and to noise. Neural variability is then characterized by the distribution of neural responses given a fixed stimulus, p(r|s). These two are related via Bayes’ rule,

$$p(s|\mathbf{r})\propto p(\mathbf{r}|s)p(s).$$ (Equation 1)

Since suboptimal inference changes uncertainty (the left hand side), it must change the neural variability too (the right hand side).

Given Equation 1, it would be tempting to conclude that an increase in uncertainty (e.g., in the variance of the posterior distribution, p(s|r)) implies a decrease in the signal to noise ratio of single neurons, as measured by, say, the single-cell variance or the Fano factor. Unfortunately, such simple reasoning is invalid. The term p(r|s) that appears on the right hand side of Equation 1 is the conditional distribution of the whole population of neural activity. It thus captures correlations and higher order moments, not just single cell variability. As a result the relationship between uncertainty and neural variability is complex.

In the case of a population of neurons with Gaussian noise and a covariance matrix that is independent of the stimulus, the variance of the posterior distribution is given approximately by (Paradiso, 1988; Seung and Sompolinsky, 1993)

$${\sigma }^2\approx \frac{1}{\mathbf{f}\prime ·{\sum }^{-1}\mathbf{f}\prime }$$ (Equation 2)

where Σ is the covariance matrix of the neural responses, f is a vector of tuning curves of the neurons, and a prime denotes a derivative with respect to the stimulus, s. For population codes with overlapping tuning curves, the single cell variability (given by the diagonal elements of the covariance matrix) has very little effect on the posterior variance, σ²—changes in the single-cell variability introduce changes in σ² that are proportional to 1/n, where n is the number of neurons. Thus, if correlations are such that the posterior variance is independent of n (as it must be whenever there is external noise and n is large), single-cell variability has very little effect on behavioral variability. This is why the uncertainty of the optimal network asymptotically converges with increasing n to the minimal achievable behavioral variance (Figure 4). This convergence has an interesting consequence for large networks: if we eliminate the stochastic spike generation mechanism, thus removing all internal noise, behavioral variability would not decrease much at all, as it simply erases the tiny gap between the blue and red curves in Figure 4.

The insignificant impact of the stochastic spike generation mechanisms on network performance underscores the limitation of a very common assumption in systems neuroscience, namely that a decrease in single cell variance (or Fano factor) is associated with a decrease in behavioral variability. This assumption seems consistent with experimental data showing that Fano factors appear to decrease when attention is engaged (Mitchell et al., 2007). However, as we have just seen, the single cell variability has minimal impact on uncertainty, and therefore behavioral variability.

This has important implications for how suboptimal inference affects neural variability. A suboptimal generative model can substantially increase uncertainty. If uncertainty changes, then something about the neural responses must change to satisfy Equation 1. And if it is not the single-cell variance, it must be the tuning curves, the correlations, or higher moments. This claim can be made more precise if neural tuning curves and correlations depend only on the difference in preferred stimulus (Zohary et al., 1994). Under this scenario, improving the quality of inference performed by the network results in smaller correlations as long as the tuning curves remain the same (Bejjanki et al., 2011). Again, this is by no means a general rule. If the tuning curves change as a result of making an approximation less severe, it is in fact possible to decrease uncertainty while increasing correlations.

In summary, the relationship between suboptimal inference and neural variability is complex. With population codes, suboptimal inference increases uncertainty by reshaping the correlations or the tuning curves or both. Suboptimal inference may also have an impact on single-cell variability, but in large networks, changes in single-cell variability alone have only a minor impact on behavioral performance.

What Suboptimal Inference Explains

Recently, Osborne et al. (2005) argued that 92% of the behavioral variability in smooth pursuit is explained by the variability in sensory estimates of speed, direction, and timing, suggesting that very little noise is added in the motor circuits controlling smooth pursuit. If one were to build a model of smooth pursuit, a natural way to capture these results would be to inject a large amount of noise into the networks prior to the visual motion area MT and very little noise thereafter. Although this is possible, it is a strange explanation: why would neural circuits be noisy before MT but not after it? We propose instead that most of the uncertainty (in this case, the variability in the smooth pursuit) comes from suboptimal inference and that suboptimal inference is large on the sensory side and small on the motor side. This would explain the Osborne et al. (2005) finding without having to invoke different levels of noise in sensory and motor circuits. And it is, indeed, quite plausible. MT neurons are unlikely to be ideal observers of the moving dots stimulus used in their study; they are more likely tuned to motion in natural images. Therefore, the approximations involved in processing the dot motion will result in large stimulus uncertainty in MT. By contrast, it is quite possible that the smooth pursuit system is near optimal. Indeed, the eyeball has only 3 degrees of freedom and it is one of the simplest and most reliable effectors in the human body (it is so reliable that proprioceptive feedback plays almost no role in the online control of eye movements; Guthrie et al., 1983).

If this explanation is correct, these results could be modified by comparing performance for two stimuli that are equally informative about direction of motion, but for which one stimulus is closer to the optimal stimulus for MT receptive fields. We predict that the percentage of the variance in smooth pursuit attributable to errors in sensory estimates would decrease when using the near-optimal stimulus. By contrast, if the variance of the sensory estimates is dominated by internal noise, such a manipulation should have little effect.

A related prediction can be made about speed perception. Weiss et al. (2002) have shown that a wide variety of motion percepts can be accounted for by a Bayesian model with a single parameter, namely, the ratio of the width of the likelihood function to the standard deviation of the prior distribution. The width of the likelihood is meant to model any internal noise that may have corrupted the neural responses (Stocker and Simoncelli, 2006; Weiss et al., 2002). If this is indeed internal noise, this variance should not be affected by the type of stimulus (e.g., dot versus Gabor). By contrast, in the framework we propose, the width of the likelihood is due to a combination of noise and suboptimal inference. Therefore, this variance should depend on the stimulus type even when stimuli are equally informative, since different motion stimuli are unlikely to be processed equally well. More specifically, let us assume that the cortex analyzes motion through motion energy filters. Such filters are much more efficient for encoding moving Gabor patches than moving dots. Therefore, we predict that the width of the likelihood function, when fitted with the Bayesian model of Weiss et al. (2002), will be much larger for dots than Gabor patches, when matched for information content. This prediction can be readily generalized to other domains beside motion perception.

Similar ideas could be applied to decision making. Shadlen et al. (1996) argue that the only way to explain the behavior of monkeys in a binary decision making task given the activity of the neurons in area MT is to assume an internal source of variability, called “pooling noise” between MT and the motor areas. More recent results, however, suggest that, contrary to what was assumed in this earlier paper, animals do not integrate the activity the MT cells throughout the whole trial, but stop prematurely on most trials due to the presence of a decision bound (Mazurek et al., 2003). This stopping process integrates only part of the evidence and, therefore, generates more behavioral variability than a model that integrates the neural activity throughout the trial. Once this stopping process is added to the decision-making model, we predict that there will be no need to assume that there is internal pooling noise.

In the domain of perceptual learning and attention, it is common to test whether Fano factors—a measure of single-cell variability—decrease as a result of learning or engaging attention (Mitchell et al., 2007). Such a decrease is often interpreted as a possible neural correlate of the improvements seen at the behavioral level. Once again, suboptimal inference provides an alternative explanation: behavioral improvement can also result from better models of the statistics of the incoming spikes for the task at hand, without necessarily having to invoke a change in internal noise. As shown by Dosher and Lu (1998) and Bejjanki et al. (2011) experimental results are in fact more consistent with this perspective than a decrease in internal noise (see also Law and Gold, 2008). Similar arguments can be made for attention (L. Whiteley and M. Sahani, 2008, COSYNE, abstract).

The notion of suboptimal inference also applies to sensorimotor transformations. To reach for an object in the world, we need to know its position. At the level of the retina, position is specified in eye-centered coordinates but, to be usable to the arm, it must be recomputed in a frame of reference centered on the hand, a computation known as a coordinate transformation. Sober and Sabes (2005) have demonstrated that this coordinate transformation appears to increase positional uncertainty. If there is internal noise in the brain, this makes perfect sense: the circuits involved in coordinate transformations add noise to the signals, and increase their uncertainty. However, once again, there is no need to invoke noise. As long as some deterministic approximations are involved in the coordinate transformations, one expects this kind of computation to result in extra behavioral variability and added uncertainty about stimulus location.

Discussion

We have argued that in complex tasks, the main cause of behavioral variability may not be internal noise, but suboptimal inference caused by approximating the generative model of the sensory input. We have also proposed that this suboptimal inference is primarily reflected in the correlations among neurons and their tuning curves.

Outside of neuroscience, the conclusion that suboptimal inference is the main cause of behavioral variability is not particularly original. In fact, this was the conclusion reached a long time ago in fields like machine learning. It is clear, for example, that the main factor that limits the performance of image recognition software is not the amount of internal noise in the camera: most digital cameras have better optics than the human eye and more pixels than we have cones. Nonetheless humans remain extraordinarily better at image recognition than computers. Instead, the bottleneck lies in the quality of the algorithm performing the inference; that, in turn is determined primarily by the severity of the approximations required. In neuroscience, however, we rarely hear the perspective that suboptimal inference may be the major cause of variability. As we saw, many models tend to blame internal variability instead (Deneve et al., 2001; Fitzpatrick et al., 1997; Kasamatsu et al., 2001; Pouget and Thorpe, 1991; Reynolds and Heeger, 2009; Reynolds et al., 2000; Rolls and Deco, 2010; Schoups et al., 2001; Shadlen et al., 1996; Stocker and Simoncelli, 2006; Teich and Qian, 2003; Wang, 2002). In fact, in most of these models, internal variability is the only cause of behavioral variability.

A consequence of this conclusion is that internal sources of noise can be large without affecting behavioral performance—so long as their impact on behavioral variability is small compared to the variability introduced by suboptimal inference. Thus, we propose an explanation for the surprisingly poor quality of both the optics of the eye and of proprioceptive signals. Conversely, if an internal source of noise could have a large impact on behavioral variability, it should be small. In the context of decision making, one source that could significantly affect the behavior of the animal is a noisy integrator. Interestingly, recent experiments appear to suggest that, indeed, this integrator has very small internal noise (B.W. Brunton and C.D. Brody, 2011, COSYNE, abstract; Stanford et al., 2010).

Note that we are not claiming that the brain is noiseless. There is internal variability, but we argue that its impact on behavioral variability is small compared to the impact of suboptimal inference. Also, we would agree that there are situations in which stochastic behavior might be advantageous, such as during motor learning (Olveczky et al., 2005; Sussillo and Abbott, 2009), when exploring a new environment, or when unpredictable behavior is used to confuse a predator. In these situations, the brain might produce internal variability that has a significant impact on behavior. Stochasticity in the brain could also be used to perform probabilistic inference via sampling, a well-known technique in machine learning (Fiser et al., 2010; Moreno-Bote et al., 2011; Sundareswara and Schrater, 2008). We emphasize, however, that sampling in the brain may or may not lead to significant extra variability at the behavioral level. On the one hand, when behavior is based upon the average of a large numbers samples, added variability due to sampling is small. On the other hand, when probability distributions are relatively flat (or multimodal), a small number of samples could lead to a large increase in variability (Bialek and DeWeese, 1995; Moreno-Bote et al., 2011). Finally, when the numbers of neurons is small, as is the case for instance in insects, it is quite possible that internal variability is no longer negligible and has an impact comparable to suboptimal inference.

In summary, we propose that because of the vast redundancy of neural circuits, noise internal to the brain is a minor contributor to behavioral variability. Rather, in light of the computational shortcuts the brain must exploit, we suggest that suboptimal inference accounts for most of our behavioral variability, and thus uncertainty, on complex tasks.