Abstract
Although the human cerebellum has been increasingly identified as an important hub that shows potential for helping in the diagnosis of a large spectrum of disorders, such as alcoholism, autism, and fetal alcohol spectrum disorder, the high costs associated with manual segmentation, and low availability of reliable automated cerebellar segmentation tools, has resulted in a limited focus on cerebellar measurement in human neuroimaging studies.
We present here the CATK (Cerebellar Analysis Toolkit), which is based on the Bayesian framework implemented in FMRIB’s FIRST. This approach involves training Active Appearance Models (AAM) using hand-delineated examples. CATK can currently delineate the cerebellar hemispheres and three vermal groups (lobules I–V, VI–VII, and VIII–X). Linear registration with the low-resolution MNI152 template is used to provide initial alignment, and Point Distribution Models (PDM) are parameterized using stellar sampling. The Bayesian approach models the relationship between shape and texture through computation of conditionals in the training set. Our method varies from the FIRST framework in that initial fitting is driven by 1D intensity profile matching, and the conditional likelihood function is subsequently used to refine fitting.
The method was developed using T1-weighted images from 63 subjects that were imaged and manually labeled: 43 subjects were scanned once and were used for training models, and 20 subjects were imaged twice (with manual labeling applied to both runs) and used to assess reliability and validity. Intraclass correlation analysis shows that CATK is highly reliable (average test-retest ICCs of 0.96), and offers excellent agreement with the gold standard (average validity ICC of 0.87 against manual labels). Comparisons against an alternative atlas-based approach, SUIT (Spatially Unbiased Infratentorial Template), that registers images with a high-resolution template of the cerebellum, show that our AAM approach offers superior reliability and validity. Extensions of CATK to cerebellar hemisphere parcels is envisioned.
Keywords: Cerebellum, MRI, Segmentation, Active Appearance Models, Automated Analysis
1. Introduction
Segmentation of magnetic resonance images (MRI) of the brain into its anatomic components is one of the most difficult tasks in image processing. Many techniques exist to help divide a brain MRI into its subregions. Early techniques based on signal intensity features such as histogram thresholding, edge-based segmentation, and region-based segmentation generally did not perform well on images with complex anatomy, such as the brain [1]. State of the art approaches for segmenting medical images include: machine learning [2, 3], probabilistic graphical models [4, 5], atlas-based methods [6, 7, 8], and deformable models [9, 10, 11]. Segmentation of the cerebellum into its components is especially challenging because cerebellar foliations are on the order of 0.5mm, smaller than the standard 1mm3 resolution T1-weighted structural brain images. Additionally, the cerebellum’s close proximity to the base of the skull causes image contrast nonuniformity resulting in inferior gray matter/white matter (GM/WM) discrimination [12, 13]. Methods that seek to delineate more than the outer cerebellar boundary must use the prior knowledge of shape, image intensities and inter-shape relationships that human experts use to infer object boundaries in medical images.
Initial attempts at semi-automated cerebellar segmentation used an atlas-based approach [14]. Atlas-based segmentation relies on appropriate atlas formation and accurate registration (alignment) of the atlas to new images prior to segmentation. The first brain atlases were based on a single individual, such as the well-known Talairach atlas [15], and did not adequately reflect anatomical variability. Other early atlases derived from averaging multiple brain images after affine normalization (i.e., correcting for translation, rotation, scale, and shear), resulted in blurry templates [16, 17]. The utility of such atlases for defining anatomic structures and propagating them to individual images is thus limited by the spatial uncertainty present in blurry atlases that reduces label propagation accuracy. Modern registration methods use nonlinear transformations, that allow nonrigid deformation, and better account for inter-subject shape differences that are beyond the capabilities of linear mappings. Registration accuracy for nonlinear registration methods is directly related to the degrees of freedom of the underlying transformation [18]. The curse of dimensionality usually diminishes the advantage of high-order parameterizations due to increased computational requirements and difficulties in ensuring convergence. However, the sophisticated techniques employed by modern nonlinear registration algorithms have led to successful registration even with millions of parameters. A comparison of several popular nonlinear registration methods applied to the brain [19] shows that the top performers achieve median overlap of between 65% and 70% for the 40 images that comprise the LONI Probabilistic Brain Atlas (LPBA40), and 40% to 50% for other similar data sets. (A total of 14 algorithms applied exhaustively to 80 images were evaluated, resulting in over 45,000 registrations.) Most methods performed robustly, although a number of outliers were observed in the LPBA40 images. Supplemental material [20] indicated that overlap measures for segmentations of GM/WM parcels for the left and right cerebellar hemispheres were between 55% and 76%. These results indicate that off-the-shelf nonlinear registration methods are not sufficiently reliable for detailed cerebellar segmentation.
There are a number of automated tools that provide limited cerebellar segmentation. FreeSurfer [21] delineates the cerebellar hemispheres, but they are inclusive of the vermis. To our knowledge the only automated tool that provides comprehensive labeling of the cerebellum is the SUIT (Spatially Unbiased Infratentorial Template) [22, 23], which offers plugin functionality for SPM (Statistical Parametric Mapping) [24], and uses atlas-based registration. More recently, a few novel methods have also emerged, but are not readily available for evaluation: In [25], artificial neural network (ANN) and support vector machine (SVM) approaches were shown to outperform template and probabilistic approaches when applied to the cerebellum. Similarly, a combined atlas and voxel-based appearance model (derived from a nearest-neighbor classifier) has been proposed in [26] for delineating the cerebellar hemispheres. Finally, [27] shows encouraging results for a 28 label parcellation of the cerebellum using a multi-object levelset formulation that allows boundary-based speed functions to be derived.
We have developed a Cerebellar Analysis Tool Kit (CATK) that was funded by the National Institute for Alcohol Abuse and Alcoholism (NIAAA) and was motivated by studies showing these cerebellar regions are impacted by chronic alcohol abuse [28, 29, 30]. Our approach uses the Bayesian Active Appearance Modeling (AAM) framework that forms the basis of the FSL subcortical brain segmentation tool FIRST [31], which follows a deformable surfaces paradigm, but includes a mechanism for incorporating contextual knowledge. CATK differs from the FIRST framework [31] by: 1) implementing a multi-template linear registration pipeline capable of robustly normalizing the cerebellum; 2) introducing a simplified mesh representation based on stellar sampling that assures approximate point correspondence; and 3) adding an intermediary surface fitting stage based on intensity profile matching. We obtained expert hand delineations on T1-weighted images for 63 subjects from Neuromorphometrics Inc. that are considered the gold standard for brain segmentation analyses. From this data, 43 subjects were used to train AAMs of the cerebellar hemispheres and major vermal lobules, and 20 subjects who were imaged and hand-labeled in two separate imaging sessions were used solely for reliability and validity assessment.
To establish reliability and validity, we applied CATK, FreeSurfer, and SUIT to the 20 validation subjects with repeat scans (i.e., 40 test images). We used the Intraclass Correlation Coefficient [32] (ICC) and Dice Overlap [33] (DO) to assess segmentation performance. We note that the SRI24 atlas [34], which uses template-free nonlinear registration, also provides cerebellar labels. However, our current atlas-based comparisons are based on SUIT because of its specific focus on the cerebellum, and the fact that preliminary analyses showed comparable cerebellum segmentation accuracy for SRI24 and SUIT. We acknowledge that we were unable to take full advantage of SRI24’s ability to use multi-channel data to improve registration because the Neuromorphometrics imaging data we examined consists only of T1-weighted images.
2. Material and Methods
2.1. Manual Segmentation and Data Preparation
A series of 1mm3 T1-weighted images from 63 healthy subjects that were manually segmented by Neuromorphometrics Inc (NMI) was used to develop CATK. AAM models were trained using 43 subjects that were scanned once, while 20 subjects that had two scan sessions (and were hand-labeled on both occasions) were held out for the assessment of reliability and validity. When delineating neuroanatomical regions, Neuromorphometrics uses protocols and custom software that were originally developed at the Center for Morphometric Analysis at Massachusetts General Hospital (Harvard Medical School). All labels are verified by a neuroanatomy expert. The manual labels parcellate the cerebellar volume into: left and right hemispheres, left and right white matter, and three vermal parcels defined as lobes I–V (superior anterior), VI–VII (superior posterior), and VIII–X (inferior posterior). These subdivisions are shown in Figure 1a.
Figure 1.
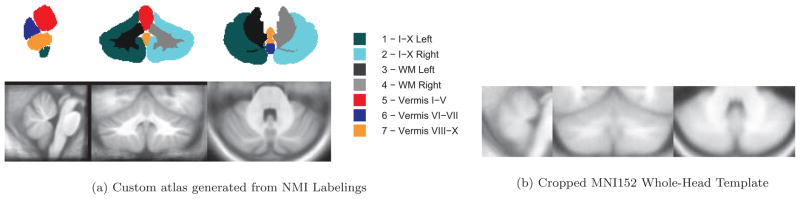
Top-Left: Cerebellar parcellation under manual labeling protocol by Neuromorphometrics Inc. (NMI). Images show slices from our custom atlas that was generated by SUIT’s standard registration functions on our training data. Bottom-Left: Average NMI T1-weighted template. Bottom-Right: Cropped MNI152 whole-head T1-weighted template for comparison.
Subjects used for training
The average age was 44 (5–96 years) and included 13 children (5–17 years), 19 adults (18–70 years), and 11 elderly (71–96 years). There were 21 males and 22 females, and only one subject was left-handed.
Subjects used for validation
The availability of repeat scans and manual labels for 20 subjects (that were not used for training) enabled us to assess the test-retest reliability of both the manual and automated methods. The average age of the 20 subjects with repeat scans was 23 (19–34 years), with 8 men and 12 women, all of whom were right-handed. Test-retest reliability was assessed using the single-rater intraclass correlation coefficient (ICC) [32], which ranges between 0 and 1, corresponding to the rating reflecting 0 to 100% of the true underlying measure. Note that the narrow age gap in the validation set corresponds to lower inter-subject variance making it more difficult to achieve high ICCs. Note also that the labels from the repeat scans from separate imaging sessions reflect variability in the labeling process and variability due to differences in voxel boundaries between the scans (i.e., partial voluming).
2.2. Atlas-based segmentation
The SRI24 atlas [34] developed at the Stanford Research Institute, and SUIT [23], developed by the UCL Institute of Cognitive Neuroscience, are templates to which MR images can be aligned using linear or nonlinear registration in order to parcellate the cerebellum. SRI24 was created from 24 healthy subjects to enable multi-channel (i.e., T1, T2, PD, and DTI) atlas-to-subject image registration for atlas-based segmentation (based on cortical parcellation maps) or spatial normalization. It uses a novel template-free technique that jointly adjusts individual subjects, which reduces bias, as opposed to using a single reference. Registration of new images can be accomplished using either template-based registration with the atlas or using the template-free method via the open-source CMTK package [35]. Although the SRI24 parcellation maps contain cerebellar labels, the atlas creation was not focused on the cerebellum. In contrast, SUIT was specifically designed to improve cerebellar co-registration across subjects during atlas creation. SUIT’s authors recognized that aligning subjects using a multi-subject whole-head template, such as MNI152, tends to result in poor cerebellar alignment, which is evident by the blurry template seen in Figure 1b. This problem is further compounded by using Schmahmann’s atlas labels that are derived from a single subject [36]. To build a comprehensive probabilistic atlas, shown in Figure 2, SUIT follows Schmahmann’s protocol of labeling (starting at the midsagittal slice and moving outwards laterally) but incorporates the normalized brains of 20 diverse subjects (ages between 19 and 27). The resulting 1mm3 T1-weighted template (also shown in Figure 2) is formed by averaging the normalized subjects. We compared CATK to SUIT because SUIT had been optimized for the cerebellum. Cerebellar segmentation of new images using SUIT (version 2.7) is achieved with SPM (version 12)[24, 37]. Normalization between the template and new image is achieved using affine registration (with the whole-head template) followed by tissue classification to roughly isolate the cerebellum using probabilistic priors. Finally, a nonrigid deformation using cosine basis functions is estimated to account for individual subject variation. While the entire procedure can be applied automatically through SPM, the isolation algorithm is not infallible, and documentation recommends that the user review (and correct) the isolation mask prior to nonlinear registration. For comparison with fully automated CATK, we only used SUIT in the automated fashion. SUIT also offers an alternative deformation method based on the DARTEL engine [38] that uses gray and white matter segmentation maps produced during cerebellar isolation to generate a flowfield using Large Deformation Diffeomorphic Metric Mapping (LDDMM) [39]. Parameterization with DARTEL is more flexible, which allows more detailed deformations and theoretically more precise registration. In our experiments, both SPM registration engines were used, but for brevity only results from the cosine basis deformation method, which achieved better results on our data, are shown. This is discussed further in Section 4.
Figure 2.
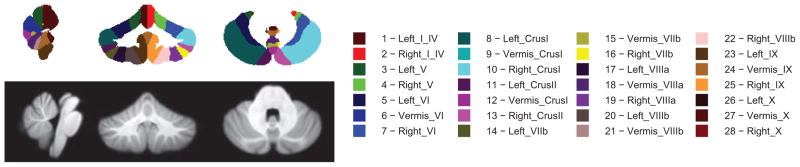
SUIT atlas (top) and template (bottom) showing central slices from each axis. The atlas does not explicitly identify white matter (apart from the dentate nuclei), but this can be deduced from the T1 template.
It is not possible to directly compare measurements between SUIT and the manual labels since the parcellations differ. SUIT produces 28 parcels compared with 7 parcels for the manual labels. The major difference is in the vermis. Whereas the manual labels delineate the superior anterior portion of the vermis (lobules I–V), SUIT does not distinguish between hemispheres and vermis for this region. To address this difference, we constructed additional probabilistic atlases (the non-DARTEL atlas is shown in Figure 1a) using the 43 training images from our manually labeled data. These images were registered with SUIT using the standard and DARTEL methods, failed registrations were manually removed from the set, and the corresponding label images were combined in SUIT-space to form an atlas and template for each method (i.e., one for standard SUIT and one for SUIT with DARTEL).
2.3. CATK Algorithm
At its core, CATK comprises a 3D Active Appearance Model (AAM) [40] that uses parameterized examples of surface shape and intensity to drive an optimization framework that fits the model to new images. This methodology has led to advances in adaptive face recognition systems [41], and has shown great promise in difficult medical imaging segmentation problems [42]. Unlike intensity-only boundary segmentation or energy minimizing curves (active contours [43, 44]), AAMs encapsulate variation from real examples and restrict the search space to plausible combinations. Since the variability of cerebellar appearance tends to be closely distributed, the use of contextual knowledge results in reliable estimation and sensible transitions between parameters.
The key distinction between the AAM and its cousin the ASM (Active Shape Model) [45] is that it generates statistical models for both shape and texture (intensity pattern), and allows fitting to take advantage of their interrelationship. Where an ASM adjusts shape parameters towards optimizing image heuristics (e.g. maximum boundary gradient), an AAM minimizes the error between a hypothesized image driven by the shape parameters and the original image. There are numerous ways to model the prior relationship between shape and texture, hence a number of AAM variations exist, e.g., [40, 31, 10, 42].
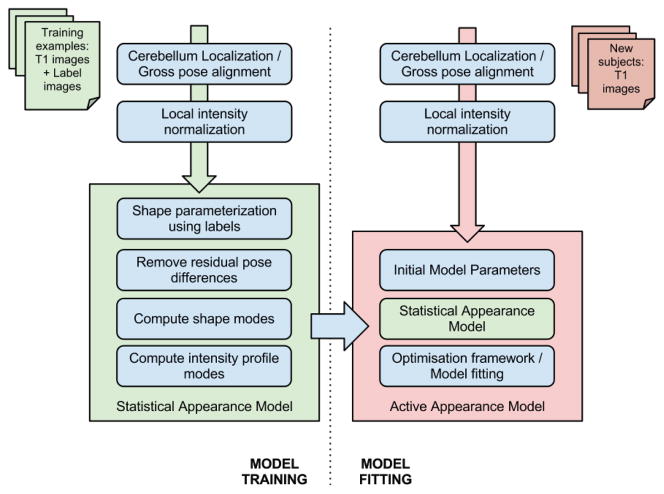
CATK uses an adptation of the Bayesian AAM framework devised by Patenaude [31] upon which his development of FSL’s subcortical brain segmentation tool FIRST [31, 46] is based. The method’s primary distinction as a Bayesian approach is that it uses conditional distributions (as opposed to arbitrary weightings) to model the relationship between shape and texture. Our implementation extends the original framework, in order to segment the cerebellum, by using an alternative shape parameterization based on stellar meshes (as opposed to polygonization with Marching Cubes [47]), and introduces a multi-stage fitting process that combines both ASM-style profile-matching and AAM posterior optimization; as opposed to Patenaude’s implementation which relies solely on the latter. In addition, a robust localization algorithm has been developed that is used for pose correction and cerebellar isolation. Figure 3 provides a graphical overview of CATK’s functionality.
Figure 3.
Functional Overview of CATK.
2.3.1. Localization, Normalization, and Parameterization
Statistical shape within the AAM is specified by a Point Distribution Model (PDM) [40] that describes each shape as a linear combination of characteristic modes of variation. This requires that each shape is modeled by a set of corresponding landmarks. To achieve this, the cerebellum must be localized and its pose and intensities normalized. First, any image in homogeneity is corrected (using N4ITK [48]) and the intensity distribution rescaled by removing the upper and lower tails with a threshold. A skull-stripped [49] version of the image is then linearly registered using AIR [50, 51, 52] with the MNI152 whole-head template in order to account for gross pose differences, namely position, scale, and orientation. (A 9 parameter model is used.) Since cerebellar pose relative to the rest of the brain varies across subjects the initial registration leaves significant residual differences, which contribute higher variability between point correspondences. If left unchecked, this causes the AAM to account for variability that does not correspond to inter-subject variation. To address this, CATK uses a bootstrapping process whereby a rough cerebellar ASM, constructed from the initial alignment, is fitted and used to mask the cerebellum. A second linear alignment using the higher resolution SUIT template is then used to refine the cerebellar region-of-interest.
Following localization and image normalization, which is common to both training and fitting (shown by the first two steps in Figure 3), the training examples are parameterized by creating triangular surface meshes from the hand-labeled voxel volumes using stellar projection of a subdivided icosahedron. (This subdivided surface approaches a sphere as the number of subdivision levels is increased.) Since the base mesh has known topology, this provides a convenient and efficient means of obtaining a consistent number of correspondences across the training data. Following sampling, residual translations are removed by centering each mesh. The resulting surfaces follow the boundary interface defined by a selected label group that corresponds to a particular parcel. For instance, parameterization of the hemispheres includes the exterior GM/CSF and interior GM+WM hemisphere/vermis interfaces. Therefore, attention to concavities, such as gaps between inter-lobule fissures that are more predominant when atrophy occurs, depends on the quality of manual segmentations used for training. (I.e., high model flexibility requires adequate examples of extreme cases.)
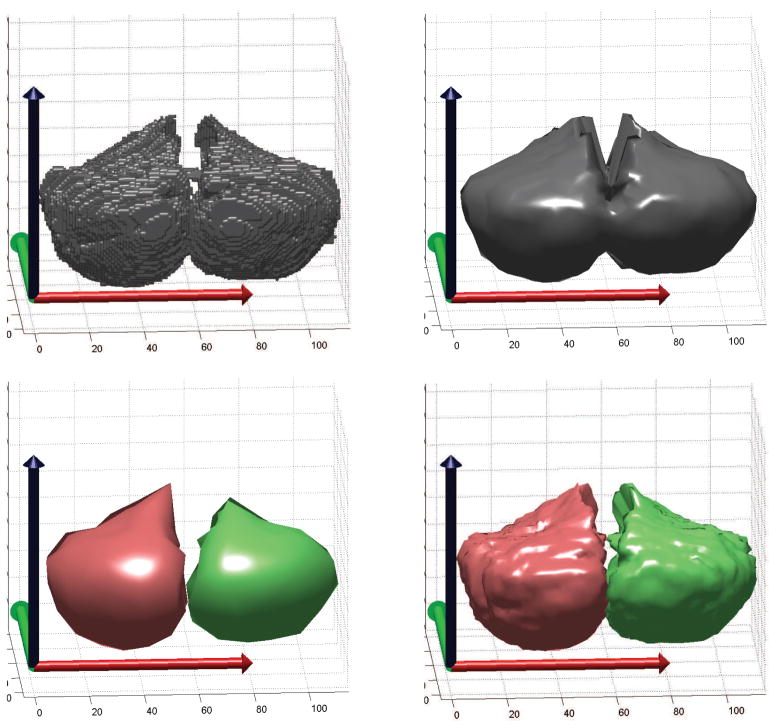
Unfortunately, enforcing stellar topology to arbitrary shapes is not possible, however, the stellar approximations closely match the original surfaces of the cerebellar substructures we have labeled. An example of degradation due to this assumption can be seen when modeling the entire cerebellar cortex with a single projection center. In this case, the white matter peduncles protrude in an overlapping manner thereby causing additional volume to be enclosed within the brainstem. To resolve this difficulty, CATK uses multiple projection centers determined from the manual labels. An example for the cerebellar hemispheres is shown in Figure 4, where the top-left image shows the labeled voxels that we wish to parameterize. Sampling with a single projection center produces the model shown in the top-right, while using a projection center for each hemisphere results in a closer approximation to the desired shape as seen in the bottom-right image. This approach allows efficient representation of multiple parcels.
Figure 4.
Stellar parameterization of the cerebellar hemispheres. Top: Isosurface of original labels (left), and stellar mesh with a single projection center and 4 levels of subdivision (right). Note that the isosurface cannot be used directly since the number of vertices (parameters) is dependent on the surface area and therefore variable. Bottom: Stellar meshes using two projection centers with 2 levels of subdivision (left), and 5 levels of subdivision (right). Stellar sampling produces a manifold with a fixed number of vertices per subject that is required for statistical modeling.
2.3.2. Bayesian Framework
The model is trained according to the method presented in [31], which is based on the assumption of a multivariate Student Distribution that offers better adaptation for smaller training sets. With the exception of our implementation-specific adjustments discussed in the last paragraph, this section provides a conceptual overview of the Bayesian AAM framework that we have adopted; the interested reader is referred to the original work for further details [31, 46].
Meshes are generated for each parcel group and represented by a concatenated parameter vector hs that is added to a data matrix Xs whose columns span the number of training examples m (Equation 1). The mean shape, represented by Equation 2, is computed by averaging the columns of Xs and is removed from each column (Equation 3) to produce the demeaned data matrix Zs. Singular value decomposition of Zs (Equation 4) produces the two main ingredients of the PDM: the eigenvectors Us that describe the modes of variation, and the singular values Ds that describes their importance.
| (1) |
| (2) |
| (3) |
| (4) |
(Vs is a weighting matrix that reconstructs the original training data.)
Since there are typically far fewer training examples (columns) than parameter dimensions (rows) in Zs, this potentially leads to very large covariance matrices. Fortunately, the resulting matrices are also of low rank which allows a number of computational simplifications; for instance, only the first m eigenvectors need be calculated. By choosing parameters bs, that represent weights for each mode (eigenvector), any shape within the multivariate distribution can be generated:
| (5) |
where γ is a scalar relating to parameters of the multivariate Student Distribution. We can also invert this process and obtain model parameters bs, or the closest shape, for any set of mesh vertices.
Texture (intensity distribution) is modeled in the same manner where the example vectors hI are derived from 1D intensity profiles sampled normal to the surface at each vertex. (Experience has shown that the order of 15 samples per profile works well for cerebellar surfaces.) In order to ensure consistent spatial sampling without additional resampling noise, sample coordinates are always generated in the normalized reference frame and projected into the original (subject) image for interpolation. As for shape, the demeaned intensity PDM is approximated through eigen-decomposition:
| (6) |
(Whereas Zs has 3 dimensions for each vertex, i.e. 3n rows, ZI has 15 dimensions for each vertex, i.e. 15n rows.) Modeling each entity (shape and texture) in this way amounts to partitioning a generalized data matrix Z = {ZsT, ZIT}T, which allows the distribution of intensity conditioned on shape to be constructed by partitioning the joint precision matrix λ:
| (7) |
| (8) |
| (9) |
assuming a Student Distribution St with α degrees of freedom where alpha is determined according to . Equation 9 forms the basis of the Bayesian Appearance Model and intrinsically handles the weighting between shape and intensity.
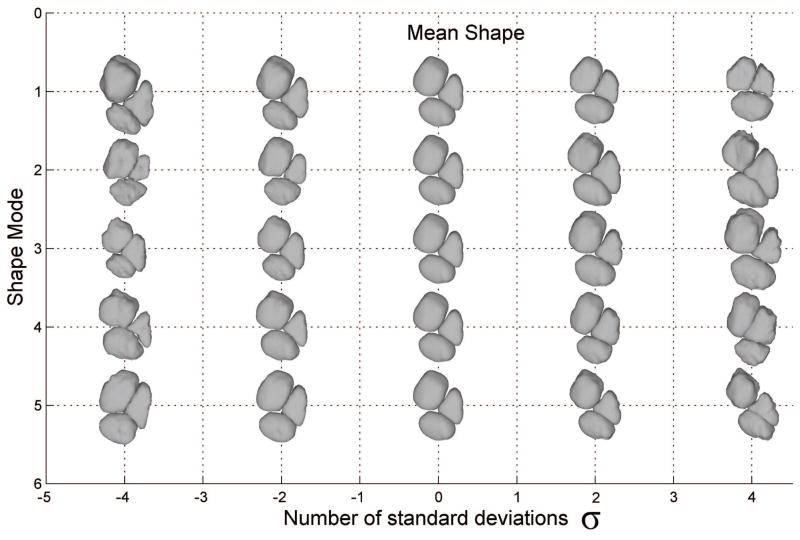
Since the underlying data can be arbitrary, it is therefore possible to apply the same approach to other data partitions. For instance, shape–shape relations can be modeled that predict the shape distribution of one parcel given the location (or intensity distribution) of several others. While the same effect can be achieved by performing eigen-decomposition on the entire unpartitioned data matrix, this increases the dimensionality of each input vector significantly and can result in poor generalization given the finite number of training examples. However, we have found that modeling inter-structure relationships through conditional modeling can also suffer from lower generalization due to compression of the conditional covariance which is also simplified though eigen analysis. When initializing models of subparcels (like the vermis), we found conditional shape–shape relations to be very effective, but parcel groups like the three vermal lobes tended to perform better when modeled as a whole since most of the covariance can be explained through the joint PDM. Therefore, CATK uses conditional partitions to initialize sub-parcellations using the full cerebellum model as a reference, while hemispheres and vermal lobes are each modeled as a group (i.e. 2 meshes for the hemispheres, and 3 meshes for the vermis). Figure 5 shows parcel shapes sampled from the model of the vermis which is jointly modeled by 3 projection centers. Each row illustrates how the average shape (center column) varies along the first 5 modes of variation. By choosing a linear combination of these modes one can define a family of shapes that resemble the original examples. Although the total dimensionality of the shape vector is over 7000, the PDM adequately explains 90% of the variance with only 40 modes.
Figure 5.
Shape variation of CATK vermis model. The central column (zero deviation) represents the average shape while each row shows how parcel shape is affected by varying the parameters for the 5 most influential modes.
2.3.3. Model Fitting
Fitting is achieved by first using the two-stage normalization procedure discussed and initializing the search using the result of the rough ASM solution. Drawing upon insights gained by experimenting with different approaches, CATK applies a multi-stage fitting process that incorporates both ASM and AAM techniques. One of the drawbacks of the Bayesian AAM is that it is slow to converge and is easily trapped in local minima. While the conditional distribution between shape and intensity (Equation 9) can be fine-tuned through priors (intended to condition the covariance matrix), smoother surfaces that over segment the underlying volume tend to be favored irrespective of these parameters. In addition, the cerebellar structural boundaries are not all well-defined (in terms of tissue contrast), and the close proximity to nearby structures with similar intensity distributions tends to result in a small capture region. (Models that are initialized close to the “capture region” generally have a high convergence rate, hence large capture regions are desirable.) Another possibility is that the low number of training examples is insufficient to completely characterize the texture variations, because the fine foliations within the cerebellum cause intensity to fluctuate near the boundary thereby increasing variance across subjects.
Contrastingly, a naive ASM that simply selects the maximum gradient along each intensity profile offers a large capture area since the model parameters can jump farther between iterations. This comes at the cost of discarding the context of the intensity distribution and its relation to shape, which also presents problems. Therefore, we use an ASM/AAM hybrid approach that uses 1D template matching to propagate the shape parameters. This is very fast to compute, and is more robust in low contrast images.
Intensity profiles comprise 15 samples centered about each vertex and extend from the interior to the exterior of a parcel along the local surface normal. Gradient-based template matching is used to match each profile to the corresponding mean intensity profile drawn from the conditional distribution during fitting. First, μI|s is calculated from the candidate bs, and gradients are computed for both the conditional profile gI|s and the profile sampled from the current mesh vertex gi. Convolution using the Fast Fourier Transform (
 ):
):
| (10) |
provides the linear shift t that best aligns each sampled profile with the model. (We perform 1D convolution in parallel for each vertex by reshaping each 15n length profile g to 15 × n arrays and operating row-wise. Output vector t has length n.) Vertices are then adjusted to these optimum points along each surface normal, and the closest shape is selected (using the inverse of Equation 5). This process is applied iteratively until convergence is detected.
After the ASM terminates, stage two refines the solution using the Bayesian AAM: A conjugate gradient descent optimization adjusts shape parameters bs to maximize the posterior function [31]:
| (11) |
which is equivalent to minimizing the negative log-likelihood. This drives the process to select the most probable shape given the observed intensities.
2.4. Evaluation Measures
2.4.1. Reliability and Validity
We assessed both reliability and validity using the intraclass correlation coefficient (ICC) on measurements from the 20 validation subjects that were scanned and hand labeled twice. The ICC for a measure indexes the proportion of variance of that measure that reflects the true variable being measured as compared to measurement error. When applied to repeated scans, the error (1 - ICC) includes both variability in the measurement and variability in the scans due to the different voxel boundaries (and thus differences in partial voluming) that occurs whenever the subject is positioned within the MR Imager. The ICC is always measured relative to the variability of the underlying phenomena being measured. For example, the test-retest images used to assess reliability here only contains variability in cerebellar measures present in normal individuals 19–34 years of age. The reliability measured here would be higher if it was measured across data with larger intersubject variability (e.g., including alcoholic and non-alcoholic subjects, and perhaps including individuals from 19–60 years of age). Reliability for CATK was assessed by computing the ICC for each cerebellar measure across the two repeat scans.
Validity (i.e., agreement with the gold standard Neuromorphometrics manual measures) was assessed by computing the ICC for four-tuples of measures (the two repeat measures for the measure of interest and the two corresponding Neuromorphometrics measures). The higher the ICC, the greater the agreement of the measure of interest with the gold standard. Additionally, because the vermis lacks clear-cut anatomical demarcations from the cerebellar hemispheres [53, 54], we also report reliability and validity for midsagittal areas for the vermal lobules, which have been used as a surrogate measure of vermis volume in numerous studies [55, 56, 29, 30].
2.4.2. Dice Similarity
Dice overlap (DO) [33] is a well-used metric that compares the spatial overlap between two discrete segmentations by measuring the proportion of voxels that have the same label as a percentage of the total masked volume:
| (12) |
where the contributing elements are the True Positive (TP), False Positive (FP), and False Negative (FN) voxels respectively. DO results are useful as a means of verifying that some volumetric correspondence exists between the ground truth and estimated labels. However, we point out that: (1) DO is sensitive to quantization error due to the discretization process (fitted meshes must be converted back to voxels), and (2) it does not account for variability in the ground truth labeling. The latter is an important factor when trying to determine whether a method can be considered “good enough”, and is the case here since our objective is to achieve validity with respect to manual labeling.
Owing to the sensitivity of vermal segmentations to partial voluming of different tissues at the vermal lateral boundaries, we compute midsagittal vermal DO by masking the volume comprising the midsagittal slice and 4 slices on either side. Using 3D voxels (volumetric) instead of 2D pixels (area-based) to define midsagittal vermal DO also avoids the need to reslice the manual labels to a normalized orientation prior to measurement that would contribute additional quantization error.
3. Results
Reliability and validity results, based on the 20 validation subjects with repeat scans (refer to Section 2.1), are presented in Table 1.
Table 1.
Reliability and validity ICC scores for the 20 validation subjects with repeat scans for each cerebellar measure. Reliability indexes test-retest repeatability of the measure, while validity indexes the agreement of the measure with the Neuromorphometrics manually measured gold standard.
| Cerebellar Measure | Intraclass Correlation | ||||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Test-Retest Reliability
|
Validity
|
||||||
| Manual | CATK | SUIT | FreeSurfer | CATK | SUIT | FreeSurfer | |
|
|
|
||||||
| Volume Measurements: | |||||||
| Total Cerebellum | 0.987 | 0.998 | 0.679 | 0.989 | 0.977 | 0.773 | 0.980 |
| Left Hemisphere | 0.987 | 0.997 | 0.522 | 0.983 | 0.964 | 0.705 | 0.975 |
| Right Hemisphere | 0.983 | 0.997 | 0.622 | 0.983 | 0.960 | 0.699 | 0.978 |
| Vermis I–V | 0.795 | 0.951 | 0.192 | 0.717 | 0.246 | ||
| Vermis VI–VII | 0.878 | 0.876 | 0.658 | 0.604 | 0.573 | ||
| Vermis VIII–X | 0.940 | 0.971 | 0.408 | 0.851 | 0.524 | ||
| Midsagittal Area Measurements: | |||||||
| Vermis I–V | 0.954 | 0.983 | 0.078 | 0.943 | 0.258 | ||
| Vermis VI–VII | 0.924 | 0.967 | 0.487 | 0.909 | 0.523 | ||
| Vermis VIII–X | 0.964 | 0.967 | 0.366 | 0.920 | 0.401 | ||
3.1. Reliability
Manual measurements
On average, hemisphere manual labels have a reliability ICC of 0.98, while vermal lobes have an average reliability ICC of 0.87, all consistent with the manual labels being trustworthy indications of the cerebellum. Much research on the cerebellar vermis uses midsagittal area rather than volume as measures of vermal size because of the difficulty in delineating vermal lateral extent. We also derived measures of midsagittal vermal area in all our analyses. Midsagittal vermal lobe area had ICCs averaging 0.95, consistent with the literature, showing improvements in the precision and reliability of midsagittal area vs. volume measurements for the cerebellar vermis.
Automated measurements
For the total cerebellum and the hemispheres, CATK and FreeSurfer perform excellently, each with reliabilities over 0.98. SUIT, on the other hand, exhibits reliabilities of 0.52 to 0.67. For vermal volumes and areas, CATK is only compared to SUIT since FreeSurfer does not measure the vermis. For vermal volumes, CATK test-retest reliabilities (averaging 0.93) were comparable to or higher than test-retest reliabilities for manual labeling (averaging 0.87). In contrast, SUIT test-retest reliabilities were poor to moderate for vermal volumes (ranging from 0.19 to 0.66, averaging 0.42). For midsagittal vermal areas, test-retest reliabilities increased for both CATK (averaging 0.97) and manual labeling (averaging 0.95). SUIT had worse test-retest reliabilities for midsagittal vermal areas (ranging from 0.078 to 0.487 and averaging 0.31) compared to vermal volume measures.
3.2. Validity (agreement of automated methods with expert manual labels)
As noted above, validity (i.e., agreement with the gold standard Neuromorphometrics manual measures) was assessed by computing the ICC for four-tuples of measures: the two repeat measures for the automated procedure under investigation and the two corresponding Neuromorphometrics measures. The higher the ICC, the greater the agreement of the automated measures with the gold standard. For the total cerebellum and right and left cerebellar hemisphere volumes, for which we have FreeSurfer data, both CATK and FreeSurfer have over 0.96 agreement (1.0 is perfect) with the Neuromorphometrics manual labels. In comparison, SUIT agreement with the manual labels is only 0.70–0.77. For the vermis measures, we only have CATK and SUIT to compare. For vermis volumes, CATK agreement with the manual labels varied between 0.60 and 0.85. SUIT performed much worse, with agreement varying between 0.25 and 0.57. For the midsagittal area measurements, CATK had excellent agreement with the manual labels (between 0.91 and 0.94), while SUIT performance was no better than for the vermal volume measures (between 0.26 and 0.52). Based on these results, we use midsagittal vermal area measurements in our clinical applications of CATK [57, 58].
3.3. Dice Comparison
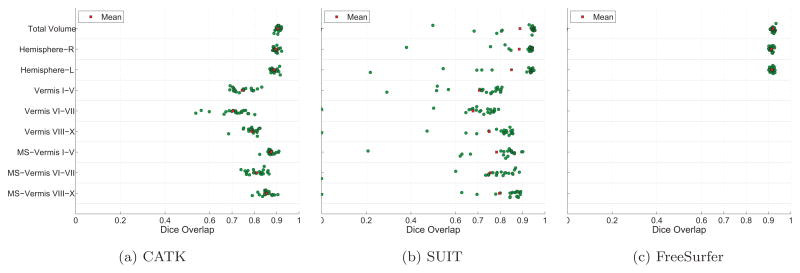
Figure 6 shows the DO results obtained for CATK, SUIT, and FreeSurfer. MS-Vermis refers to masked midsection volumes of the vermis centered about the midsaggital slice as discussed in Section 2.4.2, and is different from midsagittal vermal area ICCs that were computed from the single midsagittal slice.
Figure 6.
Dice Overlap scores for manual labels vs. CATK, SUIT, and FreeSurfer. “MS-Vermis” refers to midsection volumes of the vermis computed over 9 slices centered laterally to illustrate that central measurements (e.g. areas) are more reliable due to improved lateral boundary definition.
Average CATK DO scores were 90% for the total cerebellar volume, 89% for the left and right hemispheres, 70–79% for the vermal volume, and 81–88% for the midsagittal vermal volume, with little variability of agreement across subjects for the total cerebellum and cerebellar hemisphere volume measures. FreeSurfer performed similarly to CATK for the total cerebellar and cerebellar hemisphere volumes it measures. SUIT also achieved reasonably high average DO scores: close to 90% for the total cerebellum and hemispheres, an average of 71% for the vermal volume, and an average of 78% for the midsagittal vermal volume. However, as illustrated in Figure 6b, overlap scores are more variable for SUIT than CATK or FreeSurfer, with agreement for individual subjects for several measures being below 40%.
4. Discussion
CATK has surprising test-retest reliability (average ICC of 0.96) evaluated from repeat scans on 20 subjects not included in the data used for training. Given that the test set only contained individuals in a narrow age range (19–34 years), the reliability results for the manual labeling says reliable differences in cerebellar measures are present in such individuals, and the CATK reliability results show that CATK can also reliably detect differences between individuals in this narrow age range. CATK also demonstrated high validity (i.e., agreement with gold standard Neuromorphometrics hand labeling), with validity ICCs of over 0.96 for total cerebellum and cerebellar hemisphere volumes, between 0.60 and 0.85 for vermal volume measures, and between 0.91 and 0.94 for midsagittal vermal area measures. DO scores for CATK also indicate close agreement with the manual labels, with a range of: 87%–93% for the total cerebellum and cerebellar hemispheres, 52%–84% for vermis volumes, and 72%–91% for midsection vermal volumes. The minimum of 52% corresponds to vermis lobule VI–VII, which has proved to be one of the most difficult parcels to segment because of its high variability. However, higher scores are achieved using midsection volumes of the vermis that are less sensitive to the poorly defined lateral boundaries of the vermis. CATK’s agreement with the gold standard is thus very encouraging, with the agreement being close to the test-retest reliability of the gold standard itself.
FreeSurfer and CATK showed comparable reliability and validity for total cerebellum volume and for cerebellar hemisphere volumes—the only cerebellar measures that are part of FreeSurfer. As is apparent in Figure A.7c in the appendix, FreeSurfer volumes were consistently somewhat smaller than manual volumes, consistent with FreeSurfer having a small bias in its volume estimates. CATK produces segmentations in the form of 3D triangular mesh surfaces that interpolate the discrete manual volumes in the training set. These measurements also tend to be slightly smaller than the corresponding manual volumes, and are adjusted through calibration on the training set. Given these adjustments on the training data, this potential bias is not present on the test set. We speculate that FreeSurfer’s bias could be linked to a similar phenomenon, and could be corrected in a similar manner.
SUIT’s much lower reliability and validity ICCs and lower average DO scores compared to CATK (or FreeSurfer where appropriate), indicates that CATK has much higher validity for volume measures than SUIT. Our analyses show that SUIT as implemented in the SPM toolbox is not sufficiently robust as a volume measurement tool. SUIT registration was applied using both the standard functions (that use cosine basis functions during nonrigid registration) and the DARTEL engine (that defines the deformation by a LDDMM-based flowfield). While DARTEL offers greater model flexibility and more refined fitting, this comes at the cost of larger errors when the solution fails to converge. We found that both implementations failed on exactly the same images, leading us to conclude that poor initialization was to blame. However, because of DARTEL’s higher dimensionality, the resulting segmentations were much worse for DARTEL, leading to lower average scores than the standard approach. Therefore, we chose to report results from the standard method. To examine whether SUIT’s dense nonlinear registration offers some advantage, we implemented a hybrid approach where the cerebellar isolation algorithm is replaced with CATK. Essentially, this uses CATK as an initial solution to dense registration. While several registrations still produced irregularly skewed transforms, the majority met with success. This raised the average test-retest reliability of SUIT measurements to 0.90 from 0.45, and improved the average validity ICC to 0.80 from 0.52. Although these results are still lower than those achieved by CATK, the fact that CATK and SUIT approaches can be applied successfully in tandem is of interest for future applications in which shape parameterization of the target structure may be more difficult.
One of the reasons we think CATK performs so reliably is because the 1D template matching used within the ASM stage, that uses gradient information, is extremely robust to differences in the intensity distribution. This allows the model to converge even when there is significant blurring due to effects like subject motion. In recent published work [57], we used CATK to compare measures of cerebellar volumes between adolescents with histories of prenatal alcohol exposure (PAE) and non-exposed controls. CATK detected smaller cerebellar volumes and mid-sagittal vermal areas in the PAE group compared to controls, with the exception of the superior posterior vermis, consistent with prior studies that used manual cerebellar measurement. In addition, we were able to show that smaller anterior superior vermis areas were present over and above the generally smaller brain evident in the PAE group, an interesting new finding. We note that the PAE vs. control comparison shows that CATK does well in measuring pathologically small cerebellar, and particularly vermal, size despite such cases not being part of the training set. Finally, in our recent experience applying CATK to more than 300 scans of adults and adolescents with alcohol use disorders and controls, the method has failed on less than 2% of images while detecting hypothesized cerebellar size differences (work in preparation). In summary, our work in clinical samples suggests the utility of using CATK in large clinical studies to sensitively detect disease-related cerebellar volume effects.
A limitation of CATK in its current form is that it does not segment the cerebellar hemispheres into their parcels. CATK was developed with limited funding and made use of the standard Neuromorphometrics labels as available on their web site. Extending CATK to delineate parcels of the cerebellar hemispheres would involve significant additional work, which we have proposed in pending funding applications, and where we also propose using prospective motion tracking and correction to obtain higher image quality that will allow better delineation of the cerebellar foliations.
Highlights.
We apply an active appearance modelling framework to cerebellar segmentation
Validation using manual delineations indicate high reliability and validity
Comparison with FreeSurfer and SUIT show better performance than atlas-based methods
Detected teratogenic effects in adolescents with history of Prenatal Alcohol Exposure
Acknowledgments
This work was made possible by the National Science Foundation (SBIR R43 AA021945).
Appendix A. Measurement Comparisons for Validation Subjects
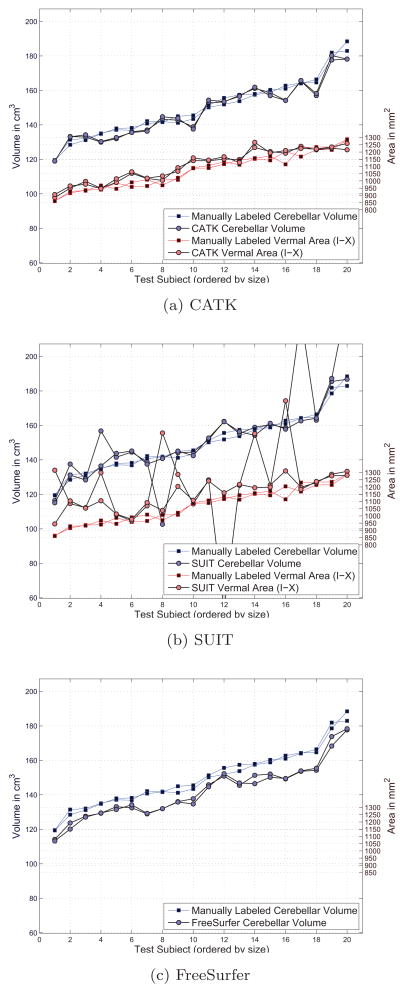
Comparative plots of total cerebellar volumes and combined vermal areas are shown against manually labeled examples in Figure A.7. Since CATK produces segmentations in the form of 3D triangular mesh surfaces that interpolate the discrete volume, measurements must be adjusted through calibration (i.e., scaled up by a small factor) in order to be comparable with those taken directly from discrete volumes. Consequently, values in Figure A.7a have been adjusted accordingly using a correction factor computed from the training data. Also note that each data series (i.e., volume and area) is sorted in terms of the manually labeled measurements to facilitate visualization, and the apparent covariation between cerebellar volume and vermal area is as a result of this ordering.
Figure A.7.
Measurement comparison for cerebellar volumes and vermal areas for the 20 validation subjects. Both test and retest images are plotted illustrating the repeatability of each method.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Sharma N, Aggarwal LM. Automated medical image segmentation techniques. Journal of medical physics/Association of Medical Physicists of India. 2010;35(1):3–14. doi: 10.4103/0971-6203.58777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Magnotta VA, Heckel D, Andreasen NC, Cizadlo T, Corson PW, Ehrhardt JC, Yuh WTC, Westmoreland P, Westmoreland-Corson P, Ehrhardt C, James, West-morland Corson P. Measurement of Brain Structures with Artificial Neural Networks: Two-and Three-dimensional Applications. Radiology. 1999;211(3):781–790. doi: 10.1148/radiology.211.3.r99ma07781. URL http://www.ncbi.nlm.nih.gov/pubmed/10352607. [DOI] [PubMed] [Google Scholar]
- 3.Akselrod-Ballin A, Galun M, Gomori MJ, Basri R, Brandt A. Atlas guided identification of brain structures by combining 3D segmentation and SVM classification. Medical image computing and computer-assisted intervention: MICCAI … International Conference on Medical Image Computing and Computer-Assisted Intervention. 2006;9(Pt 2):209–216. doi: 10.1007/11866763\_26. [DOI] [PubMed] [Google Scholar]
- 4.Van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of MR images of the brain. IEEE transactions on medical imaging. 1999;18(10):897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
- 5.Despotović I, Segers I, Platisa L, Vansteenkiste E, Pizurica A, Deblaere K, Philips W. Automatic 3D graph cuts for brain cortex segmentation in patients with focal cortical dysplasia. Conference proceedings: Annual International Conference of the IEEE Engineering in Medicine and Biology Society IEEE Engineering in Medicine and Biology Society Conference. 2011;2011:7981–7984. doi: 10.1109/IEMBS.2011.6091968. URL http://www.ncbi.nlm.nih.gov/pubmed/22256192. [DOI] [PubMed] [Google Scholar]
- 6.Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33(3):341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- 7.Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage. 2006;31(3):968–980. doi: 10.1016/j.neuroimage.2006.01.021. URL http://www.sciencedirect.com/science/article/B6WNP-4JFHF4P-1/2/0ec667d4c17eafb0a7c52fa3fd5aef1c. [DOI] [PubMed] [Google Scholar]
- 8.Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33(1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- 9.Cootes T, Baldock E, Graham J. An Introduction to Active Shape Models. Image Processing and Analysis. 2000:223–248. [Google Scholar]
- 10.Babalola KO, Patenaude B, Aljabar P, Schnabel J, Kennedy D, Crum W, Smith S, Cootes T, Jenkinson M, Rueckert D. An evaluation of four automatic methods of segmenting the subcortical structures in the brain. NeuroImage. 2009;47(4):1435–1447. doi: 10.1016/j.neuroimage.2009.05.029. [DOI] [PubMed] [Google Scholar]
- 11.Sun H, Frangi AF, Wang H, Sukno FM, Tobon-Gomez C, Yushkevich PA. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) Vol. 6361. LNCS; 2010. Automatic cardiac MRI segmentation using a biventricular deformable medial model; pp. 468–475. [DOI] [PubMed] [Google Scholar]
- 12.Suckling J, Sigmundsson T, Greenwood K, Bullmore ET. A modified fuzzy clustering algorithm for operator independent brain tissue classification of dual echo MR images. Magnetic Resonance Imaging. 1999;17(7):1065–1076. doi: 10.1016/s0730-725x(99)00055-7. [DOI] [PubMed] [Google Scholar]
- 13.Datta S, Sajja B, He R, Dieber J, Narayana P. Segmentation of MR Brain Images with Intensity Correction and Partial Volume Averaging. Proceedings 16th Scientific Meeting, International Society for Magnetic Resonance in Medicine; Toronto. 2008. p. 3165. [Google Scholar]
- 14.Hartmann SL, Parks MH, Martin PR, Dawant BM. Automatic 3-D segmentation of internal structures of the head in MR images using a combination of similarity and free-form transformations: Part II, validation on severely atrophied brains. IEEE transactions on medical imaging. 1999;18(10):917–926. doi: 10.1109/42.811273. [DOI] [PubMed] [Google Scholar]
- 15.Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain: 3-dimensional proportional system: an approach to cerebral imaging. 1988;39 [Google Scholar]
- 16.Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J. A probabilistic atlas of the human brain: theory and rationale for its development. The International Consortium for Brain Mapping (ICBM) NeuroImage. 1995;2(2):89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- 17.Mazziotta J, Toga A, Evans A, Fox P, Lancaster J, Zilles K, Woods R, Paus T, Simpson G, Pike B, Holmes C, Collins L, Thompson P, MacDonald D, Iacoboni M, Schormann T, Amunts K, Palomero-Gallagher N, Geyer S, Parsons L, Narr K, Kabani N, Le Goualher G, Boomsma D, Cannon T, Kawashima R, Mazoyer B. A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM)., Philosophical transactions of the Royal Society of London. Series B. Biological sciences. 2001;356(1412):1293–1322. doi: 10.1098/rstb.2001.0915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hellier P, Barillot C, Corouge I, Gibaud B, Le Goualher G, Collins DL, Evans A, Malandain G, Ayache N, Christensen GE, Johnson HJ. Retrospective Evaluation of Intersubject Brain Registration. IEEE Transactions on Medical Imaging. 2003;22(9):1120–1130. doi: 10.1109/TMI.2003.816961. [DOI] [PubMed] [Google Scholar]
- 19.Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, Christensen GE, Collins DL, Gee J, Hellier P, Song JH, Jenkinson M, Lepage C, Rueckert D, Thompson P, Vercauteren T, Woods RP, Mann JJ, Parsey RV. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage. 2009;46(3):786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Klein A. Supplementary material for: Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Tech Rep. 2009;3 doi: 10.1016/j.neuroimage.2008.12.037. URL http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2747506&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dale A, Fischl B, Sereno MI. Cortical Surface-Based Analysis: I. Segmentation and Surface Reconstruction. NeuroImage. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 22.Diedrichsen J. A spatially unbiased atlas template of the human cerebellum. NeuroImage. 2006;33(1):127–38. doi: 10.1016/j.neuroimage.2006.05.056. URL http://discovery.ucl.ac.uk/167934/ [DOI] [PubMed] [Google Scholar]
- 23.Diedrichsen J, Balsters JH, Flavell J, Cussans E, Ramnani N. A probabilistic MR atlas of the human cerebellum. NeuroImage. 2009;46(1):39–46. doi: 10.1016/j.neuroimage.2009.01.045. [DOI] [PubMed] [Google Scholar]
- 24.Wellcome Trust Centre for Neuroimaging. SPM: Statistical Parametric Mapping. 2012 URL http://www.fil.ion.ucl.ac.uk/spm/software/
- 25.Powell S, Magnotta VA, Johnson H, Jammalamadaka VK, Pierson R, Andreasen NC. Registration and machine learning-based automated segmentation of subcortical and cerebellar brain structures. NeuroImage. 2008;39(1):238–247. doi: 10.1016/j.neuroimage.2007.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Van der Lijn F, De Bruijne M, Hoogendam YY, Klein S, Hameeteman R, Breteler MMB, Niessen WJ. Cerebellum segmentation in MRI using atlas registration and local multi-scale image descriptors. Proceedings - 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, ISBI; 2009; 2009. pp. 221–224. [Google Scholar]
- 27.Bogovic JA, Bazin PL, Ying SH, Prince JL. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) Vol. 7917. LNCS; 2013. Automated segmentation of the cerebellar lobules using boundary specific classification and evolution; pp. 62–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cavanagh JB, Holton JL, Nolan CC. Selective damage to the cerebellar vermis in chronic alcoholism: a contribution from neurotoxicology to an old problem of selective vulnerability. Neuropathology and applied neurobiology. 1997;23(5):355–363. [PubMed] [Google Scholar]
- 29.Sowell ER, Jernigan TL, Mattson SN, Riley EP, Sobel DF, Jones KL. Abnormal development of the cerebellar vermis in children prenatally exposed to alcohol: size reduction in lobules I–V. Alcoholism, clinical and experimental research. 1996;20(1):31–34. doi: 10.1111/j.1530-0277.1996.tb01039.x. [DOI] [PubMed] [Google Scholar]
- 30.Webb SJ, Sparks BF, Friedman SD, Shaw DWW, Giedd J, Dawson G, Dager SR. Cerebellar vermal volumes and behavioral correlates in children with autism spectrum disorder. Psychiatry Research - Neuroimaging. 2009;172(1):61–67. doi: 10.1016/j.pscychresns.2008.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Patenaude B. Phd thesis. University of Oxford; 2007. Bayesian Statistical Models of Shape and Appearance for Subcortical Brain Segmentation. [Google Scholar]
- 32.Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychological Bulletin. 1979;86(2):420–428. doi: 10.1037//0033-2909.86.2.420. URL http://www.ncbi.nlm.nih.gov/pubmed/18839484. [DOI] [PubMed] [Google Scholar]
- 33.Crum WR, Camara O, Rueckert D, Bhatia KK, Jenkinson M, Hill DLG. Generalised overlap measures for assessment of pairwise and groupwise image registration and segmentation. Medical image computing and computer-assisted intervention: MICCAI … International Conference on Medical Image Computing and Computer-Assisted Intervention. 2005;8(Pt 1):99–106. doi: 10.1007/11566465_13. [DOI] [PubMed] [Google Scholar]
- 34.Rohlfing T, Zahr NM, Sullivan EV, Pfefferbaum A. The SRI24 multichannel atlas of normal adult human brain structure. Human brain mapping. 2010;31(5):798–819. doi: 10.1002/hbm.20906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rohlfing T. Computational Morphometry Toolkit. 2011 URL http://www.nitrc.org/projects/cmtk/
- 36.Schmahmann JD, Doyon J, McDonald D, Holmes C, Lavoie K, Hurwitz AS, Kabani N, Toga A, Evans A, Petrides M. Three-dimensional MRI atlas of the human cerebellum in proportional stereotaxic space. NeuroImage. 1999;10(3 Pt 1):233–260. doi: 10.1006/nimg.1999.0459. [DOI] [PubMed] [Google Scholar]
- 37.Friston KJ. Statistical Parametric Mapping: The Analysis of Functional Brain Images. Academic Press; 2006. [Google Scholar]
- 38.Ashburner J. A fast diffeomorphic image registration algorithm. NeuroImage. 2007;38(1):95–113. doi: 10.1016/j.neuroimage.2007.07.007. [DOI] [PubMed] [Google Scholar]
- 39.Beg MF, Miller MI, Trouve A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International Journal of Computer Vision. 2005;61(2):139–157. doi: 10.1023/B:VISI.0000043755.93987.aa. [DOI] [Google Scholar]
- 40.Cootes TF, Taylor CJ. Statistical models of appearance for medical image analysis and computer vision. Proceedings of SPIE. 2001;4322:236–248. doi: 10.1117/12.431093. [DOI] [Google Scholar]
- 41.Cootes TF, Edwards GJ, Taylor CJ. Active appearance models. Pattern Analysis and Machine Intelligence. 2001;23(6):681–685. [Google Scholar]
- 42.Heimann T, Meinzer HP. Statistical shape models for 3D medical image segmentation: a review. Medical image analysis. 2009;13(4):543–563. doi: 10.1016/j.media.2009.05.004. [DOI] [PubMed] [Google Scholar]
- 43.Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. 1988. [DOI] [Google Scholar]
- 44.Hwang J, Kim J, Han Y, Park H. An automatic cerebellum extraction method in T1-weighted brain MR images using an active contour model with a shape prior. Magnetic Resonance Imaging. 2011;29(7):1014–1022. doi: 10.1016/j.mri.2011.01.005. [DOI] [PubMed] [Google Scholar]
- 45.Cootes T, Taylor C, Cooper D, Graham J. Active Shape Models-Their Training and Application. Computer Vision and Image Understanding. 1995;61(1):38–59. URL http://www.sciencedirect.com/science/article/pii/S1077314285710041. [Google Scholar]
- 46.Patenaude B, Smith SM, Kennedy DN, Jenkinson M. A Bayesian model of shape and appearance for subcortical brain segmentation. NeuroImage. 2011;56(3):907–922. doi: 10.1016/j.neuroimage.2011.02.046. URL http://www.ncbi.nlm.nih.gov/pubmed/21352927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lorensen WE, Cline HE. Marching cubes: A high resolution 3D surface construction algorithm. Computer Graphics. 1987;21(4):163–169. [Google Scholar]
- 48.Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC. N4ITK: improved N3 bias correction. IEEE transactions on medical imaging. 2010;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Smith SM. Fast robust automated brain extraction. Human brain mapping. 2002;17(3):143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Woods RP. Automated Image Registration (AIR) 2011 URL http://bishopw.loni.ucla.edu/air5/
- 51.Woods RP, Grafton ST, Holmes CJ, Cherry SR, Mazziotta JC. Automated image registration: I. General methods and intrasubject, intramodality validation. Journal Of Computer Assisted Tomography. 1998;22(1):139–152. doi: 10.1097/00004728-199801000-00027. URL http://www.ncbi.nlm.nih.gov/pubmed/9448779. [DOI] [PubMed] [Google Scholar]
- 52.Woods RP, Grafton ST, Watson JD, Sicotte NL, Mazziotta JC. Tech Rep. Vol. 1. Department of Neurology, UCLA School of Medicine; USA: 1998. Automated image registration: II. Intersubject validation of linear and nonlinear models. URL http://www.ncbi.nlm.nih.gov/pubmed/9448780. [DOI] [PubMed] [Google Scholar]
- 53.Deshmukh AR, Desmond JE, Sullivan EV, Lane BF, Lane B, Matsumoto B, Marsh L, Lim KO, Pfefferbaum A. Quantification of cerebellar structures with MRI. Psychiatry Research: Neuroimaging. 1997;75(3):159–171. doi: 10.1016/s0925-4927(97)00051-6. [DOI] [PubMed] [Google Scholar]
- 54.Press GA, Murakami J, Courchesne E, Berthoty DP, Grafe M, Wiley CA, Hesselink JR. The cerebellum in sagittal plane–anatomic-MR correlation: 2. The cerebellar hemispheres. American Journal of Roentgenology. 1989;153(4):837–846. doi: 10.2214/ajr.153.4.837. [DOI] [PubMed] [Google Scholar]
- 55.Bookstein FL, Streissguth AP, Connor PD, Sampson PD. Damage to the human cerebellum from prenatal alcohol exposure: the anatomy of a simple biometrical explanation. The Anatomical Record Part B: The New anatomist. 2006;289(5):195–209. doi: 10.1002/ar.b.20114. [DOI] [PubMed] [Google Scholar]
- 56.O’Hare ED, Kan E, Yoshii J, Mattson SN, Riley EP, Thompson PM, Toga AW, Sowell ER. Tech Rep. Vol. 12. Laboratory of Neuro Imaging, Department of Neurology, University of California; Los Angeles, California, USA: 2005. Mapping cerebellar vermal morphology and cognitive correlates in prenatal alcohol exposure. [DOI] [PubMed] [Google Scholar]
- 57.Cardenas VA, Price M, Infante MA, Moore EM, Mattson SN, Riley EP, Fein G. Automated cerebellar segmentation: Validation and application to detect smaller volumes in children prenatally exposed to alcohol. NeuroImage: Clinical. 2014;4(0):295–301. doi: 10.1016/j.nicl.2014.01.002. URL http://www.sciencedirect.com/science/article/pii/S2213158214000035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Greenstein D, Fein G. Gait and Balance Ataxia in Abstinent Alcoholics. Proceedings of 41st Annual Meeting of the International Neuropsychological Society; Hawaii. 2013. [Google Scholar]