Refinement by shifting secondary structure elements improves sequence alignments

Abstract

Constructing a model of a query protein based on its alignment to a homolog with experimentally determined spatial structure (the template) is still the most reliable approach to structure prediction. Alignment errors are the main bottleneck for homology modeling when the query is distantly related to the template. Alignment methods often misalign secondary structural elements by a few residues. Therefore, better alignment solutions can be found within a limited set of local shifts of secondary structures. We present a refinement method to improve pairwise sequence alignments by evaluating alignment variants generated by local shifts of template-defined secondary structures. Our method SFESA is based on a novel scoring function that combines the profile-based sequence score and the structure score derived from residue contacts in a template. Such a combined score frequently selects a better alignment variant among a set of candidate alignments generated by local shifts and leads to overall increase in alignment accuracy. Evaluation of several benchmarks shows that our refinement method significantly improves alignments made by automatic methods such as PROMALS, HHpred and CNFpred. The web server is available at http://prodata.swmed.edu/sfesa.

INTRODUCTION

Prediction of protein three-dimensional (3D) structures from amino acid sequences is important for biologists to study proteins lacking experimental structures and is one of the key problems in computational biology ¹. With the accumulation of experimentally determined protein structures in the PDB database ², homology modeling (also known as template-based modeling) is the most reliable approach to protein structure prediction ^1,3. The 3D structure for a given query sequence can be modeled by aligning the query to one or several protein templates with known structures^4–5. The model quality relies heavily on the quality of the pairwise or multiple sequence alignment (MSA) between the query and the templates ^6–8. Currently, most MSA methods use a progressive approach that builds up an MSA by aligning the most similar two sequences as a pre-aligned group first and gradually adding more distant sequences or other pre-aligned groups. At each step of progressive alignment, a pairwise alignment method is used to align two sequences, a sequence and a pre-aligned group, or two pre-aligned groups. Thus, pairwise alignment is an integral component in most MSA methods ^9–13. An accurate pairwise alignment between the query and the template is essential regardless of whether one or multiple templates are used for homology modeling.

Although pairwise alignment construction has been extensively researched, alignments are still not sufficiently accurate for sequences with low similarity ¹⁴. For example, the latest significant advance, CNFpred ¹⁵, only has Q-score of 52.4 for the MUSTER benchmark ¹⁶ (13.0% average sequence identity by MUSTER’s own reference). A number of approaches have been developed for the task. Earlier work focused on dynamic programming recursion in construction of a global or local alignment ^17–18. Heuristic methods such as FASTA and BLAST ^19–20 were developed to significantly increase the speed of alignment. Subsequently, sequence profiles and hidden Markov models (HMMs) ²¹ were introduced for comparison of a single sequence and an MSA. Furthermore, profile-profile ^22–25 and HMM-HMM ^11–12,26 comparisons improved pairwise alignments by scoring the similarity between sequence positions in protein families. In addition to pure sequence methods, 3D structural information is valuable for alignment construction because protein structures tend to evolve more slowly than protein sequences ^27–28. 3D-COFFEE¹⁰ as well as PROMALS3D ¹² use alignment constraints derived from known 3D structures and do not use structure energy-based scoring to explicitly compare a structure to a sequence without 3D structure. Scoring of observed and predicted structural properties, such as secondary structure, solvent accessibility, residue depth, residue contacts and backbone torsion angles, was included in a number of alignment methods ^{15–16,29–34}. Information extracted from structure-based alignments of homologous proteins was used to derive amino acid substitution matrices ^32,35–36 or position-specific scoring matrices (PSSMs) ^37–38. 3D profile is a position-dependent 20xn scoring matrix derived from protein structures. Such profiles were used to improve sequence-structure alignment ^37–38. Moreover, a 400x400 contact-mutation matrix was proposed to improve sequence alignment by using the contacts in template ^39–40. However, how to efficiently and effectively use structural (especially energy-based) information to improve pairwise alignment remains an open question in the field ⁴¹.

Query-template alignment quality is poor when the query is distantly related to the template, and alignment errors remain the main bottleneck in homology modeling ^42–43. Inevitable shortcomings in each alignment strategy lead to alignment errors. Application of a refinement algorithm to a given alignment can correct such errors. Refinement methods have been used to improve structure-based alignments and progressively constructed MSA ^44–48. MSA refinement was often conducted by iteratively dividing an MSA into two sub-alignments and realigning them. However, one obvious drawback of these methods is that no additional information (such as structural information) was added to the iterative refinement.

A template structure can be viewed as regular secondary structure elements (SSEs, i.e., α-helices and β-strands) ^49–50 alternating with loops (such as turns and coils) connecting these SSEs. SSEs are typically more conserved ⁵¹ and accurate alignments between SSEs are essential, whereas loops tend to be more evolutionarily plastic and difficult to align. In a given alignment, we define an “alignment block” as the residues in an SSE in the template and their aligned residues in the query. Automatic aligners such as PROMALS ¹¹ frequently misalign alignment blocks by a few residues. Better alignment solutions can frequently be found among a limited set of local shifts of alignment blocks (moving residues in the query relative to the template). This observation motivated us to develop a pairwise alignment refinement method, SFESA, which generates candidate alignment variants for each alignment block by shifting the query region. We developed a scoring function to judge whether an alignment variant is likely to be more accurate than the original alignment. Our scoring function combines a profile-based sequence score and a novel structural contact-based score derived from residue contacts in template. This combined score was often able to select the best alignment solution among a set of candidates and lead to overall increase in alignment accuracy. Our approach improves alignments generated by a number of methods such as PROMALS ¹¹, HHpred ²⁶ and CNFpred ¹⁵ on several benchmarks that include both reference-dependent and reference-independent assessment.

MATERIAL AND METHODS

Generation of alignment variants

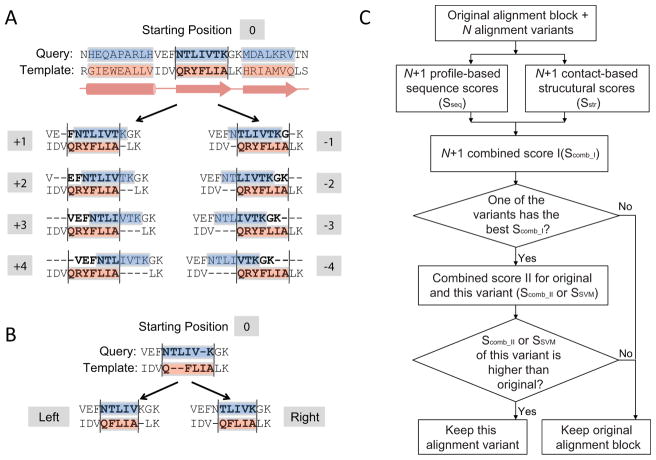
We partition a pairwise alignment into alignment blocks according to template SSEs defined by the program PALSSE ⁵². Short secondary structures (α-helices less than 8 residues and β-strands less than 4 residues) are not considered and are treated as loop regions. Each alignment block is defined as the residues in one template SSE and their aligned residues in the query. Eight additional alignment variants can be generated for one alignment block by shifting the original alignment in the block up to ±4 residues (Fig. 1A). We use +K shift to refer to the alignment variant that shifts the query in the alignment block toward the C-terminus by K residues. Residues in the neighboring loop regions can be placed inside an alignment block after the shift (e.g., residue “F” in the query in +1 shift in Fig. 1A). Similarly, negative shift numbers refer to shifting the query towards the N-terminus. SFESA does not allow residues in neighboring alignment blocks to shift. For example, in the +4 shift, the neighboring residue “V” is the last one shifted into the alignment block (Fig. 1A), while the residues neighboring but belonging to a different SSE (such as residue “H” in Fig. 1A) are not allowed to shift.

Figure 1. An overview of the SFESA method.

(A) For each alignment block, SFESA generates up to ±4 variants by shifting (marked as -1, -2, -3, -4, +1, +2, +3, and +4). The pink boxes show the SSEs recognized from template structure and the blue boxes are corresponding regions in the query aligned to such SSEs. Residues and gaps in one corresponding blue and pink boxes compose an alignment block. The corresponding black lines provide the boundaries between which sequence and structure scores are calculated for each aligned residue pairs. (B) If gap shifting is considered, two variants (left and right) are generated by putting gaps on the same side (left or right) before generating the above 8 variants. (C). Flowchart of the SFESA method.

When there are no gaps in the original alignment block, SFESA can generate 8 alignment variants according to above procedure. If gaps are present in the query and/or template in the alignment block, there are two gap processing strategies. The first one is to keep the gap pattern in the original alignment block when shifting ±K (up to 4) residues, resulting in 8 alignment variants. This strategy is used in SFESA (O) mode (described below).

The second gap treatment strategy is to preprocess gaps before shifting ±K (up to 4) residues. As gaps rarely occur in the middle of SSEs, we move the gaps to the same side (left or right) without interrupting the SSEs. Residues in an alignment block can be pushed to leftmost or rightmost while all gaps are put to the opposite side, resulting in two alignment variants (left and right, Fig. 1B). Each of these two alignment variants is then used as a starting point to generate 8 additional alignment variants by ±4 shifting while keeping the modified gap patterns. Therefore, if gaps exist in the original alignment, SFESA with gap shifting can generate up to 18 (1+8+1+8) alignment variants. This strategy is used in SFESA (O+G), SFESA (O+G+M) and SFESA (O+G+M+S) (described below).

Profile-based sequence score

Profiles are generated from multiple sequence alignments (MSAs) generated from three PSI-BLAST⁵³ iterations. Score for the similarity of residue content in MSA columns is measured by the formula originally implemented in the COMPASS method ²⁴.

$$S_{\mathit{seq}}=c_1\sum _i{n}_i^{1}ln\frac{Q_i^2}{p_i}+c_2\sum _i{n}_i^{2}ln\frac{Q_i^1}{p_i}$$ Eq (1)

where $n_i^1$ and $n_i^2$ are effective numbers of residue type i in the query column 1 and template column 2, $Q_i^1$ and $Q_i^2$ are estimated residue frequencies of the two compared columns, and p_i is the background residue frequency. Parameters c₁ and c₂ are calculated as:

$$c_1=\frac{{\displaystyle \sum _i}{n}_i^2-1}{{\displaystyle \sum _i}{n}_i^1+{\displaystyle \sum _i}{n}_i^2-2}$$ Eq (2)

$$c_2=\frac{{\displaystyle \sum _i}{n}_i^1-1}{{\displaystyle \sum _i}{n}_i^1+{\displaystyle \sum _i}{n}_i^2-2}$$ Eq (3)

SFESA further incorporates secondary structure (SS) information into the sequence score. For query, SS is predicted by PSIPRED ⁵⁴; for template, SS information in DSSP ⁵⁰ is used. A three-by-three secondary structure substitution matrix is derived from the structural alignment FAST ⁵⁵ ₍considered as query aligned to template) of protein domains from ASTRAL compendium ⁵⁶ based on SCOP 1.75 ⁵⁷ (see Training dataset below). For each residues pair, the SS score S_ss and S_seq are combined to get the new sequence score $S_{\mathit{seq}}^{\prime }$ as:

$$S_{\mathit{seq}}^{\prime }=S_{\mathit{seq}}+w_{ss}{S}_{ss}$$ Eq (4)

where w_ss is the constant weight for the secondary structure score term and is set to 0.06 in our study.

Contact-based structure score

A residue contact is defined as a residue pair within a distance cutoff. In the template of one alignment, the residue contacts can be identified using the known structure of the template. Correctly aligned equivalent residues in the query should have similar structural environment as in the template. Based on a residue-residue contact energy matrix, e.g., the one derived by Miyazawa and Jernigan ⁵⁸, the total contact energies of query residues in an alignment block can be inferred from the query-template alignment and the contacts defined by the template structure (Fig. 2, explained below). Our contact-based structure score, corresponding to the negative of the inferred contact energies of the query, should reflect the fitness of the query residues in the structural environment defined by the template structure. Our hypothesis is that an alignment variant with a higher inferred contact energy score is likely to be more accurate.

Figure 2. The template contact residue pairs are transferred to the query by original alignment to calculate structure score for the original alignment block and alignment variants.

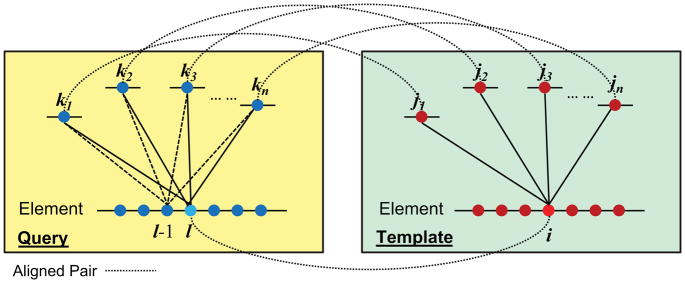
The blue and red filled circles represent residues in query and template, respectively. The dashed lines connect aligned residue pairs in the original alignment. Residue i is in contact with residues j₁, j₂, j₃… j_n based on template structure. Residue I in the query is aligned with i and is inferred to be in contact with residues k₁, k₂, k₃… k_n that are aligned to j₁, j₂, j₃… j_n. The contact-based score for residue l is calculated by Eq (5). In the case of +1 shift, residue l-1 is aligned to residue i, and the inferred contacts are between residue l-1 and k₁, k₂, k₃… k_n (shown as dashed lines).

In Fig. 2, i is one residue in an SSE of template, and j₁, j₂, …, j_n are the contact residues of i based on the template structure. According to the alignment, l is the residue in the query aligned to i, and k₁, k₂, …, k_n in the query are aligned to j₁, j₂, …, j_n, respectively. Thus, the contact residues of l are inferred to be k₁, k₂, …, k_n. The inferred structure score for residue l based on the alignment and the template contact definitions is:

$$S_{\mathit{contact}}(l)=-\sum _{m=1}^n{e}_{l,k_m}$$ Eq (5)

where e_l,km is the pairwise contact energy for residues l and k_m in the query.

The total structure score of the alignment block is the sum of the contact energy scores for all the query residues.

$$S_{\mathit{str}}=\sum _l{S}_{\mathit{contact}}(l)$$ Eq (6)

When a profile is used instead of a sequence, the structure score is the average of all contact energies of equivalent residues in homologs of query (including the query itself):

$$S_{\mathit{str}}^{\prime }=\frac{1}{N}\sum _{a=1}^N{S}_{\mathit{str}}(a)$$ Eq (7)

where N is the total number of homologs of the query in the PSI-BLAST multiple sequence alignment, and S_str (a) is the structure score calculated by Eq(6) for the homologous sequence a.

Two contact energy matrices are explored. One is the Miyazawa-Jernigan contact energy matrix with contacts defined as residue pairs with side chain centers less than 6.5Å. The other matrix is a new contact energy matrix trained on PROMALS alignments. For each alignment, each alignment block is allowed to shift ±4 residues (eight variants), and then the best-scoring variant (showing the best agreement with DALI reference ⁵⁹, that is, the variant having the most number of common aligned positions with DALI alignment) among the original alignment and the eight variants (nine total) is selected based on and the other eight variants (alignment variants or the original alignment) are considered as background. The contact energy is formulated as follows:

$$e_{ij}=-ln(\frac{b_{ij}}{d_{ij}/8})+C$$ Eq (8)

Where b_ij is the occurrence of aligned residue pair of i and j in the best-scoring alignment; d_ij is the occurrence of aligned residue pair of i and j in background alignments; C is a constant ( C = 0.25). The cutoff for contact definition is 6.5Å between any side chain atoms of two residues.

Evaluation of the original alignment and alignment variants for an alignment block

Two filtering steps to evaluate the combined (sequence and structure) score are used to determine whether the original alignment block is kept or replaced by one of the alignment variants (Fig. 1C). “Original alignment block” refers to blocks prior to refinement by SFESA. In the first filtering step, if the best-scoring alignment variant has a higher score (S_{comb_I}) than the original alignment block, this variant will be selected and passed to the second filter. Otherwise, SFESA keeps the original alignment block. In the second filtering step, the selected alignment variant (with the best S_{comb_I}) is again compared to the original alignment block by using a different score: S_{comb_II} or S_svm. If the selected alignment variant also has a better S_{comb_II} or S_svm than the original alignment block, this alignment variant will replace the original alignment block. Otherwise, the original alignment block is kept.

S_{comb_I} and S_{comb_II} are linear combinations of sequence score and structure score with different weights:

$${\mathrm{S}}_{\text{comb}\_\mathrm{I}}=w_1{S}_{\mathit{seq}}^{\prime }+(1-w_1)S_{\mathit{str}}^{\prime }$$ Eq (9)

$${\mathrm{S}}_{\text{comb}\_\text{II}}=w_2{S}_{\mathit{seq}}^{\prime }+(1-w_2)S_{\mathit{str}}^{\prime }$$ Eq (10)

where $S_{\mathit{seq}}^{\prime }$ is the sequence score combined with secondary structure score (Eq(4)) and $S_{\mathit{str}}^{\prime }$ is the contact-based structure score with consideration of query homologs (Eq(7)). SFESA has four modes (described below). w1 and w2 are optimized to be 0.8 and 0.1 in SFESA (O), 0.4 and 0.1 in SFESA (O+G), and 0.12 and 0.02 in SFESA (O+G+M). In SFESA (O+G+M+S), w1 is optimized to be 0.12. S_svm used in second filter of SFESA (O+G+M+S) is a score generated by a SVM classifier described below.

The SVM score

A support vector machine (SVM), implicitly mapping its inputs into high-dimensional feature space, is widely used in binary classification ⁶⁰. In our strategy, if any alignment variant passes the first filter (with the top S_{comb_I} compared to all other variants and the original alignment block), the second filter is a two-category classification problem – either accepting this selected alignment variant or keeping the original alignment block. Besides S_{comb_II}, an SVM was trained in the second filter to aid this decision. Ten features were used in such an SVM binary classifier. Two features are binary representatives for secondary structure type: helix as (1, 0) and strand as (0, 1). Four features represent the scores of the original alignment block: S_seq, S_ss, $S_{\mathit{str}}^{\prime }$ and S_rsa, and another four corresponding features are used for the selected alignment variant. Similarly to S_ss, S_rsa is based on a three-by-three relative solvent accessibility (rsa) substitution matrix derived from FAST ⁵⁵ structural alignments of SCOP domains. Notably, for query, three categories of neural network-predicted rsa values (with PSI-BLAST PSSMs as input) ⁵¹ were used based on three equal-sized bins; for template, the real rsa values calculated by NACCESS ⁶¹ are used to generated three categories based on three equal-sized bins. Two-fold cross validation was used in our SVM training. The linear, polynomial and radial basis functions were tried as kernels. The linear model was found to be optimal. The criterion to accept the alignment variant is set to SVM score above −0.6 for optimal performance of alignment accuracy.

Training dataset

The training dataset consists of protein domain pairs with sequence identity less than 20% from the ASTRAL compendium ⁵⁶ based on SCOP 1.75 ⁵⁷. All domain pairs with COMPADRE e-value less than 1e-30 were used. For all domain pairs, we generated DALI structure alignments. Then, we discarded domain pairs with GDT-TS score ⁶² less than 0.5 in DALI alignment. We also included at most 10 domains from any individual SCOP superfamily, and ensured that each domain is present no more than twice in domain pairs. The final training dataset consists of 1675 domain pairs with 2305 protein domains. We generated PROMALS alignments for these domain pairs and deduced 16347 alignment blocks in these alignments. There are 3061 incorrectly aligned alignment blocks (at least one residue misaligned compared to DALI reference alignment) in PROMALS alignments. The parameters of w_ss in Eq (4), C in Eq (8), w₁, w₂ in Eq (9) and Eq (10) and all SVM parameters were trained on this dataset. The assessment of alignment quality is Q-score (alignment quality score, described below) compared with reference DALI alignment and reference-independent GDT-TS score ⁶³.

Testing benchmarks

We used the following four public datasets to test the method:

1. The MUSTER benchmark ¹⁶. This dataset consists of 110 ProSUP protein pairs ⁶⁴ and 190 pairs selected by the Zhang group with TM-score ⁶⁵ > 0.5.

2. The SALIGN benchmark ⁶⁶. This dataset has 200 protein pairs with about 20% sequence identity, and these pairs have on average about 65 structurally equivalent residues with RMSD < 3.5Å. Proteins in each pair have very different lengths.

3. The SABmark benchmark ⁶⁷. This benchmark is designed for testing multiple sequence alignments (MSAs). SABmark dataset (version 1.65) has two benchmark sets: the “twilight zone” set has 209 groups of SCOP fold-level domains with very low similarity, whereas the “superfamilies” set has 425 groups of same-superfamily domains. We randomly selected one domain pair from each group to test our pairwise alignment refinement method.

4. The PREFAB benchmark (version 4.0) ⁶⁸. This dataset contains 1682 alignments, and it provides its own reference that is based on the consensus of FSSP structure alignment ⁶⁹ and CE alignment ⁷⁰.

For these four benchmarks, we applied our refinement method to PROMALS alignments, as well as alignments generated by two profile-based and structure-aided methods: HHpred ⁷¹ and CNFpred ¹⁵. Here, HHpred was used in the global alignment mode as its local alignment mode often results in short alignments and shows lower alignment accuracy than global alignments (Table S1).

The evaluation criteria include:

1. Reference-dependent evaluation. (1) Q-score is the fraction of correctly aligned residue pairs in a test alignment among all aligned residue pairs in a reference alignment. In this paper, the range of Q-score is from 0 to 100 (e.g. 100 means 100% agreement with reference).The reference alignments were constructed by several structure alignment methods: DALI ⁵⁹, TM-align⁶⁵, Matt ⁷² and Deepalign ⁷³. (2) The number of alignment blocks improved and deteriorated in different benchmarks after refinement by different SFESA modes. Above-mentioned structural alignment methods are used as references. One alignment block is considered as an improved block when the correctly aligned residue pair number (compared with reference) in the block is increased. One alignment block with less correctly aligned residue pairs (compared with reference) is treated as a deteriorated block. (3) The number of aligned positions improved and deteriorated in different benchmarks after refinement by different SFESA modes. Abovementioned structural alignment methods are used as references. This number provides the residue position-level alignment accuracy comparison.

2. Reference-independent score. Alignment-based GDT-TS ⁶³ score and TM-score ⁶⁵ were used in our study to evaluate alignment quality. GDT-TS score is based on the number of structurally equivalent pairs of C-alpha atoms that are within specified distance cutoffs (1Å, 2Å, 4Å and 8Å) based on the sequence-independent superpositions of two protein structure. TM-score is a simpler template modeling score, which evaluates the similarity of two protein structures in a single superposition by weighting the close atom pairs stronger than the distant matches. For TM-score, a 3D model was built for the query protein by MODELLER ⁸ based on its alignment to the template, and subsequently the score between the query model and the experimental structure was computed.

RESULTS

An overview of the SFESA method for pairwise alignment refinement

SFESA is a post-processing tool that can be applied to any pairwise alignment between a query and a template with known spatial structure. It increases alignment quality by locally shifting residues in alignment blocks defined by template SSEs. First, SFESA recognizes alignment blocks in an existing alignment. Each alignment block corresponds to residues in one SSE of the template and their aligned residues in the query. Then, proceeding from N-terminus to C-terminus, SFESA determines if each alignment block should be changed to one of the alignment variants generated by local shifts. Our analysis of PROMALS alignments revealed that SSEs are often misaligned by several residues. Thus, a better alignment solution can be found within a limited set of local shifts of SSEs (Fig. S1).

SFESA generates N (up to 18) alignment variants (Fig. 1C) by shifting query residues in alignment blocks locally (see MATERIALS and METHODS). Then, both profile-based sequence score (including scoring of secondary structure similarity) and contact-based structure score of aligned residue pairs of the original alignment block and all alignment variants are calculated. We found that a two-filter strategy offers the best performance. The first filter detects alignment variants with a higher combined score I (S_{comb_I}) than the original alignment block. If the original alignment block has the best S_{comb_I}, SFESA keeps it and move to the next alignment block. Otherwise, the alignment variant with the highest S_{comb_I} is selected and passed to the second filter. The second filter compares the selected alignment variant and the original alignment block by using a different combined score. This combined score is either combined score II (S_{comb_II}) or the SVM score (S_SVM) (see MATERIALS AND METHODS). If the selected alignment variant has a higher S_{comb_II} or S_SVM, SFESA accepts the alignment variant. Otherwise, SFESA keeps the original alignment block. This refinement procedure is performed for each block in the alignment, starting from the N-terminal block and moving towards the C-terminus.

Here we report results of four modes for SFESA (see MATERIALS AND METHODS for details): SFESA (O) uses up to 8 variants generated by ±4 shifts that keep the gap patterns in the original alignment block and the Miyazawa-Jernigan (MJ) contact matrix for structure score calculation; SFESA (O+G) uses up to 18 variants by considering gap shifts and the MJ contact matrix; SFESA (O+G+M) uses our newly derived contact matrix in addition to gap processing; SFESA (O+G+M+S) differs from SFESA (O+G+M) in that the S_SVM instead of S_{comb_II} is used in second filter.

Parameter optimization

Using an in-house dataset of 1675 remote homologous domain pairs (see MATERIALS AND METHODS), we optimized the parameters of four SFESA modes: SFESA (O), SFESA(O+G), SFESA(O+G+M) and SFESA (O+G+M+S). Best parameters were found for each mode separately. The Q-score and GDT-TS of the original PROMALS are 62.3 and 0.464, respectively. Each of these SFESA modes improve PROMALS alignments in both reference-dependent (Q-score of DALI) and reference-independent (GDT-TS) assessments. Even the basic mode SFESA (O) that locally shifts up to ±4 residue positions can increase the average DALI Q-score by 2.0 (from 62.3 to 64.3) and the GDT-TS score by 0.008 (from 0.464 to 0.472). By shifting gaps in the original alignment blocks, the mode that considers 18 alignment variants, SFESA (O+G), can increase Q-score by 3.0 (from 62.3 to 65.3) and GDT-TS by 0.012 (from 0.464 to 0.476). Our new contact matrix, used in SFESA (O+G+M), further increases the alignment quality compared to the MJ matrix. The Q-score and GDT-TS improvement over the original PROMALS are 3.6 (from 62.3 to 65.9) and 0.014 (from 0.464 to 0.478), respectively. Finally, SFESA (O+G+M+S), using S_SVM in the second filter instead of S_{comb_II}, increases 3.7 in Q-score (from 62.3 to 66.0) and 0.014 (from 0.464 to 0.478) in GDT-TS. The comparison of numbers of improved and deteriorated alignments also shows that all SFESA modes can improve the original alignments generated by PROMALS (Fig. S2).

The above results are based on the entire training dataset. To address the possibility of overfitting in parameter training, we divided the training dataset into four subsets based on the four SCOP classes: class a (all α proteins), class b (all β proteins), class c (α and β proteins (a/b)) and class d (α and β proteins (a+b)) (Fig. 3). We trained the SFESA (O+G+M) parameters (including our new contact energy matrix) on the SCOP class b alignments and tested these parameters on the four subsets separately. Similarly, we trained the parameters on the SCOP class c alignments. There was no significant drop in Q-score on the class b when using parameters trained on class c (the purple column in Fig. 3 class b) compared to using parameters trained on class b (the green column in Fig. 3 class b) or using parameters derived from all data (the red column in Fig. 3 class b). The average Q-scores of class b using parameters trained on class b, class c and all data are 59.5, 59.3 and 59.4, respectively. Similar results were observed on class c, with no significant Q-score difference between using the parameters trained on the class b (the green column in Fig. 3 class c) and using the parameters trained on the class c (the purple column in Fig. 3 class c). Overtraining was not a major issue even in our very stringent, class-specific cross-validation scheme.

Figure 3. Tests on our training subsets divided by four SCOP classes.

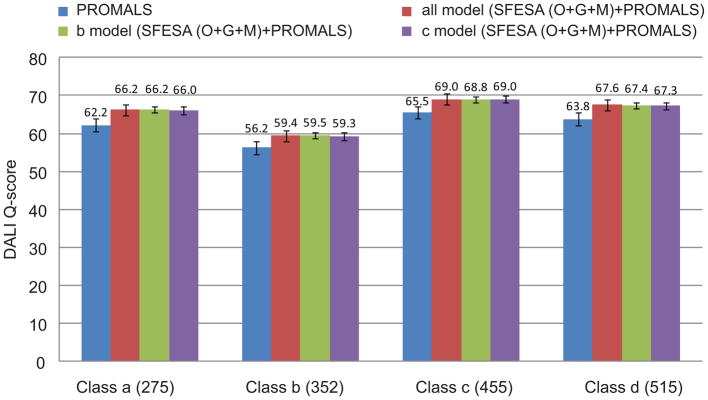
DALI Q-score is compared in different subsets: 275 class a alignments (all α proteins), 352 class b alignments (all β proteins), 455 class c alignments (α and β proteins (α/β)) and 515 class d alignments (α and β proteins (α+β)). The blue column represents the performance of PROMALS alignments. The red column shows the SFESA (O+G+M) results with parameters derived from all data (1675 alignments). The green and purple columns are the SFESA (O+G+M) results trained on class b and class c, respectively. The error bars (standard error of the mean) are showed.

Furthermore, we analyzed the distribution of improved and deteriorated alignment block numbers in one alignment (SFESA (O+G+M+S) vs. PROMALS; DALI as a reference) for our training dataset. We found that SFESA sometimes improved several alignment blocks in one alignment, while mostly deteriorating none or only one alignment block (Fig. 4A). Among 1675 alignments in our training dataset, there are 562 alignments with one improved alignment block while 292 alignments contain only one deteriorated alignment block. There are 268 alignments with two improved alignment blocks while 55 alignments contain two deteriorated alignment blocks. The total number of alignments with more than two improved alignment blocks is 121. In contrast, only 6 alignments contain more than two deteriorated alignment blocks.

Figure 4. Alignment block-level evaluation of SFESA performance on different datasets.

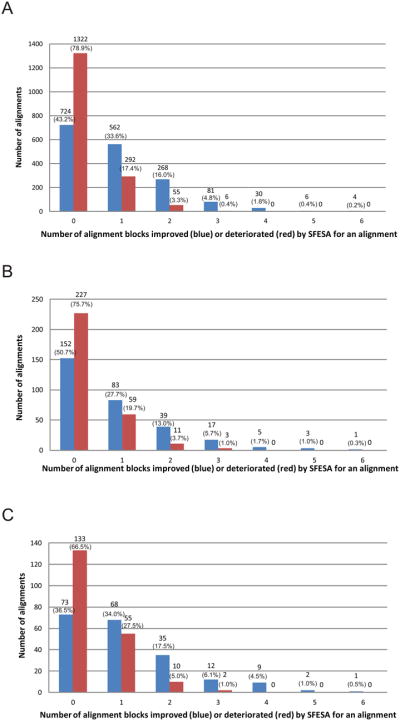
(A) Evaluation on our training dataset (1675 alignments). (B) Evaluation on the MUSTER benchmark (300 alignments). (C) Evaluation on the SALIGN benchmark (200 alignments). SFESA (O+G+M+S) is used to refine alignments generated by PROMALS and Dali structure alignment is used as the reference. The blue column represents the number of alignments in which a certain number of aligned blocks were improved by SFESA. The red column represents the number of alignments in which a certain number of aligned blocks were deteriorated by SFESA. Columns of the “0” in the x-axis show the number of alignments where none of the alignment blocks were improved (blue) by SFESA and the number of alignments where none of the alignment blocks were deteriorated (red) by SFESA. The number of alignment cases in each category and the percentage is shown above each column.

Tests on the MUSTER benchmark

The MUSTER benchmark consists of 300 protein pairs ¹⁶. It is a more challenging benchmark with an average DALI Q-score of 51.6 for PROMALS alignments compared to 62.3 of our inhouse dataset. We used a number of structure-based alignment methods as a reference: DALI⁶⁹, TMalign ⁶⁵, Matt ⁷², MUSTER ¹⁶ and DeepAlign ⁷³. SFESA (O+G+M) and SFESA (O+G+M+S) applied to PROMALS alignments outperform other methods (Table 1), regardless of the reference alignments used. SFESA can at most increase 2.6, 2.1, 2.6, 2.5 and 2.2 in Q-score compared with original PROMALS method when either Dali, TMalign, Matt, Muster or DeepAlign is used as a reference. In terms of Q-score based on DALI reference, all SFESA modes are statistically better than the original PROMALS based on the Wilcoxon signed-rank test (p-value less than 0.005, Table S2). When applied to alignments generated by HHpred and CNFpred, SFESA also shows improved alignment quality in terms of DALI Q-score, although the improvement is smaller (Table 1). Based on the alignment block level and aligned position level comparisons (Table S3–S8), all SFESA modes generate more improved alignment blocks as well as aligned residue pairs than the deteriorated ones when compared with the original PROMALS. The similar trends can be observed in most SFESA modes applied on HHpred and CNFpred (Table S3–S8).

Table 1.

Test on MUSTER database.

Methods	Reference-dependent (Q-score)					Reference-independent (TM-score)
	Dali	TMalign	Matt	MUSTER	Deep Align
PROMALS	51.6	48.1	49.5	51.5	53.5	0.515
SFESA (O)+PROMALS	53.4	49.6	51.5	53.2	55.0	0.521
SFESA (O+G)+PROMALS	53.6	49.6	51.6	53.4	55.1	0.522
SFESA (O+G+M)+PROMALS	54.2	50.2	52.1	54.0	55.3	0.523
SFESA (O+G+M+S)+PROMALS	54.2	50.0	52.0	53.8	55.7	0.525
HHpred	49.3	45.3	46.7	49.0	49.7	0.490
SFESA (O)+HHpred	49.2	45.2	46.8	48.8	49.8	0.490
SFESA (O+G)+HHpred	49.4	45.2	47.0	49.1	50.0	0.491
SFESA (O+G+M)+HHpred	49.4	45.1	47.2	49.0	49.7	0.490
SFESA (O+G+M+S)+HHpred	49.6	45.3	47.3	49.1	49.9	0.491
CNFpred	51.5	48.2	49.2	52.4	53.7	0.511
SFESA (O)+CNFpred	52.0	48.3	49.9	52.5	54.0	0.511
SFESA (O+G)+CNFpred	52.2	48.4	50.1	52.5	54.1	0.512
SFESA (O+G+M)+CNFpred	52.6	48.7	50.4	52.9	54.0	0.512
SFESA (O+G+M+S)+CNFpred	52.7	49.0	50.7	53.3	54.8	0.515

Columns 2–6 indicate five different structure alignment methods to generate reference alignments (Reference-dependent evaluation). Column 7 indicates the average of query model’s TM-score built by Modeller (Reference-independent evaluation). Bold indicates the best performance in the subsection. Bold with underscore indicates the overall best performance in one column. Average Q-score and TM-score are reported.

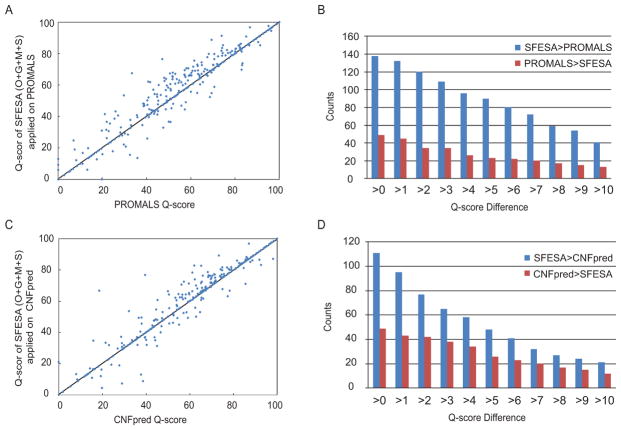
SFESA (O+G+M+S) significantly improves PROMALS alignments on the MUSTER benchmark, making 138 alignments better and degrading 49 alignments (Fig. 5A). In a more detailed comparison, we counted the number of the alignments SFESA improves over PROMALS and the number of alignments PROMALS is descended by SFESA at different Qscore difference cutoffs (Fig. 5B). SFESA (O+G+M+S) improves PROMALS by at least 5 Qscore on 90 alignments and degrades by this margin on 23 alignments (Fig. 5B). SFESA (O+G+M+S) also improved CNFpred alignments on this benchmark (Fig. 5C) with 111 better alignments and 49 worse alignments. SFESA (O+G+M+S) improves CNFpred by at least 5 in Qscore on 48 alignments and failed by this margin on 26 alignments (Fig. 5D).

Figure 5. DALI Q-score for the MUSTER benchmark.

(A) Scatter plot of SFESA (O+G+M+S) Q-score (applied to PROMALS) vs. PROMALS Q-score. Each point represents one domain pair. (B) The number of alignments that SFESA is better than PROMALS in Q-score and the number of alignments that PROMALS is better than SFESA at different Q-score difference cutoffs. (C) Scatter plot of SFESA (O+G+M+S) Q-score (applied to CNFpred) vs. CNFpred Q-score. (D) The number of the alignments that SFESA is better than CNFpred in Qscore and the number of the alignments that CNFpred is better than SFESA at different Q-score difference cutoffs.

Besides the above reference-dependent assessments, reference-independent average TM-score of query models built by MODELLER ⁸ also shows that SFESA can improve PROMALS, HHpred and CNFpred alignments (Table 1, last column). SFESA (O+G+M+S) applied to PROMALS (Table 1, last column) offers the best performance.

Based on the analysis of the improved and deteriorated alignment block numbers in one alignment (SFESA (O+G+M+S) vs. PROMALS; DALI as a reference) for this dataset (Fig. 4B), we also found that SFESA sometimes improved several alignment blocks in one alignment and mostly deteriorated none or only one alignment block. Among 300 alignments in the MUSTER benchmark, there are 83 alignments with one improved alignment block while 59 alignments contain only one deteriorated alignment block. There are 39 alignments with two improved alignment blocks while 11 alignments contain two deteriorated alignment blocks. The total number of the alignments with more than two improved alignment blocks is 26. In contrast, only 3 alignments contain more than two deteriorated alignment blocks.

Tests on the SALIGN benchmark

The SALIGN benchmark consists of 200 protein pairs. Although it has a similar DALI Q-score of 61.4 on PROMALS alignments compared to 62.3 of our inhouse dataset, this benchmark is very challenging because proteins in each pair have very different lengths. SFESA applied to PROMALS shows maximal improvement compared to that applied to HHpred and CNFpred (Table 2). SFESA improves PROMALS Q-scores by 2.5, 1.9, 2.1 and 2.5 when using either DALI, TMalign, Matt or DeepAlign as a reference. For these references, SFESA shows 0.7, 0.5, 0.5 and 0.5 increases for HHpred and 0.6, 0.5, 0.4 and 0.2 for CNFpred. The reference-independent evaluation (Table 2, the last column) shows a similar trend that SFESA has the maximal improvement on PROMALS. The improvement on the SALIGN benchmark is less than that on the MUSTER benchmark, especially for the CNFpred with DALI as a reference (improvement of 1.2 Q-score in MUSTER and 0.6 Q-score in SALIGN). Nevertheless, alignments refined in all SFESA modes are statistically better than PROMALS based on the Wilcoxon signed-rank test (p-value less than 0.005, Table S9) in terms of Q-score based on DALI reference. SFESA modes except SFESA (O) are statistically better than HHpred, despite of an increase of less than 1.0 Q-score on HHpred (Table S9). For CNFpred, the Wilcoxon signed-rank test shows statistically significant improvement in SFESA (O), SFESA (O+G) and SFESA (O+G+M+S) (Table S9) in terms of Q-score. The alignment block level and aligned position level comparisons show that the number of improved alignment blocks or aligned residue pairs is larger than the number of deteriorated ones for all SFESA modes applied on PROMALS and most SFESA modes applied on HHpred and CNFpred (Table S10–S14).

Table 2.

Test on SALIGN database.

Methods	Reference-dependent (Q-score)				Referenceindependent (TM-score)
	DALI	TMalign	Matt	DeepAlign
PROMALS	61.4	59.5	60.2	62.6	0.582
SFESA (O)+PROMALS	62.7	60.5	61.2	63.9	0.585
SFESA (O+G)+PROMALS	63.4	61.0	61.9	64.6	0.588
SFESA (O+G+M)+PROMALS	63.7	61.1	62.2	64.8	0.589
SFESA (O+G+M+S)+PROMALS	63.9	61.4	62.3	65.1	0.589
HHpred	63.0	60.6	62.7	64.4	0.589
SFESA (O)+HHpred	63.1	60.6	62.7	64.4	0.590
SFESA (O+G)+HHpred	63.1	60.6	62.7	64.5	0.590
SFESA (O+G+M)+HHpred	63.7	61.1	63.2	64.9	0.592
SFESA (O+G+M+S)+HHpred	63.5	61.1	63.2	64.8	0.592
CNFpred	64.7	62.2	62.6	66.3	0.595
SFESA (O)+CNFpred	65.1	62.5	62.6	66.4	0.596
SFESA (O+G)+CNFpred	65.3	62.7	62.5	66.4	0.598
SFESA (O+G+M)+CNFpred	64.8	62.2	62.6	66.0	0.595
SFESA (O+G+M+S)+CNFpred	65.2	62.7	63.0	66.5	0.598

Columns 2–5 indicate five different structure alignment methods to generate reference alignments (Reference-dependent evaluation). Column 6 indicates the average of query model’s TM-score built by Modeller (Reference-independent evaluation). Bold indicates the best performance in the subsection. Bold with underscore indicates the overall best performance in one column. Average Q-score and TM-score are reported.

Among 200 alignments in the SALIGN benchmark (SFESA(O+G+M+S) vs. PROMALS; DALI as a reference), there are 68 alignments with one improved alignment block while 55 alignments contain only one deteriorated alignment block (Fig. 4C). 35 alignments contain two improved alignment blocks while 10 alignments contain two deteriorated alignment blocks (Fig. 4C). In addition, the total number of the alignments with more than two improved alignment blocks is 24 while only 2 alignments contain more than two deteriorated alignment blocks (Fig. 4C). Thus SFESA refinement improves many alignment blocks without introducing many incorrectly aligned blocks.

Tests on the SABmark benchmark

We separately tested on SABmark’s two datasets ⁶⁷: the “superfamilies” set and the “twilight zone” set. The “superfamilies” set has an average Q-score of 71.1 for PROMALS alignments. On the “superfamilies” set SFESA improved 1.0, 0.7 and 1.3 for PROMALS, HHpred and CNFpred, respectively (Table 3). The “twilight zone” set is a more difficult benchmark than the “superfamilies” set with an average Q-score of only 46.2 for the PROMALS alignments. On the “twilight zone” set SFESA improved Q-score for PROMALS, HHpred and CNFpred by 1.9, 0.7 and 0.9, respectively (Table 3). Reference-independent average TM-scores of query models built by MODELLER displayed similar trends (Table 3). In terms of Q-score based on SABmark’s own reference, all SFESA modes in “twilight zone” set as well as SFESA (O+G), SFESA (O+G+M) and SFESA (O+G+M+S) in “superfamilies” set are statistically better than the original PROMALS based on the Wilcoxon signed-rank test (p-value less than 0.005, Table S15). Based on the alignment block and aligned position level comparisons, all SFESA modes surpassed the original PROMALS. In terms of Q-score, TM-score and alignment block/aligned position level, most SFESA modes improved HHpred and CNFpred, but not as much as PROMALS (Table 3, table S16–S19).

Table 3.

Test on SABmark database.

Methods On subsets	Reference-dependent (Q-score)		Reference-independent (TM-score)
	SABmark_TWI	SABmark_SUP	SABmark_TWI	SABmark_SUP
PROMALS	46.2	71.1	0.413	0.583
SFESA (O)+PROMALS	47.3	71.3	0.416	0.585
SFESA (O+G)+PROMALS	48.0	71.8	0.416	0.585
SFESA (O+G+M)+PROMALS	47.9	71.9	0.416	0.586
SFESA (O+G+M+S)+PROMALS	48.1	72.1	0.416	0.587
HHpred	40.7	68.9	0.371	0.570
SFESA (O)+HHpred	40.6	69.0	0.371	0.570
SFESA (O+G)+HHpred	41.3	69.1	0.372	0.571
SFESA (O+G+M)+HHpred	41.4	69.6	0.372	0.571
SFESA (O+G+M+S)+HHpred	41.3	69.4	0.373	0.571
CNFpred	41.5	66.1	0.368	0.543
SFESA (O)+CNFpred	41.6	66.4	0.367	0.545
SFESA (O+G)+CNFpred	42.3	67.0	0.370	0.545
SFESA (O+G+M)+CNFpred	42.4	67.4	0.371	0.545
SFESA (O+G+M+S)+CNFpred	42.2	66.9	0.370	0.545

Columns 2–3 indicate the alignment Q-score based on their reference on two subsets of the SABmark benchmark: “twilight zone” and “superfamilies” respectively (Reference-dependent evaluation). Columns 4–5 indicate the average of query model’s TM-score built by Modeller on two subsets of the SABmark benchmark: “twilight zone” and “superfamilies” respectively (Reference-independent evaluation). Bold indicates the best performance in the subsection. Bold with underscore indicates the overall best performance in one column.

Based on the analysis of the improved and deteriorated alignment block numbers in one alignment (SFESA (O+G+M+S) vs. PROMALS; compared with SABmark’s own reference) for “twilight zone” set (Fig. S3, 209 alignments totally), there are 45 alignments with one improved alignment block while 21 alignments contain one deteriorated alignment block. And there are 8 alignments containing more than one improved alignment blocks in contrast to 5 alignments containing more than one deteriorated alignment blocks. The same analysis on “superfamilies” set (Fig. S4, 425 alignments totally) shows a similar trend. There are 71 alignments with one improved alignment block while 37 alignments contain one deteriorated alignment block. And there are 16 alignments containing more than one improved alignment blocks while 6 alignments have more than one deteriorated alignment blocks in each alignment. Thus SFESA improves quality of several alignment blocks while avoiding deterioration of many alignment blocks in one alignment.

Tests on the PREFAB benchmark

The PREFAB benchmark ⁶⁸ contains 1682 protein pairs and is less difficult compared to the previous three benchmarks, with a PROMALS Q-score of 80.3. PREFAB reference alignments⁶⁸ are based on a consensus of FSSP ⁶⁹ structural alignment and CE alignment ⁷⁰. SFESA (O+G+M+S) can increase the Q-score of PROMALS (80.3) and CNFpred (80.5) to 81.3 (Table 4, the first column).

Table 4.

Test on PREFAB database.

Method	All (1682/23.0)	Set 1 (420/6.8)	Set 2 (421/14.9)	Set 3 (420/23.1)	Set 4 (421/48.4)
PROMALS	80.3	56.7	80.2	90.0	94.2
SFESA (O)+PROMALS	80.4	57.4	80.5	89.9	93.8
SFESA (O+G)+PROMALS	80.1	57.6	80.3	89.4	93.2
SFESA (O+G+M)+PROMALS	80.3	57.3	81.1	89.7	93.1
SFESA (O+G+M+S)+PROMALS	81.3	58.7	81.7	90.5	94.1
HHpred	78.0	46.6	80.2	90.3	94.7
SFESA (O)+HHpred	78.0	46.7	80.2	90.3	94.7
SFESA (O+G)+HHpred	78.3	47.2	80.6	90.5	94.9
SFESA (O+G+M)+HHpred	78.6	47.8	81.3	90.6	94.8
SFESA (O+G+M+S)+HHpred	78.6	47.7	81.1	90.6	94.9
CNFpred	80.5	56.3	81.7	89.6	94.5
SFESA (O)+CNFpred	81.0	57.1	82.1	90.2	94.6
SFESA (O+G)+CNFpred	81.2	57.3	82.3	90.3	94.7
SFESA (O+G+M)+CNFpred	81.2	57.2	82.8	90.3	94.6
SFESA (O+G+M+S)+CNFpred	81.3	57.5	82.8	90.4	94.6

Average Q-score is reported. The total 1682 PREFAB alignments are divided to four semi-equalsized sets according to sequence identity of the PROMALS alignment. The number of alignments and the average sequence identity are in parenthesis beneath the set names. Bold indicates the best performance in the subsection. Bold with underscore indicates the overall best performance in one column.

In addition, we divided the PREFAB alignments into four equal-sized subsets by sequence identity (Table 4). The average sequence identities of the four subsets are 6.8%, 14.9%, 23.1% and 48.4%. In “set1” and “set2” subsets with the lower sequence identity (6.8% and 14.9%), we observed the most prominent improvement of more than 1.0 Q-score unit over PROMALS, HHpred and CNFpred. In the other two less difficult subsets (“set3” and “set4”, Table 4), SFESA improvement is less dramatic. According to the Wilcoxon signed-rank test, there are statistically significant improvement in “set1” and “set2” (Table S20) in terms of Q-score based on PREFAB’s own reference. We also observed more improvement in “set1” and “set2” compared with “set3” and “set4” based on alignment block and aligned position comparisons (Table S21–25).

Based on the analysis of the improved and deteriorated alignment block numbers in one alignment (SFESA (O+G+M+S) vs. PROMALS; PREFAB’s own reference) for this dataset (Fig. S5–S9), we also found that SFESA sometimes improved several alignment blocks in an alignment and mostly deteriorated none or only one alignment block. Among 1682 alignments in the PREFAB benchmark, there are 390 alignments with one improved alignment block, while 249 alignments contain only one deteriorated alignment block. And there are 90 alignments containing one improved alignment blocks while 36 alignments contain two deteriorated alignment blocks in each alignment. In addition, 21 alignments are found to have at least two improved alignment blocks, and 17 alignments contain more than two deteriorated alignment blocks.

Examples of alignments improved by SFESA

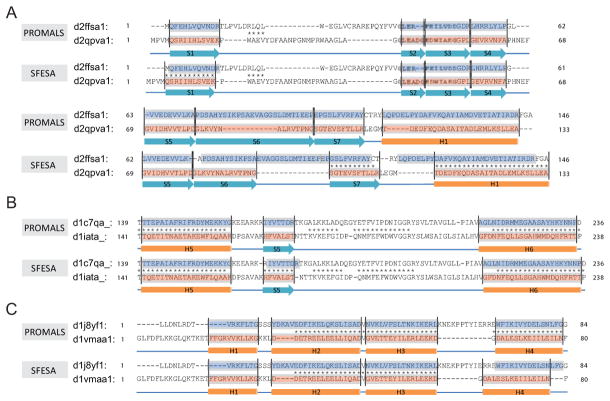
Here, we discuss four examples of alignments improved using SFESA. In the first, and very challenging, example (Fig. 6A), SFESA refined the PROMALS alignment of two SCOP domains from the same superfamily (d.129.3): d2ffsa1 (query) and d2qpva1 (template). The PROMALS alignment of these domains consists of eight alignment blocks. All eight blocks are misaligned by PROMALS, and the Q-score (with the DALI alignment as reference) is only 3.2 (4 out of 125 aligned positions correctly aligned). SFESA changed the alignment in five blocks (S1, S5, S6, S7 and H1) and improved three of them (S1, S7 and H1), resulting in a Q-score of 39.2 (49 out of 125 aligned positions correctly aligned). We observed that both sequence score and structure score contribute to the selection of a better alignment variant. For example, the S1 alignment block in the original PROMALS alignment has a SFESA sequence score of −1.8 and a structure score of 6.0, which increased to 1.8 and 11.4, respectively, in the SFESA alignment.

Figure 6. Three examples of SFESA refinement.

(A) The alignments between d2ffsa1 (query) and d2qpva1 (template) generated by PROMALS and SFESA (O+G) + PROMALS. (B) The partial alignments between d1c7qa_ (query) and d1iata_ (template) generated by PROMALS and SFESA (O) + PROMALS. (C) The alignments between d1j8yf1 (query) and d1vmaa1 (template) generated by PROMALS and SFESA (O) + PROMALS. The pink boxes show the SSEs recognized from template and the blue boxes are those regions in the query aligned to such SSEs. Each corresponding blue and pink regions is an alignment block. The asterisk between two aligned residues indicates this aligned residue pair is in agreement with DALI alignment (reference).

The second example shows a case with the Q-score increase (1.7) close to the average Q-score difference (the DALI alignment as reference) (Fig. 6B). The two SCOP domains d1c7qa_ (query) and d1iata_ (template) are from the same SCOP superfamily (c.80.1). Both of them are phosphoglucose isomerases but are from different organisms. The PROMALS alignment of these domains consists of 22 alignment blocks (13 helices and 9 strands). The original PROMALS alignment has a Q-score of 72.4 when compared with the DALI alignment (296 out of 409 aligned positions correctly aligned). SFESA changed the alignment in one block (S5) and improved this strand, resulting in a Q-score increase of 1.7 (7 out of 409 aligned positions were corrected by SFESA).

Besides these improved alignments, there are a few alignments with accuracy decrease. The third example shows an alignment with accuracy dropping more than 20 Q-score units (Fig. 6C). These two SCOP domains d1j8yf1 (query) and d1vmaa1 (template) are from the same SCOP superfamily (a.24.13, Domain of the SRP/SRP receptor G-proteins). SFESA incorrectly refined one of the four blocks corresponding to alpha-helices (H4) and led to a decrease of Q-score from 78.7 (48 out of 61 aligned positions correctly aligned) to 52.5 (32 out of 61 aligned positions correctly aligned) when compared with the DALI alignment. We observed a large increase of sequence score (from −1.32 to 4.13) after shifting +3 residues. On the other hand, the original alignment block and the +3 alignment variant have the similar structure score (original: 0.96, +3 variant: 0.94). Thus, +3 alignment variant has the highest combined score 1 among the original alignment block and 8 alignment variants, and this variant has a higher combined score 2 when compared with the original alignment block. As a result, SFESA incorrectly refined the alignment block by +3 shifting. The procedure of +3 shifting in SFESA introduced additional gaps to the right side of the template element (Fig. 6C). However, no gap penalty is used in SFESA, as our scoring is restricted to the alignment block. From the structure similarity perspective, the C-terminal helix (H4) has a relatively large RMSD (2.81Å) based on DALI alignment compared with other three helices (H1: 2.21Å, H2: 1.47Å and H3: 1.97Å), suggesting that elements showing large structural deviations between target and template are prone to mistakes by SFESA.

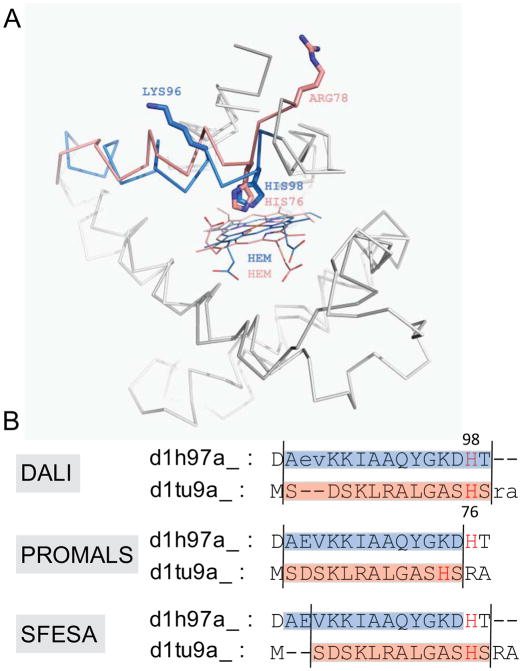
Prediction of active site residues is one of the key goals in alignment construction. Misaligned active site residues can lead to faulty experimental design. The last example shows (Fig. 7) that SFESA can correct a misaligned active site residue in the alignment of two SCOP domains d1h97a_ (query) and d1tu9a_ (template). Both protein domains are from the SCOP globin family: d1h97a_ is a trematode hemoglobin ⁷⁴, and d1tu9a_ is a globin-like hypothetical bacterial protein (unpublished). HIS76 in the template and HIS98 in the query are the active site residues (heme-binding) and they occupy structurally equivalent positions according to the DALI alignment. However, in PROMALS alignment, HIS76 in the template is misaligned to LYS96 in the query (Fig. 7). All SFESA modes succeed in recognizing the misaligned alignment block and correcting it by a shift of -2 (Fig. 7).

Figure 7. An example of SFESA correction of a misaligned active site residue.

(A). Superposition of d1h97a_ (query) and d1tu9a_ (template) based on the DALI structure alignment (reference). The blue (query) and pink (template) α-helical regions indicate the alignment block. The histidine residues are the active site residues in contact with hemes (shown in lines). LYS96 and HIS98 in the query are incorrectly aligned to HIS76 and ARG78in the template in the PROMALS alignment, respectively. The sidechains of these residues are shown in sticks. (B). Alignments of DALI (reference), PROMALS and SFESA in this region. All SFESA modes can generate such alignment refinement.

DISCUSSION

For divergent sequences, alignments generated by automatic methods are error-prone despite significant research efforts. Alignment errors are still the major reason for poor quality of homology models. Alignment refinement is a promising addition to existing alignment methods. Alignment methods often misalign secondary structures by a few residues, and more accurate solutions can be found within a limited set of local shifts of SSEs (Fig. S1). SFESA aims to refine pairwise alignments by locally shifting alignment blocks defined by template SSEs to correct misaligned blocks.

A limitation of the SFESA approach is that shifting involves only residues within an alignment block and its adjacent loops. Residues in other alignment blocks are not allowed to move into the current alignment block. Therefore, SFESA will not correct blocks with residues misaligned to non-equivalent SSEs. However, such errors frequently occur in alignments of proteins with very different lengths, e.g., those in the SALIGN benchmark. Thus, SFESA shows less improvement on SALIGN alignments compared to the other benchmarks. Alternative methods need to be developed to deal with non-local alignment errors.

Alignment errors are frequently caused by incorrect placement of gaps. The simplest SFESA (O) mode keeps original gap patterns while shifting SSEs. This approach generates up to 8 alignment variants for an alignment block. Considering that gaps rarely occur within SSEs, we implemented the SFESA (O+G) mode in which all gaps in an alignment block are moved to one side of the block. This gap shifting approach allows generation of up to 18 alignment variants. Our results show that SFESA (O+G) improves alignments more than SFESA (O).

In addition to the profile-based sequence score, we included a contact-based structure score. A residue-residue contact is defined as a residue pair within a distance cutoff. In the template, a residue’s contacts contribute to its structural environment. The correctly aligned equivalent residues in the query should pack more favorably in such a structural environment than incorrectly aligned residues. Thus, the estimated contact energy is an essential source of structural information and could be used as a scoring function for alignment evaluation. Unlike position-specific profile scores used in programs such as PSI-BLAST and HHpred, pairwise contact scores, in the form of two-body interactions, are difficult to incorporate into a polynomial-time algorithm (e.g. dynamic programming) to find the optimal alignment, since the interaction partners for a position are not known before the alignment is obtained. Thus, heuristic methods are needed to deal with this NP-hard problem ⁷⁵, such as linear programming ^76–77, branch and bound ^78–79 and dead end elimination ⁸⁰. However, our task is to refine an existing alignment. Using the existing alignment, contacts for a position in the query can be deduced from those contacts defined in its aligned position in the template and the query-template alignment. The resulting contact score is a positional score like the profile-based sequence score. If the initial alignment is generally accurate, with only a few blocks misaligned, such a deduction works well.

We tested a number of contact energy matrices to derive the contact-based structure score. Firstly, we used Miyazawa and Jernigan (MJ) ⁵⁸ contact energy matrix in SFESA (O) and SFESA (O+G). This matrix was designed for threading improved alignments. Secondly, we designed secondary structure-dependent contact energy matrices (data not shown), but they did not lead to additional improvement. Thirdly, we tested four body contact potentials ⁸¹, and they also did not give promising results. These more complex matrices were not designed for the alignment refinement task. Since our task is to select the most accurate alignment among a set of alignment variants generated by local shifts, we finally computed a new contact energy matrix specific for this task by log-odds scoring that compares contacts deduced from the correctly aligned positions to those deduced from the incorrectly aligned positions. Using the new contact energy matrix, SFESA (O+G+M) outperformed SFESA (O+G) using the MJ matrix. Another direction to improve contact energy is to explore the definition of contacts. MJ contacts are limited to one fixed distance (6.5Å) between centers of side chains. We tested several definitions of contacts to deduce our contact energy matrix. The best definition was a fixed distance (6.5Å) between any side chain atoms of two residues. A number of distance-based potentials such as DFIRE ⁸², DOPE ⁸³ and EPAD energy ⁸⁴ have been proposed, and some of them consider side chain orientation-dependent terms ^85–86. Many of these potentials are all-atom based, and their application to alignment refinement would require constructing structure models at the atomic level. A simple coarse-grained residue-contact energy matrix we used may be more appropriate for alignment scoring than atomic-level energy potentials, because atomic details of contacts may differ greatly between distant homologs, while residues could still be in similar environments and the residue-residue contacts for homologous positions are largely preserved in the structures of the template and the query.

SFESA uses a combination of profile-based sequence score and contact-based structure score to maximize the chance that the correct alignment variant is selected. First, we tested a one-filter strategy by choosing the variant with the best combination score after weight optimization. However, this strategy resulted in many false positives, i.e., the alignment variant with the best score has, on average, fewer correctly aligned positions. In practice, we found that a two-filter strategy performs better. The first filter is to inspect if there are any alignment variants with a higher combined score I. If not, the original alignment block is kept. Otherwise the alignment variant with the highest combination score is selected and passed into the second filter. If this variant has a higher combination score II than the original alignment block, the alignment variant is accepted. Otherwise the original alignment block is kept. The optimal weights for sequence vs. structure score are different in the two filtering steps. More weight is placed on the sequence score in the first filtering step, but the opposite is true for the second step.

We observed that contact-based structural information can improve alignment, but it has limitations. We found that this structure scoring works well when there are sufficient contacts in the template as well as sufficient corresponding aligned residues in the query. However, if an SSE is involved in too few contacts (e.g. exposed edge β-strands) the remaining contacts are insufficient to define a complete structural environment and SFESA is less effective. To probe the effects of contact number and secondary structure type, we divided alignment blocks in our inhouse dataset into three categories: helix, edge strand (with hydrogen bonds on only one side) and non-edge strand (with hydrogen bonds on two sides) (Table S26. Edge strands have fewer contacts (average contact number is 12.2) than non-edge strands (average contact number is 25.7). Indeed, SFESA is more likely to succeed in correctly shifting non-edge strands (3.0 success/failure rate) than edge strands (1.5 success/failure rate) (Table S26). The helices have an average contact number of 23.7 and have a 1.8 success/failure rate. Moreover, success/failure rate positively correlates with the increase of contact number for SSEs in each of the three categories. For example, helices with less than 11 contacts have a 0.8 success/failure rate while helices with more than 36 contacts have a 9.8 success/failure rate. The same general trend is also observed in edge strands and non-edge strands. Thus, SFESA performs better when there are more contacts in an alignment block.