Methicillin-resistant Staphylococcus aureus in hospitals and the community: Stealth dynamics and control catastrophes

Abstract

Methicillin-resistant Staphylococcus aureus (MRSA) represents a serious threat to the health of hospitalized patients. Attempts to reduce the spread of MRSA have largely depended on hospital hygiene and patient isolation. These measures have met with mixed success: although some countries have almost eliminated MRSA or remained largely free of the organism, others have seen substantial increases despite rigorous control policies. We use a mathematical model to show how these increases can be explained by considering both hospital and community reservoirs of MRSA colonization. We show how the timing of the intervention, the level of resource provision, and chance combine to determine whether control measures succeed or fail. We find that even control measures able to repeatedly prevent sustained outbreaks in the short-term can result in long-term control failure resulting from gradual increases in the community reservoir. If resources do not scale with MRSA prevalence, isolation policies can fail “catastrophically.”

Methicillin-resistant Staphylococcus aureus (MRSA) is one of the most widespread and virulent nosocomial pathogens. It is usually resistant to multiple antibiotics, making infections difficult to treat, and accounts for an increasing proportion of staphylococcal infections among hospitalized patients in countries where it has become established. It appears to add to the total burden of staphylococcal infection in hospitals, rather than replacing methicillin-sensitive S. aureus (MSSA), and is associated with a sharp rise in mortality attributable to staphylococcal infection (1). Although S. aureus is carried asymptomatically in ≈30% of healthy adults (the vast majority being MSSA), it is a major cause of invasive disease among hospitalized patients.

The recent emergence and transmission of strains with full resistance to glycopeptides (2) (until recently, the only antibiotic for which resistance had not been seen in vivo in S. aureus) and reports of resistance to linezolid (3, 4), the only commercially available oxazolidinone (the only new class of antibiotic for >20 years), make development of effective policies to control the spread of MRSA an urgent priority.

At present, control policies primarily consist of the isolation of both infected and colonized (asymptomatic) patients and increased staff hygiene measures (principally handwashing compliance). Both of these are intended to reduce patient-to-patient transmission mediated by transiently colonized healthcare workers. In the strongest form of isolation, patients carrying MRSA are placed in dedicated isolation units (IUs). If operated appropriately with designated staff, such units should be effective at preventing almost all transmission to patients elsewhere in a hospital.

Despite a body of evidence that such measures can, in combination, be effective at reducing transmission (5), they have met with mixed success both at the hospital and national levels. Some countries, such as Denmark and The Netherlands, have succeeded in maintaining MRSA at very low levels by using control policies based on the prompt isolation of MRSA-positive patients (6, 7). In this situation, MRSA is limited to “epidemic” behavior; long periods without MRSA are punctuated by short outbreaks of infection, often traceable to imported cases. Elsewhere, similar approaches have failed and an endemic state is attained (i.e., MRSA is continuously present). Thus, in England and Wales, the “search and destroy” approach recommended by national guidelines was abandoned by many hospitals in light of limited resources (8). Subsequent guidelines (which advocated an approach targeted to protect the most vulnerable patients) were forced to recognize that higher MRSA levels had made the original more stringent control measures infeasible (9). Over this period, MRSA increased from <2% of S. aureus bacteraemias in 1990 to 42% in 2000 (10, 11).

Currently, MRSA as a proportion of invasive S. aureus isolates ranges from <1% in hospitals in Denmark and the Netherlands to 44% in the United Kingdom and Greece (data are from European Antimicrobial Resistance Surveillance System, www.earss.rivm.nl).

At the hospital level, stringent isolation measures in conjunction with other interventions appear, in some cases, to have contributed to controlling MRSA, whereas in others, these measures have been unable to prevent MRSA from becoming endemic (5). Local control failure is often associated with primary isolation facilities becoming overwhelmed (12–14).

Here we use a simple stochastic mathematical model of MRSA transmission to explore the conditions under which isolation policies can successfully control MRSA transmission, both preventing an endemic state, and eradicating MRSA where it is already endemic. The results show that control by isolation induces bistability and that a switch from low to high prevalence can be explained in terms of catastrophic failure of control. We conjecture that this dynamic has relevance for all situations where curtailment of the infectious period is used as a control measure and the effort is resource-limited.

Methods

To capture transmission dynamics without isolation, we modeled a fixed capacity hospital, where patients may either be MRSA positive (whether infected or colonized) and infectious, or MRSA negative and susceptible to infection/colonization. We assumed that all MRSA transmission took place in the hospital. No explicit assumptions about the transmission route were made, but new cases occurred at a rate proportional to the product of the number of colonized/infected and susceptible patients in the hospital (the mass action assumption) (15). When discharged from the hospital, patients entered a population of former patients, where they were either free of MRSA or colonized with the organism. The rate of readmission of former patients decreased as the time since hospital discharge increased, in accordance with observed data (modeled by allowing former patients to move into compartments with lower hospitalization rates). Every discharged patient was immediately replaced by a new admission from the community. We assumed no difference in the rate at which MRSA carriage was lost between hospitalized patients and those in the community.

To investigate the impact of isolation, we considered the addition of a fixed capacity IU. The unit was assumed to prevent all transmission from isolated MRSA-positive patients to MRSA-negative patients elsewhere in the hospital. All patients were still admitted to the general hospital population, but provided there was spare isolation capacity, the rate at which MRSA-positive patients were isolated was set to the rate at which these patients were detected. Otherwise, it was taken as the minimum of the detection rate and the rate of discharge of isolated patients. We assumed that a fraction of isolated patients were successfully cleared of MRSA carriage at the time of discharge from the IU. This model reduces to the previous model if the number of isolation beds or the isolation rate is set to zero.

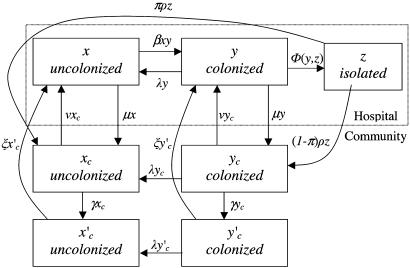
The differential equations specifying these models in deterministic form are given in the appendix and the model illustrated schematically in Fig. 1. In the stochastic formulation the differential equations were replaced by corresponding Poisson processes with time-varying intensities. These stochastic models were investigated with Monte Carlo simulation experiments using standard techniques (16).

Fig. 1.

Flow diagram of the model with the IU.

Estimates of Reproduction Numbers. In the early stages of an epidemic when prevalence is very low or in settings without endemic MRSA the depletion of susceptibles can be ignored and the epidemic approximated by a branching process. If the patients who are MRSA positive on admission can be distinguished from the new hospital-acquired cases this approximation allows estimates of the reproduction number associated with a single hospital admission (R_A).

Standard approaches to estimating reproduction numbers using the number of primary and secondary cases condition on extinction of the epidemic, and are thus not suitable when the reproduction number could be greater than one. The modified approach we used overcomes this problem by considering outbreaks above a threshold size to be censored (17). We assumed a geometric distribution for the number of secondary cases caused by each primary case and a threshold level of one case per week to obtain a maximum likelihood estimate for R_A.

Parameter Values. Parameter values were estimated from sources identified by a systematic review of the MRSA control literature (Table 1) (5). No published data were available for patient readmission rates, and for these we used data from unique patient episodes over 1 year from a 1,000-bed teaching hospital (5). Maximum likelihood estimates were obtained for patient discharge and readmission rates and persistence of MRSA colonization.

Table 1. Parameters used in the model.

Parameter	Symbol	Default values (range)	Source
Transmission rate	β	Chosen to give R0 values ranging from 1.1 to 1.3
Isolation rate, days-1	ϕ	0.1 (0.02–0.1)
Number of beds in isolation unit	ni	20 (5–30)
Number of beds in hospital	n	1,000
Community population size	Nc	1.7 × 105	Defined by other parameters
Mean duration of carriage, days	1/λ	370	Scanvic et al. (18)
Mean length of stay, days	1/μ	8	Local data
Readmission rate
High, days-1	ν	0.0057	Local data
Low, days-1	ξ	0.00063	Local data
Rate of change from high to low readmission rate, days-1	γ	0.030	Local data
Mean length of stay in isolation, days	1/ρ	20	Fitzpatrick et al. (19)
Proportion of isolated patients cleared of MRSA	π	0.25	Fitzpatrick et al. (19)

Results

Dynamics Without Isolation Measures. In the absence of effective isolation of patients carrying MRSA, two key numbers govern the dynamics: R_A, the single admission reproduction number, and R₀, the basic reproduction number. We define R_A as the average number of secondary cases caused by one primary case when other patients are susceptible during a single hospital admission of the primary case. R₀ is the average number of secondary MRSA cases caused by one primary case over all admissions of the primary case until carriage is cleared, again assuming that all other patients are susceptible. R_A corresponds to the basic reproduction number used in previously published hospital epidemiology models (20–22). In contrast, we explicitly consider repeated admissions in calculating R₀; these are important because MRSA carriage can persist for several months (18). Clearly, R_A ≤ R₀.

Three distinct patterns of behavior are possible. If 0 < R₀ < 1, there can never be a major outbreak (regardless of the value of R_A). Although some transmission will still occur, it will be restricted to sporadic self-limiting clusters of secondary cases when primary MRSA cases are imported into the hospital. When R₀ > 1 and R_A > 1, the admission of an MRSA-positive patient to the hospital is able to cause an immediate major outbreak leading to the rapid establishment of endemic MRSA. Faced with repeated introductions, endemic MRSA will be inevitable.

The third scenario is especially pertinent (Fig. 2 a–c, e, and g). When R₀ > 1 but R_A < 1, there will be insufficient transmission to sustain an outbreak in the short term: again sporadic, self-limiting transmission will be seen, and all outbreaks will appear to be controlled. However, repeated admission provides an opportunity for an infectious case to spark many such self-limiting outbreaks, each potentially resulting in several further cases. There is now a chance that the linked outbreaks become more frequent and of greater duration, eventually resulting in endemic MRSA. If there are repeated challenges, despite the short-term successes, eventual long-term control failure is inevitable.

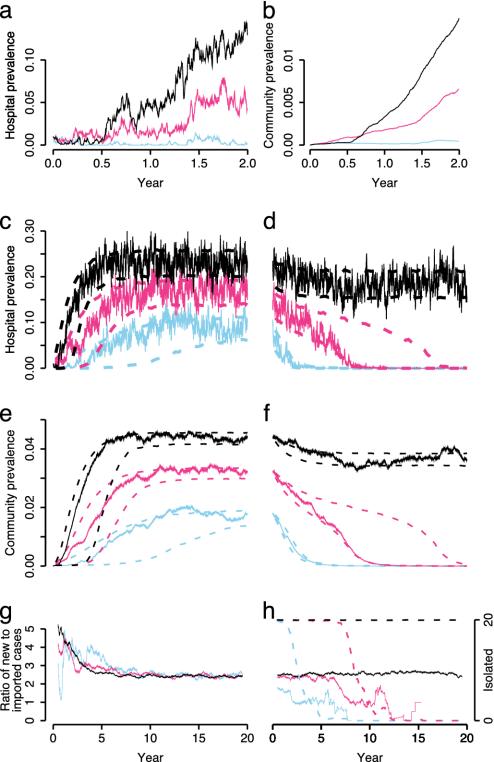
Fig. 2.

Simulation output from the stochastic model with three R₀ values: 1.1 (blue); 1.2 (red); and 1.3 (black). Respective R_A values are 0.77, 0.85, and 0.92. (a) Hospital prevalence over 2 years. Ten hospitalized patients were initially colonized with MRSA. (b) Corresponding community prevalence. (c) The same simulation runs over 20 years (solid lines). Dashed lines indicate 10th and 90th percentiles calculated from 1,000 simulations conditioning on fadeout (i.e., extinction of the epidemic) not occurring (40, 16, and 9% of simulations faded out by chance for R₀ values of 1.1, 1.2, and 1.3, respectively). (d) Hospital prevalence after opening a 20-bed IU starting from the endemic level reached in c. Dashed lines indicate 10th and 90th percentiles from 1,000 simulations. (e and f) Community prevalence corresponding to c and d. (g and h) Ratio of new hospital-acquired to imported cases corresponding to single runs in c and d (1 year moving average). Dashed lines in h shows the number of isolated patients (1 year moving average).

For the single run with the lowest transmissibility (Fig. 2 a–c, blue line, R₀ = 1.1), MRSA levels remain low for >2 years. During this period, only clusters of limited extent are seen. Eventually, as community prevalence rises and the number of imported cases increases, MRSA becomes endemic to the hospital. Similar patterns on a shorter time scale are seen for higher R₀ values. The 10th percentile lines show that many epidemics remain at very low levels for several years before taking off.

There are three other important features of these results. First, although MRSA prevalence approaches a steady endemic level in a sigmoidal fashion, there are large stochastic fluctuations in the hospital prevalence. Because these may appear as trends even over time scales as long as 3 years, naïve assessments of such time series may mistakenly attribute these changes to external causes (5). Second, although the increase in hospital prevalence is driven by a build-up of cases in the community (Fig. 2 b and e), the absolute community prevalence remains low. For the scenario most representative of U.K. hospitals (blue line), the predicted community prevalence of between 1% and 2% is in accordance with estimated values (23). This stable community prevalence is predicted even though all transmission is assumed to occur in the hospital. Third, although the early stages of the epidemic are dominated by hospital-acquired cases, over time, the ratio of new nosocomial acquisitions to imported cases decreases, approaching a stable level that is independent of the within-hospital transmission rate (Fig. 2g).

Model with Isolation Measures. When a 20-bed IU is introduced to control endemic MRSA that has reached equilibrium levels (Figs. 2 d, f, and h), we find that, in the low and intermediate transmissibility scenarios, MRSA is always eradicated eventually, although this takes several years. Again, stochastic fluctuations mean that there are frequent and extended reversals in trend. For the intermediate level of transmissibility, there is large variation between simulation runs in the time to eradication, which frequently exceeds 15 years. Eradication occurs even though the IU is initially fully occupied (Fig. 2h, dashed lines), and no effective control measures are in place for unisolated patients. During the course of eradication, the proportion of MRSA cases that are newly acquired decreases substantially (Fig. 2h, solid lines).

In contrast, in the high transmissibility scenario the IU is again initially fully occupied, but thereafter it remains at full capacity. Eradication is not achieved, and the system reaches a new stable endemic level only slightly lower than that achieved without control measures.

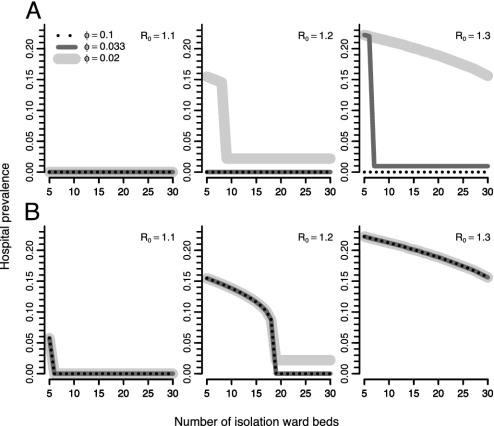
An unusual and important feature of this system is that the final state can depend critically on the timing of interventions (Fig. 3). This is a consequence of the existence of two stable equilibria over a wide range of parameter values. When isolation is in place from the start of the epidemic (Fig. 3 Upper) the system reaches the low stable equilibrium (total eradication, or a very low level of MRSA). At this low equilibrium, the IU is never full, and MRSA patients are isolated as soon as they are identified. However, if the IU is introduced when MRSA is at a high-level (Fig. 3 Lower), it will fill up immediately; now the rate at which newly detected MRSA cases can be isolated is limited by the rate at which patients leave the IU. Thus, the high equilibrium level is unaffected by the detection rate, but decreases as the IU size increases. The greater patient turnover associated with the larger IU enables faster patient isolation and hence decreased transmission. In contrast, the level of the lower equilibrium decreases with a higher detection rate, but is not affected by the IU size because there is always spare capacity.

Fig. 3.

Hospital prevalence at the stable equilibria (deterministic model) as a function of IU size, isolation rate (φ), and R₀.

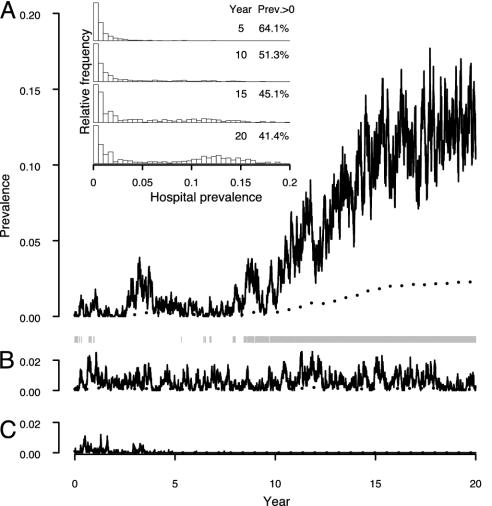
Although Fig. 3 represents the deterministic equilibria, in practice stochastic effects will be important in populations as small as those under consideration here. These effects mean that there can be a nonnegligible probability of the system jumping (by chance) from the low to the high stable equilibrium (Fig. 4). Three runs are shown, with identical starting conditions and parameter values. In run A, a low prevalence is maintained for ≈10 years, despite occasional episodes when the IU becomes full. However, unusually large outbreaks lead to increases in the community prevalence, resulting in more patients who are MRSA positive on admission. Eventually, the IU becomes full on an almost permanent basis, causing the time to effective isolation of patients to increase, pushing the system to the high endemic state.

Fig. 4.

Three simulation runs with the same parameter values [10-bed IU, R₀ = 1.2, isolation rate (φ) = 0.02] and the same starting conditions (0.1% of community population initially carrying MRSA, all with a low hospitalization rate). Run A shows a stochastic transition from the low to high stable state; run B shows persistence in the low stable state; run C shows stochastic fadeout. Hospital (solid lines) and community (dotted line) prevalence are shown. Gray bars underneath run A indicate periods when the IU is full. (Inset) Results at 5-year intervals of 1,000 simulations with the same parameters and starting conditions. The percentage of simulation runs where stochastic fadeout has not occurred is shown in the column headed Prev. > 0.

Run B shows that the system can stay in the low endemic state over long periods, without explosive increases in MRSA numbers. In run C, a third pattern is seen: fadeout occurs (i.e., the epidemic comes to an end) after ≈5 years. Even though, in this case, an endemic state never becomes established, MRSA is able to persist for a long time because of multiple reintroductions that cause a series of clusters of cases.

The Fig. 4 Inset summarizes the behavior of 1,000 such simulations. After 5 years, ≈36% of runs have faded out by chance, as in run C. The rest are at the low stable level. With time, the runs that have not faded out all have some probability of moving to the high endemic level. After 20 years, in a substantial proportion of the 41% of runs that have not faded out, stochastic control failure has occurred and the system has reached the high endemic level. Once at the high level, the chance of moving to the low endemic level without further intervention is negligible.

Estimates of R_A and R₀. To our knowledge, there are no studies allowing direct estimates of R₀ for MRSA. However, estimates for R_A can be obtained by using a branching process approximation when patients who are MRSA positive on admission can be distinguished from the new hospital-acquired cases.

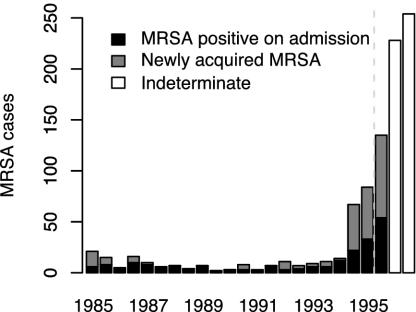
A systematic review identified two major studies allowing direct estimates of R_A (5). The first came from a report describing long-term successful control over a period of 10 years, followed by ultimate control failure in a 1,000-bed tertiary hospital employing an MRSA IU (Fig. 5) (12). We obtained a maximum likelihood estimate for R_A over the period 1985–1995 (and 95% confidence interval) of 0.57 (0.48, 0.68). The 1985–1989 and 1990–1994 data alone gave R_A estimates of 0.34 (0.23, 0.51) and 0.55 (0.41, 0.74), respectively.

Fig. 5.

Time series of MRSA cases detected at a large teaching hospital employing an IU to control MRSA (from Farrington et al., ref. 12). Dashed line indicates the timing of a relaxation of the control measures necessitated by the increasing MRSA numbers.

Therefore, there is good evidence that R_A remains below one throughout the entire period for which it can be estimated. No direct estimates of R₀ values are possible with these data, but using independent estimates of readmission and loss of carriage rates (see Methods) gave 95% confidence intervals for R₀ estimates over the three periods of (0.68, 0.96), (0.32, 0.72), and (0.58, 1.04). These results indicate that, for much of this period, R₀ could have been close to one. Thus, even before the explosive increase in MRSA numbers seen after 1994, there was evidence that the local control policy was vulnerable to long-term failure. Either the emergence of a new strain with enhanced transmissibility or persistence, or reduced effectiveness of isolation measures resulting from local resources becoming overwhelmed (possibly initially because of imported MRSA cases acquired at other hospitals) may have been enough to hasten the transition to endemicity resulting in the observed control failure. The estimated R₀ values will be biased toward zero if some transmission events were missed, if persistence of carriage was underestimated, or if the patients most likely to acquire MRSA were also those most likely to be rapidly readmitted. The branching process approximation will also cause some bias in the same direction, although this is likely to be small in the early stages of an epidemic (17). Together, these biases may mean that the true R₀ value was in fact above one for much of the study period.

The second source uses data from returned questionnaires sent to all Dutch hospitals challenged with MRSA (24). The experience in The Netherlands, where MRSA has been controlled, provides an important contrast to the U.K. Esveld et al. (24) reported that source cases of MRSA imported into hospitals led to secondary spread on four of 73 occasions when patients were immediately isolated according to national guidelines. When there was a delay in isolation or national guidelines were not followed, there was found to be at least one secondary case in 19 of 95 cases. Estimated R_A values (and 95% confidence intervals) are 0.06 (0.02, 0.14) for patients who were isolated immediately, and 0.25 (0.15, 0.40) when there was a delay. Corresponding 95% confidence intervals for R₀, calculated as above, are (0.03, 0.20) and (0.21, 0.56). Thus, in this case, we can be confident that R₀ was below one, and MRSA strains should be controlled in the long-term provided control measures are flexible enough to cope with transient spikes and no large increases in transmissibility or persistence of carriage are seen.

Discussion

For MRSA, as with all infectious diseases, ultimate control depends on keeping the mean number of secondary cases caused by each case below one. In a nonendemic setting, provided that control measures are flexible enough to withstand transient increases in pathogen numbers, if the average number of secondary cases is less than one, all battles against MRSA will eventually be won and so will the war. However, when carriage can persist for a long time, the secondary cases caused by each case may be distributed over several hospital admissions. Reducing only the secondary cases generated during a single admission to below one will lead to control in the short term, but if sufficient transmission occurs during readmissions, an endemic state can occur by stealth: all battles against MRSA will initially be won, but there will be some probability of losing the war. We believe these results have much wider applicability; the model structure is appropriate for any pathogen that is primarily hospital-acquired but can be carried asymptomatically for periods long enough to make reintroduction from the community important.

Prompt and effective patient isolation can contribute to control by reducing transmission. However, because the isolation rate decreases when isolation capacity is exceeded, for a wide range of parameters, high-level persistence can occur even though the control measures could have prevented such a high level from becoming established. This result should apply equally to any effective intervention that fails to scale with the size of the problem. In particular, isolation methods such as staff cohorting (where staff numbers are the limiting factor), if effective at reducing spread, should be subject to similar effects. More generally still, any strategy to control infectious disease (in hospitals or the community) by identification and removal of infectious cases will be vulnerable to such catastrophic control failure if the removal process is constrained.

We found that stochastic fluctuations in MRSA numbers provided one mechanism able to account for transitions from the low to high stable state. Control failure at nearby hospitals provides another. Increases in MRSA numbers at one hospital could be expected to lead to more imported MRSA cases at neighboring hospitals (caused by transfers and overlapping catchment areas). Such increases could cause a hospital to move from low to high stable MRSA levels. This would explain the observed spatial clustering of hospitals with high MRSA levels.

Limitations and Future Developments. The major simplification in these models has been in treating the patient population as homogenous. In practice, those most vulnerable may have longer lengths of stay, higher readmission rates, and require more staff contact, resulting in more transmission to other patients. Patient heterogeneities are likely to increase the propensity of MRSA to cause an epidemic, but, for a given R₀, may give a reduced prevalence. Targeting such high-risk groups for special attention should increase the cost-effectiveness of any control program.

The assumption that there is no transmission in the community cannot be strictly correct, although as a first approximation we believe it is reasonable. Studies have repeatedly found little evidence of sustained community spread of important nosocomial MRSA strains, and most patients carrying MRSA in community prevalence studies have had recent hospital exposure (25, 26). Nonetheless, as Smith et al. (27) observe, even limited community transmission, although difficult to detect, may profoundly alter the dynamics. Quantifying such transmission is an important area for future research.

Recently, MRSA strains have emerged that do seem to spread well in the community. It seems that these have fewer antibiotic-resistance determinants than common hospital strains, and extensive hospital transmission has not been documented (28). Their distinct epidemiology suggests that these strains should not be considered in the same framework as nosocomial MRSA. For strains where transmission in more than one setting is important, the theoretical framework proposed by Smith et al. (27) would be required.

We have assumed that only true MRSA carriers are isolated. Further work is required to understand the dynamic consequences of false positive and negative results, and their interaction with screening effort.

Clinical and Policy Implications. Preventing control failure is a matter of ensuring that sufficient resources can be made available to cope with transient outbreaks. In this regard, the optimal allocation of resources should be determined at regional or national rather than local organizational levels. A policy that allows temporary reallocation of nonlocal resources (such as isolation beds or staff time) when local resources became fully engaged should use no more resources than a policy allocating fixed resources to each hospital, but should have a much greater ability to withstand such challenges.

Monitoring R_A (and estimating R₀), could represent an important component of routine surveillance activities in settings free of endemic MRSA. Such key parameters can be estimated even when detailed epidemiological and genotyping data are not available (29, 30). By identifying policies vulnerable to long-term failure, additional control measures could be taken at an early stage. A similar approach has been advocated for monitoring community pathogens (31).

The model emphasizes the importance of the readmission of already-colonized MRSA patients in determining the long-term dynamics and the role of prompt isolation in curtailing transmission. This suggests that a policy of screening newly admitted patients for MRSA coupled with rapid and effective isolation and treatment could make a major contribution to controlling its spread. Discharge screening followed by eradication therapy or immediate isolation on readmission could also be an effective strategy. We believe that the clinical importance of MRSA should make the rigorous evaluation of such policies a research priority.

Our results show that, although eradication of endemic MRSA is possible, it is far easier to prevent it from becoming endemic in the first place (Fig. 3). With this in mind, we note that MRSA exhibits an “epidemic” population structure, characterized by repeated waves of new successful clones (32). The observed temporal patterns suggest that such clonal replacements are likely to have been driven by external causes, such as changing patterns of antibiotic use, rather than by direct competition. If so, the beginning of each new wave, when prevalence is low, provides an opportunity for isolation to prevent establishment of a new clone, with ultimate eradication following as a result of changing selection pressure. This may have occurred in Denmark, where the prevalence of the predominant MRSA phage type 83A fell from 18% of all hospital S. aureus isolates in 1969 to 0.6% in 1989 (6). Similar reductions in the predominant MRSA phage type were seen in the U.K. and elsewhere over the same period. In Denmark, however, control policies were able to prevent new strains from becoming established. In the U.K., as elsewhere, new epidemic clones later emerged and became endemic to many hospitals. To be effective, detailed surveillance would be required to identify the epidemic threat posed by emerging strains.

Appendix

The deterministic version of the basic model can be described by the differential equations:

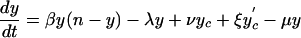[1]

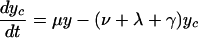[2]

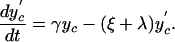[3]

Here, y represents the number of hospitalized (unisolated) patients carrying MRSA, and y_c and y′_c represent the number of MRSA carriers in the community with high and low readmission rates, respectively. Definitions and default values of parameters are given in Table 1. Expressions for R₀ and R_A are given in the supporting information, which is published on the PNAS web site.

For the model with isolation measures hospital and community populations are not fixed and the full set of differential equations is needed to model the system:

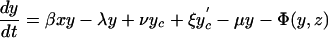[4]

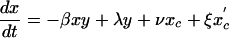[5]

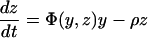[6]

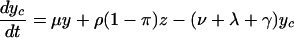[7]

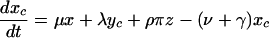[8]

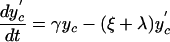[9]

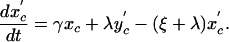[10]

Here x represents the population size of those free of MRSA in the hospital and x_c and x′_c the corresponding population sizes in the community with high and low hospital admission rates. The patient isolation rate, Φ(y, z), is a function of the number of isolated patients (z) and the number of colonized patients (y):

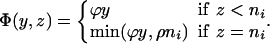[11]