Slow Internal Dynamics and Charge Expansion in the Disordered Protein CGRP: A Comparison with Amylin

Abstract

We provide the first direct experimental comparison, to our knowledge, between the internal dynamics of calcitonin-gene-related peptide (CGRP) and amylin (islet amyloid polypeptide, IAPP), two intrinsically disordered proteins of the calcitonin peptide family. Our end-to-end contact formation measurements reveal that in aqueous solution (i.e., in the absence of structure-inducing organic solvents) CGRP preferentially populates conformations with short end-to-end distances. However, the end-to-end distance of CGRP is larger than that of IAPP. We find that electrostatic interactions can account for such a difference. At variance with previous reports on the secondary structure of CGRP, we find that the end-to-end distance of the peptide increases with decreasing pH and salt concentration, due to Coulomb repulsion by charged residues. Interestingly, our data show that the reconfiguration dynamics of CGRP is significantly slower than that of human IAPP in water but not in denaturant, providing experimental evidence for roughness in the energy landscape, or internal friction, in these peptides. The data reported here provide both structural and dynamical information that can be used to validate results from molecular simulations of calcitonin family peptides in aqueous solution.

Introduction

Calcitonin-gene-related peptide (CGRP) is an intrinsically disordered neuropeptide of the calcitonin peptide (Ct) family, produced in the central and the peripheral neurons. It is involved in the transmission of pain signals in the nervous system and acts as a vasodilator upon binding to the CGRP receptor (1,2). Because it triggers migraine attacks, CGRP has recently become a major therapeutic target for the prevention of migraines (3,4). CGRP is a member of the Ct family, which includes calcitonin, CGRP; adrenomedullin; intermedin; and amylin (i.e., islet amyloid polypeptide, IAPP). These are structurally and genetically related intrinsically disordered hormone peptides, which share sequence homology ranging between 20 and 50% (5–7). Some Ct family members, including IAPP, have been shown to bind to the CGRP receptor and are able to activate cell response, though with varying degrees of affinity (5,8). Understanding the cross reactivity of CGRP and IAPP is of considerable interest to drug development (7,8). Although the precise mechanism of receptor binding and activation is not yet known, cross reactivity between these two peptides and their receptors has been attributed to their sequence homology (47%) and possible structural similarities (5,8). Because in physiological conditions these peptides are intrinsically disordered, binding to their receptors (or to drugs) will depend strongly on the structural and the dynamical properties of their disordered unbound state. Detecting such properties is challenging because Ct peptides have a low molecular mass (∼4 kDa) and sample a large ensemble of conformations on fast timescales. While some experimental information is available on the unbound disordered state of IAPP in solution (9–14), very little is known about CGRP. With the exception of low-resolution circular-dichroism (CD) experiments (15–18), no direct comparison exists between IAPP and CGRP in aqueous solvent (i.e., in the absence of helix-inducing solvents). A direct comparison of the structural and dynamical properties of these two peptides is also of more general biophysical interest (these peptides have the same contour length, yet differ in both charged and hydrophobic residue content).

The sequences of CGRP and IAPP are shown in Fig. 1 for comparison. Under physiological conditions, both peptides are amidated at the C-terminus and contain a disulfide bond at the N-terminus, between C2 and C7. This constrains residues 1–7 into an essentially rigid, ringlike structure (N_loop) (19–21). An intact disulfide bond is required for the peptides to activate cell response upon binding to the receptors (8,22–24). By combining two-dimensional solution nuclear magnetic resonance (NMR), Fourier transform infrared spectroscopy, and CD experiments with replica exchange molecular dynamics simulations, we have recently proposed a structural model of the N_loop of IAPP (21). In the absence of residues 9–37, this structure is conducive to self-aggregation and leads to the formation of extremely stable non-amyloid fibers (21). In the context of the full-length peptide, the N_loop structure favors interactions with disordered backbone groups (12). The sequence of the N_loop of CGRP is almost identical to that of IAPP (Fig. 1), suggesting a similar N_loop structure. Following this structured region, the linear portion of the sequence (residues 8–37) is disordered in both peptides, with a somewhat higher propensity to locally sample α-helical dihedral angles in the N-terminal half of the sequence (relative to random coil). The precise region of the sequence involved in helical sampling varies with the peptide, and the amount of helicity depends strongly on the solvent. This is reflected in the CD spectra of the peptides, which indicate a disordered structure with a small percentage of apparent α-helical content in water. The helical content increases in the presence of helix-inducing solvents, such as TFE (trifluoroethanol), HFIP (hexafluoroisopropanol), DMSO (dimethyl sulfoxide), or SDS (sodium dodecyl sulfate) micelles and other membrane-mimicking solvents (15–17,25–28). Secondary chemical shifts from two-dimensional NMR experiments of IAPP in aqueous solution indicate a modest helical propensity in residues 5–19, indicating transient helical sampling in this region (10,11). In the presence of diphenylamine-2-carboxylate vesicles and other membrane-mimicking environments, this region assumes a well-defined α-helix conformation (27,29). At variance with human IAPP (hIAPP), NMR experiments of CGRP in aqueous solution failed to detect sequential nuclear Overhauser effects. This is consistent with rapid conformational fluctuations and/or with a lack of well-defined three-dimensional structure (19). In 50% TFE/50% H₂O solutions, residues 8–18 of CGRP assume a well-defined helical structure while residues thereafter remain largely disordered (19). A similar helical region is observed in 100% DMSO (20). While two-dimensional NMR has provided important information on the local (secondary) structural preferences of CGRP in the presence of helix-inducing solvents, no experimental information is available (to our knowledge) on the nonlocal (i.e., long-range, or tertiary) structural properties of CGRP, nor on the dynamics of conformational sampling under near-native solution conditions. A direct comparison of these properties in CGRP and IAPP is missing. Nonlocal interactions and large-scale conformational motions are expected to play an important role in intrinsically disordered protein (IDP) function and binding (30–37). Moreover, understanding how specific changes in the sequence affect the structure and dynamics of disordered and unfolded states in proteins is a problem of general biophysical interest (38–55).

Figure 1.

Sequences of CGRP and hIAPP. C2–C7 disulfide bond (blue). Charged residues (red, positive; green, negative). The N-terminus is free while the C-terminus is amidated. In our experiments, residue 37 is mutated to W. To see this figure in color, go online.

Here we study the long-range conformational and dynamical properties of CGRP in solution under near-native solution conditions (in the absence of helix-inducing solvents), and we compare them to those previously measured for IAPP under identical solution conditions (12). For this purpose, we use the same nanosecond laser-pump spectroscopy technique, based on tryptophan triplet quenching by cystine (TCQ) (56,57), previously used to study IAPP (12). This technique provides a measure of the rate of end-to-end contact formation and of the relative end-to-end distance of the peptide at equilibrium. The advantage of this technique over Förster resonance energy transfer and fluorescence correlation spectroscopy combined is that it uses the phosphorescence properties of natural amino acids, so it does not require labeling these small proteins with large prosthetic dyes, and it provides the short-distance sensitivity required to study Ct peptides, which are only 37 residues long.

Materials and Methods

Samples

Peptides (with N-terminal amidation, W37 mutation, and with a disulfide between C2 and C7) were either synthesized by Fmoc (9-fluorenylmethoxycarbonyl) solid peptide synthesis and then purified and lyophilized (as described in the Supporting Material), or else purchased from GenScript (Piscataway, NJ). For TCQ experiments, samples were prepared by dissolving the lyophilized peptide directly into freshly filtered buffer (0.2 μm Millex-GV; Millipore, Billerica, MA). The peptide concentration was measured by absorbance and adjusted to 100 μM if needed (ε = 5774 cm⁻¹ mol⁻¹). Buffer was 50 mM NaAc at pH 3 or 4.9, or 20 mM NaPO4 pH 8 (Sigma-Aldrich, St. Louis, MO). Guanidinium chloride (Sigma-Aldrich) GdmCl solutions were prepared at 6 M in 50 mM NaAc, pH 4.9. Salt was 99.0% purity KCl (Sigma-Aldrich). Solutions at different viscosities were prepared by varying the sucrose concentration from 0 to 40% w/v in buffers, and 0–32% w/v in 6 M GdmCl. In all cases the pH of the solution was measured and adjusted if needed (Accumet BASIC AB15 pH meter; Thermo Fisher Scientific, Waltham, MA). Fresh samples were immediately filtered (Anotop 10 0.2 μm; Whatman, Little Chalfont, Buckinghamshire, UK) into gas tight cuvettes, deoxygenated by bubbling in NO for at least 2 h, and used immediately for TCQ measurements.

End-to end contact formation by Trp-Cystine quenching

As described elsewhere, the tryptophan triplet state is quenched by close contact with cysteine and disulfides (at distances <0.4 nm) (12,56–58). After nanosecond ultraviolet excitation of W37 to the triplet state, this can contact C2–C7 at a rate k_D+ (by diffusion), and either be quenched with a rate q or diffuse away with a rate k_D− (59) (Fig. 2)

Figure 2.

Kinetic scheme of tryptophan triplet quenching by cystine (TCQ) experiment. Tryptophan (W37) side chain is represented in red, cystine (C2–C7) in yellow.

The observed lifetime of the W-triplet state, 1/k_obs, is

$$\frac{1}{k_{\text{obs}}}=\frac{k_{D-}+q}{q{k}_{D+}}=\frac{1}{k_R}+\frac{1}{k_{D+}},$$

where k_R = q(k_D+/k_D−) is the reaction-limited rate and depends on the probability of forming a contact at equilibrium, k_D+/k_D−, and on the quenching rate upon contact, q. Because k_R is independent of the solvent viscosity (η) while k_D+ is a function of η, one can experimentally obtain k_R and k_D+ by measuring k_obs as a function of solvent viscosity (57). In the limit for η→0, 1/k_D+(η) will be a linear function of η. Plotting 1/k_obs as a function of viscosity therefore yields 1/k_R as the intercept and 1/ηk_D+ as the slope in the limit for zero viscosity. We note that for all peptides and solution conditions presented throughout this work, 1/k_obs was found to be a linear function of η, with no apparent curvature (Fig. S3 in the Supporting Material).

Meaning of k_R and its relation to the end-to-end distance

From the definition of k_R above, it follows that, for peptides with identical quenchers, k_R directly measures the probability of forming a contact. If we describe the contact formation as a one-dimensional diffusion along the end-to-end distance coordinate, k_R can be related to the end-to-end distance distribution P(r) by (57)

$$k_R=\underset{a}{\overset{l_c}{\int }}P\left(r\right)q\left(r\right)dr,$$ (1)

where q(r) is the distance-dependent quenching rate (measured by Lapidus et al. (58)), a is the distance of van der Waals contact, and l_c is the contour length of the peptide. In this work we provide an empirical (model-free) comparison between measured k_R values for different peptides, as well as P(r) distributions estimated from Eq. 1, in the simple case of a Gaussian P(r).

Meaning of k_D+ and relation to end-to-end distance

The average time for contact formation between the two ends of the chain is 1/k_D+. This depends on the probability of forming a contact (i.e., on P(r)) and on the intrinsic rate at which the polypeptide backbone can reconfigure itself. That is, if the two ends of the peptide are close together the contact formation time will be shorter than if they are farther apart, even if the intrachain diffusion coefficient is the same. For example, in the framework of SSS theory (57), describing the contact formation as one-dimensional diffusion along the end-to-end distance coordinate, the reaction-limited rate k_D+ can be related to P(r) and to the intrachain diffusion coefficient D. Alternative models can be used to describe the intrachain dynamics (52). A detailed description of these can be found elsewhere in Cheng et al. (52) and Lapidus et al. (57) and goes beyond the scope of this article, which is to present an empirical (model-free) comparison between measured k_D+ values for different peptides of the same length.

TCQ experimental methods and data analysis

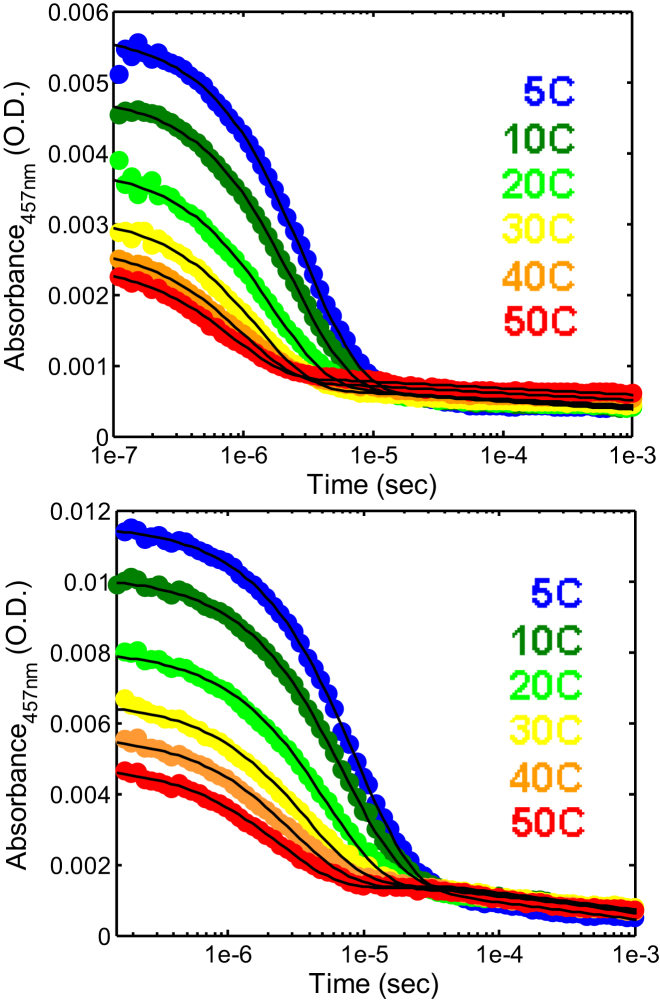
Values of k_obs were measured as a function of temperature at different solvent viscosities, using a home-built nanosecond laser-pump spectrometer similar to that of Vaiana et al. (12). Briefly, samples were placed in a temperature-controlled Peltier stage (Cat. No. TLC50; Quantum Northwest, Liberty Lake, WA) and irradiated with a 7-ns pulse at 290 nm, generated by pumping a deuterium Raman cell with the fourth harmonic of a Nd:YAG laser (Continuum, San Jose, CA). The decay of the tryptophan triplet-state population was measured by time-resolved triplet-triplet absorption at 458 nm (argon ion laser; Coherent, Santa Clara, CA). Each trace was averaged over 256 laser pulses and five of these traces were acquired at each temperature, in a range from 5° to 50°C. Time-resolved absorption was detected using nanosecond photodetectors (New Focus; Newport, Irvine, CA), and data were recorded by Cat. No. DPO3032 digital oscilloscopes (Tektronix, Beaverton, OR). After correcting for background, the temperature- and viscosity-dependent data for each set of buffer conditions were assembled into an array containing ∼120 traces. To reduce the noise, singular-value decomposition was performed and the 12 largest components were used to reconstruct the data at each temperature (Fig. 3). We note that this procedure yielded the same rates as the ones obtained from averaging over individual traces at each temperature, but significantly reduced the noise and decreased the uncertainty in the fit (Figs. S4 and S5 and Table S1 in the Supporting Material). This array of data was then used as input for the global fitting procedure described in the following.

Figure 3.

Decay of tryptophan triplet-triplet absorption measured after nanosecond excitation in solutions of CGRP (50 mM NaAc, pH 4.9) at different temperatures in aqueous buffer (top) and in 6 M GdmCl (bottom). (Solid lines) Fits to an exponential decay followed by a slower decay. The rate of initial exponential decay, k_obs(T), corresponds to the quenching of the W37 triplet state by cystine (C2–C7) upon (end-to-end) contact formation. To see this figure in color, go online.

As in Vaiana et al. (12), each trace in the array (Fig. 3) was fit to an exponential relaxation (yielding the exponential relaxation rate k_obs), with a time-independent offset and a second offset function that was constant for times <∼10⁻⁵ s and varied linearly with log(t) for times longer than 10⁻⁵ s (this empirically accounted for the observed slower decay due to a radical photoproduct (56)). When k_obs⁻¹ data obtained from individual fits were plotted as a function of viscosity for each temperature, they followed a simple linear dependence. A first-order polynomial fit yields the intercept (1/k_R) and the slope (1/ηk_D+) for each temperature (Fig. S3). To reduce the uncertainty in the values of k_R(T) and of k_D+(T), we globally fit the array of viscosity and temperature-dependent data for each set of buffer conditions, according to the general function

$$\frac{1}{k_{\text{obs}}\left({\eta }_T,T\right)}=\frac{1}{k_R\left(T\right)}+\frac{1}{k_{D+}\left({\eta }_T,T\right)},$$

where we can separate the intrinsic temperature dependence of k_D+ from its viscosity dependence, and write the latter as a general first-order polynomial:

$$k_{D+}\left({\eta }_T,T\right)=f\left({\eta }_T\right)k_{D+}^{\prime }\left(T\right)={\eta }_T^{-1}{k}_{D+}^{\prime }\left(T\right).$$

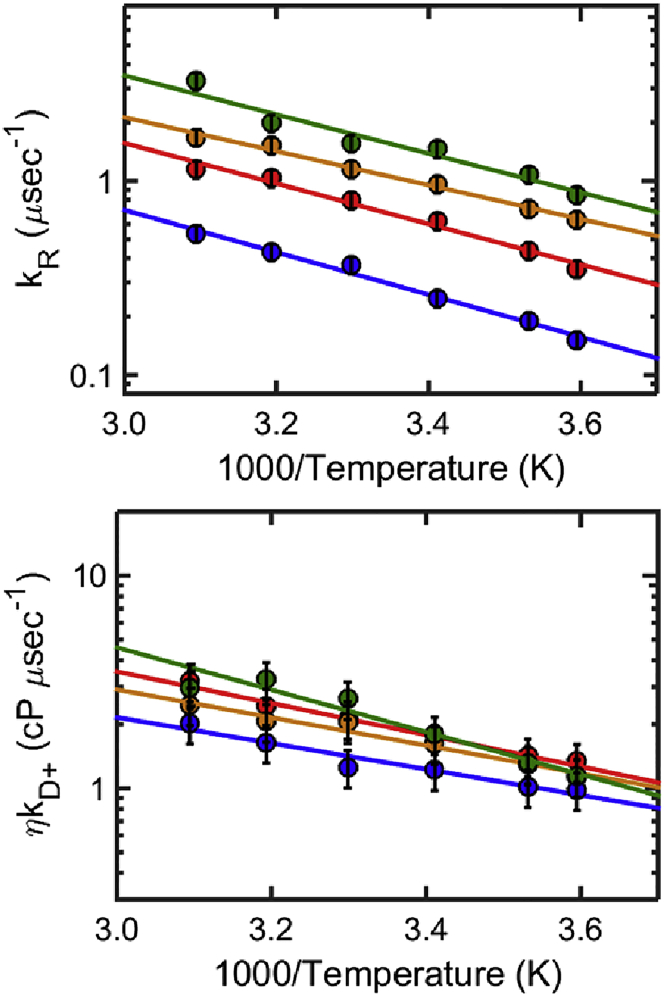
Here T is temperature and η_T is the solution viscosity measured at the given temperature (Fig. S3). We note that this global fitting procedure differs from some of the previous methods used to fit TCQ data (56–59) in that it does not assume a fixed functional dependence of k_R and k_D+ on temperature, and yields unbiased, model-free, temperature-dependent values of k_R(T) and k_D+(T), while globally fitting the data and reducing the uncertainty in the fits. Plots of k_R(T) and ηk_D+(T) obtained in this way exhibit an apparent Arrhenius dependence in the temperature range studied (see Figs. 7 and 9).

Figure 7.

Reaction-limited rates k_R (top) and diffusion-limited rates corrected for viscosity ηk_D+(T) (bottom) of CGRP in buffer at different pH values, and in 6 M GdmCl: pH 3 net charge +6 (red), pH 4.9 net charge +5 (orange), pH 8 net charge +4 (green), and 6 M GdmCl (blue). Large values of k_R indicate short end-to-end distances; large values of ηk_D+ can reflect short end-to-end distances or indicate fast intrachain dynamics. To see this figure in color, go online.

Figure 9.

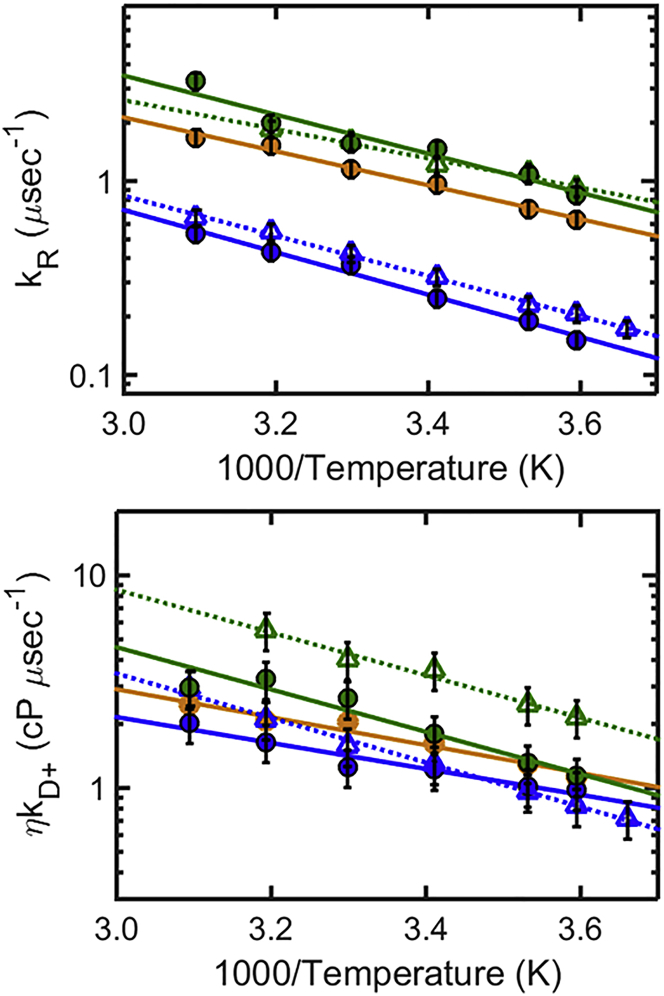
Reaction-limited rates k_R (top) and diffusion-limited rates corrected for viscosity ηk_D+(T) (bottom) of CGRP (circles), compared to hIAPP (triangles) from Vaiana et al. (12), in denaturant (blue, 6 M GdmCl) and in aqueous buffer (green and orange). Color-coding indicates the peptide’s net charge: net charge +4 (green) (CGRP pH 8, hIAPP pH 4.9); net charge +5 (orange) (CGRP pH 4.9); and 6 M GdmCl is shown for reference (blue). Large values of k_R indicate short end-to-end distances; large values of ηk_D+ can reflect short end-to-end distances or indicate fast intrachain dynamics. To see this figure in color, go online.

Debye length calculation

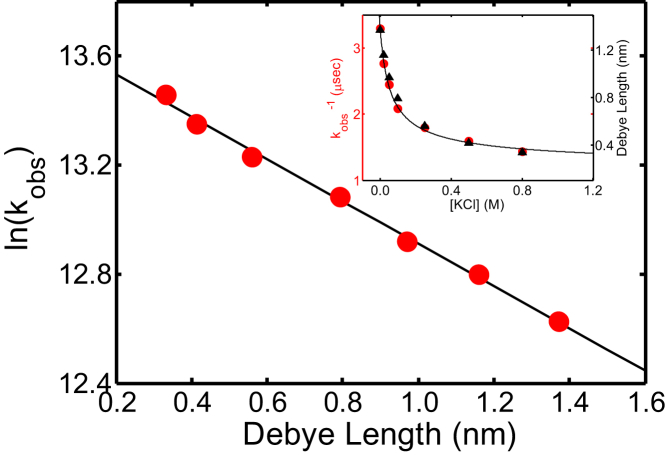
Values of the Debye length κ⁻¹ seen later in Fig. 6 were calculated at each salt concentration from

$${\kappa }^{-1}=\sqrt{\frac{{\epsilon }_r{\epsilon }_o{k}_{\text{B}}T}{2N_A{e}^{2}I}},$$

where ε_r is the dielectric constant, ε_o is the permittivity in free space, k_B is the Boltzmann constant, T is the temperature in Kelvin, N_A is Avogadro’s’ number, e is the elementary charge, and I is the ionic strength of the solution in mole/m³.

Figure 6.

(Inset) Observed relaxation times k_obs⁻¹ (red) measured for D3N CGRP at pH 3 at different concentrations of KCl, and corresponding Debye lengths κ⁻¹ (black). A plot of ln(k_obs) versus the Debye length reveals an empirical linear dependence. (Best fit line) ln(k_obs) = aκ⁻¹+ b (a = 0.773 nm⁻¹, b = 13.68). Data shown for 10°C. To see this figure in color, go online.

Further details may be found in the Supporting Material.

Results and Discussion

CGRP populates states with short end-to-end distances

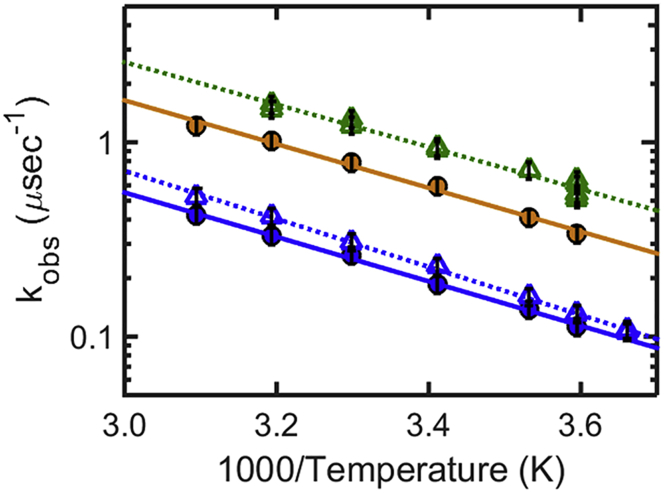
For a direct comparison of contact formation rates in CGRP and IAPP, we labeled the peptide as in Vaiana et al. (12). Briefly, we mutated the C-terminal phenylalanine F37 of CGRP to tryptophan and used the native N-terminal disulfide bond between C2 and C7 as the quencher of the tryptophan triplet state (Fig. 1). We note that the F37W mutation represents a minimal perturbation to the sequence. Although F37 may be involved in direct interactions with the receptor, NMR experiments have shown that this residue does not affect CGRP’s structure in solution (18) (comparison of CD spectra is also shown in Fig. S1). We monitored the decay of the tryptophan triplet-state population by measuring the time-resolved triplet-triplet absorption at 458 nm after nanosecond excitation at 290 nm. The raw data obtained for CGRP in 6 M GdmCl and in aqueous buffer (50 mM NaOAc, pH = 4.9) at various temperatures are shown in Fig. 3. As observed for IAPP, the data exhibit a fast exponential decay followed by a slowly decaying tail of much smaller amplitude (12). The fast exponential decay corresponds to the triplet-state decay due to contact with cystine, while the slower tail corresponds to the decay of a radical photoproduct (56). As described elsewhere, the exponential rate of triplet-state decay (k_obs) depends on two contributions: 1) the probability of forming a tryptophan-cystine contact, through the equilibrium end-to-end distance distribution P(r) (a structural property of the peptide); and 2) the rate at which the backbone can reconfigure itself to allow the two ends to come into contact (the intrachain diffusional dynamics) (57,59). For simplicity, we will assume in the following that the differences in k_obs primarily reflect differences in P(r). The analysis of the viscosity and temperature dependence of k_obs presented later confirms the validity of this assumption. This analysis will allow separating the reaction-limited rate k_R, which depends only on P(r), from the diffusion-limited rate k_D+, which depends on intrachain diffusion (see Materials and Methods). This will provide additional information on the intrachain dynamics, which will be discussed in a separate paragraph. In the following, small values of k_obs indicate large end-to-end distances, while large values of k_obs indicate short end-to-end distances. In Fig. 4 we show the Arrhenius plots of k_obs(T) measured for CGRP in two different solvents (obtained from fitting the data of Fig. 3), compared to the values previously measured for hIAPP under identical solution conditions (12). The observed rates follow an empirical Arrhenius behavior in the temperature range studied, consistent with previous findings using this technique (12,59), with apparent activation energies of ∼5 kcal/mol for all peptides/solvent conditions (respectively 5.0, 5.2, 5.7, and 5.2 kcal/mol for hIAPP and CGRP in buffer and for hIAPP and CGRP in 6 M GdmCl). Therefore, the relative changes in k_obs discussed in the following, as a function of peptide sequence or solvent conditions, occur consistently at all temperatures.

Figure 4.

Observed rates, k_obs, measured for CGRP (circles) compared to those of hIAPP (triangles) from Vaiana et al. (12), in 6 M GdmCl (blue), and in aqueous buffer (orange, CGRP; green, hIAPP): 50 mM NaAc pH 4.9. Small values of k_obs indicate large end-to-end distances; large values of k_obs indicate short end-to-end distances. To see this figure in color, go online.

We first compare k_obs for the two peptides under highly denaturing conditions (6 M GdmCl). This is a convenient reference state for measuring basic polymer properties of peptides. In this good solvent, unfolded proteins and IDPs behave like wormlike chains with excluded volume (41,43,45,48,59–62). The small values of k_obs measured in 6 M GdmCl indicate that both peptides preferentially populate states with large end-to-end distances, consistent with expanded denatured states (59). The slightly smaller values observed for CGRP indicate that this peptide has a slightly larger end-to-end distance and therefore a slightly larger persistence length or excluded volume compared to hIAPP. This is consistent with CGRP’s larger number of bulky (hydrophobic) side chains.

Next, we compare the values measured for the two peptides in aqueous buffer, in the same conditions used previously for hIAPP (50 mM NaAc buffer, pH = 4.9) (12). Fig. 4 shows that, at all temperatures, k_obs values for CGRP are ∼3 times larger in buffer than in 6 M GdmCl (Table 1). CGRP therefore populates states with significantly shorter end-to-end distances in aqueous buffer with respect to those in denaturant (this is confirmed by the values of k_R presented later). A similar result was found by Vaiana et al. (12) for hIAPP and was attributed to intraprotein interactions occurring between the N_loop (residues 1–7) and the backbone of the remaining disordered chain (residues 8–37), with the rigid structure of the N_loop (21) acting as a nucleus. A similar increase in rates was observed for hIAPP, for the rat variant of IAPP (rIAPP), and for a model hydrophilic sequence that contains the N_loop (residues 1–7) of IAPP. By contrast, a much smaller variation in rates (i.e., in the end-to-end distance) was observed when the disulfide bond of the N_loop was reduced, thus opening the loop (12). The presence of nonlocal contacts between residues in the N_loop and the rest of the linear chain is also supported by molecular simulations of the IAPP monomer in solution (63,64). Given that the N_loop sequence of CGRP is almost identical to that of hIAPP (Fig. 1), a similar mechanism could also occur in CGRP.

Table 1.

Measured rates at 20°C

Peptide	CGRP				D3N		IAPPa
6 M GdmCl	pH 3	pH 4.9	pH 8	6 M GdmCl	pH 3	6 M GdmCl	pH 4.9
kobs (μs−1)	0.19 ± 0.02	0.43 ± 0.04	0.57 ± 0.06	0.74 ± 0.07	0.18 ± 0.02	0.39 ± 0.04	0.23 ± 0.02	0.93 ± 0.07
kR (μs−1)	0.25 ± 0.03	0.58 ± 0.06	0.93 ± 0.09	1.3 ± 0.1	0.23 ± 0.02	0.56 ± 0.06	0.32 ± 0.03	1.2 ± 0.1
ηkD (cP μs−1)	1.2 ± 0.2	1.7 ± 0.3	1.6 ± 0.3	1.8 ± 0.4	1.3 ± 0.2	1.4 ± 0.3	1.3 ± 0.2	3.6 ± 0.6
kD (μs−1)	0.72 ± 0.14	1.7 ± 0.3	1.5 ± 0.3	1.7 ± 0.3	0.75 ± 0.15	1.3 ± 0.3	0.7 ± 0.1	3.6 ± 0.6

^aIAPP values from Vaiana et al. (12).

Comparing the values of k_obs for the two peptides in aqueous buffer indicates that hIAPP has shorter end-to-end distances than CGRP (Fig. 4). Inspection of the sequences (Fig. 1) shows that CGRP is slightly more hydrophobic, and has a higher net charge than hIAPP at pH = 4.9 (the average hydrophobicity per residue is +0.21 and −0.097 on the Kyte and Doolittle scale (65), and the net charge is roughly +5 and +4 for CGRP and hIAPP, respectively, at this pH). Based on its larger hydrophobicity, CGRP would be expected to populate more compact states with respect to hIAPP in water, contrary to observations. On the other hand, the higher net charge of CGRP would cause greater Coulomb repulsion, leading to larger end-to-end distances (44,46), consistent with our observations. We therefore set out to study whether the relatively small difference in net charge between hIAPP and CGRP (+4 and +5, respectively) could account for the observed differences.

Electrostatic interactions modulate the end-to-end distance of CGRP

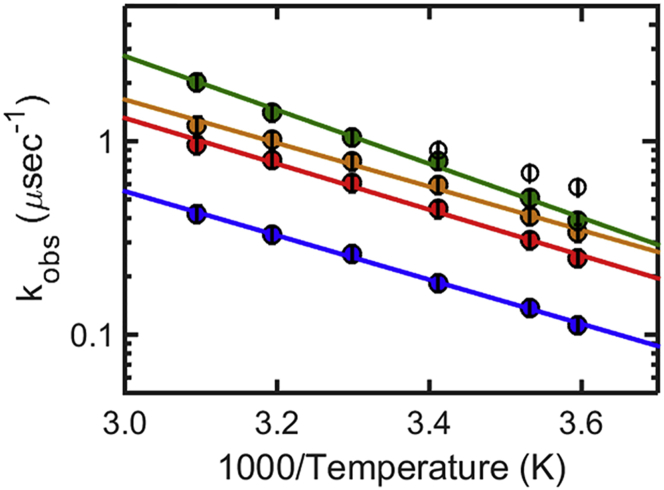
To investigate the effect of charge on the end-to-end distance of CGRP, we first measured k_obs(T) at different pH values. We found that the end-to-end distance of CGRP increases at decreasing pH (i.e., at increasing net charge), indicating that Coulomb repulsion causes significant expansion of CGRP in buffer. In the pH range 3–8, the net charge of CGRP decreases from roughly +6 to +4, due to two titrating side chains (assuming that the N-terminus remains fully protonated at pH = 8): the histidine H10, which has a measured pKa of 6.5 (16) and is positively charged at pH = 4.9; and the aspartic acid D3, which has an expected pKa of ∼4 and is negatively charged at pH = 4.9. Fig. 5 shows plots of k_obs(T), measured for CGRP at pH 3, 4.9, and 8 in buffer (corresponding to a peptide net charge of roughly +6, +5, and +4, respectively), and in denaturant (6 M GdmCl) for comparison. As in Fig. 4, larger values of k_obs indicate smaller end-to-end distances. At all temperatures, the observed rates increase monotonically as the net charge of CGRP decreases from +6 to +4, indicating that the peptide samples shorter end-to-end distances as the net charge decreases. This suggests that Coulomb repulsion in CGRP reduces the probability of sampling short end-to-end distances. To check whether the decrease in k_obs from pH 4.9 to pH 3 was truly due to the loss of charge on the aspartic acid and not to other possible direct effects of pH, we measured k_obs for a D3N CGRP mutant at pH 4.9. The results were virtually indistinguishable from those of wild-type CGRP at pH 3 (Fig. S2). Similar results were also obtained when comparing D3N at pH 8 with wild-type CGRP at pH 4.9, both corresponding to a net charge of ∼+5 (Fig. S2). When 1 M KCl was added to the solution, the rates increased further, indicating that complete screening of charges by salt leads to a maximally compact state (Fig. 5).

Figure 5.

Observed rates k_obs for CGRP at different pH values: pH 3 (red) net charge +6, pH 4.9 (orange) net charge +5, pH 8 (green) net charge +4, and after addition of 1 M KCl (open black circles). 6 M GdmCl data are shown for comparison (blue). At all temperatures, the values of k_obs decrease (i.e., the end-to-end distance increases) monotonically as the net charge increases. To see this figure in color, go online.

To further test this, and to gain a more quantitative understanding of the electrostatic contribution to the free-energy cost of forming a van der Waals contact between the ends of the peptide, we measured k_obs as a function of salt concentration. At variance with the pH titrations (which only affect the charges of two specific side chains, D3 and H10), the salt is expected to screen all seven charges in CGRP, without significantly altering the distribution of charges along the chain (i.e., the charge patterning). Fig. 6 (inset) shows the relaxation times (1/k_obs) of D3N CGRP measured as a function of KCl concentration, at pH 3 (these conditions were chosen to maximize the peptide net charge). Fig. 6 (inset) also shows the values of the Debye screening length, κ⁻¹. The observed correlation between the Debye length and the relaxation times (Fig. 6, inset) confirms that charge screening causes shorter end-to-end distances in CGRP at high salt concentrations. Interestingly, we find a linear dependence between ln(k_obs) and the Debye length, κ⁻¹ (Fig. 6). This provides information on the electrostatic contribution to the free-energy cost of forming a contact between the two ends of the peptide. By analyzing the viscosity- and temperature-dependent behavior of k_obs at 0 M KCl and 500 mM KCl (see the Supporting Material and Fig. S3) we find that k_obs is proportional to k_R. Because quenching of tryptophan triplet state by cystine occurs when the two side chains are roughly within a distance of 0.4 nm (58), the reaction-limited rate k_R is proportional to the fraction of peptides with R_end-to-end < 0.4 nm (i.e., the population of the contact subensemble) over the fraction of peptides with R_end-to-end > 0.4 nm (i.e., the population of the open subensemble). The relative population of these two subensembles is directly related to their free-energy difference. The linear dependence of ln(k_obs) on κ⁻¹ (Fig. 6) therefore implies that the free-energy difference between the two subensembles (i.e., the free-energy cost of forming a van der Waals contact) varies linearly with the Debye length.

Our data clearly show that the end-to-end distance of CGRP is modulated by electrostatic interactions between charged residues in the sequence: the peptide expands when the net charge increases. We note that previous far-ultraviolet CD measurements of CGRP in aqueous buffer showed no variation in secondary structure content as a function of pH, in the same pH range studied here (16). This data is also confirmed by our own CD measurements under the same solution conditions of Fig. 5 (Fig. S1). This behavior is at odds with that of natively folded proteins, for which local (secondary) and nonlocal (tertiary) structural properties are generally strongly coupled. However, it is not surprising in the case of IDPs, as they lack cooperative interactions. Secondary structure content in IDPs has in fact been shown to be uncorrelated with long-range structural properties such as the hydrodynamic radius (45). Our findings further underline the importance of measuring nonlocal (long-range) structural properties of IDPs (as the end-to-end distance or the radius of gyration), in addition to local properties.

End-to-end distance and internal dynamics of CGRP

To separate the dynamical from the structural information contained in k_obs, we measured the rate of triplet-state decay (k_obs) as a function of viscosity and temperature (Fig. S3). The data analysis described in Materials and Methods yields the reaction-limited rate, k_R(T), and the diffusion-limited rate, k_D+(T) at each temperature. While k_R (Eq. 1) depends only on the equilibrium (structural) properties of CGRP (i.e., its end-to-end distance distribution, P(r)), k_D+ depends on both the structure (P(r)), and the dynamics of the chain (intrachain diffusion). By providing both values of k_R and k_D+ our experiments allow distinguishing whether large values of k_D+ are due to the peptide’s short end-to-end distance (i.e., to a high probability of forming a contact), or to its fast conformational sampling (i.e., fast intrachain diffusion). We note that measurements of k_D+ alone, obtained for example using a diffusion-limited technique, would not allow us to distinguish between these two scenarios. Arrhenius plots of k_R(T) and η(T)k_D+(T) (the diffusion-limited rate corrected for the viscosity value of the given solvent at each temperature, η(T)) are shown in Fig. 7. The temperature dependence of k_R and of η(T)k_D+ both follow an empirical Arrhenius dependence, with apparent activation energies that are consistent with those found by Buscaglia et al. (59) for model peptides of similar length (the apparent activation energies for k_R are 4.6, 4.0, 4.8 and 5.0 kcal/mol, and those for ηk_D+ are 4.6, 3.0, 3.4, 2.8 kcal/mol, respectively, in buffer at pH 8, 4.9, 3, and in 6 M GdmCl). As noted in Buscaglia et al. (59), the temperature dependence of k_R primarily reflects the temperature dependence of the quenching rate of tryptophan by free cystine q(r) (Eq. 1). The small variations observed in the activation energies of different peptides and different pH values, may reflect slight differences in the temperature dependence of P(r). In the following, we focus on the relatively large differences observed between the measured rates at different pH and solvent conditions.

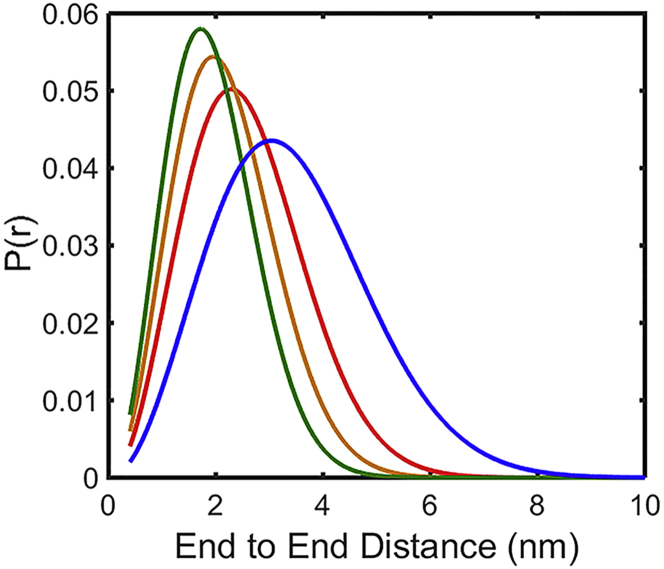
The reaction-limited rates k_R (Fig. 7, top) confirm the qualitative conclusions drawn in the previous paragraphs, namely that CGRP has a higher probability of sampling short end-to-end distances in aqueous buffer versus denaturant, and that this probability increases with increasing pH (i.e., with decreasing net charge). The corresponding end-to-end distance distributions, P(r), calculated from k_R values at 20°C, using SSS theory (57) and assuming a simple Gaussian distribution (Eq. 1), are shown in Fig. 8. Under this assumption, the average end-to-end distance decreases from 3.7 nm in 6 M GdmCl, respectively, to 2.8, 2.4, and 2.1 nm at pH 3, 4.9, and 8 (these values are calculated assuming an initial value of 3.7 nm for the end-to-end distance of CGRP in 6 M GdmCl, consistent with data for a typical wormlike chain peptide of 31 residues long (59)). We note that if the actual P(r) differs from a simple Gaussian, the corresponding end-to-end distances can be recalculated for the specific distribution, using SSS theory and our measured k_R values from Eq. 1 (57).

Figure 8.

Estimate of the end-to-end distance distributions of CGRP in different solvents, calculated from experimental values of k_R at 20°C (Fig. 6, top) using SSS theory and assuming a Gaussian P(r) (Eq. 1). Color-coding as in Fig. 6. To see this figure in color, go online.

The diffusion-limited rates (Fig. 7, bottom) give additional information on the dynamics of conformational sampling in CGRP. First we note that, unlike k_R, the values of η(T)k_D+ barely change as a function of pH. The average time it takes to form an end-to-end contact (1/k_D+) in fact remains roughly 0.6 μs at 20°C at all pH values (Fig. 7, bottom, and Table 1). It is particularly informative to compare the rates in buffer and in denaturant (Table 1). While the values of k_R increase by a factor 5.2 between 6 M GdmCl and buffer (pH = 8), the corresponding values of ηk_D+ change by barely a factor 1.5. In other words, despite the fact that the end-to-end distance of CGRP is considerably shorter in aqueous solvent than in denaturant (Fig. 8), it takes almost the same time for the two ends of the peptide to form a contact. This implies that the end-to-end diffusional dynamics of CGRP is slower in aqueous solution than in denaturant.

The observed slowing down of intrachain dynamics in water can be interpreted in terms of the appearance of many small barriers in the potential of mean force describing end-to-end distance diffusion (i.e., roughness in the energy landscape) (66,67). The appearance of a rougher energy landscape in water with respect to that in denaturant could be a direct consequence of the fact that the peptide samples more compact states (consistent with observations that diffusional dynamics slows down and internal friction of proteins increases as a function of compaction (40,47,49,50,68,69)) and/or could be due to the presence of intrachain interactions in water, which are specific to the CGRP sequence. As we shall see in the following paragraph, the slowing down of intrachain diffusion in water is unique to CGRP and is not observed in hIAPP, even though this peptide samples similarly compact states.

Comparison between the end-to-end distance and the internal dynamics of CGRP and IAPP

We now compare more closely the end-to-end distance and the intrachain dynamics of CGRP and hIAPP in solution, taking into consideration the effect of net charge. Fig. 9 shows the values of k_R(T) and η(T)k_D+(T), measured for CGRP (circles) and hIAPP (triangles) (12) in denaturant (blue) and in aqueous buffer at two different pH values. The data points in buffer are color-coded according to the peptide’s net charge (net charge +5: orange; net charge +4: green). The values of k_R (Fig. 9, top) confirm our initial conclusions, namely that both peptides sample significantly shorter end-to-end distances in aqueous buffer with respect to those in denaturant. Specifically, k_R increases by a factor 5.2 for CGRP in buffer (pH 8) relative to denaturant, and by a factor 3.8 for hIAPP (Table 1), corresponding to a factor 1.8 (44%) and 1.6 (36%) decrease in the average end-to-end distance of the two peptides, respectively (assuming a simple Gaussian P(r) as in Fig. 8). We now directly compare the values of k_R measured for the two peptides in buffer. The data confirm that at pH 4.9, CGRP samples larger end-to-end distances compared to hIAPP. This is consistent with CGRP’s larger net charge causing greater Coulomb repulsion (the net charge is, respectively, +5 and +4 for CGRP and hIAPP). Consistent with this interpretation, the k_R values of the two peptides become virtually undistinguishable when the net charge is the same (green data points: +4 for both peptides, i.e., pH 4.9 for hIAPP and pH 8 for CGRP). Under these conditions, it is now possible to compare the intrachain dynamics of CGRP and hIAPP in aqueous solution by directly comparing their diffusion-limited rates (Fig. 9, bottom, green data points). Strikingly, we find that even though hIAPP and CGRP have the same reaction-limited rates k_R (i.e., the same probability of forming a contact), the two peptides have significantly different diffusion-limited rates, ηk_D+(T). The values in Table 1 show that at 20°C it takes an average time (1/k_D+) of 0.6 μs to form an end-to-end contact in CGRP, but only 0.3 μs in hIAPP. This data clearly show that in aqueous buffer CGRP has slower intrachain diffusional dynamics than hIAPP. By contrast, we do not observe any difference in the diffusional dynamics of CGRP and hIAPP in denaturant, where the peptides are both maximally expanded (blue data points).

If we interpret the slowing down of diffusional dynamics in terms of roughness in the end-to-end distance potential of mean force, our data implies that CGRP has a rougher energy landscape compared to hIAPP, in water, but not in denaturant. This, together with the observation that our peptides are highly compact in water and maximally expanded in denaturant, is in agreement with the observation that the roughness in the energy landscape and internal friction tend to increase as a function of IDP compaction (40,47,49,50,68,69). A number of factors have been proposed to contribute to rough energy landscapes or increased internal friction in IDPs and unfolded states of proteins. These include intrachain collisions, concerted dihedral angle rotations, and the occurrence of salt bridges, hydrogen bonds, hydrophobic interactions, and other specific intrachain interactions (38,42,52,54,70–72). As the probability for collisions increases and short-range interactions become more significant when the protein samples more compact states, the protein dynamics is expected to slow down. Interestingly, data in Fig. 9 show that, while hIAPP is as compact as CGRP in aqueous buffer, its intrachain dynamics does not slow down relative to GdmCl, as instead we observe in CGRP. As noted in Vaiana et al. (12), the reaction- and diffusion-limited rates of hIAPP (corrected for viscosity) increase by the same proportionality constant in water relative to denaturant, as expected from SSS theory when the end-to-end distance decreases without affecting the intrachain diffusion coefficient (assuming a Gaussian P(r)). We note that while different models can be used to quantitatively describe the dynamics of intrachain diffusion, each potentially leading to a different dependence of k_D+ on the end-to-end distance (52), this will not change our basic conclusion. The data in Fig. 9 imply that in water, the roughness in CGRP’s energy landscape arises from interactions specific to CGRP’s sequence, interactions which are absent in hIAPP.

Conclusions

The structural and dynamical properties of IDPs in their unbound disordered state can affect both the affinity and rate of binding to receptors and to drugs. By measuring the rate of end-to-end contact formation in CGRP under near-native conditions (in aqueous solution and in the absence of structure-inducing solvents), we find that the peptide samples highly compact conformations, characterized by short end-to-end distances. At variance with previous reports on the (local) secondary structure of CGRP (16), we find that its end-to-end distance (a nonlocal property) is extremely sensitive to pH and salt concentration. Lowering the solution pH from 8 to 4.9 and to 3, or decreasing the salt concentration, causes expansion of the peptide, due to increased electrostatic repulsion between charged residues in the sequence. These findings could be relevant to current theories on migraine pathology, which suggest an important role of pH in the generation of headache pain (73–76). It is known that CGRP can be released at pH below 7.5. A decrease in extracellular pH from basal levels (7.5) to values below pH 5.5 has been shown to stimulate the release of CGRP from trigeminal neurons, and has been implicated in triggering migraines (74,77,78). Our data show that variations in pH in this same range can significantly affect the ensemble of conformations sampled by CGRP.

By comparing our data to previous data on IAPP (12), we find that both CGRP and IAPP populate conformations with short end-to-end distances in water, yet their dynamics differs significantly. The dynamics of end-to-end contact formation of CGRP is in fact two-times slower than that of IAPP. Moreover, we find that intrachain diffusion of CGRP (adjusted for viscosity) dramatically slows down in water (where the peptide is compact), versus denaturant (where the peptide is maximally expanded), an effect that is not observed in IAPP. We interpret this slowing down of diffusional dynamics in terms of increased roughness in the energy landscape of CGRP in water with respect to that in denaturant. This is consistent with the finding that intrachain dynamics slows down and internal friction increases when IDPs or unfolded states of proteins sample more compact conformations (40,47,49,50,68,69). However, because this effect was not observed in IAPP (12), the roughness in CGRP’s energy landscape must arise from intrachain interactions and/or interactions between the chain and the solvent, which are specific to CGRP’s sequence, and are absent in IAPP. Slow intrachain diffusion in CGRP could play a functional role in CGRP-receptor binding and activation. The specific interactions and molecular mechanisms giving rise to such roughness in CGRP remain to be investigated.

Author Contributions

S.M.S. carried out peptide characterization, performed experiments and data analysis, and contributed to writing the article. S.M.C. measured viscosities and assisted in sample characterization, experiments, and analysis. A.R. and G.G. designed peptide synthesis and purification protocols; A.R. carried out the synthesis and assisted in peptide characterization. G.G. contributed writing and editing to the final article. S.M.V. conceived and designed the project, analyzed the results, and wrote the article with S.M.S. and G.G.

Editor: Elizabeth Rhoades.