Measuring Local Viscosities near Plasma Membranes of Living Cells with Photonic Force Microscopy

Abstract

The molecular processes of particle binding and endocytosis are influenced by the locally changing mobility of the particle nearby the plasma membrane of a living cell. However, it is unclear how the particle’s hydrodynamic drag and momentum vary locally and how they are mechanically transferred to the cell. We have measured the thermal fluctuations of a 1 μm-sized polystyrene sphere, which was placed in defined distances to plasma membranes of various cell types by using an optical trap and fast three-dimensional (3D) interferometric particle tracking. From the particle position fluctuations on a 30 μs timescale, we determined the distance-dependent change of the viscous drag in directions perpendicular and parallel to the cell membrane. Measurements on macrophages, adenocarcinoma cells, and epithelial cells revealed a significantly longer hydrodynamic coupling length of the particle to the membrane than those measured at giant unilamellar vesicles (GUVs) or a plane glass interface. In contrast to GUVs, there is also a strong increase in friction and in mean first passage time normal to the cell membrane. This hydrodynamic coupling transfers a different amount of momentum to the interior of living cells and might serve as an ultra-soft stimulus triggering further reactions.

Introduction

A biological cell can be considered as a minimal living system to respond to external disturbances. Among the many different kinds of stimuli that a cell is exposed to, mechanical contacts at the cell surface play a superordinate role (1,2), because cells are in constant mechanical interaction with their environment. The question of how a cell reacts to an approaching particle is of principal interest for various disciplines ranging from immunology (3,4) to drug delivery (5–7), and it is connected to the preceding question of how much time is given to a cell to react adequately to an approaching disturbance such as a bacterium, a virus, a vesicle, or inorganic particles delivered deliberately or unintentionally from outside.

The characteristic reaction time of a cell can be defined by a time period that starts with a stimulus of transmembrane receptors or of molecules in the pericellular/extracellular matrix (8), which can be measured by, e.g., small changes in the fluctuation amplitude of the approaching particle (9). The end of the reaction time can be defined by a measurable reorganization of membrane proteins or cytoskeleton proteins. This reaction can be further amplified by the duration and the amplitude of the stimulus, e.g., the ongoing approach of the particle. During the stimulus, the particle typically diffuses passively nearby the cell membrane on a timescale that is dominated by the viscosity of the extracellular fluid. Generally, the equilibrium association constant for two binding partners does not depend on the viscosity—provided reaction time is not limited. However, an increase of the viscosity η nearby the cell membrane is accompanied by a decrease of the collision rate f_c ∼1/η with the cell membrane and thus by decreased binding and reaction probability (10,11). The variation in the viscous drag γ ∼ η of the approaching particle regulates the transfer of hydrodynamic momentum to the cell and thereby the amplitude of a stimulus and eventually of the cellular response. In this study we investigate the distance-dependent behavior of the mobility μ = 1/γ near the membranes of living cells, which has been measured so far only in specific viscoelastic relaxation experiments (8).

The change of the viscosity experienced by a particle near a stiff plane interface, i.e., its hydrodynamic coupling to the wall, has been put on a solid theoretical basis by the 1963 work of Happel and Brenner (12), who were able to predict the increase of a particle’s viscous drag parallel and perpendicular to the interface as a function of the separation distance. Theoretical studies by Lee (13,14) and Bickel (15,16) showed that the increase in static viscous drag at a fluid interface is very similar to that of a stiff interface in perpendicular direction, but is hardly visible parallel to the fluid interface. The theoretical work of Bickel (15) was extended to deformable membrane interfaces, considering different spatial and temporal frequencies at the deforming membrane (16).

A variety of experimental efforts were undertaken to confirm the theoretical predictions of the space variant viscous drag or diffusion constants of microbeads at stiff planar interfaces and alterations thereof. This was either realized by video tracking of a diffusing particle (17), by evanescent wave scattering (18–20), by analyzing the bead fluctuations inside an optical trap (21,22) or attached to the cantilever of an atomic force microscopy (23), or by using fluorescence correlation spectroscopy of fluorescent beads (24). In this context, optical traps enabled the measurement of the Derjaguin-Landau-Verwey-Overbeek potential in combination with viscous relaxation experiments near the interface (25). Instead of mapping the position-dependent local diffusion normal to the interface, Pralle et al. (26) succeeded in mapping the changes in lateral diffusion inside plasma membranes revealing sphingolipid-cholesterol rafts.

More complex situations of hydrodynamic coupling lengths and temporal mode relaxation of several particles were investigated by either time multiplexed point traps (27–29), holographic optical traps (30,31), and optical line traps, enabling direct contact between the particles (32–34).

The most elegant way to measure local diffusion coefficients or viscous drags is to analyze the thermal position fluctuations of trapped particles. Whereas the analysis of fluctuation amplitudes provides information about the trapping potential and the local environment (35), the analysis of the position autocorrelation (AC) functions or the power spectral density (PSD) also enables the extraction of the viscous drag of the particle’s motion (36). On very short timescales, this enables a three-dimensional (3D) viscosity mapping of small volume elements on the length scale of 10 to 30 nm (37).

Although the combination of optical traps and fast 3D position particle tracking, preferably by using back focal plane (BFP) interferometry, is quite established, no experiments have been performed to measure the distance-dependent change of the viscous drag near the plasma membrane of a living cell.

In this study, we investigate the change of the viscous drag close to the plasma membrane for three different types of mammalian cells and giant unilamellar vesicles (GUVs) (38). We analyze the 3D position fluctuations on a μs timescale to extract the viscous drag at the position of the diffusing particle, which is controlled by an optical trap. We show that the hydrodynamic coupling lengths normal to the cell membrane can be measured with good reproducibility, and demonstrate that this length can vary significantly for different cell types.

Theoretical background

Thermal position fluctuations

The bead’s stochastic motion in the presence of linear external forces can be theoretically described by a Langevin equation (39). In our case, it can be well approximated by the following:

$$\overleftrightarrow{\mathbf{\gamma }}\left(d\right)\times \dot{\mathbf{b}}+\left({\overleftrightarrow{\mathbf{\kappa }}}_{opt}-{\overleftrightarrow{\mathbf{\kappa }}}_{cell}\left(d\right)\right)\times \mathbf{b}={\mathbf{F}}_{th}\left(t\right),$$ (1)

where the position vector b(t) denotes the bead’s displacement with respect to the trap center at a given time t, and d is the distance of the cell membrane to the center of the laser focus; see Fig. 1B, The trap center is ∼0.2 μm behind the laser focus because of the radiation pressure (9). As the condition for overdamped motion for a high-enough viscous drag γ (i.e., ${\gamma }^2>4m\kappa$) is fulfilled, the inertia term $m\cdot \ddot{\mathbf{b}}$ was neglected. The spherical particle is driven by an uncorrelated random thermal force F_th(t) with 〈F_th,j(t) × F_th,j(t + τ)〉 = 2γ_jj × k_BT × δ(τ), which accounts for the Brownian motion of the particle with thermal energy k_BT. Choosing the cell surface normal to one coordinate axis, $\overleftrightarrow{\mathbf{\gamma }}$ is approximately a diagonal tensor with diagonal elements γ_jj being the viscous drag coefficients for each spatial dimension j = x,y,z. As all nondiagonal matrix elements ${\mathit{\gamma }}_{i\ne j}\left(d\right)=0$ vanish, we can refer to the diagonal elements as γ_j(d) instead of γ_jj(d). In general, γ_j(d) varies with the distance d to an obstacle, which in our case is the membrane of a living cell. To fit the data presented in the results section, we assume the diagonal drag coefficients γ_j to have the following form:

$${\gamma }_j\left(d\right)\approx {\gamma }_0\times \text{exp}\left(-\left(d-R\right)/{\mathit{\Lambda }}_j\right)+{\gamma }_{\infty },$$ (2)

where Λ_j is the hydrodynamic coupling length in direction j and γ_∞ represents the viscous drag far away from the interface. γ₀ = γ(d = R) describes the drag, when the bead with radius R is in contact with the cell membrane at d = R. ${\overleftrightarrow{\mathbf{\kappa }}}_{opt}$ denotes the stiffness tensor of the optical trap and reflects the linearized restoring force F = ${\overleftrightarrow{\mathbf{\kappa }}}_{opt}\times \mathbf{b}$ for sufficiently small displacements, which is a valid assumption in all our experiments. Upon binding to a cell, an additional, a priori unknown stiffness parameter ${\overleftrightarrow{\mathbf{\kappa }}}_{cell}$ ≈ (κ_cell,ij ×δ_ij) contributes to the bead’s motion. ${\overleftrightarrow{\mathbf{\kappa }}}_{cell}$ can be approximated by a step-function, which is zero for distances d > R to the membrane, such that the total force constant experienced by the particle in direction j is ${\kappa }_j\left(d\right)={\kappa }_{cell,\text{j}}\left(d\right)+{\kappa }_{opt,j}$ such that ${\kappa }_j\left(d>R\right)\approx {\kappa }_{opt,j}$. Because both the optical force ${\overleftrightarrow{\mathbf{\kappa }}}_{opt}\times \mathbf{b}$ and the friction force $\overleftrightarrow{\mathbf{\gamma }}\left(d\right)\times \dot{\mathbf{b}}$ point in the opposite direction of b and $\dot{\mathbf{b}}$, respectively, they have the same sign. However, the force exerted by the cell, $-{\overleftrightarrow{\mathbf{\kappa }}}_{cell}\times \mathbf{b}$, which only applies when d < R, tends to push the particle out of the trap, i.e., acts in the opposite direction and therefore has a negative sign.

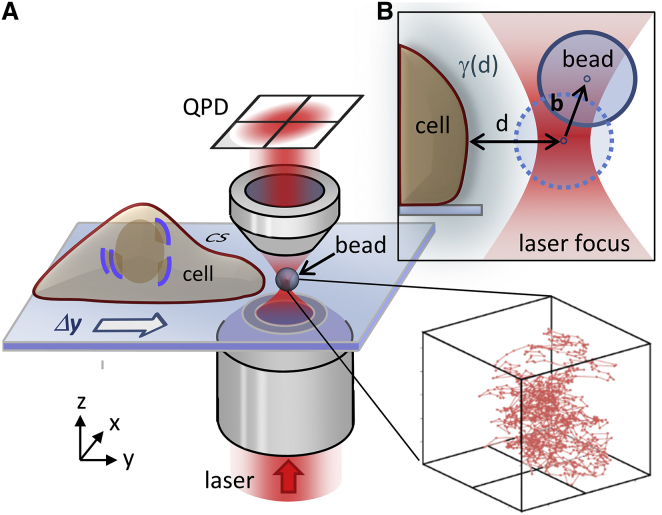
Figure 1.

Sketch of the experimental setup. (A) A 1 μm polystyrene bead is fluctuating in the proximity of a living cell. An optical trap confines the motion of the particle to a small volume around the trap center with FWHM = 18 nm in x and y, and FWHM = 40 nm in z direction. The trap is moved toward the cell membrane with Δy = 20 nm steps by means of a 3D piezo stage. The bead’s fluctuation data are recorded in three dimensions (lower right) with 2 MHz temporal resolution via two QPDs. For simplicity, only one QPD is drawn in this setup sketch. (B) The distance between the center of the optical trap and the cell membrane is denoted as d, whereas b symbolizes the bead’s displacement from the trap center. The blue halo surrounding the cell membrane indicates the spatially varying viscous drag γ(d). To see this figure in color, go online.

A suitable and common method to determine the quantities κ and γ from the fluctuation data is correlation analysis (39). Assuming a linear force and friction acting on the particle in thermal equilibrium, the autocorrelation function for the particle’s position is given by the following:

$$\begin{array}{c}AC\left(b_j\left(t\right)\right)=\langle b_j\left(t\right)\times b_j\left(t+\tau \right)\rangle \approx \langle b_j{\left(0\right)}^2\rangle \times e^{-\tau /{\tau }_{0j}}\\ \approx \frac{k_{B}T}{{\kappa }_j\left(d\right)}\times \text{exp}\left(-\tau \times {\kappa }_j\left(d\right)/{\gamma }_j\left(d\right)\right)\end{array}.$$ (3)

For time delays τ much shorter than the AC time τ_0j = γ_j /κ_j, $AC\left(b_j\left(t\right)\right)=A{C}_j\left(\tau \right)$ is approximately linear, resulting in the following:

$$A{C}_j\left(\tau \ll {\tau }_{0j}\right)\approx \frac{k_{B}T}{{\kappa }_j\left(d\right)}\left(1-\tau \times {\kappa }_j\left(d\right)/{\gamma }_j\left(d\right)\right)=\frac{k_{B}T}{{\kappa }_j\left(d\right)}-\frac{k_{B}T}{{\gamma }_j\left(d\right)}\times \tau .$$ (4)

The static part (τ = 0) of the AC yields the stiffness parameter κ. The dynamical information extracted from the slope $k_{B}T/{\gamma }_j\left(d\right)$ of the AC for short time delays τ yields the friction coefficient γ.

Mean first passage time

The average time a particle needs to diffuse over a given distance is defined as the mean first passage time (MFPT). Often, diffusion of a particle over its own radius R is considered. In the absence of interfaces or for distances large enough that no disturbance of the diffusive motion occurs, i.e., d-R >> Λ_j, the MFPT simply reads $t_0=\left(R^2/2k_{B}T\right)\times {\mathit{\gamma }}_{\infty }$, which can be derived from the particle’s mean squared displacement (39). If hydrodynamic coupling to the interface has to be considered, i.e., for d-R ≈ Λ_j, the spatial variation of the viscous drag has to be taken into account. For our exponential approach in Eq. 2, the following is the modified formula for the MFPT t_j(d₁,d₂):

$$t_j\left(d_1,d_2\right)=\frac{R^2}{2k_{B}T}\times \frac{1}{d_2-d_1}\underset{d_1}{\overset{d_2}{\int }}{\mathit{\gamma }}_{\infty }+{\mathit{\gamma }}_{0j}{e}^{-\left(d-R\right)/{\Lambda }_j}\mathrm{d}d,$$ (5)

where the multiplication with a constant factor γ_∞ has been replaced by an integral accounting for the distance-dependent change of γ_j(d), normalized by the prefactor (d₂-d₁)^-1, and d₁ and d₂ are the boundaries confining the diffusion area in perpendicular direction.

Interferometric particle tracking and signal acquisition

The determination of the particle’s displacement b(t) in our situation is not straightforward. The tracking scheme is based on intensities $I_{tot,2}={\left|{\mathbf{E}}_i\mathbf{+}{\mathbf{E}}_p\right|}^2$ generated by the interference of the electric field of the unscattered trapping light and the light scattered at the particle, E_i and E_p. These intensities in the BFP are recorded by one or two quadrant photo diodes (QPDs); see Fig. 1. A QPD measures four voltage signals, each proportional to the interference intensity $I_{tot}$, which is integrated over the area of each quadrant. The voltage signals are then combined to result in three position signals S_j(t) that are functions of the particle position b_j(t). S_x is obtained from the difference of the two left and the two right quadrant signals, and S_y from the difference between the upper and lower two quadrant signals. The axial position signal S_z is provided by the sum of all four QPD signals and varies linearly with small axial displacements b_z of the particle. Therefore, the position signal recorded in the BFP of the detection objective lens (Fourier plane) with coordinates $\left(k_x,k_y\right)$ can be described as $S_j\left(b_j\right)={\iint }_{QPD}{I}_{tot,2}\left(k_x,k_y,b_j\right)H_j\left(k_x,k_y\right)d{k}_{x}d{k}_y$ (40). The vector function H is a filter selecting the three directions j = x,y,z out of the interference pattern I_tot,2 through $\mathbf{H}\left(k_x,k_y\right)=step\left(k_{0}N{A}_{\det }-\left|\mathbf{k}\right|\right)\times \left(2step\left(k_x\right)-1,2step\left(k_y\right)-1,1\right)$. k₀ = 2π/λ is the vacuum wave number of the trapping light with wavelength λ = 1.06 μm and NA_det is the numerical aperture of the detection lens.

Within the small spatial displacements b_j occurring in all our experiments, the signals S_j are proportional to the actual displacements. The conversion factor is the detector sensitivity g_j and is given by $\text{S}\left(\mathrm{t}\right)=\overleftrightarrow{\text{g}}\left(\mathrm{t}\right)\times \text{b}\left(\mathrm{t}\right)$. Before each experiment, i.e., in the absence of the cell, the undisturbed detector sensitivities g_∞j are determined by the Langevin calibration procedure (41).

If a particle diffuses nearby the cell, the incident trapping light can be scattered at the periphery of the cell as well, such that three beams with electric fields E_i, E_p, and E_c (i = incident, p = particle, c = cell) can interfere. The three-beam interference generates an intensity pattern $I_{tot}\left(k_x,k_y\right)$ in the BFP of the detection objective lens (Fourier plane) with coordinates $\left(k_x,k_y\right)$ (40), which is imaged onto the QPD and can be described by (42) the following:

$$I_{tot,3}\left(\mathbf{b},d\right)={\left|{\mathbf{E}}_i+{\mathbf{E}}_p\left(\mathbf{b}\right)+{\mathbf{E}}_c\left(d\right)\right|}^2={\left|{\mathbf{E}}_i\right|}^2+{\left|{\mathbf{E}}_p\right|}^2+{\left|{\mathbf{E}}_c\right|}^2+2\left|{\mathbf{E}}_i\right|\left|{\mathbf{E}}_p\right|\text{cos}\left({\varphi }_i-{\varphi }_p\left(\mathbf{b}\right)\right)+2\left|{\mathbf{E}}_i\right|\left|{\mathbf{E}}_c\right|\text{cos}\left({\varphi }_i-{\varphi }_c\left(-d\right)\right)+2\left|{\mathbf{E}}_p\right|\left|{\mathbf{E}}_c\right|\text{cos}\left({\varphi }_p\left(\mathbf{b}\right)-{\varphi }_c\left(d\right)\right).$$ (6)

The three-beam interference consists of six terms, with three additional intensities generated by the distance-dependent electric field E_c(d) scattered at the cell periphery. For large distances d, these terms vanish and the well-known two-beam interference formula is left over. Because the distance d is a positive number, we indicated the origin of the scattered phase ${\varphi }_c\left(-d\right)$ by a negative argument, because the cell is placed left to the optical axis and the particle is right to the optical axis. Equation 6 can be summarized to the incoherent parts $I_i+I_p\left(\mathbf{b}\right)+I_c\left(d\right)$, two terms with sine functions both defined by the interference of the incident field and a scattered field, which are phase shifted by π/2, and, a cosine term defined by the interference between the two scattered fields, E_p and E_c:

$$I_{tot,3}\left(k_x,k_y,\mathbf{b},d\right)\approx I_i+I_p\left(\mathbf{b}\right)+I_{ip}\left(\mathbf{b}\right)\text{sin}\left(\Delta {\varphi }_{ip}\left(\mathbf{b}\right)\right)+I_c\left(d\right)-I_{ic}\left(d\right)\text{sin}\left(\Delta {\varphi }_{ic}\left(d\right)\right)+I_{pc}\left(\mathbf{b},d\right)\text{cos}\left(\Delta {\varphi }_{pc}(\mathbf{b},d)\right).$$ (7)

The second sine term does not change on timescales smaller than the measurement time, because it does not depend on the fluctuating particle position b(t). The cosine term, defined by both scattered fields, is small and can be neglected. According to Fig. 1B, the cell is displaced in the one and the bead in the other direction relative to the center of the field’s focus with phase ϕ_i. In this way, the two sine functions in Eq. 7 have different signs, because the phase difference $\Delta {\varphi }_{ic}\left(d\right)={\varphi }_i-{\varphi }_c\left(-d\right)$ is an odd function, i.e., $\Delta {\varphi }_{ic}\left(d\right)=-\Delta {\varphi }_{ic}\left(-d\right)$. Thereby, the distance-dependent term $I_{ic}\left(d\right)\text{sin}\left(\Delta {\varphi }_{ic}\left(d\right)\right)$ flattens the total interference pattern across the QPD and reduces the mean value of the total signal S_j(b_j,d) according to the following:

$$S_j\left(b_j,d\right)\approx \underset{QPD}{\iint }{I}_{tot,2}\left(b_j\right)H_{j}d{k}_{x}d{k}_y+\underset{QPD}{\iint }\left(I_c\left(d\right)-I_{ic}\left(d\right)\text{sin}\left(\Delta {\varphi }_{ic}\left(d\right)\right)\right)H_{j}d{k}_{x}d{k}_y=S_{ip,j}\left(b_j\right)-S_{ic,j}\left(d\right).$$ (8)

For small displacements, the position signal $S_{ip,j}\left(b_j\left(t\right)\right)\approx S_{0j}+g_{\infty j}\times b_j\left(t\right)$ is a linear function of displacements b_j(t). According to Eq. 8, the distance-dependent signal S_ic,j(d) generated by the cell reduces the measured signal S_j(b_j,d) with decreasing distance d, but does not depend on the particle displacements b_j and thereby on the fluctuation width 〈b_j(0)²〉. As shown by the green trajectory in Fig. 3A, the vicinity of the cell will affect the mean signal offset, leading to an apparent particle displacement perpendicular to the cell surface, which is merely an optical effect. However, the amplitude of the position fluctuations 〈b_j(0)²〉 is hardly affected.

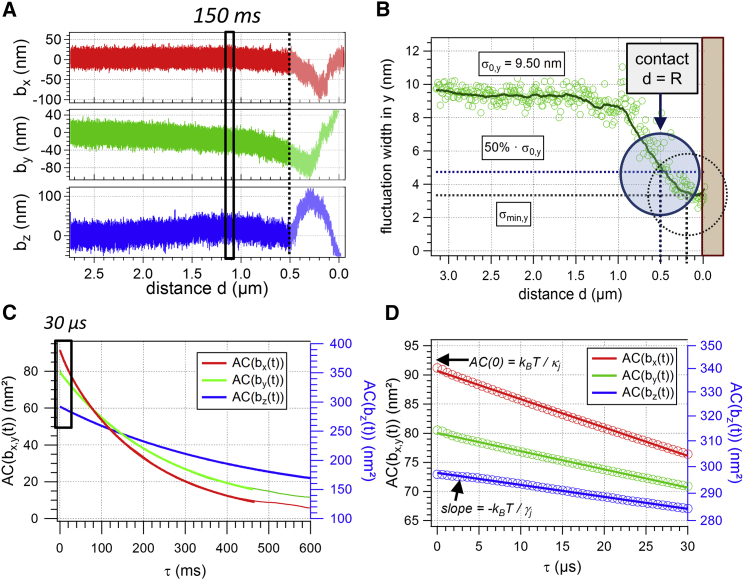
Figure 3.

Analysis of a 1 μm bead’s fluctuation data while approaching the membrane of a HT29 cell. (A) Distance-dependent position trajectories b_x(d,t), b_y(d,t), b_z(d,t) calculated from the QPD data after calibration. y data correspond to scan direction. The regions d ≤ R, in which the membrane is already in contact with the bead, are grayed out. The three-dimensional QPD data are divided into subsequent parts with duration τ_mes = 150 ms as indicated by the black box; each spatial dimension is analyzed separately. (B) Upon contact to the membrane, i.e., d = R, the histogram width σ_y(d) of the bead’s fluctuations perpendicular to the cell membrane decreases (circles: data points, solid line: running average over 10 data points). The values at 50% of σ₀ and σ_min are used to determine the likely and the latest membrane contact point. The shaded region right of the vertical d = 0 line represents the cell. (C) The parts of the trajectory that correspond to one specific cell-focus distance d are analyzed by means of AC functions. (D) The AC is approximately linear on a τ ≤ 30 μs timescale, which is used to obtain κ_j(d) and γ_j(d). To see this figure in color, go online.

Following Eq. 8, the AC of the particle’s position signal is the sum of a time-varying and a temporally constant function, $AC\left(S\left(b\left(t\right),d\right)\right)=AC\left(S_{ip}\left(b\left(t\right)\right)-S_{ic}\left(d\right)\right)$ and can be written as the sum of two AC functions: $AC\left(S\left(b\left(t\right),d\right)\right)=AC\left(S_{ip}\left(b\left(t\right)\right)\right)+AC\left(S_{ic}\left(d\right)\right)-2\times CC\left(S_{ip}\left(b\left(t\right)\right),S_{ic}\left(d\right)\right)$. The cross correlation between the conventional fluctuation signal and the DC signal from the cell is zero. The first AC function is the exponential of Eq. 3, the second is a wedge function characterized by the time-constant signal amplitude $S_{ic}\left(d\right)$.

$$AC\left(S_j\left(b_j,d\right)\right)=g_j^2\frac{k_{B}T}{{\kappa }_j}\times \text{exp}\left(-\frac{\tau {\kappa }_j}{{\gamma }_j\left(d\right)}\right)+S_{ic,j}{\left(d\right)}^2\left(1-\frac{\tau }{{\tau }_{mes}}\right)\stackrel{\tau <<{\tau }_{0j}}{\approx }{g}^2\left(\frac{k_{B}T}{{\kappa }_j}-\frac{k_{B}T}{{\gamma }_j\left(d\right)}\cdot \tau \right)+S_{ic,j}{\left(d\right)}^2.$$ (9)

However, on short timescales τ << τ_0j,τ << τ_mes, the additional signal $S_{ic}\left(d\right)$ generated by the cell does not affect the slope $k_{B}T/{\gamma }_j\left(d\right)$ of the AC function and thereby the viscosity γ_j(d). Here, the measurement time at each trap position, τ_mes = 150 ms, equals ∼100 times the AC time τ_0j.

Materials and Methods

Optical microscope

An inverted microscope (Axio Observer, Carl Zeiss, Jena, Germany) equipped with a high NA water immersion objective lens (C-Apochromat 63×/1.20W Corr M27, Carl Zeiss) was used for differential interference contrast (DIC) and bright-field microscopy. The DIC images were acquired by a 12-bit monochrome charge-coupled device camera (AxioCam MRm, Carl Zeiss).

Photonic force microscope

In brief, the photonic force microscope consists of an optical trapping unit and an interferometric tracking unit. The optical trap is formed by a 2 W Nd:GdVO₄ solid-state laser (Smart Laser Systems, Berlin, Germany) operating at 1064 nm in cw mode, which is focused onto the sample via the objective lens. An acousto-optical modulator (AA.MT.110/A1-ir, AA Opto-Electronique, Orsay, France) allowed for the control of the laser power in the focus. The laser power is stabilized by a noise eater (miniNE 2.1, TEM Messtechnik, Hanover, Germany), which analyzes the laser intensity fluctuations by a reference photo diode (G8370-81, InGaAs photo diode, Hamamatsu, Japan) and controls the transmission of the acousto-optic modulator via an external regulation circuit. A simplified sketch of the experimental setup is shown in Fig. 1.

Tracking unit

A second high NA objective lens (W Plan-Apochromat 63×/ NA_det = 1.0, Carl Zeiss) is used to collect the unscattered laser light and the light scattered at the bead and the cell periphery, respectively. The resulting interference patterns in the BFP are imaged onto two QPDs (InGaAs PIN photodiodes, G6849 series, Hamamatsu). The beam is split up by 50% beam splitter cubes after passing the detection objective and is imaged onto the QPDs with different magnifications, accounting for the different detection sensitivities for axial and lateral signals, respectively (43–45). The use of InGaAs photodiodes enables high-speed tracking with good quantum efficiency at 1064 nm. Incoming voltage signals are amplified by two miniSupply QUAD pre-amplifiers (TEM Messtechnik) and digitalized via two analog-digital converter cards (NiDAQ PCI-6110 and PCIe-6259, National Instruments, Austin, TX).

Cell preparation

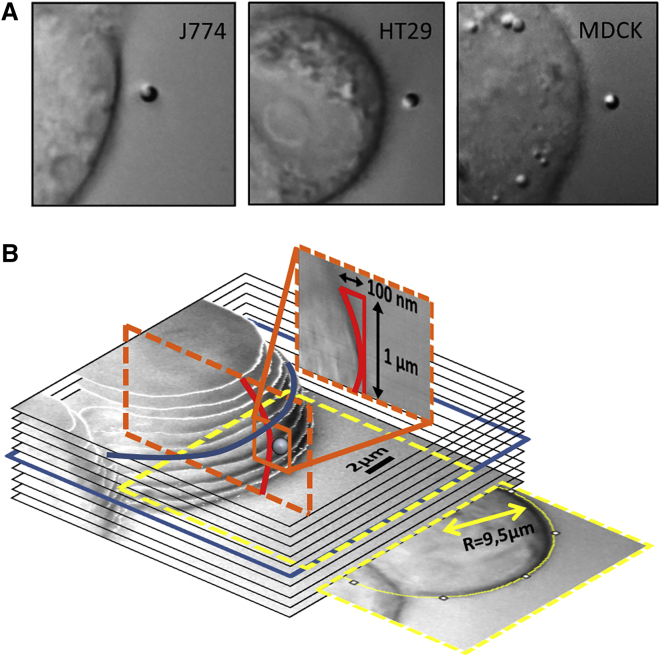
For our cell experiments, we used J774 mouse macrophages (American Type Culture Collection ATCC, Manassas, VA) as an example for cells that exhibit phagocytic activity as well as HT29 human colorectal adenocarcinoma cells and Madin-Darby canine kidney (MDCK) epithelial cells, the latter two showing no phagocytic activity. The cells, shown in Fig. 2, were cultured at 37°C in an atmosphere containing 5% CO₂. During growth and experiments, the cells were suspended in cell medium (Dulbecco’s Modified Eagle Medium (DMEM GlutaMAX, Invitrogen Life Technologies, Carlsbad, CA) with 10% fetal bovine serum added). Before each experiment, the cells were detached from the bottom of the cell culture flask and transferred onto an uncoated microscope cover glass that has been sterilized before in an autoclave. No substrate coating of the microscope glass slides is necessary, as all cell types used in this study are adherent cells. The measurement chamber containing the cover glass and freshly added cell medium was kept at 37°C during all the experiments.

Figure 2.

Three-dimensional configuration of the cell membrane interface. (A) DIC images of different cell types with a 1 μm diameter polystyrene bead. From left to right: J774 macrophage, HT29 adenocarcinoma cell, and MDCK epithelial cell. (B) Three-dimensional cell image of a HT29 cell, reconstructed from x-y-slices taken at different z-positions, which are Δz = 1 μm apart. The blue frame indicates the height above the cover slip at which the bead was placed. The additional slices illustrate the estimation of the cell’s radii of curvature (yellow frame: x-y-plane, orange and red lines: y-z-plane). To see this figure in color, go online.

Sample chamber with heating unit

The temperature of the cell medium inside the sample chamber can be controlled by a surrounding heating element (TC-CSC, Bioscience Tools, San Diego, CA), which has an integrated temperature sensor and is regulated via a proportional-integral-derivative controller (TC-2-100, Bioscience Tools). The heating unit is switched on ∼1 h before the experiments to allow the system to equilibrate, thus reducing thermal drifts during measurement. The sample chamber is connected to 3D piezo stage (NanoView LP200, Mad City Labs, Madison, WI) that provides a 200 μm range of motion with a step response of 20 ms for each dimension and with a positioning accuracy smaller than 1 nm. Moving the sample chamber relative to the static optical trap thus enables an accurate distance control.

Results

Geometrical arrangement

The geometry of the interfaces is an important factor in all experiments. We have approximated the cell to be planar over the cross section of the bead. To back up this assumption, the cell’s radii of curvature were measured with the public domain software ImageJ (http://rsbweb.nih.gov/ij/) and compared with the bead’s radius. For the sample cell shown in Fig. 2B, the radius of curvature in the x-y-plane of ∼9.5 μm is 19 times larger than the bead radius R_bead = 0.5 μm, so that R_cell >> R_bead is a valid assumption. All other cells used were of comparable size. In fact, the curvature of the cell has only a minor effect of <2.5% on the measured viscous drag γ(d) that can be estimated by some geometrical considerations (see Figs. S1 and S2 in the Supporting Material).

The z-distance of the bead to the cover slip was chosen high enough, i.e., at least five times the bead diameter, where the hydrodynamic effects are low, such that no interaction between bead and cover slip could deteriorate our measurements. The direction of light propagation is always denoted as z, whereas the in-plane coordinates x and y are chosen such that x always denotes the direction parallel to the interface and y corresponds to the scan direction, i.e., perpendicular to the interface; see also Fig. 1. In the analysis of the hydrodynamic decay lengths and MFPTs, we limit ourselves to x and y data, to which we refer as ‖ and ⊥, respectively.

Measuring the position signals

QPD signals were recorded with a sampling rate of 2 MHz, from which the bead’s position trajectories b_x(t), b_y(t), b_z(t) were calculated as shown above; see Fig. 3A. During data acquisition, the piezo stage holding the cell sample was moved in y direction with 20 nm steps, hereby subsequently reducing the distance d between the center of the laser focus and the cell membrane. At each step, 300,000 data points were recorded, corresponding to a measurement time τ_mes = 150 ms per position. This equals ∼100 times the AC time, which has been shown to be beneficial for the reliability of the AC analysis presented in Fig. 3, C and D. The complete trajectories b_x(t), b_y(t), b_z(t) were cut into single segments corresponding to one fixed piezo position and analyzed separately. Although the full range of data points up to d = 0 is shown in Fig. 3A, only distances d ≥ R are considered for data evaluation. For d < R, bead and membrane are already in close contact, so that the fluctuation width of the bead is narrowed and causing the bead to be shifted out of the laser focus, which can be seen as a strong displacement of the trajectories in all spatial dimensions. A control experiment of an empty trap approaching a cell membrane is presented and discussed in the Supporting Material; see Fig. S3.

Estimating the contact between bead and membrane

From the fluctuation data in scan direction, i.e., y data, position histograms were determined and the distance-dependent standard deviation of the bead trace σ_y(d) was analyzed; see Fig. 3B. A decay of σ_y(d = R) = 50% × σ₀ to half of its bulk value reveals the position d = R, where the bead and a stiff interface are in mechanical contact (46). The rationale behind this choice is further explained in the Supporting Material, alongside data from Brownian dynamics simulations that back up this criterion; see Figs. S4–S7.

However, if the bead comes into contact with a soft interface, such as the pericellular matrix (PCM), the bead’s fluctuation width can decay to σ₀ /2 before contact with the cell membrane, which might be only reached at a minimal width of about σ_y(d = R) ≈ σ₀ /3 = σ_min. At this point, stiff membrane contact is very probable, as the bead starts to get pushed out of the optical trap by the cell and the QPD signals merely arise from laser light scattered at the cell. The true membrane contact point is likely located between these two estimates. More precise values for the membrane contact point cannot be specified, because a certain influence of the PCM on the measured signals remains. Analysis of all σ(d) curves from each cell experiment reveals that the latest membrane contact point at σ_min is in average 0.22 μm ± 0.09 μm behind the 50% σ₀ estimate and differs slightly between different cell types (J774: 0.27 ± 0.09 μm, MDCK: 0.19 ± 0.07 μm, HT29: 0.21 ± 0.11 μm).

Force constants and distance-dependent viscosities

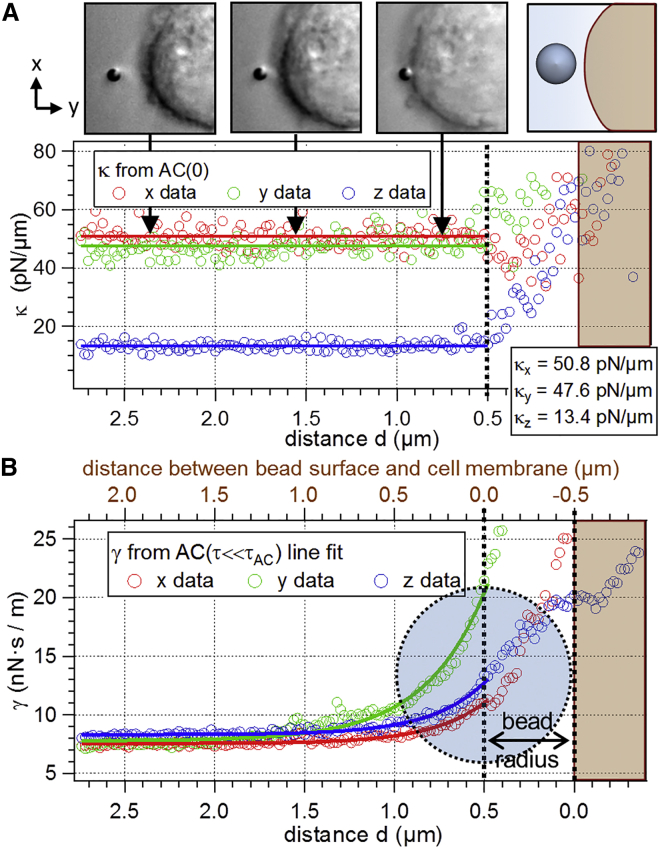
We can assume the system to be in thermal equilibrium as long as no contact between bead and membrane is established. Then, the fluctuation data can be analyzed by means of correlation analysis to obtain information about the force constants κ_j and the friction coefficients γ_j; see Eq. 4. Fig. 4 A shows the stiffness κ(d) for varying distance d between the center of the laser focus and the cell membrane. All its components κ_j (j = x,y,z) remain constant until mechanical contact between the bead and the cell membrane is established, as indicated by additional line fits. The values obtained from these fits (κ_x = 50.8 pN/μm, κ_y = 47.6 pN/μm, κ_z = 13.4 pN/μm) agree well with the trap stiffnesses obtained from a Langevin-calibration before the experiment (not shown).

Figure 4.

The bead’s distance d to the cell membrane of a HT29 cell is subsequently decreased, as illustrated in the DIC images and the schematic sketch. Contact between the bead surface and the cell membrane is marked by a vertical dotted black line at d = 0.5 μm. (A) The stiffness parameter κ_j(d) and (B) the viscous drag γ_j(d) are plotted as a function of d. Solid lines in (B) indicate exponential fits to the data points. The positions of bead and cell (according to the 50% σ₀ criterion) are indicated by the filled circle and the shaded region right of d = 0. To see this figure in color, go online.

At the same time, the friction coefficients γ_j(d) increase as the bead approaches the cell membrane, starting ∼1 μm before contact. The increase of the friction component perpendicular to the cell membrane, i.e., γ_y(d) displayed in green, is significantly higher than γ_x(d) and γ_z(d) in parallel direction (red and blue circles). This phenomenon has also been observed qualitatively in experiments of a spherical bead approaching a stiff wall (22).

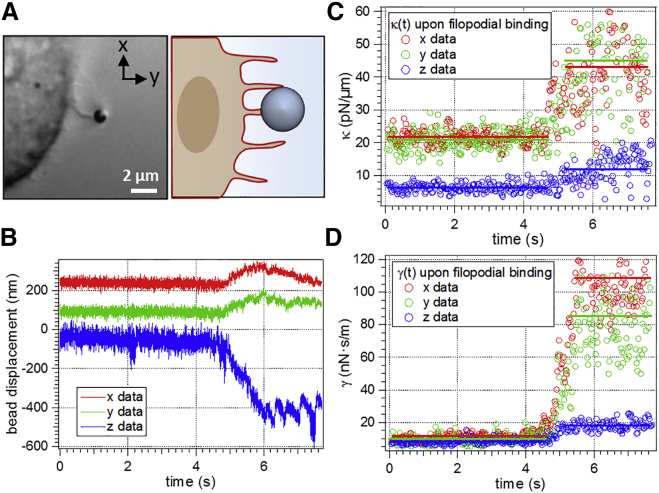
Influence of filopodial binding on the fluctuation data

Macrophages are components of the mammalian immune system and possess small cell protrusions called filopodia, which can act as tentacles to pull bound objects toward the cell to initiate a process called phagocytosis (47,48). The measurements performed with macrophages require special attention because of possible binding events to cellular protrusions such as filopodia. Binding to such protrusions would make it impossible to extract information about pure hydrodynamic coupling out of the fluctuation data. During all experiments with cells, care was taken to investigate only parts of the membrane where no protrusions could be observed in the DIC images. However, binding to tiny filopodia that are invisible in the microscope can still have an influence on the measurement data and must be disregarded, if any changes in the fluctuation width become visible in the particle tracking data before cell contact. Upon binding to the membrane, the particle fluctuation width reduces strongly and considerable forces would be required to detach the particle from the cell (49).

Fig. 5 illustrates how filopodial binding can be identified in the fluctuation data. First, the bead’s positions trajectories change slowly in their mean position values. Further analysis of the fluctuation behavior reveals that both κ_j(t) and γ_j(t) increase abruptly upon binding of a filopodium, while at the same time the fluctuation volume is restricted by the filopodium, resulting in a narrowed fluctuation width. The increase in κ_j(t) and γ_j(t) is most pronounced in the direction of filopodial retraction. As shown in Fig. 5, κ_x(t) and κ_y(t) increase rapidly to ∼250% of their original values. γ_x(t) and γ_y(t) increase even by a factor of 10. Note that this behavior is fundamentally different to the smooth increase shown in Fig. 4. In this way possible filopodial binding can be identified with the help of the fluctuation data. For all results shown in the following chapters, we could verify that no filopodial binding occurred.

Figure 5.

(A) DIC image and illustration of binding events to filopodia of a J774 macrophage. (B) Binding events can be seen in a relatively slow temporal change of the fluctuation data. Here, the binding process takes place at approximately t = 4.8 s. (C and D) An abrupt increase of both κ_j(t) and γ_j(t) in all three dimensions j = x,y,z of up to one order of magnitude is observed upon binding, as filopodial retraction takes place in three dimensions. To see this figure in color, go online.

The pericellular matrix of living cells

A large variety of eukaryotic cells including those examined in this study are known to have a structure that is covalently linked to the outer side of the plasma membrane, the so-called glycocalyx or PCM (8,49–51). It consists in particular of proteoglycans and associated polymer chains and is involved in plenty of cellular functions from cell adhesion and migration to receptor functions and immune response, only to mention a few. The thickness of the glycocalyx can exceed a few micrometers. As the PCM is invisible in brightfield or DIC microscopy, its occurrence is difficult to observe. However, its possible influence on the bead’s fluctuation upon cell approach must not be ignored. A discussion of possible effects will be provided later in the manuscript.

Change of the local hydrodynamics close to a living cell

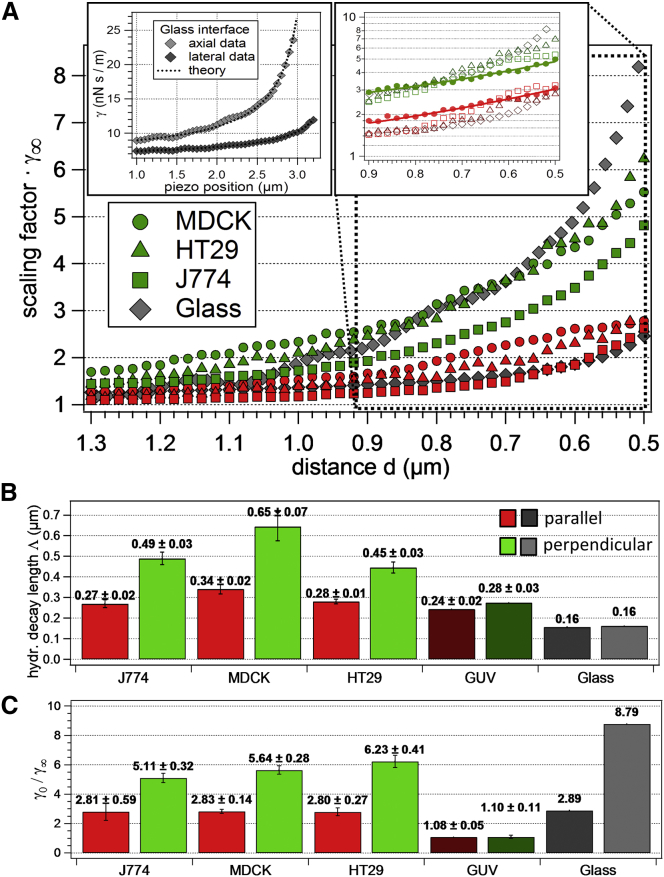
The distance-dependent viscous drag close to an interface is displayed in Figs. 4 and 6. The exponential function given in Eq. 2 was fitted to the data points γ_j(t). The good fit results show that our exponential model is a suitable approach, which has the great advantage, that the hydrodynamic coupling of particles to the interface can be described by just two values for each direction, γ_0j and Λ_j. The hydrodynamic decay length Λ_j is a measure for the distance, on which hydrodynamic coupling between the particle and cell increases the friction. In the limit $d\to \infty$, i.e., far away from the cell, we measured a viscous drag γ_∞ = 8.0 × 10⁻⁹ Ns/m, which is the viscosity of the cell medium at T = 37°C (52). γ_∞ + γ_0j is the maximum viscous drag that occurs when cell membrane and bead surface are in close contact.

Figure 6.

Hydrodynamic coupling of a 1 μm bead close to different interfaces. (A) Comparison of γ_⊥(d) in green and γ_‖(d) in red for all cell types and a stiff glass interface, shown in gray diamonds and in the upper left inset together with fits. Data points for all available measurements belonging to the respective cell type were averaged to get the resulting curves. The linear behavior in semi-logarithmic representation (right inset) confirms the nearly exponential decay, highlighted for the case of the MDCK cells. (B) Bar diagram of hydrodynamic decay lengths Λ_⊥ and Λ_‖ for all investigated cell types, the GUVs and the glass interface. (C) Summary of the measured values γ_0⊥ and γ_0‖ in units of γ_∞ = 8.0 × 10⁻⁹ Ns/m. Numbers in (B) and (C) are mean values ± standard deviation. GUV data in (B) and (C) are displayed in darker colors and glass data in gray, where dark gray represents parallel and light gray perpendicular data. To see this figure in color, go online.

Fig. 6 summarizes the fit results to the measured γ_j(d) curves for different cell samples using the contact point estimate at σ₀. In total, we investigated N = 16 J774 macrophages, N = 15 MDCK cells, N = 24 HT29 cells, and N = 11 GUVs. γ_⊥(d) reveals comparable slopes for all cell types, but does not increase as steeply as for the case of a stiff wall at small distances, i.e., 0.5 μm < d < 0.65 μm. Although Λ_⊥ is significantly higher than Λ_‖ for all living cells, this is not the case for a GUV or a glass interface. The hydrodynamic decay lengths for perpendicular motion are approximately the same for the J774 (Λ_⊥ = 0.49 μm) and the HT29 cells (Λ_⊥ = 0.45 μm), whereas the decay length for the MDCK cells is ∼30% longer (Λ_⊥ = 0.65 μm). A similar result can be observed for the parallel decay lengths, which are generally ∼1.5 to 1.8 times smaller: J774: Λ_‖ = 0.27 μm, HT29: Λ_‖ = 0.28 μm, MDCK: Λ_‖ = 0.34 μm. The viscous drag increases with decreasing distance d between focus and interface and, within our measurement accuracy, reaches a finite value γ_j(d = R) = γ_0j + γ_∞; see Eq. 2 with j = ⊥,‖. The obtained γ₀ values are displayed in Fig. 6C as a multiple of γ_∞ = 8.0 × 10⁻⁹ Ns/m. In the case of diffusion parallel to the interface, the viscous drag γ_0‖ is effectively the same for all cell types investigated and increases to roughly 280% of the bulk value. The perpendicular friction factor γ_0⊥ is generally higher than γ_0‖ and the values for different cell types differ by up to 20% from one another (HT29: γ_0⊥ = 6,23 × γ_∞, MDCK: γ_0⊥ = 5,64 × γ_∞, J774: γ_0⊥ = 5,11 × γ_∞).

Using the σ_min criterion for the contact point, the measured decay lengths Λ_j are slightly decreased (by maximally 12%) and the maximum friction coefficients γ_0j are increased by a factor of 1.39 to 2.31, depending on the cell type. A detailed comparison of all the results is given in the Supporting Material; see Tables S1–S3, together with a revision of Figs. 6, B and C, and 7 accounting for the uncertainty of the membrane position (see Figs. S8–S10).

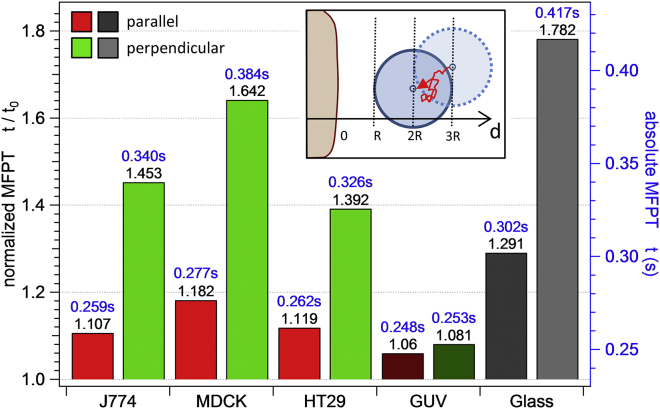
Figure 7.

Anisotropic diffusion nearby interfaces. Mean first passage times t_⊥(d₁,d₂) and t_‖(d₁,d₂) for a 1 μm bead diffusing nearby an interface from d₁ = 3R toward d₂ = 2R, as illustrated in the inset. Color coding is the same as in Fig. 6. To see this figure in color, go online.

The change in γ(d) of a bead approaching a plane stiff interface as a function of distance is well understood and can be theoretically calculated according to Happel’s and Brenner’s law (12). The corresponding measurement data is shown in the left inset of Fig. 6A. The uncoated glass cover slip of the measurement chamber was used to study the viscosity close to a stiff and planar interface, which leads to a different experimental geometry, as explained in the following and in the Supporting Material; see Figs. S11 and S12. In contrast to the cell experiments, where the surface was approached in y direction, the glass cover slip was approached in –z direction, i.e., in (reverse) propagation direction of the laser light with Δz = 20 nm steps as in the cell experiments. To compensate for the weaker trap stiffness in z direction compared with x and y, the laser power was increased by 50% compared with the cell experiments.

The good agreement between our experimental data and the decay predicted by Happel and Brenner for the glass interface proves the validity of our measurement procedure. Applying our exponential decay model to the glass interface data yields decay lengths of Λ_⊥ = 0.162 μm and Λ_‖ = 0.157 μm. These values do not exhibit a difference in both directions, but are significantly lower than those for living cells, i.e., about a factor of 3.5 for perpendicular and 1.9 for parallel motion. One should note that fitting the Happel and Brenner functions

$${\gamma }_{\parallel }={\gamma }_{\infty }{\left(1\text{-}9/16\left(R/d\right)+1/8{\left(R/d\right)}^3\text{-}45/256{\left(R/d\right)}^4\text{-}1/16{\left(R/d\right)}^5\right)}^{\text{-}1}$$ (10)

$${\gamma }_{\perp }={\gamma }_{\infty }\left(6{\left(d\text{-}R\right)}^2+9\times \left(d\text{-}R\right)\times R+2R^2\right)/\left(6{\left(d\text{-}R\right)}^2+2\times \left(d\text{-}R\right)\times R\right)$$ (11)

to the γ(d) curves belonging to cell membranes or GUVs fails and that our exponential model shows more accurate fit results (not shown).

Measurements on GUVs as artificial cells

We have used GUVs as the simplest biomimetic model system for mammalian cells. As described in further detail by Meinel et al. (38), the GUVs were ∼20 μm in diameter and were prepared from egg phosphatidylcholine (Egg PC, Sigma-Aldrich, St. Louis, MO), utilizing the method of electroformation. Different to the cells used, the GUVs are characterized by a lipid bilayer that separates two approximately identical fluids. Measurements on GUVs were performed with 1 μm–sized polystyrene beads and the same experimental parameters as described above, but with reduced laser power, resulting in slightly larger fluctuation volumes of the bead. The GUV was trapped in a sandwich configuration consisting of two uncoated glass cover slips separated by a 75 μm–thick spacer ring. Glass beads (2R = 20 μm) were attached to the downside of the upper cover slip to ensure the immobilization of the GUV, which has moved to the upper cover slip upon laser irradiation because of the scattering force.

Remarkably, and in contrast to the results for living cells, no significant difference in perpendicular and parallel hydrodynamic decay lengths (Λ_⊥ = 0.28 μm, Λ_‖ = 0.24 μm) could be observed; see Fig. 6B. Both decay lengths are very similar to those Λ_‖ measured nearby living cells. The maximal friction close to the GUV membrane in perpendicular and in parallel direction are about the same (γ_0⊥ = 1.10 × γ_∞ and γ_0‖ = 1.08 × γ_∞), again significantly different compared with the results of living cells. The fluctuation data from the GUV experiments and the extraction of κ_j(d) and γ_j(d) similar to the procedure shown in Fig. 4 is presented in the Supporting Material; see Fig. S13, together with Fig. S14 displaying the bead’s trajectory upon approaching the GUV membrane.

Mean first passage times

By means of Eq. 5, we analyzed the time a 1 μm bead needs to diffuse toward an interface from the distance d₁ = 3R toward d₂ = 2R with $t_0=\left(R^2/2k_{B}T\right)\times {\mathit{\gamma }}_{\infty }=0.234\mathrm{s}$ for d-R >> Λ_j using the σ₀/2 criterion for the contact point. As Fig. 7 shows, the increase in viscous drag nearby an interface causes the MFPTs to rise significantly. For living cells, an anisotropy of the MFPT is apparent. The diffusion perpendicular to the membrane is slowed down by a factor of up to 1.64 in the case of MDCK cells (J774: t_⊥(3R,2R) = 1.45 × t₀, HT29: t_⊥(3R,2R) = 1.39 × t₀). In contrast, however, the MFPT for diffusion parallel to the interface is not affected severely, with a maximum increase of t_‖(3R,2R) = 1.18 × t₀ for the case of MDCK cells. The significantly increased t_⊥ is unique to living cells and is not that pronounced at the GUV membrane with t_⊥(3R,2R) = 1.08 × t₀ and t_‖(3R,2R) = 1.06 × t₀. As the uncertainty in the determination of the true membrane contact point affects both Λ_j and γ_0j, the t_j are also influenced. Using the σ_min contact estimate results in an overall increase of t_j, which is again most pronounced in perpendicular direction. The results accounting for this contact point uncertainty are presented in the Supporting Material; see Table S3 and Fig. S10.

To calculate the MFPTs at the glass interface, we performed a numerical integration of Eq. 5, where the term ${\gamma }_{\infty }+{\gamma }_0{e}^{-\left(d-R\right)/\Lambda }$ was replaced by the respective approximation formula as given by Happel and Brenner (Eqs. 10 and 11). This analysis resulted in t_‖,Glass(3R,2R) = 0.302 s = 1.291 × t₀ and t_⊥,Glass(3R,2R) = 0.417 s = 1.782 × t₀. Those results are both even higher than those of all living cells, which is understandable, because the stiff character of the glass interface is expected to slow down the bead’s diffusion more drastically than the presence of a flexible plasma membrane.

Discussion

Short summary of the experimental results

In this study, we measured the diffusive behavior of 1 μm–sized particles in the vicinity of the plasma membranes of living cells, of a GUV, and a glass interface. We used a photonic force microscope equipped with a 3D interferometric tracking system, which allows us to record the Brownian motion of the particle at a 2 MHz sampling rate and with nanometer precision. By analyzing the short timescale diffusion via the AC of the particle’s trajectory, we could observe and quantify a generally increased viscous drag near surfaces. For all cell types, the viscous drag perpendicular to the membrane is increased more significantly than in parallel direction. This behavior could not be observed for the GUV.

Accuracy of determining the bead-membrane-distance

Although the distance was reduced in steps of 20 nm, the relatively strong laser power restricted the bead diffusion to an area with radius of roughly 9 nm, both for parallel and perpendicular diffusion, which is less than 50% of the chosen step size. The piezo stage itself has a positioning accuracy of <1 nm. Because of this choice of parameters, the presence of the cell interface itself hardly influences the bead’s fluctuations and therefore does not affect the results of the diffusion analysis. This is further supported by computer simulations shown in Figs. S4–S6.

The membrane of a living cell or a GUV is not rigid but is subject to thermal fluctuations. We have estimated the membrane fluctuations in two different ways: first, by trapping and calibrating the membrane in a weak laser focus and recording its thermal fluctuations analogously to the bead’s motion as described in (53); second, by recording the fluctuations of a 1 μm bead that was bound to the membrane. Both methods gave an estimate that the membrane fluctuations are in the range of 4 nm, which is five times smaller than the step size, so that we can conclude that the role of the membrane fluctuations is negligible in this study.

However, because the PCM at the outside of the cell membrane gets first into contact with the bead, it might reduce the bead’s position fluctuation width σ. In this way σ might drop off to 50% before the bead touches the membrane. Therefore, we estimated the latest-possible (worst-case) contact point, where the bead fluctuations reach a minimum σ_min of around typically 30% to 40% of the bulk value σ₀. The alternative contact point, where the bead fluctuation is minimal, is, in average, 0.22 μm ± 0.09 μm behind our initial contact estimate for the cells. It is likely that the true contact point between bead and cell membrane is in between these two estimates.

Reliability of the local viscous drag measurements

As described in the methods section, the values of the local viscous drag γ(d) were obtained by the AC of the measured bead’s trajectory on a short timescale of τ < 30 μs. As the AC is calculated from a vast number of data points, corresponding to roughly 100 times the AC time τ₀, the results obtained from linear fitting are statistically reliable. Besides our short time analysis based on Eqs. 4 and 9, we have tested other methods to recover γ and κ, such as the analysis of the complete exponentially decaying AC, of the mean square displacement, or of the PSD. All methods yielded the same results for κ_j(d) and γ_j(d) (not shown). As mentioned above, the γ values extracted from $AC\left(\tau \ll {\tau }_0\right)$ coincide well with the theoretically predicted behavior of γ close to a glass surface according to Happel and Brenner. A frequency resolved analysis of γ(ω), shown in Fig. S12, reveals that γ_j(d) has no relevant frequency-dependent contribution and that taking the average over all frequencies ω is justified. However, particle fluctuations nearby the cell membrane can be damped because of the PCM (glycocalyx) (8), which is not visible with DIC. This is possibly the reason for the decay of the perpendicular fluctuation width over a distance of ∼0.2 μm in Fig. 3C and the slight increase in the stiffness κ_y over the last 0.1 μm before cell contact as shown in Fig. 4A. This length may be an indication for the thickness of the glycocalyx. Nevertheless, it is significantly shorter than the hydrodynamic decay length measured for several cells, the GUV, and the glass surface.

Influence of transient binding to the glycocalyx on the fluctuation data

Figs. 3B, and 4 both contain hints that transient binding to the PCM can be identified in the fluctuation data. In Fig. 3B, a drop of the fluctuation width in approach direction (y) can be observed already at roughly 250 nm before contact point (0,75 μm > d > 0,5 μm), whereas the drop-off to 50% × σ_0y because of steric interaction between bead and cell is expected to take place only within one fluctuation width of the bead, which is σ_0y = 9,5 nm in this study. This is further discussed in connection with Fig. S7.

It has been reported (8) that the PCM is not deformed or compressed by optically trapped beads passing though the PCM toward the cell membrane. Rather, the bead penetrates the PCM that thereon recovers in the vicinity of the bead. The transient binding to the PCM may reduce the fluctuation width as seen in Fig. 3B, such that the drop to 50% of the bulk value σ₀ is reached before the actual contact with the cell membrane. By using an alternative estimate of the contact point, where σ₀ is reduced to the minimum width of ∼0.3σ₀ to 0.4σ₀, the hydrodynamic decay lengths Λ_‖ and Λ_⊥ are slightly decreased in average by 9% and 12%, respectively. At the same time, the viscous drags γ_0‖ and γ_0⊥ are increased in average by 40% to 63% and even 62% to 131% in the perpendicular case. However, even this worst-case estimation does not affect the overall analysis, data interpretation, and message of our study.

In Fig. 4, a rise of the stiffness parameter κ_y(d) in approach direction of up to 20% is observed at roughly 0.1 μm before contact. Interaction with filopodia is unlikely according to the argumentation around Fig. 5, as there is no jump in γ_y(d) (or in the parallel directions) at the same time. Also, Figs. S12 and S13 show sample approach traces for the glass interface and the GUV, which, in contrast to the cell approach, do not show a change in κ_j(d) before the contact point.

Alongside Fig. S16, a passive microrheological analysis of the data in Fig. 4 is shown to estimate whether the transient binding to the PCM corrupts the measurement of γ_j(d) and the associated hydrodynamic decay lengths. This becomes possible by calculating κ and γ from the real and imaginary part of the complex shear modulus, respectively, through the Kramers and Kronig relations. A comparison of the results obtained from AC analysis in Fig. 4 with the fluctuation range of the data obtained by microrheology (see Fig. S16) brings us to the conclusion that the determination of γ_j(d) and Λ_j is still valid despite the apparent interaction of the bead with the PCM. Other studies, e.g., (8,51), show how bead-optical tweezers-assays can be used to probe the structure of the PCM, which is however beyond the scope of this study.

Error estimation for tracking nearby cells

As pointed out in the derivation of Eq. 9, the additional signal $S_{ic}\left(d\right)$ generated by the cell leads to an apparent additional particle displacement. This optical effect leads to a wedge function with axis intercept ${\overline{b}}_y^2$ adding up to the undisturbed AC and thereby slightly changing its slope and the resulting γ(d). We roughly estimate from Fig. 3A that the mean particle displacement is shifted by maximum ${\overline{b}}_y$ = 50 nm when in close proximity to the cell membrane, which is a worst-case assumption, as the actual mean shift is always below 50 nm. It follows from geometrical considerations that the additional slope can be expressed as $\Delta AC/{\tau }_{max}={\overline{b}}_y^2/{\tau }_{mes}$, where the linear part of the AC has been analyzed up to τ_max = 30 μs and τ_mes = 150 ms represents the measurement time at a distance d. Given these values, Eqs. 3 and 9 together with ${\overline{b}}_y^2=S_{ic,y}{\left(d\approx R\right)}^2/g_y^2$ then provide an upper limit estimate of the systematic error: $\left(k_{B}T/{\gamma }_{max}^{\ast }\right)=\left(k_{B}T/{\gamma }_{max}\right)+\left({\overline{b}}_y^2/{\tau }_{mes}\right)$. Assuming γ_max = γ_∞ = 8.0 × 10⁻⁹ Ns/m results in Δγ_max = –2.4 × 10⁻¹⁰ Ns/m, which is only 3.0% of γ_∞ (with $\Delta {\gamma }_{max}={\gamma }_{max}^{\ast }-{\gamma }_{max}$). In conclusion, the systematic error originating from the additional signal $S_{ic}\left(d\right)$ is negligibly small in the short-time AC analysis based on Eqs. 3 and 9.

Suitability of the exponential model

Our simplified assumption of the exponentially decaying viscous drag for decreasing distance between the particle and the cell membrane fits remarkably well to our measurement data. It offers the great advantage that the changing hydrodynamics at smooth interfaces such as the lipid membranes of different cells or of artificial vesicles can be described by just two quantities, the maximum viscous drag γ_0j and the hydrodynamic decay length Λ_j. Furthermore, a comparison between viscosities at different interfaces becomes easily possible.

However, the exponential decay fails to give a correct approximation of the diffusive behavior of a bead close to a glass interface. In the right inset of Fig. 6A, the deviation of the data points from the exponential behavior can be seen, which may lead to a misinterpretation of the calculated hydrodynamic decay lengths and MFPT for glass. A realistic estimation of the MFPTs at glass interfaces could be achieved by the numerical integration of Eq. 5 as discussed in the results section. Calculation of the MFPTs at the glass interface by using the approach of Eqs. 2 and 5 would result in t_‖(3R,2R) = 1.016 × t₀ and t_⊥(3R,2R) = 1.024 × t₀, which is unrealistically low because of the nonexponential increase of γ_j(d) at a glass interface. The realistic results (t_‖,Glass(3R,2R) = 0.302 s = 1.291 × t₀ and t_⊥,Glass(3R,2R) = 0.417 s = 1.782 × t₀) for the MFPT, which are given in the results section, are in fact significantly higher than t_‖(3R,2R) = 1.016 × t₀ and t_⊥(3R,2R) = 1.024 × t₀.

The increase of the static viscous drag close to a plane membrane separating two identical fluids as predicted theoretically by Lee et al. (13,14) and Bickel (15,16) is of the form $\gamma \left(d\right)/{\gamma }_0={\left(1-\alpha \times \left(R/d\right)\right)}^{-1}$ and does not resemble an exponentially decaying function (α is a constant and R is the sphere radius). However, a bead close to a spherical surface—like it is the case for our cells—can drag the water more easily to the side, compared with the case of a plane surface. Therefore, one can expect a less-steep increase in viscous drag close to a spherical surface, which could partly explain the difference between our measured curves and the theoretical predictions for the static viscous drag. However, further investigations are required to model the decay of the viscous drag considering dynamic effects, nonplane and elastic membranes, as well as different viscosities on both sides of the membrane.

Anisotropy of hydrodynamic decay lengths for living cells

All measurements performed on cells show the common result that the hydrodynamic decay lengths in perpendicular direction are significantly longer than in parallel direction. This behavior cannot be seen with the GUV, where Λ_⊥ and Λ_‖ are of comparable length. Interestingly, GUVs and cells, which both have a phospholipid bilayer membrane, show the same decay lengths of Λ_‖ ≈ 0.3 μm for parallel diffusion.

A possible physical explanation for a significantly stronger increase in viscous drag for perpendicular diffusion could be the following: without an interface, the hydrodynamic drag can be transferred from one particle to another via the surrounding fluid, depending on the distance (10,54). A transfer of hydrodynamic momentum through an interface is also possible, if the interface can deform and relax its shape or can transmit fluid molecules to a certain extent. Lipid membranes behave like this, and therefore can transfer hydrodynamic momentum from the outside of the GUV to its interior, i.e., in normal direction equally well as in lateral direction. In front of a stiff wall the hydrodynamic drag cannot be transferred anymore, which leads to a local fluid compression. In consequence, the motion of a bead is hindered and damped, leading to a strong increase in viscosity; see Fig. 6B. Simply because of geometric constraints, it is obvious that the fluid can be dragged more easily parallel to the interface than in direction to the interface. This coincides with the theoretical prediction that the normal component of the viscous drag close to a glass surface increases to infinity with decreasing distance according to the theory of Happel and Brenner, i.e., γ_0⊥ → ∞, but also diverges in the experiments. Unlike solid surfaces, lipid membranes behave like two-dimensional fluids and a hydrodynamic drag from the environment can result in lateral membrane motion, thus reducing friction in parallel direction.

The hydrodynamic momentum produced by the drag of the sphere is completely repelled at a stiff interface, thus doubling the amount of mechanical momentum taken up by the stiff medium. A thin elastic membrane transfers most of the incoming momentum without significant repulsion. Cells represent an intermediate case, where part of the momentum is transferred and the other part is repelled, leading to an increase in viscous drag with a specific decay length. This hydrodynamic coupling length is the distance within which the momentum transfer to the interface starts to increase relative to the case of a homogeneous fluid.

At the cell membranes, the perpendicular drag coefficients γ_0⊥ = 5.1 × γ_∞ (J774) and γ_0⊥ = 6.2 × γ_∞ (HT29) are five to six times larger than the bulk value γ_∞ = 8.0 × 10⁻⁹ Ns/m, whereas the increase in viscous drag close to a GUV membrane is fundamentally smaller (γ_0⊥ = 1.10 × γ_∞). In other words, momentum transfer through a membrane is better possible, if the fluid on both sides of the membrane is approximately the same regarding viscosity and osmolarity, as in the case of the GUV. However, the situation is different with living cells, because the plasma membrane exhibits a more complex composition of different lipids and lipid rafts, pores, and membrane proteins, many of them linked to the cytoskeleton (55). The interior of the cell is crowded with vesicles, macromolecules, cytoskeletal filaments, organelles, and other membranes, resulting in a higher density and a more rigid structure that apparently dampens the transfer of hydrodynamic momentum. The difference in γ_0⊥ for different cell types is probably a result of different compositions of the cell interior and also of the PCM, both because of the different functions of these cell types.

Our calculations show that the MFPTs are also influenced, as shown in Fig. 7. For a sphere diffusing over R = 0.5 μm toward the cell from distance d₁ = 3R toward d₂ = 2R, the parallel MPFTs are hardly changed. In perpendicular direction, however, the MPFT is increased significantly by 30% to 65%. These times become the longer, the closer the particle approaches the cell.

Biological interpretation

The hydrodynamic coupling of the approaching particle in perpendicular direction exerts a hydrodynamic pressure, i.e., momentum transfer, onto the cell, which, in consequence, must apply a force to the membrane and mechano-sensitive proteins therein. The pronounced increase in viscous drag slows down the particle’s diffusion and thus reduces the rate of collisions with membrane components and thereby reduces the interaction probability in a given time window. The denser and more viscous the cell, the more hydrodynamic momentum is transferred to its interior, but the more the mobility and the collision rate are reduced outside the cell. The reduced collision rate corresponds to a limited temporal bandwidth of information (momentum) transfer. In this way, less broad-band noise is transferred to the cell. Thereby, the local increase of viscosity leads to a low-pass filtering of incoming signals, and one may conclude that only distinct, pronounced momentum changes can be transferred to the cell interior.

For example, as a response to the hydrodynamic pressure of the particle, the cell can reorganize the cytoskeleton connected to the membrane or can initiate the growth of cell protrusions such as filopodia.

The larger parallel mobility compared with the bead’s perpendicular motion allows a particle to diffuse faster parallel to the membrane and to better find specific or unspecific binding sites across the cell surface. Because the particle fluctuations are faster in parallel than in perpendicular direction, also the particle’s collision rate is higher in parallel direction. This might, for example, help cells to improve their endocytosis efficiency by a facilitated search of the particle for membrane binding sites.

Conclusions

The viscosity of a fluid determines the mobility of a particle on a macroscopic scale and the dissipation of particle fluctuations on a microscopic scale. Close to different cellular interfaces, this behavior changes strongly—an effect that can significantly influence the probability of particle binding to the interface. Using a photonic force microscope with a fast 3D interferometric particle tracking system, we show for the first time, to our knowledge, that the viscous drag increases nearly exponentially with decreasing distance to the membranes of living cells and of GUVs. Similar to the direction-dependent changes of the viscosity nearby stiff interfaces, but nevertheless unexpected, we found that three different types of cells show a significantly stronger increase in viscosity in perpendicular direction than in parallel direction. However, all three different cells and the GUVs are characterized by a strongly different hydrodynamic coupling length and maximum viscosity, which we believe are a consequence of the cell’s composition and its regulation of proteins and lipids inside the cell or the membrane and also the PCM. It is remarkable that the correlation of the particle position fluctuations encode the cellular membrane composition and the ability to transfer information. However, further investigations need to uncover the relation between the cellular constituents near the membrane, the hydrodynamic coupling length and strength outside the membrane, and the connected physiological function. Fast particle fluctuations, as measurable by photonic force microscopy, encode a lot of relevant information to understand the molecular processes of endocytosis or drug delivery.

Author Contributions

F.J. performed cell experiments, analyzed and interpreted the data, and prepared the figures; F.K. designed and constructed the microscope setup; A.M. performed GUV experiments; T.M. developed the BD simulation framework; R.N. and B.E. provided and prepared the cells; and A.R. initiated and supervised the project, obtained financial funding, interpreted the data, and wrote the manuscript together with F.J.

Editor: Jochen Guck.

Supporting Citations

References (56–60) appear in the Supporting Material.