Do Molecular Markers Inform About Pleiotropy?

Abstract

The availability of dense panels of common single-nucleotide polymorphisms and sequence variants has facilitated the study of statistical features of the genetic architecture of complex traits and diseases via whole-genome regressions (WGRs). At the onset, traits were analyzed trait by trait, but recently, WGRs have been extended for analysis of several traits jointly. The expectation is that such an approach would offer insight into mechanisms that cause trait associations, such as pleiotropy. We demonstrate that correlation parameters inferred using markers can give a distorted picture of the genetic correlation between traits. In the absence of knowledge of linkage disequilibrium relationships between quantitative or disease trait loci and markers, speculating about genetic correlation and its causes (e.g., pleiotropy) using genomic data is conjectural.

THE interindividual differences for a trait or disease risk that can be explained by genetic factors, such as trait heritability (h²), the genetic correlation (r_G), and the coheritability between two traits (r_Gh₁h₂), are very important parameters in quantitative genetic studies of animals, humans, and plants. These quantities play a role in the study of evolution due to artificial and natural selection, and knowledge thereof is required for statistical prediction of outcomes in animal and plant breeding as well as medicine. Traditionally, these parameters have been estimated using phenotypes and pedigrees, e.g., family and twin data in human genetics. The availability of dense panels of common single-nucleotide polymorphisms (SNPs) and of sequence data more recently has made it possible to assess kinship among distantly related individuals (Morton et al. 1971; Thompson 1975; Ritland 1996; Lynch and Ritland 1999). This development has opened new opportunities for study of the genetic architecture of complex traits and diseases. For instance, Yang et al. (2010) suggested using whole-genome regressions (WGRs) (Meuwissen et al. 2001) to assess the proportion of variance of a trait or disease risk that can be explained by a regression of phenotypes on common SNPs or genomic heritability and a related parameter, the “missing heritability.” More recently, WGR models have been extended for the analysis of systems of multiple traits, so the concept of genomic correlation also has entered into the picture (Jia and Jannink 2012; Lee et al. 2012). For instance, Maier et al. (2015) used multivariate WGR models and reported estimates of genetic correlations between psychiatric disorders, and Furlotte and Eskin (2015) presented a methodology that incorporates genetic marker information for the analysis of multiple traits that, according to the authors, “provide fundamental insights into the nature of co-expressed genes.” In a similar spirit, Korte et al. (2012) argued that multitrait-marker-enabled regressions can be useful for understanding pleiotropy. More recently, Bulik-Sullivan et al. (2015) proposed a methodology for “estimating genetic correlation” using statistics derived from single-marker genome-wide association studies (GWAS) and reported estimates of such correlations among 25 human traits.

de los Campos et al. (2015) discussed potential problems that emerge when trying to infer genetic parameters using molecular markers that are imperfectly associated with the genotypes at the causal loci. In this paper, the framework described in de los Campos et al. (2015) is extended for the analysis of systems of traits, and it is demonstrated that correlation parameters inferred using markers can give a distorted picture of the genetic correlation between traits. For instance, it is shown that an analysis based on markers may suggest a genetic correlation when none exists or may fail to detect a genetic correlation when one does exist. It is concluded that in the absence of knowledge about linkage disequilibrium (LD) relationships between quantitative trait loci (QTL) and markers, speculating about genetic correlations, and even more about their causes (e.g., pleiotropy), using genomic data is conjectural.

Theory

To set the stage, consider a single-locus model. In an additive-inheritance framework, a phenotype (y) is regressed on a QTL genotype code Q (0, 1, and 2 for genotypes aa, Aa, and AA, respectively) according to the linear model

$$y={\text{α}}_0+{\text{α}}_{1}Q+E$$ (1)

where ${\text{α}}_0$ and ${\text{α}}_1$ are fixed parameters, and Q and E are independent random variables, the latter representing a model residual. The proportion of phenotypic variance explained by the linear regression on Q, or narrow-sense heritability, is

$$h^2=\frac{{\text{α}}_1^2{\mathrm{\Sigma }}_Q}{{\text{α}}_1^2{\mathrm{\Sigma }}_Q+{\sigma }_E^2}$$

where ${\mathrm{\Sigma }}_Q=\text{var}\left(Q\right)$ is the variance in allelic content, and ${\sigma }_E^2=\text{var}\left(E\right)$ is the residual variance. If Q is standardized to a unit variance,

$${\mathrm{\Sigma }}_Q=1\hspace{1em}\text{and}\hspace{1em}{h}^2=\frac{{\text{α}}_1^2}{{\text{α}}_1^2+{\text{σ}}_E^2}$$

In quantitative genomic analysis, marker genotypes (X) are used in lieu of the QTL genotypes Q because the latter are unknown or unobserved. The marker-based or instrumental model, assuming a single marker, is a linear regression on marker genotype X with form

$$y={\text{α}}_0+{\text{β}}_{1}X+E^{\prime }$$ (2)

where E′ is a regression residual. Assuming without loss of generality that both X and Q are in standard deviation units, the marker effect can be shown to be ${\text{β}}_1={\text{ρ}}_{QX}{\text{α}}_1$, where ${\text{ρ}}_{QX}$ is the correlation between the marker and the QTL genotypes, which depends on their LD. In this setting, the proportion of variance of phenotypes explained by the linear regression on the marker, or genomic heritability, is $h_{\text{marked}}^2={\text{ρ}}_{QX}^2{h}^2$, and missing heritability is $h_{\text{missing}}^2=\left(1-{\text{ρ}}_{QX}^2\right)h^2$. Hence, missing heritability is a function of the LD between the marker and the QTL. Genomic heritability has h² as an upper bound (de los Campos et al. 2015).

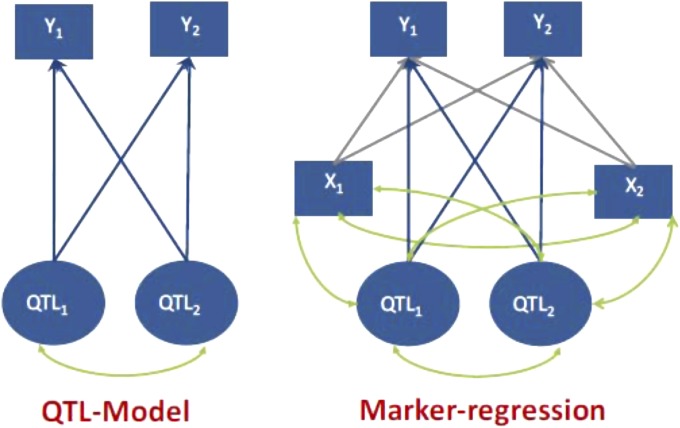
The regression model just described can be extended to the analysis of multiple traits affected by multiple QTL. For simplicity, we consider only two markers (X₁ and X₂) and two QTL (Q₁ and Q₂). A multivariate representation of the model with an arbitrary number of QTL and markers is provided in the Appendix. Figure 1 depicts a system with two traits, two QTL, and two markers. The left panel represents the regression of the phenotypes on the two QTL, with blue arrows denoting effects from QTL on traits and green arcs denoting LD between QTL. In the QTL model of Figure 1, the genetic correlation is (see Appendix)

$$r_G=\frac{{\alpha }_1\prime {\mathrm{\Sigma }}_Q{\alpha }_2}{\sqrt{\left({\alpha }_1\prime {\mathrm{\Sigma }}_Q{\alpha }_1\right)\left({\alpha }_2\prime {\mathrm{\Sigma }}_Q{\alpha }_2\right)}}$$ (3)

where ${\mathbf{\alpha }}_1\prime =\left(\begin{array}{cc}{\text{α}}_{11}& {\text{α}}_{12}\end{array}\right)$ contains the effects of QTL 1 and 2 on trait 1, and ${\mathbf{\alpha }}_2\prime =\left(\begin{array}{cc}{\text{α}}_{21}& {\text{α}}_{22}\end{array}\right)$ contains the effects of QTL 1 and 2 on trait 2. The variance-covariance matrix between QTL genotypes is given by ${\mathbf{\Sigma }}_Q$. If genotypes are standardized,

$${\mathbf{\Sigma }}_Q=\left[\begin{array}{cc}1& {\text{ρ}}_{Q_{12}}\\ {\text{ρ}}_{Q_{21}}& 1\end{array}\right]$$

with ${\text{ρ}}_{Q_{12}}$ being the correlation between genotypes at QTL 1 and 2. In the QTL model of Figure 1, there are two sources of genetic correlation: pleiotropy (i.e., the same QTL affects more than one trait) and LD between QTL, in this case represented by ${\text{ρ}}_{Q_{12}}\ne 0$. This is well known in quantitative genetics (Falconer and Mackay 1996; Knott and Haley 2000).

Figure 1.

Two-trait system. A system of two traits (Y) involving two QTL and two markers (X). Single-pointed blue arrows denote causal effects, green double-pointed arrows denote LD, and single-pointed gray arrows represent regression coefficients.

We now bring the two markers into the picture, as shown in the right panel of Figure 1; here gray arrows are regressions on markers (these are distinct from regressions on QTL genotypes), and arcs denote correlations between genotypes due to LD. In the Appendix, we show that the genomic correlation is

$$r_{G\text{,marked}}=\frac{{\alpha }_1\prime {\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}{\mathbf{\alpha }}_2}{\sqrt{\left({\mathbf{\alpha }}_1\prime {\Sigma }_{QX}{\Sigma }_X^{-1}{\Sigma }_{XQ}{\mathbf{\alpha }}_1\right)\left({\mathbf{\alpha }}_2\prime {\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}{\mathbf{\alpha }}_2\right)}}$$ (4)

In this expression, ${\mathbf{\Sigma }}_{QX}$ is the covariance matrix between QTL and marker genotypes (reflecting marker-QTL LD), and ${\mathbf{\Sigma }}_X$ is the covariance matrix between marker genotypes, reflecting mutual LD relationships among markers. If markers and genotypes are in standard deviation units,

$${\mathbf{\Sigma }}_X=\left[\begin{array}{cc}1& {\text{ρ}}_{X_{12}}\\ {\text{ρ}}_{X_{21}}& 1\end{array}\right]\hspace{1em}\text{and}\hspace{1em}{\mathbf{\Sigma }}_{QX}=\left[\begin{array}{cc}{\text{ρ}}_{Q_1{X}_1}& {\text{ρ}}_{Q_1{X}_2}\\ {\text{ρ}}_{Q_2{X}_1}& {\text{ρ}}_{Q_2{X}_2}\end{array}\right]$$

Comparison of the genomic correlation (4) with the genetic correlation (3) indicates that in $r_{r_{G\text{,marked}}}$, ${\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}$ replaces ${\mathbf{\Sigma }}_Q.$ Inspection of (4) reveals that the sources of the genomic correlation are (1) pleiotropic QTL effects via ${\mathbf{\alpha }}_1$ and ${\mathbf{\alpha }}_2$, (2) marker-QTL LD patterns conveyed by ${\mathbf{\Sigma }}_{QX}$, and (3) among-marker LD relationships, as conveyed by ${\mathbf{\Sigma }}_X.$ Notably, one of the sources of genetic correlation, i.e., LD between QTL, as conveyed by ${\mathbf{\Sigma }}_Q$, has no effect on $r_{G\text{,marked}}$. Conversely, there are sources that contribute to the genomic correlation, i.e., marker-marker and marker-QTL LD, that do not enter into $r_G.$

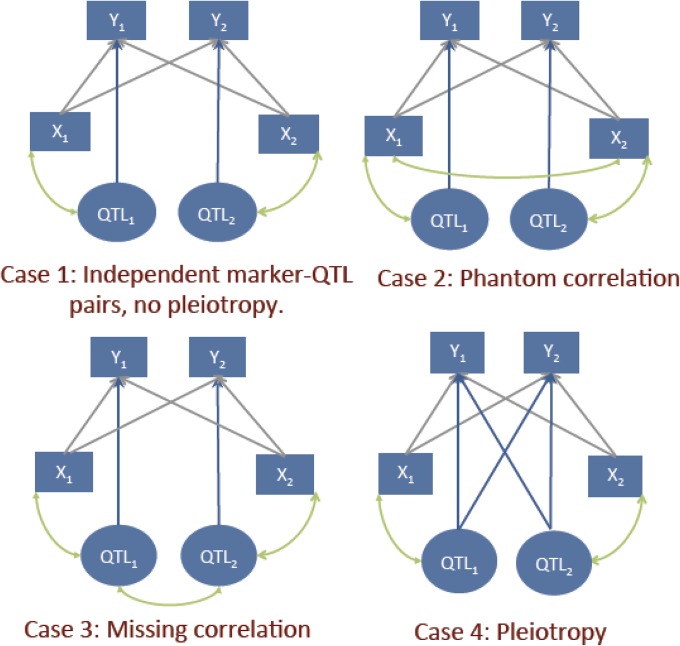
Because the sources affecting genetic and genomic correlations are distinct, the two parameters can differ greatly. This point is strengthened by considering four stylized cases represented in Figure 2. All the demonstrations supporting the discussion that follows can be found in the Appendix.

Figure 2.

Two-trait system. Four possible cases of interplay between QTL, markers, and phenotypes. The arrows have the same interpretation as in Figure 1.

Application to Four Situations

Case 1: Independent marker-QTL pairs and absence of pleiotropy (Figure 2, upper-left panel)

This is the simplest case: it consists of two marker-QTL pairs with linkage equilibrium (LE) between pairs but LD within pairs. Each trait is affected by only one QTL; QTL 1 affects trait 1, and QTL 2 affects trait 2. Several simplifications take place here. For instance, because of LE between pairs, ${\text{ρ}}_{Q_1{X}_2}=0$, so ${\mathbf{\Sigma }}_{QX}$ becomes an identity matrix. Therefore, the genetic covariance in the numerator of (3) reduces to ${\mathbf{\alpha }}_1\prime {\mathbf{\alpha }}_2$. In the absence of pleiotropy, ${\mathbf{\alpha }}_1\prime =\left(\begin{array}{cc}{\text{α}}_{11}& 0\end{array}\right)$ and ${\mathbf{\alpha }}_2\prime =\left(\begin{array}{cc}0& {\text{α}}_{22}\end{array}\right)$ are orthogonal; i.e., ${\mathbf{\alpha }}_1\prime {\mathbf{\alpha }}_2=0$. Therefore, the genetic correlation is null. Furthermore, with LE between pairs, ${\text{ρ}}_{Q_1{X}_2}={\text{ρ}}_{Q_2{X}_1}={\text{ρ}}_{X_1{X}_2}=0$, leading also to an absence of genomic correlation. Thus, in case 1 there is complete agreement between the genomic and genetic correlations: both are null.

Case 2: Phantom correlation (Figure 2, upper-right panel)

The setting is obtained by adding LD between the two markers to case 1. There is no pleiotropy, and the two QTL are in LE, so the genetic correlation is zero (genetically, the system is equivalent to case 1). However, because of the LD between markers, ${\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{\mathbf{-1}}{\mathbf{\Sigma }}_{XQ}$ in (4) is no longer diagonal. Consequently, there will be nonzero genomic correlation even in absence of genetic correlation: markers can induce genomic correlation when traits are genetically uncorrelated—a crucial issue.

Case 3: Missing correlation (Figure 2, lower-left panel)

This scenario illustrates a situation in which the genetic correlation is undetected by the markers and is obtained from case 1 by adding LD between QTL, which, in the absence of pleiotropy, is the only source of genetic correlation between traits. However, ${\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}$ remains diagonal as in case 1. Furthermore, in the absence of pleiotropy, ${\mathbf{\alpha }}_1\prime {\mathbf{\alpha }}_2=0$ (orthogonality); consequently, $r_{G\text{,marked}}$ is null. This example shows how one source of genetic correlation, namely, LD among QTL, may be completely lost in a genomic analysis.

Case 4: Pleiotropy (Figure 2, lower-right panel)

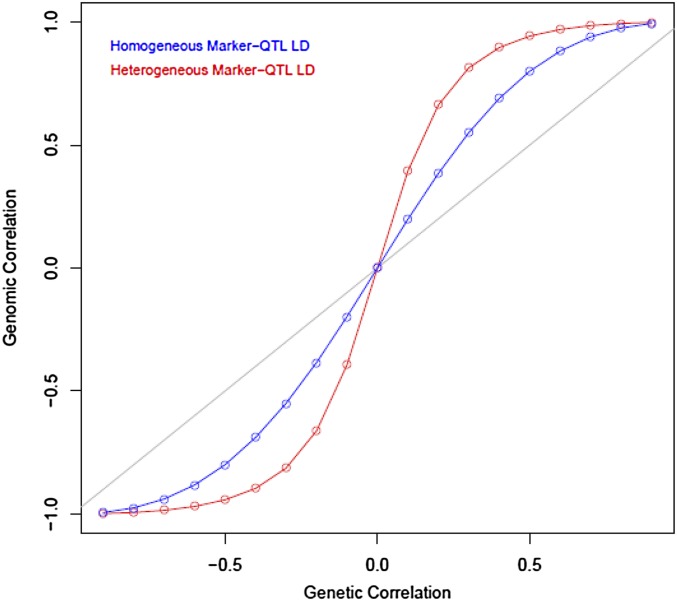
Here we allow each of the two QTL to affect both traits; otherwise, the setting is as in case 1. Pleiotropy now induces a genetic and a genomic correlation. However, $r_G$ and $r_{G,\text{marked}}$ differ in magnitude depending on the patterns of LD and on the magnitude of the pleiotropic effects. To illustrate, we set ${\mathbf{\Sigma }}_X={\mathbf{\Sigma }}_Q=I_2$, an identity matrix of order 2; this implies LE between pairs of QTL and pairs of markers. Further, we take

$${\mathbf{\Sigma }}_{QX}=\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right]\hspace{1em}\text{or}\hspace{1em}{\mathbf{\Sigma }}_{QX}=\left[\begin{array}{cc}0.2& 0\\ 0& 0.8\end{array}\right]$$

i.e., homogeneity or heterogeneity of marker-QTL LD, respectively. Finally, QTL effects are set to ${\mathbf{\alpha }}_1\prime =\left(\begin{array}{cc}1& {\text{α}}_{12}\end{array}\right)$ and ${\mathbf{\alpha }}_2\prime =\left(\begin{array}{cc}{\text{α}}_{21}& 1\end{array}\right)$, with ${\text{α}}_{12}={\text{α}}_{21}$; this pleiotropic effect was varied over the set of values $\left[-0.9,-0.8,\dots ,0.8,0.9\right]$. Figure 3 displays the resulting values of the genomic (vertical axis) vs. genetic (horizontal axis) correlations computed using (3) and (4); the blue curve represents the case where marker-QTL LD was the same for both pairs, and the red curve represents the case where LD differed between pairs 1 and 2. The figure shows how different patterns of LD induce different magnitudes of genomic and genetic correlations that, however, do not differ in sign in this example.

Figure 3.

Genomic vs. genetic correlation in the system described by case 4.

The genomic covariance does not always preserve the sign of the genetic covariance. Suppose that the two QTL are not pleiotropic but are in LD, with effects ${\mathbf{\alpha }}_1\prime =\left(\begin{array}{cc}\text{α}& 0\end{array}\right)$ and ${\mathbf{\alpha }}_2\prime =\left(\begin{array}{cc}0& -\text{α}\end{array}\right)$ and with

$${\mathbf{\Sigma }}_Q=\left[\begin{array}{cc}1& \frac{1}{2}\\ \frac{1}{2}& 1\end{array}\right]$$

Using the expression in the numerator of (3), the genetic covariance is

$$\left(\begin{array}{cc}\text{α}& 0\end{array}\right)\left[\begin{array}{cc}1& \frac{1}{2}\\ \frac{1}{2}& 1\end{array}\right]{\left(\begin{array}{cc}0& -\text{α}\end{array}\right)}^{\prime }=-\frac{{\text{α}}^2}{2}$$

which is negative at any nonnull value of α. Now let the LD relationships between markers and between QTL and markers be such that

$${\mathbf{\Sigma }}_X=\left[\begin{array}{cc}1& \frac{4}{5}\\ \frac{4}{5}& 1\end{array}\right]\hspace{1em}\text{and}\hspace{1em}{\mathbf{\Sigma }}_{QX}=\left[\begin{array}{cc}\frac{4}{5}& 0\\ 0& \frac{4}{5}\end{array}\right]$$

The genetic system is such that QTL 1 (QTL 2) is in LD with marker 1 (marker 2), but there is LE between QTL 1 and marker 2 and QTL 2 and marker 1. In the numerator of expression (4),

$${\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}=\left[\begin{array}{cc}\frac{16}{9}& -\frac{64}{45}\\ -\frac{64}{45}& \frac{16}{9}\end{array}\right]$$

and the genomic covariance is (64/45)α², always positive. In this example, the genomic correlation is 4/5, and the genetic correlation is −1/2.

Discussion

In the analysis of systems of complex traits, none of the cases just discussed are likely to “hold” exactly as described, and there is an enormous range of possibilities in terms of within and between marker-QTL genotypes as well as allelic effects sizes and signs. However, the underlying mechanisms that our examples describe are an integral part of the multivariate system involving QTL and markers and are key to an understanding of why genomic and genetic correlations are distinct parameters. Importantly, there is an ambiguous link between the two parameters. For instance, all or a fraction of the component of $r_G$ that is due to LD among QTL is likely to be missed by an analysis based on markers that are in imperfect LD with QTL. Also, a fraction of the genetic correlation due to pleiotropy is likely to be missed as a result of imperfect LD between marker and QTL. Finally, LD between markers can create illusory genetic correlations.

What happens if all QTL genotypes are included in the panel of markers, as may be expected if full DNA sequence information is available? Here the sequence can be partitioned into neutral markers (x) and QTL (q) such that for a given individual the genomic data presents as $x_{\text{seq}}=\left(x^{\prime },q^{\prime }\right)$. Thus, the sequence covariance matrix is

$$\text{var}\left(x_{\text{seq}}\right)={\mathbf{\Sigma }}_{{\mathbf{x}}_{\text{seq}}}=\left[\begin{array}{cc}{\mathbf{\Sigma }}_X& {\mathbf{\Sigma }}_{XQ}\\ {\mathbf{\Sigma }}_{QX}& {\mathbf{\Sigma }}_Q\end{array}\right]$$ (5)

The marked genotype for trait i using the DNA sequence is

$${\widehat{G}}_i={\mathbf{\alpha }}_i\prime {\mathbf{\Sigma }}_{Q{x}_{\text{seq}}}{\mathbf{\Sigma }}_{x_{\text{seq}}}^{-1}{x}_{\text{seq}},\hspace{1em}i=1,2$$ (6)

and the genomic or marked covariance is

$$\text{cov}\left({\widehat{G}}_1,{\widehat{G}}_2\right)={\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_{Q{x}_{\text{seq}}}{\mathbf{\Sigma }}_{x_{\text{seq}}}^{-1}{\mathbf{\Sigma }}_{x_{\text{seq}}}{\mathbf{\Sigma }}_{x_{\text{seq}}}^{-1}{\mathbf{\Sigma }}_{x_{\text{seq}}Q}{\mathbf{\alpha }}_2={\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_{Q{x}_{\text{seq}}}{\mathbf{\Sigma }}_{x_{\text{seq}}}^{-1}{\mathbf{\Sigma }}_{x_{\text{seq}}Q}{\mathbf{\alpha }}_2^{\prime }$$ (7)

Using partitioned matrix techniques for obtaining the inverse of ${\mathbf{\Sigma }}_{x_{\text{seq}}}$ de los Campos et al. (2015) showed that

$${\mathbf{\Sigma }}_{Q{x}_{\text{seq}}}{\mathbf{\Sigma }}_{x_{\text{seq}}}^{-1}{\mathbf{\Sigma }}_{x_{\text{seq}}Q}=\left[\begin{array}{cc}{\mathbf{\Sigma }}_{QX}& {\mathbf{\Sigma }}_Q\end{array}\right]\left[\begin{array}{c}\mathbf{0}\\ I\end{array}\right]={\mathbf{\Sigma }}_Q$$ (8)

Hence, $\text{cov}\left({\widehat{G}}_1,{\widehat{G}}_2\right)={\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_Q{\mathbf{\alpha }}_2$, the genetic covariance defined in equation (A2) in the Appendix. This shows that if the sequence information contains the variants at the causal loci, the marked covariance is equal to the genetic covariance between traits, and therefore, the genomic correlation is identical to the genetic correlation in that case. However, the genetic correlation depends on allelic frequencies and allele effect sizes at the QTL as well as on LD relationships between the QTL; these parameters, as well as the trait-specific QTL, will still need to be learned properly. Apart from finite-sample-size statistical problems, technical issues such as a large percentage of singleton reads and incomplete gene coverage will complicate matters (Kerr Wall 2009). Hence, when sequence data become available for quantitative genetic studies, unraveling the structure of the genetic correlation will not be an easy task, even under the simplifying assumptions of an additive model of inheritance.

In conclusion, multivariate quantitative genetic analysis based on markers can be used to obtain more accurate predictions of complex traits and to estimate genomic correlations. However, these parameters cannot always be viewed as genetic correlations because the sources of genetic and genomic correlations are distinct. Imperfect LD between markers and QTL produces missing heritability in single-trait analysis; in multivariate models, the problem becomes one of missing, excessive, or spurious (MES) correlation. Care must be exercised when interpreting estimates of genomic correlations between complex traits when these traits are assessed by molecular markers as opposed to QTL and even more so when interpreted from a causality perspective. Unfortunately, considerably more information is needed than what is now available for a meaningful interpretation of estimates of genomic correlations between pairs of traits when gene action involves many additive QTL. Speculating on the multivariate statistical genetic architecture of complex traits using imperfect instruments such as markers seems risky at this time.

Appendix

Genetic Correlation

Let $G_1={\mathbf{\alpha }}_1\prime q$ and $G_2={\mathbf{\alpha }}_2\prime q$ be additive genetic values for a pair of traits, where ${\mathbf{\alpha }}_1$ and ${\mathbf{\alpha }}_2$ are vectors of fixed allelic substitution effects affecting traits 1 and 2, respectively, and q is a random vector indicating the incidence of genotypes at the corresponding QTL. Following de los Campos et al. (2015), the additive genetic variance of trait i is

$$\text{var}\left(G_i\right)={\mathbf{\alpha }}_{\mathrm{i}}\prime {\mathbf{\Sigma }}_Q{\mathbf{\alpha }}_i,\hspace{1em}i=1,2$$ (A1)

The additive genetic covariance between traits 1 and 2 is then

$$\text{cov}\left(G_1,G_2\right)={\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_Q{\mathbf{\alpha }}_2$$ (A2)

where ${\mathbf{\Sigma }}_Q$ is a covariance matrix between allelic contents at loci affecting the traits. For example, with two QTL (assuming Hardy-Weinberg equilibrium at each of the two QTL),

$${\mathbf{\Sigma }}_Q=\left[\begin{array}{cc}2p_1\left(1-p_1\right)& 2D_{12}\\ 2D_{12}& 2p_2\left(1-p_2\right)\end{array}\right]$$ (A3)

where p_j is the frequency of the reference allele at locus j (j = 1,2), and D₁₂ is the LD statistic between alleles at the two loci. In scalar notation, (A2) takes the more explicit form

$$\text{cov}\left(G_1,G_2\right)=2\left[p_1\left(1-p_1\right){\text{α}}_{11}{\text{α}}_{21}+p_2\left(1-p_2\right){\text{α}}_{12}{\text{α}}_{22}\right]+2D_{12}\left({\text{α}}_{12}{\text{α}}_{21}+{\text{α}}_{11}{\text{α}}_{22}\right)$$ (A4)

The genetic covariance has a pleiotropy component (the first part of the expression) plus a LD component that vanishes if the QTL are in pairwise equilibrium, i.e., $D_{12}=0.$ The genetic correlation (Falconer and Mackay 1996) is

$$r_G=\frac{{\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_Q{\mathbf{\alpha }}_2}{\sqrt{\left({\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_Q{\mathbf{\alpha }}_1\right)\left({\mathbf{\alpha }}_2\prime {\mathbf{\Sigma }}_Q{\mathbf{\alpha }}_2\right)}}$$ (A5)

Genomic Correlation

Let x be a vector of genotypes at p marker loci. The multiple linear regressions of $G_1$ and $G_2$ on x produce as fitted values ${\widehat{G}}_i={\mathbf{\alpha }}_i^{\prime }{\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}x$. The genomic covariance (or marked genetic covariance) is defined as

$$C_{\text{marked}}=\text{cov}\left({\widehat{G}}_1,{\widehat{G}}_2\right)={\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}{\text{α}}_2$$ (A6)

The genomic correlation is

$$r_{G\text{,marked}}=\frac{C_{\text{marked}}}{\sqrt{\left({\mathbf{\alpha }}_1\prime {\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}{\mathbf{\alpha }}_1\right)\left({\mathbf{\alpha }}_2\prime {\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}{\text{α}}_2\right)}}$$ (A7)

Interpreting this parameter meaningfully requires knowledge of (1) bivariate QTL effects at all loci, (2) LD relationships between QTL affecting the two traits and the markers via the ${\mathbf{\Sigma }}_{QX}$ matrices, and (3) LD relationships among markers. Unfortunately, only phenotypes, marker genotypes, and LD relationships between markers are observable. Most of the required ingredients in the formula are yet unknown. Importantly, note that ${\mathbf{\Sigma }}_Q,$ conveying LD between QTL, does not enter into the genomic correlation.

Independent QTL-Marker Blocks (Case 1 in Figure 2)

Each of two independently segregating QTL is in LD with a marker, with the two markers being in mutual LE, and there is no pleiotropy. Here

$${\mathbf{\Sigma }}_{QX}={\mathbf{\Sigma }}_{XQ}={\mathbf{\Sigma }}_X=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$ (A8)

so the genetic and genomic correlations both become

$$r_G=r_{G\text{,marked}}=\frac{{\mathbf{\alpha }}_1\prime {\mathbf{\alpha }}_2}{\sqrt{\left({\mathbf{\alpha }}_1\prime {\mathbf{\alpha }}_1\right)\left({\mathbf{\alpha }}_2\prime {\mathbf{\alpha }}_2\right)}}$$ (A9)

Because there is no pleiotropy, ${\mathbf{\alpha }}_1\prime {\mathbf{\alpha }}_2={\left(\begin{array}{cc}{\text{α}}_{11}& 0\end{array}\right)}^{\prime }\left(\begin{array}{cc}0& {\text{α}}_{22}\end{array}\right)=0$, and both correlations are null.

Phantom Correlation (Case 2 in Figure 2)

Consider ${\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\Sigma }_{XQ}$ in (A6), where (given standardized genotypes)

$$\begin{array}{l}{\mathbf{\Sigma }}_{QX}=\left[\begin{array}{cc}{\text{ρ}}_{Q_1{X}_1}& {\text{ρ}}_{Q_1{X}_2}\\ {\text{ρ}}_{Q_2{X}_1}& {\text{ρ}}_{Q_2{X}_2}\end{array}\right]=\left[\begin{array}{cc}{\text{ρ}}_{Q_1{X}_1}& 0\\ 0& {\text{ρ}}_{Q_2{X}_2}\end{array}\right]\\ {\mathbf{\Sigma }}_X^{-1}={\left[\begin{array}{cc}1& {\text{ρ}}_{X_1{X}_2}\\ {\text{ρ}}_{X_1{X}_2}& 1\end{array}\right]}^{-1}=\frac{1}{1-{\text{ρ}}_{X_1{X}_2}^2}\left[\begin{array}{cc}1& -{\text{ρ}}_{X_1{X}_2}\\ -{\text{ρ}}_{X_1{X}_2}& 1\end{array}\right]\\ {\mathbf{\Sigma }}_{XQ}=\left[\begin{array}{cc}{\text{ρ}}_{Q_1{X}_1}& 0\\ 0& {\text{ρ}}_{Q_2{X}_2}\end{array}\right]\end{array}$$ (A10)

Then

$${\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}=\frac{1}{1-{\text{ρ}}_{X_1{X}_2}^2}\left[\begin{array}{cc}{\text{ρ}}_{Q_1{X}_1}^2& -{\text{ρ}}_{Q_1{X}_1}{\text{ρ}}_{Q_2{X}_2}{\text{ρ}}_{X_1{X}_2}\\ -{\text{ρ}}_{Q_1{X}_1}{\text{ρ}}_{Q_2{X}_2}{\text{ρ}}_{X_1{X}_2}& {\text{ρ}}_{Q_2{X}_2}^2\end{array}\right]$$ (A11)

The off-diagonals of this matrix are nonnull, so a genomic correlation will arise when there is no genetic correlation.

Missing Correlation (Case 3 in Figure 2)

Because the markers are in LE, ${\mathbf{\Sigma }}_X^{-1}$ is an identity matrix, so

$${\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_X^{-1}{\mathbf{\Sigma }}_{XQ}={\mathbf{\Sigma }}_{QX}{\mathbf{\Sigma }}_{XQ}=\left[\begin{array}{cc}{\text{ρ}}_{QX}^2& 0\\ 0& {\text{ρ}}_{QX}^2\end{array}\right]$$

Therefore, in the absence of pleiotropy, $C_{\text{marked}}$ in (A6) and, thus, $r_{G\text{,marked}}$ will be null no matter what the value of the genetic correlation.

Pleiotropy (Case 4 in Figure 2)

The results in Figure 3 were obtained using expressions (3) and (4) with the parameter values described in the main body of the paper.