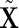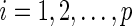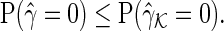Abstract
We study the estimation of a Gaussian graphical model whose dependent structures are partially identified. In a Gaussian graphical model, an off-diagonal zero entry in the concentration matrix (the inverse covariance matrix) implies the conditional independence of two corresponding variables, given all other variables. A number of methods have been proposed to estimate a sparse large-scale Gaussian graphical model or, equivalently, a sparse large-scale concentration matrix. In practice, the graph structure to be estimated is often partially identified by other sources or a pre-screening. In this paper, we propose a simple modification of existing methods to take into account this information in the estimation. We show that the partially identified dependent structure reduces the error in estimating the dependent structure. We apply the proposed method to estimating the gene regulatory network from lung cancer data, where protein–protein interactions are partially identified from the human protein reference database. The application shows that proposed method identified many important cancer genes as hub genes in the constructed lung cancer network. In addition, we validated the prognostic importance of a newly identified cancer gene, PTPN13, in four independent lung cancer datasets. The results indicate that the proposed method could facilitate studying underlying lung cancer mechanisms and identifying reliable biomarkers for lung cancer prognosis.
Keywords: Concentration matrix, Gaussian graphical models, Gene regulatory network, Lung cancer, Partially identified graph, Protein–protein interaction
1. Introduction
In recent years, statistical approaches have been developed to construct gene regulatory networks (GRNs) from mRNA expression data. A GRN describes the interactions among genes and how the genes work together to form modules of cell functions under specific contexts, such as disease status. It provides a systematic understanding of the molecular mechanisms underlying the biological processes (Friedman, 2004). In GRNs, highly connected genes are called hub genes. Because the hub genes are in key positions, their activities may affect many genes in the network and hence play an important role in biological processes. Recently, analysis of hub genes has shown to be a promising approach in identifying key disease driver genes (Akavia and others, 2010) and important biomarkers for predicting disease progression (Taylor and others, 2009; Tang and others, 2013). Currently, most of the existing computational methods use purely data-driven approaches to construct gene regulatory networks from gene expression data. These approaches do not rely on any prior knowledge about the network and are widely suited to many applications. However, for gene regulatory networks, information about many known connections (edges) between genes has been accumulated over decades of biological research, such as protein–protein interactions or transcriptional factor-binding sites. Using these known edges, we can turn a network construction problem into a statistical completion of a partially identified graph problem, which could lead to much better power in identifying the unknown edges. In this paper, we propose a statistical completion of a partially identified graph (SCPG) method, which is a modification of existing methods to incorporate the information about known edges. We show that the information on known edges reduces the error in identifying the unknown edges and improves the accuracy of the constructed networks.
Consider a 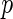 -dimensional random vector from a multivariate Gaussian distribution with mean
-dimensional random vector from a multivariate Gaussian distribution with mean  and covariance matrix
and covariance matrix 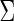 , or the concentration matrix
, or the concentration matrix 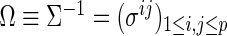 . In the Gaussian graphical model, the dependent structure among
. In the Gaussian graphical model, the dependent structure among 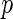 variables
variables 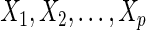 can be expressed using a graph
can be expressed using a graph 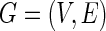 , where a vertex set
, where a vertex set 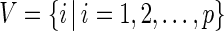 represents
represents 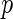 variables and an edge set
variables and an edge set 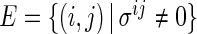 represents pairs of random variables that are dependent on each other, given all other variables. In other words, that
represents pairs of random variables that are dependent on each other, given all other variables. In other words, that 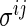 , the
, the 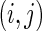 th element of
th element of 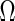 , is equal to
, is equal to  implies that
implies that 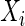 and
and 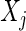 are conditionally independent given all other variables
are conditionally independent given all other variables 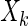 ,
, 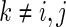 .
.
Covariance selection, first introduced by Dempster (1972), is a class of problems that estimate dependent structures among multivariate Gaussian variables by detecting non-zero elements of the concentration matrix 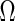 . Recently, researchers revisited the problem and studied the estimation of large-scale concentration matrices from a small number of observations. The
. Recently, researchers revisited the problem and studied the estimation of large-scale concentration matrices from a small number of observations. The 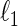 -regularization on a concentration matrix or a partial correlation matrix is popularly used to obtain a sparse estimate of the dependent structure. Yuan and Lin (2007) propose the
-regularization on a concentration matrix or a partial correlation matrix is popularly used to obtain a sparse estimate of the dependent structure. Yuan and Lin (2007) propose the 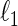 -regularized maximum likelihood estimator (MLE) of the concentration matrix and an algorithm to solve it using the determinant maximization problem (MAXDET), which has computational complexity of order
-regularized maximum likelihood estimator (MLE) of the concentration matrix and an algorithm to solve it using the determinant maximization problem (MAXDET), which has computational complexity of order 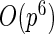 and becomes slower as
and becomes slower as 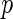 increases. Friedman and others (2007) propose a block coordinate descent procedure to solve the
increases. Friedman and others (2007) propose a block coordinate descent procedure to solve the 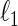 -regularized MLE, namely the graphical lasso. Meinshausen and Bühlmann (2006) formulate the covariance selection problem as a set of lasso regression problems and solve each of the lasso regression problems independently. Peng and others (2009) propose the sparse partial correlation estimation (SPACE) method, which solves the set of lasso regression problems jointly under the symmetry of the concentration matrix
-regularized MLE, namely the graphical lasso. Meinshausen and Bühlmann (2006) formulate the covariance selection problem as a set of lasso regression problems and solve each of the lasso regression problems independently. Peng and others (2009) propose the sparse partial correlation estimation (SPACE) method, which solves the set of lasso regression problems jointly under the symmetry of the concentration matrix  . However, this symmetry is not guaranteed by Meinshausen and Bühlmann (2006). Recently, Cai and others (2011) propose the constrained
. However, this symmetry is not guaranteed by Meinshausen and Bühlmann (2006). Recently, Cai and others (2011) propose the constrained 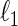 -minimization for inverse matrix estimation (CLIME) that directly minimizes the
-minimization for inverse matrix estimation (CLIME) that directly minimizes the 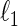 -norm of the concentration matrix with a relaxed constraint for the condition
-norm of the concentration matrix with a relaxed constraint for the condition 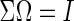 .
.
In this paper, we consider a simple modification of existing methods that incorporates “partially identified” dependent structures. The dependent structure to be estimated is often partially identified in practice. We also denote partially identified structures as “pre-identified” to emphasize that these structures are previously known. For example, GRNs and protein–protein interaction (PPI) networks are available in the public databases that were constructed for many previous laboratory experiments. In comparison, the pre-screening procedures recently proposed by many authors identify pairs of variables that are conditionally independent (Bair and others, 2006; Wasserman and Roeder, 2009). The existing methods do not take into account these partially identified structures. They frequently estimate a known dependence as independence, or vice versa, due to a lack of data information from small samples.
The modification is done by simply redefining the existing 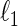 -regularization. To be specific,
-regularization. To be specific, 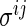 and
and 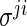 are not penalized in the objective function or its constraints if
are not penalized in the objective function or its constraints if 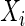 and
and 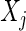 are pre-identified as conditionally dependent. The modification can be applied to the
are pre-identified as conditionally dependent. The modification can be applied to the 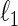 -regularized MLE, the
-regularized MLE, the 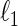 -minimization and the regression-based methods. However, in this paper, we restrict our discussion to the modification of the regression-based method, i.e., the SPACE method.
-minimization and the regression-based methods. However, in this paper, we restrict our discussion to the modification of the regression-based method, i.e., the SPACE method.
The paper is organized as follows. In Section 2, we briefly introduce the SPACE method and propose the SCPG method as a modification to incorporate pre-identified dependent structures. In Section 3, we analytically show that the SCPG method reduces the asymptotic probability of mistakenly identifying an independent pair of variables as dependent. In Section 4, we numerically investigate the gains in accuracy by estimating the network from assuming the pre-identified graph structure. In Section 5, we apply the SCPG method to estimating the gene regulatory network from lung cancer data. We conclude the paper in Section 6.
2. Modification for partially identified graph
Suppose 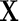 random vector with mean
random vector with mean  and positive definite covariance matrix
and positive definite covariance matrix 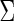 . The partial correlation between
. The partial correlation between 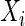 and
and 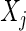 , denoted by
, denoted by 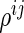 , is the conditional correlation of
, is the conditional correlation of 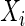 and
and 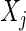 given
given 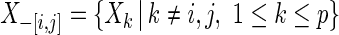 . This partial correlation is closely related to the concentration matrix
. This partial correlation is closely related to the concentration matrix 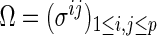 . It is known that
. It is known that 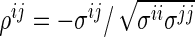 . Also, for every
. Also, for every 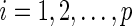 ,
,
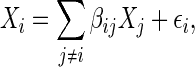 |
(2.1) |
where 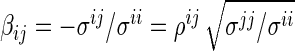 , and
, and 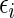 is uncorrelated with
is uncorrelated with 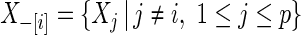 and has mean 0 and variance
and has mean 0 and variance 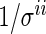 .
.
The identity (2.1) introduces a regression-based method to estimate 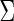 or
or 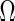 . Let
. Let 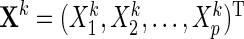 be the
be the 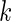 th observation of the random vector
th observation of the random vector 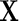 for
for 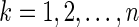 . Meinshausen and Bühlmann (2006) propose the neighborhood selection method to solve a set of lasso regression problems with respect to
. Meinshausen and Bühlmann (2006) propose the neighborhood selection method to solve a set of lasso regression problems with respect to 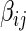 s;that is, for
s;that is, for 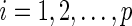 ,
,
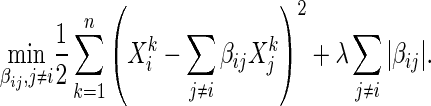 |
(2.2) |
Later, Peng and others (2009) propose the SPACE method, which minimizes the weighted sum of 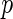 squared loss functions in (2.2) with a penalty term on the
squared loss functions in (2.2) with a penalty term on the 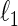 -norm of the partial correlation
-norm of the partial correlation 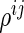 s:
s:
 |
(2.3) |
where 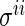 is the
is the 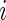 th diagonal element of the concentration matrix and
th diagonal element of the concentration matrix and 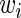 is a nonnegative weight for the
is a nonnegative weight for the 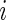 th squared loss function.
th squared loss function.
The SPACE method has several advantages over the neighborhood selection method by Meinshausen and Bühlmann (2006) in estimating the concentration matrix and the graph structure. First, the SPACE method estimates the partial correlations and the diagonal elements of the concentration matrix. Thus, the estimation of the concentration matrix can easily be calculated by the relationship 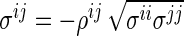 in the SPACE method, while the neighborhood selection method only obtains information about whether or not each off-diagonal element of the concentration matrix is zero. Second, the estimated edges from the SPACE method are symmetrical in the sense that
in the SPACE method, while the neighborhood selection method only obtains information about whether or not each off-diagonal element of the concentration matrix is zero. Second, the estimated edges from the SPACE method are symmetrical in the sense that  ; thus, if
; thus, if 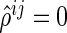 (or
(or 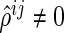 ), then
), then 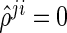 (or
(or 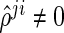 ). Conversely, the neighborhood selection method separately solves
). Conversely, the neighborhood selection method separately solves 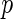 problems in (2.2) and may obtain the contradictory edges (i.e.,
problems in (2.2) and may obtain the contradictory edges (i.e., 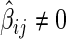 and
and 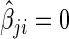 ). Finally, the SPACE method outperforms the neighborhood selection method in estimating graph structure and finding hubs in practice. This comparison study is reported in Peng and others (2009).
). Finally, the SPACE method outperforms the neighborhood selection method in estimating graph structure and finding hubs in practice. This comparison study is reported in Peng and others (2009).
We now introduce the SCPG method as a modification of the SPACE method to take into account the pre-identified graph structure. The same modification can be applied to the 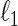 -regularized MLEs and the
-regularized MLEs and the 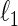 -minimization, but those examples are omitted here. We consider the concentration matrix
-minimization, but those examples are omitted here. We consider the concentration matrix 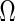 and its induced graph
and its induced graph 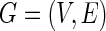 . Let
. Let 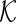 be a set of pre-identified edges in
be a set of pre-identified edges in 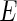 . In this paper, we propose to solve
. In this paper, we propose to solve
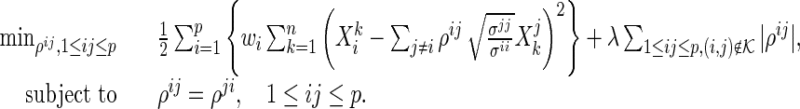 |
(2.4) |
The modification in (2.4) only removes the penalties on the partial correlations corresponding to the pre-identified edges from (2.3). Thus, we can directly apply the active shooting algorithm, proposed by Peng and others (2009), to solve the modified problem. To be specific, we first rewrite the main problem (2.4) using matrix notation. The problem (2.4) without symmetry constraints becomes
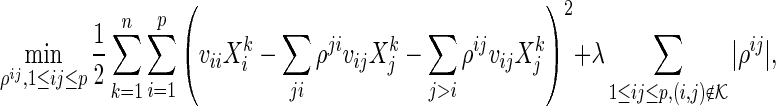 |
where 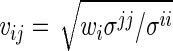 for
for 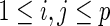 .
.
Let 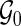 denote a set of pairs such that
denote a set of pairs such that 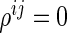 (i.e.,
(i.e.,  ) and
) and 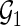 denote a set of edges such that
denote a set of edges such that 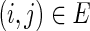 and
and 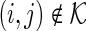 (i.e.,
(i.e., 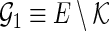 ). Let
). Let 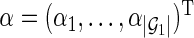 be a
be a 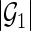 -dimensional vector of
-dimensional vector of 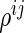 s for
s for 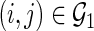 ; let
; let 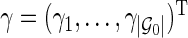 be a
be a 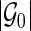 -dimensional vector of
-dimensional vector of 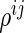 s for
s for 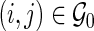 ; and let
; and let 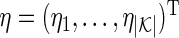 be a
be a 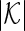 -dimensional vector of
-dimensional vector of 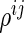 s for
s for 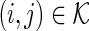 . For
. For 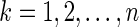 , let
, let
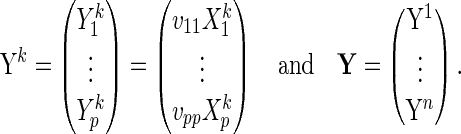 |
We define a covariate matrix 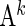 of
of 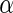 , for
, for  , as a matrix with a size of
, as a matrix with a size of 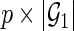 and, if
and, if 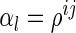 , its
, its  th column vector
th column vector 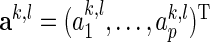 is defined as
is defined as
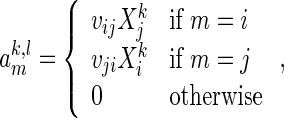 |
(2.5) |
where 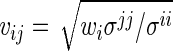 for
for 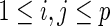 .
.
The covariate matrices  and
and 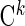 with sizes of
with sizes of 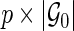 and
and 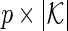 , respectively, are defined similarly for coefficient vectors
, respectively, are defined similarly for coefficient vectors 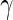 and
and 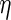 . The whole group of covariate matrices
. The whole group of covariate matrices 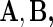 and
and  are then defined as
are then defined as
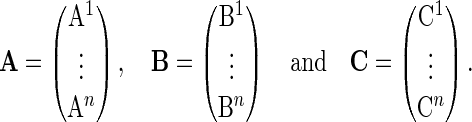 |
The first part of the objective function in (2.3) is read as the least square error of the linear model
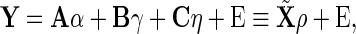 |
(2.6) |
where 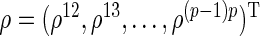 is a
is a 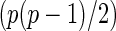 -dimensional vector,
-dimensional vector, 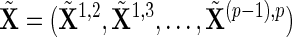 is a design matrix with a size of
is a design matrix with a size of 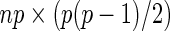 ,
, 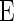 is from the
is from the 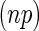 -dimensional multivariate normal distribution with mean
-dimensional multivariate normal distribution with mean  and covariance matrix
and covariance matrix 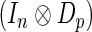 , where
, where 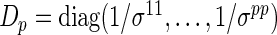 and an operator
and an operator  denotes the Kronecker product. Thus, we can represent the problem (2.4) as
denotes the Kronecker product. Thus, we can represent the problem (2.4) as
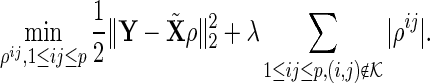 |
Note that we set weights 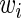 s to one in this paper since we do not assume any strengths for nodes. We can only assume that we have partial information about true edges. If there is information about strength or importance for specific nodes, that information can be incorporated by changing the weights.
s to one in this paper since we do not assume any strengths for nodes. We can only assume that we have partial information about true edges. If there is information about strength or importance for specific nodes, that information can be incorporated by changing the weights.
Now we briefly describe the proposed algorithm, which depends largely on the algorithm in Peng and others (2009). We first set initial values 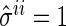 for
for  . The proposed algorithm alternately updates the estimates
. The proposed algorithm alternately updates the estimates 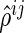 s and
s and 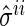 s by the following steps:
s by the following steps:
- Step 2: Based on the identity (2.1), for a given
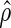 and
and 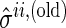 for
for 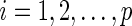 ,
,
where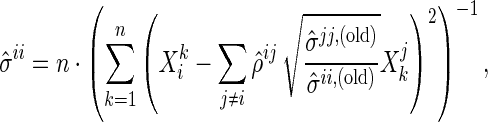
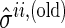 is the estimate of
is the estimate of 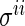 from the previous iteration.
from the previous iteration. Step 3: Repeat Steps 1 and 2 until the convergence occurs.
In Step 1, we apply the modified active shooting algorithm to incorporate the pre-identified edges 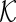 . Details on the active shooting algorithm we propose are given in Appendix A of Supplementary material available at Biostatistics online.
. Details on the active shooting algorithm we propose are given in Appendix A of Supplementary material available at Biostatistics online.
3. Asymptotic error probabilities
In this section, we analytically find the changes in asymptotic error probability by using the information on pre-identified edges. As shown in Section 2, our main problem can be rewritten as the estimation of the sparse linear model (lasso regression), and we are able to compute the asymptotic true negative/positive probabilities of the model both with and without the information on dependent pairs of variables. The computation shows that the pre-identified dependent information asymptotically increases the true negative probability (the probability of identifying independent pairs as independent) while the true positive probability (the probability of identifying dependent pairs as dependent) of both methods converge to 1. Thus, the SCPG method reduces the error probability asymptotically. Our analysis of this section relies heavily on the results of Knight and Fu (2000) and Anderson (1955), which are reviewed in Appendix B of Supplementary material available at Biostatistics online.
For the asymptotic true negative probability, we consider the simplified model
 |
(3.1) |
where  and
and 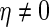 . Under this model, we compare the true negative probabilities of the SCPG and SPACE methods.
. Under this model, we compare the true negative probabilities of the SCPG and SPACE methods.
Theorem 3.1 —
Suppose we have knowledge about
. Let
and
be the solutions of the SPACE and SCPG methods, respectively. Then, the asymptotic true negative probabilities
and
satisfy the inequality
Proof —
See Appendix C.1 of Supplementary material available at Biostatistics online.
We next compare the asymptotic true positive probabilities of the SCPG and SPACE methods. Here, we consider the simplified model
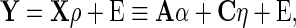 |
where both 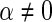 and
and 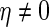 . Suppose we have knowledge on
. Suppose we have knowledge on 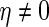 . Let
. Let 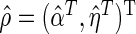 and
and 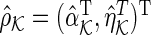 be the solutions of the SPACE and SCPG methods, respectively. This section shows the following theorem:
be the solutions of the SPACE and SCPG methods, respectively. This section shows the following theorem:
Theorem 3.2 —
The asymptotic true positive probabilities of both the SPACE and SCPG models (which are
and
, respectively) converge to one as
.
Proof —
See Appendix C.2 of Supplementary material available at Biostatistics online.
In comparing the asymptotic error probabilities between the SPACE and SCPG models, we show that the SCPG model asymptotically improves the true negative probability with the same performance as the true positive probability. Note that there is a difference between the asymptotic biases for  and
and 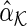 . However, a direct comparison of these asymptotic biases is difficult since the difference varies with the signs and structures of partial correlations in the model.
. However, a direct comparison of these asymptotic biases is difficult since the difference varies with the signs and structures of partial correlations in the model.
4. Numerical study
In the previous section, we showed that the SCPG method improves the asymptotic true negative probability and has the same performance for the asymptotic true positive probability in estimating graph structure for a given 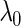 . This is mainly due to the bias reduction by using the prior information about partially identified edges. In practice, however, we generally encounter datasets with finite samples and choose a tuning parameter that minimizes an information criterion, such as the Bayesian information criterion (BIC) (Schwarz, 1978). Thus, we additionally investigate the performance of the SCPG method with finite samples for several graph structures and also compare the SCPG method with the SPACE method to confirm the improvements of the SCPG method in estimating a graph structure.
. This is mainly due to the bias reduction by using the prior information about partially identified edges. In practice, however, we generally encounter datasets with finite samples and choose a tuning parameter that minimizes an information criterion, such as the Bayesian information criterion (BIC) (Schwarz, 1978). Thus, we additionally investigate the performance of the SCPG method with finite samples for several graph structures and also compare the SCPG method with the SPACE method to confirm the improvements of the SCPG method in estimating a graph structure.
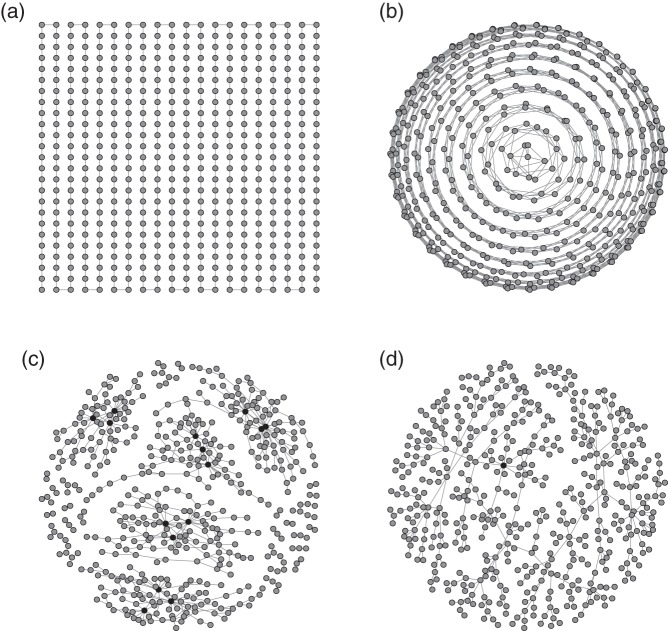
We first consider the Gaussian graphical model accompanied by the following AR(1), AR(2), hub and scale-free networks in simulation. The AR(1) and the AR(2) networks are from the time series model and the hub and scale-free networks reflect real biological networks. These four networks are illustrated in Figure 1. The details of the four networks, including how they are generated, are given in Appendix D of Supplementary material available at Biostatistics online.
Fig. 1.
Graphs of four networks used in simulation. Black nodes ( ) denote nodes whose degrees are
) denote nodes whose degrees are 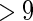 . (a) (N1) AR(1), (b) (N2) AR(2), (c) (N3) hub network, and (d) (N4) scale-free.
. (a) (N1) AR(1), (b) (N2) AR(2), (c) (N3) hub network, and (d) (N4) scale-free.
We consider moderate-sized networks with 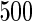 nodes and sample sizes of
nodes and sample sizes of 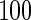 ,
, 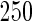 , and
, and 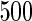 . To apply the SCPG method, we define two pre-identified edge sets
. To apply the SCPG method, we define two pre-identified edge sets 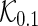 and
and 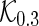 by randomly selecting 10 and
by randomly selecting 10 and 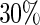 of the true edges, respectively. These two pre-identified edge sets are also used to find the effects of the amount of information on estimating a graph structure. In each network, we generate 50 datasets from a Gaussian distribution with mean 0 and covariance matrix
of the true edges, respectively. These two pre-identified edge sets are also used to find the effects of the amount of information on estimating a graph structure. In each network, we generate 50 datasets from a Gaussian distribution with mean 0 and covariance matrix 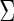 defined with the
defined with the 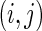 th element
th element 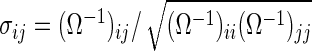 . Note that, for the hub and scale-free networks, we make the network have five exclusive sub-networks, each of which has
. Note that, for the hub and scale-free networks, we make the network have five exclusive sub-networks, each of which has  nodes; the nodes in one sub-network are not connected to those in other sub-networks. This procedure is applied in Peng and others (2009) to describe the module-based networks frequently observed in real networks.
nodes; the nodes in one sub-network are not connected to those in other sub-networks. This procedure is applied in Peng and others (2009) to describe the module-based networks frequently observed in real networks.
Let 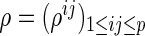 and
and 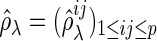 be a
be a 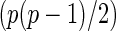 -dimensional vector of the true partial correlations and the estimates of partial correlations at
-dimensional vector of the true partial correlations and the estimates of partial correlations at 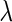 , respectively. To investigate the theoretical properties of the SCPG method with finite samples, we introduce the true positive rate (TPR) and the true negative rate (TNR) defined as follows:
, respectively. To investigate the theoretical properties of the SCPG method with finite samples, we introduce the true positive rate (TPR) and the true negative rate (TNR) defined as follows:
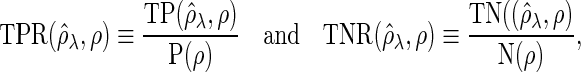 |
where 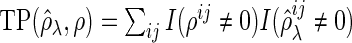 ,
, 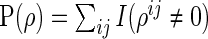 ,
, 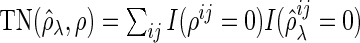 ,
, 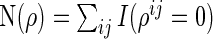 , and
, and 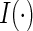 denotes an indicator function. We additionally define the false discovery rate (FDR) as
denotes an indicator function. We additionally define the false discovery rate (FDR) as
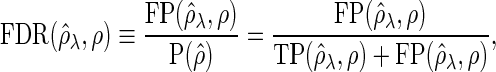 |
where 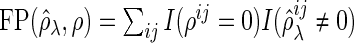 and
and 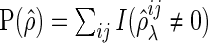 . Note that the FDR is not defined if
. Note that the FDR is not defined if 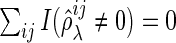 . In this case, we consider the FDR value to be 0 to summarize results with all datasets.
. In this case, we consider the FDR value to be 0 to summarize results with all datasets.
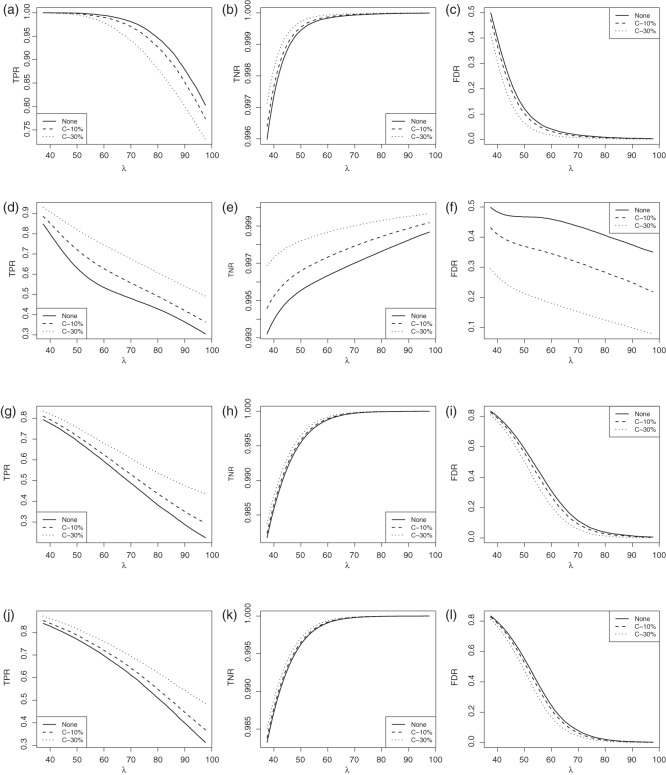
Figure 2 plots the average of TPRs, TNRs, and FDRs for various 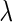 s in the aforementioned four networks and shows several interesting features containing the result that are related to the theoretical properties in the previous section. Compared with SPACE, the SCPG method improves TPRs in all networks considered except the AR(1) network for a given
s in the aforementioned four networks and shows several interesting features containing the result that are related to the theoretical properties in the previous section. Compared with SPACE, the SCPG method improves TPRs in all networks considered except the AR(1) network for a given 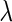 .
.
Fig. 2.
The averages of TPR, TNR, and FDR for (N1)–(N4) networks in Figure 1 with 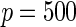 and
and 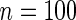 . “None”, “C-10%”, and “C-30%” denote the SPACE method (solid), the SCPG method with 10% (dashed) and 30% (dotted) partially identified edges, respectively. (a) (N1) TPR
. “None”, “C-10%”, and “C-30%” denote the SPACE method (solid), the SCPG method with 10% (dashed) and 30% (dotted) partially identified edges, respectively. (a) (N1) TPR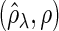 , (b) (N1) TNR
, (b) (N1) TNR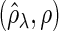 , (c) (N1) FDR
, (c) (N1) FDR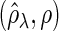 , (d) (N2) TPR
, (d) (N2) TPR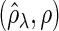 , (e) (N2) TNR
, (e) (N2) TNR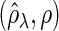 , (f) (N2) FDR
, (f) (N2) FDR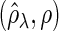 , (g) (N3) TPR
, (g) (N3) TPR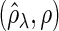 , (h) (N3) TNR
, (h) (N3) TNR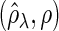 , (i) (N3) FDR
, (i) (N3) FDR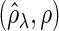 , (j) (N4) TPR
, (j) (N4) TPR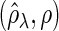 , (k) (N4) TNR
, (k) (N4) TNR , and (l) (N4) FDR
, and (l) (N4) FDR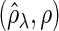 .
.
In view of TNRs, however, the SCPG method improves on the SPACE method for any given 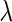 s in all networks we consider and also increases TNRs as the amount of pre-identified information increases. This result shows that the theoretical result for the true negative probability described in the previous section still holds with finite samples. Moreover, the SCPG method decreases FDRs for any given
s in all networks we consider and also increases TNRs as the amount of pre-identified information increases. This result shows that the theoretical result for the true negative probability described in the previous section still holds with finite samples. Moreover, the SCPG method decreases FDRs for any given 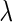 s in all networks compared with the SPACE method. Interestingly, the SCPG method decreases FDRs while the TPRs decrease as the amount of pre-identified information increases in the AR(1) network.
s in all networks compared with the SPACE method. Interestingly, the SCPG method decreases FDRs while the TPRs decrease as the amount of pre-identified information increases in the AR(1) network.
The tuning parameter 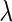 in both the SCPG and SPACE methods plays an important role in estimating the network, where a large (or a small) value of
in both the SCPG and SPACE methods plays an important role in estimating the network, where a large (or a small) value of 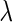 results in a sparse (or a dense) estimate of the network with low false positives (or low false negatives). Several information criteria, such as the Akaike information criterion and Bayesian information criterion (BIC), are heuristically used for the network model of these papers (Danaher and others, 2014; Yuan and Lin, 2007; Peng and others, 2009). They are originally designed for the linear regression model and some of them are theoretically shown to select the correct model (Wang and others, 2009; Fan and Tang, 2013). However, these are limited to the linear regression model, and there is no optimal rule for choosing
results in a sparse (or a dense) estimate of the network with low false positives (or low false negatives). Several information criteria, such as the Akaike information criterion and Bayesian information criterion (BIC), are heuristically used for the network model of these papers (Danaher and others, 2014; Yuan and Lin, 2007; Peng and others, 2009). They are originally designed for the linear regression model and some of them are theoretically shown to select the correct model (Wang and others, 2009; Fan and Tang, 2013). However, these are limited to the linear regression model, and there is no optimal rule for choosing 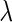 in the network model. In this paper, we adopt the generalized information criterion (GIC) proposed by Fan and Tang (2013), which is shown to outperform the BIC in identifying the correct model in the linear regression. The “GIC-type” criterion used in this paper is defined like the “BIC type” criterion in Peng and others (2009) as
in the network model. In this paper, we adopt the generalized information criterion (GIC) proposed by Fan and Tang (2013), which is shown to outperform the BIC in identifying the correct model in the linear regression. The “GIC-type” criterion used in this paper is defined like the “BIC type” criterion in Peng and others (2009) as
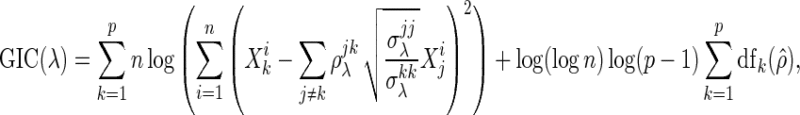 |
where 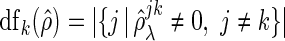 and
and  is a cardinality of a set
is a cardinality of a set 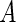 . For each dataset, we evaluate the
. For each dataset, we evaluate the 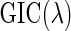 on a grid of
on a grid of 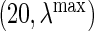 and choose a tuning parameter
and choose a tuning parameter 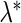 such that
such that 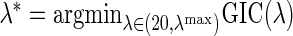 , where
, where 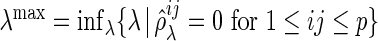 . In addition, the selected models of the SPACE and SCPG methods by the GIC are evaluated by the TPR, TNR, FDR, the mis-specification rate (MISR), and the Matthews correlation coefficient (MCC). The first three measures have been defined already. Here, we introduce the MISR and MCC, defined as
. In addition, the selected models of the SPACE and SCPG methods by the GIC are evaluated by the TPR, TNR, FDR, the mis-specification rate (MISR), and the Matthews correlation coefficient (MCC). The first three measures have been defined already. Here, we introduce the MISR and MCC, defined as
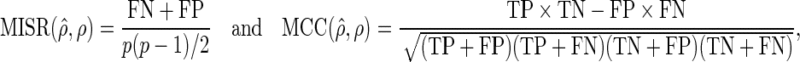 |
where 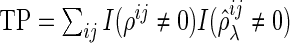 ,
,  ,
, 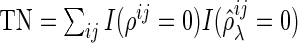 , and
, and 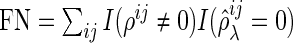 . Here, the MISR corresponds to the total error rate of a classifier and the MCC, with a value between
. Here, the MISR corresponds to the total error rate of a classifier and the MCC, with a value between 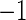 and
and 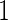 , measures the accuracy of a classifier, where
, measures the accuracy of a classifier, where 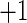 ,
,  , and
, and 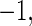 respectively, denote a perfect classification, a random classification, and a total discordance of classification.
respectively, denote a perfect classification, a random classification, and a total discordance of classification.
Tables 1 and 2 report the average of these five measures over 50 datasets, which reveals some interesting features of the proposed SCPG method. First, compared with the SPACE method, the TNRs and the MCCs of the SCPG method increase as the amount of pre-identified information increases, for all the cases we consider. Second, the SCPG method has smaller error rates than the SPACE method in terms of the FDRs and the MISRs. Finally, the TPRs of the SCPG method are approximately equal to or higher than those of the SPACE method (without pre-identified information) in all the cases we consider except the AR(1) model. In summary, these features indicate that the SCPG method's performance is superior to the SPACE method in all aspects.
Table 1.
The averages of 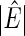 , TPR, TNR, FDR, MISR, and MCC for AR
, TPR, TNR, FDR, MISR, and MCC for AR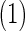 and AR
and AR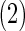 networks over
networks over 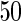 datasets
datasets
| Network | 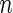 |
Info. | 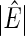 |
TPR | TNR | FDR | MISR | MCC |
|---|---|---|---|---|---|---|---|---|
AR(1) 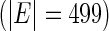
|
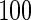 |
None | 627.64 | 99.97 | 99.9 | 20.45 | 0.1 | 89.12 |
| (2.55) | (0.01) | (0) | (0.32) | (0) | (0.18) | |||
| 10% | 613.7 | 99.92 | 99.91 | 18.7 | 0.09 | 90.08 | ||
| (2.22) | (0.02) | (0) | (0.29) | (0) | (0.16) | |||
| 30% | 584.38 | 99.82 | 99.93 | 14.68 | 0.07 | 92.24 | ||
| (2.51) | (0.03) | (0) | (0.36) | (0) | (0.19) | |||
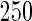 |
None | 609.58 | 100 | 99.91 | 18.09 | 0.09 | 90.46 | |
| (2.24) | (0) | (0) | (0.3) | (0) | (0.17) | |||
| 10% | 596.62 | 100 | 99.92 | 16.3 | 0.08 | 91.44 | ||
| (2.4) | (0) | (0) | (0.33) | (0) | (0.18) | |||
| 30% | 570.74 | 100 | 99.94 | 12.52 | 0.06 | 93.5 | ||
| (1.87) | (0) | (0) | (0.28) | (0) | (0.15) | |||
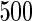 |
None | 600.84 | 100 | 99.92 | 16.9 | 0.08 | 91.12 | |
| (2.18) | (0) | (0) | (0.3) | (0) | (0.17) | |||
| 10% | 584.68 | 100 | 99.93 | 14.61 | 0.07 | 92.37 | ||
| (1.83) | (0) | (0) | (0.26) | (0) | (0.14) | |||
| 30% | 566.2 | 100 | 99.95 | 11.83 | 0.05 | 93.87 | ||
| (1.62) | (0) | (0) | (0.25) | (0) | (0.13) | |||
AR(2) 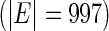
|
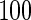 |
None | 1431.8 | 75.21 | 99.45 | 47.59 | 0.74 | 62.4 |
| (14.03) | (0.63) | (0.01) | (0.14) | (0) | (0.24) | |||
| 10% | 1509.6 | 87.28 | 99.48 | 42.29 | 0.61 | 70.68 | ||
| (10.81) | (0.37) | (0.01) | (0.2) | (0) | (0.11) | |||
| 30% | 1403.8 | 94.87 | 99.63 | 32.56 | 0.41 | 79.8 | ||
| (7.23) | (0.19) | (0) | (0.25) | (0) | (0.12) | |||
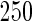 |
None | 1873.38 | 100 | 99.29 | 46.75 | 0.7 | 72.71 | |
| (6.57) | (0) | (0.01) | (0.19) | (0.01) | (0.13) | |||
| 10% | 1724.14 | 100 | 99.41 | 42.14 | 0.58 | 75.84 | ||
| (6.22) | (0) | (0.01) | (0.21) | (0) | (0.14) | |||
| 30% | 1455.84 | 100 | 99.63 | 31.49 | 0.37 | 82.61 | ||
| (4) | (0) | (0) | (0.19) | (0) | (0.11) | |||
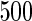 |
None | 1801.44 | 100 | 99.35 | 44.61 | 0.64 | 74.17 | |
| (7.39) | (0) | (0.01) | (0.23) | (0.01) | (0.15) | |||
| 10% | 1665.48 | 100 | 99.46 | 40.09 | 0.54 | 77.18 | ||
| (6.52) | (0) | (0.01) | (0.23) | (0.01) | (0.15) | |||
| 30% | 1418.54 | 100 | 99.66 | 29.69 | 0.34 | 83.7 | ||
| (3.67) | (0) | (0) | (0.18) | (0) | (0.11) |
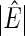 denotes the number of estimated edges. All values except for
denotes the number of estimated edges. All values except for 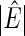 are multiplied by
are multiplied by 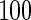 . The numbers in parentheses denote the standard errors of measures.
. The numbers in parentheses denote the standard errors of measures.
Table 2.
The averages of 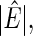 TPR, TNR, FDR, MISR, and MCC for hub and scale-free networks over
TPR, TNR, FDR, MISR, and MCC for hub and scale-free networks over 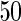 datasets
datasets
| Network | 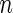 |
Info. | 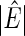 |
TPR | TNR | FDR | MISR | MCC |
|---|---|---|---|---|---|---|---|---|
Hub 
|
 |
None | 318 | 48.94 | 99.97 | 12.15 | 0.26 | 65.38 |
| (4.5) | (0.5) | (0) | (0.49) | (0) | (0.26) | |||
| 10% | 343.1 | 53.79 | 99.97 | 10.56 | 0.24 | 69.2 | ||
| (4.17) | (0.44) | (0) | (0.44) | (0) | (0.21) | |||
| 30% | 363.4 | 60.18 | 99.98 | 5.61 | 0.2 | 75.24 | ||
| (3.69) | (0.42) | (0) | (0.35) | (0) | (0.18) | |||
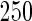 |
None | 586.38 | 87.05 | 99.93 | 15.43 | 0.13 | 85.71 | |
| (3.34) | (0.18) | (0) | (0.37) | (0) | (0.17) | |||
| 10% | 574.96 | 87.45 | 99.94 | 13.39 | 0.12 | 86.96 | ||
| (2.74) | (0.18) | (0) | (0.31) | (0) | (0.14) | |||
| 30% | 564.5 | 88.56 | 99.95 | 10.68 | 0.1 | 88.88 | ||
| (2.54) | (0.17) | (0) | (0.29) | (0) | (0.13) | |||
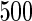 |
None | 654.32 | 97.01 | 99.92 | 15.57 | 0.1 | 90.44 | |
| (2.78) | (0.09) | (0) | (0.33) | (0) | (0.17) | |||
| 10% | 644.34 | 96.99 | 99.93 | 14.31 | 0.09 | 91.12 | ||
| (2.29) | (0.08) | (0) | (0.28) | (0) | (0.14) | |||
| 30% | 619.42 | 96.92 | 99.95 | 10.92 | 0.07 | 92.88 | ||
| (2.21) | (0.08) | (0) | (0.29) | (0) | (0.15) | |||
Scale-free 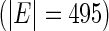
|
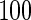 |
None | 396.6 | 66.73 | 99.95 | 16.58 | 0.19 | 74.49 |
| (3.02) | (0.26) | (0) | (0.42) | (0) | (0.18) | |||
| 10% | 399.04 | 69.17 | 99.95 | 14.04 | 0.17 | 77 | ||
| (3.11) | (0.24) | (0) | (0.45) | (0) | (0.16) | |||
| 30% | 402.3 | 73.28 | 99.97 | 9.72 | 0.14 | 81.25 | ||
| (2.74) | (0.24) | (0) | (0.38) | (0) | (0.15) | |||
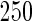 |
None | 526.1 | 89.28 | 99.93 | 15.87 | 0.11 | 86.59 | |
| (3.3) | (0.18) | (0) | (0.42) | (0) | (0.2) | |||
| 10% | 518.12 | 89.57 | 99.94 | 14.31 | 0.1 | 87.54 | ||
| (3.12) | (0.17) | (0) | (0.41) | (0) | (0.19) | |||
| 30% | 500.22 | 90.47 | 99.96 | 10.37 | 0.08 | 89.99 | ||
| (2.9) | (0.18) | (0) | (0.39) | (0) | (0.17) | |||
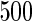 |
None | 561.52 | 96.79 | 99.93 | 14.61 | 0.08 | 90.86 | |
| (2.26) | (0.09) | (0) | (0.34) | (0) | (0.19) | |||
| 10% | 551.34 | 96.63 | 99.94 | 13.18 | 0.07 | 91.55 | ||
| (2.2) | (0.09) | (0) | (0.34) | (0) | (0.19) | |||
| 30% | 536.6 | 97.14 | 99.96 | 10.33 | 0.06 | 93.29 | ||
| (2.09) | (0.07) | (0) | (0.33) | (0) | (0.17) |
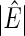 denotes the number of estimated edges. All values except for
denotes the number of estimated edges. All values except for 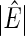 are multiplied by
are multiplied by 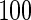 . The numbers in parentheses denote the standard errors of measures.
. The numbers in parentheses denote the standard errors of measures.
Before we end this section, we implement three additional numerical studies. First, we compare the performances of the SCPG and naive methods in estimating the structure of the network. Here, the naive method implies the direct addition of pre-identified edges to the estimated network by the SPACE. The results show that the SCPG method outperforms the naive method in all cases considered. The details of this comparison are detailed in Appendix H of Supplementary material available at Biostatistics online and the results are summarized in Table H.1 of Supplementary material available at Biostatistics online. It indicates that incorporating information of pre-identified edges help the estimation of network structure. In the second study, we investigate how the SCPG method is sensitive to the misspecification rates (the ratio of false positives in the pre-identified edges). Both details of the second study and results are reported in Appendix I of of Supplementary material available at Biostatistics online. The results show that the SCPG method still works better than the SPACE method in terms of error rates unless the misspecification rate is low (not  15% in the study). However, we recommend readers choose the pre-identified edges in a conservative way. Finally, to understand how the SCPG performs in a large-scale network, we repeat the same numerical study as above for the hub and scale-free networks with 1000 nodes; these two networks are the most common assumptions for a large-scale network. The results are similar to what we had in Table 2. They are reported in Table J.1 in Appendix J of of Supplementary material available at Biostatistics online.
15% in the study). However, we recommend readers choose the pre-identified edges in a conservative way. Finally, to understand how the SCPG performs in a large-scale network, we repeat the same numerical study as above for the hub and scale-free networks with 1000 nodes; these two networks are the most common assumptions for a large-scale network. The results are similar to what we had in Table 2. They are reported in Table J.1 in Appendix J of of Supplementary material available at Biostatistics online.
5. Applications with lung cancer adenocarcinoma
Two recent studies have shown that the hub genes in lung cancer gene regulatory networks may be potential robust biomarkers for lung cancer progression. To study whether our proposed method could discover novel gene biomarkers for cancer progression, we applied the proposed method to construct a network based on a microarray dataset from the Lung Cancer Consortium dataset (Shedden and others, 2008). This dataset measures the gene levels in 442 lung cancer adenocarcinoma patients. We identified 794 genes whose expression levels are significantly associated with patients’ survival time, after adjusting for clinical variables based on a univariate Cox regression (See Appendix E of of Supplementary material available at Biostatistics online). In addition, we used a list of PPIs from the human protein reference database (HPRD), which provided 39 240 pairs of PPIs for 9617 genes. Only 222 pairs of PPIs for 211 genes were matched to 794 genes in the lung cancer dataset. We used these 222 pairs as the pre-identified information.
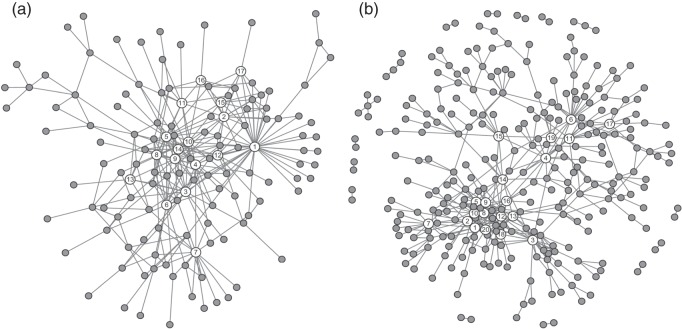
In this study, we compared performances in constructing the gene regulatory network using (i) the SPACE method and (ii) the proposed SCPG method, with 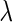 determined by the GIC. An overview of the networks constructed using the SPACE method and the proposed method is shown in Figure 3. The SPACE method estimated 297 edges for 135 genes of 794 genes (659 genes had no connection). The SCPG method estimated 455 edges for 299 genes (495 genes had no connection). To identify hub genes in the estimated graph, we applied a procedure similar to that described in Peng and others (2009). From the estimated graph structures, we first selected genes whose degrees lie over 0.95 quantiles of degree distribution. Then, we calculated the ranks of degrees of selected genes for various
determined by the GIC. An overview of the networks constructed using the SPACE method and the proposed method is shown in Figure 3. The SPACE method estimated 297 edges for 135 genes of 794 genes (659 genes had no connection). The SCPG method estimated 455 edges for 299 genes (495 genes had no connection). To identify hub genes in the estimated graph, we applied a procedure similar to that described in Peng and others (2009). From the estimated graph structures, we first selected genes whose degrees lie over 0.95 quantiles of degree distribution. Then, we calculated the ranks of degrees of selected genes for various 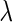 values. We selected potential hub genes such that the averages of the ranks of degrees were
values. We selected potential hub genes such that the averages of the ranks of degrees were 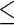 20, and the standard deviations were
20, and the standard deviations were 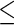 2. Following this procedure, we identified 17 hub genes from the SPACE method and 20 hub genes from the proposed method by incorporating the PPI network information. The identified hub genes are summarized in Table 3. There were 11 genes (highlighted in bold in Table 3) identified by both approaches, among which there were several key lung cancer genes, NKX2-1, HOP, and SFTPB (Further information is given in Appendix F of Supplementary material available at Biostatistics online). In comparing the two methods, we noted that the SCPG method identified nine genes that were missed by the SPACE method, including CTNNB1, CSNK2A1, ESR1, NEDD9, FYN, BRCA1, PTPN13, PIK3R1, and SLC34A2. Seven of these nine genes (identified only by SCPG) had been reported to play important roles in lung cancer, while two (UBE2C and TYMS) of six genes identified only by SPACE method are, based on our literature search, associated with lung cancer. (Further details are given in Appendix G of Supplementary material available at Biostatistics online.)
2. Following this procedure, we identified 17 hub genes from the SPACE method and 20 hub genes from the proposed method by incorporating the PPI network information. The identified hub genes are summarized in Table 3. There were 11 genes (highlighted in bold in Table 3) identified by both approaches, among which there were several key lung cancer genes, NKX2-1, HOP, and SFTPB (Further information is given in Appendix F of Supplementary material available at Biostatistics online). In comparing the two methods, we noted that the SCPG method identified nine genes that were missed by the SPACE method, including CTNNB1, CSNK2A1, ESR1, NEDD9, FYN, BRCA1, PTPN13, PIK3R1, and SLC34A2. Seven of these nine genes (identified only by SCPG) had been reported to play important roles in lung cancer, while two (UBE2C and TYMS) of six genes identified only by SPACE method are, based on our literature search, associated with lung cancer. (Further details are given in Appendix G of Supplementary material available at Biostatistics online.)
Fig. 3.
Estimated graph structures for the SPACE and SCPG methods. The nodes with numbers denote the detected hub genes reported in Table 3. (a) SPACE and (b) SCPG with PPI networks.
Table 3.
List of potential hub genes that identified by the SPACE and SCPG methods
| SPACE |
SCPG |
||||||
|---|---|---|---|---|---|---|---|
| No. | Gene symbol | Degree | CR | No. | Gene symbol | Degree | CR |
| 1 | PRC1 | 39 | 1 | GPR116 | 18 | ||
| 2 | RRM2 | 18 | 2 | NKX2-1 | 18 |  |
|
| 3 | CYP2B7P1 | 17 | 3 | RRM2 | 18 | ||
| 4 | GPR116 | 17 | 4 | CTNNB1 | 17 |  |
|
| 5 | SFTPB | 17 |  |
5 | CYP2B7P1 | 17 | |
| 6 | NKX2-1 | 16 |  |
6 | CSNK2A1 | 16 |  |
| 7 | TFF1 | 16 | 7 | TFF1 | 15 | ||
| 8 | HOP | 15 |  |
8 | C1orf116 | 14 | |
| 9 | C1orf116 | 14 | 9 | HOP | 14 |  |
|
| 10 | FMO5 | 14 | 10 | SFTPB | 14 |  |
|
| 11 | CD302 | 12 | 11 | ESR1 | 13 |  |
|
| 12 | HSD17B6 | 12 | 12 | FMO5 | 12 | ||
| 13 | HOXD1 | 9 | 13 | CD302 | 11 | ||
| 14 | TMPRSS2 | 9 | 14 | NEDD9 | 11 |  |
|
| 15 | TPX2 | 9 | 15 | FYN | 10 |  |
|
| 16 | UBE2C | 8 |  |
16 | PTPN13 | 10 | |
| 17 | TYMS | 7 |  |
17 | BRCA1 | 9 |  |
| 18 | HSD17B6 | 9 | |||||
| 19 | PIK3R1 | 9 |  |
||||
| 20 | SLC34A2 | 9 | |||||
Bold font highlights the genes identified by both methods. “CR” denotes cancer-related genes identified by previous studies.
In addition, the SCPG method identified the PTPN13 gene, which had not been previously reported as a lung cancer related gene. To further study this gene, we have downloaded the mRNA expression together with the clinical annotation from four public lung cancer datasets, including (1) Tomida and others (2009) (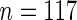 ), (2) Bhattacharjee and others (2001) (
), (2) Bhattacharjee and others (2001) (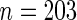 ), (3) Raponi and others (2006) (
), (3) Raponi and others (2006) (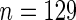 ), and (4) Jones and others (2004) (
), and (4) Jones and others (2004) (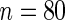 ). These four datasets were selected because they were published in high-profile journals, contained relatively large sample sizes (at least 80 samples), and were measured from different microarray platforms. Interestingly, the under-expression of the PTPN13 gene is consistently associated with the poor prognosis of lung cancer patients in the four independent datasets, which were measured using different platforms (see Fig. G.1 of Supplementary material available at Biostatistics online). The results show that the mRNA expression of the PTPN13 gene is a novel and robust prognostic biomarker of potential clinical importance.
). These four datasets were selected because they were published in high-profile journals, contained relatively large sample sizes (at least 80 samples), and were measured from different microarray platforms. Interestingly, the under-expression of the PTPN13 gene is consistently associated with the poor prognosis of lung cancer patients in the four independent datasets, which were measured using different platforms (see Fig. G.1 of Supplementary material available at Biostatistics online). The results show that the mRNA expression of the PTPN13 gene is a novel and robust prognostic biomarker of potential clinical importance.
6. Conclusion
Recently, reconstructions of GRNs based on genome-wide mRNA expression data have been widely used to study biological mechanisms and identify novel biomarkers. Learning the gene network structures from gene expression data is a challenge because of the extremely large number of possible network edges and the small number of sample sizes in gene expression data to infer the true edges. However, for GRN, there are many previously identified edges (i.e., gene regulations) from pathway information, protein–protein interaction databases, and transcriptional factor binding databases. So instead of learning the structure of GRN from scratch, we can incorporate the known edges to mitigate the daunting task of network reconstruction. In this study, we proposed the SCPG method, a simple but effective modification of the SPACE method, to incorporate partially identified edges in estimating graph structure with a Gaussian graphical model. The SCPG method asymptotically increases the true negative probability and obtains the same performance in terms of the true positive probability compared with the SPACE method. Moreover, we numerically show that the SCPG method not only increases the true negative rate but also reduces the false discovery rate. The SCPG method was applied here to estimate the gene regulatory network of lung cancer data with pre-identified edges from the HPRD database, and it identified more cancer-related hub genes than the SPACE method. More importantly, the SCPG method identified a novel prognostic biomarker, the PTPN13 gene. We validated the prognostic performance of PTPN13 gene expression using four independent lung cancer mRNA expression datasets across different experimental platforms. The results indicate that the proposed SCPG method performs well in reconstructing a gene regulatory network and could be used to identify novel biomarkers for predicting disease outcomes.
In this study, we demonstrated that inferring gene network structures can be improved by incorporating information about previously identified edges from other resources. However, we need to be cautious because gene regulation could vary among different tissues or biological conditions, while most information available about previously identified edges (gene–gene interactions) is not condition specific. As a result, some edges reported in existing databases may not really be edges in the specific conditions under study, which may lead to false-positive edges. A reasonable way to avoid this is to select only the reported edges with high expression correlations for the corresponding gene pairs in the expression data to be used for constructing the network (Ahn and others, 2011). This step helps to identify the gene-gene interactions that are appropriate for the specific conditions under study. In addition, we used GIC to select the tuning parameter, which produced satisfactory results in the real data application. However, it is possible that there exist other examples where the GIC performs poorly. It is also possible that there are other methods for selecting the tuning parameter that could be superior to the GIC. In summary, methodology for objectively selecting tuning parameters is an interesting area for future research.
Supplementary Material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
This work was supported by the National Institutes of Health (R01CA172211 to Guanghua Xiao) and National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2011-0029104 to Johan Lim).
Supplementary Material
References
- Ahn J., Yoon Y., Park C., Shin E., Park S. (2011). Integrative gene network construction for predicting a set of complementary prostate cancer genes. Bioinformatics 27(13), 1846–1853. [DOI] [PubMed] [Google Scholar]
- Akavia U. D., Litvin O., Kim J., Sanchez-Garcia F., Kotliar D., Causton H. C., Pochanard P., Mozes E. and others (2010). An integrated approach to uncover drivers of cancer. Cell 143(6), 1005–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson T. W. (1955). The integral of a symmetric unimodal function over a symmetric convex set and some probability inequalities. Proceedings of the American Mathematical Society 6(2), 170–176. [Google Scholar]
- Bair E., Hastie T., Paul D., Tibshirani R. (2006). Prediction by supervised principal components. Journal of the American Statistical Association 101, 119–137. [Google Scholar]
- Bhattacharjee A., Richards W. G., Staunton J., Li C., Monti S., Vasa P., Ladd C., Beheshti J. and others (2001). Classification of human lung carcinomas by mrna expression profiling reveals distinct adenocarcinoma subclasses. Proceedings of the National Academy of Sciences of the United States of America 98(24), 13790–13795. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Cai T., Liu W. D., Luo X. (2011). A constrained
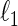 minimization approach to sparse precision matrix estimation. Journal of the American Statistical Association
106(494), 594–607. [Google Scholar]
minimization approach to sparse precision matrix estimation. Journal of the American Statistical Association
106(494), 594–607. [Google Scholar] - Danaher P., Wang P., Witten D. (2014). The joint graphical lasso for inverse covariance estimation across multiple classes. Journal of the Royal Statistical Society: Series B 76(2), 373–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster A. (1972). Covariance selection. Biometrics 28, 157–175. [Google Scholar]
- Fan Y., Tang C. Y. (2013). Tuning parameter selection in high dimensional penalized likelihood. Journal of the Royal Statistical Society: Series B 75(3), 531–552. [Google Scholar]
- Friedman N. (2004). Inferring cellular networks using probabilistic graphical models. Science 303(5659), 799–805. [DOI] [PubMed] [Google Scholar]
- Friedman J., Hastie T., Tibshirani R. (2007). Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9(3), 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones M. H., Virtanen C., Honjoh D., Miyoshi T., Satoh Y., Okumura S., Nakagawa K., Nomura H., Ishikawa Y. (2004). Two prognostically significant subtypes of high-grade lung neuroendocrine tumours independent of small-cell and large-cell neuroendocrine carcinomas identified by gene expression profiles. The Lancet 363(9411), 775–781. [DOI] [PubMed] [Google Scholar]
- Knight K., Fu W. (2000). Asymptotics for lasso-type estimators. The Annals of Statistics 28(5), 1356–1378. [Google Scholar]
- Meinshausen N., Bühlmann P. (2006). High-dimensional graph and variable selection with the lasso. Annals of Statistics 34(3), 1436–1462. [Google Scholar]
- Peng J., Wang P., Zhou N., Zhu J. (2009). Partial correlation estimation by joint sparse regression models. Journal of the American Statistical Association 104, 735–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raponi M., Zhang Y., Yu J., Chen G., Lee G., Taylor J. M., Macdonald J., Thomas D. and others (2006). Gene expression signatures for predicting prognosis of squamous cell and adenocarcinomas of the lung. Cancer Research 66(15), 7466–7472. [DOI] [PubMed] [Google Scholar]
- Schwarz G. (1978). Estimating the dimension of a model. Annals of Statistics 6(2), 461–464. [Google Scholar]
- Shedden K., Taylor J. M., Enkemann S. A., Tsao M. S., Yeatman T. J., Gerald W. L., Eschrich S., Jurisica I. and others (2008). Gene expression-based survival prediction in lung adenocarcinoma: a multi-site, blinded validation study. Nature Medicine 14(8), 822–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H., Xiao G., Behrens C., Schiller J., Allen J., Chow C. W., Suraokar M., Corvalan A. and others (2013). A 12-gene set predicts survival benefits from adjuvant chemotherapy in non-small cell lung cancer patients. Clinical Cancer Research 19(6), 1577–1586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor I. W., Linding R., Warde-Farley D., Liu Y., Pesquita C., Faria D., Bull S., Pawson T. and others (2009). Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nature Biotechnology 27(2), 199–204. [DOI] [PubMed] [Google Scholar]
- Tomida S., Takeuchi T., Shimada Y., Arima C., Matsuo K., Mitsudomi T., Yatabe Y., Takahashi T. (2009). Relapse-related molecular signature in lung adenocarcinomas identifies patients with dismal prognosis. Journal of Clinical Oncology 27(17), 2793–2799. [DOI] [PubMed] [Google Scholar]
- Wang H., Li B., Leng C. (2009). Shrinkage tuning parameter selection with a diverging number of parameters. Journal of the Royal Statistical Society Series B 75(3), 531–552. [Google Scholar]
- Wasserman L., Roeder K. (2009). High dimensional variable selection. The Annals of Statistics 37(5), 2178–2201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M., Lin Y. (2007). Model selection and estimation in the Gaussian graphical model. Biometrika 94(1), 19–35. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.