Abstract
Pattern-dependent collective behaviors of cells have recently raised intensive attention. However, the underlying mechanisms that regulate these behaviors are largely elusive. Here, we report a quantitative study, combining experiment and modeling, on cell polarization and arrangement on a micropatterned substrate. We show that cells exhibit position-dependent collective behaviors that can be regulated by geometry and stiffness of the patterned substrate. We find that the driving force for these collective behaviors is the in-plane maximum shear stress in the cell layer that directs the arrangement of cells. The larger the shear stress, the more the cells preferentially align and polarize along the direction of the maximum principal stress. We also find that the aspect ratio of cell polarization shape and the degree to which cells preferentially align along the direction of maximum principal stress exhibit a biphasic dependence on substrate rigidity, corresponding to our quantitative predictions that the magnitude of the maximum shear stress is biphasically dependent on the stiffness of the substrate. As such, the driving force of these cell collective behaviors can be quantified using the maximum shear stress.
Introduction
Pattern formation is an indispensable requirement for the process of tissue morphogenesis (1,2). Although it is thought to be regulated primarily by spatial gradients of chemical factors known as morphogens (2–4), recent evidence shows that the mechanical factors also play crucial roles. For instance, there is a wealth of information showing that geometric constraints, such as systematic changes of the area and shape of the substrate using micropatterning techniques, can remarkably influence adhesion-based cell behaviors, regulating the structure of the cytoskeleton, cell migration, differentiation, and apoptosis (5–13). Particularly at the multicell level, the geometry of the substrate also regulates the orchestration of cell behaviors (14–17). For example, human adipose-derived stem cells (hASCs) exhibit geometry- and position-specific morphology, proliferation, and differentiation on patterned substrate in a collective manner. The highest cell proliferation occurs in the regions with large and well-spreading cells at the outer edge of a ring pattern, whereas differentiation localizes in the regions containing small and elongated cells at the inner edge (14). Human mesenchymal stem cells (hMSCs) at the edge of a circular pattern differentiate into osteogenic lineage, whereas those in the center become adipogenic (16,17). In addition, changing the shape of the cellular layer modulates the locations of osteogenic versus adipogenic differentiation (16). Moreover, a recent study showed that cells on a ring pattern exhibit directional migration and biased alignment—the cell populations exhibit an intrinsic phenotype-specific left-right asymmetry or chirality (18).
Besides the geometry, the stiffness of the substrate is another key factor influencing cell collective behaviors. For instance, cells adhere (19–25) and spread (12,19,21,26) better on stiff substrates than on soft ones. Cell proliferation rate is positively correlated with substrate stiffness (21,27). Stem-cell-lineage specification depends on substrate stiffness (28), and the osteogenic lineage of hMSCs is favored on rigid micropost arrays whereas adipogenic differentiation is favored on soft ones (22). Moreover, cells preferentially polarize and migrate toward or along the direction of stiffer substrates (19,29,30). In particular, cell migration speed depends on the substrate stiffness in a biphasic manner (31–36). Recent studies have demonstrated that increasing substrate stiffness enhances the persistence and directionality of collective cell migration and coordination among the cells (37).
The above collective behaviors of cells on patterned substrates have drawn growing interest in recent years. However, the driving force for these collective manners of pattern formation and its dependence on the geometric and mechanical properties of the substrate remains quite elusive. Here, we employ a combined approach with experiments and quantitative analyses to investigate the effects of geometry and rigidity of the micropatterned substrate on cell polarization and alignment. We find that the driving force of the collective behaviors is the in-plane maximum shear stress in the cell layer. The larger the maximum shear stress, the more the cells prefer to align along the direction of the maximum principal stress, and the higher the degree to which cells polarize. The stiffness and geometry of the pattern can influence the magnitude of the maximum shear stress and thus regulate cell collective behaviors. We apply our model to various patterns, and the predictions of cell polarization and alignment agree with our experiments.
Materials and methods
Micropatterning and cell seeding
The micropatterned substrate was prepared using soft lithography techniques. Briefly, the pattern with the designed geometric features was first fabricated on a mask, which was then replicated on a master with an AR-P3210 photoresist layer of 5 μm in thickness on a silicon wafer exposed to ultraviolet (UV) radiation. The mixture of Dow Corning 184 gel (Midland, MI) and curing agent (10:1) was poured onto the master in a petri dish, which was further vacuumized for 2 h and permitted to cure at 60°C for 8 h. The polydimethylsiloxane stamp was washed with acetone and alcohol in a bath sonicator and then treated with oxygen-ion sputtering to make it hydrophilic. A droplet of comb-polymer, nonadhesive to proteins or cells (38), was placed on the stamp surface and then uniformed by centrifugation at 1500 rpm. The stamp with the comb-polymer was immediately impressed onto a slide with precoated collagen. The micropatterned slide was immersed in phosphate-buffered saline for 2 h and sterilized by UV radiation for 2 h before seeding cells.
Osteoblast-like MC3T3-E1 cells (ATCC, Manassas, VA) were cultured with α-MEM medium (Hyclone, Logan, UT) containing 10% FBS (Gibco, Grand Island, NY) and 1% P/S (Invitrogen, Carlsbad, CA). After reaching 70% confluency, cells were trypsinized and seeded onto the micropatterned surfaces. The cells were then cultured at 37°C and 5% CO2 until they reached confluency.
Preparation of gel substrates
The polyacrylamide substrates were prepared according to protocols in the existing literature (39). In brief, a coverslip was pretreated with a drop of NaOH (Sinopharm Chemical Reagent, Beijing, China) and allowed to dry in air, and then a drop of 3-aminopropyltrimethoxysilane (Sigma, St. Louis, MO) was smeared evenly on the surface. After 4–5 min, the coverslip was washed three times and then incubated with 0.5% glutaraldehyde (Sinopharm Chemical Reagent) for 30 min. Acrylamide and N,N-methylene-bis-acrylamide (Bio-Rad, Hercules, CA) were mixed with fluorescent beads (Sigma) and curing agent. The mixture of 50 μL was sandwiched between the activated coverslip and a blank coverslip, which allows a formation of a flat gel layer of ∼100 μm in thickness. The surface of the gel substrate was washed with HEPES and applied with sulfo-SANPAH (Pierce Chemical, Rockford, IL) under UV irradiation for 30 min. Then, 300 μL type-I collagen (Sigma) solution was coated on the substrate and stayed at 4°C overnight. The gel substrate then was washed extensively with phosphate-buffered saline, drained off, micropatterned, and finally incubated with culture medium for 2 h.
Measurement of traction force and in-plane stresses of the cell layer
To measure the traction force and the in-plane stresses, the surface deformation of the substrate should first be measured. Briefly, for a specific location, a fluorescent image of the beads embedded within the substrate was recorded. Then, after the cell layer was released from the gel substrate with trypsin, a second fluorescence image of the beads was recorded. Based on the two fluorescent images, the displacement field in the substrate was calculated using digital image correlation.
Constrained Fourier transform traction microscopy (FTTC) (40) was used to calculate the corresponding traction stress maps according to the following procedure. 1) The traction field was calculated using unconstrained FTTC. First, the displacement field in Fourier space was calculated using fast-Fourier transform. The transformed displacements were multiplied by the Fourier transform of the Green function to get the transformed traction. Then, we took the inverse Fourier transform of the result to obtain the traction. 2) The new traction field was defined by setting the traction outside the cell boundary to zero and the displacement field was calculated using this new traction field. 3) A new displacement field was defined by replacing the displacements of the calculated displacement field within the cell boundary with the experimentally observed displacements. 4) Steps 1–3 were repeated until convergence was reached at a given level of tolerance. We chose to terminate the iteration when the relative variation in maximal magnitude of the tractions within the cell was <0.001 in the succeeding steps.
To determine the in-plane stresses in the cell layer, a finite-element model of the cell layer was constructed with the commercial software ABAQUS, in which the traction obtained from the experiment was applied to the model (41,42). The meshes of the FEM model were deliberately set to be the same as the meshes on the substrates for calculating the traction with FTTC, so that the position in the cell layer on which the corresponding traction should be applied can be easily determined. Once the traction was loaded, the corresponding stress fields in the cell layer were calculated and mapped through postprocessing with ABAQUS.
Analysis of cell alignment
Phase-contrast images of the micropatterned cells were recorded and then analyzed using ImageJ software, by which the profile of each cell was fitted with an ellipse. The degree of cell polarization was denoted by the aspect ratio of the ellipse, i.e., the ratio of its major axis to its minor axis, and cell orientation was denoted by the angle between the direction of the major axis of the cell and the circumferential direction of the ring pattern or the direction of maximum principal stress in the cell layer on patterns of other geometry. All experiments were performed at least in triplicate, and >150 cells were measured for each replicate.
The data were presented as the mean ± SD if not specifically claimed. One-way analysis of variance with Bonferroni’s post hoc analysis was performed to determine the statistical significance among the mean values of different groups. The difference is regarded as statistically significant if the p value is <0.05.
Theoretical and numerical modeling
Assuming the cells are connected perfectly through the cell-cell junction, the cell monolayer is considered as a homogeneous elastic membrane. The cell layer adheres to the substrate via adhesion molecules at the cell-substrate interface. It is believed that cell-cell and cell-substrate interactions are the physical basis of cells developing and sustaining the in-plane stresses in the cell layer via contractility of the cytoskeleton. The Young’s modulus, Poisson’s ratio, and prestrain of the cell layer are denoted by Ec, , and , respectively. The magnitude of the prestrain, , is thought to be ∼0.1 under physiological conditions (43–45). The two-dimensional plane stress constitutive relation of the cell layer is written as
| (1) |
where and are the stress and strain tensors, respectively. The second term in Eq. 1 accounts for the cytoskeletal contractility. can be derived from the displacement of the cell layer according to the small-deformation theory.
We model the molecular bonds as elastic springs, without considering the dynamic binding and unbinding of the bonds (46), and we consider the mean stiffness of the molecular bond from a statistical point of view. For simplicity, here we adopt the two-spring model (47) to effectively consider the stiffness of substrate and adhesion molecules, denoted by . For a cell layer of ringlike shape, the strain in the cell layer in polar coordinates is given by
| (2) |
where u is the radial displacement. The equilibrium equation of the cell layer can be derived as (see Section S1 and Fig. S1 in the Supporting Material for more details)
| (3) |
where
| (4) |
Substituting Eqs. 1, 2, and 4 into Eq. 3, we have
| (5) |
where , in which is the bond density of adhesion molecules, the effective stiffness of the substrate, and the thickness of the cell layer. Because the inner and outer edges of the ringlike cell layer are traction free, the boundary conditions for the governing equation, Eq. 5, are written as
| (6) |
where and are the inner and outer radii, respectively. Solving Eq. 5, we obtain
| (7) |
where and are constants and are to be determined by the boundary conditions (Eq. 6). Then, the traction can be obtained by Eq. 4. Substituting Eq. 7 into Eq. 2, and then into Eq. 1, we can obtain the radial and circumferential normal stresses, and , i.e., the in-plane minimum and maximum principal stresses,
| (8) |
and
| (9) |
The absolute value of the difference between and gives twice the in-plane maximum shear stress as
| (10) |
which is a function of the radial position and stiffness of the substrate, and and are constants, which are given in Section S2 in the Supporting Material. In the calculation, , , and . According to the two-spring model (47), , where and are the spring constants of the substrate and molecular bond, respectively. , in which and are the Young’s modulus and the Poisson ratio of the substrate, and d is the diameter of the adhesion molecules (48). Given , , , and Es = 10∼60 kPa, we can obtain the value of . And , the effective areal stiffness of the substrate and adhesion molecules, varies from to 0.625 in our analysis.
The commercial software ABAQUS was adopted in the calculation of stress fields in the cell layer, except on the ring pattern, where analytical solutions could not be obtained. The cell layer was modeled as a prestrain membrane adhering on a micropattern. The four-node linear membrane element was used to discretize the cell layer. The element size was chosen to be 1 μm. The contractility of cell layers was simulated by a thermal contraction with a thermal expansion coefficient of 0.1; thus, a temperature drop of 1°C corresponds to a strain of −0.1. The cell layer is connected with the substrate via a layer of adhesion molecules with areal stiffness that can be set in the Interaction module of ABAQUS.
Results
Collective cell alignment and polarization on the ring pattern
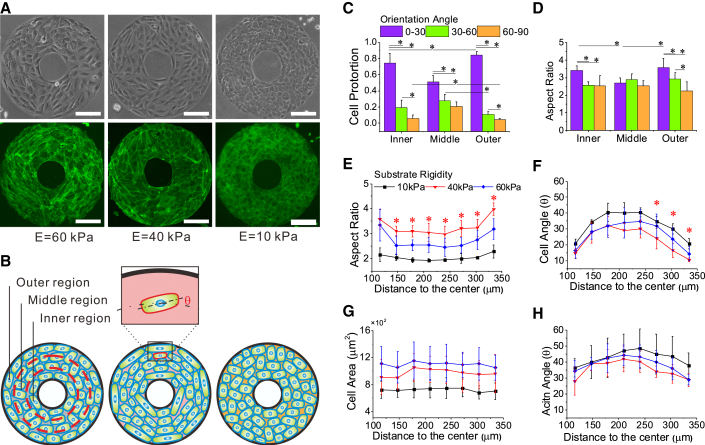
To study cell alignment, we seeded the MC3T3-E1 cells on the ring-like micropatterns of five different rigidities (60 kPa, 40 kPa, 30 kPa, 18 kPa, and 10 kPa; see Materials and Methods for details). The phase-contrast images of the MC3T3-E1 cell monolayer on patterns of three typical rigidities, stiff (60 kPa), medium (40 kPa), and soft (10 kPa), and the corresponding fluorescence images of actin, are shown in Fig. 1 A. The results of all five rigidities of the pattern are given in Fig. S2. We noted that the cells on the stiff and medium patterns (60 kPa gel and 40 kPa gel, respectively) tended to align along the circumferential direction of the ring, especially at the ring edges, whereas cells on the soft pattern (10 kPa gel) did not clearly show this feature, as indicated in Fig. 1 A and shown schematically in Fig. 1 B. To describe the position-dependent alignment of cells on the pattern, we divided the area of the annular ring into three regions—the inner, middle, and outer rings, represented by I, M, and O, respectively, as shown in Fig. 1 B. We depicted the cell alignment by an orientation angle represented by the angle between the long axis of the cell and the circumferential direction of the ring pattern, , which is in the range 0°∼90°. We further divided the range of the orientation angle into three subranges, 0°∼30°, 30°∼60°, and 60°∼90°. We found that the proportions of cells in the 0°∼30° orientation range were significantly larger in both the inner and outer rings than in the middle ring (Fig. 1 C). This result suggests that cells preferred to align along the circumferential direction at the ring edges, whereas cells in the middle region exhibited more random orientation.
Figure 1.
Cell polarization and alignment on ring patterns of different substrate stiffnesses. (A) Phase-contrast images of cell morphology and alignment, and associated fluorescence images of actin on ring patterns of three different stiffnesses, i.e., 60 kPa gel, 40 kPa gel, and 10 kPa gel. Scale bars,200 μm. (B) Schematic diagram of cell morphology and alignment corresponding to the phase-contrast images in (A), where the ring pattern is divided into three regions, the inner, middle, and outside regions. (C) Histograms of the statistics of cell population for three different angle ranges in the three different regions of the ring pattern on the stiffest matrix. (D) Histograms of statistics of the cell aspect ratio for different angle ranges in the different regions of the ring pattern on the stiffest matrix. (E) The mean aspect ratio of cells versus their distance from the center of the ring pattern at different stiffnesses. (F) The mean cell orientation angle as a function of the distance for three different stiffnesses. (G) The mean cell area as a function of the distance. (H) The alignment of actin as a function of the distance. Note that the asterisks indicate that the differences between the results on 40 kPa gel and those on both 60 kPa and 10 kPa gel are statistically significant (p < 0.05). To see this figure in color, go online.
To represent the polarization shape of the cell, we use the aspect ratio, defined as the ratio of the long axis to the short axis of the cell. We showed that in the inner and outer rings, the mean aspect ratio of 0°∼30° cells was significantly larger than that of 30°∼60° and 60°∼90° cells, whereas in the middle ring, there was no marked difference in mean aspect ratio among the three angle ranges (Fig. 1 D). In addition, the mean aspect ratios of 0°∼30° cells in the inner and outer ring were significantly larger than that in the middle ring. The mean aspect ratio of the 30°∼60° and 60°∼90° cells showed no significant difference among the three different regions (inner, middle, and outer) of the ring pattern (Fig. 1 D). These results suggest that cells at the ring edges exhibited larger aspect ratio compared with those in the middle region. Interestingly, the mean aspect ratio exhibited a biphasic dependence on substrate stiffness, i.e., cells adopted a less polarized morphology on both the softest and the stiffest substrates, but had more polarized morphology on the substrate of intermediate stiffness (Fig. 1 E). Correspondingly, the cell orientation angle also showed a biphasic dependence on substrate stiffness (Fig. 1 F). The mean angle of cells at the intermediate stiffness was smaller than that on the softest and stiffest substrates, indicating that cells preferentially aligned along the circumferential direction on the substrate of intermediate stiffness.
We also analyzed the orientation of actin. The alignment of actin was consistent with that of cells, i.e., the actin is more parallel to the circumferential direction in the inner and outer rings than in the middle region (Fig. 1 H). In addition, the larger the aspect ratio of cells, the smaller the angle of actin, consistent with the relation between cell angle and cell aspect ratio. There also existed a weak biphasic dependence of the actin angle (Fig. 1 H) on substrate rigidity, consistent with the biphasic dependence of the cell angle. Of note, different from the cell shape and alignment, the cell area did not depend on the distance from the center of the ring, keeping a somewhat constant value on the ring for a given substrate rigidity. However, the cell area increased with substrate rigidity, consistent with reports in the existing literature (12).
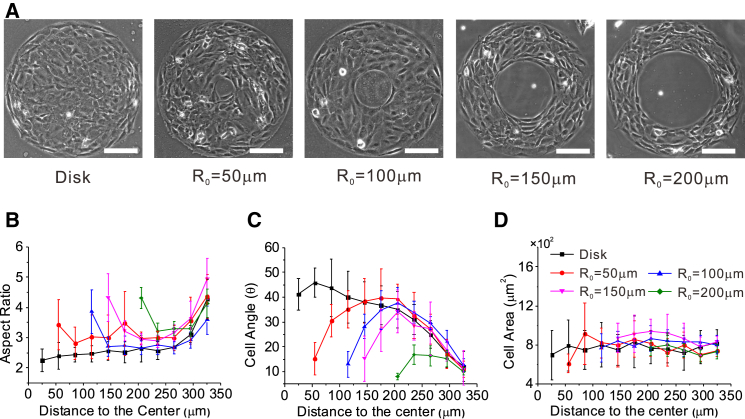
We noted that the width of the ring pattern (i.e., the difference between the outer and inner radii) had a notable effect on cell alignment and polarization. By increasing the inner radius from 0 to 200 μm (see Fig. 2 A) to change the ring width, we found that the larger the inner radius (i.e., the thinner the ring), the larger the mean aspect ratio, and the smaller the mean orientation angle of cells, suggesting that more cells polarized and aligned parallel to the circumferential direction with the increase in inner radius, as shown in Fig. 2, B and C. However, the cell area depended on neither the inner radius nor the radial position (Fig. 2 D).
Figure 2.
Cell polarization and alignment on ring patterns with different inner radii. (A) Phase-contrast images of cell morphology and alignment in the cell layer on ring patterns with five different inner radii. (B and C) The mean cell aspect ratio (B) and mean cell angle (C) as functions of cell distance from the ring center for rings of different inner radius. (D) The mean cell area shows an independence of distance and inner radius. Scale bars, 200 μm. To see this figure in color, go online.
The in-plane stresses in the cell layer
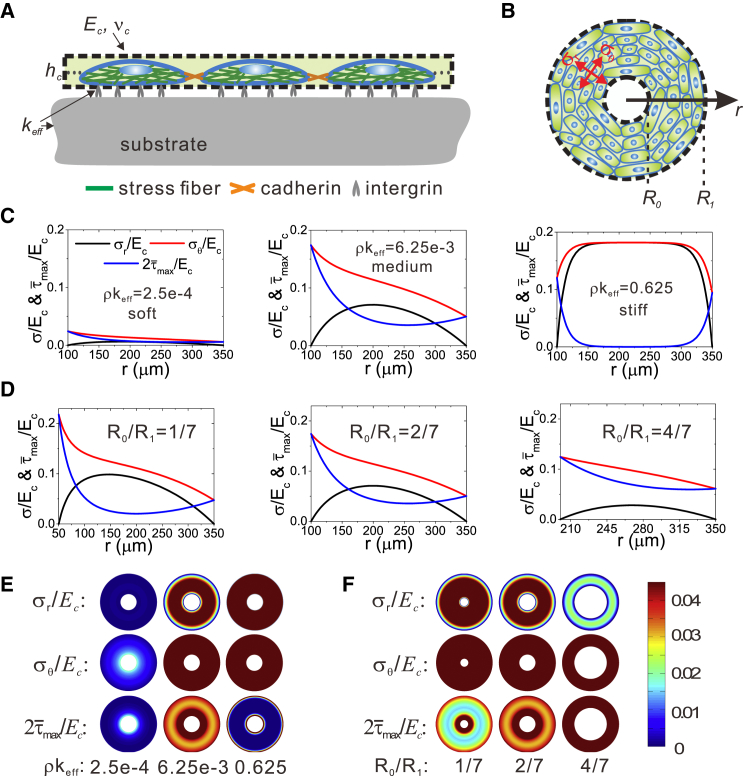
Here, we assumed that the above geometry- and rigidity-induced cell responses are closely related to the mechanical stresses in the cell layer (41,42,49). We analyzed the stresses in the cell layer on the ring pattern (Fig. 3, A and B) and their dependency on substrate stiffness and ring width using the mechanical model described in this study (see Materials and Methods). Fig. 3 C shows the distribution of the principal stresses, and , and the maximum shear stress, , along the r axis for three different substrate stiffnesses, . Note that the distribution of shows a pattern consistent with those of cell alignment and polarization (Fig. 1, A and B): the value of at the ring edge is larger than in the interior region. In particular, it exhibited a biphasic dependence on substrate stiffness, i.e., it was larger at intermediate stiffness than at lowest and highest stiffnesses, corresponding to the biphasic dependence of the aspect ratio and alignment of cells on substrate stiffness (Fig. 1, E and F). Fig. 3 D shows the effect of the inner radius on distribution of , , and . The larger the inner radius, the more uniform the principal stresses and the maximum shear stress along the r axis.
Figure 3.
Predictions of the in-plane principal stresses and maximum shear stress in the cell layer. (A) Side view of the mechanical model of the cell layer adhering to the patterned substrate via adhesion molecules. (B) Top view of the model. The cell monolayer is considered as a homogeneous membrane of a ring shape, with the inner and outer radii denoted by R0 and R1, respectively. (C) Predictions of the distribution of the in-plane minimum and maximum principal stresses, and , as well as the in-plane maximum shear stress, , for three different substrate stiffnesses. (D) Predictions of the distribution of the principal stresses and shear stress, , , and , for rings of different inner radius. (E) Color maps of the maximum and minimum principal stresses and the maximum shear stress in the cell layer on the ring pattern for three different stiffnesses, corresponding to the results in (C). (F) Color maps of the maximum and minimum principal stress and the maximum shear stress in the cell layer on ring patterns with three different inner radii, corresponding to the results in (D). To see this figure in color, go online.
Fig. 3, E and F, further illustrates the distribution of , , and in color maps for the various stiffnesses and inner radii, respectively. Comparing with our experimental results, we found that the high shear stress (Fig. 3, E and F, red) corresponds to the region with large aspect ratio and small orientation angle of cells in Figs. 1 A and 2 A, respectively; in contrast, the low shear stress (Fig. 3, E and F, blue) corresponds to the region with small aspect ratio and random orientation in Figs. 1 A and 2 A. These results suggest that the maximum shear stress might be the driving force for regulating collective cell polarization and alignment; the larger the value of the maximum shear stress, , the more the cells preferentially align along the direction of the maximum principal stress, , and the larger the aspect ratio of cells as well.
Of note is that the circumferential stress also exhibits a transition from a monotonic to a biphasic dependence on the radial position (Fig. 3 C). The mechanism behind this switch is that the displacement distribution observed in the cell layer changes with the substrate stiffness. On soft substrate, the entire cell layer contracts toward the center of the ring, i.e., the displacement of the cell layer is negative, and its absolute value linearly increases with the radial coordinate r (see Fig. S3, A and B). However, on the medium and stiff substrates, the deformation pattern is different. The displacement of the inner part of the cell layer becomes positive, i.e., it expands away from the center of the ring, whereas that at the outer edge is negative (Fig. S3 C). In particular, on stiff substrate, there is almost no deformation at the middle range of the ring (Fig. S3 A).
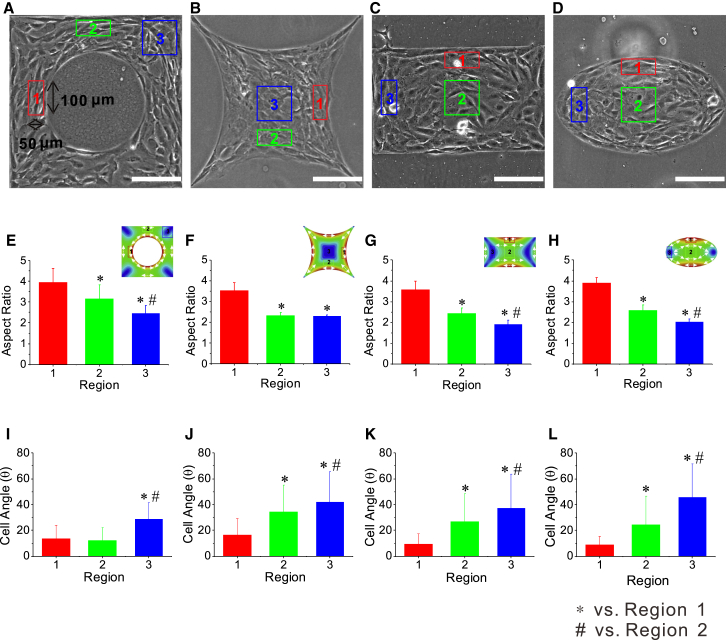
To validate our model, we further applied it to four other, different micropatterns—a square with a hole, an indented square, a rectangle, and an ellipse (see Fig. 4, A–D)—and calculated the in-plane maximum shear stress in the cell layer, as shown in Fig. 4, E–H. The inset color map of the maximum shear stress for each pattern in Fig. 4, E–H, is consistent with the cell alignment and polarization on the corresponding pattern in Fig. 4, A–D. The red color indicates the highest in-plane maximum shear stress, whereas green and blue correspond to the intermediate and minimal values (Fig. 4, E–H), respectively. Correspondingly, the aspect ratio in the red boxes was significantly larger than that in either the blue or the green box, whereas the aspect ratio in the green box was larger than that in the blue one (Fig. 4, E–H). In addition, in the red box, the cell alignment was more preferentially along the direction of the maximum principal stress (Fig. 4, I–L). As expected, in the region where the maximum shear stress was small, the cells exhibited no preferred orientation. These results again suggest that our model predictions of the distribution of in-plane principal stress and maximum shear stress are consistent with the pattern of cell collective polarization and alignment on the various micropatterns observed in our experiments.
Figure 4.
Measurements of cell alignment and polarization on various geometrical patterns compared with model predictions. (A–D) Phase-contrast images of cells on a square pattern with a circular hole (A), an indented-square pattern (B), a rectangular pattern (C), and an elliptical pattern (D). The colored boxes indicate typical regions of different magnitudes of maximum shear stress. (E–H) Histograms of the mean aspect ratios of cells at different regions in accordance with the colored boxes labeled in (A)–(D), respectively. (E–H insets) Color maps showing model predictions of the maximum shear stress of the corresponding pattern geometries. (I–L) Histograms of the mean cell angle in different regions are in accordance with the colored boxes labeled in (A)–(D), respectively. Scale bars, 200 μm. To see this figure in color, go online.
Measured in-plane stresses in the cell layer
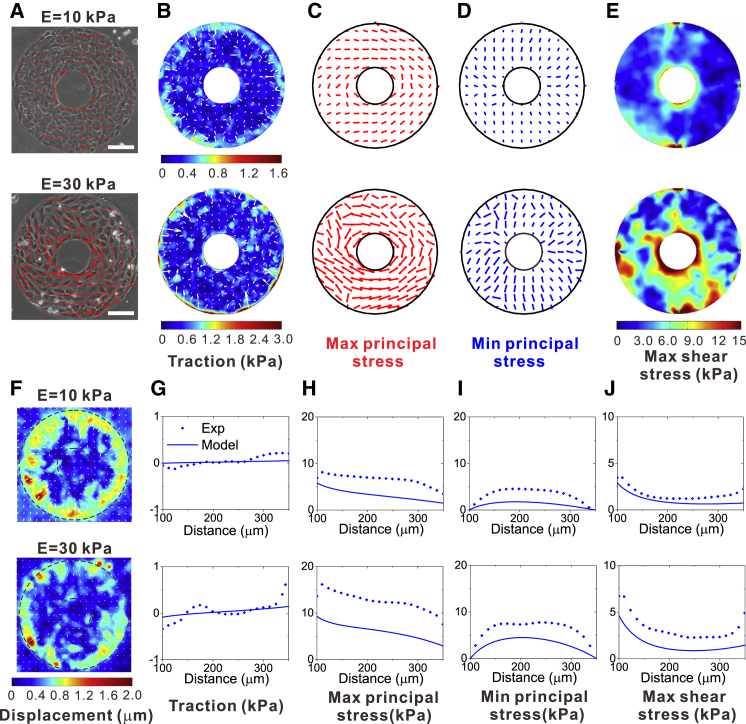
To further verify the role of maximum shear stress in the collective cell behaviors, we examined the measured in-plane stresses of the cell layer and compared them with the predictions of our theoretical model. The in-plane stresses were obtained based on the measured traction force. The traction forces on patterned substrates of two different stiffnesses, i.e., 10 kPa and 30 kPa, were measured. The phase-contrast images of cell layers are shown in Fig. 5 A, and the corresponding displacement fields of the substrates are shown in Fig. 5 F. The results show that the traction force was generally in the radial direction (Fig. 5 B), and its radial component increased as a function of the distance to the ring center (Fig. 5 G). There was generally a linear relationship between the traction force and the distance to the ring center for the soft substrate (Fig. 5 G, 10 kPa gel), whereas the traction force concentrated at the boundary of the ring for the stiff substrate (Fig. 5 G, 30 kPa gel). The distribution of the traction force is consistent with theoretical predictions in this work (Eq. 4) and with those of a previous study (50).
Figure 5.
Measurement of the traction force and in-plane stresses in the cell layer. (A) Phase-contrast images of cells on ring patterns on 10 kPa and 30 kPa gels. The vectorial representation of the maximum principal stress is given to show the orientation of cells relative to the stress tensor. (B) Color maps and vectorial representation of traction on ring patterns of two different stiffnesses, showing that the traction is generally in the radial direction. (C) Vectorial representation of the in-plane maximum principal stress on ring patterns of two different stiffnesses, calculated based on the measurement of the traction force. (D) Vectorial representation of the in-plane minimum principal stress. (E) Color maps of the in-plane maximum shear stress. (F) Color maps of the displacement fields of the ring substrates for the 10 kPa gel and the 30 kPa gel. (G) Radial component of traction as a function of the cell distance from the center of the ring pattern for the two different substrate stiffnesses, where the solid lines represent model predictions, and the dots represent experimental measurements. (H) In-plane maximum principal stress as a function of the cell distance from the center of the ring pattern, where the solid lines represent model predictions and the dots represent calculations based on experimental measurements of traction. (I) The in-plane minimum principal stress; (J) the in-plane maximum shear stress. To see this figure in color, go online.
The maximum principal stress was in general along the circumferential direction (Fig. 5, C and H), and the minimum principal stress was along the radial direction (Fig. 5, D and I). The in-plane maximum shear stress on the ring pattern localized at the ring edge, and the shear stress was low on the soft substrate, but high on the stiff one (Fig. 5, E and J). This measurement of the in-plane principal stress and maximum shear stress was also consistent with our observation of cell alignment and polarization along the circumferential direction, as shown in Figs. 1 and 5 A. That is, for the soft matrix, the cell alignment was more random and the aspect ratio was relatively small, whereas for the stiff matrix, the cell alignment was in general along the circumferential direction and the aspect ratio was larger. This comparison of our measurement of in-plane principal stresses and maximum shear stress with our experimental observation of cell alignment and polarization supports our theories about the driving force of cell collective behaviors.
We note that in our experiments, the edge of the cell layer could not be as smooth as the ideal circular edge in our theoretical model, and there might have been imperfections at the boundary of the cell layer. To reduce the effect of these imperfections, we tried our best to choose samples of cell layers with the smallest possible boundary imperfections. We showed that those imperfections had only a slight effect on the value and direction of the maximum principal stress, and that the effect was localized in a very small region near the imperfections. The direction of the maximum principal stress was in general along the circumferential direction, consistent with our theoretical predictions (Fig. S4).
Inhibition of actin, cell-cell adhesion, and cell-matrix adhesion
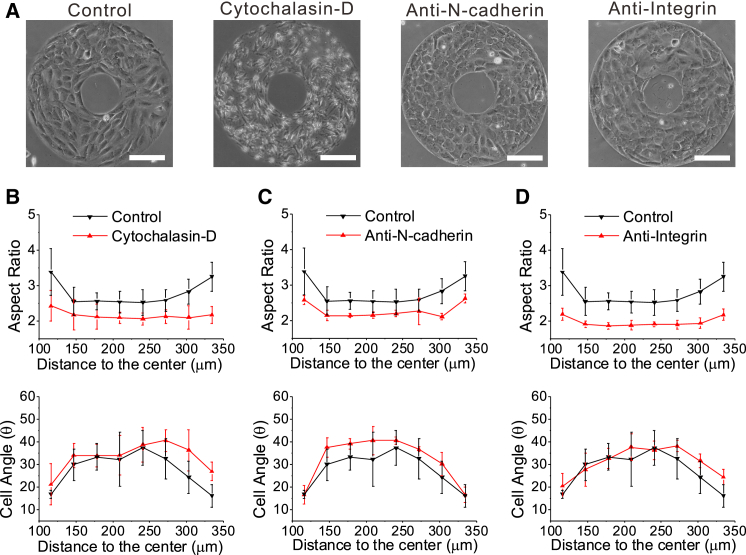
To gain additional insight into the molecular mechanisms of cell mechanosensing, we examined the effect of inhibition of actin and adhesion molecules on cell alignment and polarization. To do so, on the 60 kPa gel, we inhibited the contractility of the cytoskeleton with cytochalasin-D, inhibited cell-cell adhesion with the monoclonal anti-N-cadherin antibody (N-cadherin is one of the important adhesion molecules of cell-cell adhesion for MC3T3-E1 cells (51)), and inhibited cell-substrate adhesion with the CD29 antibody of integrin (α4β1) (Fig. 6 A).
Figure 6.
Polarization and alignment of cells depend on cell contractility, cell-cell adhesion, and cell-matrix adhesion. (A) Phase-contrast images of the cell layer on the ring pattern for the cases of control, treatment by cytochalasin-D, treatment by anti-N-cadherin, and treatment by anti-integrin. (B) Cytochalasin-D treatment dramatically reduced the aspect ratio of cells and increased the cell angle, particularly at the ring edge. (C) Anti-N-cadherin treatment also reduced the aspect ratio and increased the cell angle, with a slightly reduced effect compared to treatment by cytochalasin-D. (D) Anti-integrin treatment decreased the aspect ratio more dramatically than treatment by either cytochalasin-D or anti-N-cadherin, but it increased the cell angle only slightly. To see this figure in color, go online.
Our experiments showed that when cell contractility was blocked by cytochalasin-D, the degree of cell alignment and polarization both decreased (see Fig. 6 B). That is, the aspect ratio dramatically decreased, and the cell angle with respect to the circumferential direction increased, particularly at the ring edge. Also, the inhibition of N-cadherin and the inhibition of integrin both suppressed the collective cell alignment and polarization (Fig. 6, C and D). Note that all inhibition treatments caused a significant decrease in the aspect ratio of cells. However, the effect of inhibition on the cell angle was less significant. The reason for this is that cell alignment may still more or less follow the original alignment (before the drug was added) because of a dramatic decrease in the driving force for a new alignment due to the inhibition.
In addition, to examine the effect of adhesion perturbation on the biphasic dependence, we performed further experiments by inhibiting N-cadherin on substrates of different rigidity, 10 kPa, 40 kPa, and 60 kPa (Fig. S5 A). The adhesion perturbation by inhibition of N-cadherin impaired the biphasic behaviors (Fig. S5 B). Note that in addition, the aspect ratio of cells was dramatically reduced and its biphasic dependence became weak, with much less statistical significance, compared with the corresponding data in Fig. 1. In addition, the biphasic dependence of the cell angle completely disappeared. The reason that the biphasic behavior of the aspect ratio was not completely lost might be that there are multiple types of cadherin for MC3T3-E1 cells, and the inhibition of N-cadherin could not completely destroy the cell-cell adhesion. Therefore, the in-plane tension force could still be transferred via the residual cell-cell adhesion. However, when we inhibited the actin to block the contractility of cells, the biphasic behavior was completely lost (Fig. S5 C).
Discussion
In-plane stresses versus cell alignment and polarization
In this study, we have demonstrated that cells preferred to align and polarize along the direction of the maximum principal stress, and that the in-plane maximum shear stress was the driving force for these pattern-determined cell arrangements. But how are the cell behaviors related to the in-plane principal and shear stresses? The answer to this question lies in the intrinsic responses of the cytoskeleton to mechanical force. The cytoskeleton is believed to provide structural support and shape to cells, and it mainly sustains tensile stress, but hardly bears shear stress. Shear stress in cells will thus induce rotation of the cytoskeleton to align along the direction of principal stress, where the shear stress is equal to zero. A myriad of evidence shows that cells preferentially align along the direction of maximum principal stress under the contractile force of the cytoskeleton (to maintain a tensional homeostasis in the cytoskeleton) (52–54). Therefore, the larger the maximum shear stress, the larger the driving force for the rotational alignment (via reconstruction of the cytoskeleton instead of only elastic deformation). It is thus also reasonable that the maximum shear stress determines the cell aspect ratio in the cell layer.
To validate our findings that the in-plane maximum shear stresses induced collective cell alignment and polarization, we examined the evolution of the cell layer from a very early stage of its formation on the pattern. We observed that at the early stage, before the cells filled the surface of the pattern, the cells exhibited random alignment because the in-plane stress had not been developed due to the lack of cell-cell connection. Once the cells completely filled the surface of the pattern via proliferation and migration and the cells were connected through cell-cell adhesion, cells started to reorientate and polarize preferentially along the maximum principal stress driven by the in-plane shear stress and finally reached a steady state (Figs. S6 and S7). However, when cell-cell interaction was inhibited, the collective cell alignment and polarization were suppressed. These results reveal the important roles of the in-plane stress and cell-cell interaction for position-dependent polarization and arrangement of cells.
Our predictions and experiments are consistent with recent studies of collective migration of cells by Trepat and co-workers (41,42,49,55), showing that cells align and migrate along the direction of maximum principal stress. The authors denoted the in-plane maximum shear stress as the degree of anisotropy of the local in-plane stress field. They showed that the region of higher-stress anisotropy exhibits stronger alignment between the direction of the maximum principal stress and that of the cellular migration velocity. Here we further showed that the cell shape (aspect ratio) was correlated with the in-plane maximum shear stress, i.e., the higher the maximum shear stress, the larger the aspect ratio of the cells. We also showed that the in-plane maximum shear stress as the driving force of cell alignment and polarization could be modulated by matrix stiffness and geometry from both the theoretical and the experimental standpoint.
Effect of the stiffness and geometry of the patterned substrate
Our experiments showed that the collective behavior of cell alignment and polarization depended on the stiffness (Fig. 1) and geometry (Figs. 2 and 4) of the patterns, and in particular, they exhibited biphasic dependence on substrate stiffness. What are the mechanisms underlying these cell responses? We showed that these behaviors were attributed to the effect of the stiffness and geometry of the micropattern on the in-plane stresses in the cell layer. It has been shown that substrate stiffness has a significant impact on the magnitude and distribution of cell traction force (cell-matrix interaction) (50,56), as well as on the in-plane stresses (cell-cell interaction) (57,58). Consistent with those prior works, this study showed that the stiffness of the substrate influenced the in-plane principal stresses and in-plane maximum shear stress. Because the maximum shear stress was the driving force for the collective cell behaviors, directing cells to align along the direction of maximum principal stress, the level of the alignment and polarization was positively correlated with the magnitude of maximum shear stress. In addition, according to our quantitative analyses, it is rational to have biphasic behavior of cells in alignment and polarization, since the maximum shear stress biphasically depended on the substrate stiffness (Fig. 3). We also demonstrated that different geometries of the micropattern induced different distributions of the in-plane principal stresses and maximum shear stress, which thus caused different patterns of cell alignment and polarization (Fig. 4).
Effect of the orthotropic property of the cell layer
When cells polarize and align along the circumferential direction on the ring pattern, the cell layer might become orthotropic because there would be more cytoskeletons parallel to the circumferential direction than in the radial direction, which renders the cell layer orthotropic. This raises a question as to whether our predictions using the isotropic model are still valid. To answer this question, we remodeled the cell layer as an orthotropic membrane, with the Young’s moduli in the radial direction, , and the circumferential direction, , to study the effect of the orthotropic property on the principal stresses and maximum shear stress. Note that because of cell polarization along the circumferential direction. The details of the model are given in Section S3 in the Supporting Material. Our results showed that the decrease in did not change the general distribution of maximum shear stress and the principal stresses. In particular, in most areas of the pattern, except near the inner edge, the smaller the ratio, the larger was the maximum shear stress (Fig. S8). This result ensures stable cell polarization and alignment driven by the maximum shear stress.
Effect of curvature of the ring edge
Of note is that our model prediction of the maximum shear stress is higher at the inner edge than at the outer edge. Inconsistent with that, in Figs. 1 and 2, the angles in the inner radius are higher than in the outer radius, whereas the aspect ratio of cells at the inner edge seems to be smaller than that at the outer edge. The difference between our model predictions and Figs. 1 and 2 may be caused by the high curvature of the inner edge of the pattern. The radius of curvature of the inner edge is close to the size of a single cell. Thus, the bending resistance of the cytoskeleton makes it difficult for the cell to align along the inner edge to follow the direction of maximum principal stress and to comply with such high curvature. However, in our theoretical model, the cell layer is considered as a continuum membrane, and the bending rigidity of the cytoskeleton was not considered, which might account for the difference between our model predictions and the experimental results. This effect of bending rigidity decreased for a larger inner radius, as shown in Fig. 2 C (for R0 = 200 μm), where the cell angle is smaller at the inner edge than at the outer edge. Therefore, our model predictions of cell alignment in general agree with experimental results, except in the case of the ring pattern with a small inner radius. Improvements of our model, such as taking into consideration the bending rigidity of the cytoskeleton, will be left for future efforts.
Conclusions
Collective cell arrangement, as a key component in the processes of tissue formation, has now been a focus of inquiry. In this study, we determined that the driving force for the collective alignment and polarization of cells was the in-plane maximum shear stress, which originates from active contractility of the cells in the cell layer and can be regulated by altering the stiffness and geometry of the patterned substrate. This finding was achieved via a combination of experiments and theoretical modeling, which enables us to construct a quantitative relationship between the driving force and the mechanical and geometric properties of the substrate, and to predict how mechanical force drives collective cell behaviors. This relationship has been demonstrated by the close correlation of the cell alignment and polarization with the distribution of the in-plane maximum principal stress and maximum shear stress, as well as by the consistency between the biphasic dependence of the degree of cell alignment and cell polarization on substrate stiffness and the corresponding biphasic behavior of the maximum shear stress. This study demonstrates the important role of quantitative modeling in predicting collective cell behaviors and pattern formation, which will provide powerful tools for precise control of the pattern formation in tissue engineering for potential biomedical applications.
Author Contributions
S.H., B.H., and B.J. designed the research; C.L., X.L., and S.H. performed the research; C.L. and X.L. performed the experiment; S.H. contributed to the development of the model and numerical calculations; S.M. contributed the tools for measuring surface deformation; C.L., X.L., and S.H. analyzed data; and C.L., S.H., B.H., and B.J. wrote the article. All authors reviewed the manuscript.
Acknowledgments
This research was supported by the National Natural Science Foundation of China through grants 11025208, 11372042, 11221202, and 11372043.
Editor: Rong Li.
Footnotes
Shijie He and Chenglin Liu contributed equally to this work.
Supporting Materials and Methods and eight figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00669-4.
Contributor Information
Bo Huo, Email: huobo@bit.edu.cn.
Baohua Ji, Email: bhji@bit.edu.cn.
Supporting Material
References
- 1.Salazar-Ciudad I., Jernvall J., Newman S.A. Mechanisms of pattern formation in development and evolution. Development. 2003;130:2027–2037. doi: 10.1242/dev.00425. [DOI] [PubMed] [Google Scholar]
- 2.Keller R.E. The cellular basis of epiboly: an SEM study of deep-cell rearrangement during gastrulation in Xenopus laevis. J. Embryol. Exp. Morphol. 1980;60:201–234. [PubMed] [Google Scholar]
- 3.Nilsson O., Parker E.A., Baron J. Gradients in bone morphogenetic protein-related gene expression across the growth plate. J. Endocrinol. 2007;193:75–84. doi: 10.1677/joe.1.07099. [DOI] [PubMed] [Google Scholar]
- 4.Huang S., Ingber D.E. The structural and mechanical complexity of cell-growth control. Nat. Cell Biol. 1999;1:E131–E138. doi: 10.1038/13043. [DOI] [PubMed] [Google Scholar]
- 5.Théry M., Pépin A., Bornens M. Cell distribution of stress fibres in response to the geometry of the adhesive environment. Cell Motil. Cytoskeleton. 2006;63:341–355. doi: 10.1002/cm.20126. [DOI] [PubMed] [Google Scholar]
- 6.Rape A.D., Guo W.H., Wang Y.L. The regulation of traction force in relation to cell shape and focal adhesions. Biomaterials. 2011;32:2043–2051. doi: 10.1016/j.biomaterials.2010.11.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen C.S., Mrksich M., Ingber D.E. Geometric control of cell life and death. Science. 1997;276:1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 8.Fu R., Liu Q., Huo B. Spreading area and shape regulate apoptosis and differentiation of osteoblasts. Biomed. Mater. 2013;8:055005. doi: 10.1088/1748-6041/8/5/055005. [DOI] [PubMed] [Google Scholar]
- 9.Elineni K.K., Gallant N.D. Regulation of cell adhesion strength by peripheral focal adhesion distribution. Biophys. J. 2011;101:2903–2911. doi: 10.1016/j.bpj.2011.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kilian K.A., Bugarija B., Mrksich M. Geometric cues for directing the differentiation of mesenchymal stem cells. Proc. Natl. Acad. Sci. USA. 2010;107:4872–4877. doi: 10.1073/pnas.0903269107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.McBeath R., Pirone D.M., Chen C.S. Cell shape, cytoskeletal tension, and RhoA regulate stem cell lineage commitment. Dev. Cell. 2004;6:483–495. doi: 10.1016/s1534-5807(04)00075-9. [DOI] [PubMed] [Google Scholar]
- 12.Tee S.Y., Fu J., Janmey P.A. Cell shape and substrate rigidity both regulate cell stiffness. Biophys. J. 2011;100:L25–L27. doi: 10.1016/j.bpj.2010.12.3744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen B., Kumar G., Ho C.C. Geometric control of cell migration. Sci. Rep. 2013;3:2827. doi: 10.1038/srep02827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wan L.Q., Kang S.M., Vunjak-Novakovic G. Geometric control of human stem cell morphology and differentiation. Integr. Biol. (Camb.) 2010;2:346–353. doi: 10.1039/c0ib00016g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nelson C.M., Jean R.P., Chen C.S. Emergent patterns of growth controlled by multicellular form and mechanics. Proc. Natl. Acad. Sci. USA. 2005;102:11594–11599. doi: 10.1073/pnas.0502575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ruiz S.A., Chen C.S. Emergence of patterned stem cell differentiation within multicellular structures. Stem Cells. 2008;26:2921–2927. doi: 10.1634/stemcells.2008-0432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Luo W., Jones S.R., Yousaf M.N. Geometric control of stem cell differentiation rate on surfaces. Langmuir. 2008;24:12129–12133. doi: 10.1021/la802836g. [DOI] [PubMed] [Google Scholar]
- 18.Wan L.Q., Ronaldson K., Vunjak-Novakovic G. Micropatterned mammalian cells exhibit phenotype-specific left-right asymmetry. Proc. Natl. Acad. Sci. USA. 2011;108:12295–12300. doi: 10.1073/pnas.1103834108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ghibaudo M., Saez A., Ladoux B. Traction forces and rigidity sensing regulate cell functions. Soft Matter. 2008;4:1836–1843. [Google Scholar]
- 20.Saez A., Buguin A., Ladoux B. Is the mechanical activity of epithelial cells controlled by deformations or forces? Biophys. J. 2005;89:L52–L54. doi: 10.1529/biophysj.105.071217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Weng S., Fu J. Synergistic regulation of cell function by matrix rigidity and adhesive pattern. Biomaterials. 2011;32:9584–9593. doi: 10.1016/j.biomaterials.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fu J., Wang Y.-K., Chen C.S. Mechanical regulation of cell function with geometrically modulated elastomeric substrates. Nat. Methods. 2010;7:733–736. doi: 10.1038/nmeth.1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Balaban N.Q., Schwarz U.S., Geiger B. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
- 24.Riveline D., Zamir E., Bershadsky A.D. Focal contacts as mechanosensors: externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J. Cell Biol. 2001;153:1175–1186. doi: 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tan J.L., Tien J., Chen C.S. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc. Natl. Acad. Sci. USA. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sen S., Engler A.J., Discher D.E. Matrix strains induced by cells: computing how far cells can feel. Cell. Mol. Bioeng. 2009;2:39–48. doi: 10.1007/s12195-009-0052-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mih J.D., Marinkovic A., Tschumperlin D.J. Matrix stiffness reverses the effect of actomyosin tension on cell proliferation. J. Cell Sci. 2012;125:5974–5983. doi: 10.1242/jcs.108886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Engler A.J., Sen S., Discher D.E. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 29.Saez A., Ghibaudo M., Ladoux B. Rigidity-driven growth and migration of epithelial cells on microstructured anisotropic substrates. Proc. Natl. Acad. Sci. USA. 2007;104:8281–8286. doi: 10.1073/pnas.0702259104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lo C.M., Wang H.B., Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Stroka K.M., Aranda-Espinoza H. Neutrophils display biphasic relationship between migration and substrate stiffness. Cell Motil. Cytoskeleton. 2009;66:328–341. doi: 10.1002/cm.20363. [DOI] [PubMed] [Google Scholar]
- 32.Peyton S.R., Putnam A.J. Extracellular matrix rigidity governs smooth muscle cell motility in a biphasic fashion. J. Cell. Physiol. 2005;204:198–209. doi: 10.1002/jcp.20274. [DOI] [PubMed] [Google Scholar]
- 33.Pathak A., Kumar S. Independent regulation of tumor cell migration by matrix stiffness and confinement. Proc. Natl. Acad. Sci. USA. 2012;109:10334–10339. doi: 10.1073/pnas.1118073109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhong Y., He S., Ji B. Mechanics in mechanosensitivity of cell adhesion and its roles in cell migration. Int. J. Comput. Mater. Sci. Eng. 2012;1:1250032. [Google Scholar]
- 35.Zhong Y., Ji B. Impact of cell shape on cell migration behavior on elastic substrate. Biofabrication. 2013;5:015011. doi: 10.1088/1758-5082/5/1/015011. [DOI] [PubMed] [Google Scholar]
- 36.Zhong Y., Ji B. How do cells produce and regulate the driving force in the process of migration? Eur. Phys. J. Spec. Top. 2014;223:1373–1390. [Google Scholar]
- 37.Ng M.R., Besser A., Brugge J.S. Substrate stiffness regulates cadherin-dependent collective migration through myosin-II contractility. J. Cell Biol. 2012;199:545–563. doi: 10.1083/jcb.201207148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ma H., Hyun J., Chilkoti A. Fabrication of biofunctionalized quasi-three-dimensional microstructures of a nonfouling comb polymer using soft lithography. Adv. Funct. Mater. 2005;15:529–540. [Google Scholar]
- 39.Dembo M., Wang Y.L. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Butler J.P., Tolić-Nørrelykke I.M., Fredberg J.J. Traction fields, moments, and strain energy that cells exert on their surroundings. Am. J. Physiol. Cell Physiol. 2002;282:C595–C605. doi: 10.1152/ajpcell.00270.2001. [DOI] [PubMed] [Google Scholar]
- 41.Tambe D.T., Hardin C.C., Trepat X. Collective cell guidance by cooperative intercellular forces. Nat. Mater. 2011;10:469–475. doi: 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Serra-Picamal X., Conte V., Trepat X. Mechanical waves during tissue expansion. Nat. Phys. 2012;8:628–634. [Google Scholar]
- 43.Zhong Y., Kong D., Ji B. Frequency-dependent focal adhesion instability and cell reorientation under cyclic substrate stretching. Cell. Mol. Bioeng. 2011;4:442–456. [Google Scholar]
- 44.Deguchi S., Ohashi T., Sato M. Tensile properties of single stress fibers isolated from cultured vascular smooth muscle cells. J. Biomech. 2006;39:2603–2610. doi: 10.1016/j.jbiomech.2005.08.026. [DOI] [PubMed] [Google Scholar]
- 45.Lu L., Feng Y., Yin F.C.P. Actin stress fiber pre-extension in human aortic endothelial cells. Cell Motil. Cytoskeleton. 2008;65:281–294. doi: 10.1002/cm.20260. [DOI] [PubMed] [Google Scholar]
- 46.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 47.Schwarz U.S., Erdmann T., Bischofs I.B. Focal adhesions as mechanosensors: the two-spring model. Biosystems. 2006;83:225–232. doi: 10.1016/j.biosystems.2005.05.019. [DOI] [PubMed] [Google Scholar]
- 48.Kendall K. The adhesion and surface energy of elastic solids. J. Phys. D Appl. Phys. 1971;4:1186. [Google Scholar]
- 49.Trepat X., Wasserman M.R., Fredberg J.J. Physical forces during collective cell migration. Nat. Phys. 2009;5:426–430. [Google Scholar]
- 50.He S., Su Y., Gao H. Some basic questions on mechanosensing in cell–substrate interaction. J. Mech. Phys. Solids. 2014;70:116–135. [Google Scholar]
- 51.Tsutsumimoto T., Kawasaki S., Takaoka K. TNF-α and IL-1β suppress N-cadherin expression in MC3T3-E1 cells. J. Bone Miner. Res. 1999;14:1751–1760. doi: 10.1359/jbmr.1999.14.10.1751. [DOI] [PubMed] [Google Scholar]
- 52.Théry M. Micropatterning as a tool to decipher cell morphogenesis and functions. J. Cell Sci. 2010;123:4201–4213. doi: 10.1242/jcs.075150. [DOI] [PubMed] [Google Scholar]
- 53.De R., Zemel A., Safran S.A. Dynamics of cell orientation. Nat. Phys. 2007;3:655–659. [Google Scholar]
- 54.Bischofs I.B., Schwarz U.S. Cell organization in soft media due to active mechanosensing. Proc. Natl. Acad. Sci. USA. 2003;100:9274–9279. doi: 10.1073/pnas.1233544100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Trepat X., Fredberg J.J. Plithotaxis and emergent dynamics in collective cellular migration. Trends Cell Biol. 2011;21:638–646. doi: 10.1016/j.tcb.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Mertz A.F., Banerjee S., Dufresne E.R. Scaling of traction forces with the size of cohesive cell colonies. Phys. Rev. Lett. 2012;108:198101. doi: 10.1103/PhysRevLett.108.198101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Reinhart-King C.A., Dembo M., Hammer D.A. Cell-cell mechanical communication through compliant substrates. Biophys. J. 2008;95:6044–6051. doi: 10.1529/biophysj.107.127662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Guo W.H., Frey M.T., Wang Y.L. Substrate rigidity regulates the formation and maintenance of tissues. Biophys. J. 2006;90:2213–2220. doi: 10.1529/biophysj.105.070144. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.