Abstract
The behavior of the well-characterized nematode, Caenorhabditis elegans (C. elegans), is often used to study the neurologic control of sensory and motor systems in models of health and neurodegenerative disease. To advance the quantification of behaviors to match the progress made in the breakthroughs of genetics, RNA, proteins, and neuronal circuitry, analysis must be able to extract subtle changes in worm locomotion across a population. The analysis of worm crawling motion is complex due to self-overlap, coiling, and entanglement. Using current techniques, the scope of the analysis is typically restricted to worms to their non-occluded, uncoiled state which is incomplete and fundamentally biased. Using a model describing the worm shape and crawling motion, we designed a deformable shape estimation algorithm that is robust to coiling and entanglement. This model-based shape estimation algorithm has been incorporated into a framework where multiple worms can be automatically detected and tracked simultaneously throughout the entire video sequence, thereby increasing throughput as well as data validity. The newly developed algorithms were validated against 10 manually labeled datasets obtained from video sequences comprised of various image resolutions and video frame rates. The data presented demonstrate that tracking methods incorporated in WormLab enable stable and accurate detection of these worms through coiling and entanglement. Such challenging tracking scenarios are common occurrences during normal worm locomotion. The ability for the described approach to provide stable and accurate detection of C. elegans is critical to achieve unbiased locomotory analysis of worm motion.
Keywords: C. elegans, deformable shape registration, image analysis, multi-object tracking, WormLab
Abbreviations
- NGM
nematode growth medium
- FP
false positive
- FN
false negative
Introduction
Caenorhabditis elegans (C. elegans) is a free-living, semi-transparent soil nematode that is widely used as a model organism in the fields of genetics, animal development, and neurobiology. C. elegans are fecund and have a rapid life-cycle (3.5 d from egg to adulthood). In addition, self-fertilizing hermaphrodites create homozygous progeny. From an experimental perspective, the small size (1 mm) and transparency of this organism makes it ideal for microscopy-based analysis. The worms are easy and inexpensive to maintain. In addition, this species is ideally suited to forward and reverse genetic approaches that have elucidated the entire genome1 and complete cell lineage,2,3 including the position and synaptic connectivity of all neurons.4 The locomotion patterns of C. elegans can be impacted by a variety of factors. Numerous studies have shown that locomotion analysis provides extremely useful insight into how environmental factors 5,6 and genetic factors 7-12 affect behavior. Subtle changes in locomotion patterns must be isolated through statistical analysis of worm motion,13,14 which requires a large number of replicate screens, each consisting of the visual observation of worms over a period of time. The large number of observations required argues for automated, high throughput tracking of C. elegans from time-lapse video sequences.
From a computer vision perspective, reliable detection of nematodes can be a very challenging task as illustrated in Figure 1. Standard shape descriptors and simple motion models cannot be applied to the detection of nematodes because their shape lacks usable contour features and their motion patterns are non-rigid and very complex (e.g., omega bending and coiling). Additionally, common imaging artifacts and clutter found on nematode growth medium (NGM) plates further complicate the process.
Figure 1.
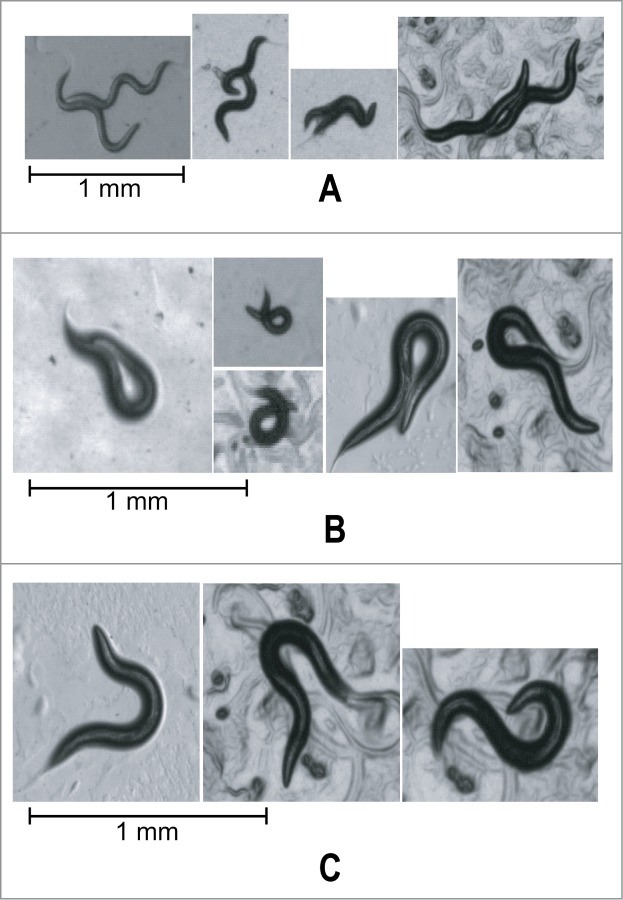
Illustrative images of C. elegans on nematode growth medium (NGM) plates in challenging tracking scenarios: (A) interaction between 2 worms, (B) coiling with self occlusion of the worm contour, (C) high amplitude bending. Challenging scenes such as these are common occurrences during normal worm locomotion. Stable and accurate detection of worms at different maturation states through such scenarios is critical to achieve reliable and automated multi-worm tracking.
C. elegans are morphologically complex organisms and have been the subject of many studies aimed at quantifying their morphological and locomotory properties. In early attempts, videos featuring C. elegans worms were analyzed and detected as connected regions after image thresholding.15,16 During tracking, the position of each worm was searched for within a neighborhood of its position in the previous video frame. The algorithm handled collisions—when 2 worms touch one another—by abandoning both tracks. This approach was used in several worm tracker systems and applied in a number of studies focusing on locomotory phenotypes of C. elegans.15,17
The aforementioned tracking strategies focused only on worm position, leaving out critical shape characteristics such as length, thickness, and posture. In later publications by several authors, worm shapes were extracted from a binary image generated through thresholding, refined using morphological operations, and skeletonized to define the worm spinal axis (centerline).14,18-22 This additional information allowed the behavioral characterization of the worms.
With these tracking approaches, here denoted as “basic detection,” tracking repeats the segmentation for every video frame without taking into account any relation of the results in successive frames. These approaches fail when multiple worms interact with one another or when one worm exhibits complex posture with significant self-overlap (coiling) because these conformations are not handled by classical thinning methods used to extract the worm centerline.23
Recently, edge linking strategies have been successfully applied to separate homogeneous populations of overlapping C. elegans worms in a fluidic environment.24,25 These approaches are based on skeleton analysis and require worm populations of homogeneous size to be effective. In addition, disambiguation is only possible for a limited range of overlap patterns due to the nature of the skeletonization operator. An approach used by Huang et al. employs a worm model of 6 articulated rectangular elements.26,27 Each element accepts a limited number of discrete angular orientations, and model estimation is done through dynamic programming. However, this model is overly simplistic and does not reflect realistic locomotion patterns of freely moving worms. In addition, the relative coarseness of the model will impair measurement precision and impact negatively on critical tasks such as head detection. None of the previous methods are robust to the wide variety of morphology and locomotion in extended observations of C. elegans. Complex behaviors such as frequency of coiling are defining characteristic of many C. elegans strains, for example genotypes such unc-32, unc-34 and unc-17 are defined as “severe coilers” in literature.28 Limiting the locomotion analysis of worms to their non-occluded, uncoiled state is incomplete and fundamentally biased. Thus, new models that specifically address worm interaction and overlap are needed to advance research in this field.
Our goal is to create a novel tracking algorithm that is robust to worm interaction and overlap to address this need. To that end, we reviewed the existing worm tracking systems capable of both detection and tracking of multiple worms within a field of view. We found that the overwhelming majority of tracking systems29-31 currently available do not support tracking through occlusion, coiling, or entanglement. These systems rely on a “basic detection” approach where binary images are generated through thresholding, and skeletonised using morphological thinning methods to define the worm spinal axis. This approach has been used extensively in past biological studies and can be considered classical.32 For example, in Tracker 3.0,29 tracking is limited to only one worm at a time and relies exclusively on a standard worm detection algorithm. As a result, the system drops a track as soon as occlusion occurs. A more recent tracking system14 allows the tracking of multiple worms within the field of view, but because this system relies on detection-based tracking, it does not handle coiling or entanglement either.
The focus of this paper is to demonstrate how our shape registration algorithm can successfully be used to track adult C. elegans worm through coiling, interaction with other worms, and in a cluttered environment. A direct comparison between our work and published tracking systems not designed to address occlusions would not be informative. Instead, a tracking system utilizing a variant of the “basic detection” algorithm was implemented and its output was compared to WormLab. In addition, we evaluated the performance of WormLab against the tracking system developed as part of our previous work, here denoted as Roussel 2007.34 We define robustness – the likelihood of successful detection of the worm – and accuracy – the quality of the worm outline – to quantify the performance of these systems.
This paper presents a sophisticated model-based approach for the simultaneous tracking of multiple worms in a manner that is both efficient and robust to occlusions. This approach furthers our previous work33,34 and incorporates formalisms from Fontaine et al.35,36 to create a framework for the automated detection, tracking, and quantification of C. elegans shape and motion. Our focus is to demonstrate the effectiveness of our model-based shape registration specifically when tracking C. elegans worms through coiling, entanglement, and in a cluttered environment.
Mathematical modeling of worm anatomy and worm dynamics
The geometric model
Following recent approaches, the worm centerline is modeled as a parametric curve, , represented by a function of centerline's length, where is the distance along the centerline from the midpoint of the worm.33-36 The parameter is normalized over the range such that is the midpoint position of the detected worm shape, its tail, and its head. The bending angle along the centerline is similarly defined and modeled using a third order periodic B-spline basis composed of a default number of splines (1).
| (1) |
The relevance of such a curvature representation of the worm centerline to model and analyze worm crawling movement has been confirmed by a more recent study by Padmanabhan et al.37 The worm width profile is defined as a continuous function for the localized radius as a function of distance along its length. It is similarly parameterized using a third order periodic B-spline basis with splines (2).
| (2) |
The worm model is a 2-dimensional surface defined around the centerline curve. Roussel demonstrated that points within the worm body can conveniently be cast into the Frenet frame 38 of coordinate where is the point along the worm centerline, the curve tangent vector and the curve normal vector (Fig. 2A).39,40 Each point of the worm surface can be located using the curvilinear coordinates where is the normalized distance along the worm central axis and is the radial distance from the centerline. We express the Cartesian coordinates of a point within a worm body as
| (3) |
where is the overall length of the worm, M(0) its midpoint position,
| (4) |
Figure 2.
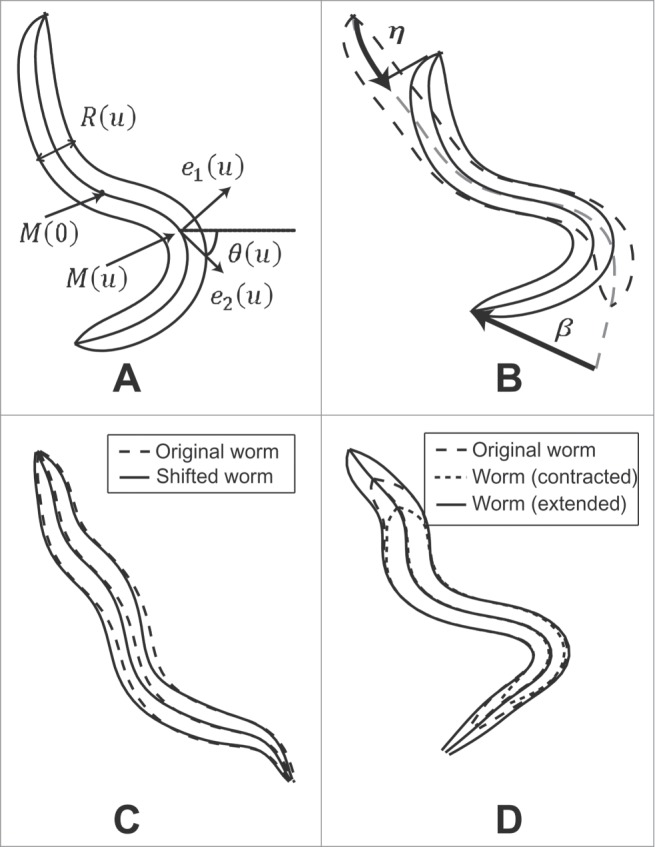
Illustration of the geometric and motion model for C .elegans: (A) Illustration of the notations used to define the worm centerline and width profile. (B) The worm crawling motion model can be characterized by a peristaltic progression factor along the worm central axis and deformation . (C) Illustration of the radial displacement of the midpoint. (D) Illustration of the contraction/extension operator.
In the earlier publications on C. elegans tracking listed earlier, the natural variation of the worm length occurring during peristaltic progression was considered negligible.34,35 Fontaine and colleagues 36 briefly present, without applying it experimentally, how their model could be modified to allow for elongations and contractions via a “rate of length function” () augmenting the generative model in (3) to
This approach, however, does not model the natural variation in length of the worm body in a viscous environment. Because the bending angle and length function are coupled, changing one function has an adverse effect on the position of the outline.
In this paper, we model worm length elasticity in a manner that more closely resembles the natural worm crawling movements by decoupling the length and bending angle functions. We introduce an elasticity factor to the generative model (3), which acts as a length multiplier (Fig. 2D). An elasticity factor greater than one increases worm length, while a factor less than one decreases it. The final generative model becomes
| (5) |
The advantage of this formalism is that it only influences the worm outline at its extremities which is consistent with the peristaltic movements of nematodes in a viscous environment. This formalism requires the bend angle function to be defined outside its original support as if and if . The model thus becomes parameterized by a state vector containing the midpoint position, length , bending parameters , width parameters , and elasticity factor .
The motion model
Fontaine et al. and Roussel et al. each have previously demonstrated that the natural crawling motion of worms in a viscous environment can be characterized by a peristaltic progression factor along the worm axis and a deformation of the curvature of the worm.33-36 In a previous publication, Roussel et al defined crawling as a combination of peristaltic progression and radial displacement. In this paper, crawling is modeled as peristaltic progression and change of the angle model parameters. This new approach is more powerful because it enables modeling large changes in bending angle and therefore supports image sequences acquired at low frame rates.
The equations of motion illustrated in Figure 2B calculate the predicted state vector after the worm has undergone a peristaltic progression, and deformation, . We added the elasticity factor, to Fontaine's original state prediction equation introduced in the previous section.
| (6) |
where is the matrix of B-spline bases evaluated at sampled grid points in .
One critical weakness in this motion model is that it does not allow any degree of freedom at the midpoint located at position. While displacement of the worm midpoint is usually negligible from one frame to the next, during long-term tracking positioning error accumulates at the worm midpoint, as illustrated in Figure 3, and can result in detection and tracking failure. In order to ensure long-term tracking stability, an additional degree of freedom illustrated in Figure 2C was added to the motion model,
| (7) |
Figure 3.
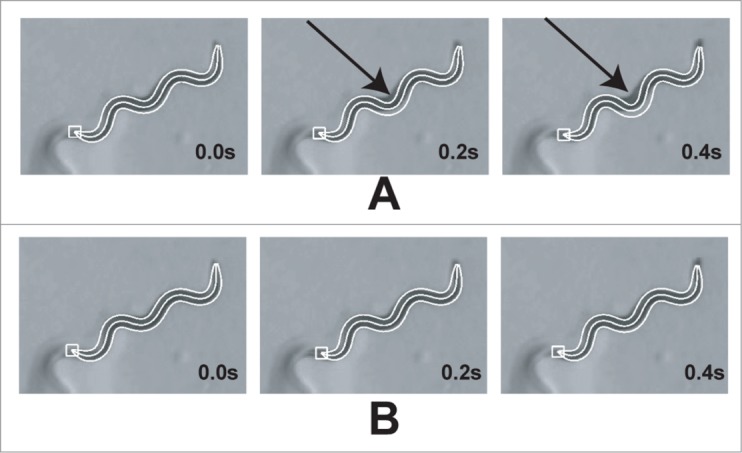
The effect of cumulative positioning error at the worm midpoint. (A) When radial midpoint shift deformation is disabled from the fitting algorithm, cumulative error shown with an arrow tends to aggregate at the midpoint of the worm. (B) Adding radial midpoint shift deformation to the deformation model allows the fitting algorithm to compensate for this error and produces a stable tracking output. This deformation operator is critical for long term tracking stability.
This radial shift of the midpoint of the worm must be compensated for by a local change of the worm curvature localized at the worm mid-section :
| (8) |
Incorporating the radial shift of the midpoint and curvature correction into our motion model, our equation of motion becomes:
| (9) |
Motion estimation
In this section, we describe how the model parameters are estimated based on measurement from the image. Model estimation approaches can be separated into feature-based and region-based approaches. Our research focuses on a region-based model estimation algorithm inspired from our earlier work.33 The worm surface is modeled as a piecewise-constant Mumford–Shah model40 and we use a curve evolution formalism inspired by Chan and Vese41 to fit the model to the image data. Model estimation is defined as a deformable shape fitting process using a deformable template formalism. The geometric template here is the worm contour recorded at the previous frame and characterized by the contour points . In the context of worm tracking, the worm structure to be estimated in the current video frame is considered a deformed version of this template. The new object structure is thus captured by the deformation parameters .
Let denote the grayscale image on a domain . We define the region of space occupied by the worm object from the previous frame to which the deformation parameters have been applied, we define the region outside . Fitting the region-based active contour model as defined in the previous section can be seen as an optimization process where a quantity is minimized with respect to the deformation parameter and appearance.
| (10) |
For deformation parameters , the optimal appearance levels are estimated as the average pixel intensity within their respective spatial supports and .
Given known intensity values , the problem is to estimate the shape deformation parameter that minimizes the objective function. Minimizing the objective function is performed by gradient descent requiring the gradient of with respect to the deformation parameters . Using classical integral calculus42 the derivative can be expressed in the form of an integral over the contour around the worm region as:
| (11) |
where is the unit normal associated with the contour . This provides the basic tools for fitting deformable worm templates. We use the fitting forces in conjunction with an iterative gradient search optimization approach to fit the worm templates to the image data. If the Chan and Vese energy functional is applied to a binary image, the mean intensity values and are known quantities (1 and 0, respectively) and need not be estimated. Our motion estimation algorithm does not differentiate between moving and static worms. A paralyzed worm will have measured deformation parameters of amplitude zero.
Occlusion
Limited overlap between worms or self-occlusion within a single worm are very common occurances and explain in part why tracking C. elegans worms can be such a challenging task. Fontaine et al.35,36 describe a feature-based algorithm inspired by Blake et al.43,44 in which the model is matched to contour-based features extracted from a binary image. When a contour point cannot be matched to any detected contour, it is marked as occluded and excluded from the fitting process.
In contrast, we modify equation (11) by limiting the integral over the object contour to the portion of the contour that does not overlap with other worms. At each fitting iteration we compute an initial fitting force assuming that the entire model is visible, then determine which portion of the worm contour is occluded, and finally recompute an updated fitting force.
Multiple hypotheses tracking
In highly cluttered environments, tracking systems can suffer from frequent mis-associations.45 We previously demonstrated that a multiple hypotheses tracking approach can be successfully incorporated into a chain of recursive estimations of the worm shape to greatly improve tracking performance in cluttered environments.33,34 During the fitting process, it is very common for several hypotheses to converge toward the same worm position and shape, making these hypotheses redundant. To adress this redundancy issue and to keep the number of tracked hypotheses to a manageable number, we added an advanced hypotheses management system, where redundant hypotheses are detected then discarded using a deterministic hyerarchical clustering algorithm.46 Only representatives of the4 fittest clusters are retained.
Detection and tracking system
We present the detection and tracking framework developed for WormLab (MBF Bioscience, Williston, VT), software for analyzing the locomotion of C. elegans. The software maintains the successive position of each worm in the field of view. As a new frame is analyzed, it cycles through the active worm tracks and tries to estimate the worm structure for each of them. Estimated worms denoted as observations which are then assigned to their corresponding track (denoted hereafter as observation to track association). The tracking process can be performed backward, which allows worms with no predecessor—those suddenly appearing in the field of view—to be tracked backward in time. The tracking system provides the user with various image processing operators to maximize worm contrast, compensate for illumination irregularities and obtain a clean binary image. These operators include greyscale closing to eliminate background gradient,47 gaussian smoothing and binary closing to clean up holes inside the worm body.48 Optimal Image processing is highly dependent on the experimental condition and beyond the scope of this paper. For the purpose of the study presented here, all video sequences are well contrasted, have uniform illumination and are in focus. Plate and stage remain at a fixed position at all time during video recording.
Figure 4 outlines the major components of the tracking framework:
Figure 4.
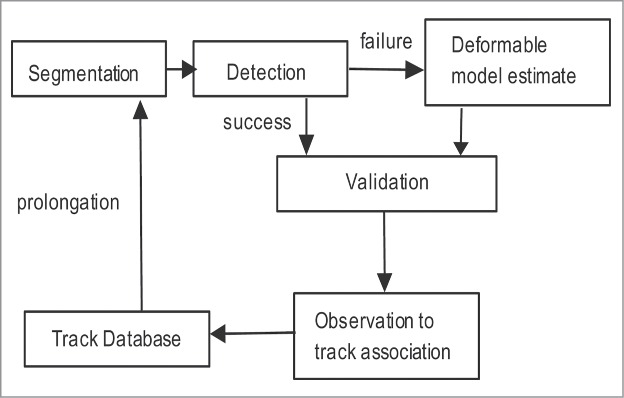
Illustration of the detection and tracking framework developed for the novel C. elegans tracking software presented here. Estimation of worm position and shape is done with a combination of a detection process, deformable model estimate, and an observation to track fusion module.
Detection
The tracking algorithms require initial detection of the worms. We used the approach described in,34 which assumes that the intensity of pixels that belong to the worm follow a different distribution than those belonging to the background agar (i.e. darker worm on lighter background or lighter worm on darker background). The detection algorithm relies on measuring 2 points of high curvature from a closed planar B-spline curve fit to the object contour to automatically estimate the initial center line of the worm object.49 This approach is straightforward and robust; it can be used for initial object detection and long-term tracking in situations when the worm is isolated and uncoiled.
Deformable model estimate
When worm coiling, entanglement, or the presence of background artifacts prevents direct detection of the worm, we use the deformable shape registration. In this case a deformable model estimation algorithm is used to fit the geometric model from the previous frame to the current image.
Observation to track association
Observation to track fusion is achieved using a combined shape filtering (gating) and Multiple Hypothesis data association. Shape filtering (gating) eliminates very unlikely observation to track pairs and/or perform a focused detection on a restricted region of space.
At present, WormLab is not a real-time tracker, processing time largely depends on the number of tracked animals as well as the complexity of the tracking scenario. Typically,10 Wild-Type (N2) C. elegans evolving in a relatively clean agar plate can be processed at an average of 7–10 frames per second but background artifacts, frequent coiling or interactions will have a negative impact on processing speed.
Material and methods
We demonstrate our tracking algorithm on 10 video sequences of wild-type (N2) adult C. elegans nematodes residing on standard NGM, generously provided by Dr. Deborah Neher, University of Vermont, Burlington VT, Dr. Christoph Schmitz, Ludwig-Maximilians-Universität, Munich, Germany, and Randy D. Blakely, Vanderbilt University, Nashville TN. Our videos were acquired with the WormLab software using a purpose-built illumination stand (MBF Bioscience) equipped with a Nikon 60 mm Micro lens (Nikon Inc., Melville, NY, USA) and an AVT Stingray F-504B digital camera (Allied Vision Technologies GmbH, Stadtroda, Germany) connected to the host computer via Firewire/IEEE1394 interface. Video was captured at rates between 7 – 25 frames per second and saved as AVI files with MPEG-4 20:1 compression. The validation data set was compiled to encompass a wide range of imaging conditions with scaling between 0.63 to 4.46 μm/pixel, frame rate between 5 and 15 frame/s. All our videos are relatively short and did not exceed 500 frames (Table 1).
Table 1.
Tracking performance summary of WormLab.
| WormLab |
Roussel 2007 |
Basic Detection |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sequence Id | Worm Count | Frame Count | Frame rate | scaling | FP | FN | Error | FP | FN | Error | FP | FN | Error |
| 1 | 19 | 19 | 7.5 | 0.63 | 0 | 0 | 0.01 | 0 | 0 | 0.02 | 0 | 5 | 0.28 |
| 2 | 28 | 28 | 7.5 | 6 | 0 | 0 | 0.03 | 0 | 0 | 0.04 | 0 | 8 | 0.3 |
| 3 | 112 | 56 | 7.5 | 6 | 0 | 0 | 0.02 | 0 | 0 | 0.03 | 0 | 8 | 0.09 |
| 4 | 128 | 32 | 7.5 | 6 | 0 | 0 | 0.03 | 0 | 0 | 0.04 | 1 | 8 | 0.1 |
| 5 | 76 | 50 | 7.5 | 1.49 | 1 | 0 | 0.04 | 1 | 0 | 0.05 | 3 | 22 | 0.34 |
| 6 | 80 | 20 | 9 | 4.46 | 0 | 0 | 0.04 | 0 | 0 | 0.04 | 0 | 0 | 0.04 |
| 7 | 159 | 40 | 7 | 4.46 | 1 | 0 | 0.04 | 1 | 0 | 0.05 | 1 | 15 | 0.13 |
| 8 | 70 | 14 | 25 | 20 | 0 | 0 | 0.04 | 0 | 0 | 0.04 | 0 | 8 | 0.15 |
| 9 | 134 | 12 | 15 | 4.46 | 11 | 0 | 0.11 | 13 | 5 | 0.16 | 15 | 16 | 0.24 |
| 10 | 100 | 20 | 15 | 4.46 | 0 | 0 | 0.07 | 0 | 31 | 0.36 | 0 | 51 | 0.54 |
| TOTAL | 906 | 13 | 0 | 0.049 | 15 | 36 | 0.081 | 20 | 141 | 0.172 | |||
A set of image sequences are analyzed with WormLab then validated against manually labeled worms. False positive (FP), false negative (FN), average fitting error as a fraction of the worm length, frame rate (frame/s), scaling (μm / pixel),worm count (validated) and frame count (validated) are reported for each sequence. Our tracking system shows significant improvement in robustness and accuracy over both the basic detection and the Roussel 2007 tracking algorithms.
In order to quantify the performance of our automated worm tracking system, its output must be compared to ground truth data. In the simplest, most direct approach, a human observer manually labels the head, tail, midpoint and centerline points for each worm in the sequence. The result of this process is the ground truth against which multiple tracking algorithms can be compared. This approach is very labor intensive and the range of object features that can be generated by a user is limited.
As an alternative to exhaustive manual labeling of the entire dataset, we can process all the validation sequences using WormLab and then correct any detection and tracking errors to obtain an acceptable ground truth for the extensive range of worm metrics available within WormLab. Similar validation approaches have been used previously to quantify the performance of a detection process.50 The rich validation data set would allow the quantification of tracking system performance broken down by worm geometry (length, length-to-width ratio, etc.), conformation (coiling angle, self-overlap, etc.) or interaction scenario (overlap with other worms). There are drawbacks to using this approach, however, because the edit-based ground truth is biased in favor of the software used to generate the initial detection data. Small sub-pixel detection errors are likely to be ignored by the user, thus artificially increasing the average detection accuracy for this system. Ground truth datasets obtained by editing the output of WormLab are only acceptable to quantify the detection rate (i.e., false positive, false negative) of the tracking software. They should not be used to quantify the accuracy of this worm tracker.
To address this shortcoming, we adopted a hybrid validation approach combining classical and edit-based validation. We perform a 3-step process to generate the ground truth: (i) the image sequence is processed using WormLab, (ii) the result is edited using the WormLab editing tools, (iii) finally, the user manually marks the location of the head and tail extremities for each worm present in the sequence. These manually labeled markers will be used to estimate the system accuracy.
Even in our short videos the detected worm objects can number in the thousands. To manually label each of these instances of a worm at every frame would be extremely labor intensive. To avoid this problem, we took advantage of the inherent redundancy of the tracking data set and manually validated a subset of the video frames taken at a one second interval.
This validation protocol was used to evaluate the performance of WormLab against the tracking system developed as part of our previous work33 and a “basic detection” method that is our approximation of the typical approach used in many worm trackers.14,18-22 With this method, shapes are extracted from a binary image generated through thresholding and refined using a closing morphological operation. The extremities of the worm are detected as points of high curvature from the worm contour. The worm spinal axis is finally extracted using a skeletonization operator. This “Basic detection” technique is very similar to the detection algorithm implemented in WormLab. The main difference is that WormLab can use a deformable model estimation technique as an alternative when detection fails due to coiling, entanglement or imaging clutter.
Results
The tracking system described in this paper provides excellent tracking results. Figures 5–7 provide a visual indication of the system performance; it shows that our model provides stable tracking output even in complex tracking environment such as coiling or entanglement. Figures 6–7 illustrate the result of tracking worms through coiling. In Figure 6 the worm starts in a complex coiled conformation (s) and initially cannot be detected, when it uncoils (s), the worm is detected and tracked backward through coiling.
Figure 5.
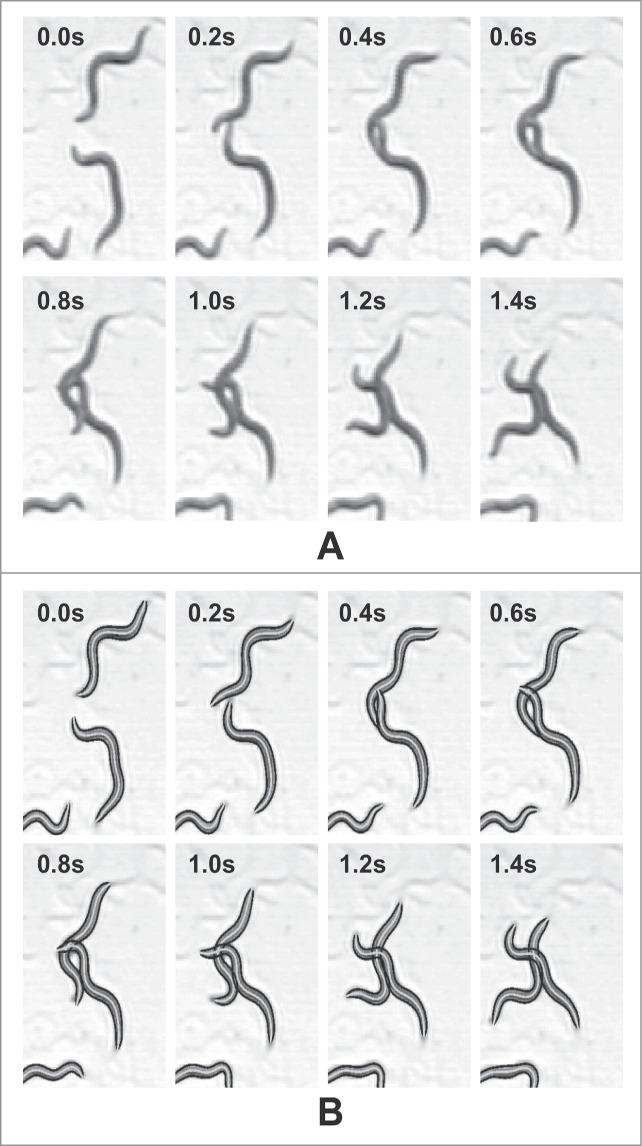
Illustration of the tracking output for 2 worms through entanglement: (A) original images (B) tracking result overlaid on the original images.
Figure 6.

Illustration of the tracking output for a worm undergoing coiling (self-overlap): (A) original images (B) tracking result overlaid on the original images. When the analysis starts, the worm is in coiled configuration and cannot be detected. The tracking algorithm can detect the worm when it uncoils and track the worm backward in time using our shape registration algorithm.
Figure 7.
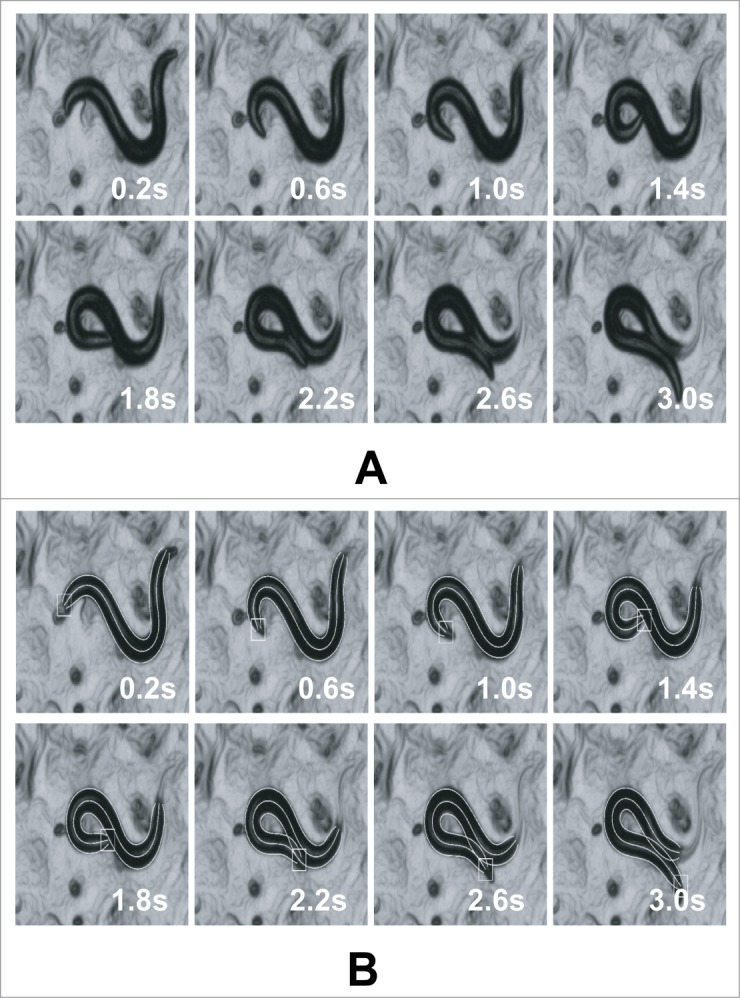
Illustration of the tracking output for a worm undergoing coiling (self-overlap): (A) original images (B) tracking result overlaid on the original images. The tracking process is made more challenging due to the presence of food and eggs clutter. Precise position and conformation of the worm can be measured using our shape registration algorithm.
Validation data in Table 1 is represented as the percentages of false positive and false negative identifications. A false positive identification is an automatically generated worm structure that cannot be matched by a manually generated one across all images in the video sequence. False positives are typically due to background artifacts mistakenly identified as worms. Conversely, a false negative identification is a manually marked worm that is not automatically detected in the image of the video sequence.
The error between automatically and manually detected worms is estimated as the average absolute distance between their respective extremities. In the case of false negatives, when the tracking algorithm fails to detect a worm, we set the error to half the length of the missed worm. In order to be able to compare detection accuracy between worms of various sizes, the error is normalized and expressed as a percentage of worm length. The results of our validation are presented in Table 1.
Across all validation sequences, a total of 906 worms have been labeled with a false positive rate of 1.4%, a false negative rate of 0.0%, and a normalized detection error of 4.9%. One of the difficulties with validating the software is that performance is highly dependent on the complexity of the tracking scenario, such as coiling or interaction with other worms. For example, most of the error reported in Table 1 is from the sequences 9 and 10 where worms are coiling extensively. WormLab uses detection-based tracking whenever possible, i.e., when the worm is uncoiled and un-occluded. In sequences where C. elegans crawl on clean uncluttered plates with no coiling or interaction, we expect the tracking results for any detection-based system to be quite good. In sequence 6 where worms remain in unoccluded, uncoiled state the performance of the 3 tracking algorithms are virtually identical. In order to provide a fair assessment of the performance of our tracking system in difficult scenarios, we quantify the complexity of the tracking scene using the following complexity metrics: A the width of the worm in pixels to estimate optical resolution, B overlap as the proportion of the worm contour that is occluded by itself, other worms, or a background artifact, C the degree of coiling defined as the angle formed by the head, midpoint and tail locations. Using these complexity metrics, we focused our performance assessment on the more challenging tracking scenarios and performed meaningful comparisons between tracking systems. We evaluated the performance of WormLab against (A) the tracking system developed as part of our previous work33 and (B) a standard detection based tracking algorithm, “basic detection”.20,29 The result of this performance analysis is shown in Figure 8.
Figure 8.
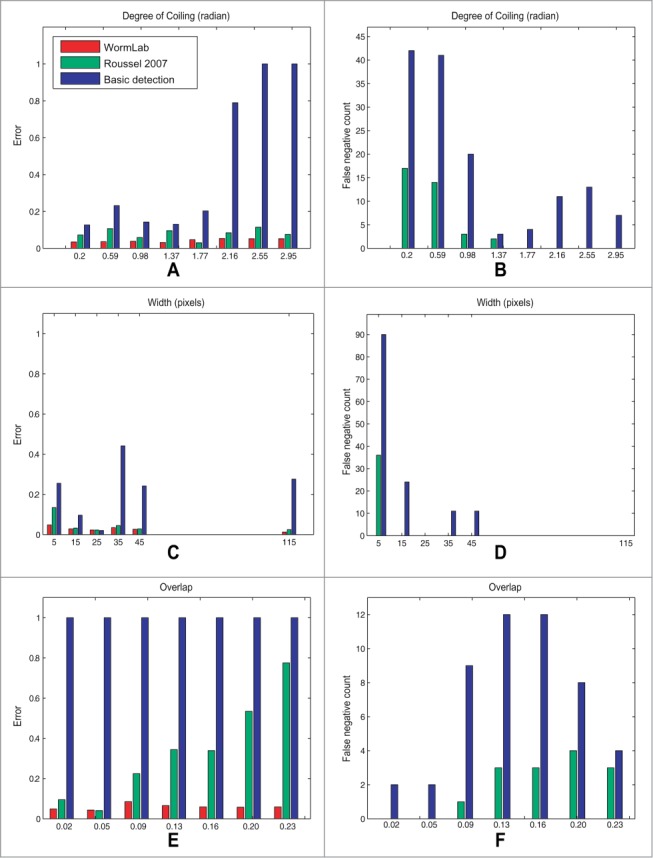
Normalized detection error and false negative count as a function of scene complexity metrics. The left column shows that the detection error tends to increase with scene complexity that we measure with: (A) degree of coiling; (C) worm width (in pixels) and (E) overlap. On the right, the evolution of the false negative count is similar, it tends to increase with scene complexity that we measure with: (B) degree of coiling; (D) worm width (in pixels) and (F) overlap. It consistently outperforms Roussel 200734,35 and the standard “basic detection” tracking algorithm. During validation, the WormLab tracking system did not return a single false negative detection error.
Discussion
In this paper we have validated this approach by evaluating the performance of our tracking system qualitatively and quantitatively. Using complexity metrics, we focused our performance assessment on the more challenging tracking scenarios to perform meaningful performance assessments. When the complexity of the tracking scenario increases the tracking performance and accuracy is expected to diminish. On the performance analysis shown on Figure 8, the 3 systems under consideration exhibit similar tracking accuracy in scenarios with low complexity, such as large worm width, low occlusion, and small degree of coiling. When the complexity of the scenario increases, however, the accuracy of the tracking system in WormLab barely diminishes and WormLab consistently outperforms the 2 other tracking algorithms by a significant margin.
The relatively poor performance of detection-based systems shown in Figure 8 can be explained by the fact that these systems rely exclusively on a standard worm detection algorithm based on a classical thinning method to extract the worm centerline. These systems do not handle coiling or entanglement and are expected to drop a track as soon as occlusion occurs.
Factors that contribute to higher detection error include: clutter, overlap (plate density), and low resolution. When subtle body deformations need to be quantified, the detection error can be significantly reduced by using clean, low density plates acquired at high resolution and/or high magnification.
We addressed the problem of tracking multiple C. elegans worms in a manner that is efficient and robust to entanglement and coiling. A modeling approach for the shape and motion of the C. elegans body was successfully applied to the tracking of multiple worms observed in time-lapse video data. Many of the weaknesses identified in our previous tracking algorithm33 have been addressed, notably the inability to identify individual worms in an entangled cluster at the first frame. Our tracking algorithm can now detect the worm when it becomes un-occluded and track the worm backward in time using our shape registration algorithm. Another issue identified in our previous algorithm was the loss of accuracy when tracking worms in coiled state. By incorporating occlusion information into our new model estimation approach we can now track worms in all but the most complex occlusion scenarios without any noticeable loss of tracking robustness or accuracy. One noticeable weakness, inherent to our modeling approach, can be observed in instances of prolonged occlusion of 10 frames or longer for both worm extremities. This is typically the case in tail chase coiling behavior or when 2 worms adhere to one another. Further research is needed to improve tracking in these scenarios.
Additional degrees of freedom have been added to our initial motion model: the worm centerline is now extensible and can be adjusted allowing the capture of the subtle length variation occurring naturally in the crawling motion of worms and similar organisms. The addition of the radial shift of the midpoint to our deformation model has proven very beneficial for the tracking of worms over an extended duration. While our algorithms can back-track the worm to a position of entanglement, overall performance would benefit from the inclusion of an additional module to detect worms even in entangled state.
Our study is restricted to the tracking of adult C. elegans. Younger worms at the larvae stage are very challenging objects to track because of their low contrast and tendencies to adhere to adult worms causing occlusion of both their extremities. Practical tracking of C. elegans larvae should only be attempted on clean plates in the absence of adults.
The algorithms presented in this paper focus exclusively on the tracking of C. elegans worms through crawling motion, in the future, using alternative deformation pattern and equation of motion, we will expand the framework to different modes of worm locomotion such as swimming in fluid environments.
Disclosure of Potential Conflicts of Interest
No potential conflicts of interest were disclosed.
Acknowledgments
We thank Dr. Deborah A. Neher of the University of Vermont, Dr. Christoph Schmitz of Ludwig-Maximilians-Universität and Randy D. Blakely of the Vanderbilt University for the C. elegans biological material used in our study. We thank Drs. Ebraheem Fontaine and Brian Eastwood for helpful discussion.
Funding
This work was supported by the Small Business Innovation Research program of the National Institute of Environmental Health Sciences (Award 2R44 ES 017180).
References
- 1. The CeSC. Genome sequence of the nematode C. Elegans: a platform for investigating biology. Science 1998; 282:2012-8; PMID:9851916; http://dx.doi.org/ 10.1126/science.282.5396.2012 [DOI] [PubMed] [Google Scholar]
- 2. Sulston JE, Horvitz HR. Post-embryonic cell lineages of the nematode caenorhabditis elegans. Dev Biol 1977; 56:110-56; PMID:838129; http://dx.doi.org/ 10.1016/0012-1606(77)90158-0 [DOI] [PubMed] [Google Scholar]
- 3. Sulston JE, Schierenberg E, White JG, Thomson JN. The embryonic cell lineage of the nematode caenorhabditis elegans. Dev Biol 1983; 100:64-119; PMID:6684600; http://dx.doi.org/ 10.1016/0012-1606(83)90201-4 [DOI] [PubMed] [Google Scholar]
- 4. Jorgensen EM, Mango SE. The art and design of genetic screens: caenorhabditis elegans. Nat Rev Genet 2002; 3:356-69; PMID:11988761; http://dx.doi.org/ 10.1038/nrg794 [DOI] [PubMed] [Google Scholar]
- 5. Wang D, Xing X. Assessment of locomotion behavioral defects induced by acute toxicity from heavy metal exposure in nematode Caenorhabditis elegans. J Environ Sci (China) 2008; 20:1132-7; PMID:19143322; http://dx.doi.org/ 10.1016/S1001-0742(08)62160-9 [DOI] [PubMed] [Google Scholar]
- 6. Yu Z, Jiang L, Yin D. Behavior toxicity to Caenorhabditis elegans transferred to the progeny after exposure to sulfamethoxazole at environmentally relevant concentrations. J Environ Sci (China) 2011; 23:294-300; PMID:21517004; http://dx.doi.org/ 10.1016/S1001-0742(10)60436-6 [DOI] [PubMed] [Google Scholar]
- 7. Boender AJ, Roubos EW, van der Velde G. Together or alone?: foraging strategies in Caenorhabditis elegans. Biol Rev Cambr Philos Soc 2011; 86:853-62; PMID:21314888; http://dx.doi.org/ 10.1111/j.1469-185X.2011.00174.x [DOI] [PubMed] [Google Scholar]
- 8. Bono Md, Bargmann CI. Natural variation in a neuropeptide Y receptor homolog modifies social behavior and food response in C. elegans. Cell 1998; 94:679-89; PMID:9741632; http://dx.doi.org/ 10.1016/S0092-8674(00)81609-8 [DOI] [PubMed] [Google Scholar]
- 9. Hofler C, Koelle MR. AGS-3 alters Caenorhabditis elegans behavior after food deprivation via RIC-8 activation of the neural G protein G αo. J Neurosci: Off J Soc Neurosci 2011; 31:11553-62; PMID:21832186; http://dx.doi.org/ 10.1523/JNEUROSCI.2072-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Liu Y, LeBeouf B, Guo X, Correa PA, Gualberto DG, Lints R, Garcia LR. A cholinergic-regulated circuit coordinates the maintenance and Bi-stable states of a sensory-motor behavior during caenorhabditis elegans male copulation. PLoS Genet 2011; 7:e1001326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Sternberg SR. Biomedical image processing. Computer 1983; 16:22-34; http://dx.doi.org/ 10.1109/MC.1983.1654163 [DOI] [Google Scholar]
- 12. White JQ, Jorgensen EM. Sensation in a single neuron pair represses male behavior in hermaphrodites. Neuron 2012; 75:593-600; PMID:22920252; http://dx.doi.org/ 10.1016/j.neuron.2012.03.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Geng W, Cosman P, Baek JH, Berry C, Schafer WR. Quantitative classification and natural clustering of C. elegans behavioral phenotypes. Genetics 2003; 165:1117-36; PMID:14668369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Tsibidis GD, Tavernarakis N. Nemo: a computational tool for analyzing nematode locomotion. BMC Neurosci 2007; 8; PMID:17941975; http://dx.doi.org/ 10.1186/1471-2202-8-86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Dhawan R, Dusenbery DB, Williams PL. Comparison of lethality, reproduction, and behavior as toxicological endpoints in the nematode Caenorhabditis elegans. J Toxicol Environ Health Part A 1999; 58:451-62; PMID:10616193; http://dx.doi.org/ 10.1080/009841099157179 [DOI] [PubMed] [Google Scholar]
- 16. Soil DR, Kwang WJaJJ. The Use of Computers in Understanding How Animal Cells Crawl. International Review of Cytology: Academic Press, 1995:43-104. [PubMed] [Google Scholar]
- 17. de Bono M, Maricq AV. Neuronal substrates of complex behaviors in C. elegans. Ann Rev Neurosci 2005; 28:451-501; PMID:16022603; http://dx.doi.org/ 10.1146/annurev.neuro.27.070203.144259 [DOI] [PubMed] [Google Scholar]
- 18. Baek J, Cosman P, Feng Z, Silver J, Schafer WR. Using machine vision to analyze and classify C. elegans behavioral phenotypes quantitatively. J Neurosci Methods 2002; 118:9-21; PMID:12191753; http://dx.doi.org/ 10.1016/S0165-0270(02)00117-6 [DOI] [PubMed] [Google Scholar]
- 19. Cronin CJ, Mendel JE, Mukhtar S, Kim Y-M, Stirbl RC, Bruck J, Sternberg PW. An automated system for measuring parameters of nematode sinusoidal movement. BMC Genetics 2005; 6:5; PMID:15698479; http://dx.doi.org/ 10.1186/1471-2156-6-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Feng Z, Cronin CJ, Wittig JH, Sternberg PW, Schafer WR. An imaging system for standardized quantitative analysis of C. elegans behavior. BMC Bioinformatics 2004; 5:115; PMID:15331023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gonzalez RC, Woods RE. Digital Image Processing. Upper Saddle River, N.J: Prentice Hall, 2007. [Google Scholar]
- 22. Hoshi K, Shingai R. Computer-driven automatic identification of locomotion states in Caenorhabditis elegans. J Neurosci Methods 2006; 157:355-63; PMID:16750860 [DOI] [PubMed] [Google Scholar]
- 23. Zhang TY, Suen CY. A fast parallel algorithm for thinning digital patterns. Commun ACM 1984; 27:236-9; http://dx.doi.org/ 10.1145/357994.358023 [DOI] [Google Scholar]
- 24. Babaii Rizvandi N, Pizurica A, Rooms F, Philips W. Skeleton analysis of population images for detection of isolated and overlapped nematode C. elegans. 16th Eur Signal Proc Conf (EUSIPCO 2008) C3 - Eur Signal Proc Conf, 16th, Proc, 2008. [Google Scholar]
- 25. Rizvandi NB, Pizurica A, Philips W, Ochoa D. Edge linking based method to detect and separate individual C. Elegans worms in culture. Digital Image Comput: Tech Appl (DICTA), 2008, 2008:65-70. [Google Scholar]
- 26. Huang K-M, Cosman P, Schafer WR. Machine vision based detection of omega bends and reversals in C. elegans. J Neurosci Methods 2006; 158:323-36; PMID:16839609; http://dx.doi.org/ 10.1016/j.jneumeth.2006.06.007 [DOI] [PubMed] [Google Scholar]
- 27. Huang K-M, Cosman P, Schafer WR. Automated tracking of multiple C. Elegans with articulated models. 4th IEEE Int Symp Biomed Imaging: From Nano to Macro 2007. ISBI 2007, 2007:1240-3. [Google Scholar]
- 28. WormBase web site , http://www.wormbase.org", release WS241, date 20 Mar 2014. [Google Scholar]
- 29. Brown AEX, Yemini EI, Grundy LJ, Jucikas T, Schafer WR. A dictionary of behavioral motifs reveals clusters of genes affecting Caenorhabditis elegans locomotion. Proc Nat Acad Sci 2013; 110:791-6; PMID:23267063; http://dx.doi.org/ 10.1073/pnas.1211447110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Delta Informatika Z. Dvision [Google Scholar]
- 31. Ramot D., “Tracker” (Wormsense), [online] 2006, http:wormsense.stanford.edutracker (Accessed: 24 May 2006) 2006. [Google Scholar]
- 32. Husson SJ, Costa WS, Schmitt C, Gottschalk A. Keeping track of worm trackers. WormBook: The Online Rev of C Elegans Biol 2013; 1-17; PMID:23436808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Roussel N. A Computational Model for Caenorhabditis Elegans Locomotory Behavior: Application to Multi-Worm Tracking. Troy, NY, USA: Rensselaer Polytechnic Institute, 2007. [Google Scholar]
- 34. Roussel N, Morton CA, Finger FP, Roysam B. A computational model for C. elegans locomotory behavior: application to multiworm tracking. IEEE Transactions on Bio-Medical Eng 2007; 54:1786-97; PMID:17926677; http://dx.doi.org/ 10.1109/TBME.2007.894981 [DOI] [PubMed] [Google Scholar]
- 35. Fontaine E, Barr AH, Burdick JW. Tracking of multiple worms and fish for biological studies. [Google Scholar]
- 36. Fontaine E, Burdick J, Barr A. Automated tracking of multiple C. Elegans. Conf Proc: Ann Int Conf IEEE Eng Med Biol Soc IEEE Eng Med Biol Soc Conf 2006; 1:3716-9; PMID:17945791 [DOI] [PubMed] [Google Scholar]
- 37. Padmanabhan V, Khan ZS, Solomon DE, Armstrong A, Rumbaugh KP, Vanapalli SA, Blawzdziewicz J. Locomotion of C. elegans: a piecewise-harmonic curvature representation of nematode behavior. PLoS One 2012; 7:e40121; PMID:22792224; http://dx.doi.org/ 10.1371/journal.pone.0040121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Salas Hille. Calculus, One and Several Variables. Seventh Edition John Wiley & Sons, 1995. [Google Scholar]
- 39. Malladi R, Sethian J, Vemuri BC. Shape modeling with front propagation: a level set approach. 1995; 17:158-75. [Google Scholar]
- 40. Mumford D, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun Pure Appl Math 1989; 42:577-685; http://dx.doi.org/ 10.1002/cpa.3160420503 [DOI] [Google Scholar]
- 41. Chan TF, Vese LA. Active contours without edges. IEEE Trans on Image Proc 2001; 10:266-77; http://dx.doi.org/ 10.1109/83.902291 [DOI] [PubMed] [Google Scholar]
- 42. Jehan-Besson Sp, Barlaud M, Aubert G. DREAM2S: deformable regions driven by an eulerian accurate minimization method for image and video segmentation. Int J Comput Vision 2003; 53:45-70; http://dx.doi.org/ 10.1023/A:1023031708305 [DOI] [Google Scholar]
- 43. Blake A, Curwen R, Zisserman A. A framework for spatio-temporal control in the tracking of visual contours. Int J Comput Vision 1993; 11:127-45; http://dx.doi.org/ 10.1007/BF01469225 [DOI] [Google Scholar]
- 44. Blake A, Isard M, Reynard D. Learning to track the visual motion of contours. Artif Intell 1995; 78:179-212; http://dx.doi.org/ 10.1016/0004-3702(95)00032-1 [DOI] [Google Scholar]
- 45. Blackman SS, Popoli RF. Design and analysis of modern tracking systems. Artech House 1999. [Google Scholar]
- 46. Sibson R. SLINK: an optimally efficient algorithm for the single-link cluster method. Comput J 1973; 16:30-4; http://dx.doi.org/ 10.1093/comjnl/16.1.30 [DOI] [Google Scholar]
- 47. Geng W, Cosman P, Berry CC, Feng Z, Schafer WR. Automatic tracking, feature extraction and classification of C. elegans phenotypes. IEEE Transactions on Biomed Eng 2004; 51:1811-20; PMID:15490828; http://dx.doi.org/ 10.1109/TBME.2004.831532 [DOI] [PubMed] [Google Scholar]
- 48. Srinivasan J, von Reuss SH, Bose N, Zaslaver A, Mahanti P, Ho MC, O’Doherty OG, Edison AS, Sternberg PW, Schroeder FC. A modular library of small molecule signals regulates social behaviors in caenorhabditis elegans. PLoS Biol 2012; 10:e1001237; PMID:22253572; http://dx.doi.org/ 10.1371/journal.pbio.1001237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Al-Kofahi O, Radke RJ, Roysam B, Banker G. Object-level analysis of changes in biomedical image sequences: application to automated inspection of neurons in culture. IEEE Transactions Biomed Eng 2006; 53:1109-23; PMID:16761838; http://dx.doi.org/ 10.1109/TBME.2006.873565 [DOI] [PubMed] [Google Scholar]
- 50. Chen Y, Ladi E, Herzmark P, Robey E, Roysam B. Automated 5-D analysis of cell migration and interaction in the thymic cortex from time-lapse sequences of 3-D multi-channel multi-photon images. J Immunol Methods 2009; 340:65-80; PMID:18992251; http://dx.doi.org/ 10.1016/j.jim.2008.09.024 [DOI] [PMC free article] [PubMed] [Google Scholar]


