Partial covariance based functional connectivity computation using Ledoit-Wolf covariance regularization

Abstract

Functional connectivity refers to shared signals among brain regions and is typically assessed in a task free state. Functional connectivity commonly is quantified between signal pairs using Pearson correlation. However, resting-state fMRI is a multivariate process exhibiting a complicated covariance structure. Partial covariance assesses the unique variance shared between two brain regions excluding any widely shared variance, hence is appropriate for the analysis of multivariate fMRI datasets. However, calculation of partial covariance requires inversion of the covariance matrix, which, in most functional connectivity studies, is not invertible owing to rank deficiency. Here we apply Ledoit-Wolf shrinkage (L₂ regularization) to invert the high dimensional BOLD covariance matrix. We investigate the network organization and brain-state dependence of partial covariance-based functional connectivity. Although RSNs are conventionally defined in terms of shared variance, removal of widely shared variance, surprisingly, improved the separation of RSNs in a spring embedded graphical model. This result suggests that pair-wise unique shared variance plays a heretofore unrecognized role in RSN covariance organization. In addition, application of partial correlation to fMRI data acquired in the eyes open vs. eyes closed states revealed focal changes in uniquely shared variance between the thalamus and visual cortices. This result suggests that partial correlation of resting state BOLD time series reflect functional processes in addition to structural connectivity.

Introduction

The brain is highly active even in the absence of observable behavior (Raichle, 2011). Intrinsic brain activity is not random, but rather exhibits a stereotypical correlation structure (Biswal et al., 2010). Spontaneous fluctuations in the blood oxygen level dependent (BOLD) signal (Ogawa et al., 1993) have been used to investigate the organization of intrinsic activity in the resting-state, i.e., in the absence of explicit task performance (Biswal et al., 1995). This phenomenon commonly is referred to as functional connectivity; the associated topographies define resting-state networks (RSNs). Seed based correlation mapping (Biswal et al., 2010) and spatial independent component analysis (sICA) (Beckmann et al., 2005) account for the vast majority of functional connectivity studies. These techniques define RSN topographies but do not isolate variance unique to brain region pairs. Partial covariance techniques isolate pairwise regional variance and offer the possibility of improved understanding of brain organization by more precisely partitioning widely and uniquely shared variance in different brain states. However, partial covariance analysis of fMRI datasets has been difficult owing to the rank deficiency, hence non-invertibility, of high dimensional fMRI datasets (Schafer and Strimmer, 2005). Extant strategies for dealing with this problem in the context of resting-state fMRI are listed in Table 1.

Table 1.

Literature Review. Table summarizing previous reports utilizing partial correlation/ covariance approaches. Table shows the reference, solution adopted to allow partial correlation estimation, number of regions on interest (ROIs) and number of subject included. The general area of scientific inquiry is also noted.

Reference	Conditioning Strategy	# of ROIs/ components	# of Subjects	Scientific Topic
Liu et al., 2008	No conditioning	90	31 controls, 31 schizophrenics	Small world structure in schizophrenia
Balenzuela et al., 2010	No conditioning	90	12 controls, 12 back pain patients	Graph analysis of functional connectivity in lower back pain
Zhang et al., 2011	No conditioning	90	63 controls, 30 MDD	Small world structure in major depressive disorder
Marrelec et al., 2006	Limit # of ROIs	6	7	Motor system organization
Fransson and Marrelec, 2008	Limit # of ROIs	9	17	DMN organization
Zhang et al., 2008	Limit # of ROIs	5	17	Thalamic organization
Liang et al., 2011	ICA dimensionality reduction	38	6 rats	Network organization in the awake rate
Yu et al., 2011	ICA dimensionality reduction	57	19 controls, 19 schizophrenics	Small world structure in schizophrenia
Smith et al., 2013 *	ICA dimensionality reduction	22/78	20	Methods development for the connectome project
Varoquaux et al., 2010	L1 Normalization	122	20	Covariance model selection
Fiecas et al., 2013	L1 Normalization	90	25	Test-retest reliability assessment
Smith et al., 2013 *	L1 Normalization	22/78	20	Methods development for the connectome project
Ryali et al., 2012	Elastic Net Normalization	90	22	Stability of different regularization techniques
Varoquaux et al., 2012	Markov Structure (L1 and Ledoit-Wolf)	105	12	RSN vs small-world brain organization
Deligianni et al., 2014	Ledoit-Wolf shrinkage	82	17	Relationship between BOLD and EEG functional connectivity

^*Smith et al., 2013 compared multiple approaches so is presented twice

Covariance Matrix Conditioning via Shrinkage

BOLD time-series give rise to an empirical covariance matrix of the form: $\widehat{\Sigma }=\frac{1}{T}{(X-\stackrel{‒}{X})}^t(X-\stackrel{‒}{X}),\text{where}X\in {\mathbb{ℝ}}^{T\times M}$ (T time points and M regions of interest [ROI]) with the overbar indicating the column mean. When M is large, $\widehat{\Sigma }$ typically is ill-conditioned, i.e., not invertible. Ledoit-Wolf shrinkage describes a process wherein rank deficient covariance matrices can be made invertible by shrinkage (Ledoit and Wolf, 2003). Defining $\tilde{\Sigma }=(1-\alpha )\widehat{\Sigma }+\alpha \Delta$, where α is a tuning parameter and Δ is the shrinkage target (Ledoit and Wolf, 2004), yields an invertible matrix. Shrinkage targets vary in form but generally have some favorable property. In this case, the shrinkage target is full rank. The value of α that results in $\tilde{\Sigma }$ that most closely approximates the theoretical value of Σ (the true covariance matrix given infinite data) has in the past been determined using cross-validation e.g., (Efron and Morris, 1975). However, it has been shown that the optimal value of α can be calculated in closed form under weak assumptions (Ledoit and Wolf, 2003)¹. Matrix shrinkage is a low bias strategy in the sense that $\tilde{\Sigma }$ is close to the true theoretical covariance matrix. Given $\tilde{\Sigma }$, partial covariance and related quantities in high dimensional covariance matrices can be calculated.

Ledoit-Wolf regularization has previously been used to condition resting-state BOLD covariance matrices (Varoquaux et al., 2012, Deligianni et al., 2014) but the properties and consequences of this approach to functional connectivity have not been thoroughly investigated. In order to introduce this approach to the broader neuroimaging community, we first demonstrate the favorable properties of the partial covariance quantity. Specifically, partial covariance matrices calculated using Ledoit-Wolf regularization can be calculated with large numbers of ROIs and have improved test-retest reliability compared to full covariance matrices. We use the partial covariance quantity to investigate RSN organization. RSNs are defined by their widely shared variance; the partial covariance quantity removes this variance. It is unclear what, if any, RSN organization remains in the partial covariance matrix. Partial covariance functional connectivity has been reported to be similar to structural connectivity (i.e., constant over short time-scales). We next investigate the brain-state dependence of the partial correlation quantity using a well-established contrast: eyes open vs. eyes closed.

Methods

Subject Characteristics

Two datasets are used in this study. Dataset A consisted of 57 adults (mean age: 30 years, range: 18-45 years). All subjects were neurologically and psychiatrically normal on examination and neuropsychological testing. These subjects were enrolled as controls in ongoing imaging studies and two short resting state fMRI scans with the eyes open and fixated were collected. Dataset B consisted of 10 adults (mean age: 25 years, range: 22 – 31 years). Two long resting state fMRI scans were collected, one with eyes open and the other with eyes closed. All subjects provided written informed consent in accordance with the Washington University in St Louis Institutional Review Board.

Scanning Parameters

Image acquisition was performed using a 3T Siemens Trio scanner (Erlangen, Germany) equipped with a standard 12-channel head coil. A high-resolution structural scan was acquired using a 3-dimensional sagittal T1-weighted magnetization-prepared rapid gradient echo (MPRAGE, echo time [TE] = 16 msec, repetition time [TR] = 2,400 msec, inversion time [TI] = 1,000 msec, flip angle = 8°, 256 × 256 acquisition matrix, 1×1×1mm voxels). This scan was used for atlas registration. High-resolution 2D multi-slice oblique axial spin density/T2-weighted fast spin echo (FSE) structural images were also acquired using slice tilts and positions computed by slice preregistration (TE=455 msec, TR = 3,200 msec, 256 × 256 acquisition matrix, 1 acquisition, 1×1×1mm voxels). These T2-weighted FSE data were used for fMRI atlas registration. Resting state fMRI scans were collected using a gradient spin-echo sequence (TE = 30 msec, TR = 2200 msec, field of view = 256 mm, flip angle = 90°, 4mm isotropic voxels) sensitive to the blood oxygen level dependent (BOLD) contrast (Ogawa et al., 1993). In dataset A, two six-minute resting state fMRI runs (164 volumes per run) were acquired during which participants were asked to fixate on a visual cross-hair and not fall asleep. In dataset B, two forty-five minute resting state fMRI runs (1225 volumes per run) were acquired. During one run the participants were asked to fixate on a visual cross-hair (Eyes open; EO) and during the other run the participants were asked to keep their eyes closed (EC) but not to fall asleep. The order of these scans was counterbalanced across subjects.

Preprocessing

Initial preprocessing of resting state fMRI data followed conventional methods as previously described (Brier et al., 2014). Generic preprocessing of fMRI data included correction for slice-dependent intensity differences related to interleaved acquisition (debanding) (Hacker et al., 2013), rigid body correction for head movement within and between fMRI runs, and atlas transformation. Volumes strongly contaminated by head movement (Power et al., 2012) were removed and voxelwise replaced with linearly interpolated values (Power et al., 2013). Frame censoring was computed using the DVARS measure (Smyser et al., 2010) modified to include a 10mm FWHM Gaussian spatial pre-blur². The frame exclusion threshold was set at 0.7% root mean square (rms) BOLD signal change over successive frames, counting only voxels within the brain (Brier et al., 2014). Excluded frames were replaced with linear interpolations only for the purposes of facilitating preprocessing. Only subjects with fewer than 40% of frames excluded were passed on to the next stage of processing. Signals of non-interest were extracted from white matter, ventricles, and the global signal averaged over the whole brain (Fox et al., 2009). These signals of non-interest along with movement time-series and their first temporal derivatives were regressed from the voxelwise BOLD time-series. In order to investigate the effects of global signal regression (GSR) on the calculation of partial covariance matrices, a subset of the following analyses were performed without GSR. The residual BOLD time-series was then low-pass filtered to retain frequencies below 0.1Hz and spatially smoothed with a Gaussian blur (6mm FWHM in each direction). The linearly interpolated volumes were excluded in all subsequent analyses. Following preprocessing, an average of 308 (stdev = 30) frames were retained for each subject in Dataset A. These BOLD time-series were autocorrelated across approximately 3 frames (6.6 seconds); thus each subject had approximately 103 degrees of freedom. Dataset B had an average of 1031 frames retained.

Region of Interest Definition

In Dataset A, we used two sets of regions of interest (ROI) to examine the effects of matrix conditioning under different degrees of rank deficiency. The first ROI set contained 36 ROIs representing 5 RSNs including the default mode, dorsal attention, executive control, salience, and sensorimotor network (Brier et al., 2012). The second ROI set contained 264 ROIs representing 12 RSNs including somatomotor, cingulo-opercular, auditory, default mode, parietal encoding/retrieval, visual, fronto-parietal control, salience, subcortical, ventral attention, dorsal attention, and cerebellum networks (Power et al., 2011). For both ROI sets, each ROI was a 6mm radius sphere centered on previously published coordinates.

Covariance Calculations and Ledoit-Wolf Shrinkage

For each subject, the BOLD time-series extracted from M = 36 or M = 264 ROIs had length T, where T is the number of BOLD frames that were not contaminated with movement. Thus, define $X\in {\mathbb{ℝ}}^{T\times M}$. The sample covariance matrix is then defined as $\tilde{\Sigma }=\frac{1}{T}{(X-\stackrel{‒}{X})}^t(X-\stackrel{‒}{X})$. Because large subspaces in the covariance matrix are highly related and because the condition T >> M is not satisfied, $\widehat{\Sigma }$ is rank deficient and therefore uninvertible. We define the shrunken covariance matrix as $\tilde{\Sigma }=(1-\alpha )\tilde{\Sigma }+\alpha \Delta$ (Ledoit and Wolf, 2004, Schafer and Strimmer, 2005). α was calculated in closed-form as described in (Ledoit and Wolf, 2003) and Δ is the identity matrix (Ledoit and Wolf, 2004). The details of the calculation of α are described in Appendix 1.

Full and Partial Covariance

For each subject, the sample and conditioned covariance matrix have the form:

$$\widehat{\Sigma }=\left[\begin{array}{ccc}\hfill {\widehat{\sigma }}_1\hfill & \hfill \cdots \hfill & \hfill {\widehat{\sigma }}_{i,j}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\widehat{\sigma }}_{j,i}\hfill & \hfill \cdots \hfill & \hfill {\widehat{\sigma }}_i\hfill \end{array}\right]\tilde{\Sigma }=\left[\begin{array}{ccc}\hfill {\tilde{\sigma }}_1\hfill & \hfill \cdots \hfill & \hfill {\tilde{\sigma }}_{i,j}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\tilde{\sigma }}_{j,i}\hfill & \hfill \cdots \hfill & \hfill {\tilde{\sigma }}_i\hfill \end{array}\right]$$

where i, j ∈ [1, ...,36] or i, j ∈ [1, ...,264] and σ_i denotes the variance of the i-th time-series and σ_i,j denotes the full covariance between the i-th and j-th time-series. The off-diagonal values in ${\widehat{\Sigma }}^{-1}$ or ${\tilde{\Sigma }}^{-1}$ quantify the partial covariance between the i-th and j-th time-series accounting for all other time-series. To conform with the definition of partial correlations (Weatherburn, 1961), and resolve a sign flip associated with inverting the covariance matrix, we scaled ${\widehat{\Sigma }}^{-1}$ and ${\tilde{\Sigma }}^{-1}$ by a factor of −1. This sign manipulation ensures that the reported partial covariances have the same sign as the corresponding partial correlations. For the purpose of demonstrating the favorable properties of Ledoit-Wolf regularization as applied to fMRI data, we use covariance as it is the general case (Dataset A). However, the application of matrix shrinkage is equally valid for correlation matrices (see Supplemental Material) and is used in the investigation of Dataset B in order to conform to the extant literature.

Graphical LASSO Comparison

In Dataset A, we compared the results of partial covariance values calculated using Ledoit-Wolf shrinkage with an extant L₁-based method, namely, the graphical LASSO (Friedman et al., 2008). The inverse covariance matrix was estimated for each subject using a range of a priori defined penalty values. It is also possible to determine a penalty value by cross-validation. We calculated the ideal penalty coefficient using a popular cross-validation scheme (Bien and Tibshirani, 2011). To compare these results with the previous results, we calculated the correlation across all ROI pairs and subjects.

Identification of Topography Sensitive to Eyes Open vs. Eyes Closed

In order to investigate the changes in widely and uniquely shared variance in Dataset B, we first identified a set of ROIs that were most affected by the eyes open (EO) vs. eyes closed (EC) contrast. We divided the entire grey matter into 9mm isotropic ROIs and calculated the correlation between each ROI and all voxels for the EO and EC condition separately. The resulting parametric correlation volumes were averaged across subjects to yield C^EO(M × V) and C^EC(M × V) where M is the number of 9mm isotropic ROIs and V is the number of voxels. Given M ROIs, there exist $\left(\begin{array}{c}\hfill M\hfill \\ \hfill 2\hfill \end{array}\right)$ functional connectivity pairs; these data require data reduction. To achieve concise summary topographies we adopted a PCA approach. Let X = C^EO − C^EC. PCA is performed on X such that X(M, V ∈ GM) = USW^T where GM is the grey matter mask. The number of significant principal components is determined by an information criteria (Minka, 2000). Let w_i be the ith column of W with length M. The topography of the effect of Eyes Open vs. Eyes Closed is defined as:

$$T_i=\frac{1}{\sqrt{M}}\sum _{m=0}^M{w}_i\left(m\right)\cdot X\left(m\right)$$

T_i has length V and represents a topography. Large values (positive and negative) were extracted to form ROIs (|T_i| > 0.05; cluter size > 100 voxels).

Intersubject Variability as a Function of Eyes Open or Eyes Closed State

To quantify the level of inter-subject variability we calculated the distance between a single subject’s full/partial correlation matrix in the EO and EC condition and the group average without that single subject. For some subject n, either full or partial, EO or EC, the inter-subject variability for generic matrix C is defined as:

$${\sigma }_n=\frac{1}{N}\sum _{n=1}^N\parallel C_n-\left(\frac{1}{N-1}\sum _{\eta \ne n}C\eta \right){\parallel }_2$$

Thus, four distributions (full/partial, EO/EC) are then subjected to a matrix type (full, partial) by condition (EO, EC) repeated measures ANOVA.

Results

Matrix shrinkage accomplished significant matrix conditioning

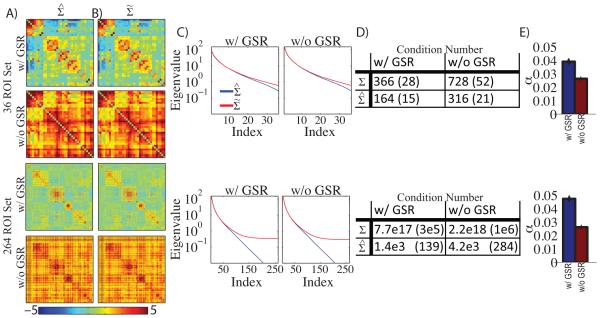
We calculated $\widehat{\Sigma }$ in the 36 and 264 ROI sets with and without GSR (Figure 1A). The covariance matrices exhibited block organization commonly observed in resting-state BOLD fMRI correlation matrices. With GSR, positive blocks along the diagonal correspond to within RSN correlations and off-diagonal blocks of negative correlations indicate anti-correlations (e.g., between the default-mode network (DMN) and dorsal attention network (DAN)). Without GSR, the same block organization was evident, but all values were shifted towards positive values. $\tilde{\Sigma }$, computed as described in section 2.5, is shown in Figure 1B. The difference between $\widehat{\Sigma }$ and $\tilde{\Sigma }$ is not apparent to the eye (Figure 1A vs 1B). However, the effect of matrix conditioning is clearly evident in the eigenspectra (Figure 1C). The critical feature evident in Figure 1C is the exponential decrease in eigenvalues of $\widehat{\Sigma }$ (blue line), especially in the larger ROI set. In contrast, the eigenvalues of $\tilde{\Sigma }$ showed a less steep decline in the smaller ROI set, and a plateau in the larger ROI set (α is the lower bound).

Figure 1. Matrix conditioning significantly improves the condition number of BOLD covariance matrices.

A: BOLD covariance matrices (Σ) calculated in the 36 and 264 ROI set with and without global signal regression (GSR). Matrices with GSR exhibit familiar block organization representing resting-state networks (RSNs). Matrices without GSR exhibit similar organization biased towards positive values. B: Conditioned BOLD covariance matrices ($\widehat{\Sigma }$) in the same configuration as A. Notably, there is no visual difference between matrices in A and B. C: Mean eigenspectra of matrices in A and B. The blue line indicates the eigenspectra corresponding to Σ and the red lines indicates the eigenspectra corresponding to $\widehat{\Sigma }$. The eigenvalues of Σ decay towards zero but the eigenvalues of $\widehat{\Sigma }$ plateau at a non-zero constant. D: Quantification of matrix invertibility by mean condition number. The condition number is defined as the ratio of the largest eigenvalue to the smallest. E: mean shrinkage coefficient (α) in each ROI set with and without global signal regression. Error bars indicate standard error of the mean estimated across subjects.

Matrix invertibility is frequently quantified as the condition number, defined as the ratio of the largest to smallest eigenvalue. In practice, matrices with condition numbers less than ~10⁴ are invertible using standard double precision arithmetic. In the larger ROI set the condition number was intolerably large but was made significantly smaller with shrinkage (Figure 1D). For the 36 ROI set matrix shrinkage improved the condition number by about a factor of 2. However, for the 264 ROI set matrix conditioning improved the condition number from a value representing the limits of machine precision (~10¹⁷) to an invertible condition (~10³). This improvement in condition number was achieved with α less than 0.05 for all conditions (Figure 1E). By way of comparison, the value of α obtained in a highly cited study of gene expression data using Ledoit-Wolf regularization with 100 variables was 0.20 (Schafer and Strimmer, 2005). In the present data, significant conditioning was achieved with a relatively small amount of shrinkage. Similar results were achieved for correlation matrices (Supplemental Figure 1).

Matrix conditioning stabilized matrix inversion and improved test-retest reliability

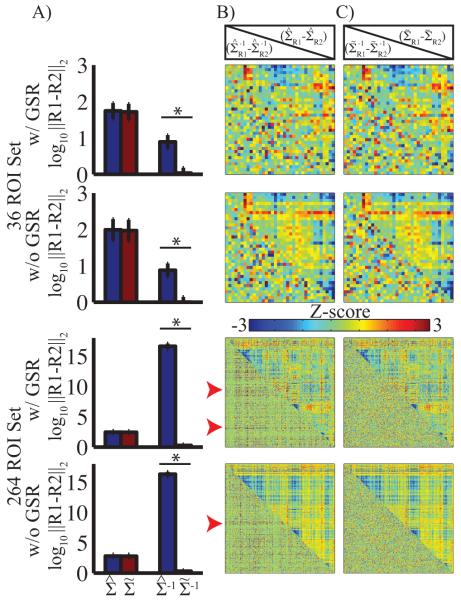
The results shown in Figure 1 also demonstrate a dramatic improvement in condition number following modest conditioning. The error in matrix inversion is bounded by the condition number (Conte and de Boor, 1980). To investigate this important effect, we report empirical results using the present data and a split sample approach. More specifically, the full and partial covariance matrices derived from the first and second fMRI runs were compared with and without conditioning. Assuming stationarity, the results obtained from both runs should be the same. Non-stationarity of BOLD time-series has been reported, e.g., (Chang and Glover, 2010, Allen et al., 2012), but recent results suggest that this effect is small when appropriate models are used (Lindquist et al., 2014). Accepting this view, the difference between the first and second runs is interpretable in terms of test-retest reliability. To quantify the difference between the matrices resulting from the first and second fMRI runs, we calculated the Euclidean distance (Frobenius norm) between the corresponding matrices. We subjected these log transformed Euclidean distance measures to a linear model investigating the effect of matrix regularization correcting for the α value. Matrix conditioning had little effect on the full covariance matrices, but reduced the distance between the inverse covariance matrices by more than 10 orders of magnitude in the case of the larger ROI set (Figure 2A) and by a factor of 10 in the smaller ROI set. We also observed a negative relationship between the distance between the inverse covariance matrices prior to regularization and α. This effect was approximately the same with and without GSR. Thus, matrix conditioning, as implemented here, was sufficient to stabilize the inversion step even for a large number of ROIs. This result follows from the relationship between condition number and inversion precision and has practical utility in improving test-retest reliability of high-dimensional partial correlations.

Figure 2. Matrix conditioning is sufficient to constrain the covariance inverse.

A: Mean Euclidean distance between covariance and inverse covariance matrices calculated from the first and second fMRI sessions. Blue bars display results without conditioning; red bars display results with conditioning. Error bars represent standard deviation across subjects. Asterisks indicate significant differences; in this case p < 0.001. Conditioning had no significant effect on distance for full covariance results, but significantly reduced the distance (error) between the inverse covariance matrices. B: Z-transformed (removal of mean and normalization by standard deviation) mean difference between the first and second sessions without conditioning. Full covariance results are above the diagonal; partial covariance results are below the diagonal. Red arrow heads indicate organized pattern of large values in the inverse matrix. C: Same as B, but with conditioning. Structured noise is absent in the conditioned result.

We next investigated the structure of the first vs second run differences, which we define as error for the present purposes. Unstructured error may be reduced by increasing numbers of subjects, increasing the amount of data acquired in a single subject, or by averaging across ROIs. However, tructured error is more difficult to remove. Thus, reduction of structured error is an ideal characteristic of an analytic approach. The mean (across subjects) error for each of the matrix types was investigated. As noted above, the magnitude of the error differs by orders of magnitude depending on conditioning and ROI number. We investigated the presence or absence of structured error. Accordingly, the error was Z-transformed (removing the mean and normalizing by the standard deviation across ROI pairs), thereby scaling all results to approximately the same range. The full covariance matrices are presented above the diagonal in Figure 2B and C. The first vs. second run differences were clustered roughly by RSN; critically these differences were not affected by conditioning. The first vs. second run differences in partial covariance matrices (below the diagonal, Figure 2B,C) exhibited no structure in the 36 ROI set. In contrast, for the 264 ROI set, the differences without conditioning were structured (red arrows); conditioning removed this structure. To quantify the effect of conditioning on error structure in inverse covariance matrices, we calculated the first eigenvalue of each difference matrix (Table 2). Large and small first eigenvalues correspond, respectively, to structured and unstructured error. A large first eigenvalue indicates similar error structure across some set of ROIs; averaging or other data reduction techniques does not remove this error. On the other hand, a small first eigenvalue indicates random error across ROIs that is removable by averaging or other approaches. Matrix conditioning significantly reduced this metric of structured error in the inverse covariance matrices, particularly in the large ROI set (all p<10⁻⁶). We emphasize that without removing the overall effect of magnitude (Z-scoring), the effect of conditioning would have been much more marked.

Table 2.

1^st eigenvalue of Z transformed difference of 1^st and 2^nd half scan session. Table shows the mean (standard deviation) of the largest eigenvalue of the Z transformed difference between the first and second fMRI runs. This is computed separately for the 36 and 264 ROI set, with and without GSR, and for the covariance and inverse covariance matrices. The far right column shows the t and p values for the comparison of the sample (unconditioned) and conditioned condition.

			Sample	Conditioned	t,p
36 ROI Set	w/ GSR	Covariance	17.8 (6.4)	17.8 (6.6)	0.7, 0.49
		Inverse	16.7 (3.4)	13.0 (2.0)	7.3, <10−8
	w/o GSR	Covariance	19.0 (4.7)	19.0 (4.8)	0.5, 0.64
		Inverse	17.2 (3.5)	13.0 (2.1)	8.5, <10−10
264 ROI Set	w/ GSR	Covariance	108.2 (34.2)	107.6 (35.4)	1.3, 0.19
		Inverse	138.9 (20.9)	35.2 (5.6)	35.5, <10−39
	w/o GSR	Covariance	128.4 (30.8)	128.3 (31.0)	1.0, 0.28
		Inverse	146.6 (22.8)	35.0 (4.5)	38.1,<10−40

The relationship between partial covariance analysis and GSR is shown in the Supplemental Material (Supplemental Figure 2).

Ledoit-Wolf shrinkage and LASSO (L₁) based methods yielded similar results

We have demonstrated the utility of Ledoit-Wolf shrinkage in the computation of partial covariance matrices. A frequently used alternative, namely, the graphical LASSO approach, enforces an L₁ penalty on the inverse solution (Friedman et al., 2008). We compared the calculated partial covariance values resulting from the graphical LASSO approach vs. the present Ledoit-Wolf based approach. As there exists no closed form method to select the weight of the L₁ penalty (β), we calculated partial covariance matrices over a range of β values [0.10 0.25 0.50 0.75 0.90]. The 264 ROI case failed to converge after 1 week of computation. Accordingly, we report a comparison between the graphical LASSO approach and the Ledoit-Wolf approach for the 36 ROI case (Figure 3A). To simulate the thresholding effect of the L₁ penalty in the Ledoit-Wolf based result, we thresholded the absolute value of the data over a range of ρ values [0.00 0.01 ... 0.25]. For all values of β and ρ, L₁:L₂ correlation was high (r > 0.50). However, there was obvious structure in the L₁:L₂ correlation results. The highest correlation was found with no L₂ thresholding (ρ=0) and minimal L₁ sparsity (β=0.10) (Figure 3B). Similarly high correlation was found between the penalty determined by cross-validation (β=0.12) (Figure 3C). Sparsity is a requirement for inversion in L₁ based methods, but increasing sparsity reduces test-retest reliability (Varoquaux et al., 2012). The present Ledoit-Wolf approach avoids sparsity altogether and is computationally feasible for larger ROI sets.

Figure 3. Ledoit-Wolf shrinkage and L₁ based methods yield similar results.

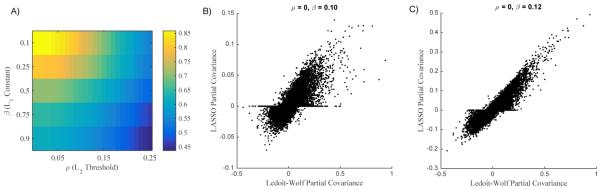
A: The correlation (using ROI pairs and subjects as samples) between the partial covariance quantities resulting from the present Ledoit-Wolf shrinkage based approach and the graphical LASSO approach are presented for varying L1 penalty weights (β) and varying absolute thresholds applied to the Ledoit-Wolf based approach (ρ). Only representative β values are shown as graphical LASSO is computationally expensive. B: Scatter plot illustrating the maximal correlation result (ρ=0 and β=0.10) between the two techniques. C: Same as B, but β=0.12 which was determined by cross-validation.

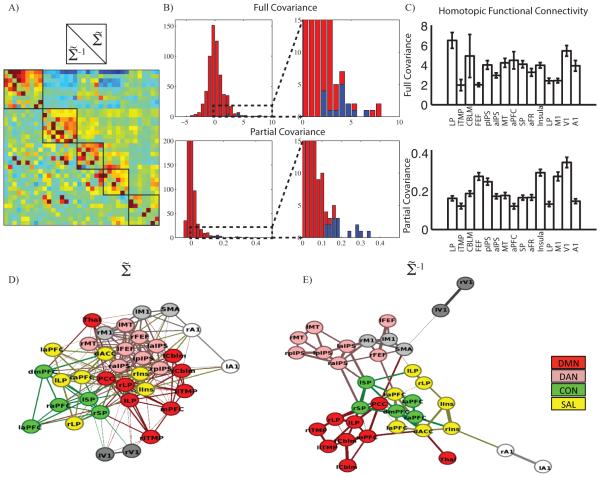
Partial covariance exhibits strong homotopy and reveals novel features of RSN organization

Having demonstrated the practical utility of Ledoit-Wolf regularization for the computation of partial covariance functional connectivity, we investigated the brain organization that is revealed by this approach. We analyzed the 36 ROI set as the larger ROI set does not explicitly include homotopic ROIs. Full covariance matrices (Figure 4A, above the diagonal) demonstrate the familiar block organization that reflects RSN organization. This feature is notably absent in the partial covariance matrix (Figure 4A, below the diagonal). Instead, the partial covariance matrix is dominated by homotopic functional connectivity, although this feature is not immediately obvious on inspection of Figure 4A. To more clearly demonstrate this feature, we display the values of Figure 4A in histogram format (Figure 4B). In both the full and partial covariance results, homotopic values (shown in blue) were concentrated in the right tail of the distribution. However, the separation between homotopic versus other covariance values was more complete using partial covariance (Figure 4B, enlargement).

Figure 4. The partial covariance matrix is dominated by homotopic functional connectivity and contains RSN organization.

A: Full (above diagonal) and partial (below diagonal) covariance matrices shown for the 36 ROI set with GSR. Black boxes denote RSN membership. B: Histogram of full and partial covariance values with homotopic covariance values in blue. Inset magnifies right side of distribution. Homotopic covariance is large in both distributions, but is better separated in the partial covariance result. C: Mean full and partial covariance between homotopic brain regions (error bars are standard error. D: The 36 ROI covariance and (E:)partial covariance matrix were transformed into a graph representations. The position of each node optimized using an automated algorithm (Hu, 2005). Colors denote a priori RSN membership. Lines indicating connections are omitted from the 264 ROI result for visual clarity.

The topography of homotopic functional connectivity differed in the full versus partial covariance results. Repeated measures ANOVA revealed that both full (F_14,786=3.44, p=0.000018) and partial (F_14,786=23.7, p<10⁻⁸) homotopic covariance values varied across brain regions (Figure 4C). However, the homotopic full and partial covariance topographies were not correlated (r = 0.088, p = 0.76). This result suggests that partial covariance reveals features in the functional organization of the brain that are not captured in the full covariance values.

Full covariance functional connectivity is dominated by clusters of widely shared variance (RSNs); partial covariance calculation removes that variance. We next investigated if RSN organization still existed after removing the variance that defines RSNs using a semi-quantitative graphical approach. Full and partial covariance matrices were thresholded using a one-sample t-test (across subjects) against the null-hypothesis of no covariance. t-statistics corresponding to suprathreshold (p<0.001, uncorrected) ROI pairs were used as edge weights in a graph. The resultant graph was displayed using a force directed algorithm (Hu, 2005). In the force directed results obtained with the 36 ROI set, nodes belonging to the same RSN were clustered for both mean $\tilde{\Sigma }$ (Figure 4D) and mean ${\tilde{\Sigma }}^{-1}$ (Figure 4E). RSNs are conventionally defined in terms of widely shared variance between multiple ROIs; partial covariance removes that shared variance. Therefore one might expect RSN structure to fall apart using a force directed graphical model derived from partial covariance analysis. However, contrary to this expectation, the separation between RSNs was more complete in the result obtained with mean ${\tilde{\Sigma }}^{-1}$. Comparable results were obtained with the 264 ROI set (Supplemental Figure 3). The critical observation here is that clustering of nodes by RSN affiliation persisted in the partial covariance results even though shared signals were removed. In full covariance matrices, RSN affiliation is reflected in block organization. This feature is not apparent in partial covariance matrices (Figure 4A, below the diagonal). Nevertheless, nodes in the same RSN remained clustered. Inspection of the force directed graph result obtained with the 36 ROI set suggests that RSNs are clustered in the partial covariance results on the basis of conditionally dependent pair-wise connections. Thus, RSNs can be defined in two ways: 1) on the basis of widely shared variance across a set of ROIs and 2) on the basis of uniquely shared variance between pairs of member ROIs.

Partial Correlation is Focally Dependent on Changes in Brain State

The organization of partial correlations has been proposed to closely approximate structural connectivity (e.g., white matter tractography). If partial correlation functional connectivity were a simple reflection of structural connectivity (Smith et al., 2013) it would be insensitive to brain state. To test this hypothesis, we investigated the partial correlation organization during EO and EC conditions (Dataset B). We began by identifying sets of brain regions sensitive to the EO vs. EC full correlation contrast (see Methods). Two significant principal components were identified (Figure 5A). From these topographies, eight ROIs were extracted. Full and partial correlation functional connectivity was calculated for this set of eights ROIs (Figure 5B). Full correlation functional connectivity was dramatically affected by the change in brain state (Figure 5C, above diagonal) whereas partial correlation functional connectivity remained relatively unchanged (Figure 5C, below diagonal). However, partial correlations between the thalamus and visual areas and the thalamus and frontal areas were affected. Thus, partial correlation organization is modifiable by brain state and those perturbations are relatively focal compared to full correlation changes.

Figure 5. Partial Correlation Organization is Modulated by Brain-state.

A: First two principal components (PC) of the eyes open (EO) compared to eyes closed (EC) full correlation contrast. Strongly affected regions (positive and negative) were extracted to form ROIs. ROIs are superimposed as colored regions. B: Full (above diagonal) and partial (below diagonal) correlation matrices using extracted ROIs in the EO and EC condition. C: ROI-pair-wise contrasts of the EO and EC condition. Cell color indicated t-statistic value. White X indicates p < 0.001, uncorrected for multiple comparisons.

Next we investigated the inter-subject variability in the full and partial correlation matrices in the EO and EC condition. The inter-subject variability was calculated as the distance (Euclidean norm) between a single subject’s matrix and the group mean (less that subject)’s matrix (Table 3). These values were subjected to a correlation type (full, partial) by condition (EO, EC) repeated measures ANOVA. There was a significant effect of correlation type (F(1,9)=11.11, p=0.0088) wherein the partial correlation matrices showed less inter-subject variability. There was no effect of condition (F(1,9)=0.0046, p=0.95) nor an interaction (F(1,9)=0.27, p=0.62).

Table 3.

Inter-subject Variability. Mean (standard deviation) values of σ as calculated in the methods. Low values correspond to low levels of inter-subject variability.

	Full Correlation	Partial Correlation
EO	1.33 (0.46)	0.91 (0.26)
EC	1.30 (0.31)	0.95 (0.25)

Discussion

Summary

We have applied an approach to covariance matrix conditioning, Ledoit-Wolf shrinkage, which facilitates calculation of high dimensional partial covariance matrices for the assessment of functional connectivity. We show that this approach yields partial covariance matrices that are stable within subjects and reproducible across subject groups. Having established the validity of this computational strategy in resting state fMRI data, we next used Ledoit-Wolf shrinkage to examine the brain’s functional organization. We found: (1) RSNs are defined by both their widely shared variance and by pair-wise unique shared variance, and (2) partial correlations are sensitive to brain state suggesting they contain mutable representations of brain connectivity which are not simple 1:1 reflections of structural connectivity.

Matrix shrinkage circumvents limitations in extant approaches to partial covariance calculation

The favorable properties of partial correlation and covariance computation in the context of resting state fMRI have been frequently recognized (Table 1). The primary challenge has been overcoming rank deficiency of high-dimensional BOLD fMRI covariance matrices. The simplest approach is to limit the dimensionality of the system (Marrelec et al., 2006, Fransson and Marrelec, 2008, Zhang et al., 2008). This approach has the advantage of avoiding ill conditioned matrices but limits the scope of the scientific inquiry. The present matrix shrinkage strategy provides computational stability and enables study of large partial covariance organizations.

The second extant approach to overcoming the rank deficiency problem is dimensionality reduction using PCA followed by ICA (Liang et al., 2011, Yu et al., 2011, Smith et al., 2013). The covariance matrix calculated over independent components is full rank and therefore invertible. However, this approach includes an arbitrary parameter (the number of components retained in the PCA step) and does not allow for investigation of partial correlations between individual regions, although, partial correlations between RSNs can be computed. Ledoit-Wolf shrinkage involves no arbitrary parameters and supports the computation of partial correlations between a priori selected ROIs.

The third approach in the extant literature for calculating partial correlations is imposing an L₁ penalty to constrain the inversion step (Varoquaux et al., 2010, Fiecas et al., 2013, Smith et al., 2013). The L₁ norm forces small values in the inverse matrix to 0. This procedure effectively reduces the number of free parameters in the inversion computation. This approach includes a tunable parameter determined by simulation but allows for the investigation of large number of ROIs. One of the consequences of the L₁ constraint is that the inverse covariance matrix is sparse (i.e., has many off-diagonal 0s). This feature has been described as an advantage (Varoquaux et al., 2010) but a recent report has argued that the L₁ constraint is too strict (Ryali et al., 2012). Ryali and colleagues have suggested using the elastic net (linear combination of the L₁ and L₂ penalty (Hastie et al., 2009)) to constrain the inversion step at the cost of an additional free parameter. The L₂ norm penalizes large values in the inverse but does not force small values to zero. The present approach is analogous to imposing a pure L₂ penalty without any tunable parameters.

Thus, the present approach for calculating partial correlation/covariance values has three primary advantages over alternative approaches. First, the calculation of Ledoit-Wolf shrinkage is possible for a large number of ROIs and computation time does not dramatically increase as in non-closed form solutions (e.g., graphical LASSO). Second, this approach does not assume a model (e.g., sparsity). Sparsity may be appropriate for some forms of connectivity (e.g., white matter tractography) but has not been conclusively demonstrated for functional measures. Finally, the arbitrary parameter is calculated in closed form, precludes simulations, reduces computational burden, and stabilizes interpretation.

Previous applications of matrix shrinkage to functional connectivity

Covariance matrix shrinkage has been recently used in the investigation of functional connectivity (Varoquaux et al., 2012, Deligianni et al., 2014, Shou et al., 2014). Stein’s paradox (Stein, 1956) asserts that a shrunken estimate of the mean outperforms the sample mean in predicting the true mean of a multivariate distribution. Shou and colleagues used knowledge of the group functional connectivity matrix to predict the retest outcome in subjects scanned twice. Shrinkage of individual functional connectivity matrices towards the group mean improved test-retest reliability. This result is consistent with the known behavior of multivariate distributions under shrinkage (Efron and Morris, 1975) but represents an application of matrix shrinkage very different from the thepresent use. We used shrinkage to improve matrix invertibility. Nevertheless, we observed that partial covariance estimates were more reliable than full covariance estimates both at the individual and group level. This work adds to previous studies which have applied Ledoit-Wolf shrinkage to calculate partial correlation values (Varoquaux et al., 2012, Deligianni et al., 2014).

Homotopy dominates partial covariance organization

Large partial covariance values identify variance uniquely shared between two variables. In the present results (Figure 4), the largest partial covariance values were observed between homotopic brain regions. Strong homotopic functional connectivity is well documented (Salvador et al., 2008) and is thought to be supported by callosal and other commissural fibers (O'Reilly et al., 2013, Shen et al., 2015). It has been suggested that that unique shared variance implies direct communication between brain regions (Smith et al., 2013). This is an appealing notion but it is not entirely supported by the present results. Over all ROI pairs, the largest partial covariance value was observed between left and right primary visual cortex (Figure 4C). The only known direct inter-hemispheric connections between primary visual cortices are representations of the vertical meridian (Van Essen et al., 1982). It seems unlikely that this anatomy alone supports the observed high degree of unique shared variance. Hence, some other mechanism may be responsible for identification of highly reliable inter-hemispheric partial correlations in primary visual cortex. One hypothesis that potentially explains the present observations is that high degrees of shared variance may arise from common efferents or afferents (Adachi et al., 2012).

RSN organization is preserved in partial covariance matrices

Direct comparison of full and partial covariance matrices reveals several striking differences. Partial covariance matrices lacked the familiar RSN-related block organization that dominates full covariance matrices. Loss of prominent RSN organization follows from the definition of both RSNs and partial covariance. RSNs are defined by shared variance between member regions; this shared variance was removed in partial covariance matrices. What remains is unique shared variance between regions. Surprisingly, this organization is sufficient to separate RSNs in force-directed graphs (Figure 4D). This result may reflect some underlying skeletonized organization of the brain (van den Heuvel et al., 2012). We note that partial covariance matrices were reliable, which suggests that they reflect some biologically important aspect of brain organization.

Partial Correlation Functional Connectivity is Sensitive to Brain State

The similar organization of partial correlation functional connectivity and structural connectivity has been previously observed (Smith et al., 2013). The extent to which partial correlations represent structural connectivity alone or dynamic brain organization is unclear. The contrast of brain organization in the eyes open vs. eyes closed state is an operationally simple manipulations that is known to elicit functional connectivity changes. Closing of the eyes elicits a change in mean BOLD signal in primary visual (Bianciardi et al., 2009) as well as non-visual cortices (Marx et al., 2003, McAvoy et al., 2008). Functional connectivity is also affected. Consistent with previous literature we found broad changes in full correlation functional connectivity (Figure 5) (Jao et al., 2013, Liang et al., 2014, Xu et al., 2014). In particular, we observed an increasingly strong negative correlation between visual cortices and the thalamus (Zou et al., 2009, McAvoy et al., 2012). In the partial correlations, functional connectivity between the thalamus and visual regions is also made more negative by eye closure. This demonstrates that the change in functional connectivity between the thalamus and visual cortex due to eye state is mediated by uniquely shared variance while the other, broader, modulations are due to widely shared variance. Speculatively, we hypothesize that the changes in broadly shared variance may be due to arousal (Tagliazucchi and Laufs, 2014) while the changes in uniquely shared variance may be more attributable to the eye condition-related brain-state change. Regardless of the exact mechanism, this result demonstrates that partial correlation based functional connectivity is modulated by brain state. This modulation indicates that uniquely shared variance reveals functional brain organization, not simply structural connectivity.

Highlights.

• We use the well characterized matrix regularization technique described by Ledoit and Wolf to calculate high dimensional partial correlations in fMRI data

• Using this approach we demonstrate that partial correlations reveal RSN structure suggesting that RSNs are defined by widely and uniquely shared variance.

• Partial correlation functional connectivity is sensitive to changes in brain state indicating that they contain functional information.

Appendix 1

In this appendix we briefly outline the calculation of the Ledoit-Wolf shrinkage parameter α. This approach was originally described in (Ledoit and Wolf, 2003) and code is generously made available by those authors³. We outline the process briefly. Capital letters denote matrices, lower case letters denote elements in a matrix, and t indicates transpose.

Given data in the form

$$X\in {\mathbb{ℝ}}^{T\times M}$$

the empirical covariance matrix is calculated as

$$\widehat{\Sigma }=\frac{1}{T}{(X-\stackrel{‒}{X})}^t(X-\stackrel{‒}{X})$$

where the overbar indicates the column mean. The shrinkage target is computed as

$$\Delta =\stackrel{‒}{\sigma }\cdot I$$

where $\stackrel{‒}{\sigma }$ = 〈 diag ($\widehat{\Sigma }$) 〉_M and I is the identity matrix of ${\mathbb{ℝ}}^{M\times M}$. The shrinkage parameter is calculated as follows. Define:

$$p_{ij}=\frac{1}{T}\sum _{t=1}^T{\{(x_{it}-{\stackrel{‒}{x}}_i)(x_{jt}-{\stackrel{‒}{x}}_j)-{\widehat{\Sigma }}_{ij}\}}^2$$

$$c=\parallel \widehat{\Sigma }-\Delta {\parallel }_2^2$$

From this, the shrinkage constant can be calculated:

$$\alpha =\frac{({\Sigma }_{ij}p∕c)}{T}$$