Skip to main content
NCBI home page
Brain logoLink to Brain
. 2015 Mar 22;138(6):1696–1709. doi: 10.1093/brain/awv075

Disconnection of network hubs and cognitive impairment after traumatic brain injury

Erik D Fagerholm 1,*, Peter J Hellyer 1,*, Gregory Scott 1, Robert Leech 1, David J Sharp 1,✉
PMCID: PMC4614120  PMID: 25808370

Traumatic brain injury (TBI) affects brain connectivity, which disrupts the large-scale networks that support cognitive function. Fagerholm et al. use graph analysis, with brain regions as nodes and white matter tracts as connections, to show that TBI particularly disrupts the connectivity of hubs, and that this disconnection predicts cognitive impairment.

Keywords: traumatic brain injury, diffusion tensor imaging, betweenness centrality, network hubs, graph theory

graphic file with name awv075fig1g.jpg

Open in a new tab

Traumatic brain injury (TBI) affects brain connectivity, which disrupts the large-scale networks that support cognitive function. Fagerholm et al. use graph analysis, with brain regions as nodes and white matter tracts as connections, to show that TBI particularly disrupts the connectivity of hubs, and that this disconnection predicts cognitive impairment.

Abstract

Traumatic brain injury affects brain connectivity by producing traumatic axonal injury. This disrupts the function of large-scale networks that support cognition. The best way to describe this relationship is unclear, but one elegant approach is to view networks as graphs. Brain regions become nodes in the graph, and white matter tracts the connections. The overall effect of an injury can then be estimated by calculating graph metrics of network structure and function. Here we test which graph metrics best predict the presence of traumatic axonal injury, as well as which are most highly associated with cognitive impairment. A comprehensive range of graph metrics was calculated from structural connectivity measures for 52 patients with traumatic brain injury, 21 of whom had microbleed evidence of traumatic axonal injury, and 25 age-matched controls. White matter connections between 165 grey matter brain regions were defined using tractography, and structural connectivity matrices calculated from skeletonized diffusion tensor imaging data. This technique estimates injury at the centre of tract, but is insensitive to damage at tract edges. Graph metrics were calculated from the resulting connectivity matrices and machine-learning techniques used to select the metrics that best predicted the presence of traumatic brain injury. In addition, we used regularization and variable selection via the elastic net to predict patient behaviour on tests of information processing speed, executive function and associative memory. Support vector machines trained with graph metrics of white matter connectivity matrices from the microbleed group were able to identify patients with a history of traumatic brain injury with 93.4% accuracy, a result robust to different ways of sampling the data. Graph metrics were significantly associated with cognitive performance: information processing speed (R2 = 0.64), executive function (R2 = 0.56) and associative memory (R2 = 0.25). These results were then replicated in a separate group of patients without microbleeds. The most influential graph metrics were betweenness centrality and eigenvector centrality, which provide measures of the extent to which a given brain region connects other regions in the network. Reductions in betweenness centrality and eigenvector centrality were particularly evident within hub regions including the cingulate cortex and caudate. Our results demonstrate that betweenness centrality and eigenvector centrality are reduced within network hubs, due to the impact of traumatic axonal injury on network connections. The dominance of betweenness centrality and eigenvector centrality suggests that cognitive impairment after traumatic brain injury results from the disconnection of network hubs by traumatic axonal injury.

Introduction

Traumatic brain injury (TBI) often results in traumatic axonal injury, which damages long-distance white matter connections (Johnson et al., 2013). Patterns of white matter damage following TBI can be measured using diffusion tensor imaging (DTI) (Basser et al., 1994; Kinnunen et al., 2011; Bonnelle et al., 2012). Damage to specific white matter tracts is sometimes associated with specific cognitive problems following TBI (Kinnunen et al., 2011). However, patterns of traumatic axonal injury are generally widespread and highly variable across individuals (Sidaros et al., 2008; Kinnunen et al., 2011; Hellyer et al., 2013). This can produce complex effects on brain network function (Sharp et al., 2014). Therefore, understanding the effects of traumatic axonal injury on brain function and behaviour is likely to require a detailed investigation of the global effects of traumatic axonal injury on brain connectivity.

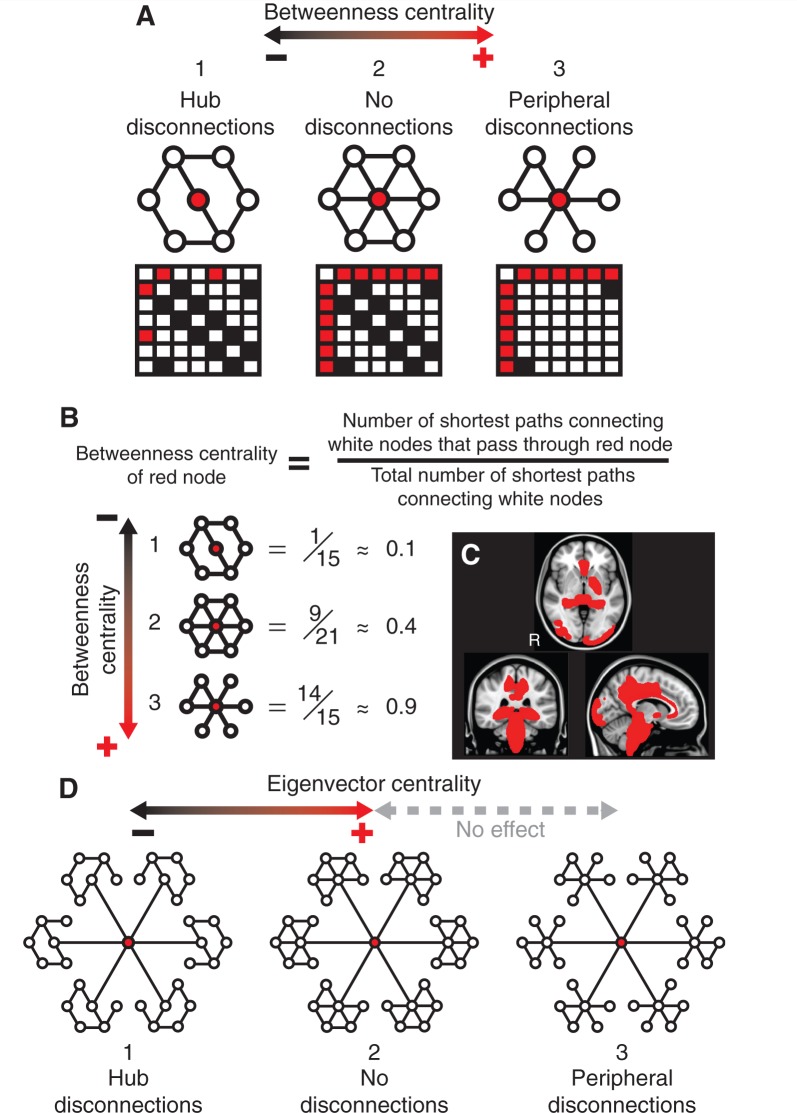
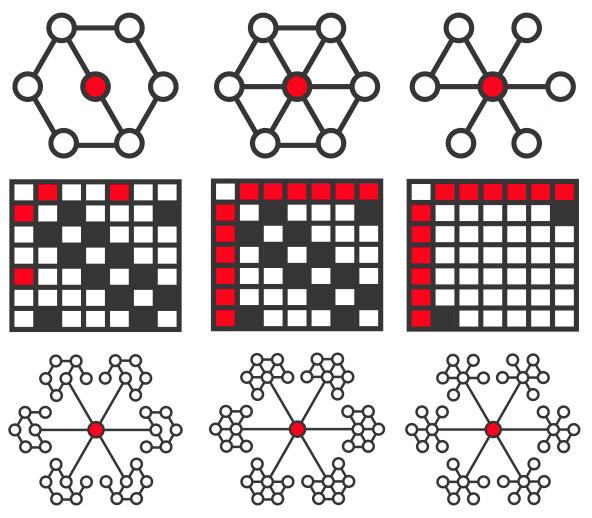
One elegant approach to studying the structure and function of brain networks is to represent connections between regions in a graphical form. A complex collection of graph metrics has been developed to describe the connective properties of ‘nodes’ within such graphs (Rubinov and Sporns, 2010). Recently, these approaches have begun to be applied to studies of the effects of TBI (Nakamura et al., 2009; Caeyenberghs et al., 2014; Han et al., 2014). Hubs of information exchange within the brain are abnormal across a range of disease states and may be particularly vulnerable to the effects of traumatic axonal injury, as diffuse damage to white matter tracts has a differentially large effect on highly connected regions (Pandit et al., 2013; Crossley et al., 2014). Betweenness centrality is a measure of the fraction of shortest paths in a network that pass through a given node (Fig. 1A–C). Hubs tend to have high values of betweenness centrality, as they efficiently connect other brain regions, and the betweenness centrality of hubs is reduced when they lose connectivity with other parts of the network. Eigenvector centrality is a self-referential metric that assigns a high level of importance to nodes if they are connected to other nodes that are themselves highly connected. The eigenvector centrality of a node is decreased if its neighbours lose connectivity with their local hubs (Fig. 1D).

Figure 1.

Figure 1

Open in a new tab

Betweenness centrality and eigenvector centrality. (A) Betweenness centrality is high for highly-connected hubs (red node), and can increase or decrease depending on the pattern of disconnection in the surrounding network. Configuration 2 in the top centre shows a fully connected network. The betweenness centrality of the red node decreases if connections to its neighbours are removed (configuration 1). Conversely, the betweenness centrality of the red node can increase if peripheral connections amongst its neighbours are removed (configuration 3). Connectivity matrices are shown below their respective networks, with the first node being defined as the central red hub, the second node as the white node ‘northwest’ of the red node, and each of the remaining five nodes being counted clockwise in the network. Note that self-connections and bi-directional paths are ignored. (B) Calculations of betweenness centrality values for the examples in A. Once again, self-connections and bi-directional paths are ignored. If two paths tie for the shortest route between two white nodes then both are counted toward the denominator of the betweenness centrality calculation. (C) Brain regions with the top 10% values of betweenness centrality for control patients, superimposed onto a standard MNI 152 T1 atlas. (D) Eigenvector centrality is high for nodes that connect to other nodes that are themselves highly connected (configuration 2). The eigenvector centrality of the red node decreases if its neighbours lose connectivity with their surrounding nodes (configuration 1). The eigenvector centrality of the red node is not affected if the hubs to which it is connected lose peripheral connections, as the central nodes in the hubs remain fully connected (configuration 3).

It is unclear which graph metrics are the most neurologically informative and how these relate to cognitive impairment after TBI (Rubinov and Sporns, 2010). We have previously studied the graph theoretical properties of brain network activity after TBI using functional MRI, showing reductions in betweenness centrality after TBI within the posterior cingulate cortex—a major hub region (Pandit et al., 2013). Here, we extend this work by comprehensively examining the graph theoretical properties of network structure after TBI, with the integrity of network connections defined using DTI.

We used a method of estimating traumatic axonal injury after TBI that does not involve tractography in patients, and so is robust to the artefacts in tracts produced in patients with low fractional anisotropy (Squarcina et al., 2012). We tested the hypotheses that changes in graph metrics following traumatic axonal injury would: (i) accurately differentiate patients with a previous history of TBI from healthy age-matched controls; and (ii) predict the extent of clinically significant cognitive impairment commonly seen following TBI. We began by mapping the location of traumatic axonal injury in a similar way to previous work (Kinnunen et al., 2011), an important initial step in interpreting the subsequent graph theoretical results. We hypothesized that traumatic axonal injury would impact most severely on the structural connections of hubs, defined in this study as brain regions showing high betweenness centrality. Therefore, we also expected to see graph metrics that describe the degree to which brain regions act as hubs as being the most discriminatory in patient/control classification, and as being the most predictive of neuropsychological outcome.

Material and methods

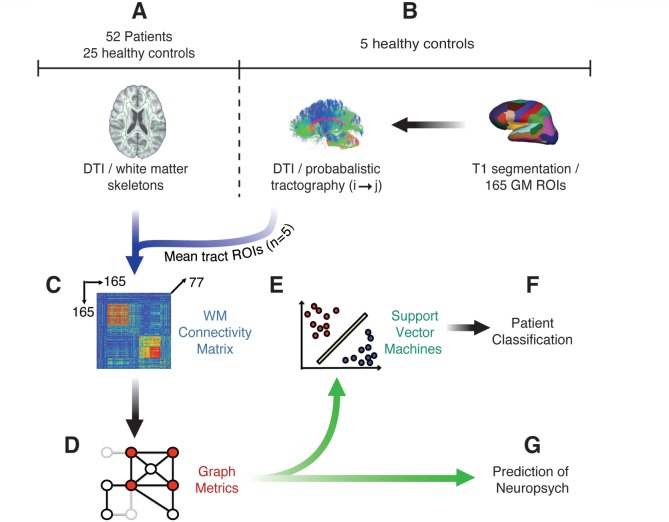
A high-level overview of our methods is provided in Fig. 2. Probabilistic tractography of DTI, performed in an independent group of five healthy control subjects, was initially used to define an atlas of masks covering the location of ∼11 000 tracts between 165 cortical and subcortical grey matter regions (Fig. 2B). This tract atlas was applied to fractional anisotropy maps preprocessed with tract-based spatial statistics (TBSS) for a separate set of 25 healthy controls and 52 patients with TBI, 21 of whom were assessed as having likely traumatic axonal injury on the basis of the presence of microbleeds on T2* imaging (Fig. 2A) (Smith et al., 2006). In this way, an individual 165-region white matter connectivity matrix was produced for each subject (Fig. 2C). Graph metrics were calculated from these connectivity matrices using the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). The metrics were then used as: (i) training variables in support vector machines (SVMs) (Fig. 2E) for patient/control differentiation (Fig. 2F); and (ii) predictor variables for regression analysis of neuropsychological outcome following TBI (Fig. 2G).

Figure 2.

Figure 2

Open in a new tab

Overview of methods. (A) Skeletonized fractional anisotropy maps were estimated for 21 patients with TBI with microbleed evidence of traumatic axonal injury and 25 healthy controls using TBSS. (B) Probabilistic tractography was used to define the location of tracts between 165 grey matter (GM) regions of interest (ROIs) in five separate healthy control subjects. These tracts were thresholded and binarized to form masks of individual white matter tracts, which were used to sample fractional anisotropy within each tract at the intersection between white matter skeletons and the tract mask. (C) A white matter (WM) adjacency matrix was filled with fractional anisotropy values for the connections between each of the 165 brain regions for every subject. (D) Graph metrics were calculated from the adjacency matrices. (E and F) Support vector machines were trained to differentiate between TBI patients and controls. (G) Graph metrics were regressed against neuropsychological testing data.

Subjects

Fifty-two TBI patients (n = 35 males, mean age ± SD 36.90 ± 11.75 years) with no present or previous drug or alcohol abuse and no neurological or psychiatric disorders prior to injury were included in this study. Structural MRI was acquired on average 37.56 months after injury. All subjects were assigned a moderate/severe classification of injury severity according to the Mayo Classification System (Reitan, 1958). Microbleeds, which are often considered as a surrogate marker of traumatic axonal injury in the absence of clear ground truth, are plainly visible on T2* sensitive gradient echo sequences. Twenty-one patients showed microbleeds on T2* images, as assessed by a senior neuroradiologist. Details of structural MRI findings and mechanism of injury are shown in Supplementary Table 1. Initial analyses were run on the group of microbleed patients, as these provided a group with high confidence of the presence of traumatic axonal injury. We then extended the cognitive analyses to the larger group of non-microbleed patients to test whether the optimal combination of graph metrics defined on the microbleed group generalized to predict cognitive function in the new group of patients. Seven of the 21 microbleed patients showed evidence of contusions. As the presence of contusions could potentially act as a confound in the results, all analyses were repeated for groups of patients with and without contusions. In addition, 25 age-matched control subjects (n = 12 males, mean age ± SD 33.40 ± 10.20 years) with no history of neurological or psychiatric disorder were recruited. All subjects provided written, informed consent prior to recruitment. The Hammersmith, Queen Charlotte’s and Chelsea Research Ethics Committee gave ethical approval for this study.

Image acquisition protocols

All subjects underwent standard T1, T2* and diffusion weighted imaging according to the following parameters: T1 images were collected using standard stock Philips sequences with a matrix of 208 × 208, in-plane resolution: 0.93 mm × 0.93 mm. 150 slices, with thickness 1.2 mm, repetition time = 9.685 ms, echo time = 4.59 ms. T2* imaging was collected using a T2*-weighted fast gradient echo sequence with a matrix of 512 × 512 in-plane resolution 0.45 mm × 0.45 mm. Twenty-four slices with thickness 4 mm, slice gap 1 mm, repetition time = 718 ms, echo time = 16 ms. Diffusion-weighted imaging was collected using four runs for diffusion-weighted volumes, with gradients applied in 16 non-collinear directions, for a total of 64 directions for each subject. Standard scanning protocols were used and the following settings applied for all scans: b-value = 1000, four images with no diffusion weighting (b = 0 s/mm2) were interleaved between blocks of 16 diffusion directions, 73 contiguous slices, slice thickness = 2 mm, matrix 128 × 128 (voxel size = 1.75 × 1.75 × 2 mm3) and field view 224 mm. All imaging data were obtained with a Philips Intera 3.0 T MRI scanner with an 8-channel array head coil. Sensitivity encoding (SENSE) was used with an under-sampling factor of 2.

Neuropsychological assessment

Patients and a subset of healthy controls underwent a detailed battery of standardized neuropsychological tests either on the same day or within a few days of their MRI scanning. In this study we focused our analysis on three measures of cognitive function: (i) information processing speed using accurate response median reaction times in a visual choice reaction task; (ii) executive function using the Trail Making Test alternating switch-cost index; and (iii) associative memory using the immediate recall measure of the People Test of the Doors and People Test (Reitan, 1958; Baddeley et al., 1994; Hellyer et al., 2013). We selected these particular tests because they are sensitive to cognitive impairment following TBI and because we have previously studied them extensively in relation to TBI (Kinnunen et al., 2011; Hellyer et al., 2013).

Probabilistic tractography

Abnormalities in DTI measures produced by TBI can bias the estimation of tractography in patient groups (Squarcina et al., 2012). Therefore, to generate an unbiased atlas of tracts, we performed probabilistic tractography between 165 cortical and subcortical grey matter regions in an independent group of five healthy control subjects (n = 2 males, mean age ± SD 31.00 ± 12.06 years) (Fig. 2B). The same T1 and DTI sequences as reported for the main study were acquired on the same scanner. All subjects gave informed consent.

Briefly, structural T1 images were segmented into 165 cortical and subcortical grey matter masks according to the Desikan-Kilaney grey matter atlas, using Freesurfer (Desikan et al., 2006; Greve and Fischl, 2009). Grey matter masks were transformed to native diffusion space by application of an affine registration between T1 and diffusion space, calculated using boundary-based registration from Freesurfer (Greve and Fischl, 2009). Each of these masks was used as a seed and target region for probabilistic tractography performed, using a two-crossing fibre model in Probtrack (Behrens et al., 2003). For each mask/target pair, 5000 streamlines were randomly seeded from each voxel within the seed mask. Only streamlines that reached any voxel within the target mask were retained. This process was iterated over each seed/target pair. Where no seed streamline reached any target voxel, probability distributions were discarded, resulting in an atlas for each subject containing a total of 11 604 tracts (5476 interhemispheric, 6128 within hemispheres). For each subject, each of these tracts was projected into MNI-152 space using FLIRT and averaged across the group, generating a mean distribution for the location of each tract across the five control subjects. To create masks from which fractional anisotropy could be sampled in the patient/control experimental groups, these tract distributions were thresholded and binarized such that the top 5% strongest voxels within the distribution were retained, providing a conservative estimate of the location of the tracts within MNI-152 space.

Estimation of individual connectivity matrices

Diffusion imaging for patients and age-matched controls were preprocessed according to standard protocols using the FMRIB Diffusion Toolbox (FDT) (Behrens et al., 2003). As a first step, a tensor model was fitted to the raw diffusion data (using the FDT) to create fractional anisotropy images, which were then brain-extracted using the brain extraction tool (BET) (Smith, 2002). The FMRIB non-linear registration tool was then used in aligning the fractional anisotropy data from all subjects into a common space using a b-spline representation of the registration warp field (Rueckert et al., 1999; Andersson et al., 2007). Next, the thinned mean fractional anisotropy images were used to create a mean skeleton, representing the centres of all tracts common to the group. The tract atlas generated by probabilistic tractography was then projected through individual skeletons in MNI-152 standard space and the mean fractional anisotropy at the intersection of the tract and mask calculated, allowing for the estimation of individual connectivity matrices (Squarcina et al., 2012).

We explored the effects of varying network sparsity by thresholding the fractional anisotropy matrices generated for patients and controls at different levels. Matrices were thresholded in terms of standard deviations of fractional anisotropy values below the mean of the control group. A range of standard deviation multiples was used, from 0.5 to 5.0 in steps of 0.5 (i.e. decreasing penalization with increasing threshold). Connections from each individual’s connectivity matrix that were smaller than the given threshold were set to 0. The inclusion of the weakest fractional anisotropy values in connectivity matrices may sometimes result in overfitting due to increased noise levels (Li et al., 2013). As such, we ran our analyses for a range of different thresholds, in order to demonstrate that the results remained consistent once the weaker fractional anisotropy values were eliminated from the data.

Furthermore, we tested the robustness of results using different initial parcellation schemes. These were created by combining pairs of adjacent regions to generate a scheme with approximately half the number of regions. Average fractional anisotropy values for the tracts from the new combined regions were then re-estimated. As all regions have more than one neighbour in the original parcellation scheme, the adjacent regions used to create the new averaged scheme were selected at random. This process was performed twice with different randomly selected adjacent regions. This resulted in two new sets of connectivity matrices (sizes 91 × 91 and 92 × 92) for all subjects.

Voxelwise diffusion tensor imaging analysis

Voxelwise analysis of the fractional anisotropy was carried out using TBSS in the FMRIB Software Library Diffusion Toolkit (Smith et al., 2004). Briefly, the steps involved in TBSS preprocessing were as follows: (i) all subjects’ fractional anisotropy data were aligned into a common space using the FMRIB non-linear registration tool, which uses a b-spline representation of the registration warp field; (ii) the group mean registered fractional anisotropy image was thinned to create a mean fractional anisotropy skeleton that represents the centres of all tracts common to the group; and (iii) each subject's aligned fractional anisotropy data were then projected onto this skeleton. Non-parametric permutation-based statistics were used to explore differences in fractional anisotropy between patients and controls, using FMRIB’s randomize function with 5000 unique permutations (Smith, 2002). Multiple comparison correction was performed using threshold-free cluster enhancement and thresholded at P < 0.05 for presentation. A detailed description of the voxelwise analysis of this group of patients has previously been presented (Hellyer et al., 2013).

Graph theoretical analysis

A total of 24 graph metrics (Fig. 2D) were calculated from the white matter connectivity matrices (Fig. 2C). Only graph metrics applicable to undirected connectivity matrices were used, as fractional anisotropy does not provide information about the directionality of water diffusion. It is unknown, a priori, whether binary or weighted metrics are more useful for accurate classification. Weighted connections reflect more information about the range of fractional anisotropy values, whereas binary metrics make fewer assumptions about the relationship between fractional anisotropy and graph topology. Given this uncertainty, both binary and weighted versions of applicable metrics were included in the analyses.

Summaries of all graph metrics used in this study are provided in Supplementary Table 2 and more in-depth descriptions of the metrics in the Supplementary material. In brief, the simplest graph metric is ‘degree’, defined as the number of neighbours connected to a given node (Göttlich et al., 2013; Jan et al., 2013; Vives-Gilabert et al., 2013). ‘Strength’ is closely related to degree, but with the weightings (here mean fractional anisotropy values) of the connections taken into account (Hwang et al., 2013; Goñi et al., 2014; Xue et al., 2014). A number of graph metrics build upon the concept of ‘path length’. If nodes A and B are separated by one other node C, then the path length between A and B is equal to 2 (regardless of physical distance), as a total of two edges must be traversed. ‘Betweenness centrality’ is a metric that depends upon the deconstruction of a graph into path lengths and is defined as the ratio of the number of shortest paths passing through a given node to the total number of shortest paths between all other nodes in the network. Another measure of network hubs that has gained considerable attention in recent years with the rise of the page-rank algorithms of internet search engines is ‘eigenvector centrality’. This is a self-referential metric that assigns a high level of importance to a node if it is connected to other nodes that are themselves important.

Support vector machine analysis: identification of TBI

We investigated which graph metrics produced the most accurate classification of patients and controls. This was performed using SVMs implemented in the LIBSVM classification library (Platt, 1999; Chang and Lin, 2011). We used a linear kernel, as this allows for interpretation of the weight vector (i.e. the relative importance of each feature in the prediction), which was subsequently used to rank the importance of the metrics in identifying TBI. SVMs were initially trained using all 24 (network average) graph metrics, as derived from white matter connectivity matrices. To identify the most informative metrics, after each round of SVM training, the least important metric (in terms of its weight vector) was removed and a new SVM trained with the remaining metrics. This process was repeated until only a single metric remained. The accuracy of the classifier was recorded at each stepwise removal. Data from healthy controls and patients with microbleeds were used to train the SVMs. We used repeated random subsampling validation, with a random selection of n subjects removed from both the patient and control group for each machine, repeated 1000 times for each n from 1 to 10. We tested a range of training/validation split sizes because leave-one-out cross-validation methods, although low in bias, are sometimes associated with high degrees of variance (Cawley, 2006).

We then investigated which brain regions were the most important for the identification of TBI. This was achieved by calculating the vector output (i.e. 165 values per subject) of the most influential metric in the combination of metrics with the highest classification accuracy. This resulted in one value of the graph metric being assigned to each of the 165 brain regions across all subjects. We then performed a t-test across brain regions to assess which of the 165 brain regions were significantly different (in terms of their graph metric outputs) between patients and controls. Each t-test was performed at a significance level of 5%. Multiple comparison correction was performed via the false discovery rate (FDR) method, at a significance level of 5%.

Prediction of cognitive outcome

Next, we explored whether graph metrics could be used to predict cognitive outcome following TBI. We used variable selection via the elastic net at various degrees of regularization to associate linearly independent graph metrics with each of the three behavioural measures considered, using the MATLAB Statistics Toolbox (MathWorks; Zou and Hastie, 2005). Model accuracy was assessed by the explained variance and statistical significance of the model with the minimum mean squared error. We then investigated the influence of individual brain regions in predicting clinical outcome. This was achieved by using variable selection and regularization via the elastic net for the vector output of the most influential metric (i.e. with the highest regression coefficient) against neuropsychological testing data. We used an elastic net fit with α = 0.5 and 10-fold cross-validation and display results for a range of the Lambda shrinkage parameter. Further details on the elastic net are provided in the Supplementary material. This allowed us to track the effect that increasing penalization has on the relative importance of graph metrics in predicting cognitive outcome. The exclusion of a certain graph metric at one value of Lambda does not necessarily mean that it is redundant across all models, as a change in the shrinkage parameter Lambda may result in it reappearing in a different combination of metrics. This is advantageous, as the exclusion of a graph metric at one value of Lambda does not mean it is ‘lost’ going forward, as would be the case with stepwise regression techniques. Rather, we were able to treat each new level of shrinkage in a ‘blind’ manner and assess the relative importance of the non-redundant metrics within each new model. The cross-validation technique allows us to track the mean squared error of the elastic net fitting across the explored range of Lambda. We can thereby arrive at an optimal value of Lambda, for which the associated combination of graph metrics achieves minimum mean squared error. Regression was performed first for the subset of healthy controls and patients with microbleeds for which neuropsychological testing data were available (choice reaction task: n = 28, executive function: n = 29, associative memory: n = 29), and then separately for the subset of controls and the larger group of patients without microbleeds for which neuropsychological testing data were available (choice reaction task: n = 40, executive function: n = 50, associative memory: n = 52).

Definition of network hubs

Next we wished to explicitly test the hypothesis that the brain regions identified in the analyses function as network hubs. As such, we identified the regions with the highest values of betweenness centrality in the healthy control group. Network hubs were defined as being in the top 10% of betweenness centrality values for all of the regions investigated.

Results

Evidence of traumatic axonal injury in the patient group

Microbleeds are a marker of underlying traumatic axonal injury. Therefore, we expected the voxelwise analysis of fractional anisotropy in patients with TBI to show evidence of abnormal DTI. We have previously shown that fractional anisotropy is reduced in groups of patients with microbleeds (Kinnunen et al., 2011) and, as expected, our TBI group showed widespread significant reductions in fractional anisotropy across most of the white matter (Fig. 3). In keeping with previous work, peaks of statistical difference between the groups were seen in the corticospinal tracts, forceps major, left inferior fronto-occipital fasciculus, uncinate fasciculus, anterior thalamic radiation, and cingulum bundle (Supplementary Table 3). These results suggest that structural damage to white matter connections partially disconnects brain networks, in particular affecting long-range connections, which would be expected to impact significantly on graph metrics.

Figure 3.

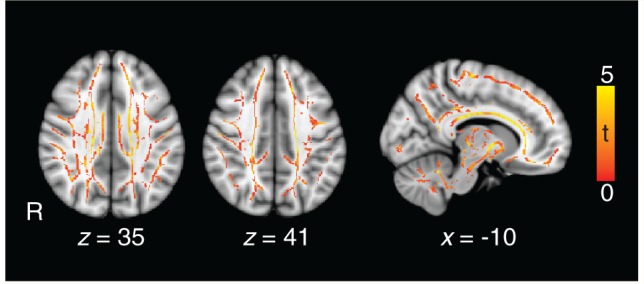
Figure 3

Open in a new tab

Evidence of traumatic axonal injury in patients. The contrast of patients against controls shows white matter where fractional anisotropy is significantly lower (red/yellow), providing evidence for the presence of traumatic axonal injury. T-scores show where P < 0.05 (corrected for multiple comparisons using threshold-free cluster enhancement). Significant differences are shown superimposed on a green white matter skeleton and the standard MNI 152 T1 atlas.

Identification of traumatic axonal injury from graph metrics

We next assessed whether graph metrics could be used to differentiate patients and controls. Through stepwise removal of graph metrics we were able to arrive at an optimal combination that identified patients in 93.4% of cases (Fig. 4). This is comparable to the sensitivity that can be achieved (94%) using raw voxelwise fractional anisotropy measures in a similar SVM framework (Hellyer et al., 2013). The top performing SVM achieved high accuracy for different training/validation split sizes of repeated random subsampling validation (Supplementary Table 4). Progressive removal of the first 16 graph metrics (in order of increasing feature importance) increased classification accuracy, as a result of reduced overfitting in the SVMs. Betweenness centrality had the highest feature importance within the most accurate combination of graph metrics, with the value of its weight vector lying >1 SD above that of the next highest metric. SVM accuracy decreased when additional metrics were either added or subtracted from the optimal combination. Using random permutation testing, the most accurate SVM was significant (P < 0.001) with high accuracy for all white matter connectivity matrix thresholds considered (Supplementary Table 5). In almost all combinations of metrics, either binary or weighted betweenness centrality had the highest feature importance. For the best performing SVM in the microbleed group, the peri-callosal part of the cingulate gyrus (encompassing both anterior and posterior regions adjacent to the corpus callosum), the right inferior and middle frontal regions and the left caudate region showed significantly decreased betweenness centrality for patients versus healthy controls (Fig. 4B) (FDR P = 0.05). In contrast, the brainstem showed a significant increase in betweenness centrality (FDR P = 0.05) for patients versus healthy controls. Qualitatively similar results were observed for the subgroup of patients without contusions, with the most accurate machine being significant (P < 0.001) across the same range of fractional anisotropy thresholds (Supplementary Table 5). The bilateral caudate and peri-callosal cingulate gyrus were in the top 10% of betweenness centrality values (Fig. 1C), suggesting that the effects of traumatic axonal injury affects network hub regions with respect to patient/control classification.

Figure 4.

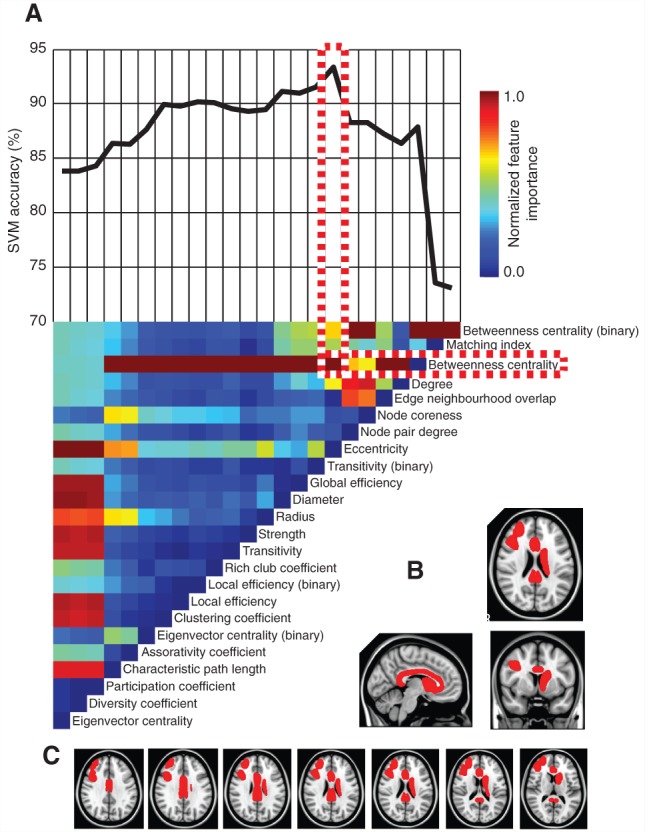
Figure 4

Open in a new tab

Prediction of traumatic axonal injury using graph metrics. (A) The vertical colour bar (top left) represents the relative feature importance of all graph metrics when used together in training a SVM to differentiate between patients and healthy controls. Eigenvector centrality was found to be the least important feature and was removed from the training data. The vertical colour bars (A, bottom) represents the relative (renormalized) feature importance of each of the remaining 23 metrics for a retrained SVM. This stepwise removal of least influential metrics was repeated until a single metric (binary betweenness centrality) remained. At each stage of metric removal, the accuracy of the retrained SVMs was recorded above the colour bars. The most influential metric (betweenness centrality) is outlined in red and white, within the combination of metrics that yielded the highest achievable SVM accuracy. (B) Sagittal, coronal and axial brain slices with brain regions overlaid in red where betweenness centrality was significantly lower in patients with microbleed evidence of TBI, for the optimal combination of graph metrics in A. (C) Additional axial brain slices as in B.

Prediction of behaviour

Information processing speed: choice reaction task

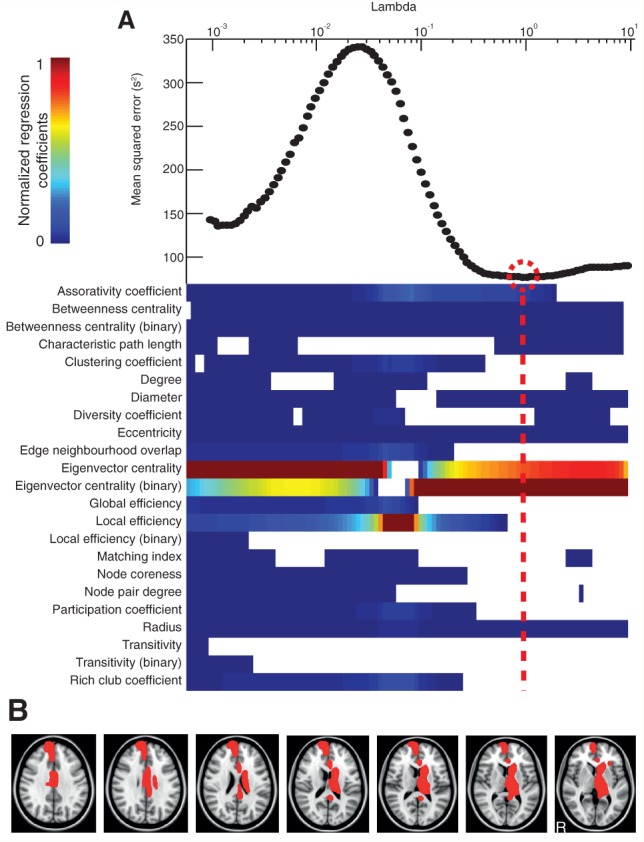
Eigenvector centrality (binary) was found to be the most influential metric in the model with the lowest mean squared error in predicting information processing speed (P = 0.01, R2 = 0.64), with its regression coefficient lying >2 SD above that of the next highest metric in the optimized selection (Fig. 5). The results remained significant when one potential outlier with information processing speed > 3 SD above the group mean was excluded (P = 0.02, R2 = 0.61). Results were qualitatively similar for the subgroup of patients without contusions, in which eigenvector centrality (binary) was the most influential metric (regression coefficient lying > 2 SD above that of the next highest metric) in the combination with the lowest mean squared error (P < 0.01, R2 = 0.83). Eigenvector centrality (binary) fell with slowing information processing speed in the left peri-callosal region, right cingulate cortex (anterior and posterior) and right superior frontal gyrus. Scatter plots showing the relationship between eigenvector centrality (binary) and information processing speed in these regions are shown in Supplementary Fig. 1.

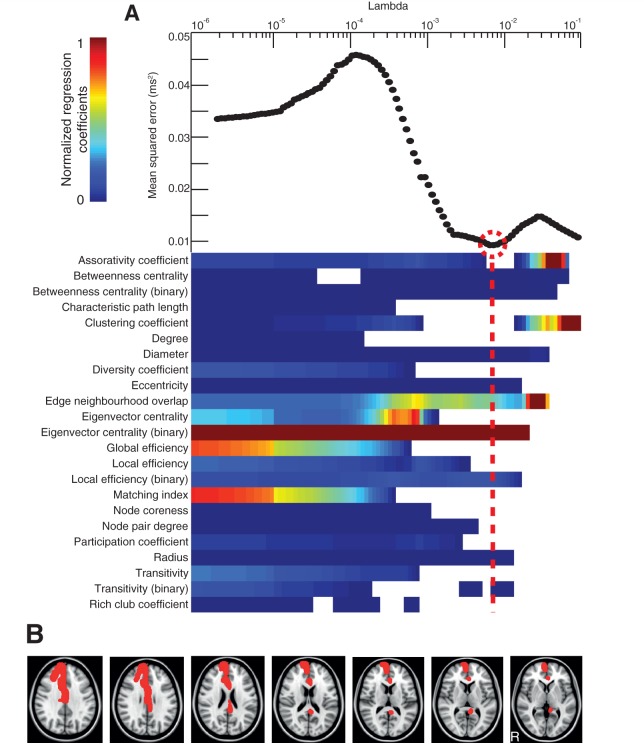
Figure 5.

Figure 5

Open in a new tab

Prediction of reaction time on the choice reaction task. (A, bottom) The relative importance of graph metrics in the regression against reaction time via elastic net. The regularization is performed at 100 different levels of penalization (Lambda)—with increasing penalization from left to right. The colour bar limits are renormalized for every new level of penalization, with hotter colours representing higher regression coefficients. Top: the mean squared error is plotted for every value of Lambda. (B) Axial brain slices with brain regions overlaid in red where reduction in eigenvector centrality (binary) significantly predicted reaction time on the choice reaction task.

Executive function

As with information processing speed, eigenvector centrality (binary) was the most influential measure (2 SD above that of the next highest metric) in explaining executive function in the combination of metrics with the lowest mean squared error (P = 0.03, R2 = 0.56) (Fig. 6). Results were qualitatively similar for the subgroup of patients without contusions, in which eigenvector centrality (binary) was the most influential metric (regression coefficient lying 2 SD above that of the next highest metric) out of the combination with the lowest mean squared error (P = 0.02, R2 = 0.73). Eigenvector centrality (binary) fell with deteriorating executive function in the left peri-callosal region, right superior frontal gyrus, left thalamus, left caudate, left insula and right cingulate cortex. Scatter plots showing the relationship between eigenvector centrality (binary) and executive function in these regions are shown in Supplementary Fig. 2.

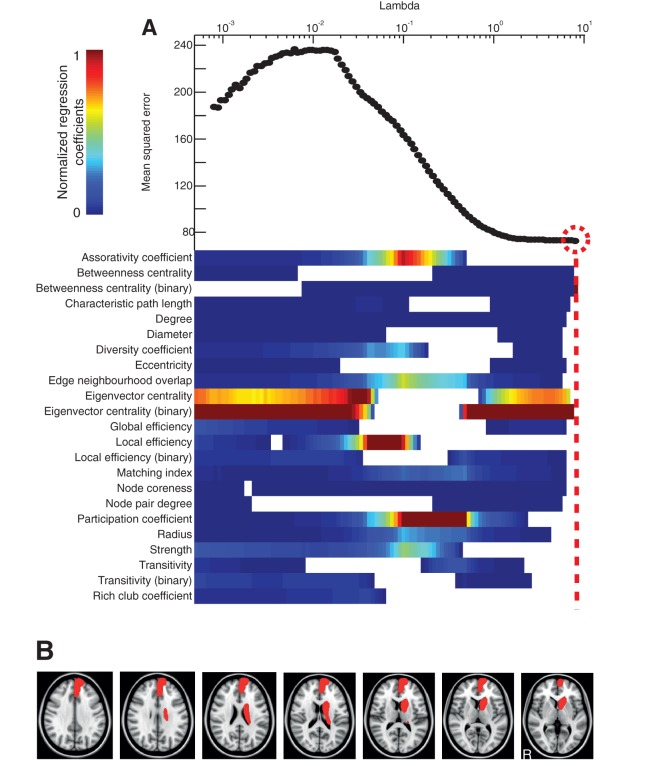
Figure 6.

Figure 6

Open in a new tab

Prediction of executive function. (A) Regression of graph metrics against executive function via elastic net as described in Fig. 5. (B) Axial brain slices with brain regions overlaid in red where reduction in eigenvector centrality (binary) significantly predicted executive function.

Associative memory

Betweenness centrality (binary) in isolation had the lowest mean squared error in predicting associative memory (P < 0.01, R2 = 0.25) (Fig. 7). Similar results were observed for the subgroup of patients without contusions, in which betweenness centrality (binary) in isolation had the lowest mean squared error in predicting associative memory (P < 0.01, R2 = 0.54). Betweenness centrality (binary) fell with deteriorating associative memory in the left superior frontal gyrus, left orbitofrontal cortex and left caudate. Scatter plots showing the relationship between betweenness centrality (binary) and associative memory in these regions are shown in Supplementary Fig. 3.

Figure 7.

Figure 7

Open in a new tab

Prediction of associative memory. (A) Regression of graph metrics against executive function via elastic net as described in Figs 5 and 6. (B) Axial brain slices with brain regions overlaid in red where reduction in betweenness centrality (binary) significantly predicted associative memory.

Replication cohort and alternative parcellation schemes

The best predictive models for the cognitive analyses from the microbleed positive group of patients were ‘locked’ and applied to a completely separate group of moderate/severe TBI patients without microbleeds. The same entry variables (i.e. graph metrics) were used but the coefficients in the multiple linear regression models were allowed to vary. The application of these models to the new data showed a significant association between graph metrics and information processing speed (P = 0.02, R2 = 0.44), executive function (P < 0.01, R2 = 0.47) as well as associative memory (P < 0.01, R2 = 0.18). For information processing speed and executive function there were significant associations between cognitive performance and eigenvector centrality (binary) in similar regions for both the microbleed and non-microbleed cohorts. For information processing speed all regions showing a significant association in the microbleed group also showed a significant association in the non-microbleed group (Supplementary Fig. 4). In addition, the left frontal pole also showed a significant association. For executive function there were significant associations in all regions except for the left insula (Supplementary Fig. 5). In addition, there was a significant association for the region around the left anterior collateral sulcus. The regions in which betweenness centrality (binary) showed significant associations with memory in the microbleed group failed to show significant associations in the non-microbleed group. However, the right precuneus showed a significant association (Supplementary Fig. 6). The results were also robust to both alternative parcellation schemes used, with the optimal combination of metrics being significant for patient classification (P < 0.001) and neuropsychological assessment, with choice reaction task (P < 0.02, R2 > 0.48), executive function (P < 0.03, R2 > 0.22) and associative memory (P < 0.03, R2 > 0.36) across the two alternative parcellation schemes.

Discussion

The brain can be described as a complex network with white matter tracts connecting brain regions. TBI often damages white matter tracts, as a result of traumatic axonal injury (Kinnunen et al., 2011; Bonnelle et al., 2012; Squarcina et al., 2012). This type of damage affects the function of brain networks and is often associated with poor clinical outcome (Sharp et al., 2014). An important goal is to identify the relationship between complex varying patterns of axonal injury and abnormal behaviour. Widespread white matter damage is often present after TBI (Kinnunen et al., 2011), as we have again demonstrated here. However, the cognitive effects of this damage to brain network connections are unclear. Graph theory provides an elegant way of describing complex networks and so is potentially an informative way of investigating the effects of traumatic axonal injury on network structure and function (Caeyenberghs et al., 2012; Pandit et al., 2013). A wide range of graph metrics have been developed for the analysis of brain networks, but it is uncertain which are the most biologically informative (Rubinov and Sporns, 2010). In this study, we performed a comprehensive analysis of changes in graph metrics following TBI, demonstrating that graph metrics can be used to predict the presence of TBI and explain significant amounts of individual variability in cognitive impairment following TBI. Hub regions within the brain are high cost and high value, and are particularly vulnerable to abnormality across a range of disorders (Crossley et al., 2014). Our findings converge with our previous study of brain function after TBI, and suggest that cognitive impairment is particularly produced after TBI when highly connected hub regions such as the cingulate cortex and caudate nuclei are disconnected as a result of axonal injury (Pandit et al., 2013).

Betweenness centrality and eigenvector centrality were prominently affected by TBI. The relationship between white matter disruption and betweenness centrality is potentially complex, but can be better understood by considering a simplified example of a brain network (Fig. 1). In the fully connected version of this toy network (Fig. 1A), the central hub node is connected to all other nodes. White matter injury has the effect of removing or damaging connections in the network, which is illustrated by the removal of edges. The effect of this disconnection depends on the type of connections removed. If connections to the central node are affected (hub disconnections), then the betweenness centrality of the central node decreases, as fewer shortest paths now pass through that region. In contrast, if connections at the edge of the network (peripheral disconnections) are removed, then this has the effect of increasing the central node’s betweenness centrality, due to a larger number of shortest paths passing through the region. Similar increases or decreases in betweenness centrality could theoretically be produced by the addition of new connections. However, this is unlikely to be relevant to the interpretation of network changes following TBI, as although brain plasticity can produce new synaptic connections after TBI at the microscopic level, new large-scale white matter tracts do not tend to form (Wieloch and Nikolich, 2006; Kinnunen et al., 2011). Eigenvector centrality is also affected by disconnections within the simplified network shown in Fig. 1D. Eigenvector centrality measures a form of ‘nested’ connectivity, whereby a node’s eigenvector centrality is dependent on the number of connections made by its neighbours. As such, the eigenvector centrality of the central node in the toy network decreases if its neighbours suffer hub disconnections, but remains unaffected if they suffer peripheral disconnections. In other contexts this definition of centrality has proved valuable in analysing the importance of individuals within social networks by measuring the importance of their acquaintances, as well as in determining the importance of websites in page rank algorithms i.e. by calculating how many high profile websites link back to a given site.

Across our analyses we found that reductions in the betweenness centrality and eigenvector centrality of highly connected hub regions were prominently associated with the presence of TBI and/or greater cognitive impairment across TBI patients. As predicted, reductions in betweenness centrality and eigenvector centrality were particularly observed in parts of the cingulate cortex. Other brain hubs were also related to cognitive function, the caudate (associative memory) and the thalamus (processing speed). These hubs have high metabolic rates and are thought to be important for the integration of information processing by connecting neural processing in functionally distinct intrinsic connectivity networks (Raichle and Snyder, 2007; van den Heuvel and Sporns, 2013; Leech and Sharp, 2014). As shown by our simplified example, reductions in the betweenness centrality of hub regions signify disconnections of hubs from the rest of the network, in keeping with the voxelwise TBSS analysis that provides evidence of widespread white matter damage. Similarly, generalized disconnection of hubs would reduce eigenvector centrality. As network hubs are a central part of a high-capacity backbone for global brain communication, damage to their connections would have the effect of reducing the ability of the brain to efficiently transmit information, by increasing the number of connections it takes for one region to communicate with another (van den Heuvel et al., 2012). Therefore, our results suggest that the relative disconnection of network hubs by traumatic axonal injury is an important mechanism by which long-term cognitive impairment in the domains of information processing, memory and information processing speed are produced.

The brainstem showed an increase in betweenness centrality in following TBI. This is a highly connected region that participates in a large number of shortest paths between other brain regions, and therefore should be viewed as a network hub (Fig. 1C). The brainstem’s betweenness centrality may increase as a result of traumatic axonal injury on other nodes which are situated more centrally in the graph. If more of the shortest paths between other regions are damaged as a result of traumatic axonal injury, it is possible that a larger number of shortest paths may pass through the brainstem post injury. This effect might be accentuated by the eccentric position of the brainstem in the graph, as illustrated by the effect of peripheral disconnection in our simplified model (Fig. 1A and B).

We have previously shown, in an overlapping group of subjects, that the betweenness centrality of the posterior cingulate cortex is reduced following TBI in graphs generated from functional MRI data (Pandit et al., 2013). In this study, connectivity was assessed between regions involved in cognitive control, rather than across the whole brain. A similar graph theoretical analysis to the current study showed evidence for a shift away from a small-world architecture, with reduced network efficiency and increased path lengths, associated with a marked reduction in betweenness centrality within the posterior cingulate cortex. In the current work, our results provide convergent evidence from measures of structural connectivity for the importance of betweenness centrality as a measure of network dysfunction after TBI, and also highlight the importance of disruption to the cingulate cortex region in the long-term effects of TBI. Structural and functional connectivity are highly related, with regions showing dense white matter connections being likely to exhibit highly synchronized brain activity (high functional connectivity) (van den Heuvel et al., 2009). Therefore, changes in betweenness centrality seen in functional brain networks are likely to reflect the underlying structural disconnection of the same regions produced by traumatic axonal injury.

Our results are broadly in keeping with another recent study that used graph theoretical analysis of DTI data to demonstrate cognitively important network abnormalities after TBI (Caeyenberghs et al., 2014). Their results also suggested that TBI showed network features in keeping with a less efficient capacity to integrate information across the brain. We extend this work by using machine learning techniques to identify the most biologically important graph metrics in a data-driven way. We also explicitly explore the relationship between changes in graph metrics, and the extent to which affected regions are indeed functioning as network hubs. Finally, we use a distinct way of assessing underlying fractional anisotropy, which is less prone to artefacts than other existing methods.

The graph theoretical results we explored are dependent on the accuracy of the underlying DTI analyses. A particularly important factor is how accurately the amount of damage in each white matter tract can be estimated in the TBI patients. Graph analysis can be calculated from connectivity matrices derived from tractography performed in individual patients. This approach has the potential limitation that tractography may fail or produce spurious results when tracts are damaged, as low fractional anisotropy values generate significantly increased uncertainty for the tractography algorithms (Hua et al., 2008; Squarcina et al., 2012). To avoid this confound, we used a method for estimating tract structure that does not involve tractography performed in the patient group, but instead involves the generation of tract templates in an independent group of healthy controls, which may then be used as a mask to sample fractional anisotropy in the patient population (Squarcina et al., 2012). This approach depends on accurate registration between standard and patient space, which we achieve using non-linear registration algorithms that we have previously found to be highly accurate when applied to DTI data (Bonnelle et al., 2012).

A potential limitation in our study is the presence of partial volume effects, which are present if the registration of individual images into standard space is not sufficiently accurate. We deal with this issue by using TBSS to skeletonize the white matter tracts, thereby minimizing the chance of partial volume effects, due to the fact that only the centres of the tracts are being included in the analysis. However, by dealing with one potential limitation in this way, we produce a second. Axonal injury can occur at the boundaries between grey and white matter, and this will not be identified by our TBSS analysis. This could lead to an overestimation of tract integrity, as areas of damage are not identified. It will be important for further work to investigate this possibility using alternative methods. A further issue is the presence of cortical contusions in some of the patients. To rule out any related confound, we conducted our main analyses both with and without contusion patients, resulting in qualitatively similar results, showing the consistent importance of both betweenness centrality and eigenvector centrality in the context of this work. It is also possible that the machine learning techniques produce a solution that is only relevant to the group of subjects used in the training phase. However, the results were robust to varying the number of subjects left out in the cross-validation, making this less likely to be a major issue. We also locked the best performing combination of graph metrics in the cognitive analyses and applied them to a completely new set of patients. A significant relationship remained for all neuropsychological testing data, suggesting that the findings were generalizable. The weighted and binary forms of betweenness centrality and eigenvector centrality are distinct measures and were important in the prediction of TBI and the association with neuropsychological variables, respectively. However, the distinction between the binary and weighted versions of these metrics cannot be easily interpreted in terms of any biological significance in this study, due to the high degree of correlation between the two metrics (P < 0.001).

In conclusion, our study demonstrates the importance of hub-based metrics such as betweenness centrality and eigenvector centrality as measure of network disconnection after TBI. Hub regions within the brain, which are important for integrating information processing, show reduced betweenness centrality, which in turn is related to the degree of disconnection of the hubs from the rest of the brain as a result of traumatic axonal injury. Combinations of graph metrics were able to explain large amounts of individual variability in all three cognitive domains studied, suggesting that graph metrics describing structural brain connectivity could prove to be a useful description of the underlying cause for cognitive impairments produced by TBI.

Supplementary Material

Supplementary Table 1
brain_awv075_index.html (3.1KB, html)

Acknowledgements

We thank the subjects who took part in this study.

Glossary

Abbreviations

DTI

diffusion tensor imaging

SVM

support vector machine

TBI

traumatic brain injury

TBSS

tract-based spatial statistics

Funding

The work has been supported by an MRC (UK) Clinician Scientist Fellowship (D.J.S.) and a National Institute of Health Research Professorship - RP-011-048 (D.J.S.). The research was also supported by the National Institute for Health Research (NIHR) Imperial Biomedical Research Centre. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health. This work is also supported by an MRC DTA studentship (E.D.F.).

Supplementary material

Supplementary material is available at Brain online.

References

  1. Andersson JL, Jenkinson M, Smith S. Oxford, UK: FMRIB Analysis Group of the University of Oxford; 2007. Non-linear registration, aka Spatial normalisation FMRIB technical report TR07JA2. [Google Scholar]
  2. Baddeley AD, Emslie H, Nimmo-Smith I. Doors and people: a test of visual and verbal recall and recognition. Bury St Edmunds, Suffolk, UK: Thames Valley Test Company; 1994. [Google Scholar]
  3. Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994;66:259–67. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, et al. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med. 2003;50:1077–88. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
  5. Bonnelle V, Ham TE, Leech R, Kinnunen KM, Mehta MA, Greenwood RJ, et al. Salience network integrity predicts default mode network function after traumatic brain injury. Proc Natl Acad Sci USA. 2012;109:4690–5. doi: 10.1073/pnas.1113455109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Caeyenberghs K, Leemans A, Heitger MH, Leunissen I, Dhollander T, Sunaert S, et al. Graph analysis of functional brain networks for cognitive control of action in traumatic brain injury. Brain. 2012;135(Pt 4):1293–307. doi: 10.1093/brain/aws048. [DOI] [PubMed] [Google Scholar]
  7. Caeyenberghs K, Leemans A, Leunissen I, Gooijers J, Michiels K, Sunaert S, et al. Altered structural networks and executive deficits in traumatic brain injury patients. Brain Struct Funct. 2014;219:193–209. doi: 10.1007/s00429-012-0494-2. [DOI] [PubMed] [Google Scholar]
  8. Cawley GC. Proceedings of the International Joint Conference on Neural Networks (IJCNN-2006), New York, USA. 2006. Leave-one-out cross-validation based model selection criteria for weighted LS-SVMs; pp. 1661–8. [Google Scholar]
  9. Chang C-C, Lin C-J. LIBSVM: a library for support vector machines. ACM Trans Instell Syst Technol. 2011;2:27. [Google Scholar]
  10. Crossley NA, Mechelli A, Scott J, Carletti F, Fox PT, McGuire P, et al. The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain. 2014;137(Pt 8):2382–95. doi: 10.1093/brain/awu132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31:968–80. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
  12. Goñi J, van den Heuvel MP, Avena-Koenigsberger A, de Mendizabal NV, Betzel RF, Griffa A, et al. Resting-brain functional connectivity predicted by analytic measures of network communication. Proc Natl Acad Sci USA. 2014;111:833–8. doi: 10.1073/pnas.1315529111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Göttlich M, Münte TF, Heldmann M, Kasten M, Hagenah J, Krämer UM. Altered resting state brain networks in Parkinson’s Disease. PLoS One. 2013;8:e77336. doi: 10.1371/journal.pone.0077336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Greve DN, Fischl B. Accurate and robust brain image alignment using boundary-based registration. Neuroimage. 2009;48:63–72. doi: 10.1016/j.neuroimage.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Han K, Mac Donald CL, Johnson AM, Barnes Y, Wierzechowski L, Zonies D, et al. Disrupted modular organization of resting-state cortical functional connectivity in U.S. military personnel following concussive ‘mild’ blast-related traumatic brain injury. Neuroimage. 2014;84:76–96. doi: 10.1016/j.neuroimage.2013.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hellyer PJ, Leech R, Ham TE, Bonnelle V, Sharp DJ. Individual prediction of white matter injury following traumatic brain injury. Ann Neurol. 2013;73:489–99. doi: 10.1002/ana.23824. [DOI] [PubMed] [Google Scholar]
  17. Hua K, Zhang J, Wakana S, Jiang H, Li X, Reich DS, et al. Tract probability maps in stereotaxic spaces: analyses of white matter anatomy and tract-specific quantification. Neuroimage. 2008;39:336–47. doi: 10.1016/j.neuroimage.2007.07.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hwang K, Hallquist MN, Luna B. The development of hub architecture in the human functional brain network. Cereb Cortex. 2013;23:2380–93. doi: 10.1093/cercor/bhs227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Jan H, Chao Y-P, Cho K-H, Kuo L-W. Engineering in Medicine and Biology Society (EMBC), 2013 35th Annual International Conference of the IEEE. 2013. Investigating the effects of streamline-based fiber tractography on matrix scaling in brain connective network; pp. 523–6. [DOI] [PubMed] [Google Scholar]
  20. Johnson VE, Stewart W, Smith DH. Axonal pathology in traumatic brain injury. Exp Neurol. 2013;246:35–43. doi: 10.1016/j.expneurol.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kinnunen KM, Greenwood R, Powell JH, Leech R, Hawkins PC, Bonnelle V, et al. White matter damage and cognitive impairment after traumatic brain injury. Brain. 2011;134(Pt 2):449–63. doi: 10.1093/brain/awq347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Leech R, Sharp DJ. The role of the posterior cingulate cortex in cognition and disease. Brain. 2014;137(Pt 1):12–32. doi: 10.1093/brain/awt162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Li Y, Qin Y, Chen X, Li W. Exploring the functional brain network of Alzheimer's disease: based on the computational experiment. PLoS One. 2013;8:e73186. doi: 10.1371/journal.pone.0073186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Nakamura T, Hillary FG, Biswal BB. Resting network plasticity following brain injury. PLoS One. 2009;4:e8220. doi: 10.1371/journal.pone.0008220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Pandit AS, Expert P, Lambiotte R, Bonnelle V, Leech R, Turkheimer FE, et al. Traumatic brain injury impairs small-world topology. Neurology. 2013;80:1826–33. doi: 10.1212/WNL.0b013e3182929f38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Platt JC. Advances in large margin classifiers. PA, USA: Citeseer; 1999. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. [Google Scholar]
  27. Raichle ME, Snyder AZ. A default mode of brain function: a brief history of an evolving idea. Neuroimage. 2007;37:1083–90. doi: 10.1016/j.neuroimage.2007.02.041. discussion 97–9. [DOI] [PubMed] [Google Scholar]
  28. Reitan RM. Validity of the Trail Making Test as an indicator of organic brain damage. Percept Mot Skills. 1958;8:271–6. [Google Scholar]
  29. Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52:1059–69. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
  30. Rueckert D, Sonoda LI, Hayes C, Hill DL, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans Med Imaging. 1999;18:712–21. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
  31. Sharp DJ, Scott G, Leech R. Network dysfunction after traumatic brain injury. Nat Rev Neurol. 2014;10:156–66. doi: 10.1038/nrneurol.2014.15. [DOI] [PubMed] [Google Scholar]
  32. Sidaros A, Engberg AW, Sidaros K, Liptrot MG, Herning M, Petersen P, et al. Diffusion tensor imaging during recovery from severe traumatic brain injury and relation to clinical outcome: a longitudinal study. Brain. 2008;131(Pt 2):559–72. doi: 10.1093/brain/awm294. [DOI] [PubMed] [Google Scholar]
  33. Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–55. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31:1487–505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
  35. Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–19. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
  36. Squarcina L, Bertoldo A, Ham TE, Heckemann R, Sharp DJ. A robust method for investigating thalamic white matter tracts after traumatic brain injury. Neuroimage. 2012;63:779–88. doi: 10.1016/j.neuroimage.2012.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. van den Heuvel MP, Kahn RS, Goni J, Sporns O. High-cost, high-capacity backbone for global brain communication. Proc Natl Acad Sci USA. 2012;109:11372–7. doi: 10.1073/pnas.1203593109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. van den Heuvel MP, Mandl RC, Kahn RS, Hulshoff Pol HE. Functionally linked resting-state networks reflect the underlying structural connectivity architecture of the human brain. Hum Brain Mapp. 2009;30:3127–41. doi: 10.1002/hbm.20737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. van den Heuvel MP, Sporns O. An anatomical substrate for integration among functional networks in human cortex. J Neurosci. 2013;33:14489–500. doi: 10.1523/JNEUROSCI.2128-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Vives-Gilabert Y, Abdulkadir A, Kaller CP, Mader W, Wolf RC, Schelter B, et al. Detection of preclinical neural dysfunction from functional connectivity graphs derived from task fMRI. An example from degeneration. Psychiatry Res. 2013;214:322–30. doi: 10.1016/j.pscychresns.2013.09.009. [DOI] [PubMed] [Google Scholar]
  41. Wieloch T, Nikolich K. Mechanisms of neural plasticity following brain injury. Curr Opin Neurobiol. 2006;16:258–64. doi: 10.1016/j.conb.2006.05.011. [DOI] [PubMed] [Google Scholar]
  42. Xue K, Luo C, Zhang D, Yang T, Li J, Gong D, et al. Diffusion tensor tractography reveals disrupted structural connectivity in childhood absence epilepsy. Epilepsy Res. 2014;108:125–38. doi: 10.1016/j.eplepsyres.2013.10.002. [DOI] [PubMed] [Google Scholar]
  43. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc B. 2005;67:301–20. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table 1
brain_awv075_index.html (3.1KB, html)
c6bdb81a93391bb46a7843262e51cc52_brain-2014-01275-File009.pdf (689.2KB, pdf)
fa7869103fdcf8812c02c2b34bba00c7_brain-2014-01275-File018.pdf (179.1KB, pdf)
36ee1acece0af6871d782d094a19ecef_brain-2014-01275-File019.pdf (168.1KB, pdf)
6b3921b9f6397efea0a64dc74d513131_brain-2014-01275-File020.pdf (179.6KB, pdf)
5e505a91e2db23397f34ca1db315b9bc_brain-2014-01275-File021.pdf (695.6KB, pdf)
b76f6249a7d587024358cce82a20a2d7_brain-2014-01275-File010.pdf (818.7KB, pdf)
c7df88349b741e5826d63f0080dc3324_brain-2014-01275-File011.pdf (521.4KB, pdf)
a66de2516d507644ff52e9cea19fd31c_brain-2014-01275-File012.pdf (695.4KB, pdf)
4193d3b8434d0581f9f1644e93bc0969_brain-2014-01275-File013.pdf (795.9KB, pdf)
343debe2ef70d714917c459d4fe0d877_brain-2014-01275-File014.pdf (293.8KB, pdf)
b87b05df6b91ed14bd221ed85bb3666b_brain-2014-01275-File015.pdf (97.3KB, pdf)
4c353c618a713d3ecbe1cc8076adb23c_brain-2014-01275-File016.pdf (161.1KB, pdf)
6cca03255babdd45de1ba070dec087ff_brain-2014-01275-File017.pdf (101.3KB, pdf)
621e56a9fcf405bf0ca4d9ff58a63261_brain-2014-01275-File022.jpg (644.3KB, jpg)

Articles from Brain are provided here courtesy of Oxford University Press

RESOURCES