Critical Timing without a Timer for Embryonic Development

Abstract

Timing of embryonic development is precisely controlled, but the mechanisms underlying biological timers are still unclear. Here, a validated model for timing under control of Sonic Hedgehog is revisited and generalized to an arbitrary number of genes. The developmental dynamics where a temporal sequence of gene expression recapitulates a steady-state spatial pattern can be realized through a simple network close to criticality, controlled by the duration of exposure to a morphogen. Criticality simultaneously accounts for many observed biological properties, such as timing, multistability, and canalization of genetic expression. This process can be parsimoniously generalized in many dimensions with a minimum number of genes, all repressing each other with asymmetrical strengths, which also explains sequential activation of different fates. Separation of timescales allows for a simple analytical interpretation. Finally, it is shown that even in the presence of noise, coupling between cells preserves criticality and robust patterning. The model offers a simple theoretical framework for the study of emergent developmental timers.

Introduction

Our contemporary understanding of embryonic development has been profoundly influenced by Wolpert’s paradigmatic French Flag Model (1), proposing that morphogen concentration levels set up boundaries of different cellular domains. For instance, bicoid is generally proposed to control gap genes boundaries in Drosophila (2), or FGF gradient concentration to control the wavefront defining future somites in vertebrates (3). However, it is also well known that many differentiation processes are at least partially controlled by the duration of exposure to some morphogens (4, 5). How such timing is actually performed by the genetic and metabolic networks remains largely unknown.

A natural hypothesis is to assume some timer variable slowly accumulates to reach different activation thresholds and thus sequentially activates corresponding fates (6, 7). This constitutes, in essence, a dynamical French Flag Model, where the maximum level of the timer variable in any given cell irreversibly drives its eventual fate. The timescale of the process is then entirely controlled by the slow timer accumulation and faster variables quickly reach a quasi-stationary state (7). Such timers have yet to be clearly identified in vertebrates even though experimental data suggest candidates, e.g., overexpression of Cdx shifts Hox domains in vertebrates (8). Theoretical work has also suggested that existence of timers might drive apparitions of new bifurcations as evolutionary transitions (9).

However, experimental and computational results also suggest a more complex alternative. It has been shown that the timing of differentiation controlled by Sonic Hedgehog (Shh) in vertebrate neural tube does not use an explicit timer, but rather relies on an emergent property of the underlying differentiation network (10). Zones in mouse hindbrain are patterned under control of a dynamical Shh morphogen, and cells can go through several transient fates before stabilizing to their final state. Computational evolution of patterning networks aiming at simulating Hox-like patterning (7, 11) can also converge toward networks activating sequentially different fates before stabilizing, with slow timescales much longer that the variables’ lifetime. In both experimental and computational cases, the origins of sequential activation of genes and of the slow timescale within the patterning process are not fully understood.

In this article, we build a model for sequential activation of genes and show how criticality, defined as the proximity of a dynamical bifurcation, can explain timing. Criticality has been under scrutiny in many complex systems, from statistical biophysics (12) to ecology, brain activity (13), cardiac rhythm (14), or Drosophila development (15). We first argue that the model for the control of differentiation of Shh published in Balaskas et al. (10) is itself critical by being close to a saddle-node bifurcation, which explains the slow timescales in such system. We then generalize the model proposed in Balaskas et al. (10) to a general mechanism for morphogenesis defining an arbitrary number of regions within a simple model of embryo, where genes corresponding to final fates are sequentially activated. We argue that criticality in development is a parsimonious mechanism explaining apparently unrelated aspects of development such as timing, multistability defining final cellular states, and canalization of dynamics. Finally, we discuss the possible limits of a critical developmental mechanisms as well as experimental tests.

Materials and Methods

We consider purely transcriptional networks. Network behavior is modeled using standard continuous approximations, with one differential equation per protein. We use activating and repressing Hill functions to model interactions, and further assume that all proteins degrade linearly. Equations for specific networks considered are given in the Results.

Stochastic behaviors are simulated using a τ-leaping algorithm, as described in Gillespie (16), with propensities of transcription corresponding to deterministic transcription rates (in the form of products of Hill functions).

Simulations for Figs. 1, 2, 3, and 4 were implemented in the software MATLAB (The MathWorks, Natick, MA). Simulations of coupled cells were implemented in C++, using standard integration methods. All scripts are available upon demand.

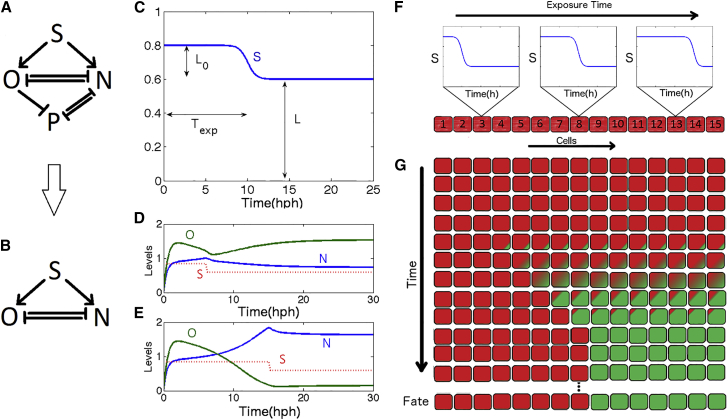
Figure 1.

Patterning under the control of a traveling wave morphogen. (A) GRN as presented in Balaskas et al. (10) for Nkx2.2 (N) Olig2 (O), Pax6 (P), and Shh (S). (Regular arrows) activation; (flat-head arrows) repression. (B) Simplified GRN with Pax6 removed. (C) S as a function of time used in simplified model. T_exp is the exposure time; L is the steady-state value of S; L₀ encodes the transient behavior. (D) Timecourse for O,N for short exposure time (6 h). (E) Timecourse for O,N for long exposure time (12 h). (F) S(t) as a traveling wave through the embryo. Cells most ventral (left) are exposed for shorter times to high concentrations of S than dorsal cells (right). (G) Schematic of the time evolution for a cell array. (Red) O-dominated; (green) N-dominated; (red/green) intermediary phase. Ventral cells reach steady state quicker than dorsal cells due to shorter exposure times. Parameters are the same as in Balaskas et al. (10) and are given in the Supporting Material. To see this figure in color, go online.

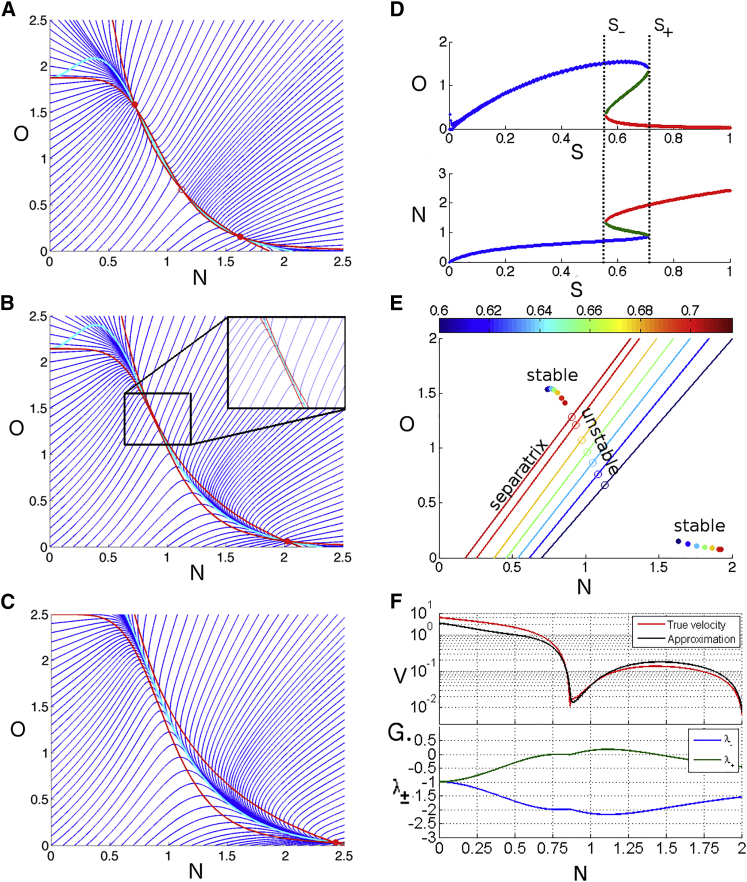
Figure 2.

Criticality provides the basis for the timing mechanism. (A) Flow in O-N phase for S = 0.6. (Red lines) Nullclines; (dark blue lines) vector field; and (cyan line) from Eq. 3. (Solid circle) Stabled fixed points; (open circle) unstable fixed point. (B) Flow for S = 0.75, just past the bifurcation. There is only one fixed point, and the flow from origin is directed to the ghost fixed point. (Inset) Zoomed-in image of the zone where saddle-node bifurcation has just happened. The flow is tangent to Eq. 3 between the nullclines. (C) Flow for S = 1. (D) Bifurcation diagram: O and N as a function of S. For S ≤ S₋ = 0.558 there is a single fixed point, the O state. At S = S₋, a saddle-node bifurcation creates a stable-unstable pair of fixed points. At S = S₊ = 0.71, a stable-unstable pair of fixed points disappear, leaving the single N state. (E) Phase plot of the separatrix and fixed points as S varies from 0.6 to 0.705. (Solid/open circles) Stable/unstable fixed points; (solid lines) separatrix. Even at the bifurcation, the origin is always attracted toward the O state. (F) Instantaneous velocity for the trajectory starting at the origin for S = 0.75 as a function of the N value. (Red) Actual velocity; (black) Eq. 4 for velocity. The two curves agree near the former fixed point, illustrating the relevance of the linear approximation. (G) Instantaneous eigenvalues λ_± for the trajectory starting at the origin. To see this figure in color, go online.

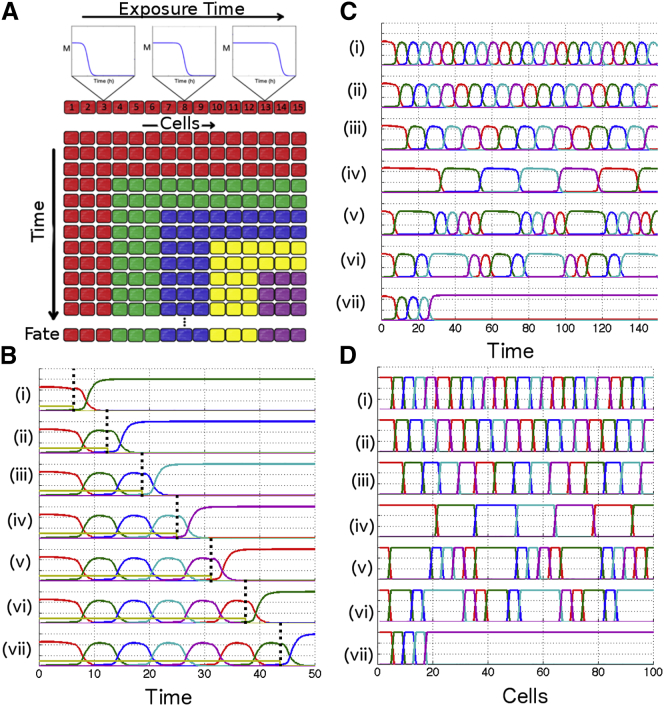
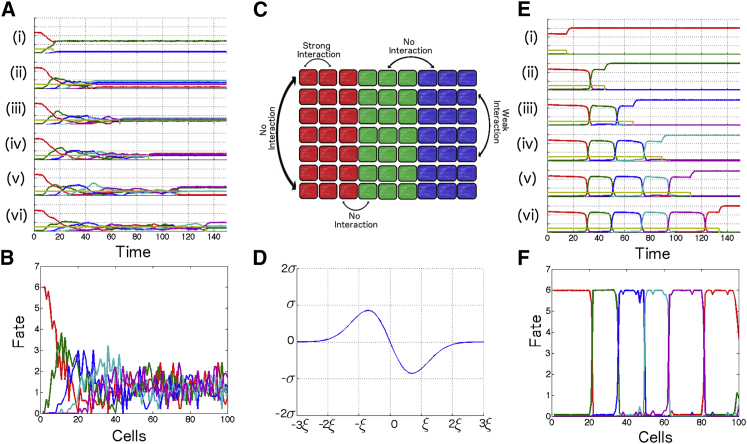
Figure 3.

Criticality for mutually repressing genes in multiple dimensions. (A) Idealization of a system generalizing the two-dimensional model in many dimensions. (B) Model of five mutually repressing genes stabilizing in different states as a function of exposure time. (i–vii) Longer exposure times. Networks are initialized with one gene high (e.g., G₁ = 4.5, G_i = 0). S steps from 1 down to 0 at various times (indicated by vertical dashed lines), and the system subsequently stabilizes at different states. (C) Evolution of multidimensional model as a function of time. Variation of parameters shapes different relative timing of expressions of genes. (i–vii) Increase of θ_iM (θ_iM = 1.50, 1.53, 1.56, 1.59, respectively) yields longer timescales. (v–vii) Asymmetrical modifications of θ_iM gives much longer expression for a given gene. (D) Spatial final pattern corresponding to (C) for a traveling step of M (speed: 1 cell per unit of time) for comparison of temporal and spatial profiles. To see this figure in color, go online.

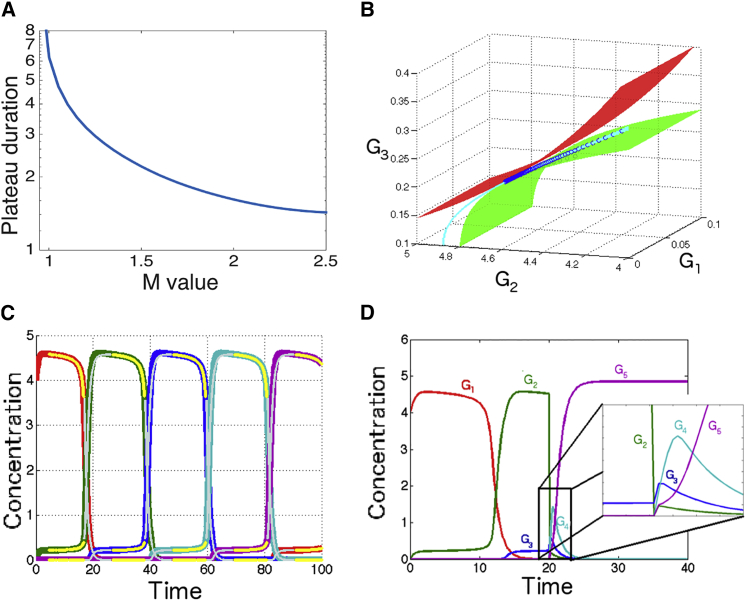
Figure 4.

Study of critical flow in multidimensional model. (A) Plateau duration for model of Fig. 3B (semilog scale) as a function of the value of input parameter M, illustrating variation of timescales even far from the bifurcation. (B) Comparison between flow (dark blue) and approximated two-dimensional valley (cyan) for multidimensional system of Fig. 3. (Green and red solid surfaces) Multidimensional nullclines of G₂ and G₃, respectively, in the three-dimensional phase space (G₁, G₂, G₃, G₄ = 0, G₅ = 0). (C) Comparison of full dynamics of a multidimensional system with two approximate regimes: slow motion on successive valleys (yellow line); fast exponential relaxation between valleys (gray lines). (D) Simulated mutant for this model: if one gene is transiently killed, the sequence of gene expression resumes but with fast typical timescales dominated by the degradation constant and not by the eigenvalues at the bifurcation. To see this figure in color, go online.

Results

Modeling dynamics of dorsal neural tube patterning

Balaskas et al. (10) and Panovska-Griffiths et al. (17) have used an approach combining experiments and mathematical modeling to show how exposure time to Shh controls differentiation in mouse hindbrain. They model explicitly the dynamics of Nkx2.2 (N), Olig2 (O), and Pax6(P) as in Fig. 1 A. Shh (S) is assumed to activate N and O via an intermediate target Gli, P represses N and is only expressed for low concentrations of S, and is repressed by both N and O. The level and duration of S and mutual repression between N and O are proposed to define the future fates. Experimentally, upon exposure to S, the system transiently expresses only P, then O, and eventually N. The dynamics is recapitulated and generalized by the proposed ACDC topology (17).

While there is some amount of positional information encoded by a graded morphogen (e.g., ventral cells in Balaskas et al. (10) never get activated, while the very dorsal cells express N very quickly), one of the main conclusion of Balaskas et al. (10) is that positional information can emerge from the dynamics of the network rather than a simple read of morphogen level. For instance, bistability is described as a crucial feature of the network (17). However, the emergent features of the dynamics of the system itself have not been studied. In particular, both experiments and models display very long transient timescales at the border of the O and N domains, which is experimentally moving for several dozens of hours (see Fig. 4 C from Balaskas et al. (10)). This is to be compared with a timescale of expression of N in the very most dorsal part (of the order of a few hours (10)) and is one order-of-magnitude longer than the half-life of proteins proposed in Balaskas et al. (10), indicating that some slowing down of the dynamics emerges at the network level.

To get more insight into this phenomenon, we introduce a simplified model of the dynamics in the dorsal region of the embryo close to the border of the O and N domains. Although P plays a role in the timing of the O and N interactions, the high P state essentially is a default state on the ventral side of the embryo. We focus on the richer dynamics between N and O in the dorsal part of the embryo (17) (Fig. 1 B), and thus ignore P. We depart from Balaskas et al. (10) and Panovska-Griffiths et al. (17) by assuming positional information is purely encoded through the dynamics of the input S, which we model as a step variable. The equations governing the simplified system are

$$S\left(x,t\right)=L+L_0\frac{T_{\text{exp}}{\left(x\right)}^{h_{\text{exp}}}}{t^{h_{\text{exp}}}+T_{\text{exp}}{\left(x\right)}^{h_{\text{exp}}}},$$

$$\dot{O}={\alpha }_O\frac{S{\left(t\right)}^{h_{OS}}}{S{\left(t\right)}^{h_{OS}}+{\theta }_{OS}^{h_{OS}}}\frac{{\theta }_{ON}^{h_{ON}}}{N^{h_{ON}}+{\theta }_{ON}^{h_{ON}}}-{\gamma }_{O}O,$$

$$\dot{N}={\alpha }_N\frac{S{\left(t\right)}^{h_{NS}}}{S{\left(t\right)}^{h_{NS}}+{\theta }_{NS}^{h_{NS}}}\frac{{\theta }_{NO}^{h_{NO}}}{O^{h_{NO}}+{\theta }_{NO}^{h_{NO}}}-{\gamma }_{N}N.$$

Apart from the removal of P, the only other difference with the models from Balaskas et al. (10) and Panovska-Griffiths et al. (17) is in the input variable S(x,t), which is assumed to be a step function between a high-state L + L₀ and a default signal of magnitude L, with a transition time depending on position x. In the full network, Shh, via Gli, activates both N and O and presents a complex adaptivelike behavior, i.e., strongly activated, then coming back to a very low activity. But Gli’s transcriptional influence is modeled in Balaskas et al. (10) as working close to saturation. As illustrated in Fig. S1 in the Supporting Material, the effect of an adaptive dynamics through a Michaelis-Menten function is essentially stepwise, from an on-phase to an off-phase, with longer switching-off times for bigger amplitude. To simplify this cascade, we thus directly model activation of the network as a Hill function depending on time and space. The Hill coefficient h_exp controls the steepness of the decline in S; the threshold T_exp(x) controls the exposure time to higher concentrations of S. To account for differences in positions, T_exp(x) is an increasing function of position (Fig. 1 C).

The reason for inclusion of a default signal L, is that, while the published model from Balaskas et al. (10) and Panovska-Griffiths et al. (17) goes through multiple bifurcations and is multistable for sufficiently high value of the modeled input Gli, Shh signaling disappears within a timescale comparable to some fate decision (∼60 h; see Balaskas et al. (10) and Panovska-Griffiths et al. (17), and Fig. 1, D and E, for Shh signaling dynamics and Fig. 3, A–C, for dynamics of boundaries), and steady states are thus maintained even in close-to-complete absence of Shh signaling. This is not explicitly accounted for by the model from Balaskas et al. (10) and Panovska-Griffiths et al. (17) because fixed points disappear when there is no Shh signal. To keep those steady states, we assume that some default signaling is maintained to keep multistability in the system. If the basal rate L is high enough, the system is bistable like the classical toggle-switch mechanism (18, 19), similar to that found by Panovska-Griffiths et al. (17). There are then two stable steady states with either high O/low N (subsequently called the “O state”) or high N/low O (the “N-state”); see Fig. 1, D and E. When S is high enough, only the N-state is stable. Note also that P does not correspond to any hypothetical third steady state in the model of Panovska-Griffiths et al. (17) for midrange signaling of S (it is simply slaved to O and N), further justifying its removal in our approach.

A noteworthy addition in this model compared to the classical model of toggle switches (such as seen in Fig. 8 a in Cherry and Adler (18), Fig. 2 a in Gardner et al. (19), or the general case presented in Jaeger and Monk (20)) is an asymmetry in mutual repressions between N and O: repression of O by N is much more stringent than repression of N by O (technically, this is done through a higher Hill coefficient h_ON = 5 vs. h_NO = 1). As consequence of the asymmetry in the parameters, the dynamics of the network is itself asymmetrical in phase space. In particular, even when only the N state is stable, before reaching the N state, the system seems to visit the O state existing for a lower value of S. This explains how positional information depends on dynamics: when S decays to its final default value, the final state of the system thus depends on the length of exposure of the system to S. It stabilizes into the O state for short exposure to S (roughly <12 h, see Fig. 1 D), and into the N state for long exposure to S (see Fig. 1 E).

So the simpler submodel from Fig. 1 B encapsulates not only the main timing characteristics observed in Balaskas et al. (10) and the trajectory in the O-N space characteristic of the ACDC network (17), but also pattern stabilization in the presence of a default signal L. Putting everything together, cells most dorsal in the embryo are then exposed for a longer time and stabilize in the N state, while cells most ventral stabilize in the O state, as schematically illustrated in Fig. 1, F and G.

Criticality and valley between ghost and stable states

To get a more mathematical understanding of what happens, the trajectory of the model is studied in the N-O plane with different constant values of S (see Fig. 2, A–C). Difference in nonlinearity in O and N repressions are clearly visible, with the O nullcline much steeper than the N one.

At medium concentrations of S (S₋ ≤ S ≤ S₊, Fig. 2 D), while the system is bistable with coexisting O and N states, the flow from the origin is biased toward the O state. This is due to the fact that separatrix between the two fates is far from the origin (assumed to correspond to initial conditions, Fig. 2 E). At S₊, the system goes through a saddle-node bifurcation (21) where the unstable fixed point moves toward the biased state O and eventually collides with it (Fig. 2, B and C). Importantly, the separatrix does not cross the origin when the bifurcation happens (Fig. 2 E), which means that the local flow from the origin hardly changes at the bifurcation.

This imposes the very particular asymmetrical flow in phase space for high S (S ≥ S₊), as seen in Fig. 2, A–C. Irrespective of S values, flow from the origin is driven toward the O state. If S is not high (S ≤ S₊), this state is stable and the system stabilizes there. If S is high, the system cannot stabilize at the O state and will inevitably flow toward the stable N state. However, the flow from the ghost O state to the stable N state will be critically slow (15, 22), because of the proximity of the bifurcation. Fig. 2 F illustrates the speed of the flow v (=$\sqrt{\dot{O}{\left(t\right)}^2+\dot{N}{\left(t\right)}^2}$) as a function of N(t) for a trajectory starting at the origin. Close to the origin, the dominating timescale is the degradation rate (or ∼1 h⁻¹ in the units from Balaskas et al. (10) we use), which, because O is scaled to be of order 1, also gives speed of order 1 in our units. Then, we clearly see a first local minima of the speed close to the ghost fixed point (here the O state with low N) with a speed of ∼10⁻². Finally, the system escapes this ghost attractor and slowly converges with a speed of ∼10⁻¹ toward the final high N fixed point.

To further illustrate this phenomenon and explicitly derive timescales, we can approximate the system by a linear Taylor expansion:

$$\begin{array}{c}\dot{N}=f\left(O\right)-N\approx f^{\prime }\left(O_0\right)O-N+f\left(O_0\right)-f^{\prime }\left(O_0\right)O_0\\ \dot{O}=g\left(N\right)-O\approx g^{\prime }\left(N_0\right)N-O+g\left(N_0\right)-g^{\prime }\left(N_0\right)N_0\end{array}\equiv \dot{\overrightarrow{x}}=A\overrightarrow{x}+\overrightarrow{B}.$$

This is valid for $\overrightarrow{x}=\left(\begin{array}{c}N\\ O\end{array}\right)$ close to an arbitrary ${\overrightarrow{x}}_0=\left(\begin{array}{c}{N}_0\\ O_0\end{array}\right)$. Eigenvalues λ_± and eigenvectors ${\overrightarrow{v}}_{\pm }$ of A are

$$\begin{array}{l}{\lambda }_{\pm }=-1\pm \sqrt{g^{\prime }\left(N_0\right)f^{\prime }\left(O_0\right)},\\ {\overrightarrow{v}}_{\pm }=\left(\begin{array}{c}\pm \sqrt{\frac{f^{\prime }\left(O_0\right)}{g^{\prime }\left(N_0\right)}}\\ 1\end{array}\right).\end{array}$$

Fixed points are defined by $\dot{\overrightarrow{x}}=A{\overrightarrow{x}}_0+\overrightarrow{B}=0$. Stability is given by the sign of λ_± at ${\overrightarrow{x}}_o$ along ${\overrightarrow{v}}_{\pm }$. In the case of the stable O state, we have of course λ_± < 0; in the case of the unstable state between the O state and the N state, we have λ_± > 0, λ₋ < 0. At the bifurcation, the O state and the unstable fixed point collide and cancel out. By continuity, this forces λ_± = 0 and as a result λ₋ = −2 at the bifurcation (Fig. 2 G) with parameters from Balaskas et al. (10). Varying S slightly past the bifurcation gives rises to a region where λ_± and $\dot{\overrightarrow{x}}$ are small and constrained by the almost touching parallel nullclines (Fig. 2 B). The general solution to the above linear system near ${\overrightarrow{x}}_o$ is $\overrightarrow{x}=a{e}^{{\lambda }_{+}t}{\overrightarrow{v}}_{+}+b{e}^{{\lambda }_{-}t}{\overrightarrow{v}}_{-}-A^{-1}\overrightarrow{B}$ with the value a,b given by initial conditions. In the case where we have slow motion and |λ_±| ≪ |λ₋|, the value $b{e}^{{\lambda }_{-}t}{\overrightarrow{v}}_{-}$ dies very quickly compared to $a{e}^{{\lambda }_{+}t}{\overrightarrow{v}}_{+}$ (Fig. 2, B and C) and the motion lies parallel to ${\overrightarrow{v}}_{+}$. Therefore the dynamics is quickly canalized on a local one-dimensional manifold defined by ${\overrightarrow{v}}_{+}$ at the bifurcation.

Strictly speaking, this approach is valid only right at the bifurcation and defines a slow manifold only in the neighborhood of the disappearing fixed point. But because the flow stays close to the nullclines (corresponding to $\dot{N}=\dot{O}=0$), it is itself very small. Thus it is reasonable to approximate it by its Taylor expansion in a full valley of near-fixed points sandwiched between the two nullclines, where $\overrightarrow{B}$ is small. Let points on the valley be denoted by ${\overrightarrow{x}}_v=\left(\begin{array}{c}{N}_v\\ O_v\end{array}\right)$.

The canalization on such a valley past the bifurcation and further from the fixed point follows a similar linear Ansatz:

$$\dot{N}=f^{\prime }\left(O_v\right)O-N+f\left(O_v\right)-f^{\prime }\left(O_v\right)O_v,$$ (1)

$$\dot{O}=g^{\prime }\left(N_v\right)N-O+g\left(N_v\right)-g^{\prime }\left(N_v\right)N_v.$$ (2)

The local eigenvalues and eigenvectors are defined in the same way as before, and if 0 ≃ |λ_±| ≪ |λ₋|, which should happen by continuity, the system relaxes quickly on the local direction ${\overrightarrow{v}}_{+}\left({\overrightarrow{x}}_v\right)$. Given that the O component of v₊ is 1 by definition, the full nonlinear system gives that ${\dot{\overrightarrow{x}}}_v\simeq \left(g\left(N_v\right)-O_v\right){\overrightarrow{v}}_{+}$, and from this the following implicit equation defining the valley in phase space is derived:

$$\left(f\left(O_v\right)-N_v\right)\simeq \left(g\left(N_v\right)-O_v\right)\sqrt{\frac{f^{\prime }\left(O_v\right)}{g^{\prime }\left(N_v\right)}}.$$ (3)

Agreement of this expression with the full system is excellent before and after the bifurcation, as illustrated in Fig. 2, A–C. Motion eventually relaxes toward the N state along this manifold between the two nullclines.

Finally, the analytical approximation for the phase-space speed along the canalized valley is given by

$$v=\Vert \dot{\overrightarrow{x_v}}\Vert =\left|g\left(N_v\right)-O_v\right|\Vert {\overrightarrow{v}}_{+}\Vert =\left|g\left(N_v\right)-O_v\right|\sqrt{1+\frac{f^{\prime }\left(O_v\right)}{g^{\prime }\left(N_v\right)}},$$ (4)

which is also in excellent agreement with the full nonlinear system as illustrated in Fig. 2 F. Equation 4 is helpful to understand the origin of the slow timescales: near the bifurcation v ∝ |g (N_v) − O_v| ≈ 0, it is the O component of $A{\overrightarrow{x}}_0+\overrightarrow{B}$ so that the system will escape the ghost fixed point in a time $\tau \sim 1/v$, which is big compared to any parameter of the system. This explains the timing effect: much of the time evolution of the system is spent close to the O ghost state. This becomes especially noticeable very close to the bifurcation as τ → ∞. It is important to note that the approximation breaks down as the flow gets further from the bifurcation and the distance between the nullclines increases, which indicates that $A{\overrightarrow{x}}_0+\overrightarrow{B}$ becomes big.

Generalization to higher dimension

The previous model combines a timing effect and canalization on a one-dimensional manifold due to criticality for high S value, and multistability ensuring the stabilization of the dynamics when S is removed. However, this model is fundamentally bidimensional and leads to only two different fates.

It is not clear that it can work in a higher dimension, because the flow a priori is less constrained. Strikingly, this mechanism can be indeed generalized to generate many steady states as long as repression strengths between pairs of genes are asymmetrical, as in the previous section.

Assume a traveling wave of a dynamical repressing morphogen M sweeping across the embryo according to Fig. 3 A, such that each cell has a different T_exp according to its position along the length of the embryo (repression mediated by morphogens is common in biology, as illustrated by the classical anterior/posterior mutual repression fates via the RA/FGF system (23)). The goal is to produce a model of gene networks generalizing the process of the previous part with several fates, i.e., a model where the system seems to visit sequentially different fates with a slow timescale, and stabilizes there if morphogen M is removed.

Consider a model where M controls a network of N_g mutually repressing genes. For simplicity, assume all transcription rates and all degradation rates are the same for every gene, and that repression is performed via multiplicative Hill functions with identical coefficients. The equation regulating time evolution of concentration protein j is

$${\dot{G}}_i={\alpha }_i\frac{{\theta }_{iM}^{h_{iM}}}{{\theta }_{iM}^{h_{iM}}+M^{h_{iM}}}\prod _{i\ne j}\frac{{\theta }_{ij}^{h_{ij}}}{{\theta }_{ij}^{h_{ij}}+G_j^{h_{ij}}}-{\gamma }_i{G}_i.$$

The only differences between genes is in their relative threshold of repression of gene i by j, θ_ij and the threshold of repressions by morphogen M, θ_iM, so that a network is completely defined by the N_g × (N_g + 1) matrix of θ-values (see Table 1).

Table 1.

Table for the N_g = 5 dimensional network

Rates	G1	G2	G3	G4	G5	M
Production α	6	6	6	6	6	—
Degradation γ	1	1	1	1	1	—
Hill coefficients hij and hiM
G1	—	5	5	5	5	3
G2	5	—	5	5	5	3
G3	5	5	—	5	5	3
G4	5	5	5	—	5	3
G5	5	5	5	5	—	3
Thresholds θij and θiM
G1	—	0.4	0.4	0.4	2.5	1.5
G2	2.5	—	0.4	0.4	0.4	1.5
G3	0.4	2.5	—	0.4	0.4	1.5
G4	0.4	0.4	2.5	—	0.4	1.5
G5	0.4	0.4	0.4	2.5	—	1.5

Taken from the systems shown in Fig. 3.

Then, a network with ${\theta }_{i+1,i}={\theta }_{1,N_g}={\theta }_{\text{weak}}$ for any i, θ_ij = θ_strong for all other couples (i,j), θ_iM = θ_M generalizes the canalized flow observed for the two-dimensional system in many dimensions as long as θ_weak > θ_strong are chosen so that the system can transition from one gene to the other. This choice of parameters essentially builds nested interactions similar to the O-N state described in the first part. See Fig. 3 B for illustration of the mechanism with a specific set of parameters giving rise to an oscillation between five genes/fates.

When there is no M, all N_g genes repress each other so that only one single gene can be expressed at steady state, leading to the existence of N_g steady states corresponding to as many different cellular fates. When M is high enough, all fixed points disappear but N_g ghost states remain where the flow is locally considerably slowed down. Consequently, as the time of exposure to morphogen increases (from (i) to (vii) in Fig. 3 B), the network goes through a sequence of plateaus corresponding to different fates. It eventually stabilizes in the fate it is in at the time when M disappears.

This mechanism can be easily modulated to give any dynamical pattern while keeping the order of gene expression constant. Parameters can be changed to modify relative timing of a given gene or global timing of the full systems, as illustrated in Fig. 3 C (dynamics in cell constantly exposed to M) and Fig. 3 D (pattern corresponding to a traveling wave of M with a speed of 1 cell per unit of time).

Changing parameter θ_M for all genes simultaneously can change the timescale of the whole system as illustrated in Fig. 3, C and D (i–iii). The system can also spend more time close to a chosen ghost state by changing only some of the parameters ${\theta }_{iM}$ in the system to go closer to one bifurcation. After M removal, this gives rise to a relatively bigger domain of expression at steady state for the corresponding gene (see Fig. 3, C and D (v–vi)). Finally, there is no need to have an actual oscillator: it is possible by a change of ${\theta }_{N_{g}M}$ to ensure that the system stabilizes in one final state, irrespective of M value.

Understanding dynamics of critical flow

A natural question arising is how far from the bifurcation can we observe a critical slowing-down? Fig. 4 A illustrates the clear dependency of the time between successive maxima of different genes as a function of constant values of M. As expected, timescale diverges close to the bifurcation. For large values of M, the time between two maxima of successive genes is approximately equal to 1.4 in our time units (and thus of the order of the inverse degradation scale as expected). Plateau duration is then getting significantly higher than its asymptotic value over a wide range of M: for instance, for M = 1.5, plateau duration is increased by 50% to reach 2.2, for $M=1.25$ it is 3, and for M = 1 it is higher than 6 (as can be seen in Fig. 3 B). Thus, the system experiences severalfold slowing-down of its timescale within a twofold range change of M, even relatively far from the bifurcation.

A simple analytical approximation fully describes the system dynamics. The order of gene expression is imposed by the fact that θ_i+1,i is higher than all other θ_i,j so that if any gene i is activated, only the successor i + 1 is not heavily repressed and therefore slowly accumulates. Because the system is now multidimensional, the full linearization of the system is much more complicated, in particular the matrix $A=d{\dot{G}}_i/d{G}_j$ contains many terms depending on G_i and is hard to visualize. However, the peaks of expression of each gene i correspond to ghost fixed points left by the bifurcation at high M. The matrix A then locally simplifies and becomes effectively two-dimensional along variables G_i and G_i+1, and we can use the exact same approximation as in the two-dimensional system to compute an implicit equation for the valley, and the corresponding slow timescales. This is illustrated in Fig. 4, B and C; the flow in a three-dimensional projection (dark blue) coincides locally with the approximated two-dimensional valley in subspace G₂-G₃ computed from Eq. 3 (cyan line, Fig. 4 B). Fig. 4 C (yellow lines) indicates when the direction of the actual vector field is within 2% of the direction of v₊, as computed in a previous section.

A different faster regime matches the successive valleys. Just like in the two-dimensional case, on the valley, G_i (like O) slowly decreases while G_i+1 (like N) slowly increases. At some point, G_i+1 reaches the threshold of repression θ_strong. It then shuts off production of G_i, which then exponentially decreases with a time constant 1 in rescaled units, i.e., much faster than the typical timescale at the bifurcation accounting for criticality and time evolution on the valley. Fig. 4 C illustrates such an exponential Ansatz (gray lines) for successive G_i, with G_i+1 and G_i+2 simply slaved to G_i using their differential equations (see the Supporting Material for details). Once G_i has completely died out, the system quickly relaxes to the next valley close to the fixed point with high G_n+1 and low G_n+2, and the process continues with slow motion on the valley. At any given time, the flow therefore approximately lies in the three-dimensional subspace of the phase space, corresponding to the gene activated, its predecessor, and its successor. Movie S1 illustrates the dynamics of the flow in the subspace defined by three consecutive genes.

Finally, a characteristic effect of this mechanism can be observed if the activity of one of the genes is artificially set to zero momentarily. In Fig. 4 D, G₂ is transiently set to zero at t = 20 h. The system then resumes its course in the determined order over a much shorter timescale and with increasing amplitude. This is to be contrasted with a timer model such as proposed in François and Siggia (7), where relative timing of the fates are independent from each other and controlled purely by the timer.

Coupling rescues degradation of the pattern by noise

As demonstrated in previous sections, a critical system tuned to be close to a bifurcation can implement sequential activation of fates, developmental timing, and multistability associated to development. One issue of concern is that biochemical noise could potentially destroy criticality and thus slow timescales, for instance by pushing the system away from the slow manifolds. This is simulated in Fig. 5, A and B, using a τ-leaping algorithm (16): considering an ensemble of 30 cells exposed to the same duration of M, the averaged concentrations of genes as a function of time exhibit a strong loss of synchrony (compare Fig. 5 A with Fig. 3 B, and Fig. 5 B with Fig. 3 D (i)). Loss of synchrony in development is well known for Notch mutants (implicated in cell-to-cell coupling), especially in the segmentation clock context (24, 25). Movie S2 illustrates the dynamics of independent cells in a simulated two-dimensional embryo (30 × 100 cells) under control of a traveling wave of M.

Figure 5.

Noise sensitivity and rescue. (A) τ-leaping simulations of uncoupled cells, showing the averages over 30 individual trajectories as a function of time for different durations of exposure to M (i–vi). (B) Average final concentration for (C) as a function of space, assuming cells are arranged as in Fig. 3A. (C) Heuristic approach used for the coupling. (D) Shape of the reaction force used to model coupling between cells. (E) Average of 30 cells using τ-leaping simulations of coupled cells within a full embryo as a function of time for different durations of exposure to M (i–vi). Rescue is almost perfect. (F) Average final concentration for same simulation as in (E). To see this figure in color, go online.

A priori, coupling between cells could help overcome this issue. However, new difficulties arise from coupling: for instance, while noise is lowered if cells in the same state are coupled, the coupling can destroy the ability of different fates to coexist to ensure multistability at steady state, leading to traveling kinks that might require other specific mechanisms such as external morphogenetic fields to stabilize (26).

We use a different heuristic. We make two hypotheses:

• 1)Coupling exponentially dies with cell-to-cell distance, and
• 2)Cells in one given state are only coupled to cells in the same state.

Hypothesis 1 is very generic and reasonable biologically. Recent quantitative studies have suggested that mechanisms similar to Hypothesis 2 are at play during development: for instance, mesodermal cells actively recognize endodermal cells and react to them to activate tissue segregation (27). Importantly, this is not done via passive tissue separation, but instead via an active sensing and modulation of Ephrins (28). In principle, other signaling pathways such as Notch could also be potentially used to recognize cells of different types and enhance pattern stabilization depending on ligand values (29).

In the absence of well-known mechanisms, we designed a phenomenological coupling accounting for Hypotheses 1 and 2, which is illustrated in Fig. 5 C. Schematically, the coupling measures an effective difference between cell expressions ξ. No assumptions are made as to how this difference is expressed or implemented; it is simply assumed that cells are able to know how different they are from their neighbors. Based on this difference, the coupling imposes reaction terms R in the dynamics, with a typical shape displayed in Fig. 5 D. This purely phenomenological coupling imposes that when cells are very different there is no coupling (R → 0 for big |ξ|), while the coupling is maximum when cells are similar but not exactly identical (intermediate |ξ|). Reaction force for an identical cell is 0. The full mathematical expression for this coupling is given in the Supporting Material.

Movie S3 illustrates the dynamics of such a simulated embryo using this coupling (to be contrasted with Movie S4 without specific interaction between fates). Clearly the coupling rescues the full dynamics of the system, with the exception of a small noise in fates for a few cells at the interface between boundaries. Average concentration for cells exposed to the same duration of M as a function of time is illustrated in Fig. 5 E, and the final pattern as a function of space in Fig. 5 F, showing almost perfect rescue. Notable here is that the long timescale is completely preserved compared to the short timescale of protein degradations (1 unit of time), showing that criticality is maintained in presence of noise and cellular coupling.

Discussion

Balaskas et al. (10) have proposed that some combination of input amplitude and duration of exposure explained the cellular fates in neural tube patterning. While influence of input amplitude is the classical hallmark of Wolpert’s French Flag Model, we focus on the latter aspect and show how cellular fates can be sequentially activated and controlled by duration of exposure to a morphogen. The proposed model explains and allows for critically slow timescales leading to multistability, without an explicit timer.

The flow in phase space sequentially visits states of the system and stabilizes according to the exposure time. This is different from classical symmetrical bistable systems where the flow is first rapidly attracted toward the unstable fixed point when mutual repression is symmetrical (see, e.g., Jaeger and Monk (20)). Importantly, we generalize our model to multiple dimensions. This can be done through a purely symmetrical network topology, and does not require any additional gene like in the ACDC model (17).

There have been discussions of the role of well-defined modules in gene networks, in particular to control timescale of gene expression (30). Interestingly, the generalized model presented here works in a very different way, because there is no modularity at the level of the network topology, in line with the idea that dynamics in gene networks is more dependent upon parameter than upon topology (31). Indeed, the observed flow is not symmetrical, and can be generated with a hierarchical structure at the level of parameters, where gene i only weakly represses gene i + 1. This translates into local flows that are canalized and defined by the three consecutively expressed genes at any given time (Fig. 4 B). This model is also parsimonious in the sense that if we assume N_g genes control N_g different fates, there is no need for extra genes to implement a timing process under control of external morphogen.

Noise in individual cells could destroy this critical timing, but we demonstrated, using a phenomenological model, that this can be almost fully attenuated by cell coupling between cells expressing similar genes. It is worth pointing out that other downstream physical mechanisms could also help in refining domain boundaries. For instance, cell-sorting associated to different Hox genes expression and levels of Shh signaling in zebrafish neural progenitors has been observed (32, 33). Sensing and sorting could both be done through active regulation of adhesion molecules, as suggested recently by Fagotto (27) and Fagotto et al. (28). While we have not accounted for sorting here, this could definitely add another layer of precision to filter out the small amount of noise remaining even in presence of cell coupling.

It is not clear how a timer based on criticality would be more advantageous or more prone to have been selected than a single slow timer accumulating, as proposed in François and Siggia (7). Timing that is under control of a timer is appealing for at least two reasons: the first is that it can well explain developmental transitions, where dynamics of development is changed. This is particularly important for the case of Hox gens (34). For instance, ancestral and short-germ insects have a dynamical mode of patterning with growth, qualitatively similar to vertebrates, while long-germ band insects pattern different regions without growth, under control of presumably static morphogen gradients. Evolutionary transitions between these two very different modes can be easily explained if an accumulating timer is turned into a morphogen (7), implementing a French Flag Model in both cases.

The second reason why a timer model is appealing is related to scaling of developmental timings with external parameters such as temperature (35). Such a global control suggests that very few parameters (such as timescale of accumulations of a few morphogens) control developmental timing. Still, in the model proposed here we can tune the timescale of our model by changing the common coupling of genes to morphogen M as shown in Fig. 3, C and D, or by changing the value of the morphogen itself. This is a feature due to the criticality and in particular to the relative sensitivity of the timescale to moderate changes of parameters as displayed in Fig. 4 A. If one of these parameters is externally controlled, e.g., by some temperature-sensitive variable, it could plausibly account for conservation of relative timing under different environments. Importantly, global regulators simultaneously tuning levels of activation or repression of many developmental genes are known to exist, such as zld in Drosophila (36), which suggests that modifications of multiple developmental thresholds to compensate for global perturbations are (at least in theory) possible. A way to test between a timer versus a critical timing mechanism as described here would be to reset the expression of differentiation genes as illustrated in Fig. 4 D: a change of relative timing would exclude an independent timer, while fast dynamics away from the normal developmental pathway would suggest critical timing in the normal unperturbed case.

Importantly, timing effects and differentiation are two interconnected aspects in our generalized model. This is in line with the idea that evolutionary development can best be described by geometric properties in phase space (9, 20, 37, 38). With a small continuous parameter change, a critical system where one gene is expressed for a very long time is turned into a system where that gene is stably expressed, defining a new steady state. Obviously, this process is thus incremental and continuous by essence: indeed the flow in phase space barely changes past the bifurcation (Fig. 2), which is the main feature explaining how one can turn a temporal sequence of expressed genes into a stable pattern. Furthermore, even far from the bifurcation, we see a clear effect on the timescale of the dynamics (Fig. 4 A), suggesting that there is no need for a strong fine-tuning of parameters in order to see the emergence of a critical slowing-down. Therefore, both critical timing and differentiation might actually be quite easy to incrementally evolve: selective pressure imposing longer and longer expression of some genes could end up selecting for multistability. Indeed, this exact process was observed for evolution of bistability in previous computational evolution works (unpublished evolutionary pathways from François and Hakim (39)). Criticality could thus be a developmental signature of incremental evolution of new bifurcations (20, 38).

Finally, it should be pointed out that many features studied here have been observed experimentally in contexts other than that of vertebrate development (13). Slow time evolution following the unstable directions along a line of attractors is very reminiscent of models of decisions in neural networks (40, 41). In particular, sequential activity in neuron networks has been modeled by a type of winnerless competition between neurons, with asymmetrical interactions very similar to those between genes that we consider (42). However, there are two important differences in our model: first, it is paramount that the developmental system can stabilize to one of these fixed points by changing a control parameter; and second, the size of the network is much smaller than typical neural networks. In Drosophila development, gap genes mutually repress, and development appears to be canalized as a consequence (43, 44). Quite interestingly, criticality due to mutual repression has been proposed as a major determinant of the boundary positions between gap domains (15). The big difference in Drosophila is that development happens under the control of steady morphogens, following a French Flag Model paradigm. Timing issues are much less relevant than spatial issues. Criticality in our model can be observed here on time correlations between genes (see Fig. S4) to be contrasted with the space correlations observed in Krotov et al. (15). In both cases, maximum anticorrelation is observed for successively expressed genes, and is the dynamical signature of canalization of the valleys. The observed criticality in Drosophila might be the trace of some ancestral timing via criticality, and the latter could still be observed in short-germ insects.

Author Contributions

P.F. initiated the project and D.E.T. and P.F. designed models, performed and analyzed simulations, and wrote the article.

Editor: Stanislav Shvartsman.

Supporting Material

Movie S1. Three-dimensional projection (G₁, G₂, G₃) of the nullclines for a typical timecourse

(Blue, green, and red solid surfaces) Multidimensional nullclines of G₁, G₂, and G₃, respectively, in the three-dimensional phase space (G₁, G₂, G₃, G₄ = 0, G₅ = 0). The timescale is slow, with θ_iM = 1.58. Initial conditions are (G_i = 0, G₅ = 4.5).

Movie S2. Stochastic simulation of a 30 × 100 cell array

Embryo of 30 × 100 cells undergoing development under the effect of a traveling wave of morphogen M. The timescale is slow with θ_iM = 1.58. The stochastic simulation is very noisy, with N = 500.

Movie S3. Stochastic simulation of a 30 × 100 cell array with cell coupling

Embryo of 30 × 100 cells undergoing development under the effect of a travelling wave of morphogen M. The timescale is slow with θ_iM = 1.58. The stochastic simulation with N = 500 is rescued by the cell-to-cell coupling.

Movie S4. Stochastic simulation of a 30 × 100 cell array with linear cell coupling

Embryo of 30 × 100 cells undergoing development under the effect of a traveling wave of morphogen M. The timescale is slow with θ_iM = 1.58. Unlike the case with nonlinear cell-to-cell coupling, the stochastic simulation with N = 500 leads to a noisy malformed embryo with no clear boundaries. Parameters are taken as the linearization of the nonlinear coupling at the origin.