Flexible Gating of Contextual Influences in Natural Vision

Abstract

Identical sensory inputs can be perceived as strikingly different when embedded in distinct contexts. Neural responses to simple stimuli are also modulated by context, but the contribution of this modulation to the processing of natural sensory input is unclear. We measured surround suppression, a quintessential contextual influence, in macaque primary visual cortex with natural images. We found suppression strength varied substantially for different images. This variability was not well explained by existing descriptions of surround suppression, but it was predicted by Bayesian inference about statistical dependencies in images. In this framework, surround suppression was flexible: it was recruited when the image was inferred to contain redundancies, and substantially reduced in strength otherwise. Our results thus reveal a surprising gating of a basic, widespread cortical computation, by inference about the statistics of natural input.

The contextual modulation of perceptual and neural responses is ubiquitous in cognition and sensory processing^1–3: how a stimulus is perceived or valued depends strongly on which other stimuli are currently present, or have recently been encountered. Contextual effects underlie phenomena as varied as visual saliency^4,5 and illusions^1,6, adaptation aftereffects², multisensory integration⁷ and value encoding of multiple alternatives⁸.

A paradigmatic example of contextual modulation is the influence of a visual stimulus placed outside a neuron’s spatial receptive field (RF)—in the ‘surround’—on the response evoked by a stimulus within the RF. This type of spatial contextual effect is thought to be central to the integration and segregation of visual information^9,10, allowing objects to be identified and the relationships between them to be understood. The surround is also widely invoked to explain perceptual salience^4,5.

Spatial contextual effects have been documented at many stages of the visual system, using simple stimuli such as bars and gratings¹¹. This work has revealed that a stimulus in the surround is often suppressive, with the strength of its influence depending on its contrast^12–14, precise location^15,16, and relation to the stimulus within the RF^16,17. The recruitment of the surround has also been shown to strongly influence responses to natural images^18,19, but whether this modulation can be explained with knowledge derived from experiments with simple stimuli is unclear^19,20. Within the RF itself, models derived from simpler stimuli have a limited ability to predict responses to natural images, constituting a recognized barrier in the study of visual processing²¹.

Here we show that existing descriptive models, derived from measurements with simple stimuli, have a limited ability to explain the surround suppression recruited by natural images in primary visual cortex (V1) of macaque monkeys. To explain this suppression, we considered how surround suppression should behave to allow cortical neurons to encode natural images optimally. In this approach, one first considers the statistical properties of natural images, then hypothesizes about the computations involved in representing them optimally, and finally uses these hypotheses to develop predictions about neuronal response properties^22–28.

Our previous modeling work using this approach showed that surround suppression should be engaged when an image provides statistically redundant (or homogeneous) signals to the RF and its surround, but be strongly reduced otherwise—a form of gating²⁷. Consistent with this prediction, we show here that surround suppression in V1 neurons is stronger for images inferred to be homogeneous. Including this gating in existing descriptive models improves considerably their ability to predict responses to scenes. Our results show that a basic cortical computation—surround suppression—can be modulated by inference about the statistical structure of visual inputs.

RESULTS

We recorded from 207 V1 neurons, in 3 anesthetized, paralyzed macaque monkeys. Neuronal spatial receptive fields were located 2–3 degree from the fovea, in the lower visual field.

Variability of surround modulation with natural images

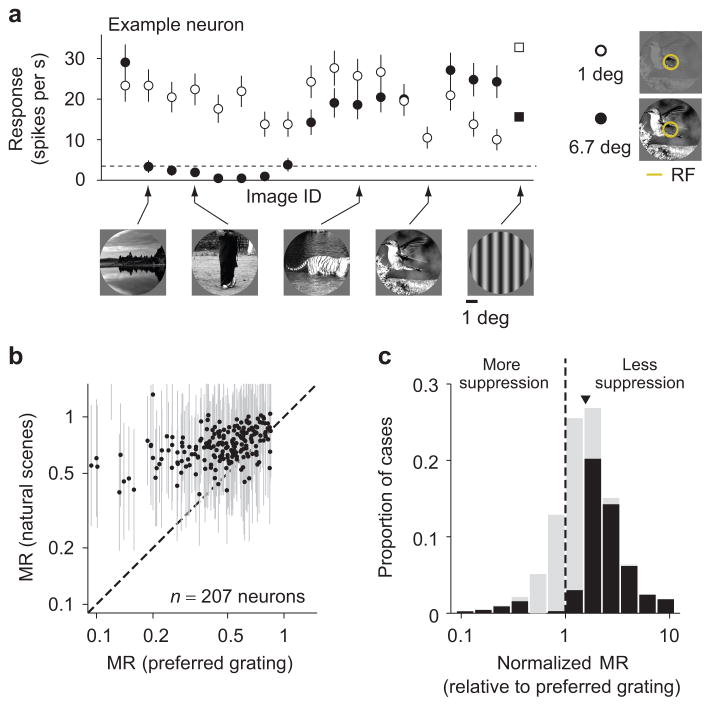
We measured responses of V1 neurons to brief presentations (100 ms) of 270 static natural images, as well as various static grating stimuli. Natural images were windowed to fit largely within the RF (1 degree) or up to 6.7 times larger (Fig. 1a, right). The example neuron in Figure 1a illustrates the effects of the surround: the neuron fired vigorously to presentations of many of the smaller images (open symbols), and usually less when these were embedded in a larger image (filled symbols).

Figure 1. Variability of surround modulation with natural images.

(a) Firing rate of a V1 neuron in response to static natural images (circles), and gratings at the preferred orientation and spatial frequency (squares), windowed to 1 degree of visual space (open symbols) or 6.7 degrees (filled). The dashed line denotes the spontaneous rate. (b) Each point represents the modulation ratio (MR) measured with gratings at the preferred orientation and spatial frequency (abscissa) and the average MR across all natural images (ordinate), for each neuron. (c) Distribution of normalized MR (NMR) across all images and neurons (N = 38,591 cases). Arrowhead indicates geometric mean, black bars indicate cases with NMR significantly different from 1 (p < 0.05). Error bars in (a) indicate 68% c.i., in (b) standard deviations.

We quantified the modulation caused by enlarging the image with a common metric^14,29, namely the ratio between the responses to each paired large and small image (termed Modulation Ratio, MR; see Methods). MR values smaller than 1 correspond to surround suppression; values larger than 1 to facilitation. The geometric mean MR for natural images which evoked a measurable response was 0.71 (68% c.i. [0.70 0.73]; n = 207 neurons), indicating clear suppression on average. Across neurons, the mean MR for images was related to that measured with a preferred grating (Spearman’s ρ = 0.42; permutation test p < 0.0001; Fig. 1b). Measurements with gratings were thus informative as to whether a neuron would show strong or weak suppression, on average, across different images.

Although the mean suppression for images was related to that for a preferred grating, we found that the suppression was often much stronger for some images than others in each neuron. For instance, in the example neuron, enlarging some images nearly eliminated all spiking activity, but it had little influence on responses to other images (Fig. 1a). To quantify the variability in suppression across images, we computed a normalized MR (NMR) by dividing the MR for each image by the MR for that neuron measured with the preferred grating. The value of NMR thus provides a measure of relative suppression strength for each image, eliminating the confounding influence of variations in mean suppression across neurons. The NMR revealed strong variations in the suppression strength across images, with values varying from 10-fold weaker than that provided by gratings (NMR = 10) to 10-fold stronger (NMR = 0.1). The geometric mean NMR was 1.48 (c.i. [1.47 1.49], Fig. 1c), indicating that suppression for images was typically weaker than for the preferred grating. Further, when the NMR value was significantly different from 1 (black bars in Figure 1c), suppression was always weaker than with a preferred grating (91.5% of 17,200 cases).

Variability in surround suppression eludes existing models

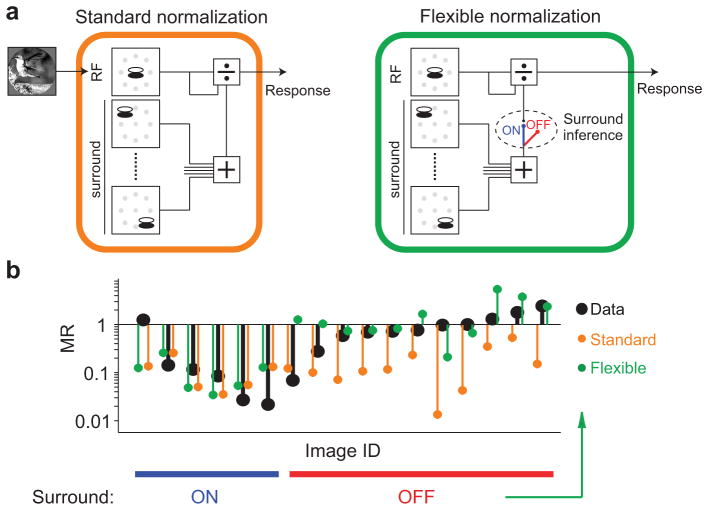
We sought to understand the variability in suppression strength recruited by natural images. Previous work with simple stimuli has shown that surround suppression involves divisive normalization^13,30, a canonical computation thought to underlie several forms of contextual modulation³. In the standard descriptive model of surround suppression, the response to a stimulus within the RF is divisively suppressed by activity in a “normalization pool”, consisting of neurons whose RFs are driven by the surround stimulus (Fig. 2a). Depending on the drive it provides to the surround pool, an image might recruit either weak or strong suppression, perhaps explaining the variability we observed.

Figure 2. Standard and flexible normalization models of surround suppression.

(a) Left: Schematic of the standard normalization model. Visual input is first passed through linear filters representing the RF (top left) and its surround (bottom left). Gray symbols denote the location of the center of each filter. The output of the RF filters is divided by the filters representing the RF and surround. Right: The flexible normalization model is identical to the standard normalization except that the surround can be turned on and off, on an image-by-image basis, depending on an inference about image homogeneity. (b) Black symbols, MR for each pair of responses shown in Fig. 1a; orange and green symbols, MR derived from the standard and flexible models, respectively, fit to the firing rates. In the flexible model, facilitation results when the surround stimulus provides additional drive to the RF, but surround suppression is inferred off.

We tested the ability of the standard normalization model to account for the observed suppression in two ways. First, we fit the model to neuronal responses to a subset of small and large images, and evaluated the cross-validated performance at predicting responses to large images (see Methods). Second, we quantified the surround drive provided by each image, and tested whether images providing stronger drive recruited greater suppression. For these analyses, we focused on the subset of neurons with measurable average surround suppression (n = 126; see Methods), to avoid trivial cases where good performance could be achieved by assuming no surround modulation for any image. All reported results were similar when we included all neurons (see Supplementary Table 1).

To evaluate the standard normalization model, we first needed to define the filters representing the RF and surround of each neuron. The drive to the RF was computed using a quadrature pair of linear filters. The surround was defined using 8 pairs of filters, spaced equally around the RF (Fig. 2a). The properties of these filters were identical to those within the RF, except their orientation preference was chosen separately for each image, to match the dominant orientation content within the RF. This choice was motivated by previous work showing that the orientation tuning of the surround changes with the stimulus presented to the RF^13,17. Finally, the model included a normalization pool inside the RF, comprising 4 pairs of filters that spanned a full range of orientations³¹. The specific parameters of the filters for each cell—the orientation preference and bandwidth, spatial frequency tuning, and size—were chosen to maximize fit quality to all images (see Methods).

We found that the standard normalization model accounted for only about half of the explainable variance in the responses to large images, on average. The mean prediction quality was 0.53 (c.i. [0.46 0.58]), where a value of 1 indicates a perfect model and 0 a model which always predicts the cell’s mean response across all images. The limited performance of the standard model appeared to arise largely from predicting strongly suppressed responses for images that provided little suppression, as illustrated for the example neuron (Fig. 2b, data in black, model predictions in orange). To test whether the failure of the standard model could be alleviated by defining the surround in a different manner, we considered several other choices of surround filters as well as variations in the normalization model itself. The average performance of the standard normalization model remained poor (Supplementary Fig. 1).

We next tested the standard model by exploring the relationship between suppression strength and surround drive (defined as the magnitude of the output of the surround filters; see Methods). For each cell, we compared the MR for the half of images providing the strongest surround drive with the half providing weakest drive, and found only slightly stronger suppression with greater drive (Fig. 3a,b; mean MR 0.53 for strong drive vs 0.62 for weak drive; p < 0.0001). Even comparing images providing particularly strong or weak drive (one standard deviation above vs. below the mean), we did not observe substantially more suppression with stronger drive (mean MR of 0.58 for both cases; p = 0.73).

Figure 3. Drive to the surround does not explain surround suppression strength.

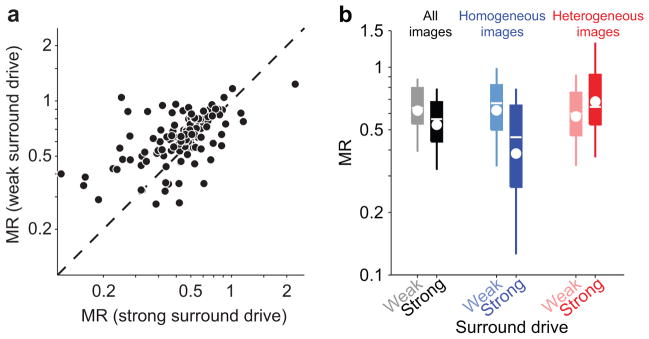
(a) Each point represents, for each neuron, the average MR for images which provide the surround with below average (ordinate) vs. above average (abscissa) drive. MR is only weakly modulated by surround drive, defined as the root mean square of the surround filters outputs. (b) Left pair: MR across all neurons, for images with weak vs. strong surround drive as in (a). Boxes denote the 25–75^th percentile; whiskers, 10–90^th percentile; white line, median; white circle, geometric mean. Middle and right pairs: same as the pair on the left, but including in the analysis only homogeneous (blue, light blue) or heterogeneous (red, pink) images.

We conclude that the surround drive provided by an image does not predict accurately the suppression it recruits. As a result, the standard normalization model provides a poor prediction of the suppression provided by images.

A principled account of surround suppression

Rather than attempting to improve the standard normalization model by searching for additional descriptive components, we instead sought to apply recent progress in understanding how contextual effects should function, given the statistics of natural images and the computational goal of representing those images efficiently. Previous work has successfully explained basic response properties of neurons in the early visual system using this approach^{22–25,32,33}. Despite this success, this approach has not been used to overcome the limited ability of models derived from simple stimuli to predict responses to images^21,34.

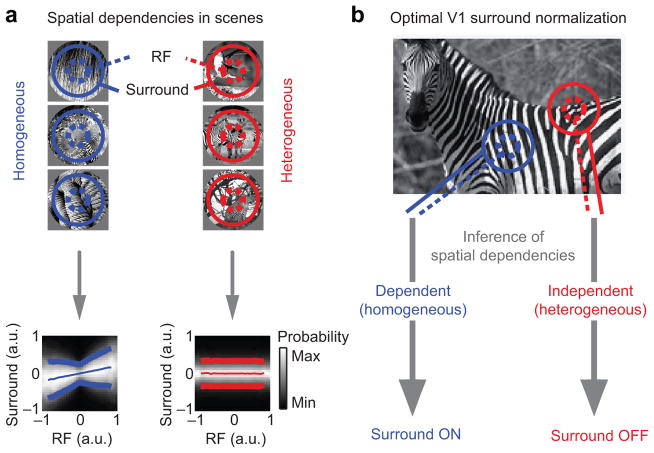
Our starting point was the observation that natural images often produce a characteristic nonlinear dependence in the output of filters representing the RF and surround²⁴ (Fig. 4a, blue; called a “bowtie” dependency because of its shape). This dependency is due to global image properties, such as the contrast or orientation of a texture, which provide common modulation to neighboring filters²⁴. This form of dependency can be effectively reduced by dividing the output of the RF by that of the surround, thus resulting in a more efficient representation²⁴. In this framework, spatial contextual effects take the form of divisive normalization because precisely this interaction is needed to remove the empirically-observed dependencies between filter outputs.

Figure 4. Surround divisive normalization is optimal only for statistically homogeneous stimuli.

(a) Left: Neighboring locations in homogeneous images contain redundant information. This produces a bowtie-shaped dependency in the outputs of filters representing the RF and surround. The dependency is illustrated in the conditional histogram (bottom): each column represents the histogram of surround filters’ outputs (position on the ordinate), given a particular output of the RF filters (abscissa). Lighter shades of gray indicate larger occurrence probability. Thin and thick lines represent conditional mean ± conditional standard deviation, respectively. Right: Neighboring locations in heterogeneous regions are independent, as evidenced by the absence of any structure in the conditional histogram (bottom). (b) Surround normalization reduces redundancy between RF and surround. Optimality requires that the normalization is turned off when the stimulus is heterogeneous. Schematic is adapted from ref. 27.

The outputs of the RF and surround filters are dependent when they fall on homogeneous regions of an image (e.g. on a single object). When the filters are driven by different objects, their outputs tend to be statistically independent (Fig. 4a, red). In such cases, no interaction between the RF and surround is needed or desired, as this would introduce a relationship between the two. Consideration of an optimal representation of images thus suggests that surround suppression should be engaged when the image patch falling on the RF and surround is homogeneous, and absent when it is heterogeneous²⁷. Previous work has shown that this principle can explain contextual effects in displays of simple stimuli⁴.

Given a specific input to the RF and surround, how to decide if it is homogeneous or heterogeneous? If one were able to calculate the dependence between the RF and surround filters’ outputs to a single input image, one could assess homogeneity and modulate suppression strength accordingly. Unfortunately, the dependence cannot be defined using a single set of filters’ responses, much like correlation between variables (a simpler form of dependency than the bowtie) cannot be defined with a single sample. Instead, one needs to infer whether that single observation is more likely to have arisen from a homogeneous or heterogeneous image. Optimal inference relies on combining the likelihood of the evidence (how likely the pattern of filters outputs arose from a homogenous or heterogeneous image) with prior knowledge about how often natural images are homogeneous, according to Bayes’ rule²⁷. An analytical expression for the resultant inferred probability is provided in Methods.

The inference about homogeneity amounts to a gating parameter on the surround influence. When the input is inferred to be homogeneous, surround suppression is fully active and takes the form of divisive normalization. When the input is inferred to be heterogeneous, the surround is muted, even if it is strongly driven by the image (Fig. 4b). When an input contains some evidence of being homogeneous and some evidence of being heterogeneous, surround suppression is engaged in proportion to the probability that the image is homogeneous—between fully active and muted.

Flexible surround suppression

We used the inference about image homogeneity to define a flexible normalization model, and asked whether it could improve our ability to predict neuronal responses to large natural images. The structure of the flexible model was identical to the standard model, and we chose its parameters in the same manner (see Methods). However, the flexible model also contained an additional gating variable that modulated the influence of the surround by the inference of homogeneity. Because we found that images were usually inferred to be homogeneous with a probability either near 1 or near 0 (Supplementary Fig. 2), we used a binary gating variable which muted the surround when the probability was less than 0.5 and left it unaffected otherwise (Fig. 2a).

Critically, the value of the gating variable was not fit to the neuronal data to improve predictions. Rather, its value was determined by learning the dependencies between the RF and surround filters representing each neuron, using an entirely independent ensemble of natural images. We then used these learned dependencies to infer whether each experimental image was homogeneous or heterogeneous, without regard to how the cell responded.

As illustrated for the example neuron, the flexible model captured the weak suppression observed for some images (Fig. 2b, green), because these were typically inferred to be heterogeneous. Across neurons, the flexible model improved prediction quality by 32% (0.53 for standard, 0.69 for flexible, p < 0.0001; see Supplementary Fig. 3 for further comparison).

While this improvement is substantial, it underestimates the true difference with the standard normalization model. In many cases, the subset of images that happened to drive a neuron were nearly entirely inferred to be either homogeneous (Fig. 5a, blue) or heterogeneous (red). For homogeneous images, the two models make identical predictions; thus, for neurons responding mostly to homogeneous images we expect little difference in performance. Similarly, for neurons responding mostly to heterogeneous images, the surround can simply always be turned off in the standard model, minimizing any difference with the flexible model. The largest difference between the models occurs when a neuron is driven by a balanced ensemble of homogeneous and heterogeneous images. We thus sorted the recorded neurons based on the proportion of effective images that were inferred homogeneous. Consistent with our reasoning, the flexible model was only slightly better than the standard model (Fig. 5b; green vs. orange line), for those neurons driven primarily by homogeneous or heterogeneous images. In neurons driven with more balanced image ensembles, the improvement was dramatic. For the tertiles of neurons with mostly heterogeneous or homogeneous images the improvement was, respectively, 20% (p < 0.0001) and 11% (p = 0.03); for the balanced tertile there was a 100% improvement (0.27 vs. 0.54, p < 0.0001). Importantly, the proportion of homogenous and heterogeneous images is roughly balanced in a large library of natural images (Supplementary Fig. 2). Thus, the flexible model will strongly outperform the standard model, across richer image ensembles than is feasible to show in an experiment.

Figure 5. Standard and flexible normalization differ most for balanced image ensembles.

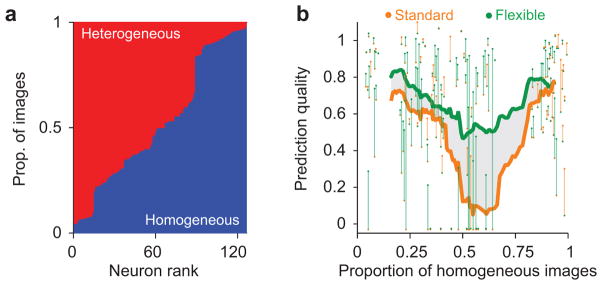
(a) Proportion of images that were inferred homogeneous (blue) vs. heterogeneous (red, stacked bars), for each neuron. (b) Cross-validated prediction quality for the flexible (green) and standard (orange) models, as a function of the proportion of effective images that were inferred homogeneous. Each dot denotes the average prediction quality for an individual neuron. Each vertical line connects the prediction quality for the two models for each neuron, and is shaded green when the flexible model performed better and orange when it did not. Thick lines indicate a running average of the performance across neurons, including 30 data points, for each model. The shaded area denotes the difference in average prediction quality between flexible and standard models. The models performed similarly in cells driven primarily by homogeneous or heterogeneous images, but the flexible model performed much better in cells driven by balanced image ensembles.

In summary, modifying the standard normalization model by including a gating variable, whose value reflects an inference of image homogeneity, provides a marked improvement in the ability to predict responses to natural images. Notably, this improvement occurs without the addition of any parameters fitted to the neuronal data.

Surround suppression is stronger for homogeneous images

The better performance of the flexible normalization model suggests that the inference about image homogeneity captures an important source of variability in surround suppression. To test this further, we compared surround suppression for images inferred as homogeneous and heterogeneous in each neuron. We found that homogeneous images were significantly more suppressive than heterogeneous ones (Fig. 6a; mean MR = 0.47 vs. 0.62; p < 0.0001). The difference in suppression strength between image classes was statistically significant in 40/126 neurons—a fraction that reflected primarily the number of images to which the cell responded. Among those neurons, suppression was stronger for homogeneous images in 80% of cases (Fig. 6b).

Figure 6. Surround suppression strength depends on image homogeneity.

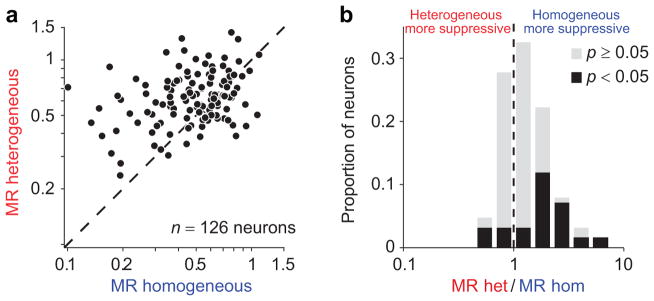
(a) MR for heterogeneous vs. homogeneous images. Each symbol represents the average MR of a neuron, for each image class. (b) The ratio between MRs for the two image categories. Values larger than 1 correspond to neurons suppressed more by homogeneous than heterogeneous images. Black bars, neurons with a ratio significantly different from 1.

The difference in suppression between homogeneous and heterogeneous images was significantly larger than that between images providing strong compared to weak surround drive (32% for homogeneity vs. 17% difference for drive shown in Fig 3a; p = 0.009). However, for homogeneous images—when the surround is engaged—suppression was 63% stronger for images providing strong drive than those providing weak drive (Fig. 3b, blue; MR of 0.38 vs. 0.62, p < 0.0001). For heterogeneous images, surround drive had little influence on suppression strength (red bars; MR of 0.68 vs. 0.58, p = 0.002), consistent with the muting of the surround. Thus, the inference about homogeneity distinguishes between images providing strong versus weak suppression better than simply measuring surround drive, the focus of the standard normalization framework. But surround drive is important for determining suppression strength, in those images inferred to be homogeneous.

Finally, we asked whether the gating of the surround was binary or continuous. As mentioned previously, the inference about homogeneity may be any continuous probability value in our framework. In practice, it often produced probability values close to 0 or 1 for our images, so we used a binary classification and gating of the surround. To test whether gating was in fact continuous, we synthetized images with intermediate probability values. Suppression of V1 neurons increased gradually as the probability of homogeneity increased (Supplementary Fig. 2), indicating that the gating of suppression is continuous, consistent with our framework.

Comparing surround suppression for images, across neurons

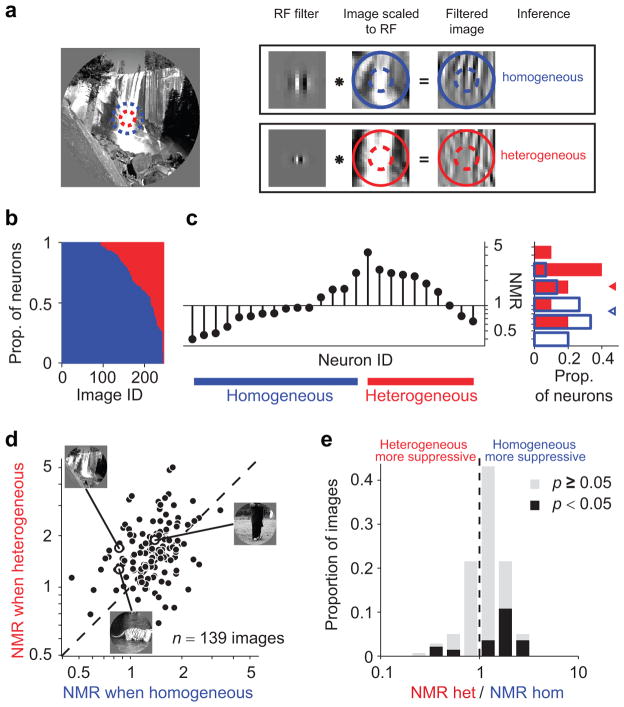
We have thus far compared the suppression in each neuron for homogeneous and heterogeneous images. Importantly, the same image may appear homogeneous to some neurons and heterogeneous to others. This is because each neuron only detects some of the structure in the image patch falling in its RF and surround, depending on its filter properties. For instance, the image shown in Figure 7a contains homogeneous structure within the RF and surround at a low spatial frequency, but appears heterogeneous at a finer scale. Figure 7b shows the proportion of neurons for which each image was inferred homogeneous (blue) or heterogeneous (red). For some images, the inference was always either homogeneous or heterogeneous, mainly because only a few neurons responded to them. However, for many images the inference differed across neurons.

Figure 7. Homogeneity depends on neuronal tuning.

(a) The same image (left) contains homogeneous structure for some neurons (RF position and size denoted with blue dashed circle; top), heterogeneous for others (red dashed circle; bottom). First column in the boxes: example filters representing two different neurons; second column: image patch scaled and centered to fit the RF; third column: the result of convolution between image and filter, indicating the image components visible to that filter. (b) Proportion of neurons for which a given image was inferred homogeneous (blue) vs. heterogeneous (red, stacked bars). Many images could be classified as either type, depending on the neuron’s tuning. (c) Stem plot: NMR for the example image in (a), across different neurons. Blue and red lines at the bottom denote neurons with surround inferred on and off, respectively. Bar plot: histogram of NMR values for each class. Triangles denote geometric mean. (d) Each symbol represents the NMR for an image, averaged separately when it was classified as heterogeneous (ordinate) or homogeneous (abscissa). Only images classified in both ways by at least 5% of neurons were included. (e) Distribution of the ratio between NMR in the two conditions. Images that were more suppressive when classified as homogeneous have values larger than 1. Black bars, images with ratios significantly different from 1.

Our framework predicts that an image should provide stronger suppression when it is inferred to be homogeneous than when that same image is inferred heterogeneous. For the example image (Fig. 7a), this was the case: normalized suppression was significantly stronger in neurons for which the image was inferred homogeneous (Fig. 7c; points above blue bar) than those neurons for which the inference was heterogeneous (above red bar; average NMR of 0.86, c.i. [0.76 0.98] vs. 1.69, c.i. [1.39 2.01] indicated in histogram to right). For the full set of images, suppression was also stronger when an image was inferred to be homogeneous than heterogeneous (Fig. 7d; average NMR = 1.32 vs. 1.58, p < 0.0001). The difference in suppression was significant for 30/139 individual images, and suppression was stronger when the inference was homogeneous in 83% of the cases (25/30; Fig. 7e).

In summary, homogeneous images provide stronger suppression than heterogeneous ones. The inference of homogeneity depends on both the image and the neuron’s properties. Thus, its role is evident not only in comparing suppression between image classes in a given cell but, notably, is also apparent in comparing the suppression caused by a given image across cells.

What determines image homogeneity?

Homogeneity is a generalized measure of similarity between RF and surround signals. An inference of homogeneity involves determining whether the outputs of the RF and surround filters for a given image are typical of those observed in homogeneous natural images (eq. (2) of Methods). The dependencies between the RF and surround outputs across different spatial positions and orientations are summarized by a set of templates (technically, the eigenvectors of a covariance matrix) learned from the ensemble of natural images. The better the match between an image and these templates, the more likely the image is to be homogeneous. The matching of RF and surround outputs to the templates has a strong intensity-dependence, with a higher probability for homogeneity when the filter outputs are larger. We found that the full inference in our framework can be approximated by a heuristic, in which the strength of the surround is gated by the product of RF and surround filter outputs divided by their sum (Supplementary Modeling and Supplementary Fig. 4).

The characterization of inference as a measure of similarity of signals in the RF and surround is reminiscent of previous descriptions—based on neuronal responses to simple stimuli^9,10,16,17. For instance a large, uniform grating is a quintessential example of a homogeneous image²⁷, consistent with uniform gratings being more suppressive than most natural images (Fig. 1b,c). Conversely, a compound grating with orthogonal orientations in the RF and surround is a clear example of a heterogeneous image²⁷, and produces weak or no suppression^16,17,30. However, the inference about homogeneity also captures effects that elude previous descriptions, in addition to its better ability to account for suppression with natural images. For instance, a large patch of white noise appears as a uniform texture, yet it is heterogeneous because random image structure inside the RF is independent from the random structure in the surround²⁷. Consistent with this prediction, white noise images elicit much weaker suppression than uniform gratings (Supplementary Fig. 5). Similarly, when high-order structure in natural images is destroyed by randomizing their Fourier phase, images become heterogeneous and a release from suppression is observed (Supplementary Fig. 5).

DISCUSSION

Understanding cortical responses to natural images is a well-recognized bottleneck in the study of visual processing, as models based on measurements with simple stimuli have struggled to predict responses to images²¹. Our model predicts V1 responses to natural images substantially better than previous models. This improved performance involves a gating of a widespread computation in cortex—divisive normalization from the surround—by an inference about image homogeneity. Our framework not only predicts this flexible form of normalization, but also explains why it exists: namely, that surround suppression is only needed to encode images efficiently when the RF and surround are statistically dependent. Our approach thus shows the advantage of studying and explaining cortical responses through an understanding of image statistics, rather than by attempting to derive more complex descriptive models.

We stress that our results in no way argue against the importance of normalization as a canonical computation. On the contrary, in our framework normalization is critical for encoding homogeneous images. The shortcoming of the standard normalization model of the surround is that it assumes suppression is only determined by the drive to the normalization pool.

We considered many previously-proposed constellations of surround filters, but none could account for the measured responses (Supplementary Fig. 1). Though there might be a complex arrangement of surround filters which would improve the performance of the standard model, the combinatorial explosion of surround configurations makes searching for this constellation impractical. Further, defining such a complex descriptive model amounts to a data fitting exercise—one is left with no understanding as to why visual cortex uses such an arrangement to encode images. We showed instead that understanding how natural image statistics should be encoded readily leads to a simple generalization of the standard model, allowing the influence of the surround to be minimized when it is driven by different image components from the RF. While our data do not directly demonstrate that V1 performs the Bayesian optimal computation, they suggest that suppression is gated in a way consistent with reducing redundancy in the outputs of the RF and surround filters.

How could the inference in our model be implemented in cortex? Such a sophisticated computation is likely to be a network-level operation, possibly occurring in higher cortical areas where neurons are sensitive to higher-order image structure. Regardless of the cortical locus, previous theoretical work has shown that populations of neurons can represent and compute with probabilities using simple, realistic neural operations: inference might boil down to simple comparisons of synaptic inputs³⁵. Another possibility is that cortical circuits do not perform the full inference but rather an approximation, perhaps using the simple heuristic—in which the sum of RF and surround outputs is compared to their product—we have derived.

How could the inference of homogeneity then be used to gate the efficacy of the surround? Surround suppression is thought to rely primarily on lateral and feedback connectivity¹¹. Gating surround suppression thus requires adjusting the gain of lateral and feedback inputs. Previous work has revealed network mechanisms^20,36 that could achieve such a gain adjustment. In particular, Miller and colleagues have argued that inhibition functions to stabilize the recurrent excitation that is recruited by strong stimulus drive^37,38. In these inhibition-stabilized networks, providing additional external excitatory drive can have the counter-intuitive effect of reducing responsivity in the network. If only homogeneous images recruit additional excitation from higher cortex, one would see the consequences of inhibitory stabilization (i.e. weaker responses) only for these images. Under this scenario, homogeneous but not heterogeneous images should result in a withdrawal of both excitation and inhibition, a distinguishing feature of an inhibition-stabilized network.

An alternative possibility is that distinct classes of inhibitory neurons might mediate surround modulation^19,39,40 and its gating⁴¹. Recently interneurons expressing vasoactive intestinal peptide (VIP) have been shown to target specific subtypes of interneurons^41–43, particularly somatostatin-expressing cells which may play a central role in surround suppression^39,40. If VIP neurons were driven by feedback signals encoding homogeneity, they could silence surround suppression. Under this hypothesis, the activity of VIP interneurons should correlate with the inferred probability of image homogeneity. Furthermore, inactivation of these interneurons should block the gating of surround suppression for heterogeneous images, yielding suppression similar to that predicted by the standard model. Recent characterization of distinct subtypes of inhibitory interneurons has also made clear that some have little surround suppression^19,39, perhaps explaining why we and others find neurons that show little suppression even with gratings, which are highly homogeneous stimuli (Fig. 1b). The absence of suppression in these neurons may be necessary for providing signals that allow the efficient encoding of images by other subpopulations of neurons (e.g. pyramidal cells which project downstream).

While our framework clearly extends the standard normalization model, it did not capture all of the explainable variance in cortical responses. Model performance might be improved by relaxing the assumption that the surround normalization pool consists of a fixed set of filters for each neuron. This could be accomplished by considering models in which the inference not only gates the surround but also determines which components of the normalization pool are included, on an image-by-image basis⁴⁴. An alternative way to improve performance would be to consider other computational goals. Our framework aims to reduce the dependencies between filter outputs in the RF and surround. Other goals might also be important, such as representing relevant information in a format that could be easily read-out by downstream neurons⁴⁵ or dynamically adjusting neuronal tuning to changing perceptual demands⁴⁶. Thus, while the principle of efficient coding which underlies our framework is consistent with the behavior of V1 neurons, we do not suggest that achieving an efficient representation is their sole goal.

It is important to note that heterogeneous (or, more broadly, non-stationary) inputs are not rare or peculiar to early visual processing. They occur frequently in natural sensory processing, since signals are often generated by different physical sources: the light reflected off occluding objects; the smell of different foods on a table; or the voices of different speakers in a room. Our approach should thus be highly relevant to the study of other types of sensory processing, as well as to other forms of sensory contextual modulation (e.g. adaptation). More generally, the inference about image homogeneity is representative of a general problem known as causal inference, which involves assessing the plausibility of different interpretations about the causal relation between objects or events in the world (which are not directly measurable) and the sensory input they provide. Causal inference is pervasive not only in sensory processing⁴⁷ but also higher cognitive function⁴⁸, suggesting relevance of our framework to higher cognitive processes, particularly those already linked to divisive normalization^8,49.

Methods

Animal preparation and data collection

Data were collected from 3 adult male monkeys (macaca fascicularis). Animal preparation and general methods were described previously⁵⁰. In brief, anesthesia was induced with ketamine (10 mg/kg) and maintained during surgery with isoflurane (1.0–2.5% in 95% O2). During recordings, anesthesia was maintained by sufentanil citrate (6–18 μg/kg/hr, adjusted as needed for each animal). Vecuronium bromide (0.15 mg/kg/hr) was used to suppress eye movements. The use of anesthesia allowed us to present a large ensemble of images, while ensuring precise and reproducible retinal positioning across trials. All procedures were approved by the Albert Einstein College of Medicine at Yeshiva University and followed the guidelines in the United States Public Health Service Guide for the Care and Use of Laboratory Animals.

We recorded neuronal activity using arrays of 10 × 10 microelectrodes (400 μm spacing, 1 mm length) inserted in the opercular region of V1. Waveform segments that exceeded a threshold (a multiple of the RMS noise on each channel) were digitized (30 kHz) and sorted offline. For all analysis we included signals from well-isolated single units as well as small multi-unit clusters, and refer to both as neurons. We obtained similar results when our analysis was based only on very well-isolated single units (see Supplementary Table 1).

Visual stimuli and presentation

We displayed stimuli on a calibrated CRT monitor (1024 × 768 pixels; 100 Hz frame rate; ~40 cd/m² mean luminance) placed 110 cm from the animal, using custom software.

We measured the spatial RF of each neuron, using small gratings (0.5 degrees in diameter; 4 orientations; 250 ms presentation) presented at a range of positions. The RF center of each neuron was defined as the location of the peak of a 2-dimensional Gaussian fit to the spatial activity map (across the population, median R² = 0.59).

We used natural images from several common databases: the Berkeley Segmentation Database, the Brodatz textures, and the Van Hateren database. We converted color images to gray scale values, and extracted 894 random patches of 320 × 320 pixels, for which the average pixel intensities were in the range 40–200 (where 255 was the maximal intensity that could be displayed) and RMS contrast was in the range 0.25–0.75. From these patches, we selected our experimental stimuli, with two objectives: (1) to drive V1 cells sufficiently well that we could measure suppression, if it occurred; (2) to maximize the diversity of image types in the experimental ensemble. To select images that would provide robust drive to V1 cells, we computed the power spectrum of the central 1 deg (50 × 50 pixel) region of each image. We excluded images for which the centroid of the rotational average of the power spectrum (a measure of the average spatial frequency content) fell outside the range 0.5–10 cycles/degree, typically preferred by V1 neurons⁵⁰. To ensure a diverse ensemble, we computed the orientation histogram of the central 1 deg using a steerable pyramid⁵¹ with 16 orientations and 3 scales. We binned images into 3 categories—low, medium, and high—based on the entropy of the orientation histogram, a measure of the “orientedness” of the image. A lower entropy indicates that more of the image energy was confined within a single orientation band. We selected the 30 images closest to the middle of each bin. For images with low and intermediate entropy, we created 4 copies rotated in steps of 45 degrees. This provided a total of 270 images (30 without a dominant orientation in the center, and 2 × 4 × 30 with a dominant orientation in the center).

We adjusted the mean pixel value and RMS contrast of each image to values of 116 and 0.6, respectively. This was done to preclude any influence of different mean luminance or contrast across images on neuronal responses. To ensure that the experimental ensemble provided an accurate and unbiased view of the role of inferred homogeneity in determining suppression strength, we adopted a resampling procedure. For each cell, we resampled responses from those images which drove the cell, to match the proportion of homogeneous and heterogeneous cases in natural images for the filters representing that cell.

Each image was included in the experimental ensemble twice: once masked by a small annular window with diameter 50 pixels (1.04 degrees), and also by a larger annular window with inner diameter of 150 pixels (3.1 degrees of visual field, used in 1 animal) or 320 pixels (6.7 degrees; 2 animals). We used an annulus of 150 rather than 320 pixels in one animal to test whether model performance would be improved by activating a smaller portion of the surround. We observed no difference between the two datasets, so the results were pooled.

To measure the tuning properties of each neuron, we interleaved static grating stimuli with the natural images. We varied grating size (7 diameters logarithmically spaced between 0.33 and 6.25 degrees, presented at 4 orientations), orientation (16 values equally spaced between 0 and 180 degrees), and spatial frequency (8 values logarithmically spaced between 0.25 and 7.26 cycles/degree, presented at 4 orientations). Variations of size and orientation were presented at a spatial frequency of 1 cycle/degree. Variations of orientation and spatial frequency were presented at a size of 1 degree. All gratings were presented at 4 spatial phases, with mean luminance and RMS contrast matched to that of the natural images.

All stimuli were displayed in pseudo-random order for 100 ms each, followed by a 200 ms uniform gray screen. Each stimulus was presented 20 times. Stimuli were presented monocularly in a circular aperture surrounded by a gray field of average luminance.

Characterization of neuronal responses

We quantified neuronal activity by the mean firing rate (R) across repeated trials of the same image, measured in a window 50 to 150 ms following stimulus onset (to account for response latency). The spontaneous activity was measured during the last 50 ms of the blank screen following each image.

The strength of surround suppression, or Modulation Ratio (MR), was defined by a common metric^14,29, namely the ratio between the raw response to a large image (3.1 or 6.7 degrees) and its small counterpart (1.04 degree) MR = R^large/R^small. To obtain reliable estimates of MR, we considered for each neuron only those images with R^small at least 1 standard deviation above the spontaneous rate.

To compare the suppression elicited by a given image across different neurons, we used a normalized MR (NMR) to account for differences in the overall suppression across neurons: NMR = MR/MR^grating, where MR^grating quantifies the suppression measured with the most preferred static grating in the stimulus ensemble. We normalized by MR^grating rather than by the average MR across natural images, because each neuron was typically driven by a different subset of images.

Inclusion criteria

The 207 neurons analyzed in Figure 1 were selected because they met the following criteria: 1) The RF was centered on the stimulus, namely either the distance between RF center and stimulus center was less than 0.2 deg (2 animals), or the maximal response to annular grating stimuli (1 deg inner diameter) was less than 15% of the maximal response across all stimuli (1 animal), thus ensuring that surround stimuli did not provide substantial drive to the RF center. 2) The neuron responded above its spontaneous rate to at least 4 small natural images. The 126 neurons on which the majority of our analyses were based (Figs. 2,3,5,6,7), met the additional criterion that they showed evidence of surround modulation with natural images. This was defined by the responses being explained better by a model that included surround modulation (standard or flexible) than one that assumed none. Similar results held when we included all well-centered and responsive neurons (n = 207), but this diluted the difference between models because of the inclusion of neurons that showed no appreciable suppression (Supplementary Table 1).

Standard normalization model

Under the standard normalization model, the response R to an image is defined by the drive to the RF, divided by the drive to the normalization pool^3,13:

$$R=\alpha {\left(\frac{E_{RF}}{\sigma +\beta E_{\mathbf{k}}+\gamma E_{\mathbf{s}}}\right)}^n$$ (1)

The E_RF term measures image drive, or energy, to the RF, computed from the outputs of filters chosen individually for each neuron; E_k and E_s capture the drive to the normalization pool inside the RF and in the surround, respectively. β and γ determine the relative strength of these normalization pools, which may differ¹³. Note that γ captures the average surround suppression strength, which can vary widely across neurons^10,12–15 (Fig. 1b). Finally, the parameters α,σ n capture the non-linear relationship between filter drive and spiking responses.

The drive to the RF, E_RF, is defined as follows. The RF of each cell was represented by a pair of linear filters (quadrature pair, of even and odd phase). The output of each filter was defined by the dot product between the image and the filter. The drive was then defined as the square root of the sum of squares of the filters’ outputs. We verified that the use of quadrature pairs (i.e. modeling the RF drive as for complex cells) was justified for our data (Supplementary Fig. 6).

The normalization signal within the RF, E_k, was computed from the output of four quadrature pairs of filters. These filters had the same size, position, and spatial frequency tuning as those of E_RF, but each pair had a different preferred orientation (0,45,90, and 135 deg), yielding a normalization signal that was unturned for orientation⁵². The normalization signal from the surround E_s included 8 pairs of filters, uniformly positioned around the RF center as on a clock face (Fig. 2a). The surround filters had the same spatial frequency preference and size as those in the RF. All surround filters had the same preferred orientation. This preferred orientation was changed from image-to-image, to match the dominant orientation in the image presented inside the RF, thus capturing the finding that the orientation tuning of surround suppression shifts with the orientation content within the RF ^13,17. The distance between the surround filters and the RF center was proportional to the RF size, allowing for a slight spatial overlap between the RF and surround and yielding a surround whose spatial extent was 2–3 times that of the RF^11–13.

Inference about homogeneity

The inference of image homogeneity was based on a Mixture of Gaussian Scale Mixtures model (MGSM), described previously^27,44 and summarized in Supplementary Modeling. This Bayesian model considers the statistical dependency between the outputs of the filters that define the RF and surround for a given neuron: k, which represents the outputs of the RF filters and the filters providing normalization within the RF; and s, which represents the outputs of the filters providing the normalization signals from the surround. The inclusion in k of both the RF filters and the within-RF normalization pool corresponds to the assumption that the outputs of spatially overlapping filters are always statistically dependent.

For a given input image, k and s are observed, but their dependence (homogeneous image) or independence (heterogeneous) must be inferred. The inferred probability that the image is homogeneous, given the observed filter responses, is⁴⁴:

$$p(\text{homogeneous}\mid \mathbf{k},\mathbf{s})\propto p(\text{homogeneous})·\frac{\mathcal{B}\left(1-\frac{n}{2};\sqrt{(\mathbf{k},\mathbf{s}){\mathbf{C}}^{-1}{(\mathbf{k},\mathbf{s})}^{\top }}\right)}{\sqrt{{(2\pi )}^{\pi }det(\mathbf{C})}{\left(\sqrt{(\mathbf{k},\mathbf{s}){\mathbf{C}}^{-1}{(\mathbf{k},\mathbf{s})}^{\top }}\right)}^{\frac{n-2}{2}}}$$ (2)

where n is the total number of filters; 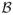is the modified Bessel function; C is the covariance matrix between k and s, and p(homogeneous)is the prior probability that k and s are dependent.

The covariance and the prior were learned by applying the filters representing each neuron to a separate database of natural images not used in the experiments. The goal of this optimization is for the model to learn which patterns in natural images distinguish homogeneous from heterogeneous images (the covariance), and how often they occur (the prior). Technically, this amounts to maximizing the likelihood of the training images under the MGSM. Further details are provided in Supplementary Modeling.

Flexible normalization model

The predicted response for the flexible normalization model was based on the standard model, eq. (1), except that the surround term in the denominator, E_s, was multiplied by a gating variable which took a value of 1 if the image was inferred homogeneous with a probability greater than 0.5, and 0 otherwise. Thus, when the image was inferred to be homogeneous, the flexible normalization model was identical to the standard model; when the image was inferred to be heterogeneous, there was no influence of the surround. The value of the gating variable was not fit to neural data. Therefore, the flexible and standard models used the same free parameters.

Model fitting

We first estimated the parameters of the normalization models (σ, n, α, β, γ) and the choice of filters for each neuron, by maximum-likelihood fitting to the raw responses to all images that drove the cell (as defined above). Likelihoods were computed assuming Gaussian variability of the spike counts, with a variance which scaled with the mean response⁵². Maximum likelihood fitting in this case amounts to minimizing the sum of squared errors between the predicted and measured responses, weighted by the inverse variances.

The maximization was performed numerically for the normalization model parameters, and by exhaustive search for the best filters. Specifically, we searched for the best filters from a set defined by a steerable pyramid⁵³. The steerable pyramid is a popular method to construct oriented bandpass filters at multiple preferred orientations, spatial frequencies, and sizes⁵¹. We used an extension that allowed us to build simultaneously both filters in a quadrature pair⁵³. The set contained filters with preferred orientations of 0, 45, 90, or 135 degrees, an orientation bandwidth (half width at full height) of 45, 22.5, or 11.25 degrees, a preferred spatial frequency (ω) of 1/12, 1/24, or 1/48 cycles/pixel, and one of four sizes: ${\left\{\frac{1}{\omega }+\frac{\omega }{12}m\right\}}_{m=2,4,6,8}$ pixels. In total, we thus considered 144 distinct filters. We constrained the choice of filter size to be within 25% of the measured RF size, defined as the peak of the neuronal area summation curve measured with gratings. Note that the relationship between the filters for the RF, the within-RF normalization pool, and the surround was fixed: the RF filters and those of the normalization pools of each neuron were the same, except that the orientation preference of the surround filters changed from image-to-image and the within-RF normalization pool always included all four orientation preferences, as described above.

Both standard and flexible models could account for the rare occurrence of response facilitation with the larger image, if that image provided additional drive to the RF but either little drive to the surround or was inferred heterogeneous.

Model comparison

We compared standard and flexible normalization models by cross-validation. We divided the measured responses into a training and test set, obtained by holding out the responses to one pair of large and small images. For the training set, we re-estimated the (σ, n, α, β, γ) parameters. We then quantified the prediction quality on the left-out data, using a normalized log-likelihood ratio⁵⁴:

$$\text{Prediction}\text{quality}=\frac{L-L_{\mathit{null}}}{L_{\mathit{oracle}}-L_{\mathit{null}}}$$

where L denotes the log-likelihood of the left-out data given the model parameters; L_null denotes the log-likelihood of a “null” model which always predicts the mean response across all images of the training set; and L_oracle denotes the log-likelihood of an “oracle” which is assumed to know the true mean response to each image, and whose error is due exclusively to the fact that the observed mean is estimated from a finite number of trials. Because of this uncertainty, the oracle’s error can be marginally larger than the model’s error on measured data, hence prediction quality can exceed a value of 1 (Fig. 5b). We repeated the procedure to compute prediction quality for all possible splits of the images into training and test sets, and then averaged the results across all held-out images (i.e. leave-one-out cross-validation).

Note that we did not update our choice of filters for each subset of responses used for training in cross-validation, because that was computationally prohibitive. To be sure that prediction quality was not inflated by using filters chosen in part using responses to the test images, we used a second independent approach to choose filters for both the standard and flexible models in a subset of neurons: we measured the tuning for orientation, spatial frequency, and size, with static grating stimuli. We then chose the filters to match these measurements. All of our core results were quantitatively indistinguishable with this method (Supplementary Fig. 7).

Statistical analysis

Error bars represent bootstrap estimates of the 68% confidence intervals, obtained by sampling 10,000 times with replacement. Statistical significance was assessed for Fig. 1b with a two-tailed permutation test, the standard choice for Spearman correlation. For all other analyses, we used non-parametric bootstrap t-tests in order to relax the assumption of normality, using 25,000 bootstrap samples (unpaired, two-sided in Fig. 6b and Fig. 7e; paired, one-sided for all other comparisons), except where noted. For the bootstrap paired t-test, we created the bootstrap distribution of t-statistics for the null hypothesis (mean difference equals zero) by subtracting the mean difference from each measured difference, sampling with replacement from this centered distribution, and calculating t-statistics for the sampled differences. The p-value was given by the proportion of cases in which the bootstrapped t-statistics had a more extreme value than the t-statistics for the actual data. The bootstrap unpaired t-test was similar, except the distribution for the null hypothesis (identical means) was constructed by subtracting the mean of each dataset from the corresponding elements of that dataset, combining the datasets, sampling with replacement to create two surrogate datasets, and computing the t-statistics for the difference in the sampled surrogates. The average MR and NMR were geometric means, and statistical significance was evaluated for the logarithm of MR and NMR. No blinding or randomization was used. No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those of previous neuronal studies of surround suppression^12–17. A methods checklist is available with the supplementary materials.