Extracting Cell Stiffness from Real-Time Deformability Cytometry: Theory and Experiment

Abstract

Cell stiffness is a sensitive indicator of physiological and pathological changes in cells, with many potential applications in biology and medicine. A new method, real-time deformability cytometry, probes cell stiffness at high throughput by exposing cells to a shear flow in a microfluidic channel, allowing for mechanical phenotyping based on single-cell deformability. However, observed deformations of cells in the channel not only are determined by cell stiffness, but also depend on cell size relative to channel size. Here, we disentangle mutual contributions of cell size and cell stiffness to cell deformation by a theoretical analysis in terms of hydrodynamics and linear elasticity theory. Performing real-time deformability cytometry experiments on both model spheres of known elasticity and biological cells, we demonstrate that our analytical model not only predicts deformed shapes inside the channel but also allows for quantification of cell mechanical parameters. Thereby, fast and quantitative mechanical sampling of large cell populations becomes feasible.

Introduction

The stiffness of cells is an important phenotypical marker that can provide insights into cellular adaptation and differentiation as well as pathological changes of cells (1, 2, 3, 4, 5, 6). Therefore, cell-mechanical phenotyping is an important contribution to biological research and medicine including applications in cell sorting and medical diagnostics (7, 8, 9, 10, 11, 12, 13, 14).

Typical methods for the measurement of cell stiffness include atomic force microscopy (AFM) indentation, magnetic twisting cytometry, optical stretching, and others (15). Cell-mechanical studies based on these methods do not allow for a throughput much beyond one cell per minute. However, the population size and heterogeneity of cells in medical and biological samples requires high-throughput methods for classification and analysis. Recently, several microfluidic techniques have been introduced that start to address this need (13, 16, 17, 18). Of these, deformability cytometry (DC) (13) and real-time DC (RT-DC) (17) deform cells purely by hydrodynamic interactions and without contact with channel walls. Although DC probes cells in an extensional flow at rates of thousands of cells per second, it operates in a dynamic regime of Reynolds numbers of $\approx 50$. This renders the calculation of associated flow fields a challenging, time-dependent, nonlinear problem. To date, no analytical or numerical modeling has been applied to this method, which leaves the cell mechanical characterization purely phenomenological. By contrast, in RT-DC, somewhat smaller rates of hundreds of cells per second together with a more viscous carrier medium lead to a fluid flow at low Reynolds numbers $\left(\approx 0.1\right)$, making it amenable to theoretical analysis. In RT-DC measurements, suspended animal cells are advected by a shear flow through a microfluidic channel at a constant speed. In this process, cells are deformed due to the existence of strong velocity gradients within the channel cross section (17). A sketch of the measurement setup is depicted in Fig. 1 A. The observed deformation of initially spherical cells in the flow channel depends on cell stiffness, but it may also be influenced by flow speed, relative cell size, and internal cell architecture. To disentangle the influence of these parameters, it is necessary to quantify the stresses exerted on the cells in the shear flow and apply cell mechanical models to predict the resulting deformations.

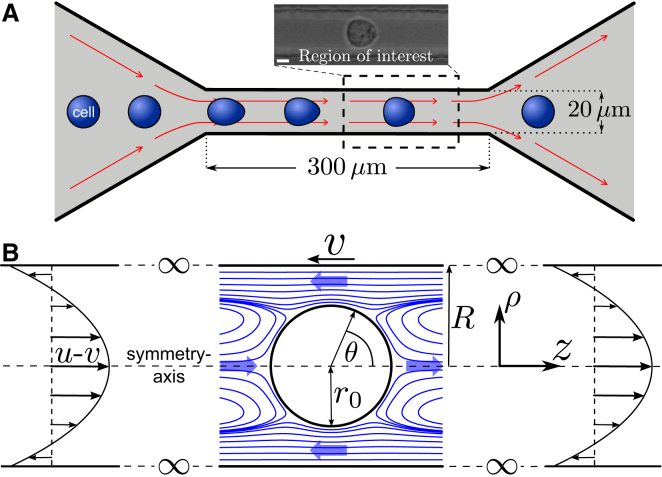
Figure 1.

RT-DC setup and flow field around an advected sphere. (A) Channel geometry for RT-DC measurements is adapted from Otto et al. (17) (not to scale). Cells enter the flow channel, start to deform, and acquire a steady shape in the end portion of the channel. There, deformations of cells are measured with RT-DC. The inset representatively shows a deformed HL60 cell. The inset scale bar is 5 μm. (B) Definition of comoving spherical coordinates $\left(r,\theta \right)$ and cylindrical coordinates $\left(\rho ,z\right)$ with azimuthal symmetry. The sketch visualizes the boundary conditions at channel walls (no-slip), $\mathbf{v}\left(R,z\right)=-v{\mathbf{e}}_z$. At the inlet and outlet of the channel at $z\to \pm \infty$, we require that $\mathbf{v}\left(\rho \right)=\left[u\left(R^2-{\rho }^2\right)/R^2-v\right]{\mathbf{e}}_z$ (Poiseuille flow). The fraction $\lambda =r_0/R$ of channel radius R and sphere radius $r_0$ defines the only independent parameter for this problem. Streamlines (blue) and thick arrows illustrate directions of the flow in different regions close to the advected sphere $\left(\lambda =0.6\right)$. Note that in the comoving frame, some streamlines change direction and thus enter and exit on the same side of the image. To see this figure in color, go online.

Previous studies have presented extensive insight into the deformation of advected red blood cells and vesicles in cylindrical and square channels (19, 20, 21). Recent work has focused in particular on numerical solutions where underlying mechanical models anticipated either a fluid-like incompressible membrane with bending stiffness (22, 23) or elastic microcapsules (23, 24, 25, 26). An analytical approach to the elastic deformation of microcapsules in a linear shear flow was given by Barthès-Biesel (27), whereas Lighthill and Fitzgerald presented analytical studies of tight-fitting elastic pellets in terms of lubrication theory (28, 29). However, to our knowledge, there exists as yet no full analytical derivation for the elastic deformation of an elastic sphere and the deformation of a thin elastic shell in a cylindrical flow channel. Our perturbation approach of small deformations aims for simple analytical expressions that allow the extraction of scaling laws of the system and rapid fitting to experimental data.

We employ an analytical expansion of the Stokes equation to calculate the flow field around a spherical object advected by a flow in a cylindrical channel (30). The obtained flow field is used to derive hydrodynamic surface stresses acting on the spherical object for the situation of a uniform, force-free motion through the channel. Surface stresses are then prompted as a boundary condition into linear elasticity theory to calculate surface displacement fields of the spherical object. As cell mechanical models, we anticipate the scenario of either an elastic sphere or a thin elastic shell with or without surface tension. We verify our theoretical results by numerical simulations and experimentally by RT-DC measurements of agar beads and accompanying AFM indentation measurements. Finally, we present to our knowledge the first data on cell stiffness, as obtained from RT-DC measurements for a human promyelocytic cell line (HL60). This work constitutes a theoretical underpinning for high-throughput RT-DC experiments directly relating measured cell deformation to elastic parameters of the cell.

Materials and Methods

Velocity measurements

We suspended commercially available polystyrene beads in a solution of phosphate-buffered saline (PBS) without Mg²⁺ and Ca²⁺ and 0.5% (w/v) methylcellulose (Sigma Aldrich, Hamburg, Germany), as used for cell measurements with RT-DC. The nominal diameters of the beads given by the manufacturer were (mean ± SD) $10.37\pm 1.27$ μm (118, Phosphorex, Hopkinton, MA), and $12.27\pm 0.12$ μm, $15.21\pm 0.31$ μm, and $19.3\pm 0.36$ μm (Q-F-0570, Q-F-KM194, and Q-F-KM223, Microparticles, Berlin, Germany), which covers a wide range of sizes that are still small enough to fit through the channel. The bead solution is driven through the channel by a high-precision syringe pump. Videos are taken using a high-speed camera built into a brightfield microscope and are later analyzed with custom-built tracking software. Further details of the experimental setup and the associated tracking software can be found in Otto et al. (17). After the flow rate of the bead suspension was set, we waited for 5 min before taking videos to ensure a stable and equilibrated flow of bead suspension. Employing the equivalent channel radius, $R_{\text{eq}}$, (Section S3 in the Supporting Material), tracked bead sizes were used to calculate the parameter $\lambda =r_0/R$, where $r_0$ is the sphere’s radius. Knowledge of channel dimensions (square channel cross section of width L) and flow rate, Q, allows calculation of the central flow velocity, u, as (31)

$$u=K_2\frac{Q}{L^2},$$

where $K_2\approx 2.096$. Measured bead velocities, v, were normalized by the flow velocity, u, and plotted against the corresponding value of λ. Measurements were repeated and taken at two different flow rates (0.04 and 0.08 μL/s), consistently yielding results as shown in Fig. 2 B. Further details of the experimental setup can be found in Otto et al. (17).

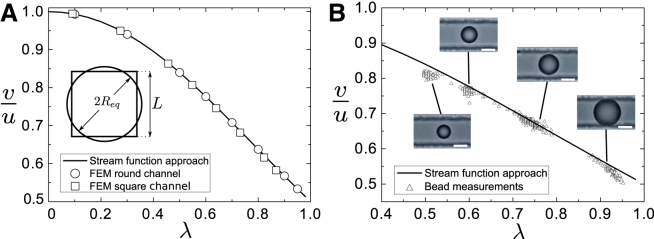
Figure 2.

Theoretical and experimental equilibrium velocities of undeformed spheres. (A) Size dependence of the velocity ratio, $v/u$, where v is the equilibrium velocity of the sphere and u is the peak velocity of the Poiseuille flow in the channel. Velocity ratios were obtained from the stream-function approach (solid line), or from finite-element simulations in a cylindrical channel (circle) or a square channel (square). The cylindrical channel was chosen such that the equivalent channel radius condition, $2R_{\text{eq}}=1.094\times L$ (inset), was satisfied (32). (B) Velocity measurement of polystyrene beads of different mean diameters (10.4 μm, 12.3 μm, 15.2 μm, and 19.3 μm) being flushed through a microfluidic channel with a square cross section (width $L=20$μm) using a high-precision syringe pump. The solid line depicts the solution derived from the stream-function approach. The graph contains 817 measurement points (triangles). The inset scale bars are 10 μm. To see this figure in color, go online.

Preparation of agar beads

Agar beads were obtained by preparing an emulsion using an aqueous solution of low-gelling-point agarose (A0701, Sigma-Aldrich) as the dispersed phase and light mineral oil (330779, density 0.84 g/mL, viscosity 30 mPa·s, Sigma-Aldrich) with 2% (v/v) Span-85 surfactant (S7135, $M=957.52$ g/mol, Sigma-Aldrich) as the continuous phase. Agarose solution was prepared by dissolving agarose powder at a concentration of 0.5% (w/w) in deionized water. The mixture was then placed for 3 min in a microwave oven. After a transparent solution was obtained, it was placed in a submersion water bath at 70°C, where it was held for at least 1 h to allow air bubbles to escape. The continuous phase was poured into a beaker on a magnetic stirrer (VMS-C4, VWR International, Darmstadt, Germany) with a stirring rate of 1250 rpm. Agar solution at 70°C (100 μL) was pipetted into the oil, 1% (v/v), and vortexed for 40 s at room temperature, generating agar beads with a diameter between 2 and 50 μm. Afterward, the bead solution was poured in a 15 mL centrifuge tube and stored in a refrigerator for 1 h. After overnight sedimentation, the oil was removed and substituted with 2 mL of metacellulose solution, after three washings with 2% w/v poly(ethylene glycol)monooleate (460176, density $1.034$ g/mL, $M=860$ g/mol, Sigma-Aldrich) aqueous solution. The final bead concentration was adjusted by pipetting 200 μL taken from the top of the solution in 1 mL of metacellulose solution. The metacellulose solution was prepared by dissolving methylcellulose (M 0512, $M=\mathrm{88,000}$ g/mol, Sigma-Aldrich) at a concentration of 1% (w/v) in PBS, with a final dilution of 50% in 2% w/v poly(ethylene glycol)monooleate aqueous solution.

HL60 cells

The HL60 cell line was cultured according to the methods of Otto et al. (17). To prepare the cell suspension for RT-DC measurements, cells were centrifuged at 115 g for 5 min (Eppendorf 5805 R, Eppendorf, Hamburg, Germany) and resuspended in a solution of PBS (without Mg²⁺ and Ca²⁺) and 0.5% (w/v) methylcellulose (Sigma Aldrich) to a final concentration of 10⁶ cells/mL. For the deformation measurements, cells were taken during log phase, ∼36 h after splitting.

Shape fitting

Deformed shapes were tracked and transformed to polar representations, ${\mathit{\varrho }}_{\text{m}}\left({\theta }_i\right)$, at 50 equidistant angles, ${\theta }_i$. To exclude tracking of nonsymmetric deformations with respect to the flow axis (e.g., due to imperfect spatial cell focusing), the upper-half area, $A_{\text{U}}$, and lower-half area, $A_{\text{L}}$, of the contours were calculated, and only objects with $\left|1-A_{\text{U}}\text{/}{A}_{\text{L}}\right|<0.005$ were used for shape fitting. Objects with $A=A_{\text{U}}+A_{\text{L}}>180$ μm² $\left({\lambda }_{\text{ECR}}\approx 0.7\right)$ were not considered for shape fitting, to avoid the influence of channel boundary effects on the deformation. Assuming volume conservation $\left(\nu =0.5\right)$ and a rotationally symmetric shape, we calculate λ with respect to the equivalent channel radius. At this point, the elasticity modulus, E, and the positioning of the theoretical shape over the tracking data (two coordinate parameters $\left(x,y\right)$) are the only remaining fitting parameters. For each value E and position $\left(x,y\right)$ tested, deformed shapes, ${\mathit{\varrho }}_{\text{t}}^E\left(\theta \right)$, predicted by our theories were calculated and sampled at angles ${\theta }_i$ in the same coordinate system as the tracked shape. Minimization of the residual $r\left(E\right)=\sum _i{\left|{\mathit{\varrho }}_{\text{m}}\left({\theta }_i\right)-{\mathit{\varrho }}_t^E\left({\theta }_i\right)\right|}^2$ was achieved by using the nonlinear regression routine provided by MATLAB R2012b (www.mathworks.com). We employed the robust fitting method with an iterative bisquare weighting to reduce the impact of outliers in the tracked shapes. Relative symmetric 95% confidence intervals (fitting errors) of the elastic parameters ranged from 5% to 40%.

Results

We study a simple cell mechanical model where suspended cells are regarded as linearly elastic, isotropic objects with a spherical reference shape. To derive cell stiffness from cell deformation in the flow channel, we pursue a perturbation approach where we only consider contributions to the first order in elastic strain. This approach is equivalent to a first-order approximation in terms of the flow rate, Q, through the channel, as small flow rates correspond to the case of small surface stresses on the sphere (see Section S1 in the Supporting Material). As a perturbation parameter, we introduce a dimensionless flow rate, $\hat{Q}=\eta Q/E{R}^3$. Here, η is the viscosity of the carrier medium, R is the channel radius, and E is the sphere’s Young’s modulus. Our perturbation calculation takes into account terms up to the first order in $\hat{Q}$. Therefore, errors of our solution scale with ${\hat{Q}}^2$ or alternatively with ${\mathit{ϵ}}^2$, where ϵ denotes the elastic strain. Accordingly, we will use in our calculations the linearized expression of the elastic strain tensor and we will neglect the feedback of the elastic deformation onto the flow field (see Section S1).

Calculation of the flow field around a sphere advected in a cylindrical channel

We model the problem of a cell in an RT-DC setup as a sphere advected in a cylindrical flow channel at constant velocity. To determine the hydrodynamic stresses acting on this sphere, we calculate the surrounding flow field. Reynolds numbers of the flows involved in RT-DC measurements are typically on the order of 0.1, and therefore, they are dominated by viscous forces. To describe the velocity distribution of the fluid flow, we solve the Stokes equation in a cylindrical channel for a Newtonian fluid together with the incompressibility condition:

$$\nabla p-\eta {\nabla }^2\mathbf{v}=0$$ (1)

$$\nabla ·\mathbf{v}=0.$$ (2)

Here, η is the dynamic viscosity of the fluid, and $\mathbf{v}$ and p are its velocity and pressure fields, respectively. For the purpose of our calculation, we consider a sphere of radius $r_0$ that is advected in the center of an infinitely long cylindrical tube of radius R at constant speed (Fig. 1 B). No-slip boundary conditions are imposed on the surface of the sphere and the cylinder walls. As boundary conditions for the flow profile at the channel inlet and outlet, i.e., at $z=\pm \infty$, we impose a Poiseuille flow (31), as the presence of the sphere is not relevant there.

For our calculation, we choose coordinates that are comoving with the sphere (Fig. 1 B). To adapt to the given domain boundaries (surface of the sphere, cylinder walls, and channel ends), cylindrical coordinates $\left(\rho ,z,\phi \right)$ and spherical coordinates $\left(r,\theta ,\phi \right)$ are employed alternately (30). The axial symmetry around the cylinder axis allows definition of a unique stream function, $\Psi \left(r,\theta \right)$, such that the components of the flow field, $\mathbf{v}$, read (33)

$$v_r=\frac{1}{r^2\text{sin}\theta }\frac{\partial \Psi }{\partial \theta }$$ (3a)

$$v_{\theta }=-\frac{1}{r\text{sin}\theta }\frac{\partial \Psi }{\partial r}.$$ (3b)

The contour lines of $\Psi$ are the streamlines of $\mathbf{v}$. Therefore, the stream function $\Psi$ encodes all the information of the flow field around the spherical object. Equations 1 and 2 lead to a single partial differential equation in $\Psi$, which is solved taking into account the described boundary conditions (30). The additional constraint of a vanishing net force acting on the sphere at steady state yields the velocity at which it passes through the channel (see Appendix A). We find that for this setting, the stream function, $\Psi$, and therefore the flow field, is uniquely parameterized by the relative sphere size, $\lambda =r_0/R$, where $r_0$ is the sphere’s radius and R is the channel radius.

Equilibrium velocity of an undeformed sphere in theory and experiment

Fig. 2 A shows the normalized steady-state velocity function, $v/u$, of an undeformed sphere in a cylindrical channel, where v is the advection velocity of the sphere and u is the peak velocity of the Poiseuille flow in the channel. The latter is related to the total flow rate, Q, by $u\propto Q/R^2$. Velocities derived from the analytical theory (solid line) and from finite-element simulations (circles) using COMSOL Multiphysics (www.comsol.com) are in good agreement. Furthermore, we employed finite-element simulations to investigate whether a similar relation can be found in a channel with a square cross section and how those results compare to the flow field in the cylindrical channel (see Fig. 2 A, squares). For this comparison, we map the flow in the square channel onto the flow in a cylindrical channel with radius $R_{\text{eq}}$, which is the so-called equivalent channel radius (32). This radius is chosen such that there is the same pressure drop along the cylindrical channel and the channel with square cross section (see Section S3). To test these predictions experimentally, we used commercially available polystyrene beads of different sizes and flushed them through a microchannel with a square cross section of $L=20$ μm width (see Materials and Methods). The results of the velocity measurements are shown in Fig. 2 B. The measured normalized bead velocities show good quantitative agreement with normalized velocities, $v/u$, as derived from the stream-function approach, using the equivalent channel radius, $R_{\text{eq}}$. Deviations of experimental results from the theoretical predictions for $\lambda <0.55$ are presumably due to an imperfect centering of the beads in the flow channel. The increasing deviation for $\lambda >0.9$ is due to the use of the equivalent channel radius, which leads to ${\lambda }_{\text{eq}}\approx 0.91$ for a bead diameter of the size of the channel width. Therefore, beads with a relative cell size >0.91 are expected to have direct contact with the channel walls. Hence, our approach of deriving the flow profiles around the sphere is correct within a useful range of λ.

Hydrodynamic stress acting on the sphere’s surface

For a velocity field, $\mathbf{v}$, of an incompressible Newtonian fluid with viscosity η, the hydrodynamic stress tensor is given in Cartesian coordinates by

$${\sigma }_{ij}^{\text{H}}=-p{\delta }_{ij}+\eta \left(\frac{\partial v_j}{\partial x_i}+\frac{\partial v_i}{\partial x_j}\right).$$

Due to the no-slip boundary condition, we have $\mathbf{v}=0$ and ${\partial }_{\theta }{v}_i=0$ on the surface of the sphere. Together with the incompressibility condition (Eq. 2), this implies also ${\partial }_r{v}_r=0$ at $r=r_0$. Further taking into account the azimuthal symmetry, the hydrodynamic stress components on the surface of the sphere read

$${\sigma }_{rr}^{\text{H}}{|}_{r=r_0}=-p$$ (4a)

$${\sigma }_{r\theta }^{\text{H}}{|}_{r=r_0}=\eta \frac{\partial v_{\theta }}{\partial r}{|}_{r=r_0}.$$ (4b)

Using Eqs. 1, 3, and 4, we find that the hydrodynamic stress is given in the form

$${\sigma }_{rr}^{\text{H}}{|}_{r=r_0}={\sigma }_{\text{c}}\underset{n\text{odd}}{\stackrel{\infty }{\sum _{n=1}}}{f}_n{P}_n\left(\text{cos}\theta \right)$$ (5a)

$${\sigma }_{r\theta }^{\text{H}}{|}_{r=r_0}={\sigma }_{\text{c}}\underset{n\text{odd}}{\stackrel{\infty }{\sum _{n=1}}}{g}_n\frac{d{P}_n\left(\text{cos}\theta \right)}{d\theta },$$ (5b)

where $P_n\left(\text{cos}\theta \right)$ denotes the nth Legendre polynomial. The coefficients $f_n$ and $g_n$ are linear functions of the expansion coefficients of the stream function, $\Psi$ (see Appendix A). Note that $f_n=g_n=0$ for even n, which reflects the symmetry of the flow field.

Although the stress components scale with the characteristic stress, ${\sigma }_{\text{c}}=\eta v/r_0$, their value changes along the sphere’s surface depending on the polar angle, θ. The expansion coefficients $f_n$ and $g_n$ quickly converge to zero for increasing n (see Fig. S2), implying that the stress components are dominated by the first few Legendre polynomials or their derivatives, respectively.

In Fig. 3, A and B, we depict the normal and tangential surface stresses for an undeformed sphere with $\lambda =0.7$ and typical experimental parameters. As for the steady-state velocity, we used the finite-element simulations to confirm the analytical results from the stream-function approach numerically (Fig. 3 B). Normal stresses are highest at the rear and front of the sphere and antisymmetric with respect to $\theta =\pi /2$. This behavior corresponds to a pushing from the back and an equal pulling at the front, which can be understood by the fact that in a steady-state situation, the peak velocity, u, of the flow is greater than the velocity of the sphere, v. The highest tangential stresses occur at regions closest to the cylinder walls as a result of the no-slip conditions on the sphere and the channel walls. Those boundary conditions produce shear rates of order $v/\left(R-r_0\right)$ at sphere surface regions close to the cylinder walls. This consequently leads to very high shear stresses for larger spheres, where $1-\lambda$ becomes small (Fig. S3). The shear stress acts tangentially on the surface of the sphere and imposes a drag force, $F_{\text{d}}$, opposite to the flow direction. The net balance between this backward drag and the forward driving normal pressure forces, $F_{\text{p}}$, then leads to the force-free, uniform motion of the sphere, i.e., $F_{\text{p}}+F_{\text{d}}=0$.

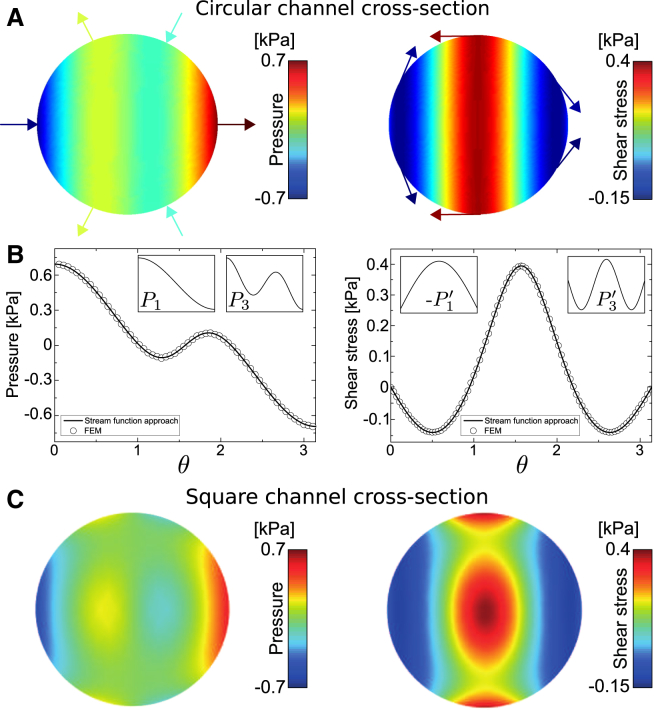
Figure 3.

Surface stresses on an undeformed sphere passing through channels of circular and square cross section. (A) Hydrodynamic pressure (normal stress, left) and hydrodynamic shear stress (right) for $Q=0.012$ μL/s, $\eta =15$ mPa·s (typical experimental parameters used for RT-DC), $R=10$μm, and $r_0=7$μm. Arrows depict the direction of locally applied forces. Forward-directed normal forces are highest at surface regions close to the symmetry axis, and backward-directed shear forces are highest at surface regions close to the cylinder wall. (B) Comparison of the solution presented in (A) (solid line) with a finite-element simulation (circles) in dependence of the polar angle θ. Insets depict the first two Legendre polynomials that appear in the expansion of the respective stress component. (C) Surface stresses from the finite-element simulation on a sphere passing through a channel with a square cross section of 20 μm width (channel walls are parallel and perpendicular to the plane of projection). Peak normal and tangential surface stresses reach values of ∼0.5 kPa and 0.4 kPa, respectively. Values are shown for a situation identified with (A) using the equivalent channel radius ($r_0=7.6$μm), with η and Q as in (A) and (B).

By choosing a rotationally symmetric description, we implicitly neglect small azimuthal surface stresses, ${\sigma }_{r\phi }$, that are present in a square channel. Hydrodynamic shear stresses, ${\sigma }_{r\theta }\left(r=r_0\right)$, in channels with square cross section are similar in their stress peak values when compared to results in a cylindrical channel using the equivalent channel radius (see Fig. 3 C).

Elastic deformation of a sphere advected in a cylindrical channel

Since the cells reach a steady-state shape toward the end of the flow channel (17), we choose to describe those shapes by time-independent, i.e., elastic, material parameters. The assumption of isotropic and linear elastic material properties additionally simplifies the theoretical treatment. We solve the general deformation problem and adapt the solution to boundary conditions that are provided by the previously calculated hydrodynamic surface stresses (Eq. 5). This approach corresponds to a perturbation expansion, where higher-order contributions coming from the feedback of the deformation onto the flow field around the object are neglected (see Section S1). The deformation of the sphere is given in terms of a displacement field, $\mathbf{u}=u_r{\mathbf{e}}_r+u_{\theta }{\mathbf{e}}_{\theta }$, such that the deformed surface is described by $\mathbf{r}\left(\theta ,\phi \right)={\mathbf{r}}_0+\mathbf{u}=\left(r_0+u_r\right){\mathbf{e}}_r+u_{\theta }{\mathbf{e}}_{\theta }$. As we aim for a description of suspended animal cells in flow channels, we will take into account different possible architectures of the spherical object corresponding to different cell mechanical models.

Solid elastic sphere

First, we consider a solid elastic sphere advected at a constant velocity in the cylindrical channel. This scenario corresponds to the case of a dominant, homogeneous cell bulk in the process of deformation. Due to the absence of external volume forces, the equilibrium equation inside the sphere reads (34)

$$\nabla ·\mathit{\sigma }=0,$$ (6)

where

$$\mathit{\sigma }=G\left[\nabla {\mathbf{u}}^{\text{T}}+\nabla \mathbf{u}+\frac{2\nu }{1-2\nu }\left(\nabla ·\mathbf{u}\right)\mathbb{I}\right].$$ (7)

Here, G and ν are the shear modulus and the Poisson ratio of the material, respectively. Using a Papkovich Neuber ansatz (see Section S6), we can find general solutions to Eq. 6 of the form (35)

$$u_r\left(r,\theta \right)=\stackrel{\infty }{\sum _{n=1}}\left[a_n\left(n+1\right)\left(n-2+4\nu \right)r^{n+1}+b_{n}n{r}^{n-1}\right]P_n\left(\text{cos}\theta \right)$$ (8a)

$$u_{\theta }\left(r,\theta \right)=\stackrel{\infty }{\sum _{n=1}}\left[a_n\left(n+5-4\nu \right)r^{n+1}+b_n{r}^{n-1}\right]\frac{d{P}_n\left(\text{cos}\theta \right)}{d\theta }.$$ (8b)

The above displacement field allows calculation of an associated elastic stress tensor, $\mathit{\sigma }$. Boundary conditions require that this elastic stress equals the hydrodynamic stress in Eq. 5 on the surface of the sphere. This condition determines the constants $a_n$ and $b_n$ (see Appendix B). On the surface of the sphere, we denote the displacement field as

$$u_r{|}_{r=r_0}=\stackrel{\infty }{\sum _{n=1}}{\alpha }_n^{\text{sp}}{P}_n\left(\text{cos}\theta \right)$$ (9a)

$$u_{\theta }{|}_{r=r_0}=\stackrel{\infty }{\sum _{n=1}}{\beta }_n^{\text{sp}}\frac{d{P}_n\left(\text{cos}\theta \right)}{d\theta },$$ (9b)

where the constants ${\alpha }_n^{\text{sp}}$ and ${\beta }_n^{\text{sp}}$ follow from Eq. 8, setting $r=r_0$ (see Appendix B).

Thin elastic shell

In the following, we consider the cell as a thin elastic, incompressible shell immersed in the shear flow. This is motivated by the actin cortex being the dominant mechanical element of the cell, as suggested by previous measurements (36).

We assume a shell of thickness $h\ll r_0$ with Young’s modulus E. In such a shell, the bending energy, $E_{\text{B}}$, is small compared to the stretching energy, $E_{\text{S}}$, of the shell surface; in fact, $E_{\text{B}}\text{/}{E}_{\text{S}}\propto {\left(h\text{/}{r}_0\right)}^2\ll 1$. The stretching energy is given by the surface integral (34):

$$E_{\text{S}}=\pi r_0^2{\int }_0^{\pi }\left[\frac{Eh}{1-{\nu }^2}\left({\mathit{ϵ}}_{\phi \phi }^2+{\mathit{ϵ}}_{\theta \theta }^2+2\nu {\mathit{ϵ}}_{\phi \phi }{\mathit{ϵ}}_{\theta \theta }\right)\right]\text{sin}\theta d\theta .$$

Furthermore, we have to consider the potential energy, $E_{\text{P}}$, of the shell (37) that is altered by a displacement, $\mathbf{u}$, of a surface element, $d\mathbf{A}$, as a result of the hydrodynamic loading, ${\mathit{\sigma }}^{\text{H}}$

$$E_{\text{P}}=-\int \mathbf{u}·{\mathit{\sigma }}^{\text{H}}·d\mathbf{A}$$

$$=2\pi r_0^2{\int }_0^{\pi }\left[-\left({\sigma }_{rr}^{\text{H}}{u}_r+{\sigma }_{r\theta }^{\text{H}}{u}_{\theta }\right)\right]\text{sin}\theta d\theta .$$

Combining expressions of stretching energy and potential energy, we find the total energy of a thin elastic shell $E_{\text{sh}}=E_{\text{S}}+E_{\text{P}}$, which yields the final Euler equations for the displacement fields $u_r$ and $u_{\theta }$:

$$\frac{\delta E_{\text{sh}}}{\delta u_r}=0\Rightarrow \frac{1}{r_0^2}\frac{Eh}{1-\nu }\left(2u_r+u_{\theta }^{\prime }+u_{\theta }\text{cot}\theta \right)-{\sigma }_{rr}^{\text{H}}=0$$ (10)

$$\frac{\delta E_{\text{sh}}}{\delta u_{\theta }}=0\Rightarrow \frac{1}{r_0^2}\frac{Eh}{1-{\nu }^2}\left(u_{\theta }{\text{cot}}^2\theta +\nu u_{\theta }-\left(1+\nu \right)u_r^{\prime }-u_{\theta }^{″}-u_{\theta }^{\prime }\text{cot}\theta \right)-{\sigma }_{r\theta }^{\text{H}}=0.$$ (11)

We use the ansatz

$$u_r=\stackrel{\infty }{\sum _{n=2}}{\alpha }_n^{\text{sh}}{P}_n\left(\text{cos}\theta \right)$$ (12a)

$$u_{\theta }=\stackrel{\infty }{\sum _{n=1}}{\beta }_n^{\text{sh}}\frac{d{P}_n\left(\text{cos}\theta \right)}{d\theta },$$ (12b)

where the first Legendre polynomial has been omitted in the expansion of $u_r$, as it would merely induce a constant shift of the object along the channel axis. The above ansatz yields a decoupled set of equations for each n that can easily be solved for ${\alpha }_n^{\text{sh}}$ and ${\beta }_n^{\text{sh}}$ $\left(n\ge 2\right)$, giving

$${\alpha }_n^{\text{sh}}=\frac{{\sigma }_c{r}_0^2}{2Eh}\frac{\left(n\left(n+1\right)+\nu -1\right)f_n+n\left(n+1\right)\left(1+\nu \right)g_n}{\frac{n\left(n+1\right)}{2}-1}$$ (13a)

$${\beta }_n^{\text{sh}}=\frac{{\sigma }_c{r}_0^2}{2Eh}\frac{\left(1+\nu \right)\left(f_n+2g_n\right)}{\frac{n\left(n+1\right)}{2}-1}$$ (13b)

and

$${\beta }_1^{\text{sh}}=\frac{{\sigma }_c{r}_0^2}{2Eh}\left(1-\nu \right)f_1.$$

Elastic shell with surface tension

Here, we again consider the advected cell as a thin elastic shell and additionally allow for a surface tension, in analogy to active mechanical tension generated by motor proteins in the cell cortex (38). In the presence of hydrodynamic stress acting on the shell, the energy functional, $E_{\text{sh}}$, for a shell without surface tension needs to be complemented by the volume work due to the hydrostatic pressure excess, P, inside the shell and by a surface-tension term that penalizes the increase of the shell’s surface area. In total, we have

$$E_{\text{tot}}=E_{\text{sh}}-P\Delta V+\gamma \Delta A.$$ (14)

Here, $\Delta V$ and $\Delta A$ denote the volume and surface area change, respectively (see Appendix C). For the undeformed, spherical shell of radius $r_0$, the surface tension, γ, is balanced by an internal hydrostatic pressure excess, $P_0$, which is given by the Laplace law, $P_0=2\gamma /r_0$ (39). The symmetry properties of the flow field imply $\Delta V=\mathcal{O}\left(u^2\right)$ (see Appendix C). As we consider only terms up to order $\mathcal{O}\left(u^2\right)$ in the energy functional, we can set $P=P_0$. Deriving the Euler equations for the displacement fields from Eq. 14, it can be shown that only Eq. 10 is modified and now reads (40)

$$\frac{1}{r_0^2}\frac{Eh}{1-\nu }\left(2u_r+u_{\theta }^{\prime }+u_{\theta }\text{cot}\theta \right)-{\sigma }_{rr}^{\text{H}}-\frac{\gamma }{r_0^2}\left(2u_r+u_r^{\prime }\text{cot}\theta +u_r^{″}\right)=0.$$ (15)

The variation of the governing energy functional (Eq. 14) with respect to the tangential displacement, $u_{\theta }$, again results in Eq. 11. We can solve the system (Eqs. 11 and 15) again with the ansatz (Eq. 12). The final analytical solution for the full problem is given by

$${\alpha }_{n,\gamma }^{\text{sh}}={\sigma }_c{r}_0^2\frac{\left(n\left(n+1\right)+\nu -1\right)f_n+n\left(n+1\right)\left(1+\nu \right)g_n}{\left[n\left(n+1\right)-2\right]\left[Eh+\gamma \left(n\left(n+1\right)+\nu -1\right)\right]}$$ (16a)

$${\beta }_{n,\gamma }^{\text{sh}}={\sigma }_c{r}_0^2\frac{\left(1+\nu \right)\left(f_n+2g_n\right)+\frac{\gamma }{Eh}\left(1-{\nu }^2\right)\left[n\left(n+1\right)-2\right]}{\left[n\left(n+1\right)-2\right]\left[Eh+\gamma \left(n\left(n+1\right)+\nu -1\right)\right]}.$$ (16b)

By construction, Eq. 13, a and b, is just a special case of Eq. 16, a and b, i.e., we formally write ${\alpha }_{n,\gamma =0}^{\text{sh}}={\alpha }_n^{\text{sh}}$ and ${\beta }_{n,\gamma =0}^{\text{sh}}={\beta }_n^{\text{sh}}$. For $\gamma \gg Eh$, this result implies ${\alpha }_{n,\gamma }^{\text{sh}}\propto 1/\gamma$ and ${\beta }_{n,\gamma }^{\text{sh}}\propto 1/Eh$. Hence, in the case of large surface tension, normal displacements are highly suppressed, whereas tangential displacements are similar to those of a shell without surface tension.

Deformed shapes

To quantify the magnitude of deformation for different sphere architectures, we use a previously introduced measure of deformation, $d=1-c$ (17), where c is the circularity, defined as

$$c=2\sqrt{\pi }\frac{\sqrt{A}}{P}.$$

In this expression, A is the area and P the perimeter of the (central) cross section of the deformed shapes. Note that $d=0$ for a circle and $d>0$ for any other shape. Hence, this measure describes the degree of deformation away from a circular cross section. Example solutions of deformed spheres at a fixed deformation, d, are depicted in Fig. 4, A and B. Comparing relative sphere sizes of $\lambda =0.7$ (top row) and $\lambda =0.9$ (bottom row), we find that increased relative sphere sizes lead to larger deformations. This observation reflects a commonly reported effect of enhanced confinement (22), which originates from an accompanying increase in hydrodynamic stress. For larger λ, there are regions of very high normal and tangential stress (see Fig. S3), resulting in shapes that show grooves and distinct bulges at $\theta \approx \pi /2$ (Fig. 4 A, bottom row).

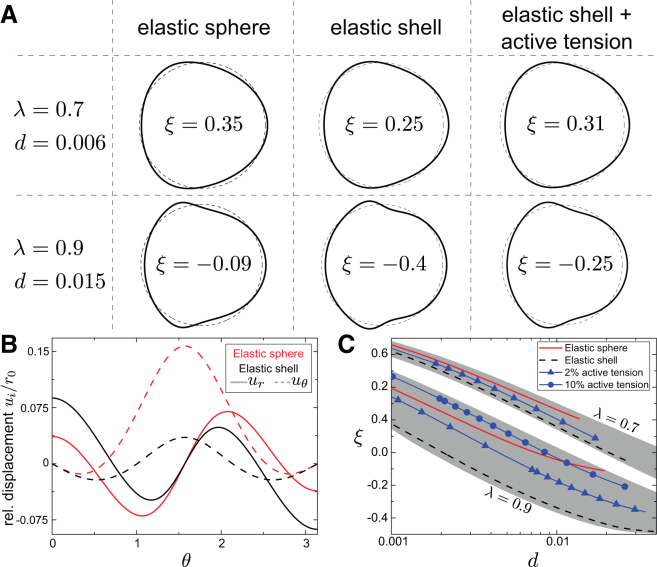
Figure 4.

Deformations of an elastic sphere and a thin elastic shell with and without surface tension generated by the hydrodynamic loading in a cylindrical channel. (A) Representative example shapes for relative cell sizes $\lambda =0.7$ (top row) and $\lambda =0.9$ (bottom row). In each row, material parameters were chosen such that shapes have the same deformation, d. The curvature fraction, ξ, discriminates between the different models. (B) Displacement fields $u_r\left(\theta \right)$ (solid lines) and $u_{\theta }\left(\theta \right)$ (dashed lines) for the elastic sphere (red) and elastic shell (black) for $\lambda =0.7$. Deformations of the elastic sphere are dominated by $u_{\theta }$, whereas deformations of the elastic shell are dominated by the radial displacement, $u_r$. (C) Interdependence of d and ξ for $\lambda =0.7$ (upper gray band) and $\lambda =0.9$ (lower gray band) for all three models under variation of material stiffness or flow rate, respectively. The solid lines with triangles correspond to $\gamma =0.02\times Eh$ (right column in A), for which shapes occupy the intermediate shape space between elastic sphere and elastic shell without surface tension in each λ band. For an increased contribution of surface tension, $\gamma =0.1\times Eh$ (solid line with circles), there can be a crossing with the elastic sphere model, i.e., regions where d and ξ can hardly discriminate between elastic sphere and elastic shell with surface tension. To see this figure in color, go online.

To quantify the differences between an elastic sphere and a thin elastic shell in more detail, we introduce a second deformation measure, ξ, defined as the fraction between minimal and maximal curvature of the shape boundary of a centered cross section $\xi ={\kappa }_{\text{min}}/{\kappa }_{\text{max}}$. Although deformation, d, quantifies the overall deviation from a spherical shape, ξ is more sensitive to local shape properties. In fact, the onset of the appearance of bulges and grooves in deformed shapes upon increasing relative cell size and/or flow rate is now simply encoded in a sign change of ξ.

In Fig. 4 C, we depict the behavior of d and ξ for $\lambda =0.7$ and $\lambda =0.9$, varying the material stiffness or, equivalently, the flow rate, Q. We can identify distinct hyperplanes occupied by sphere and shell deformations in the shape space. Therefore, extracting shape measures d and ξ from experimental data at sufficiently high accuracy would allow discrimination between the cases of an elastic sphere and a thin shell.

Incorporating surface tension into our shell model results in a reduction of normal displacements. It is therefore possible to find combinations of surface tension, γ, and shell stiffness, Eh, that produce shapes and deformation measures very similar to those of an elastic sphere with a certain shear modulus, G (Fig. 4 C). This implies that in the linear deformation regime, contributions from a surface tension, γ, can disguise a thin elastic shell as an elastic sphere.

Using deformed shapes as presented in Fig. 4 A (top row), we estimated the change in hydrodynamic stress on the sphere’s surface due to its deformation. To this end, we placed deformed shapes as rigid objects into a cylindrical channel and determined the hydrodynamic stress on their surface using finite-element simulations. We find that there is a small change of ∼3.5% on average across the surface, with peak values of 9%, which mainly result from a slight shift of stress peaks (see Section S8). Generally, we find average stress changes, $\lesssim 10\%$, for deformations of elastic spheres and elastic shells up to $d\approx 0.02$. To quantify the shape differences arising from these stress changes, we additionally performed fully coupled finite-element simulations of a solid elastic sphere that take the feedback between flow-field changes and elastic deformations into account (see Sections S8 and S12). We find good agreement between shapes generated by these fully coupled numerical simulations and shapes obtained from our analytical theory for deformations up to 0.02 (see Section S8). These numerical simulations confirm that the error in the stress on the sphere’s surface is not critical within the deformation regime considered in this work.

Testing the validity of our theory in square channels

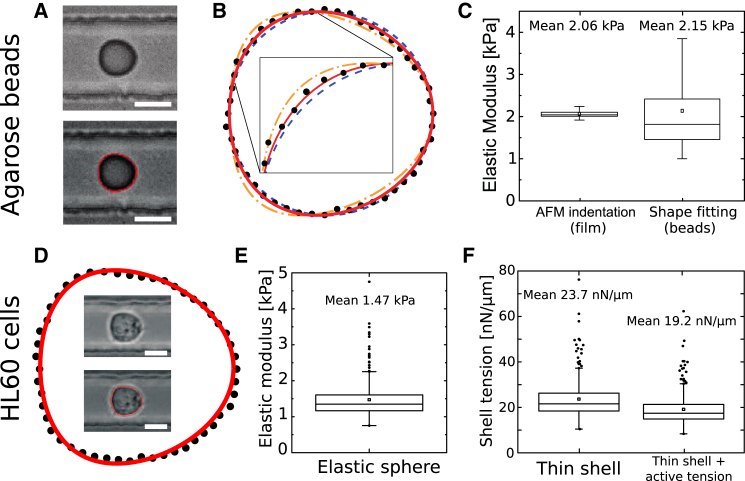
To test the predictive power of our calculations for spheres advected in square channels, we analyzed the deformation of spherical agar beads measured in an RT-DC setup (see Materials and Methods). Beads were flushed through a square channel and imaged by brightfield microscopy focusing at the channel midheight. Agar beads were detected and their boundaries extracted (see Fig. 5, A and B) using our custom-built tracking software (17). The obtained two-dimensional shapes were fit to theoretically predicted shapes of a deformed elastic sphere advected in a cylindrical channel with equivalent channel radius assuming a Poisson ratio of 0.5. Fitting results point to an average bead stiffness of $2.15\pm 1.10$ kPa (N = 228, mean ± SD). Stiffness variations originate here partly from bead inhomogeneities and partly from fitting errors, which are on average ∼0.55 kPa. Simultaneously, agar films (thickness $\mathrm{\gtrsim }1$ mm) were cast from the same agar preparation, whose stiffness was measured by AFM indentation (41) (see Section S9), giving an average elastic modulus of $2.06\pm 0.08$ kPa assuming $\nu =0.5$ (N = 48). Comparing results for the stiffness of the agar used, we find on average very good quantitative agreement between agar films measured with AFM indentation and the analysis of deformed beads in the channel (Fig. 5 C).

Figure 5.

Shape fitting of elastic agar beads and HL60 cells. (A) Deformed bead in the microfluidic channel (top left) overlaid with the contour found by the automatic contour detection (bottom left) (17). (B) Contour found by the tracking software (dotted line) overlaid by shapes from the theory for an elastic sphere for different elastic moduli, $E=1.05$ kPa (yellow dash-dotted line), $E=1.95$ kPa (red solid line, best fit, 95% confidence interval: 0.3 kPa) and $E=4.9$ kPa (blue dashed line). (C) Comparison of results from shape fitting of measured contours $\left(N=229\right)$ with AFM indentation on agar film of the same composition as the beads ($N=48$ different spots indented). (D) Deformed cell in the microfluidic channel. In the outer contour, the cell boundary found by the tracking software is shown (black dots) overlaid by the shape of a solid elastic sphere of elastic modulus $E=1.6$ kPa according to our theory (red solid line). (E and F) Cell elastic moduli from shape fitting using the cell mechanical model of (E) a solid elastic sphere or (F) a thin elastic shell without (left) and with a relative surface tension of $\gamma =0.02\times \left(Eh\right)$ (right). All measurements were taken with $Q=0.012$μL/s, $\eta =15$ mPa·s. In (C), (E), and (F), box plots show the mean value (square), first to third quartiles (horizontal lines), and 1.5× the interquartile region (whiskers). In (E) and (F), outliers are shown in addition (black circles). Scale bars in (A) and (D) are 10 μm. To see this figure in color, go online.

Measurement of cell stiffness

In addition, we measured cells of a human promyelocytic cell line (HL60) in an RT-DC setup and analyzed deformed cell shapes just as in the case of the deformed agar beads described above (see Fig. 5, D–F). Employing the cell mechanical model of an isotropic elastic sphere and assuming incompressibility $\left(\nu =0.5\right)$, we obtain on average an apparent cell elastic modulus of $E=1.48\pm 0.51$ kPa (N = 281, mean ± SD). The spread of the data may be accounted for by the fitting error of the elastic modulus (average value of 0.46 kPa) and by the biological variation of cells. Performing AFM indentation experiments, we find on average a Young’s modulus of $E=170\pm 85$ Pa (N = 169). AFM force curves were analyzed using Hertz theory, making the comparable assumption of indentation into an incompressible, isotropic elastic material (42). The smaller stiffness value from AFM indentation experiments may be accounted for by the much shorter timescales ($\approx 1$ ms) in RT-DC measurements (43). The error of the measured Young’s modulus due to uncertainties in the Poisson ratio is discussed in Section S10.

Anticipating instead that the stiffness of HL60 cells is dominated by the cell boundary, i.e., the plasma membrane and cell cortex, it is more appropriate to perform cell-shape fitting using the model of a thin, incompressible elastic shell. Performing this analysis, the same sample yields an average cell-area expansion modulus of $\left(Eh\right)=23.7\pm 8.4$ nN/μm (Fig. 5 F).

Finally, including a surface tension, γ, we find that area expansion moduli, ${\left(Eh\right)}_{\gamma }$, adopt reduced values as a result of the additional contribution of surface tension to the mechanical integrity of the cell. Setting γ to be 2% of the area expansion modulus, we find on average values that are approximately 20% smaller $\left({\left(Eh\right)}_{\gamma }=19.2\pm 6.8\text{nN/}\mu \text{m}\right)$ than without additional surface tension. This value of ${\left(Eh\right)}_{\gamma }$ corresponds to a surface tension of $\gamma \approx 0.4$ nN/μm, which is in the range of experimentally measured cell-surface tensions (38, 44).

Analysis of RT-DC experiments

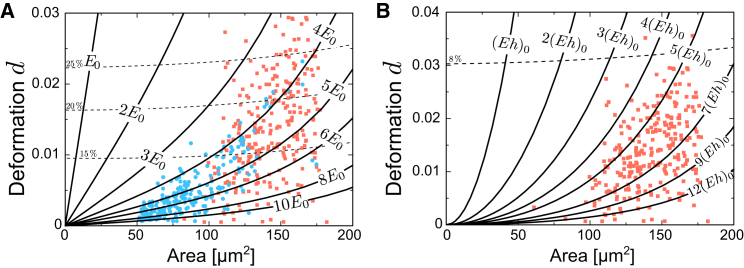
As a typical output of RT-DC measurements, cell deformation, d, is plotted versus cell size (imaged cell area), and in this representation, each cell population creates a cloud of data points (17). For further analysis, it is desirable to identify regions of similar cell stiffness in such scatterplots. In fact, cells with fixed elastic modulus but varying cell size create data points falling on a line in the deformation-versus-cell-area space. Using the equivalent channel radius together with the stream-function approach and the model of an elastic sphere or an elastic shell, we derived isoelasticity lines for a square channel with $L=20$ μm (Fig. 6, A and B).

Figure 6.

Isoelasticity lines in the area-versus-deformation space for $L=20$μm with measurement data. This representation is universal, i.e., different experimental parameters simply correspond to different values of $E_0$ and ${\left(Eh\right)}_0$. Thereby, it provides a general look-up graphic that can easily be adapted to changes in flow rate, Q, and suspension viscosity, η. The conversion rules between different experimental settings are explained in the text. Dashed lines indicate paths where the magnitude of the maximal eigenvalue of the strain tensor averaged over the sphere surface has a certain value (indicated). These lines represent an indicator for the error of our analytical solution $\left(\propto {\mathit{ϵ}}^2\right)$ and the limit of validity of the theory. (A) Isoelasticity lines of a solid elastic sphere with data points representing agarose bead measurements (blue circles) and HL60 cell measurements (red squares). For the applied experimental parameters, $E_0\approx 270$ Pa. (B) Isoelasticity lines of a thin elastic shell without surface tension with data points representing HL60 cell measurement (red squares). For the applied experimental parameters, ${\left(Eh\right)}_0\approx 3.4$ nN/μm. To see this figure in color, go online.

Isoelasticity lines are universal, i.e., they only need to be calculated once, and a subsequent change of experimental conditions only leads to a rescaling of elastic moduli. Beads and cells were measured at a flow rate of $Q=0.012$ μm/s and the fluid viscosity was $\eta =15$ mPa·s, which yields $E_0=270$ Pa or, alternatively, ${\left(Eh\right)}_0\approx 3.4$ nN/μm. Changing to a different flow rate, $Q^{\prime }$, viscosity, ${\eta }^{\prime }$, and/or channel side length, $L^{\prime }$, according to our characteristic stress scale simply leads to the conversion $E_0^{\prime }=Q^{\prime }{\eta }^{\prime }{L}^3/\left(Q\eta L^{\prime 3}\right)\times E_0$ or ${\left(Eh\right)}_0^{\prime }=Q^{\prime }{\eta }^{\prime }{L}^2/\left(Q\eta L^{\prime 2}\right)\times {\left(Eh\right)}_0$ and a rescaling of the labels written on the area axis by a factor of ${\left(L^{\prime }/L\right)}^2$. Hence, isoelasticity lines provide a general look-up graphic that can easily be adapted to a given set of experimental parameters. Plotting them together with data points from RT-DC experiments allows identification of regions of similar cell stiffness (17).

Furthermore, we indicate in this look-up graphic the range of validity of our theory for RT-DC analysis by giving an estimate of the strain magnitude. To this end, we plotted curves where the magnitude of the maximal-strain eigenvalue averaged over the sphere surface adopts a certain value (Fig. 6, A and B, dashed lines). Generally, the inaccuracy of our analytical approximation grows for larger strains and correspondingly for larger values of cell deformation. For the case of an elastic sphere, allowing for average strain values of up to 22% and thereby for errors on the order of ≈5%, the validity of our theory is limited to deformations of $d\lesssim 0.02$ in the case of an elastic sphere (Fig. 6 A). For an elastic shell, strain values are smaller and the validity limit is set by the accuracy of the stress estimate on the shell’s surface, which does not take into account changes in hydrodynamic surface stresses due to the deformation (see Section S8). Admitting average errors in stress up to 10%, our analysis is again limited to deformations of $\lesssim 0.02$.

To confirm this validity limit, we verified the predicted shapes of our analytic theory for the case of a solid elastic sphere by fully coupled finite-element simulations that take into account the coupling between flow field and elastic deformation (see Section S12). For deformations up to 0.02, we find good agreement between shapes generated with the numerical simulation and those produced by our analytical framework. Furthermore, a fit of our theory to simulated shapes reproduces the assumed Young’s modulus within an accuracy of 4% at a deformation of 0.02 (see Fig. S6).

Discussion

We have presented a theoretical analysis that allows us to relate elastic parameters directly to the deformation of entire cells in RT-DC measurements on timescales of ≈1 ms. To do so, we calculated the deformation of an elastic spherical object advected by a steady Stokes flow in a cylindrical channel using linear elasticity theory. The concept of the equivalent channel radius allows us to map our analytical results onto the problem of a sphere in a square flow channel, as is typically used in RT-DC experiments. In RT-DC, suspended animal cells, which are initially close to spherical, are advected and deformed by a steady shear flow. Our study can be used to associate cell stiffness to cell deformation as obtained from RT-DC measurements, employing simple cell mechanical models. As our calculations rely on the approximations of linear elasticity theory, our analysis is restricted to the case of small cell deformations $\left(d\lesssim 0.02\right)$ with strains ≫1.

The analytical study presented here enables us to calculate the flow field and stresses on the surface of the spherical object with minimal numerical effort (≲0.5 s computation time on a standard personal computer) (Figs. 1, 2, and 3). Calculated surface stresses are directly proportional to the peak flow velocity, u, and can therefore be tuned continuously simply by changing the flow rate, Q.

We made the simplifying assumption of the cell being composed of an isotropic elastic material, motivated by the cell shape acquiring a steady state within the RT-DC microfluidic channel. The elastic deformation of the spherical object immersed in the flow depends on its architecture and its material properties. In detail, we considered the case of a solid elastic sphere and a thin elastic shell with or without surface tension (Fig. 4).

For the case of an elastic sphere and a thin elastic shell, surface displacement fields scale with ${\sigma }_{\text{c}}\text{/}E$ $\left(E\propto G\right)$, where ${\sigma }_{\text{c}}$ is the characteristic stress and E the Young’s modulus of the material. This means, in particular, that any change in the elastic modulus, for example by a factor of f, can equivalently be interpreted as an according change in the flow rate by a factor of $1/f$. Furthermore, it highlights the need for a good experimental control of the flow rate to extract cell stiffness quantitatively. For the case of the shell, we find in addition that displacements are inversely proportional to shell thickness, h. Contributions from a surface tension, γ, reduce the radial displacement in a shell and can actually make a thin elastic shell look like an elastic sphere. To examine cells independently of surface tension during deformation experiments, cytoskeletal drugs such as blebbistatin (45) that inhibit myosin motor activity can be employed, which results in a strong reduction of cortical tension in cells (39, 46).

We used two deformation measures, deformation, d, and curvature ratio, ξ, to characterize the dependence of sphere shape deformations on sphere architecture (Fig. 4, A and C). The discriminative power of the measures d and ξ with respect to sphere architecture increases the larger the deformation. Pinpointing inherent differences between the case of a solid elastic sphere and a thin elastic shell may help to determine experimentally whether elastic deformations on short timescales are dominated by elastic properties of the cell bulk or of the membrane-cortex entity at the cell boundary. A dominant cell bulk would correspond to the scenario of an elastic sphere, whereas a dominant cell boundary would be better captured by the model of an elastic shell. Although the deformation measure d has been regularly used in RT-DC experiments so far, a precise estimate of ξ, a new cell-shape measure (to our knowledge) suggested here, is not feasible with our current imaging techniques. A distinction between the two cell mechanical scenarios according to the interdependence between d and ξ (see Fig. 4 C) calls for an enhanced imaging technique together with cell-shape predictions at large cell deformations.

Our analytical results are validated by RT-DC measurements on agar beads with known stiffness, which were independently determined by AFM measurements of films of the same agar concentration. On average, the results are in very good agreement ($E_{\text{RT}\text{-}\text{DC}}=2.15\pm 1.10$ kPa and $E_{\text{AFM}}=2.08\pm 0.08$ kPa; see Fig. 5 C). First measurements on cells (HL60) point to elastic moduli of ≈1.5 kPa (Fig. 5 E). Quantification of whole-cell mechanical properties at such short timescales constitutes a largely uncharted territory, with a first relevant publication earlier this year (18). In fact, AFM indentation experiments of the same cell line yield considerably lower average elastic moduli of 0.17 kPa for HL60 cells. This discrepancy may be accounted for by the timescale dependence of cell stiffness. This effect is absent in simple materials such as agar (47). Frequency dependence of cell stiffness has been reported to scale typically with power laws of exponents $0.1-0.5$ (43), even down to timescales of relevance here (18). In our AFM measurements, forces were applied on a timescale of $\approx 1$ s (see Section S9). Using a power-law extrapolation to a timescale of 1 ms, which is a typical timescale of an RT-DC measurement, the mean stiffness value from the AFM measurements points to elastic moduli in the range $\approx 0.34-5.4$ kPa, which is compatible with the value obtained from RT-DC (≈1.5 kPa). An additional contribution to the discrepancy between elastic moduli from AFM and RT-DC measurements could be that the underlying model of a homogeneous elastic sphere is not appropriate for an HL60 cell. If this is the case, a localized indentation as in AFM measurements and a bulk deformation as in flow cytometry may give rise to different effective elastic moduli.

Interpreting our RT-DC measurements in an alternative way, using a thin elastic shell as a cell mechanical model, HL60 cells exhibit an average cell-area expansion modulus of $\left(Eh\right)=23.7\pm 8.4$ nN/μm (Fig. 5 F). Measurements on MDCK II cells performed by Pietuch et al. (48) point to comparable values of area expansion moduli in the range $10-100$ nN/μm.

For interpretation of RT-DC data on cell populations, we have calculated a look-up graphic indicating regions of similar cell stiffness in graphs of cell deformation versus cell area (see Fig. 6). Therefore, our results facilitate the comparison between cell mechanical properties of cell populations with different average cell sizes, which is impossible by measurement of cell deformation alone. RT-DC, combined with our theoretical analysis, allows measurement of cell stiffnesses of large cell populations in a fast and efficient way and thereby opens up new possibilities for cell mechanical approaches in medical diagnostics and biology.

Author Contributions

A.M., O.O., and E.F.F. developed the theoretical analysis. A.M., O.O., S.G., P.R., A.T., and E.U. performed the experiments, S.A. performed numerical simulations, and A.M., O.O., P.R., A.T., and E.U. analyzed the data. A.M., O.O., J.G., and E.F.F. designed the research and wrote the main manuscript.

Editor: Gijsje Koenderink.

Appendix A: Solution of the flow field in terms of a stream-function approach

The scalar stream function is defined by $\Psi \left(\rho ,z\right)=q\left(\rho ,z\right)/2\pi$, where $q\left(\rho ,z\right)$ is the volumetric flow rate across a circular disk of radius ρ centered around the z axis, placed at position z (33). It can easily be transformed to spherical coordinates by $\rho =r\text{sin}\theta$ and $z=r\text{cos}\theta$. With this definition, Eqs. 1 and 2 lead to a single, fourth-order PDE (33),

$${\left[\frac{{\partial }^2}{\partial r^2}+{\left(\frac{\text{sin}\theta }{r}\right)}^2\frac{{\partial }^2}{\partial {\left(\text{cos}\theta \right)}^2}\right]}^2\Psi \left(r,\theta \right)=0.$$ (17)

The operator in square brackets is separable (33) and the part of the solution that obeys the required symmetries in θ, $\Psi \left(r,\theta \right)=\Psi \left(r,-\theta \right)$, is given by

$$\Psi \left(r,\theta \right)=\underset{n\text{even}}{\stackrel{\infty }{\sum _{n=2}}}\frac{P_{n-2}\left(\text{cos}\theta \right)-P_n\left(\text{cos}\theta \right)}{2n-1}\left(A_n{r}^n+B_n{r}^{-n+1}+C_n{r}^{n+2}+D_n{r}^{-n+3}\right),$$ (18)

with Legendre polynomials, $P_n$, and constants $A_n$, $B_n$, $C_n$, and $D_n$ to be determined from the boundary conditions (Fig. 1 A). In the following, we sketch a procedure developed in Haberman and Sayre (30) to find the solution that obeys the boundary conditions depicted in Fig. 1. Detailed expressions can be found in the Supporting Material.

Calculating the stream-function expansion coefficients

Using Eqs. 3 and 18, the no-slip boundary condition on the surface of the sphere can be translated into two conditions on the set of constants $\left(A_n,B_n,C_n,D_n\right)$, which decouple for each n as a result of the orthogonality of the Legendre polynomials. To derive the conditions that follow from the boundary conditions on cylinder walls and channel inlet and outlet, a general solution, $\tilde{\Psi }\left(\rho ,z\right)$, to Eq. 17 is additionally derived in cylindrical coordinates (30). By transforming the solution $\Psi \left(r,\theta \right)$ into cylindrical coordinates, $\Psi \left(r\left(\rho ,z\right),\theta \left(\rho ,z\right)\right)$, and comparing the coefficients of powers in ρ and z between $\tilde{\Psi }\left(\rho ,z\right)$ and $\Psi \left(r\left(\rho ,z\right),\theta \left(\rho ,z\right)\right)$, a linear system of equations is derived that determines the constants $\left(A_n,B_n,C_n,D_n\right)$ such that all boundary conditions are simultaneously satisfied ((30) and Section S2).

The resulting solution initially depends on the two dimensionless quantities $\hat{u}=u/v$ and $\lambda =r_0/R$, where v is the equilibrium velocity of the sphere, u the peak velocity of the Poisseuille flow, $r_0$ the sphere’s radius, and R the channel radius. In general, the net force resulting from the hydrodynamic stresses acting on the sphere for an arbitrary choice of $\hat{u}$ and λ will not vanish. However, we are only interested in a force-free steady-state motion of the sphere through the channel, which imposes the unique relation $\hat{u}\left(\lambda \right)$ shown in Fig. 2 A. To find $\hat{u}\left(\lambda \right)$, we need to derive the corresponding constraint that force-free motion imposes on $\left(A_n,B_n,C_n,D_n\right)$. Using Eqs. 3, 4, and 18, it can be shown that the expansion coefficients of the hydrodynamic stress (Eq. 5, a and b) read (30)

$$f_n=\frac{2}{v}\left(\frac{2n+3}{n}{r}_0^{n+1}{C}_{n+1}+\frac{2n-1}{n+1}{r}_0^{-n}{D}_{n+1}\right)$$ (19a)

$$g_n=-\frac{1}{v}\left(\frac{n-1}{n}{r}_0^{n-1}{A}_{n+1}+\frac{n+2}{n+1}{r}_0^{-n-2}{B}_{n+1}+\frac{n+3}{n}{r}_0^{n+1}{C}_{n+1}+\frac{n-2}{n+1}{r}_0^{-n}{D}_{n+1}\right).$$ (19b)

Additionally, integrating the general expansion of the surface stress (Eq. 5, a and 5) over the surface of the sphere and requiring the result to vanish leads to the constraint relation $f_1+2g_1=0$. This constraint relation, together with Eq. 19, a and b, can be used to derive a condition on $\left(A_n,B_n,C_n,D_n\right)$, such that the resulting solution, $\Psi \left(r,\theta \right)$ corresponds to a force-free motion of the sphere through the channel. Details of the solution procedure are given in Section S2.

Appendix B: Solid elastic sphere

If we use the displacement as given in Eq. 8 to calculate the nonvanishing components of $\mathit{\sigma }$ as given in Eq. 7, we find

$${\sigma }_{rr}\left(r,\theta \right)=2G\stackrel{\infty }{\sum _{n=1}}\left(a_n\left(n+1\right)\left(n^2-n-2-2\nu \right)r^n+b_{n}n\left(n-1\right)r^{n-2}\right)P_n\left(\text{cos}\theta \right)$$ (20a)

$${\sigma }_{r\theta }\left(r,\theta \right)=2G\stackrel{\infty }{\sum _{n=1}}\left(a_n\left(n^2+2n-1+2\nu \right)r^n+b_n\left(n-1\right)r^{n-2}\right)\frac{d{P}_n\left(\text{cos}\theta \right)}{d\theta }.$$ (20b)

By comparing the elastic stress components (Eq. 20) at $r=r_0$ with the hydrodynamic stress on the surface of the sphere given in Eq. 5, we find, for $n\ge 2$,

$$a_n=\frac{{\sigma }_c}{2G{r}_0^n}\frac{n{g}_n-f_n}{n^2+n+1+2n\nu +\nu }$$ (21a)

$$b_n=\frac{{\sigma }_c}{2G{r}_0^{n-2}}\frac{\left(2+3n-n^3+2n\nu +2\nu \right)f_n+\left(n^2+2n-1+2\nu \right)g_n}{\left(n-1\right)\left(n^2+n+1+2n\nu +\nu \right)}.$$ (21b)

The constant $b_1$ introduces merely a constant shift of the sphere in the direction of the channel axis and does not contribute to the stress. Therefore, we set $b_1=0$. Using the constraint $f_1+2g_1=0$ of zero net force, we find consistently for $a_1$

$$a_1=-\frac{{\sigma }_{\text{c}}}{G{r}_0}\frac{f_1}{4\left(1+\nu \right)}.$$ (22)

Now, we expand the displacement field of a solid elastic sphere on the sphere’s surface in terms of

$$u_r{|}_{r=r_0}=\stackrel{\infty }{\sum _{n=1}}{\alpha }_n^{\text{sp}}{P}_n\left(\text{cos}\theta \right)$$ (23)

$$u_{\theta }{|}_{r=r_0}=\stackrel{\infty }{\sum _{n=1}}{\beta }_n^{\text{sp}}\frac{d{P}_n\left(\text{cos}\theta \right)}{d\theta }.$$ (24)

Using the derived expressions for $a_n$ and $b_n$, ${\alpha }_n^{\text{sp}}$ and ${\beta }_n^{\text{sp}}$ can be calculated as

$${\alpha }_n^{\text{sp}}=\frac{{\sigma }_{\text{c}}{r}_0}{2G}\frac{\left(f_n\left(2\nu -2\left(\nu -1\right)n^2+\nu n-1\right)+g_{n}n\left(n+1\right)\left(\left(2\nu -1\right)n-\nu +2\right)\right)}{\left(n-1\right)\left(\nu +n^2+2\nu n+n+1\right)}$$ (25a)

$${\beta }_n^{\text{sp}}=\frac{{\sigma }_{\text{c}}{r}_0}{2G}\frac{\left(f_n\left(-\nu +\left(2\nu -1\right)n+2\right)+g_n\left(\nu -2\left(\nu -1\right)n^2+\left(3\nu -1\right)n+1\right)\right)}{\left(n-1\right)\left(\nu +n^2+2\nu n+n+1\right)}.$$ (25b)

Appendix C: Thin shell with surface tension

For a rotationally symmetric shape whose boundary is described by $\mathbf{r}\left(\theta ,\varphi \right)=\left[r_0+u_r\left(\theta \right)\right]{\mathbf{e}}_r+u_{\theta }\left(\theta \right){\mathbf{e}}_{\theta }$, surface area $A^{\left(\text{d}\right)}$, and enclosed volume $V^{\left(\text{d}\right)}$ of the deformed shape, read

$$A^{\left(\text{d}\right)}=2\pi {\int }_0^{\pi }\left|\frac{\partial \mathbf{r}}{\partial \theta }\right|\left|\frac{\partial \mathbf{r}}{\partial \varphi }\right|d\theta$$

$$=4\pi r_0^2+2\pi {\int }_0^{\pi }\left[r_0\left(2u_r+u_{\theta }\text{cot}\theta +u_{\theta }^{\prime }\right)+\left(u_r+u_{\theta }^{\prime }\right)\left(u_r+u_{\theta }\text{cot}\theta \right)+\frac{{\left(u_r^{\prime }-u_{\theta }\right)}^2}{2}\right]\text{sin}\theta d\theta +\mathcal{O}\left(u^3\right)$$

$$=A_0+\Delta A\left(\mathbf{u}\right)+\mathcal{O}\left(u^3\right)$$ (26)

$$V^{\left(\text{d}\right)}=\pi {\int }_0^{\pi }\left(r_0-u_r^{\prime }\text{cot}\theta +u_r+u_{\theta }^{\prime }+u_{\theta }\text{cot}\theta \right){\left(\left(r_0+u_r\right)\text{sin}\theta +u_{\theta }\text{cos}\theta \right)}^2\text{sin}\theta d\theta$$

$$=\frac{4}{3}\pi r_0^3+\left[\pi {\int }_0^{\pi }\left(r_0-u_r^{\prime }\text{cot}\theta +u_r+u_{\theta }^{\prime }+u_{\theta }\text{cot}\theta \right){\left(\left(r_0+u_r\right)\text{sin}\theta +u_{\theta }\text{cos}\theta \right)}^2\text{sin}\theta d\theta -\frac{4}{3}\pi r_0^3\right]$$

$$=V_0+\Delta V\left(\mathbf{u}\right),$$ (27)

where $A_0$ and $V_0$ are the surface area and volume of the undeformed sphere. By the symmetry of the problem, one has $\Delta V=\mathcal{O}\left(u^2\right)$. To see this, assume a displacement solution, $\mathbf{u}$, is given for a flow field in the z direction. Changing the direction of the flow from z to −z, leaving all other parameters unchanged, will produce the same displacement field, but with a change in sign from u to −u. For a linear contribution to the volume change, $\delta V\propto u_i$, this would imply $\delta V\to -\delta V$. However, the value of the volume cannot depend on the direction of the flow. Therefore, $\Delta V\left(\mathbf{u}\right)=\mathcal{O}\left(u^2\right)$. This also follows explicitly from Eq. 27. using the facts that $u_r\left(-\theta \right)=-u_r\left(\theta \right)$ and $u_{\theta }\left(-\theta \right)=u_{\theta }\left(\theta \right)$. Because we only consider an energy functional up to $\mathcal{O}\left(u^2\right)$, P is given by the constant Laplace pressure, $P_0=2\gamma /r_0$. Using Eqs. 14, 26, and 27, we find to linear order in $u_i$

$$\frac{\delta E}{\delta u_r}=\frac{\delta E_{sh}}{\delta u_r}-r_0\left(\left(P-\frac{2\gamma }{r_0}\right)\left(r_0+u_{\theta }^{\prime }+u_{\theta }\text{cot}\theta \right)+2\left(P-\frac{\gamma }{r_0}\right)u_r+\frac{\gamma }{r_0}\left(u_r^{\prime }\text{cot}\theta +u_r^{\mathit{″}}\right)\right)\text{sin}\theta$$

$$\frac{\delta E}{\delta u_{\theta }}=\frac{\delta E_{sh}}{\delta u_{\theta }}-r_0\left(P-\frac{2\gamma }{r_0}\right)\left(u_{\theta }-u_r^{\prime }\right)\text{sin}\theta .$$ (28)

Plugging in the Laplace pressure, $P=P_0=2\gamma /r_0$, yields the Euler equations as given in the main text (Eqs. 10 and 14).