Significance
Suboptimal fitness peaks are generally recognized as causing evolutionary stasis. Here, we show that these constraints can be overcome in an adaptive manner by reconstructing mutational trajectories for a transcription factor and its DNA binding site in variable environments. Cross-environmental tradeoffs, typically associated with evolutionary limitations, are an essential enabling component of this evolutionary mechanism. Our results underscore the importance of characterizing environmental dependencies when studying genetic interactions and provide the clearest indication so far that environmental variability can accelerate evolution hampered by stasis in constant conditions. Given that environmental variations and tradeoffs are ubiquitous, this evolutionary mechanism may be relevant to a wide range of genetically constrained phenotypes and major evolutionary transitions.
Keywords: evolution, environment, epistasis, fitness landscape, constraint
Abstract
Epistatic interactions can frustrate and shape evolutionary change. Indeed, phenotypes may fail to evolve when essential mutations are only accessible through positive selection if they are fixed simultaneously. How environmental variability affects such constraints is poorly understood. Here, we studied genetic constraints in fixed and fluctuating environments using the Escherichia coli lac operon as a model system for genotype–environment interactions. We found that, in different fixed environments, all trajectories that were reconstructed by applying point mutations within the transcription factor–operator interface became trapped at suboptima, where no additional improvements were possible. Paradoxically, repeated switching between these same environments allows unconstrained adaptation by continuous improvements. This evolutionary mode is explained by pervasive cross-environmental tradeoffs that reposition the peaks in such a way that trapped genotypes can repeatedly climb ascending slopes and hence, escape adaptive stasis. Using a Markov approach, we developed a mathematical framework to quantify the landscape-crossing rates and show that this ratchet-like adaptive mechanism is robust in a wide spectrum of fluctuating environments. Overall, this study shows that genetic constraints can be overcome by environmental change and that cross-environmental tradeoffs do not necessarily impede but also, can facilitate adaptive evolution. Because tradeoffs and environmental variability are ubiquitous in nature, we speculate this evolutionary mode to be of general relevance.
It is widely believed that epistatic interactions can direct evolutionary change (1–7). Epistasis has been implicated in shaping RNA (8) and protein (4, 6, 7, 9) sequences, sensing (5) and translation (10) functions, and developmental programs (11) and speciation (12–14). Phenotypes may be difficult to evolve not because they are impossible biochemically or physically, but because essential mutations are mutually dependent and must be fixed together to be selected positively (5, 15–17). How such genetic constraints can be overcome has been considered previously: population expansion or subdivision can limit negative selection and maintain less fit phenotypes (18, 19), and large populations and long waiting times can enable the joint fixation of multiple mutations (20), whereas recombination can join mutant alleles (21–23). Other mechanisms include drift (24–26), partial penetrance (27), and nonheritable lifetime plasticity (28, 29). However, how the constraining effects of such genetic interactions are affected by environmental variability remains poorly understood. It has been shown that mutational effects (30–33) and epistasis itself (34, 35) can depend on the environment, that bacterial resistance evolution can be contingent on the rate of antibiotic increase (36), and that adaptation in silico can be accelerated by environmental change (37–40). These observations suggest that the effects of environmental variability may go beyond merely producing variable selective pressures that favor certain phenotypes but also, could be involved in controlling phenotype accessibility and stasis.
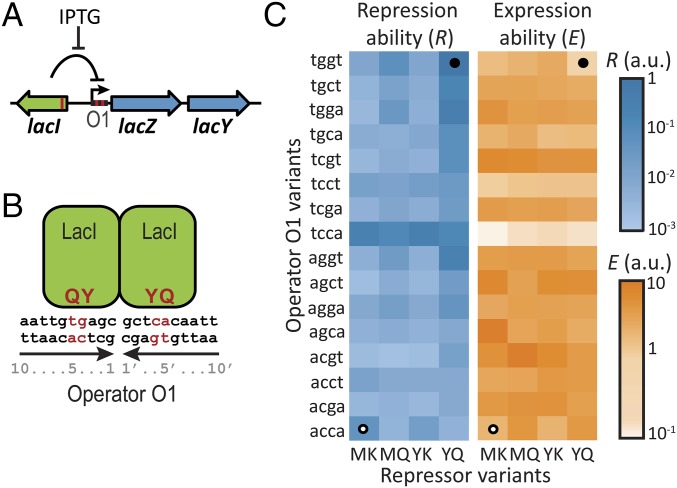
To investigate how environmental variability affects genetic constraints, we focused on a model system for genotype–environment interactions, the lac regulatory system of Escherichia coli. Its physiology has been studied extensively: in the presence of lactose, expression of the lac genes allows E. coli cells to import and metabolize lactose, whereas in the absence of lactose, repression of these genes limits physiological costs (41, 42). The ability to regulate lac expression relies on the binding of the lac repressor to the lac operator DNA sequence upstream of the coding region (Fig. 1A). We surmised that the coevolution of such protein–DNA interfaces could be severely constrained by epistatic interactions, such that some genotypes are inaccessible by positive selection in single-mutation steps. In lock–key recognition, mutating either lock or key is expected to lead to recognition loss (2, 15). At the same time, mutating both lock and key may produce a different, better-matching pair. Indeed, the lac transcription factor phylogeny suggests extensive historic adaptation of the repressor–operator interface and reveals multiple homologous repressors that bind specifically to their cognate operator (43, 44). Furthermore, the lock–key recognition of the lac regulatory system is a highly specific function that is confined to a limited number of residues, which restricts the range of adaptive solutions. Indeed, extensive mutational analysis of the lac repressor–operator interface has shown that just two repressor residues and four operator bases control binding specificity (Fig. 1 A and B) (45, 46). Moreover, in contrast to phenotypes that are affected by many unknown mutations, one can identify the genetic interactions between mutations in controlling residues that are key to genetic constraint.
Fig. 1.
Repression and expression ability of lac repressor–operator mutants. (A) Schematic representation of the E. coli lac system. β-Galactosidase (LacZ) and the lac permease (LacY) are coregulated by the repressor LacI. Expression is induced by IPTG. Red lines correspond to mutated positions. (B) The multimeric lac repressor in green bound to its operator DNA. Red indicates mutated positions responsible for specific repressor–operator binding. Y and Q are the mutated amino acid residues on positions 17 and 18 in the DNA binding helix of the lac repressor, and 4 and 4′ g–c and 5 and 5′ t–a are the mutated base pairs in the operator DNA. We note that the genotype represented here is YQ:tggt. (C) Characterization of 64 lac repressor–operator variants. The starting and final sequences are indicated by white and black circles, respectively. R is the inverse of the measured expression level in the absence of IPTG. E is the measured expression level in the presence of IPTG (Methods).
Results
Trajectories Are Not Accessible in Constant Environments.
We mutated sites in the lac operator DNA and the multimeric lac repressor that control binding specificity (Fig. 1 A and B) and measured the expression level of the downstream lac genes in two contrasting conditions (Methods). We quantified the ability to repress the lac genes, R, as the inverse of the measured lac expression level in the absence of inducing ligand (Methods and Fig. 1C). The ability to express the lac genes, E, was quantified by the measured lac expression level in the presence of ligand (Fig. 1C). Note that the repression ability (R) is, thus, not the inverse of the expression ability (E). We constructed four lac repressor–operator variants that have been predicted (45–48) to display binding: PK:agga, PS:acca, MK:acca, and YQ:tggt, where the first two letters indicate the controlling repressor residues and the last four letters indicate the controlling operator bases (Fig. 1 A and B). We focused on the latter two variants, because they displayed substantial fold changes between the induced and noninduced expression levels (R•E was 6 and 55, respectively), with E being approximately equal but R being about 20-fold lower for MK:acca. The MK:acca genotype is, thus, able to regulate lac expression but can improve repression ability by mutating the repressor (MK to YQ) and operator (acca to tggt).
We investigated the interaction between noncognate pairs by swapping around the two operators. The ability to repress (R) was found to be low (i.e., expression in the absence of ligand was high) for MK:tggt and YQ:acca (100- to 200-fold lower than for the cognate pair YQ:tggt). These data were consistent with the reciprocal sign epistasis hypothesized for lock–key interactions: changing either of the binding partners alone leads to binding loss, but changing the other partner as well restores it. This notion was supported by the overall expression levels for MK:tggt and YQ:acca, which were high and unresponsive to ligand (R•E = 1). However, although the presence of reciprocal sign epistasis is required, it is not sufficient to constrain phenotypes on suboptima (15). Indeed, the repressor and operator modifications both involve multiple mutations, and their one by one fixation in particular order (1) could confer continuous improvements in repression ability.
To test the accessibility of trajectories considering all possible orders of all essential mutations, we constructed the remaining intermediate genotypes between MK:acca and YQ:tggt. In total, 6! = 720 direct trajectories can be taken along the 26 = 64 genotypes. Whether a mutation is positively selected, and thus accessible, depends on the sign rather than the magnitude of the associated fitness change. Fitness and phenotypic changes have the same sign when the phenotype–fitness relation is monotonic. In the environment without ligand, for instance, a trajectory is then not accessible when it contains mutations that decrease R. Below, we first consider this case of monotonic phenotype fitness relations, and later, we relax this assumption to also consider a range of nonmonotonic relations.
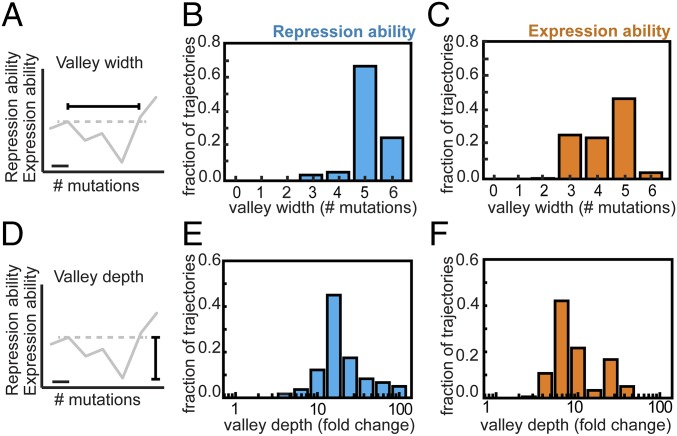
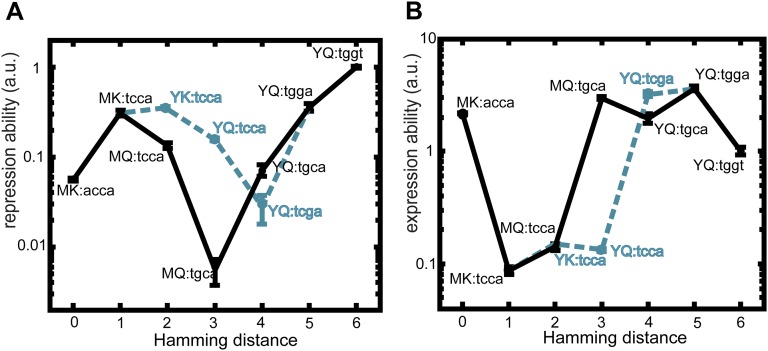
Analysis showed that all trajectories contain depressions in both R and E (Fig. 2 and Fig. S1). The depressions are at least two mutations wide and peak at a width of five mutations, whereas the involved decrease is at least 3-fold and reaches up to ∼100-fold. Thus, none of the trajectories to YQ:tggt are accessible by fixing mutations one by one in either of two environments. Although this analysis concerns only direct trajectories (i.e., without mutational reversions), allowing for reversions did not open up accessible trajectories in either of the environments (SI Results, sections S6). Overall, these data indicate that higher-order genetic interactions (i.e., epistasis involving multiple mutations) limit optimization of the lac regulatory phenotype in each of two environments.
Fig. 2.
Genetic constraints in constant environments. (A) The valley width is the number of mutations required to increase repression or expression ability above the previous suboptimum in a given mutational trajectory. For each trajectory, the widest valley is tabulated. The horizontal bar indicates one mutation. (B) Valley width in repression ability for all direct 720 mutational trajectories from MK:acca to YQ:tggt. (C) Valley width in expression ability. (D) The valley depth is the fold decrease in repression or expression ability within the valleys of a given trajectory. For each trajectory, the deepest valley is tabulated. Note that the widest and the deepest valleys for a given trajectory do not necessarily coincide. (E) Valley depth in repression ability for all direct 720 mutational trajectories from MK:acca to YQ:tggt. (F) Valley depth in expression ability. Welch’s t tests were performed to determine the statistical significance of differences in measured repression and expression ability values (Methods).
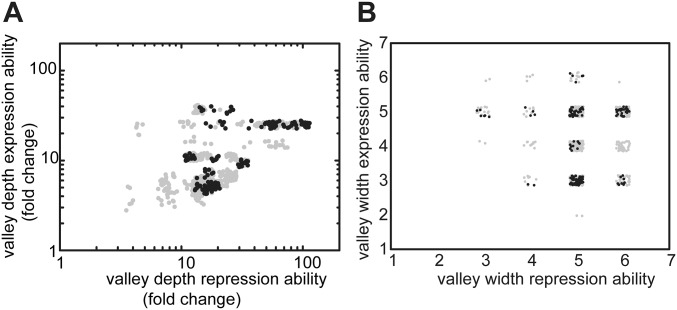
Fig. S1.
Tradeoffs in repression and expression over longer sequence space. (A) Valley depth in both environments for all direct 720 trajectories. Valley depth is the largest decrease along a mutational trajectory. (B) Valley width in both environments for all direct 720 trajectories. Valley width equals the number of mutations required to achieve a level that is greater than or equal to the previous suboptimum. Points of corresponding trajectories are depicted with a small random offset for visualization purposes. Selectively accessible trajectories are indicated in black. One does not observe selectively accessible trajectories that have a small (A) valley depth or (B) valley width in both repression and expression abilities.
Changing Environments Allows Gradual Optimization.
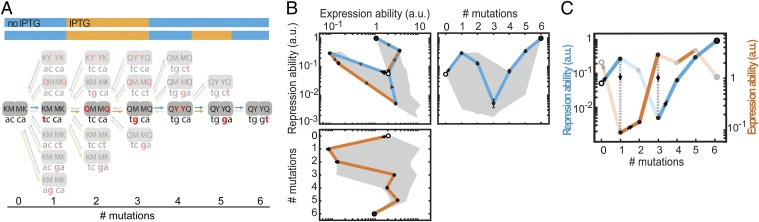
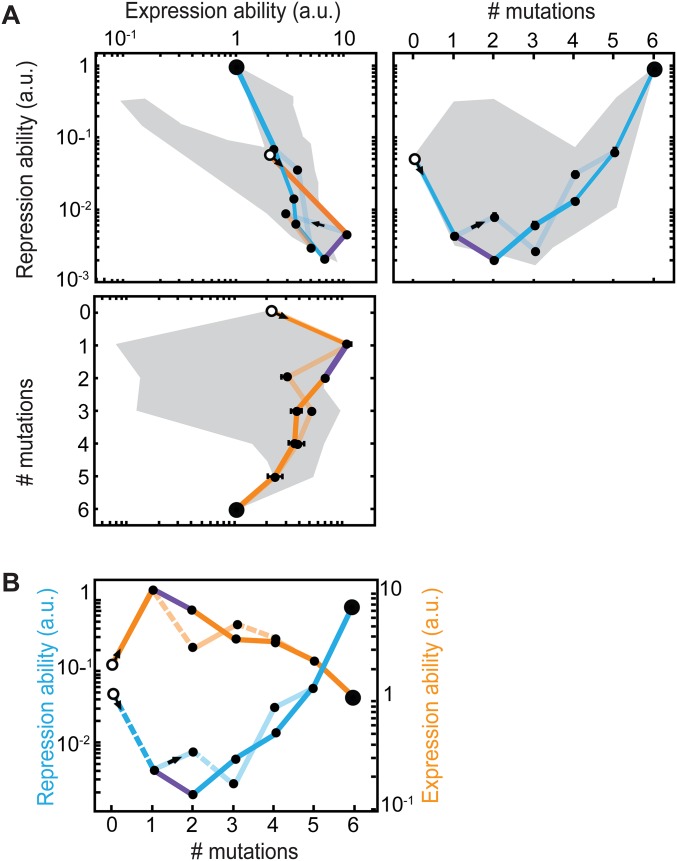
How does environmental variability affect these constraints? We first explore this question with individual trajectories starting with MK:acca. For instance, R can be increased through an operator mutation (MK:acca to MK:tcca) in the environment without ligand but then remains trapped, because the other mutations yield no additional improvements (Fig. 3 A and B and Fig. S2). However, switching to the other environment opens up various trajectories that increase E, such as the repressor mutation MK:tcca to MQ:tcca. After additional increase in E (MQ:tcca to MQ:tgca), the system becomes trapped again on a suboptimum. Concomitantly, note the low R for this genotype (Fig. S2A), which indicates an overall weakened binding between these LacI and operator variants. Switching back to the first environment now allows escape by a compensatory mutation that provides access to YQ:tggt by reestablishing binding and increasing R. We found that a significant fraction of the direct trajectories (21%) becomes accessible in this manner (Figs. S1 and S3). Accessibility was afforded by diverse patterns of environmental change, although not by all (Table S1). Interestingly, the number of accessible trajectories starting in the environment E [with isopropyl-β-d-1-thiogalactopyranoside (IPTG)] outnumbered the accessible trajectories starting in the environment R (without IPTG; 92 vs. 56), although the main improvement is made in R. Overall, these findings indicate that mutational pathways that fail to confer gradual optimization in either constant condition can do so when alternating between these same conditions.
Fig. 3.
Escape from genetic constraint in fluctuating environments. (A) Mutational trajectory accessible by continuous improvements in a changing environment corresponding to B and C. Red indicates mutated position. Forward arrows indicate mutations conferring increases in repression or expression ability, and backward arrows indicate decreasing or neutral steps. The two-color bars represent changing environments that confer continuous improvements. Without environmental changes, the system would be trapped at MK:tcca and MQ:tgca, where no additional improvements are possible in the current environment. (B) Expression and repression ability along the trajectory indicated in A. Data are represented as means (n = 3 or 4) ± SEMs. The trajectory starts at MK:acca (white circles) and ends at YQ:tggt (large black circles). This trajectory contains a valley in (Upper Right) repression ability (blue line) and (Lower) expression ability (orange line). (Upper Left) Blue lines indicate mutations that confer improvements in repression ability, and orange lines indicate mutations that confer improvements in expression ability. The gray area indicates the envelope of all trajectories. (C) Schematic representation of repression and expression ability along the trajectory indicated in A in the variable environment. Semitransparent lines indicate inaccessible mutations. Gray dotted lines indicate environmental changes allowing escape from suboptima.
Fig. S2.
Lock–key interactions trap genetic trajectories. Lock–key binding repressor–operator pairs constrain the trajectory depicted in Fig. 3 A and B (black trajectory). The black and cyan traces together form a valley in both (A) repression ability and (B) expression ability. The tcca operator is a low-expression operator in both environments (Fig. 1C and Fig. S5), which initially retains the repression ability at a high level. After this operator is mutated to tcga or tgca, the repression ability drops and is only restored to a higher repression ability when a new operator–repressor binding pair is formed at YQ:tgga. Cross-environmental tradeoffs can readily be observed by comparing A with B; initially, high levels of repression ability correspond to low levels of expression ability. The mutation to YK:tcca (in the cyan dashed trajectory) is neutral in repression ability according to the statistical test, and it is, therefore, considered not selectively accessible. Means are represented ± SEM. The same situation occurs for the mutation to YQ:tgga (in the cyan trajectory) in expression ability.
Fig. S3.
Genetic constraint in fluctuating environment circumvented by an escape route. (A) In the opaque trajectory, continuous positive selection on all mutations from MK:acca (large white circles) to YQ:tggt (large black circles) is prohibited, because the second mutation (purple) is detrimental in both environments. A mutational escape route (transparent line), bypassing the genetic constraint, is provided by a mutation that is beneficial in the absence of inducer (black arrows). The accessible (transparent) and nonaccessible (opaque) trajectories coalesce at Hamming distance 5. Dashed lines indicate detrimental effects. Means are represented ± SEM. (B) Schematic representation of the changes in repression and expression abilities vs. the number of mutations from MK:acca, with increasing levels of both repression and expression abilities on the vertical axis.
Table S1.
Environmental patterns allowing accessibility
| Pattern or concatenated pattern | Occurrence |
| A | |
| ERERRR* | 42 |
| ERRRRR† | 30 |
| REERRR‡ | 29 |
| REEERR | 12 |
| REER=R‡ | 11 |
| ERERER* | 6 |
| ERER=R* | 4 |
| ERRERR | 4 |
| REERER‡ | 4 |
| EREERR | 4 |
| ERRR=R† | 2 |
| B | |
| RE | — |
| ER | 32 |
| RER | 52 |
| ERE | — |
| RERE | — |
| ERER | 56 |
| RERER | 15 |
| ERERE | — |
| RERERE | — |
| ERERER | 10 |
For each of the 720 direct mutational trajectories from MK:acca to YQ:tggt, we analyzed for each mutational step the environmental conditions that allow fixation of the mutation. R indicates that an environment without IPTG (repression) is required for the fixation of the mutation. E indicates that an environment with IPTG (induction) is required; = indicates that there are no requirements (mutation fixation can occur in both environments). Under A are patterns of environmental requirement sorted by occurrence (i.e., the number of accessible direct paths corresponding to the given pattern of environmental requirements). Under B are statistics on the concatenated patterns. To classify the patterns regardless of the time spent in each environment, the same environmental episodes are concatenated. For example, the first pattern under A is concatenated as ERER, because there are only three environmental changes. The concatenated patterns are sorted by length. When both environments allow fixation, = is counted one time as R and one time as E; — indicates that no occurrence of the corresponding pattern of requirement is observed.
Indicated groups are to show which other patterns a pattern containing = could be associated with if one were to differentiate = as either R or E; for instance, patterns ERERRR and ERERER are specific instances of pattern ERER=R.
Ratchet Mechanism That Exploits Tradeoffs.
The above findings cannot be understood from environmental interactions that alter the magnitude of mutational effects, because they would affect only the depth of constraining valleys. Rather, they indicate the importance of cross-environmental tradeoffs, in which increases in R occur at the expense of decreases in E, and vice versa, increases in E lead to decreases in R (Fig. 3 B and C). Such tradeoffs are also referred to as GxE interactions (49) and can give rise to higher-order GxGxE (34) and sign environmental epistasis (36). In the lac repressor–operator system, cross-environmental tradeoffs between E and R were pervasive (55% of all mutational steps in the direct trajectories) (Fig. S4) and can be understood mechanistically. For example, a low but significant level of repression can be maintained in the presence of inducer through residual binding (50). We found for several genotypes (22 genotypes) that the induced expression level is significantly lower than the highest measured level for the involved operator (Fig. 1C), consistent with residual binding of induced repressors reducing expression. Mutations that increase (decrease) the overall repressor–operator affinity in both environments will increase (decrease) both the repression ability without inducer as well as the residual repression with inducer, leading to opposite effects on R and E and hence, to cross-environmental tradeoffs (Figs. S4 and S5). These tradeoffs have consequences for the relations between constraints in different conditions. We found multiple local optima for each of two environments (3 in R and 13 in E), but none coincided at the same genotype. This feature allows trajectories to repeatedly surf ascending slopes and hence, traverse valleys in a ratchet-like manner: when trapped on a local optimum, the system can wait for an environmental change that enables repositioning on a new ascending slope.
Fig. S4.
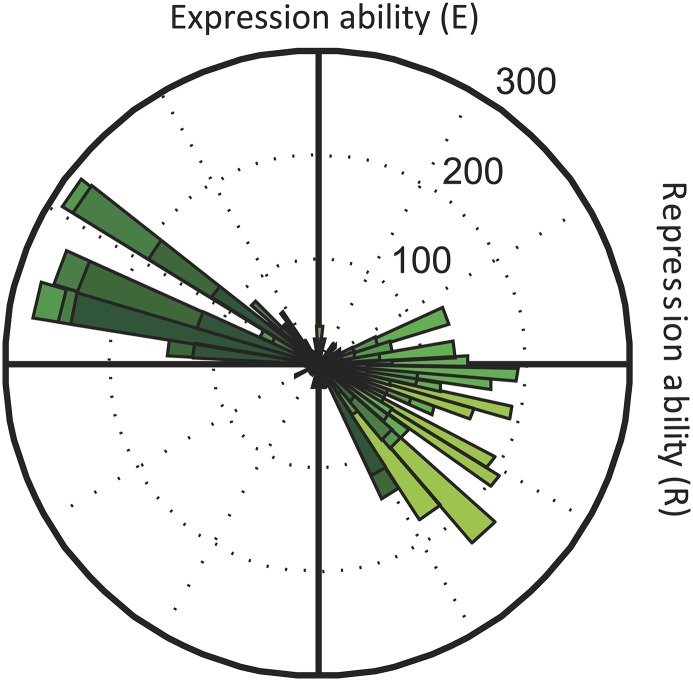
Tradeoffs between expression and repression abilities. Histogram of the changes in mean repression and mean expression ability over all mutational steps in all direct 720 trajectories, with the effect on R on the horizontal axis and the effect on E on the vertical axis. The color gradient indicates fractions of mutations occurring at increasing Hamming distance from the starting genotype, with lighter green corresponding to larger Hamming distances. Mutations in the upper left and lower right quadrants indicate tradeoffs, whereas mutations falling in the upper right quadrant are accessible in both environments. Mutations in the lower left quadrant signal inaccessibility in both environments (34). Most mutations fall in either the lower right or the upper left quadrant, which indicates that a large amount of mutational steps exhibit cross-environmental tradeoff.
Fig. S5.
Expression measurements and absolute values. Mean expression levels of all operator–repressor combinations measured as the developed fluorescence in the fluorescein di-β-d-galactopyranoside expression-level assay (Methods) in either the absence or presence of the inducer IPTG. The expression level is expressed in arbitrary units. Computation of the population transition probabilities.
Crossing Rates in Variable Environments.
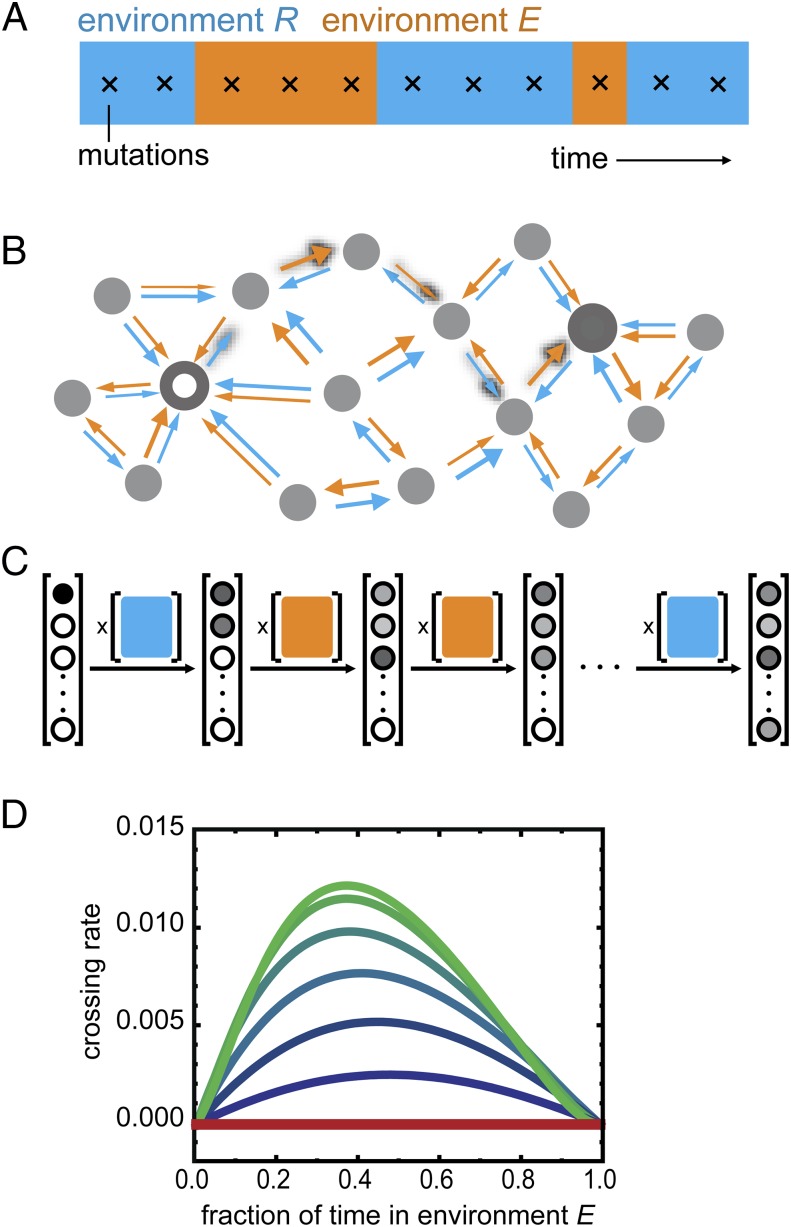
To assess the robustness of this evolutionary mode for different environmental conditions, we extended an evolution model based on a fixed environment Markov process (51) to include environmental fluctuations (Methods, Fig. 4 A–C, SI Results, sections S1–S6, and Figs. S6 and S7). We considered a discrete time Moran process in the strong selection weak mutation regime (52), in which mutational reversions are allowed and trajectories can be of arbitrary length (Methods) (53). Here, we first assume fitness and selection to be proportional to phenotype (E and R) and then, test different nonlinear and nonmonotonic phenotype–fitness relations (SI Results, section S7 and Fig. S8). Consistent with the observed constraint in fixed conditions (Fig. 2), we found that the rate to evolve to YQ:tggt from MK:acca (crossing rate kc) is null for either constant environment (Fig. 4D, fraction of time in environment E of 0 or 1). However, kc is consistently above zero when the environmental fluctuation rate kf is lower than the mutation rate km (Fig. 4D, blue and green lines) and maximized when kf = km, consistent with previous related work (39). That kc is maximal when kf = km can be understood as follows: for kf >> km, there is an effective averaging over the two environments, resulting in a constrained condition, whereas for kf << km, the waiting time for an environment-triggered escape is long enough to allow mutational escape in one of the two environments. Environmentally triggered escape is, thus, found to be robust to changes in the ratio between the times spent in the two environments (Fig. 4D).
Fig. 4.
Landscape crossing in stochastically alternating environments. (A) Environmental fluctuations and occurrence of mutations (crosses) (SI Methods and SI Results, section S1). Environments R and E refer to the environment selecting for repression or expression ability, respectively. (B) Schematic representation of genotype space. Large white and gray circles are start and end genotypes, respectively, of mutational trajectories. Arrows indicate increasing repression ability (R; blue) or expression ability (E; orange); arrow thickness reflects magnitude and hence, transition probability (SI Methods and SI Results, section S2). Shadowed arrows indicate one possible path of continuous improvement from the initial to the final genotypes. The structure of the space is schematic and does not reflect the actual system. (C) Schematic depiction of the Markov chain method for computing crossing rates. The probability vector lists all N genotypes, with the gray scale indicating the probability of populating a genotype at a given indicated time. Initially, only the beginning genotype is populated. The N × N environment-dependent transition probability matrices (colored squares) reflect the arrows in B: a matrix entry at position i,j indicates the transition probability from genotype i to genotype j. Each matrix multiplication yields a novel probability of genotype occupancy after a mutation occurred in a given environment. This illustration is schematic: we use an (infinite time limit) analytical solution for this process, considering a range of possible scenarios of environmental fluctuations. (D) Crossing rate kc as a function of the fraction of time spent in each environment for different environmental fluctuation rates kf. The unit of time is the time between two mutations. The red line indicates environment dwell time <<1, meaning that the environment fluctuates much faster than the time between mutations. The top green line to bottom blue line indicates environment dwell times of c = 1, 2, 5, 10, 20, and 50 (i.e., decreasing kf or decreasing frequency of environmental fluctuation) (SI Methods and SI Results, sections S3–S6). The crossing rate is the inverse of the mean number of mutations that are necessary to cross the landscape. The absolute maximum crossing rate is 0.17 (6−1; corresponding to six mutations being fixed).
Fig. S6.
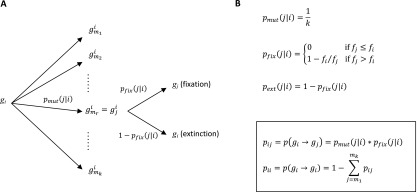
(A) Diagram for the tree of events relative to a mutation + fixation/extinction step in a given environment and their associated probabilities: gi is the isogenic population with genotype gi, is the rth neighbor mutant of gi, gji is the apparition of a mutant with genotype gj in a background population of genotype gi, is the probability for a mutant with genotype gj to appear in a background gi, and is the probability of fixation of the mutation gj in a background gi. (B) Expression of the transition probabilities (SI Results, section S2): k is the connectivity (i.e., number of neighbor mutants), fi and fj are fitness values of genotypes gi and gj, pij is the transition probability from an isogenic population with genotype gi to an isogenic population of genotype gj, and piI is the probability that the genotype of the population is unchanged after a mutation event occurred (extinction of the newly appeared mutant). The boxed area shows the resulting transition probabilities based on the combined partial probabilities expressed above.
Fig. S7.
Timeline of events for the Markov chain computation. Example of a temporal sequence of alternating environments for a scenario with an approximate 50%–50% time fraction between environment R and E () and a dwell time of mutation + fixation/extinction events per period. At the end of each period, one of two environments is chosen with a probability corresponding to their respective time fraction.
Fig. S8.
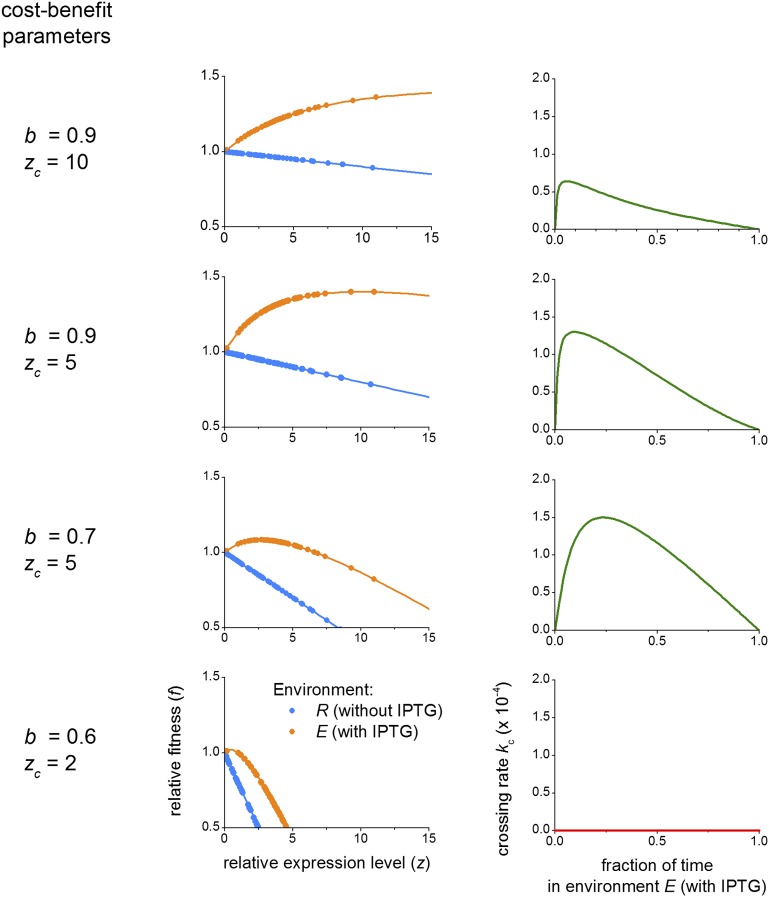
Robustness of landscape crossing for nonlinear cost–benefit tradeoffs. (Left) b and zc are cost–benefit parameters used to convert relative expression levels into relative fitness (see Eq. S10 and Eq. S11). (Center) Relative fitness in each environment as a function of the measured average relative expression level for each genotype and for the b and zc values on the left. Dots indicate experimentally measured average relative expression levels, and lines indicate Eqs. S10 and S11 plotted as a guide for the eyes. (Right) Crossing rate kc in a variable environment scenario computed as previously described (environment dwell time ) using the relative fitness values from the corresponding figure in the center to compute the transition probabilities. Except for extreme cases (row 4; b = 0.6, zc = 2), landscape crossing remains possible for moderate to strong nonlinear cost–benefit (rows 1–3). Rows 2 (b = 0.9, zc = 5) and 3 (b = 0.7, zc = 5) are qualitatively most similar to measured laboratory conditions of the WT lac operon (41).
The above result remained valid for nonlinear phenotype–fitness relations, reflecting, for instance, expression costs that make the dependence weaker for higher E (SI Results, section S7 and Fig. S8, rows 1 and 2) (41, 54). The escape mechanism also remained robust for nonmonotonic phenotype–fitness relations, in which fitness first increases with increasing E and then decreases (Fig. S8, row 3). We found that the mechanism broke down when E increases do not confer fitness increases at all, reflecting a scenario in which lac expression costs outweighs the benefits in the inducing environment (Fig. S8, row 4). However, the latter is not observed experimentally (41, 42).
Computationally Generated Landscapes.
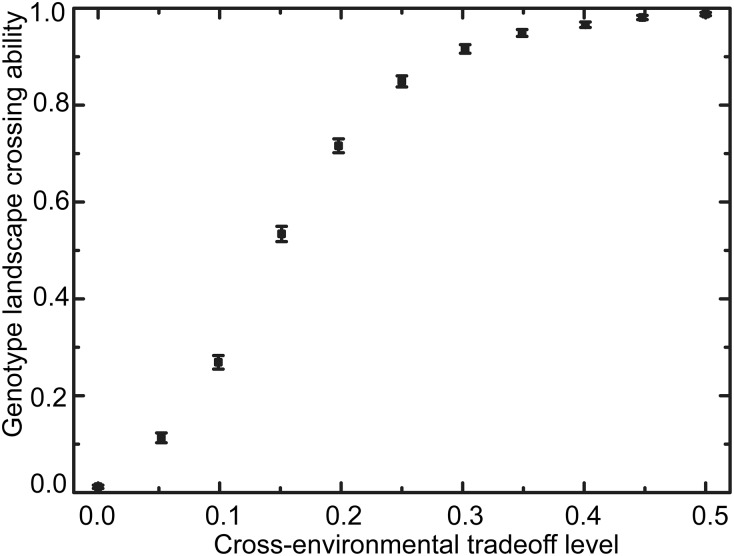
To further probe the requirements for crossing multipeaked landscapes, we considered computationally generated random landscapes. In constant conditions, mutational trajectories become trapped on these landscapes as expected, and hence, the probability to find selectively accessible paths is low (Fig. S9, absence of cross-environmental tradeoff). We found that, when we progressively increase the level of cross-environmental tradeoff (as quantified by the fraction of mutations having opposite effects in the two environments), the probability of finding accessible paths increases until practically all of the landscapes that were generated contained accessible paths in fluctuating conditions at a tradeoff level of 0.5 or more (Fig. S9). We note that this value was 0.47 for the experimentally determined landscape. Overall, these results indicated that cross-environmental tradeoffs are a central ingredient for overcoming constraining genetic interactions in fluctuating environments by positive Darwinian evolution.
Fig. S9.
Effect of cross-environmental tradeoff level between two alternating environments on the crossing ability of randomly generated landscapes. We consider a landscape over six loci of two alleles each (i.e., on a hypercube of dimension 6 and 64 genotypes). For each tradeoff level (i.e., the fraction of mutations having opposite effects in the two environments), random fitness values for each genotype and each environment are drawn to satisfy the tradeoff level between environments. The crossing ability is determined by computing for each tradeoff level the probability p over n = 1,000 (pairs of) landscapes of containing at least one selectively accessible path from the starting genotype to the final genotype in fluctuating conditions. Error bars represent the binomial error .
Discussion
To investigate how environmental variability affects genetic constraints within evolutionary trajectories, we have systematically mapped the genotype–phenotype landscape spanning two matching pairs of transcription factors and their DNA binding sites. Consistent with theoretical considerations on the evolution of molecular recognition, we find that the resulting landscapes in different contrasting environments are highly rugged: none of the mutational trajectories between the two pairs are selectively accessible by fixing one mutation at a time. Landscapes ruggedness has been studied previously for phenotypes that involve multiple possible genes and spontaneously evolved mutations (5, 16, 21, 55, 56). Here, we studied a phenotype that has a well-understood genetic basis, is restricted to one physical site, and hence, is controlled by a reduced set of mutations. The data show that epistatic interactions between these controlling mutations give rise to distinct peaks within genotype space.
Rugged landscapes constitute a specific type of genetic constraint that is distinct from, for instance, the presence of sign epistasis, which imposes specific fixation order but does allow accessible paths (1). Theoretical investigations have considered how escape from entrapment on suboptimal peaks is enabled; they addressed limiting negative selection (18, 19), simultaneously fixing mutations (20), recombination (21–23), and drift (24–26). These mechanisms do not permit adaptive evolution by positive selection of single mutations. Here, we find that such gradual adaptive evolution by positive selection is possible when considering temporal alternations between different environments, with cross-environmental tradeoffs as a second essential ingredient. These tradeoffs are pervasive in the quantified landscapes. They allow the environmental changes to displace local fitness peaks in such a way that the system can be ratcheted in an adaptive manner through fitness valleys by repeatedly climbing locally ascending slopes. We note that, at high mutation rates, such as for instance those observed in viral evolution, multiple variants may arise before one sweeps through the population, resulting in clonal interference and competition between variants. Although in this case, the sweep time rather than the time between mutations becomes the relevant timescale, the tradeoff ratchet mechanism remains valid in this regime.
Crossing fitness valleys by positive selection may seem contradictory. However, one must distinguish between the global fitness of the population and the relative fitness differences between individuals. When trapped, the relative fitness decreases conferred by mutations lead to negative selection within the population. In contrast, the global fitness decreases conferred by environmental changes affect the entire population and do not lead to negative selection. These global fitness decreases open up possibilities for mutations that confer relative fitness gains again. These repeated gains do not come completely for free, because the mechanism does not only drive forward but also backward: after a global fitness decrease induced by environmental change, the positively selected mutations that opened up point away from the ancestor but also, back to it. The occurrence of backward mutations does not cancel the positive selection of this evolutionary mode but merely reduces its efficacy. Thus, environmental changes can serve to overcome fitness decreases that constrain genotypes in constant environments.
The role of tradeoffs in facilitating adaptive change is notable, because they are typically associated with adaptive constraint. Tradeoffs can be rationalized mechanistically for regulatory phenotypes that rely on lock–key molecular recognition, which has been shown to be important genetic material for evolutionary novelties (57, 58). Evolutionary optimization in the presence of tradeoffs can be seen as a sequence of compensatory mutations; recognition loss caused by mutating one binding partner can be restored by complementary mutations in the other binding partner. Note that tradeoffs are present more generally in nature (59, 60) along with environmental fluctuations (61), and hence, the reported adaptive mechanism is not necessarily limited to regulatory phenotypes.
Organisms are known to occupy remarkable wide ranges of contrasting environments. Our findings suggest that the regulatory systems that enable these wide environmental niches are constrained by pervasive (reciprocal) sign epistatic interactions, resulting in rugged landscapes. An inability to optimize regulatory responses to environmental change can result in stasis and the emergence of environmental specialists. However, we find that the proposed mode of adaptation can overcome these constraints and facilitate the evolution of generalists that can occupy diverse niches. Interestingly, such adaptability comes at the cost of weakened environmental robustness of desirable genotypes. Indeed, the stabilizing selection of such a genotype at the top of a fitness peak can be disrupted by tradeoffs and environmental change, which together, can displace peaks. Some environmental robustness may alternatively be afforded by regions in genotype space that are flat in both environments. However, except for a “neutral chain” (YK:agga-YQ:agga-MQ:agga-MQ:tgga-MQ:tcga), no other neutral region was observed in our landscape.
Genetic constraints are commonly regarded as a key factor in adaptive stasis and major evolutionary transitions, such as for instance the evolution of sex, multicellularity or symbiosis, and eusociality (62, 63). Overcoming genetic constraints by tradeoffs in a fluctuating environment could be relevant to these transitions given its few requirements and their ubiquitous presence. Additionally, this evolutionary mode may have implications for clinically or biotechnologically relevant problems, such as the treatment of infections with multidrug protocols (64–66) and the evolutionary engineering of antibodies (67). It will be of interest to test whether this adaptive mode affects the dynamics of experimental evolution in variable environments.
Methods
Strains.
We used E. coli strain BW23473 (68) F−, Δ(argF-lac)169, ΔuidA3::pir+, recA1, rpoS396(Am), endA9(del-ins)::FRT, rph-1, hsdR514, rob-1, and creC510 (Yale Coli Genetic Stock Collection 7837) for all experiments.
Plasmid.
We used a single-copy plasmid that can be induced to a multicopy plasmid for cloning purposes (pETcoco-2; Novagen) to mimic natural expression levels. The plac, lacZ, and lacY WT sequences were derived from E. coli strain MG1655 (Yale Coli Genetic Stock Collection 6300). To facilitate the insertion of mutants (see below), the plac region was amplified until the ninth codon in the coding sequence of lacZ, and a BmtI restriction site was introduced, whereas the WT amino acid sequence was preserved. The remaining lacZ and lacY sequence was amplified and inserted in the polylinker sequence of pETcoco-2 to make pMdV53. Additional information is in SI Methods.
Mutants.
plac operator variants differed in the 4, 5, 5′, and 4′ nucleotide residues as depicted in Fig. 1 B and C. This O1 operator was made palindromic by the deletion of the central c–g base pair (69). In LacI, amino acid residues 17 and 18 were altered using optimal codons for the amino acid variants. Additional information is in SI Methods.
Media.
All growth and expression measurements were performed in Mops EZ Rich Defined Medium (Teknova) with 0.2% glucose as the carbon source and supplemented with 1 mM thiamine-HCl, 1 mM uracil, and appropriate antibiotics. For expression ability measurements, the medium was supplemented with 1 mM IPTG.
Expression-Level Measurements.
Cultures were grown at 37 °C in PerkinElmer Victor3 and VictorX3 plate readers with 200 µL medium per well in a black clear-bottom 96-well plate (NUNC 165305). Cells were fixed after the cultures had reached an OD in the plate reader of at least 0.015 and at most 0.07 by adding 20 µL fluorescein di-β-d-galactopyranoside fixation solution [109 µM fluorescein di-β-d-galactopyranoside (MarkerGene Technologies Inc.), 0.15% formaldehyde, 0.04% DMSO in deionized water]. Fluorescence development was measured every 8 min (excitation = 480 nm and emission = 535 nm), and the OD was measured at 600 nm. When cells were not induced with IPTG during growth, 1 mM IPTG was added to each well immediately before or after fixation, because the assay is sensitive to the amount of IPTG present in the medium (7). Analysis of the fluorescence to quantify the LacZ expression level was as described in ref. 7. Additional information is in SI Methods.
Statistical Tests.
For each genotype, expression measurements were performed in either triplicates or quadruplicates. Expression levels measured in one 96-well plate were normalized to a control genotype on that plate. Throughout all of the analysis, whenever the values between two genotypes were compared (either expression or repression ability values or relative fitness values obtained through the cost–benefit treatment), a two-tailed Welch’s t test was performed to test the null hypothesis that the two genotypes do not have significantly different values (hypothesis of neutrality). The null hypothesis was rejected if the p value obtained from the test was lower than a significant level of 0.05. If the null hypothesis was not rejected, the mutations distinguishing the two genotypes were considered neutral (e.g., we would take the condition in Eq. S1 in SI Results, section S2). Otherwise, the values would be considered to be significantly different, and subsequent computation would be performed accordingly.
Model for the Evolution Dynamics in Fluctuating Environment.
We modeled the dynamics of evolution in fluctuating environment using a discrete time Moran process in the regime of strong selection weak mutation and through a heterogeneous Markov process. Additional information is in SI Methods.
SI Methods
Plasmid.
We used a single-copy plasmid that can be induced to a multicopy plasmid for cloning purposes (pETcoco-2; Novagen) to mimic natural expression levels; lacI was deleted from the pETcoco-2 and replaced with the T0 and Trev terminators from the SacI-SpeI fragment of pInv-110 (70). The introduced placI was derived from the overexpressing placIq sequence from pTrc99A (71). By site-directed mutagenesis, the t at −35 was replaced with the c nucleotide (Quick Change Site-Directed Mutagenesis Kit; Qiagen), leading to native LacI expression levels. The auxiliary operator O3, located at the end of the coding sequence of the WT lacI, has a low affinity for LacI [about 300-fold lower than O1 (72)]. It is involved in weak autorepression of the lac repressor (73) and was, hence, deleted while preserving the LacI amino acid sequence (7); placI combined with lacI from pRD007 (which lacks the auxiliary O3 operator sequence) (7) and a spacer sequence derived from Drosophila Kinesin (pCascade5) by overlap PCR (Pfu Ultra; Invitrogen) were inserted in pETcoco-2. The plac, lacZ, and lacY WT sequences were derived from Escherichia coli strain MG1655 (Yale Coli Genetic Stock Collection 6300); lacA was not incorporated in the assayed operon, because it decreases the active concentration of IPTG in the cell (74, 75). To facilitate the insertion of mutants (see below), the plac region was amplified until the ninth codon in the coding sequence of lacZ (Phusion Polymerase; Finnzymes; New England Biolabs), and a BmtI restriction site was introduced, whereas the WT amino acid sequence was preserved. This fragment was inserted in the pETcoco-2 vector backbone. The remaining lacZ and lacY sequence was amplified (Phusion Polymerase; Finnzymes; New England Biolabs) and inserted in the polylinker sequence of pETcoco-2 to make pMdV53. All restriction enzymes and T4 ligase used were obtained from New England Biolabs, and all primers were obtained from MWG Eurofins.
Mutants.
lacI and plac operator mutants were constructed separately; plac operator variants differed in the 4, 5, 5′, and 4′ nucleotide residues as depicted in Fig. 1 B and C. This O1 operator was made palindromic by the deletion of the central c–g base pair (69). In LacI, amino acid residues 17 and 18 were altered using optimal codons for the amino acid variants. Half-sides of each lacI or plac operator variant were constructed using Pfu Ultra Polymerase (Invitrogen) with one flanking primer and one primer harboring the desired nucleotide variation. After gel purification (Gel Extraction Kit; Qiagen) and ExoI Treatment (New England Biolabs), the half-sides with the desired nucleotide variation in the region of overlap were amplified by overlap PCR to obtain full-length lacI or plac operator variants. Combinations of lacI-spacer-plac mutants were constructed by overlap PCR (Pfu Ultra; Invitrogen), inserted in the pMdV53 backbone, and verified by Sanger sequencing.
Expression-Level Measurements.
Cultures were grown at 37 °C in PerkinElmer Victor3 and VictorX3 Plate Readers with 200 µL medium per well in a black clear-bottom 96-well plate (NUNC 165305). OD at 600 nm was recorded every 4 min, and every 29 min, 9 µL sterile water was added to each well to counteract evaporation. Between measurements, the well plate was shaken at double orbit with a diameter of 2 mm. Cells were fixed after the cultures had reached an OD in the plate reader of at least 0.015 and at most 0.07 by adding 20 µL fluorescein di-β-d-galactopyranoside fixation solution [109 µM fluorescein di-β-d-galactopyranoside (MarkerGene Technologies Inc.), 0.15% formaldehyde, 0.04% DMSO in deionized water]. Fluorescence development was measured every 8 min (excitation = 480 nm and emission = 535 nm) along with the OD at 600 nm. Shaking and dispensing conditions were as described above. When cells were not induced with IPTG during growth, 1 mM IPTG was added to each well immediately before or after fixation, because the assay is sensitive to the amount of IPTG present in the medium (7). Analysis of the fluorescence to quantify the LacZ expression level was as described in ref. 7.
Model for the Evolution Dynamics in Fluctuating Environment.
We modeled the dynamics of evolution in fluctuating environment using a discrete time Moran process in the regime of strong selection weak mutation (SSWM) and through a heterogeneous Markov process.
Briefly, for each environment [without IPTG (environment R) or with IPTG (environment E)], a matrix of transition probabilities between the 26 = 64 isogenic states of the population is first computed based on the difference in performance between starting genotype gi and the arriving genotype gj (details are in SI Results, sections S2 and S3 and Eqs. S3 and S4):
and
To determine the landscape crossing rate in a fluctuating environment, we compute the mean first passage time, tmfp, as the mean number of time steps before reaching the final genotype for mutational trajectories going from genotype MK:acca = g1 to genotype YQ:tggt = g64 (76). Because the paths stop at the latter genotype, for the computation, we define it as an absorbing state in each environment:
Next, from matrices MR and ME, we extract the submatrices QR and QE defined over all of 63 transient states (i.e., all genotypes gj ≠ YQ:tggt, the absorbing genotype). QR and QE are, thus, matrices. QR and QE are then used to compute the fundamental matrix N(w,c) of the evolution process (76) with parameter w as the time fraction of environment R and parameter c as the number of successive mutation + fixation/extinction cycles occurring before any new possible change in environment is allowed (SI Results, sections S3 and S4). The environment is, thus, only allowed to change after a dwell time of c mutation + fixation/extinction events (corresponding to c identical steps of the Markov process), and the new environment is picked with a probability for environment R and a probability for environment E. The mean first passage time tmfp and the corresponding crossing rate kc to evolve to YQ:tggt = g64 starting from MK:acca = g1 are then obtained from the fundamental matrix using Eqs. S8 and S9 in SI Results, section S4:
SI Results
S1. Landscape Crossing Dynamics in a Varying Environment.
We compute the landscape crossing rate for different scenarios of temporally alternating environments, where the frequency of the environmental changes and the time fraction between environments are taken as parameters. To this aim, we determine the mean first passage time to genotype YQ:tggt for a population evolving from genotype MK:acca and experiencing alternately two types of selective environments: one being selective for the repression ability (environment R: absence of IPTG) and one being selective for the expression ability (environment E: presence of IPTG).
We consider an infinite-sized population following a discrete time Moran process in the regime of SSWM (52, 77). In this regime, the time for fixation (or extinction) of a newly appeared mutant allele in the population is far less than the time between mutations. The population is, therefore, essentially assumed to be isogenic.
Here, we formulate a heterogeneous Markov process that models the evolution of the population by a probability density diffusion process through a dynamic adaptive landscape. We build on similar approaches for fixed environments (51, 53). Below, we explain the construction of the model.
S2. Transition Matrices for Each Environment.
The population evolves in a landscape of 26 = 64 genotypes subject to the following dynamics, where the unit of time is taken as the time for a new mutant allele to appear in the population.
At time 0, the population is assumed to carry the starting genotype g1 = MK:acca.
At each time step, a single-point mutant genotype gj appears in the population of genotype gi, with j ≠ i, and this mutation goes to either fixation or extinction, with probabilities that depend on fj/fi, the relative fitness value of the newly appeared genotype with respect to the fitness of other individuals in the population (Fig. S6).
For each genotype, the fitness depends on the environment. Environment R selects for repression ability, whereas environment E selects for expression ability. One can consider various ways in which fitness depends on the measured phenotype. Here, we first consider a direct equivalence between fitness and ability ( and ), and in SI Results, section S7, we investigate other possible relations.
For each environment, a specific Markov matrix is computed that contains the transition probabilities between isogenic states of the population. In the Moran model, the general expressions for the fixation probabilities of a genotype gj of average fitness in a population of genotype gi and average fitness are (78)
and
where nj is the starting number of gj individuals, and ntot is the total size of the population. In the SSWM regime, where nj = 1 (apparition of a mutation in one individual) and where we assume the limit case of a very large population (ntot → ∞), the probability of fixation is nonzero only if (i.e., deleterious and neutral substitutions are negligible) (53), giving
| [S1] |
Using the probability of mutations in each genotype background and Eq. S1, one can compute the components of the transition matrices MR and ME for each environment:
| [S2] |
and
| [S3] |
where k = 6 is the connectivity (i.e., the number of single-point mutant neighbors accessible from any given genotype gi), and m1 to mk are the index of the single-point mutant neighbors of gi (Fig. S6).
S3. Mean First Passage Time and Landscape Crossing Rate.
The Markov process and the associated Markov matrices describe the evolution dynamics on the genotype space by the population submitted to the corresponding transition probabilities. Our model allows for reversal of previously fixed mutation (e.g., after reversal of the environment and/or in a modified genetic background). As such, the considered evolutionary process is not unidirectional but can be a back and forth evolution on the landscape, despite neglecting deleterious and neutral substitutions. Therefore, computing the evolution rate from genotype MK:acca = g1 to genotype YQ:tggt = g64 is equivalent to computing the mean first passage time of the population to the genotype YQ:tggt.
For a Markov process described by a single Markov matrix M, the mean first passage time of the system to a specific state sr can be computed by (i) setting sr as an absorbing state, i.e., fixing . [One should also check that this operation results in a proper absorbing Markov chain; i.e., a Markov chain where an absorbing state is reachable from any transient state—not necessarily in one step (76). That an absorbing state is reachable from any transient state means that there are no “nonescapable” circuits of transient states, which we confirmed to be the case in our system in the conditions of alternating environments.] (ii) Considering the submatrix Q over all of the other transient (i.e., nonabsorbing) states , and (iii) computing the fundamental matrix N (76):
| [S4] |
where I is the identity matrix.
The components Nij of N give the expected number of time steps in which the system is found in state sj before it is absorbed starting from state si. The mean first passage time to state sr assuming si to be the starting state is then simply given by
| [S5] |
which in turn, gives the corresponding transition rate from state si to state sr:
| [S6] |
S4. Landscape Crossing Rate in Alternating Environments.
To compute the mean first passage time to genotype YQ:tggt in alternating environments, we need to compute the mean first passage time in the case of a Markov process described by the alternating application of the two transition matrices MR and ME and their associated transient state submatrices and .
To assess different frequencies of environmental changes and different values of fraction of time spent in each environment, we define the probability w to be in environment R and a dwell time c being the number of successive mutation + fixation/extinction cycles occurring before any new possible change in environment is allowed (i.e., the transition matrix applied is allowed to change only each time a number c of mutation + fixation/extinction cycles has occurred) (Fig. 4 A–C and Figs. S6 and S7).
The fundamental matrix combines all possible scenarios and therefore, accounts for all branches of events and their respective probability at each period. Thus, for the first dwell time period of mutation + fixation/extinction cycles, there is a probability that they occur in environment R and a probability that they occur in environment E, giving
For the second period, whatever happened in the first period, the same branching of events occurs, giving the following extended expression, where only the last Q terms of order c in N1(w,c) are multiplied:
Repeating the extension, one can then write the following general expression:
where the term is defined recursively as follows:
where one can actually recognize the expression of N(w, c), which then writes:
or
with
We, thus, obtain
| [S7] |
We then obtain the mean first passage times and crossing rates from Eq. S5 and Eq. S6 with, in our particular case, the initial and final states being genotypes 1 (= 20 for MK:acca) and 64 (= 26 for YQ:tggt):
| [S8] |
and for the landscape crossing rate:
| [S9] |
S5. Conditions of Environment Fluctuating Faster than the Time Between Mutations.
When the environment fluctuates much faster than the time between mutations, the isogenic population experiences an average fitness , which we take to be the geometric mean between the fitness values and in each environment, weighted by the fraction of time w spent in the corresponding environment: . The landscape crossing rate is then computed as for a constant environment following Eqs. S1, S2, S3, S4, S5, and S6 above.
S6. Extending the Constraint Analysis to Indirect Paths.
Analyzing the accessibility of all of the paths individually (i.e., not only the 6! = 720 direct paths but also, indirect paths that allow for mutation reversal) is computationally intractable. For instance, for two genotypes distant from just five mutations, there is a total of 18,651,552,840 simple paths (79). Nevertheless, computing the landscape crossing rate kc (SI Results, sections S1–S4) indicates if the landscape is crossable, taking indirect paths into account in the analysis.
Fig. 4D shows that, for fractions of time w = 0 or 1 (i.e., for fixed environment of either R or E), the landscape crossing rates kc are identically null in all cases. This result shows that the landscape is not crossable in a fixed environment of either R or E and that, therefore, all indirect paths also contain a valley.
S7. Robustness of Landscape Crossing for Nonlinear Cost–Benefit Tradeoffs.
Fitness (or growth rate) might not be a linear or even monotonic function of expression levels. First, the benefit associated with the expression of a beneficial gene can level off beyond a certain expression level. Second, expression of a beneficial gene can also come at a cost that increases with the level of expression of the gene. To test the robustness of our results, we analyzed the landscape crossing rates in the context of a cost–benefit scenario.
To explore a range of cost–benefit scenarios, we used a parameterized version of a cost–benefit function applied previously to the lac operon (41). In the environment that selects for the expression ability (environment E), we define the following relative fitness
| [S10] |
with parameters
b [a benefit coefficient; b = benefit/(benefit + cost)],
zc (a critical relative expression level characterizing the nonlinearity of the benefit), and
z (the relative expression level of the corresponding genotype).
The term corresponds to the benefit associated with the relative expression level z and is a saturating function of z, whereas the term corresponds to the cost associated with the relative expression level z.
In the environment selecting for repression ability (environment R), there is no benefit associated with expression, and the benefit term of Eq. S10 drops. The relative fitness then simply becomes a linear decreasing function of the relative expression level:
| [S11] |
Within this framework, a benefit coefficient of implies a purely beneficial effect of the expression in environment E without any cost (whether in environment E or R), whereas a benefit coefficient of corresponds to the extreme case where expression only leads to cost, regardless of whether in environment E or R.
For given values of b and zc, the fitness values and obtained from Eqs. S10 and S11 are then used to compute the transition probability matrices using Eqs. S1, S2, and S3. Landscape crossing rates kc are then computed as before (Eq. S9). To compare average fitness values and compute the transition probabilities, statistical tests between triplicate or quadruplicate values are performed as explained in Methods.
Fig. S8 shows the result for four different sets of the b and zc parameters, exploring increasingly extreme cost–benefit scenarios.
This analysis illustrates that, except for extreme cases (uniformly null landscape crossing rate) (Fig. S8, row 4), landscape crossing stays feasible, and the mechanism can sustain saturation in benefit (Fig. S8, rows 1 and 2) or highly nonlinear cost–benefit relationships with moderate fitness decrease (Fig. S8, row 3).
Acknowledgments
We thank D. M. Weinreich, J. A. G. M. de Visser, T. Paixão, J. Polechová, T. Friedlander, and A. E. Mayo for reading and commenting on earlier versions of the manuscript and B. Houchmandzadeh, O. Rivoire, and M. Hemery for discussions and suggestions on the Markov computation. Furthermore, we thank F. J. Poelwijk for sharing plasmid pCascade5 and pRD007 and Y. Yokobayashi for sharing plasmid pINV-110. We also thank the anonymous reviewers for remarks on the initial version of the manuscript. This work is part of the research program of the Foundation for Fundamental Research on Matter, which is part of the Netherlands Organization for Scientific Research (NWO). M.G.J.d.V. was (partially) funded by NWO Earth and Life Sciences (ALW), project 863.14.015.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1510282112/-/DCSupplemental.
References
- 1.Weinreich DM, Delaney NF, Depristo MA, Hartl DL. Darwinian evolution can follow only very few mutational paths to fitter proteins. Science. 2006;312(5770):111–114. doi: 10.1126/science.1123539. [DOI] [PubMed] [Google Scholar]
- 2.Poelwijk FJ, Kiviet DJ, Weinreich DM, Tans SJ. Empirical fitness landscapes reveal accessible evolutionary paths. Nature. 2007;445(7126):383–386. doi: 10.1038/nature05451. [DOI] [PubMed] [Google Scholar]
- 3.de Visser JA, Krug J. Empirical fitness landscapes and the predictability of evolution. Nat Rev Genet. 2014;15(7):480–490. doi: 10.1038/nrg3744. [DOI] [PubMed] [Google Scholar]
- 4.Breen MS, Kemena C, Vlasov PK, Notredame C, Kondrashov FA. Epistasis as the primary factor in molecular evolution. Nature. 2012;490(7421):535–538. doi: 10.1038/nature11510. [DOI] [PubMed] [Google Scholar]
- 5.Kvitek DJ, Sherlock G. Reciprocal sign epistasis between frequently experimentally evolved adaptive mutations causes a rugged fitness landscape. PLoS Genet. 2011;7(4):e1002056. doi: 10.1371/journal.pgen.1002056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Salverda ML, et al. Initial mutations direct alternative pathways of protein evolution. PLoS Genet. 2011;7(3):e1001321. doi: 10.1371/journal.pgen.1001321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Poelwijk FJ, de Vos MGJ, Tans SJ. Tradeoffs and optimality in the evolution of gene regulation. Cell. 2011;146(3):462–470. doi: 10.1016/j.cell.2011.06.035. [DOI] [PubMed] [Google Scholar]
- 8.Meer MV, Kondrashov AS, Artzy-Randrup Y, Kondrashov FA. Compensatory evolution in mitochondrial tRNAs navigates valleys of low fitness. Nature. 2010;464(7286):279–282. doi: 10.1038/nature08691. [DOI] [PubMed] [Google Scholar]
- 9.Miller SP, Lunzer M, Dean AM. Direct demonstration of an adaptive constraint. Science. 2006;314(5798):458–461. doi: 10.1126/science.1133479. [DOI] [PubMed] [Google Scholar]
- 10.Lind PA, Berg OG, Andersson DI. Mutational robustness of ribosomal protein genes. Science. 2010;330(6005):825–827. doi: 10.1126/science.1194617. [DOI] [PubMed] [Google Scholar]
- 11.Qu X, et al. Genetic epistasis between heparan sulfate and FGF-Ras signaling controls lens development. Dev Biol. 2011;355(1):12–20. doi: 10.1016/j.ydbio.2011.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Via S. The ecological genetics of speciation. Am Nat. 2002;159(Suppl 3):S1–S7. doi: 10.1086/338368. [DOI] [PubMed] [Google Scholar]
- 13.Schluter D, Conte GL. Genetics and ecological speciation. Proc Natl Acad Sci USA. 2009;106(Suppl 1):9955–9962. doi: 10.1073/pnas.0901264106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dettman JR, Sirjusingh C, Kohn LM, Anderson JB. Incipient speciation by divergent adaptation and antagonistic epistasis in yeast. Nature. 2007;447(7144):585–588. doi: 10.1038/nature05856. [DOI] [PubMed] [Google Scholar]
- 15.Poelwijk FJ, Tănase-Nicola S, Kiviet DJ, Tans SJ. Reciprocal sign epistasis is a necessary condition for multi-peaked fitness landscapes. J Theor Biol. 2011;272(1):141–144. doi: 10.1016/j.jtbi.2010.12.015. [DOI] [PubMed] [Google Scholar]
- 16.Lozovsky ER, et al. Stepwise acquisition of pyrimethamine resistance in the malaria parasite. Proc Natl Acad Sci USA. 2009;106(29):12025–12030. doi: 10.1073/pnas.0905922106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Macken CA, Perelson AS. Protein evolution on rugged landscapes. Proc Natl Acad Sci USA. 1989;86(16):6191–6195. doi: 10.1073/pnas.86.16.6191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Burton OJ, Travis JMJ. Landscape structure and boundary effects determine the fate of mutations occurring during range expansions. Heredity (Edinb) 2008;101(4):329–340. doi: 10.1038/hdy.2008.56. [DOI] [PubMed] [Google Scholar]
- 19.Bitbol AF, Schwab DJ. Quantifying the role of population subdivision in evolution on rugged fitness landscapes. PLOS Comput Biol. 2014;10(8):e1003778. doi: 10.1371/journal.pcbi.1003778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Weinreich DM, Chao L. Rapid evolutionary escape by large populations from local fitness peaks is likely in nature. Evolution. 2005;59(6):1175–1182. [PubMed] [Google Scholar]
- 21.de Visser JA, Park SC, Krug J. Exploring the effect of sex on empirical fitness landscapes. Am Nat. 2009;174(Suppl 1):S15–S30. doi: 10.1086/599081. [DOI] [PubMed] [Google Scholar]
- 22.Watson RA, Weinreich DM, Wakeley J. Genome structure and the benefit of sex. Evolution. 2011;65(2):523–536. doi: 10.1111/j.1558-5646.2010.01144.x. [DOI] [PubMed] [Google Scholar]
- 23.Watson RA, Weinreich DM, Wakeley J. Effects of intra-gene fitness interactions on the benefit of sexual recombination. Biochem Soc Trans. 2006;34(Pt 4):560–561. doi: 10.1042/BST0340560. [DOI] [PubMed] [Google Scholar]
- 24.Kimura M. The Neutral Theory of Molecular Evolution. Cambridge Univ Press; Cambridge, United Kingdom: 1983. [Google Scholar]
- 25.Lynch M. The evolution of genetic networks by non-adaptive processes. Nat Rev Genet. 2007;8(10):803–813. doi: 10.1038/nrg2192. [DOI] [PubMed] [Google Scholar]
- 26.Weissman DB, Desai MM, Fisher DS, Feldman MW. The rate at which asexual populations cross fitness valleys. Theor Popul Biol. 2009;75(4):286–300. doi: 10.1016/j.tpb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Eldar A, et al. Partial penetrance facilitates developmental evolution in bacteria. Nature. 2009;460(7254):510–514. doi: 10.1038/nature08150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Crispo E. The Baldwin effect and genetic assimilation: Revisiting two mechanisms of evolutionary change mediated by phenotypic plasticity. Evolution. 2007;61(11):2469–2479. doi: 10.1111/j.1558-5646.2007.00203.x. [DOI] [PubMed] [Google Scholar]
- 29.Mills R, Watson RA. 2006. On crossing fitness valleys with the Baldwin effect. Proceedings of the Tenth International Conference on the Simulation and Synthesis of Living Systems (School of ECS, University of Southampton, Southampton, UK), pp 493–499.
- 30.Remold SK, Lenski RE. Pervasive joint influence of epistasis and plasticity on mutational effects in Escherichia coli. Nat Genet. 2004;36(4):423–426. doi: 10.1038/ng1324. [DOI] [PubMed] [Google Scholar]
- 31.Bataillon T, Zhang T, Kassen R. Cost of adaptation and fitness effects of beneficial mutations in Pseudomonas fluorescens. Genetics. 2011;189(3):939–949. doi: 10.1534/genetics.111.130468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hall AR, Iles JC, MacLean RC. The fitness cost of rifampicin resistance in Pseudomonas aeruginosa depends on demand for RNA polymerase. Genetics. 2011;187(3):817–822. doi: 10.1534/genetics.110.124628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stiffler MA, Hekstra DR, Ranganathan R. Evolvability as a function of purifying selection in TEM-1 β-lactamase. Cell. 2015;160(5):882–892. doi: 10.1016/j.cell.2015.01.035. [DOI] [PubMed] [Google Scholar]
- 34.de Vos MG, Poelwijk FJ, Battich N, Ndika JD, Tans SJ. Environmental dependence of genetic constraint. PLoS Genet. 2013;9(6):e1003580. doi: 10.1371/journal.pgen.1003580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Flynn KM, Cooper TF, Moore FB, Cooper VS. The environment affects epistatic interactions to alter the topology of an empirical fitness landscape. PLoS Genet. 2013;9(4):e1003426. doi: 10.1371/journal.pgen.1003426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lindsey HA, Gallie J, Taylor S, Kerr B. Evolutionary rescue from extinction is contingent on a lower rate of environmental change. Nature. 2013;494(7438):463–467. doi: 10.1038/nature11879. [DOI] [PubMed] [Google Scholar]
- 37.Kashtan N, Noor E, Alon U. Varying environments can speed up evolution. Proc Natl Acad Sci USA. 2007;104(34):13711–13716. doi: 10.1073/pnas.0611630104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tan L, Serene S, Chao HX, Gore J. Hidden randomness between fitness landscapes limits reverse evolution. Phys Rev Lett. 2011;106(19):198102. doi: 10.1103/PhysRevLett.106.198102. [DOI] [PubMed] [Google Scholar]
- 39.Mustonen V, Lässig M. Molecular evolution under fitness fluctuations. Phys Rev Lett. 2008;100(10):108101. doi: 10.1103/PhysRevLett.100.108101. [DOI] [PubMed] [Google Scholar]
- 40.Mustonen V, Lässig M. From fitness landscapes to seascapes: Non-equilibrium dynamics of selection and adaptation. Trends Genet. 2009;25(3):111–119. doi: 10.1016/j.tig.2009.01.002. [DOI] [PubMed] [Google Scholar]
- 41.Dekel E, Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature. 2005;436(7050):588–592. doi: 10.1038/nature03842. [DOI] [PubMed] [Google Scholar]
- 42.Eames M, Kortemme T. Cost-benefit tradeoffs in engineered lac operons. Science. 2012;336(6083):911–915. doi: 10.1126/science.1219083. [DOI] [PubMed] [Google Scholar]
- 43.Nguyen CC, Saier MH., Jr Phylogenetic, structural and functional analyses of the LacI-GalR family of bacterial transcription factors. FEBS Lett. 1995;377(2):98–102. doi: 10.1016/0014-5793(95)01344-x. [DOI] [PubMed] [Google Scholar]
- 44.Weickert MJ, Adhya S. A family of bacterial regulators homologous to Gal and Lac repressors. J Biol Chem. 1992;267(22):15869–15874. [PubMed] [Google Scholar]
- 45.Sartorius J, Lehming N, Kisters B, von Wilcken-Bergmann B, Müller-Hill B. lac Repressor mutants with double or triple exchanges in the recognition helix bind specifically to lac operator variants with multiple exchanges. EMBO J. 1989;8(4):1265–1270. doi: 10.1002/j.1460-2075.1989.tb03500.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lehming N, Sartorius J, Kisters-Woike B, von Wilcken-Bergmann B, Müller-Hill B. Mutant lac repressors with new specificities hint at rules for protein--DNA recognition. EMBO J. 1990;9(3):615–621. doi: 10.1002/j.1460-2075.1990.tb08153.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Poelwijk FJ, Kiviet DJ, Tans SJ. Evolutionary potential of a duplicated repressor-operator pair: Simulating pathways using mutation data. PLOS Comput Biol. 2006;2(5):e58. doi: 10.1371/journal.pcbi.0020058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Dawid A, Kiviet DJ, Kogenaru M, de Vos M, Tans SJ. Multiple peaks and reciprocal sign epistasis in an empirically determined genotype-phenotype landscape. Chaos. 2010;20(2):026105. doi: 10.1063/1.3453602. [DOI] [PubMed] [Google Scholar]
- 49.Remold SK, Lenski RE. Contribution of individual random mutations to genotype-by-environment interactions in Escherichia coli. Proc Natl Acad Sci USA. 2001;98(20):11388–11393. doi: 10.1073/pnas.201140198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lewis M. Allostery and the lac operon. J Mol Biol. 2013;425(13):2309–2316. doi: 10.1016/j.jmb.2013.03.003. [DOI] [PubMed] [Google Scholar]
- 51.Draghi JA, Parsons TL, Wagner GP, Plotkin JB. Mutational robustness can facilitate adaptation. Nature. 2010;463(7279):353–355. doi: 10.1038/nature08694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gillespie JH. Some properties of finite populations experiencing strong selection and weak mutation. Am Nat. 1983;121(5):691–708. [Google Scholar]
- 53.McCandlish DM. On the findability of genotypes. Evolution. 2013;67(9):2592–2603. doi: 10.1111/evo.12128. [DOI] [PubMed] [Google Scholar]
- 54.Perfeito L, Ghozzi S, Berg J, Schnetz K, Lässig M. Nonlinear fitness landscape of a molecular pathway. PLoS Genet. 2011;7(7):e1002160. doi: 10.1371/journal.pgen.1002160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Burch CL, Chao L. Evolution by small steps and rugged landscapes in the RNA virus phi6. Genetics. 1999;151(3):921–927. doi: 10.1093/genetics/151.3.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nahum JR, et al. A tortoise-hare pattern seen in adapting structured and unstructured populations suggests a rugged fitness landscape in bacteria. Proc Natl Acad Sci USA. 2015;112(24):7530–7535. doi: 10.1073/pnas.1410631112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wagner GP, Lynch VJ. Evolutionary novelties. Curr Biol. 2010;20(2):R48–R52. doi: 10.1016/j.cub.2009.11.010. [DOI] [PubMed] [Google Scholar]
- 58.Wu CI, Ting CT. Genes and speciation. Nat Rev Genet. 2004;5(2):114–122. doi: 10.1038/nrg1269. [DOI] [PubMed] [Google Scholar]
- 59.Stearns SC. Trade-offs in life-history evolution. Funct Ecol. 1989;3(3):259–268. [Google Scholar]
- 60.Levins R. Evolution in Changing Environments. Princeton Univ Press; Princeton: 1968. [Google Scholar]
- 61.Bell G. Fluctuating selection: The perpetual renewal of adaptation in variable environments. Philos Trans R Soc Lond B Biol Sci. 2010;365(1537):87–97. doi: 10.1098/rstb.2009.0150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.West SA, Fisher RM, Gardner A, Kiers ET. Major evolutionary transitions in individuality. Proc Natl Acad Sci USA. 2015;112(33):10112–10119. doi: 10.1073/pnas.1421402112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kondrashov FA, Kondrashov AS. Multidimensional epistasis and the disadvantage of sex. Proc Natl Acad Sci USA. 2001;98(21):12089–12092. doi: 10.1073/pnas.211214298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kim S, Lieberman TD, Kishony R. Alternating antibiotic treatments constrain evolutionary paths to multidrug resistance. Proc Natl Acad Sci USA. 2014;111(40):14494–14499. doi: 10.1073/pnas.1409800111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Schenk MF, et al. Role of pleiotropy during adaptation of TEM-1 β-lactamase to two novel antibiotics. Evol Appl. 2015;8(3):248–260. doi: 10.1111/eva.12200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Fuentes-Hernandez A, et al. Using a sequential regimen to eliminate bacteria at sublethal antibiotic dosages. PLoS Biol. 2015;13(4):e1002104. doi: 10.1371/journal.pbio.1002104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Hoogenboom HR. Selecting and screening recombinant antibody libraries. Nat Biotechnol. 2005;23(9):1105–1116. doi: 10.1038/nbt1126. [DOI] [PubMed] [Google Scholar]
- 68.Haldimann A, Daniels LL, Wanner BL. Use of new methods for construction of tightly regulated arabinose and rhamnose promoter fusions in studies of the Escherichia coli phosphate regulon. J Bacteriol. 1998;180(5):1277–1286. doi: 10.1128/jb.180.5.1277-1286.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Simons A, Tils D, von Wilcken-Bergmann B, Müller-Hill B. Possible ideal lac operator: Escherichia coli lac operator-like sequences from eukaryotic genomes lack the central G X C pair. Proc Natl Acad Sci USA. 1984;81(6):1624–1628. doi: 10.1073/pnas.81.6.1624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Yokobayashi Y, Weiss R, Arnold FH. Directed evolution of a genetic circuit. Proc Natl Acad Sci USA. 2002;99(26):16587–16591. doi: 10.1073/pnas.252535999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Amann E, Ochs B, Abel KJ. Tightly regulated tac promoter vectors useful for the expression of unfused and fused proteins in Escherichia coli. Gene. 1988;69(2):301–315. doi: 10.1016/0378-1119(88)90440-4. [DOI] [PubMed] [Google Scholar]
- 72.Oehler S, Amouyal M, Kolkhof P, von Wilcken-Bergmann B, Müller-Hill B. Quality and position of the three lac operators of E. coli define efficiency of repression. EMBO J. 1994;13(14):3348–3355. doi: 10.1002/j.1460-2075.1994.tb06637.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Oehler S. Feedback regulation of Lac repressor expression in Escherichia coli. J Bacteriol. 2009;191(16):5301–5303. doi: 10.1128/JB.00427-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Marbach A, Bettenbrock K. lac operon induction in Escherichia coli: Systematic comparison of IPTG and TMG induction and influence of the transacetylase LacA. J Biotechnol. 2012;157(1):82–88. doi: 10.1016/j.jbiotec.2011.10.009. [DOI] [PubMed] [Google Scholar]
- 75.Roderick SL. The lac operon galactoside acetyltransferase. C R Biol. 2005;328(6):568–575. doi: 10.1016/j.crvi.2005.03.005. [DOI] [PubMed] [Google Scholar]
- 76.Grinstead C, Snell L. Grinstead and Snell’s Introduction to Probability. American Mathematical Society, Washington, DC; 2006. [Google Scholar]
- 77.Gillespie JH. A simple stochastic gene substitution model. Theor Popul Biol. 1983;23(2):202–215. doi: 10.1016/0040-5809(83)90014-x. [DOI] [PubMed] [Google Scholar]
- 78.Houchmandzadeh B, Vallade M. Alternative to the diffusion equation in population genetics. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82(5 Pt 1):051913. doi: 10.1103/PhysRevE.82.051913. [DOI] [PubMed] [Google Scholar]
- 79.DePristo MA, Hartl DL, Weinreich DM. Mutational reversions during adaptive protein evolution. Mol Biol Evol. 2007;24(8):1608–1610. doi: 10.1093/molbev/msm118. [DOI] [PubMed] [Google Scholar]