A Transport Model for Estimating the Time Course of ERK Activation in the C. elegans Germline

Abstract

The Caenorhabditis elegans germline is a well-studied model system for investigating the control of cell fate by signaling pathways. Cell signals at the distal tip of the germline promote cell proliferation; just before the loop, signals couple cell maturation to organism-level nutrient status; at the proximal end of the germline, signals coordinate oocyte maturation and fertilization in the presence of sperm. The latter two events require dual phosphorylation and activation of ERK, the effector molecule of the Ras/MAPK cascade. In C. elegans, ERK is known as MPK-1. At this point, none of today’s methods for real-time monitoring of dually phosphorylated MPK-1 are working in the germline. Consequently, quantitative understanding of the MPK-1-dependent processes during germline development is limited. Here, we make a step toward advancing this understanding using a model-based framework that reconstructs the time course of MPK-1 activation from a snapshot of a fixed germline. Our approach builds on a number of recent studies for estimating temporal dynamics from fixed organisms, but takes advantage of the anatomy of the germline to simplify the analysis. Our model predicts that the MPK-1 signal turns on ∼30 h into germ cell progression and peaks ∼7 h later.

Introduction

The Caenorhabditis elegans germline is a well-studied model system for genetic studies of cell signaling (1, 2, 3). The adult hermaphrodite germline consists of two U-shaped tubes that meet at a common uterus. Each tube is filled with germ cells spatially arranged according to their maturity (4). Stem cell divisions at the distal tip of each tube (distal to the common uterus) maintain the germ cell population as the more mature cells move away from the distal tip and transition into meiosis (5, 6). After the loop, the bend in the U, a single-file line of oocytes prepare for fertilization and ovulation. Here, we focus on the anterior region of the germline, from the distal tip cell until the loop (Fig. 1), where ∼1000 germ cells line the periphery of the gonad tube and are connected to a common cytoplasmic core called the rachis (7, 8). Nuclei are separated by incomplete cell membranes that are open to the rachis, so the terms “nucleus” and “cell” in this region are essentially interchangeable. Near the loop, a large portion of healthy germ cells undergo apoptosis, which may leave more cytoplasmic material for the surviving cells that become oocytes (9). In an adult hermaphroditic nematode, the germline reaches steady state, maintaining a roughly constant number of germ cells and ovulation rate for most of the organism’s reproductive life (7, 10).

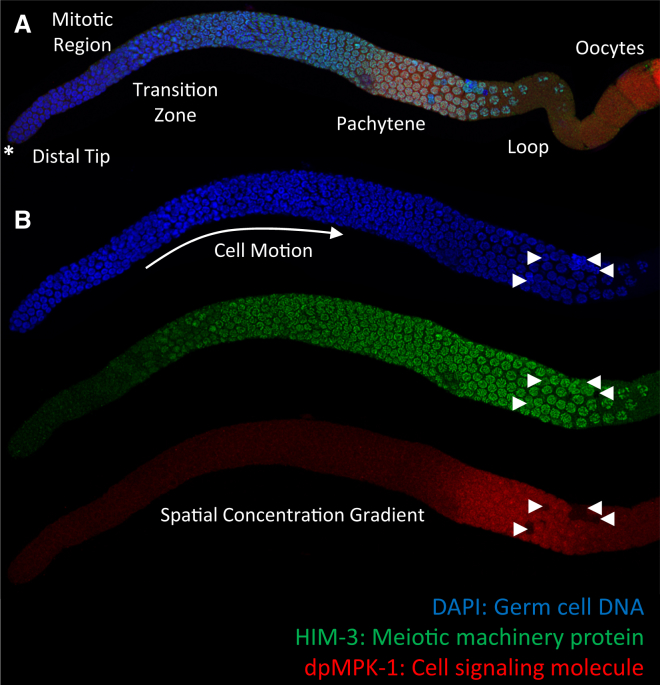
Figure 1.

An adult, hermaphrodite C. elegans germline. (A) Shows the anterior region of the germline, from the distal tip (left in the image, marked by an asterisk) through the first few cellularized oocytes (right in the image). (B) Focuses on the germline from (A), but zoomed in only on the region from the distal tip to the loop. (Blue) Nuclei stained with DAPI. Mitotic cells in the mitotic region undergo divisions that maintain the germ cell population. As the cells divide and expand the mitotic region, more mature cells are pushed toward the loop. (Green) Germ cells differentiate in the transition zone, entering meiosis, marked by the HIM-3 protein. HIM-3 labels the synaptonemal complex axis of the meiotic nuclei (53). (Red) Activation of MPK-1, which occurs in the final two-thirds of the anterior germline. Near the loop, a large fraction of arriving germ cells undergo apoptosis (apoptotic cells in each color channel marked by white arrowheads). Surviving cells pass the loop and become oocytes. To see this figure in color, go online.

Within the rachis are spatial gradients of effector molecules that regulate germ cell development as they progress through the germline (1, 2). Among the regulatory molecules in the rachis is the extracellular signal-regulated kinase (ERK), the terminal kinase of the Ras/mitogen-activated protein kinase (MAPK) signaling cascade. The C. elegans homolog of ERK is known as MPK-1 (2, 11). In the pachytene region of the germline, DAF-2 insulin-like signaling activates the MAPK cascade when the organism is in a nutritionally replete environment, resulting in MPK-1 becoming dually phosphorylated (dpMPK-1) and catalytically active (12); activation of MPK-1 then drives meiotic progression and oocyte production. The ligand to the DAF-2 receptor that results in activation of MPK-1 in the germline is unknown as of this writing. In the proximal part of the germline, MPK-1 activation by signals from sperm couples oocyte maturation to sperm availability (10).

Active MPK-1 has numerous substrates that control multiple biological functions (13). Mutations that result in complete loss of active MPK-1 cause germ cells to arrest in the early pachytene stage of meiosis I. Reduction of MPK-1 activation results in multiple phenotypes, such as delayed progression of pachytene stage germ cells and the formation of excessively large oocytes (2). Alternatively, mutations that overactivate MPK-1 result in higher and ectopic activation of MPK-1 in the loop region, causing defects in oocyte growth and maturation (2). All of these mutations render the animal infertile.

Clearly, the amplitude of the MPK-1 signal in the germline is important for normal germ cell development. The duration of MPK-1 signaling has also been shown to be important in other cell decision-making contexts, such as the proliferation versus differentiation decision in PC12 cells (14, 15, 16, 17, 18), and may also be a relevant factor in the germline. However, because existing methods for real-time monitoring of MPK-1 signaling in living organisms are not yet working in the germline, quantitative information about the dynamics of this signal is not available as of this writing (19, 20, 21, 22, 23, 24, 25, 26, 27, 28). In the early Drosophila melanogaster embryo, ERK activation dynamics were estimated from fixed samples by matching morphological features to developmental time (29, 30, 31). Here, we provide an alternative method to quantitatively estimate MPK-1/ERK activation dynamics in the C. elegans germline. Our approach builds on recent work in cultured cells estimating dynamic information from static data (32, 33). However, these studies required molecular markers to order cells according to their progress in the cell cycle; in the germline, cells are naturally ordered in space. We take advantage of this anatomical feature and develop a model-based computational approach for the reconstruction of active MPK-1 dynamics in the distal germline (which we define here as the region from the distal tip cell to the loop). While multiple mathematical models for germ cell dynamics have been proposed (34, 35, 36), all of these simulate the stem cell programs in the distal region of the germline. To our knowledge, this is the first model aimed at the quantitative estimation of signaling dynamics in the germline from fixed samples and that can be extended to multiple signaling conditions and environmental contexts.

Materials and Methods

Nematode fixation and staining

Wild-type N2 hermaphroditic animals were placed on NGM (normal growth media (37)) plates seeded with OP50 Escherichia coli bacteria at the fourth larval stage of development (L4) at 20°C for 24 h, and germlines were extruded at the end of 24 h. Dissections were performed as described in Arur et al. (13, 38). Briefly, all dissections were performed under 5 min (immediately after adding levamisole to render the animals immobile) to achieve optimal dpMPK-1 staining. The dissected germlines were then fixed in 3% paraformaldehyde for 10 min at room temperature, followed by fixation in 100% methanol at −20°C for 1 h. The fixed germlines were then processed for immuno-fluorescence staining via blocking in 30% Normal Goat Serum (in 1× PBST with 0.1% TWEEN-20) for 1 h, followed by incubation with anti-MAP Kinase antibody used at 1:200 (Clone MAPK-YT; Sigma-Aldrich, St. Louis, MO) overnight in 30% Normal Goat Serum at 4°C. Secondary antibodies were donkey anti-mouse Alexa Fluor 594. The secondary antibodies were used at 1:400. All germlines were treated with the same staining solution in the same vial to mitigate antibody-staining variation, as described in Lee et al. (2).

dpMPK-1 staining was standardized using wild-type germlines and germlines from an mpk-1 null allele, ga117, processed in the same tube (2, 12). ga117 was described in Lackner and Kim (39) and is an early stop in the mpk-1 gene, resulting in no expression of the MPK-1 protein. The MAPK-YT antibody was rigorously tested for specificity by multiple laboratories against mpk-1(ga117) null mutant germlines (2, 40). The staining conditions have been standardized such that the antibody does not detect any signal in the mpk-1 null germline, but reproducibly detects the two peaks of MPK-1 activation in wild-type N2 germlines.

Imaging

An A1 confocal microscope with a Plan-Apo VC 60× Oil objective was used for imaging germlines (Nikon, Melville, NY). Z-stacks, with 0.5 μm spacing between slices, were taken of the distal part of each germline. A single z-stack did not fit the entire distal germline in the field of view. Multiple z-stacks taken along the length of a single germline were stitched together using a custom MATLAB program (The MathWorks, Natick, MA). The overlap position between a pair of overlapping z-stacks was found by finding the position with the highest the normalized cross correlation between the DAPI images in the stacks (MATLAB normxcorr2).

Image segmentation and extracting fluorescence data

Individual germ cells were detected in each DAPI image slice of the stitched z-stacks using the two-dimensional (2D) circular Hough transform. The built-in MATLAB function imfindcircles was used to implement this. This approach was used because the germ cells took on irregular shapes in 3D when pressed by the coverslip. However, within a slice they appeared circular. As a result, the structure imposed by the 2D circular Hough transform produced more accurate detection rates than other less structured methods, such as watershed-based methods. Before applying the Hough transform, images were smoothed with a 3-pixel-wide Gaussian filter (imfilter), eroded (imerode) with a 4-pixel disk structuring element (strel), and reconstructed (imreconstruct), using the Gaussian-smoothed image as the mask. The purpose of these preprocessing steps was to blur out intracellular features, while leaving the circular cell shapes intact.

Within a slice, circles with projected area overlap above a threshold were merged by keeping the circle containing the highest average DAPI fluorescence intensity among those overlapping and removing the others. Because germ cells span multiple slices, a single germ cell would almost always be identified in multiple slices. Therefore, multiple detections of the same germ cell across slices had to be registered. This was done by starting from the bottom (or top) slice, detecting circles in that slice, and then assigning the mutually closest circle in the next slice to the same cell. This was repeated until the last slice, with the maximum allowed extent of a single cell being four slices.

To determine the effectiveness of the image segmentation code, three germlines were manually segmented in ImageJ (National Institutes of Health, Bethesda, MD) using the oval selection tool to circle cells in each slice. The result of this process was a list of cells, the slices they appear in, their 2D positions in each slice, and their radii in each slice. The automated detections then had to be matched to corresponding manual detections. For each manually detected cell, all automatically detected cells in the same slice range were considered. It was visually determined that sometimes the automated segmentation code found that cells extended one slice above or below the same cell in the manual segmentation, so the slice range for each manually detected cell was increased above and below by one slice.

Among the automatically detected cells in the same slice range as a given manually detected cell, the one with the mutually closest 2D position (averaged over slices) was found. A metric was then needed to decide whether this closest cell was actually the same cell as the manually detected one. Because we knew the two cells were in the same slice range, we only considered their projected areas. The metric used was the area of intersection of the 2D projections of the two cells divided by the area of their union. This metric is common in the object detection community and accounts for both the locations and scales of the objects being compared (41, 42). If the metric was above a preset threshold (0.3), the automatically detected cell was considered to be the same cell as the manually detected one. Otherwise, the manually detected cell was considered to be undetected by the segmentation code. An automatically-detected cell that was matched to a manually-detected one could not be matched to any other manually detected ones. After cycling through all of the manually detected cells, any cells that were automatically detected but not assigned to a manually detected one were considered false detections. Among the three manually segmented germlines, on average the detector found 90% of the germ cells present, and of the ones detected, 97% were true positives. Images comparing the automated and manual detections are provided in the Section S1 in the Supporting Material.

With the three-dimensional (3D) positions and radii of each germ cell, fluorescence intensities could be extracted from z-stacks (Fig. 2). In some cases, the segmentation code could detect faint DAPI signal even when only the tip of a cell was present in a slice. The dpMPK-1 signal from the cells in these slices was very weak and not representative of the actual dpMPK-1 content of the cell. For this reason, the slice of maximum DAPI intensity was determined for each cell, and the average nuclear dpMPK-1 intensity was measured only from that slice. If the dpMPK-1 signal in a germline significantly decreased with slice depth due to photobleaching during imaging, then only the signal from cells in the first few slices were used to measure the dpMPK-1 spatial profile. Additionally, background fluorescence was subtracted from the dpMPK-1 profiles. In each germline, background fluorescence was calculated by averaging the dpMPK-1 intensity in the mitotic and early meiotic region, where there should be much less active MPK-1 than in the pachytene region. For each experiment, ∼6–10 intact germlines were imaged with the exact same microscope settings, and each experiment was repeated at least three times. The data was internally compared for consistency.

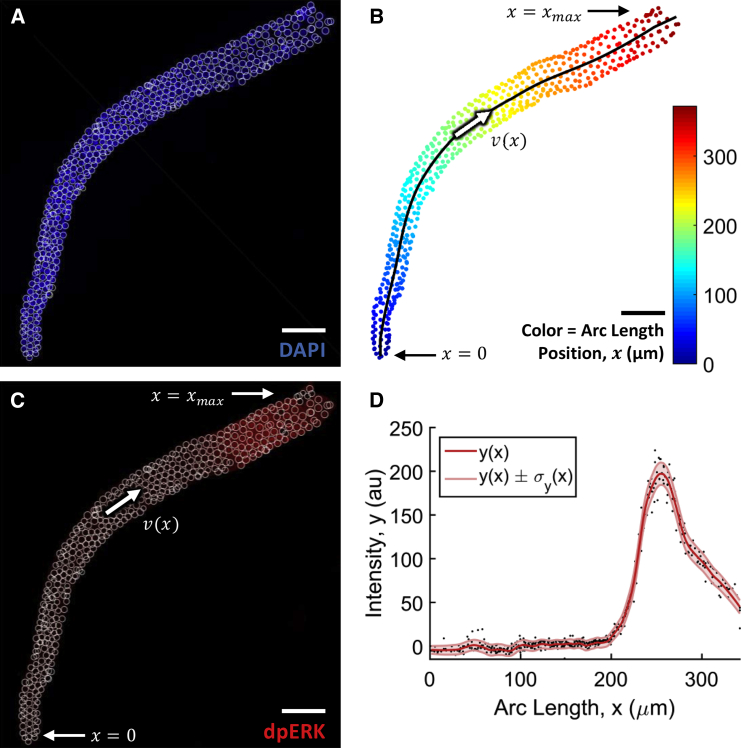
Figure 2.

Workflow of the image analysis for a given germline. (A) Confocal fluorescence microscope image of a DAPI-stained germline, extruded from a wild-type, hermaphroditic adult nematode. (White circles) Detected nuclei. Only the distal part of the germline is shown. Scale bar is 21 μm. (B) Nuclei detected from z-stack of the germline in (A). (Black) The center line estimated for this germline. Nuclei are colored by their arc length position along the center line. At the distal tip x = 0, and at the beginning of the loop x = x_max (in this germline x_max ∼ 350 μm). Germ cells are assumed to move unidirectionally through the germline with spatially-dependent velocity v(x). (C) (Red color channel image) Germline in (A), corresponding to the dpMPK-1 antibody staining. (Overlaid in white) Nuclei locations. (D) The nuclear mask in (B) was used to extract nuclear fluorescence intensity of dpMPK-1 from (C) for each germ cell. Plotted is dpMPK-1 fluorescence intensity versus arc length position. (Black dots) Measurements of dpMPK-1 intensity from each germ cell. (Dark-red line) Smoothed average across cells; (shaded region) average intensity ±1 SD. To see this figure in color, go online.

Finding the center line of the gonad tube

The scatter plot of individual cell positions in a single germline viewed from a distance appears to be a one-dimensional curve. Diffusion Maps, a nonlinear dimensionality reduction technique (43), essentially takes advantage of this coarse perspective to order the germ cells according to their positions along the one-dimensional curve, which in this case corresponds to the center line of the gonad tube. More details about the Diffusion Maps algorithm are given in the Supporting Material. Diffusion Maps is not necessarily required to find the center line; we used it because it quickly and robustly sorts cells by arc length along the center line. A user needed to manually specify which end of the one-dimensional curve corresponded to the distal tip. Once the cells had been ordered along the center line and the distal tip had been chosen, the positions of germ cells within a local neighborhood of each other were averaged, producing a noisy estimate of the center line. Following the approach of Kafri et al. (32), the ordered set of points was converted to spherical coordinates, and each of the three ordered sets of coordinates was smoothed by taking moving averages using MATLAB’s smooth function. Converting back to Cartesian coordinates resulted in a smooth estimate of the center line. Due to neighborhood averaging, the center line estimated this way did not extend all the way to the two ends of the distal germline. Each end of the center line was extended in a straight line in the direction of the tangent to the center line at that end. The center line was extended at each end until it intersected the plane containing the distal- (or proximal-) most cell with normal vector parallel to the direction in which the center line was being extended.

Estimating probability distribution functions

Germ cell positions were projected from 3D space onto the closest point on the center line of the gonad tube to calculate their arc length positions. Smooth probability density functions and cumulative distribution functions were estimated in MATLAB using Z. Botev’s code kde, available on the MathWorks website at: http://www.mathworks.com/central/fileexchange/14034-kernel-density-estimator (44, 45).

Results

Transport model for the germline

In this section, we formulate a mathematical model of germ cell transport along the germline. The prediction of this model will be the average time it takes a germ cell to travel from the distal tip to any given position in the germline. The approach, much like models used to describe unidirectional traffic flow (45), will be to estimate the local velocity as a function of spatial position. If we were given the average velocity of germ cells at each position, we could immediately calculate the average transit times. Because we do not get this information from fixed germlines, we will use our model to express velocity in terms of quantities that are measurable from fixed samples.

We will only consider distal-to-proximal motion and neglect perpendicular motion because the length of the gonad tube is much longer than its diameter. Position in the germline will be measured by arc length: if one were to measure the total distance driven down a winding road, that distance would be the arc length of the road. Arc length position, x, will be measured as distance in microns from the distal tip, with x = 0 located at the distal tip. We aim to derive an equation t(x) that describes the time it takes germ cells to travel from the distal tip to each arc length position along the germline.

In this analysis, we focus only on the distal germline. The approach described here for estimating time as a function of arc length is statistical in nature and therefore benefits from having as many cells as possible in the sample. In the proximal germline, where oocytes are in single-file, there are too few cells to make any meaningful estimates using this approach.

We will only consider adult hermaphroditic organisms (defined as 24 h past the fourth larval molt (L4)) with fully developed germlines because these germlines have reached steady state (7, 10). Specifically, we assume that the number of germ cells in the germline and the rate of oocyte ovulation are constant over time (10). Young adults are in a state of germline expansion, increasing their germ cell numbers. By 24 h past the fourth larval molt, the germline switches to a homeostatic mode, maintaining the number of germ cells more or less constant (7, 46). In normal laboratory conditions at 20°C, this state lasts until ∼72–90 h past L4 (12, 47). Time course analysis of hermaphroditic germlines assayed at 18, 20, 24, 36, and 48 h past the L4 stage of development for dpMPK-1 activation suggests that the concentration gradients inside the germline are also time-invariant in homeostatic adult germlines (12).

Next, we assume that germ cells move unidirectionally through the germline, from which it follows that germ cells are perfectly arranged according to their maturity. This is not strictly true, but there is clear directionality to germ cells’ motion when looking at timescales on the order of hours, the timescale over which germ cells develop. This assumption is weakest in the mitotic region, where it is unclear whether there is a mechanism that would prevent some cells from moving unidirectionally down the germline, such as asymmetric cell divisions (7), trapping by distal tip cell processes (7, 48), or diffusive motion created by random orientation of the axes of cell divisions (36). We acknowledge that our model does not account for effects like these. However, while an individual cell could get trapped in the mitotic region for an extended period of time before beginning unidirectional motion toward the loop, this would only add a time delay to the beginning of the time course of MPK-1 activation, without otherwise changing the dynamics.

The final assumption we make is that in a wild-type germline, germ cells undergo stereotypical dynamics, so that the population-level dynamics are representative of an individual cell. With this, we assume that the time it takes each cell to reach the loop is the same across cells.

The intuition behind the derivation is that the rate at which cells arrive at each position must be balanced by the rate at which cells leave that position for there to be no accumulation of cells at any position over time. We can construct a balance on the number of cells arriving and leaving an arbitrary arc length position:

$$0=-\frac{dJ}{dx}+S\left(x\right)-R\left(x\right).$$ (1)

Here, J(x) describes the number of cells per time that pass through each position x and is known as the convective flux. In this formulation, cell flux and cell flow rate are equivalent. S(x) is a spatially dependent source term that accounts for the production of cells by mitotic divisions, and R(x) is a sink term that accounts for the removal of apoptotic cells from the germline before they reach the loop. The average rate at which cells are produced is $s\equiv {\int }_0^{x_{\text{max}}}S\left(x\right)dx$ cells per hour, and, likewise, the average rate at which cells are removed via apoptosis is $r\equiv {\int }_0^{x_{\text{max}}}R\left(x\right)dx$ cells per hour.

We assumed that all new cells are introduced into the germline at x = 0, reducing Eq. 1 to

$$0=-\frac{dJ}{dx}-R\left(x\right),$$ (2)

with cell production included as a boundary condition on the flux at x = 0, J(x = 0) = s. The left-hand sides of Eqs. 1 and 2 correspond to the rate of accumulation of cells over time at each position x, which is equal to zero under the steady-state assumption.

The convective flux term can be expressed as J(x) = C(x)v(x), where C(x) is the concentration of cells at x, and v(x) is the average velocity of cells at x. We want to solve for v(x). The concentration of cells can be expressed as C(x) = N_totf_X(x), where N_tot is the average number of germ cells in the distal germline, and f_X(x) is the probability density function of germ cell arc length positions x (Fig. 3). The concentration C(x) is a smoothed histogram of germ cell positions, and f_X(x) is the same but normalized so that the area under the curve equals 1. We estimated the function f_X(x) empirically for each germline as follows: germ cells were automatically detected in a z-stack of an extruded germline using custom code written in MATLAB; the center line of the germline was constructed; arc length positions of cells in that germline were calculated; then f_X(x) for that germline was estimated from the collection of cell positions using kernel density estimation, a standard technique for empirically estimating probability distributions (44).

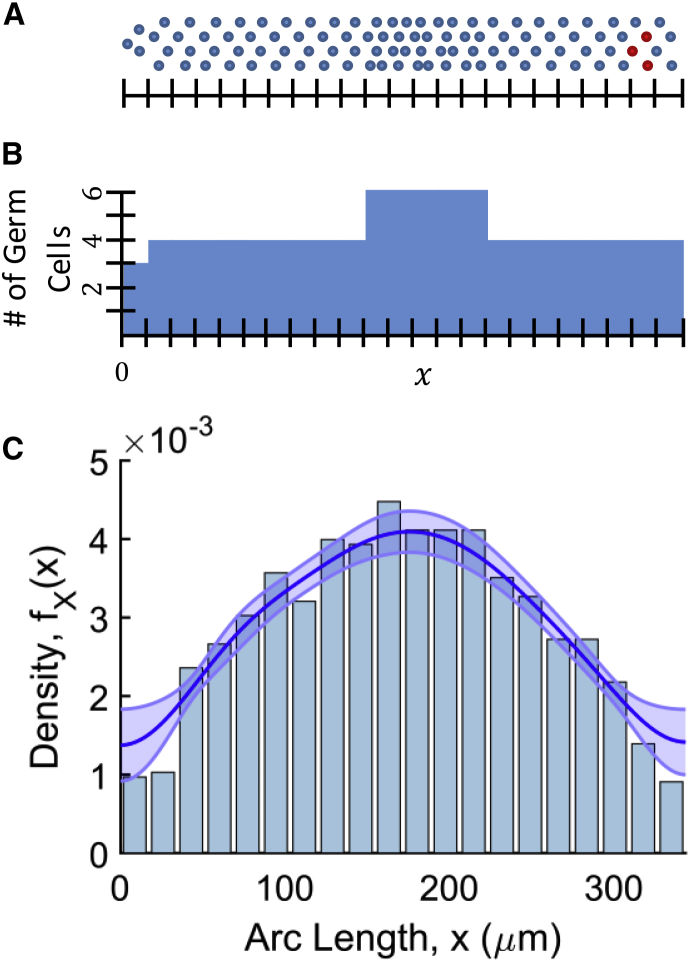
Figure 3.

(A) Schematic of a germline with a nonuniform distribution of cells over arc length position x. (Red) Cells undergoing apoptosis. (B) Histogram of germ cell arc length positions from (A). Smoothing this histogram and normalizing by the total number of cells in the germline would give an estimate of f_X(x), the probability density function over arc length positions. (C) A plot of f_X(x), calculated from germ cell positions in a real germline and overlaid on the normalized histogram of cell positions in that germline. (Shaded region) Mean estimate of f_X(x) ± the root-mean-squared error of the estimate (54). To see this figure in color, go online.

Solving the model

In this section we solve the transport model for v(x), the average local velocity, and t(x), the average transit time to each position along the gonad tube. First, we substitute J(x) = N_tot f_X(x)v(x) for the convective flux term of Eq. 2. Moving the convective flux term to the left-hand side and integrating once gives

$$N_{\text{tot}}{f}_X\left(x\right)v\left(x\right)=s-\underset{0}{\overset{x}{\int }}R\left(u\right)du,$$ (3)

where s, the rate of cell production, is the constant of integration that results from applying the boundary condition J(x = 0) = s. Solving for v(x) gives

$$v\left(x\right)=\frac{s-{\int }_0^{x}R\left(u\right)du}{N_{\text{tot}}{f}_X\left(x\right)},$$ (4)

We can draw an analogy here to unidirectional, steady-state fluid flow in a pipe. In the pipe flow problem, v(x) = Q(x)/A(x)—i.e., the average local velocity of fluid elements equals the local volumetric flow rate divided by the local cross-sectional area. The numerator of the expression on the right-hand side of Eq. 4 is the local cell flow rate (cells per unit time), analogous to the local volumetric flow rate in a pipe (volume per unit time). The cell flow rate at x = 0, where cells are produced by mitotic divisions, equals s, and the second term in the numerator reduces the local cell flow rate as cells undergo apoptosis. In the absence of cell death, the cell flow rate everywhere in the germline would be constant and equal to the production rate, s. The denominator of the expression, the local concentration of cells, is analogous to the local cross-sectional area in the pipe flow case.

The velocity v(x) is the time rate of change of a cell’s position x, or v(x) = dx/dt. Separating the variables x and t, giving dt = dx/v(x), and then integrating, produces

$$t\left(x\right)=\underset{0}{\overset{x}{\int }}\frac{N_{\text{tot}}{f}_X\left(w\right)}{s-{\int }_0^{w}R\left(u\right)du}dw.$$ (5)

The variables u and w are dummy variables of integration. The lower bound of the outer integral on the right-hand side is zero because at x = 0, t = 0. The average time cells take to transit from the distal tip at x = 0 to the loop at x = x_max will be denoted τ.

Factoring out N_tot/s from Eq. 5 shows that there are essentially two lumped parameter combinations that govern the behavior of t(x): the ratios N_tot/s and r/s. After factoring, the equation becomes

$$t\left(x\right)=\frac{N_{\text{tot}}}{s}\underset{0}{\overset{x}{\int }}\frac{f_X\left(w\right)}{1-\frac{r}{s}{\int }_0^w\hat{R}\left(u\right)du}dw,$$ (6)

where $\hat{R}\left(x\right)$ is a dimensionless function with the same shape as R(x) and, as mentioned in the previous section, r is the average rate at which cells undergo apoptosis. The first ratio, N_tot/s, is the total number of cells in the germline divided by the cell production rate and has units of time. In the absence of apoptosis, the average transit time from the distal tip to the loop would be equal to N_tot/s. The second ratio, r/s, is the fraction of germ cells that undergo apoptosis and is dimensionless. N_tot/s gives the scale of t(x) but does not affect its shape, which is determined by the expression inside the integral.

In practice, f_X(x) was estimated for each germline and R(x) was calculated by pooling data from multiple germlines. Estimation of R(x), which accounts for germ cell apoptosis and removal from the germline, required pooling data from multiple germlines and is described in the Supporting Material (Sections S3 and S4). The same values of the parameters N_tot, s, and r, were used for all germlines. In particular, N_tot and s have strong opposing effects on the model’s predictions; as a result, using a value of N_tot from an individual germline and the average value for s would give biased results. During the error analysis (Section S5 in the Supporting Material), the parameters N_tot, s, and r were sampled uniformly within ranges consistent with the literature to propagate parameter uncertainties through the model, which will be discussed in the next section. The trapezoidal rule was used to approximate all integrals.

Exploring the feasible space of physiological parameters

The model contains one equation and four physiological parameters: N_tot, the average number of cells in a germline at any given time once adulthood is reached; s, the average rate of cell production; r, the average rate of cell removal by apoptosis; and τ, the average time cells take to travel from the distal tip to the loop. The steady-state assumption provides an equation relating these physiological parameters, meaning their values are no longer entirely independent of each other. Evaluating the indefinite integral in Eq. 6 at x = x_max, where t(x_max) = τ gives

$$\tau =\frac{N_{\text{tot}}}{s}\underset{0}{\overset{x_{\text{max}}}{\int }}\frac{f_X\left(w\right)}{1-\frac{r}{s}{\int }_0^w\hat{R}\left(u\right)du}dw.$$ (7)

The density function f_X(x) is measurable for each individual germline, and $\hat{R}\left(x\right)$ can be estimated by pooling data from multiple germlines. This leaves only the physiological parameters as unknowns in the equation. Additionally, choosing values for three of the parameters constrains the value of the fourth.

Previous studies have estimated ranges for these physiological parameters from data on wild-type animals. The total number of cells in an adult hermaphroditic germline is ∼800–1000 cells (7). The cell production rate by mitotic divisions, s, has been reported to be between 16 and 24 cells per hour (7, 49). An engulfment marker shows that in wild-type animals, each gonad arm contains 2–4 apoptotic cells at a given time (50). However, the time rate of cell death, per se, has not been precisely measured. Under the steady-state assumption, the rate of cell removal via apoptosis, r, must equal the difference between the rate of cell production, s, and the rate of cell removal via ovulation. The latter has been estimated to be between 2 and 5 cells per hour per gonad arm (10). Therefore, a consistent estimate for the rate of cell death, r, lies between 11 and 22 cells per hour. Finally, pulse-chase experiments suggest that τ lies between 48 and 54 h (51).

Although there are only three independent physiological parameters after applying Eq. 7, we have information about all four parameters. To capitalize on this, we sampled the parameters N_tot, s, and r uniformly within the literature-reported ranges, then discarded all parameter combinations for which the value of τ, calculated using Eq. 7, was outside of the range consistent with the literature. This procedure carved out a sliver in the 3D parameter space consisting of the parameter combinations that are consistent with contemporary knowledge (52). This collection of consistent parameters is called the “feasible set”.

Model predictions

With Eq. 6 and the feasible set of parameters, we were able to calculate, for each germline, a prediction of the transit time to each position along that germline, t(x). These maps from position to time were used to transform the spatial profiles of dpMPK-1 fluorescence intensity to dynamic profiles for each germline. Essentially, dpMPK-1 intensity at each position in a germline was plotted against the time at which cells arrive at that position. The result was a picture of the time course of MPK-1 signaling that germ cells experience/produce as they move through that germline (Fig. 4). Doing this for multiple germlines allowed us to compare signaling dynamics across germlines.

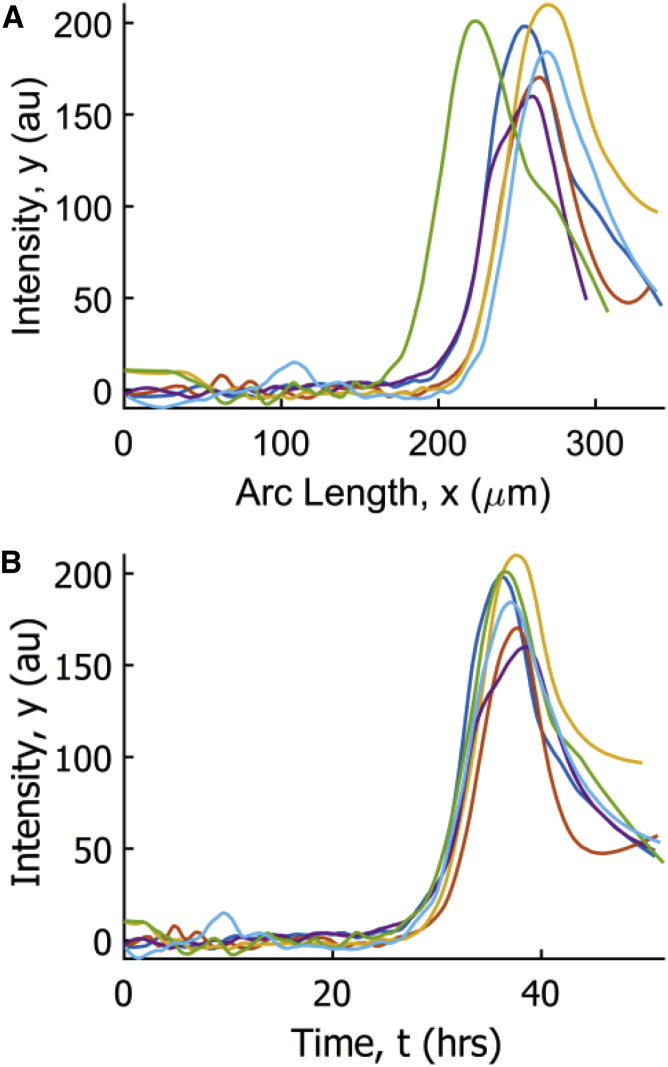
Figure 4.

(A) Raw spatial profiles of dpMPK-1 fluorescence intensity, y(x), in six germlines from a single experiment, imaged under identical conditions. (B) For each germline, the function t(x) relating arc length positions to the transit times to reach those positions was estimated using Eq. 5. Plotted are the results of transforming the spatial dpMPK-1 profiles in (A) into average time courses of dpMPK-1 seen by traveling cells. To see this figure in color, go online.

Comparing the estimated time courses of dpMPK-1 from multiple germlines shows that they approximately collapse. It was not obvious a priori that this would be the case from the raw spatial profiles of dpMPK-1. Additionally, naively plotting dpMPK-1 intensity against normalized arc length for each germline does not cause the profiles to collapse (Fig. S5 in the Supporting Material). The collapse of these curves suggests that, despite varying geometries and dpMPK-1 gradients among germlines, germ cells see stereotypical dynamics of MPK-1 activation during meiotic progression.

The average time at which germ cells in different germlines first begin to be exposed to active MPK-1 (30.5 h, SD 1.5 h) and the time of peak dpMPK-1 concentration (mean 37.7 h, SD 1.8 h) are very similar across germlines. These averages were taken over all germlines and all parameter combinations in the feasible set. The uncertainties are dominated by the uncertainty in the rate of apoptosis, r. Future experiments that constrain the range of possible values for the parameter r will dramatically reduce the uncertainty of this model’s estimates.

The model also makes quantitative predictions about the relationships between physiological parameters in an animal. From Eqs. 6 and 7, one can immediately see that because ratios of physiological parameters govern the behavior of t(x), numerous values of the individual parameters N_tot, s, and r can give rise to the same dynamics in the germline. Additionally, looking at the dependence of τ = t(x_max), the average transit time from the distal tip to the loop, on the lumped parameter ratios is also informative (Fig. 5). In a situation where the rate of ovulation decreases, germ cells will subsequently spend more time in the region distal to the loop. To maintain steady state, the animal’s physiological parameters must change. According to the model, steady state can be achieved by: 1) decreasing the rate of cell production, s; 2) increasing the number of cells in the distal region N_tot; or 3) increasing the rate of apoptosis, r. The quantitative model predictions are therefore in line with qualitative intuitions.

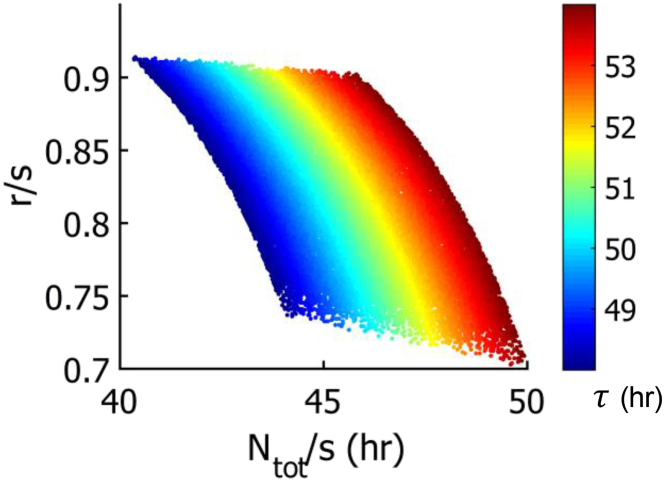
Figure 5.

Dependence of τ, the average transit time from the distal tip to the loop, on the two lumped parameter ratios in the model. The first, N_tot/s, is the ratio of the number of cells in the germline to the cell production rate. The second, r/s, is the ratio of the rate of apoptosis to the cell production rate, or the fraction of cells that undergo apoptosis. To see this figure in color, go online.

Thus, during the first wave of MPK-1 activation in the germline, each of the developing germ cells is exposed to high levels of MPK-1 signaling for several hours, during which MPK-1 activation is translated into changes in a large number of processes, including apoptosis, meiotic progression, and membrane biogenesis.

Discussion

Cell fate decision processes rely on the joint dynamics of multiple molecular players. Some of these species may be difficult to follow in real-time, calling for approaches for reconstructing dynamics based on snapshots from fixed samples. In the Drosophila melanogaster embryo, cell signaling and gene induction dynamics were estimated from fixed samples by matching embryo morphology to time (29, 30, 31). Additionally, a number of recent articles demonstrated that for a stationary process, in which cells progress unidirectionally through a sequence of states, average dynamics can be reconstructed from fixed cells. For instance, Kafri et al. (32) used data from a population of unsynchronized, fixed vertebrate cultured cells to reconstruct the average growth dynamics of an individual cell. In this work, each cell was labeled for DNA and Geminin (a protein degraded during mitosis), and this pair of signals provided a quantitative measure of cell cycle progression for each cell. The large numbers of cells available to them in each experiment enabled estimation of cell size distributions throughout the cell cycle and revealed a feedback mechanism that reduces the variability in cell sizes. A similar approach was used by Akopyan et al. (33) to reconstruct the dynamics of the mitotic entry network. In both of these studies, reconstruction of dynamics from snapshots relied on the introduction of some measure of progress, which was critical for temporal ordering of data from multiple individual cells. While this step is essential for a dataset extracted from cells that are independent of each other, it is not necessary for data from cells within the germline, where the arc length provides a natural ordering coordinate.

Assuming that the number and spatial arrangement of cells are invariant over time, we derived a transport model, in which cells move similar to cars on a packed highway, to relate arc length, rather than the cell state, to time. In doing so, we used literature estimates of the physiological parameters in the germline (7, 10, 49, 51). Finally, we pooled data from multiple germlines to estimate the average local rates of cell death. This led to the average time course of ERK activation within a developing germ cell. Looking at this pulse, one can ask, what controls the onset of ERK activation, its amplitude, and duration? It is known that this phase of ERK signaling relies on a spatially uniform insulin receptor, but the relevant ligand and the mechanisms responsible for the intracellular control of the duration of ERK activation are still unknown. As the molecular candidates for controlling these processes are proposed, such as a localized extracellular ligand, our approach can be used to probe their quantitative contributions to multiple aspects of ERK signaling.

The estimates derived from our model-based approach of cell transit times and ERK activation dynamics remain to be verified by data from studies with live reporters of ERK activation. At this point, these estimates provide the only available insight into the dynamics of a key regulatory signal in one of the most advanced experimental systems for studies of cell fate decisions. As measurements of the physiological parameters in the model become more precise, the model may be updated and its uncertainties reduced. Applying this approach to germlines at other steady states under altered conditions is relatively straightforward. Changes in the rate of cell division, rate of cell death, total number of cells, or time cells take to reach the loop can cause germlines to operate at different steady states. These alternative steady states can be achieved in the lab setting by changing the environmental conditions (temperature, crowding, or presence of a noxious substance) or by introducing genetic perturbations. However, for analysis of mutant backgrounds, the assumptions that the germline is at steady state, that the dpERK gradient is time-invariant, and that the distribution of germ cells is not changing over time, must be verified. Additionally, at least three of the four physiological parameters for that mutant background must be measured to apply to the model to alternative steady states: the average rate of cell production, the average number of cells in the germline, the average rate of apoptosis, and the average time cells take to travel from the distal tip to the loop.

Author Contributions

J.J.C. extruded, fixed, immunostained, and mounted the germlines on glass slides for imaging; H.H.M. derived the model, imaged the germlines, wrote the MATLAB code, and performed the image and data analysis; and all authors contributed to designing the research and writing the article.

Editor: Leah Edelstein-Keshet.

Supporting Citations

References (55, 56, 57) appear in the Supporting Material.